Introduction

Quantitative risk assessment, at both local and detailed scales, is becoming a fundamental tool in managing rockfall hazards (Fell et al. 2008). To assess risk in mountainous areas, exposed elements must be identified and their vulnerability quantified. Despite significant progress in recent years in assessing hazard components of the risk equation, the treatment of vulnerability has been poor. This paper focuses on investigating the response of a building to rockfall impact and developing a tool for quantifying the building’s vulnerability to it.

Rockfall risk is computed by quantifying each of the components of the hazard equation and by evaluating the consequences, which depend on the vulnerability. In terms of conditional probability, the rockfall risk to buildings may be determined by Eq. 1 (modified by Fell et al. 2005):

$$R{\left( P \right)} = {\sum\limits_{i = 1}^k {{\left[ {P{\left( {R_{i} } \right)} \times P{\left( {T:R} \right)} \times P{\left( {S:T} \right)} \times V{\left( {D{}_{i}} \right)}} \right]}} }xC$$
(1)

where,

R(P):

is expected annual loss to the property due to rockfall (i.e., € per year),

P(R i ):

is annual probability of occurrence of a rockfall having a magnitude i,

P(T:R):

is probability of a rockfall having a magnitude i reaching the element at risk,

P(S:T):

is temporal spatial probability of the element at risk,

V(D i ):

is vulnerability of the building to a rockfall of magnitude i, and

C :

is the cost of the building.

The assessment has to be summed across all rockfall-magnitude classes (from 1 to k). All of the hazard components of the risk equation are expressed as probabilities. Because the expected damage depends on both the rockfall path (i.e., the probability of impact on a given structural element) and on the kinetic energy exchange in the impact (the probability of the block traveling at a particular speed), the vulnerability has a probabilistic character as well.

In a socioeconomic context, the vulnerability of a building is associated with two parameters: the probability of physical structural failure and the consequent effects. In this paper, only the former parameter is treated. The main objective has been to develop an analytical procedure to determine the vulnerability of buildings to rockfall that could be used for the further assessment of socioeconomic damage. The value of the vulnerability is obtained by defining a correlation function between hazard intensity and structural damage.

So far, the assessment of vulnerability of buildings due to rockfall and other landslide types has been mostly subjective or empirical. Leone et al. (1996) presented a general method for quantitative evaluation of building vulnerability to mass movements. Heinimann (1999) classified the vulnerability of structures according to their typology, proposing six categories, to which Uzielli et al. (2008) attributed certain vulnerability values based on empirical criteria. The Australian Geological Survey Organisation (AGSO 2001) suggested a simple classification of building vulnerability with a difference between rockfalls on slopes steeper than 25° (vulnerability value equal to 1) and small rockfalls (vulnerability value equal to 0.25). Dai et al. (2002) proposed the use of matrices in which vulnerability is correlated with building characteristics as well as landslide properties but did not define specific vulnerability values. Cardinali et al. (2002) estimated qualitatively the vulnerability of rockfall-exposed buildings in Umbria, for the different rockfall intensities and structural typologies of the area, based on the damage that landslides had caused to the buildings. A correlation of building vulnerability to rockfalls with three levels of intensity (low, medium, and high) was also made by Glade and Jensen (2005), based on statistical analysis of rockfall and debris-flow data from Bíldudalur, NW Iceland. An interesting approach to quantification of vulnerability using a geographic information systems platform and taking into account a monetary value per unit area was made by Remondo et al. (2008). For a given Earth-debris-flow scenario, Sterlacchini et al. (2007) classified debris-flow effects into aesthetic, functional, and structural damage, and to calculate vulnerability, they estimated the economic cost for repair or reconstruction for the affected structures, differentiating between private houses, public buildings, and hotels. These researchers correlated damage with landslide intensity by empirical means. Fuchs et al. (2007) calculated the vulnerability of structures damaged by debris flows in the Austrian Alps, as the ratio of the monetary loss to the reinstatement value. Last, Wong et al. (2004, Wong and Ko 2008) derived vulnerability factors for houses by plan area by integrating the probability function of debris runout distance and a model for the degree of damage. These works provide important theoretical information for evaluating vulnerability; however, in most cases, they are based on local data from past events, and they do not always provide objective quantitative information on both damage and rock velocity that would make the methods useful for predicting future rockfall damage. Furthermore, because they lack structural data on the threatened buildings, the above-mentioned methods should not be used for local and site-specific landslide risk analysis where the building type matters.

In this paper we propose an analytical method for quantitatively evaluating vulnerability. It has the following advantages: (a) it does not require an inventory of past events; (b) it can determine vulnerability functions for any rockfall event without assumptions based on interpolation or extrapolation; (c) it takes into account the peculiarities of the threatened building and the study site; and (d) it offers objective results.

The proposed method must take into account some critical uncertainties involving rockfall properties (energy, magnitude, and path), rock interactions with structural elements (transmitted energy), and structural behavior (robustness and redundancy). Due to them, the rockfall effect of a given magnitude may vary.

Analysis of past rockfall impacts on buildings shows that either local or extensive structural damage may occur, depending on the properties of both the rockfall and the structure. However, the probability of complete building collapse is low. For example, in Venezuela, at Carabadella, Vargas, in December 1999, several blocks from a debris-flow surge hit the first two stories of an apartment building and caused its partial collapse (Lopez and Courtel 2008). In the Principality of Andorra, rockfalls are very frequent, and in 1985 and 1997, boulders struck buildings, causing severe damage and seriously injuring a person (Corominas et al. 2005). More recently in Andorra, in April 2008, a workshop was partly damaged by rockfall blocks (Fig. 1). On 13 November 2004, a rockfall in Fiumelatte (Lecco, Italy) caused two deaths and damaged several houses (Agliardi et al. 2008). Last, in June 2008 in Greece, an earthquake-induced rockfall extensively damaged a building in the village of Santameri, Peloponnesus, and led to the precautionary evacuation of the village.

Fig. 1
figure 1

Workshop damaged by the impact of a 30-m3 block, Santa Coloma, Principality of Andorra, April 2008

Full size image

Responses of buildings to rockfall impacts

To assess the performance of a structure struck by a rockfall, both the intensity and impact location must be considered. These two parameters determine whether there will be initial damage to load-bearing structural elements (i.e., columns) and whether that will affect the overall structural stability. With reference to the impact location, there are, in general, three possibilities: (1) a free-fall rock dropping on the roof, (2) a rock moving on a trajectory path and hitting the exposed façade, and (3) a rock passing through the façade and perforating a floor slab on a downward movement. In terms of impact effects, damage can be categorized into the following groups: primary structural damage (of primary structural elements such as columns, beams, etc.) that determines the overall stability of the building; secondary structural damage (of secondary load-bearing elements such as slabs, etc.); primary nonstructural damage that may cause injuries (i.e., infill walls, ceilings, etc); secondary nonstructural damage (i.e., furniture, fixtures, etc.); and damage to services (electrical and mechanical equipment, etc.).

For reinforced concrete structures, the location of the impact on the exposed façade is fundamental. Damage to a nonstructural element (e.g., an infill wall) is not critical to building stability, but collapse of a structural element, such as a column or a beam, may initiate progressive collapse. So, in a nonstructural impact, the damage is restricted to the nonstructural element itself, but in a structural impact, the final damage may vary from slight to total.

The structural response of a reinforced concrete building when a basement column is struck at midheight by a boulder has many similarities to the case of a vehicle impact on a bridge pier or to an aircraft impact on a building; such collisions are phenomena of extreme, abnormal loading, characterized by high strain rate applied locally out of the axis of the normally applied loading to one or more structural members.

According to observations of such impacts on buildings (Allen and Schrlever 1972), the initial damage to the affected columns is localized at the vicinity of the impact. Depending on the rock-motion parameters and the column’s properties, the damage may destroy the load-bearing ability of the column, such as in the case of a vehicle or an aircraft impact on a building as described by Mohamed (2006) and Ngo et al. (2003). On this basis, the first step should be assessing the primary effect of the impact on an individual column, before evaluating the overall response of the whole structural system.

One of the scenarios to simulate damage to a structural support is the instantaneous removal of the affected column (Sasani and Kropelnicki 2008). This notional removal is followed by the dynamic redistribution of structural loads throughout the load-bearing system, toward a new equilibrium state. However, if under the new stress state, the resistance of the remaining members is exceeded, a chain reaction will be triggered. As a result, to evaluate the ensuing structural response, the robustness of the structure, as defined by Starossek (2006), has to be assessed, checking whether the loss of the affected member can trigger a cascade of collapses, leading to high damage, disproportionate to the original cause. For this purpose, an analysis of potential progressive collapse may be conducted.

Despite the relative scarcity of circumstances leading to progressive failure, its existence and possible consequences have been acknowledged and included in many building codes (e.g., in the USA, Canada, and Europe), with a significant contribution from the UK, as reported in detail by Mohamed (2006) and Ellingwood (2006). Most of these codes provide guidelines for evaluating the potential for progressive collapse of a building that is subjected to an abnormal loading, such as a rockfall impact, and suggest design-protection measures. For this purpose, different analytical methods have been developed, varying mainly according to the level of simulation of inherent dynamic effects, nonlinearities, and member ductility, as reported by the US Department of Defense (UFC 2005) and the General Services Administration (GSA 2003) and by Marjanishvili and Agnew (2006).

Quantified evaluation of the performance of reinforced concrete buildings in rockfall impacts

The presented method proposes a tool for quantifying the factors that determine the vulnerability of a building to rockfalls. These are the probability of encounter of a rock with a structural element and, in case of an encounter, the damage caused to both the element and the whole structural system. However, this approach does not yet yield a vulnerability value that could be directly included in the risk equation. This is because the damage index (DI) that we will propose is not expressed in terms of relative or absolute loss, and the latter is beyond the scope of this paper. Instead, the probability of encounter and the damage extent are individually calculated for given motion properties as a first step toward the quantification of vulnerability.

The performance of a building in response to a rockfall impact is calculated in two phases: first, by evaluating the structural damage caused by impacts on primary structural key elements and, then, by analyzing the response of the whole structural system. In particular, we investigate the response of a reinforced concrete building when boulders strike its basement columns at midheight.

Description of the method

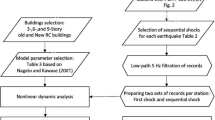
The proposed method calculates four main steps: (a) the probability of an encounter of a rock with a column; (b) the response of one or more structural elements to the hit, based on their capacity; (c) in case of failure of one or more elements in the previous step, the robustness of the whole structural system, calculating the potential for progressive collapse; and (d) the DI, being the ratio of structural elements that fail to the total number of structural elements. The procedure, including all substeps, is schematically presented in Fig. 2 and described in detail in the following sections. Last, it will be applied to the case of a simple reinforced concrete building, for alternative scenarios of rock strikes, considering various rock paths and impact energies sufficient to collapse of one or more columns.

Fig. 2
figure 2

Proposed method for evaluating the damage to a building due to rock impacts

Full size image

Probability of an encounter of a rock with a structural element

The location of the boulder impact on a building is crucial to the response of the building, and the probability of impact on a column has to be taken into account to evaluate building vulnerability.

The probability of intersection of a rock with a column depends on the boulder’s size and the geometry of the exposed façade: the width of columns and infill walls. For a symmetric façade of a building that is entirely located in the rockfall path (Fig. 3), the encounter probability (P enc) is given by Eq. 2, in a manner similar to that used by Brauner et al. (2005) to estimate the probability of impact of a boulder with a tree in a forest stand.

$$P_{{{\text{enc}}}} = \frac{{l_{{\text{c}}} + d}}{a}$$
(2)

where

l c :

is column width,

d :

is the boulder diameter,

a :

is the distance between columns \({\left( {a = l_{{\text{w}}} + l_{{\text{c}}} } \right)}\), and

l w :

is infill-wall width.

Fig. 3
figure 3

Indicative geometry of an exposed façade

Full size image

The probability (P s) of encounter with a specific column is then equal to \(P_{{\text{s}}} = {P_{{{\text{enc}}}} } \mathord{\left/ {\vphantom {{P_{{{\text{enc}}}} } n}} \right. \kern-\nulldelimiterspace} n\), where n is the total number of columns.

For simplicity, we assume a symmetrical façade, with equal-sized columns and infill walls. If the building is asymmetrical, Eq. 2 should be modified accordingly. The width of the building façade is considered to coincide with the potential width of the rockfall path.

Response of an individual column to rock impact

Past investigations of the response of structural elements to impacts show the complexity of the phenomenon, with the final effect depending on the interaction between the impacting body and the structure associated with relative masses, velocities, the contact zone, stiffness, frequency of loading, and geometry of the impact (Remennikov and Kaewunruen 2006; Kishi et al. 2002, 2007). A detailed presentation of the phenomenon of direct impact on reinforced concrete structures, including information on the development of impact forces, is presented in Delhomme (2005).

In our proposed method, the most unfavorable assumption of elastic collision between the boulder and the column mass is made. If the rock mass has the initial kinetic energy (E k) shown in Eq. 3, a fraction of this energy is transmitted to the structure and dissipated by the column.

$$E_{{\text{k}}} = \frac{1}{2}mv^{2} $$
(3)

where

m :

is the boulder mass and

v :

is the boulder speed before impact.

The fraction of the rock’s kinetic energy that is transmitted to the structure is estimated according to the suggestions of the Department of Energy of the USA for missile impact on structures (DOE 2006) and is given by Eqs. 4 and 5

$$E_{{{\text{imp}}}} = \frac{1}{2}mv^{2} \frac{{{4m} \mathord{\left/{\vphantom {{4m} M}} \right.\kern-\nulldelimiterspace} M}}{{{\left( {1 + m \mathord{\left/{\vphantom {m M}} \right.\kern-\nulldelimiterspace} M} \right)}^{2} }},\;{\text{for}}\;m \mathord{\left/{\vphantom {m M}} \right.\kern-\nulldelimiterspace} M <1$$
(4)
$$E_{{{\text{imp}}}} = \frac{1}{2}mv^{2} ,\;{\text{for}}\;m \mathord{\left/{\vphantom {m M}} \right.\kern-\nulldelimiterspace} M >>1$$
(5)

where

E imp :

is the energy of the boulder at impact and

M :

is the mass of the impacted column.

The next step is estimation of the energy-dissipation capacity of the column (E cap), up to its collapse. A review of existing experimental work on the ultimate impact resistance of reinforced concrete linear elements, such as columns, has indicated that shear is the predominant failure mode, rather than flexural failure (Remennikov and Kaewunruen 2006). This is mainly attributed to the high rate of loading. For shear failure, the piecewise linear lateral load–shear displacement model developed by Sezen (2008) is used to predict the column’s response. The model is presented in Fig. 4. The critical points in the proposed model include point A (lateral load V cr and displacement Δ cr), which represents the condition for initiation of diagonal cracking in concrete due to shear. With formation of the first crack, the stiffness of the column is lowered, up to point B (lateral load V n and displacement Δ n), where the stress-resistance limit is reached. Under the maximum shear stress, the column deforms up to point C (lateral load V n and displacement Δ u); from here, the shear strength degrades due to extensive cracking. During this phase, the column experiences additional shear deformation. The ultimate shear deformation is represented by point D (lateral load = 0 and displacement Δ af) where the axial-load carrying capacity of the column is lost.

Fig. 4
figure 4

Monotonic lateral load–shear displacement relationship (Sezen 2008)

Full size image

The critical points are calculated using Eqs. 6–11.

  1. Point A:

    Shear cracking initiation (lateral load = V cr, displacement = Δ cr)

    $$V_{{cr}} = {\left( {\frac{P}{{2*f^{\prime }_{c} *A}} + 0.10} \right)}\frac{{G*A}}{L}$$
    (6)
    $$\Delta _{{{\text{cr}}}} = \frac{{V_{{{\text{cr}}}} \times L}}{{G \times A}}$$
    (7)
  2. Point B:

    Maximum strength point (lateral load = V n, displacement = Δ n)

    $$V_{{\text{n}}} = V_{{\text{s}}} + V_{{\text{c}}} = k\frac{{A_{{\text{v}}} \times f{}_{{{\text{yv}}}} \times d}}{s} + k \times {\left( {\frac{{0.5 \times {\sqrt {f{}^{\prime }_{{\text{c}}} } }}}{{a \mathord{\left/{\vphantom {a d}} \right.\kern-\nulldelimiterspace} d}}{\sqrt {1 + \frac{P}{{0.5 \times {\sqrt {f{}^{\prime }_{{\text{c}}} } }A}}} }} \right)} \times 0.8 \times A$$
    (8)
    $$\Delta _{{\text{n}}} = {\left( {\frac{1}{{25,000}} \times \frac{{{\left( {a \mathord{\left/{\vphantom {a d}} \right.\kern-\nulldelimiterspace} d} \right)} \times f_{{{\text{yt}}}} \times \rho _{{\text{v}}} }}{{{\sqrt {\frac{P}{{A\;f^{\prime }_{{\text{c}}} }}} }}} - 0.0011} \right)} \times L$$
    (9)
  3. Point C:

    Beginning of shear degradation (lateral load = V n, displacement = Δ u)

    $$\Delta _{{\text{u}}} = {\left( {4 - 12\frac{{v_{{\text{n}}} }}{{f^{\prime }_{{\text{c}}} }}} \right)} \times \gamma {}_{{\text{n}}} \times L$$
    (10)
  4. Point D:

    Ultimate shear deformation until the lost of the axial-load capacity (lateral load = 0, displacement = Δ af)

    $$\Delta _{{{\text{af}}}} = L \times \frac{4}{{100}} \times \frac{{1 + \tan ^{2} \theta }}{{\tan \theta + P \times {\left( {\frac{s}{{A_{{\text{v}}} \times f_{{{\text{yv}}}} \times d_{{\text{c}}} \times \tan \theta }}} \right)}}}$$
    (11)

where P is the axial load, f c′ is the concrete compressive strength, A is the gross cross-sectional area (Fig. 5), L is the column length, G is the shear modulus, A v is the cross-sectional area of transverse reinforcement oriented parallel to the applied shear, s is the longitudinal spacing between transverse reinforcements, k is a constant varying according to displacement ductility (1.00 for ductility less than 2), f yv is the transverse steel yield strength, a is the shear span, d is the effective section depth, f yt is the longitudinal steel yield strength, and ρ v is the transverse steel reinforcement ratio and \(v_{{\text{n}}} = {V_{{\text{n}}} } \mathord{\left/ {\vphantom {{V_{{\text{n}}} } {{\left( {b \times d} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {b \times d} \right)}}\), where b is the width of the cross section, θ is the angle of the shear crack, and d c is depth of the core concrete, measured to the centerlines of the transverse reinforcement.

Fig. 5
figure 5

Column cross section

Full size image

Considering that the impact duration is of the order of milliseconds, the high strain-rate effect would significantly enhance the strength and ductility of reinforced concrete. To take this dynamic effect into account, the values of V cr and V n are multiplied by a dynamic increase factor of the order of 1.3 (Tsang and Lam 2008; and CEB 1990). The energy capacity E cap of the column is calculated by integrating the area under the force–deformation curve of Fig. 4.

Progressive-collapse potential

In case of failure of one or more column(s), the robustness of the whole structural system has to be investigated. We consider all the possible combinations of collapse of the basement columns. Following this collapse and given that the undamaged structure is overdetermined, it has to be checked whether the remaining structure is capable of bridging over the destroyed structural element. This depends on the overstrength of the elements and the potential for formation of alternative load paths. Guidelines developed by the US General Services Administration (GSA 2003) make some generic suggestions for this. Here, we propose a detailed step-by-step method that is summarized in the flowchart of Fig. 6. This method uses the finite-element method for structural analysis of buildings. The series of steps in the analysis are explained below.

Fig. 6
figure 6

Proposed method of progressive-collapse analysis

Full size image

First, the finite-element model is developed, omitting the impact-collapsed structural elements. The response of a reinforced concrete building following sudden loss of one or more columns is, by nature, dynamic and nonlinear. In order to take this into account, an amplified vertical load equal to 2(DL + 0.50 LL) is applied to the model, where DL stands for dead loads and LL for live loads (GSA 2003). The stress state is then calculated through a static and linear-elastic analysis.

There follows checks of every cross section of the model for failure (see Fig. 6). For the columns, the capacity ratio (PMM, stress due to loading/resistance) is calculated, considering both axial load and biaxial moment. Columns having a capacity ratio greater that 1.5 are assumed to fail. The value of 1.5 is chosen to take into account nonlinear ductility effects during progressive failure. Beams are checked in shear and bending failures at supports as well as at the midspan. Failure is assumed for a beam when the developed shear force, Q, is greater than its shear resistance, Q RS, for at least one support. For shear failure, no ductility factor is included, as it is usually brittle failure. Failure is also assumed for a beam when the span and the two supports fail due to flexural moment (three sections are checked). If only one or two of these three sections fail due to flexural moment, a hinge is placed to model the plastification of the section. Amplification of the moment resistance due to ductility (1.5 times) is considered for flexural moment failure at beams.

In the cases in which columns or beams are found to fail, they are considered to be incapable of carrying loads, and they are removed from the finite-element model. The adjacent joints are initially stressed with the loads of the eliminated member(s) at the moment of failure, in addition to their existing vertical dead and live loads. The finite-element analysis is repeated for the modified model.

After successive removals of any failed elements in the finite-element analyses, the procedure is terminated when no further sections are found to fail, indicating that the structure has reached a new equilibrium state.

When more than one alternative scenario of impact location and magnitudes are investigated, the procedure is repeated for each scenario.

Damage index

To indicate the extent of damage, a damage index is defined, which depends on the required information for determining the response of a building subjected to a rockfall impact. Here, the proposed DI has a physical, structural meaning and varies from 0 (no damage) to 1 (total damage). It is given by Eq. 12.

$${\text{DI}} = \frac{{{\text{number}}\;{\text{of}}\;{\text{failed}}\;{\text{elements}}}}{{{\text{total}}\;{\text{number}}\;{\text{of}}\;{\text{elements}}}}$$
(12)

For a comprehensive assessment of vulnerability to rockfall impact, the probability of an impact causing a certain DI value has to be calculated, and, in addition, economic and time cost factors, as well as other types of consequences and losses (e.g., social, cultural, etc.), have to be incorporated (Galli and Guzzetti 2007).

Application

The method presented above is applied to the case of a fragmented rockfall, where individual blocks up to ∼4 m3 in volume strike the building. In order to evaluate the building vulnerability, a single 2-m-diameter rock sphere is considered to move horizontally toward its façade, traveling at velocities up to 3.5 m/s, and with trajectories ranging from mostly orthogonal to 73° on either side of orthogonal (in scenario 14 of Fig. 9). In most cases, the amount of rotational energy represents just a small fraction of the total kinetic energy (Chau et al. 2002), so only the translational motion parameters of the block are considered. The impact action is assumed to be applied horizontally, normal to the face of a column. No energy is considered to be lost in the boulder during the impact. In case the hit on a column causes its collapse, it is investigated whether the remaining kinetic energy, after the crash, is sufficient to damage further columns in the rockfall path.

The investigated building is a simple, reinforced concrete frame, two-story building. The structural system has a grid of 3 × 4 columns. The number of columns that may be collapsed by the impact ranges from 0 to 4. The contribution of slabs to the continuity of the structure and to the load redistribution following the collapse of the first column is not taken into account, nor is their damage studied. It is assumed that there is no loss of kinetic energy due to friction between successive column hits or dissipation of energy by nonstructural members (walls, furniture, etc.).

Description of the structure and finite-element modeling

The two-story building was designed using Eurocode 2 (BS EN 1992), so as to withstand its anticipated dead and live loads. For the analysis and design, the finite-element method and the software SAP 2000, v10 were used. The finite-element model is presented in Fig. 7.

Fig. 7
figure 7

Finite-element model of the building

Full size image

The distance between frames in both directions is 5 m, and each floor’s height is 3 m. The geometrical and reinforcement characteristics of the typical column and beam cross sections are shown in Table 1. The concrete and steel materials are C20/25 and S500s, respectively.

Table 1 Cross-sectional dimensions and reinforcement of columns and beams
Full size table

Dead loads include the self-weight of the structure (including floor slabs and roof), the weight of infill walls (3.6 kN/m2), and an additional floor uniform load (1.5 kN/m2). The live load is taken as 2.0 kN/m2. All slab loads are distributed and applied to the adjacent beams. The model is fixed at its base.

Alternative scenarios

The alternative impact scenarios for the analysis are selected to represent all the possible damage states due to impact on one or more basement columns. Since the final damage of the building is associated with the number and location of the initial column(s) that collapse, all possible combinations of impact location and path should be investigated. It is assumed to be only one building façade exposed to the rockfall: façade A in Fig. 7. In the example, different rock paths are generated from more than one rockfall source on the cliff face. Depending on the impact kinetic energy, one or more columns may fail. There are 29 possible combinations of column(s) damage (circled in red in Fig. 8 with symmetrical cases included).

Fig. 8
figure 8

Schematic representation of all 29 possible combinations of column impact and damage. Façade A is located at the bottom of each grid. Red circles outline the hit column(s) and red lines the block path

Full size image

To evaluate the different building responses for each of these cases, 16 basic scenarios that are representative of the possible combinations are analyzed (Fig. 9). For each one, the level of kinetic energy E k is sufficient to destroy the columns marked in red. The rock path is indicated with an arrow.

Fig. 9
figure 9

Basic hazard scenarios. Columns marked in red are destroyed along the paths indicated by the arrows

Full size image

The response of the building for each case shown in Fig. 8 can be obtained using the basic hazard scenarios shown in Fig. 9.

Probability of encounter

For a 2-m-diameter rock, the encounter probability P enc with a building column is given by Eq. 2. In order to calculate the encounter probability with a specific column P s, P enc is divided by the number of columns on the face. In cases 9 to 16 of Fig. 9, where the boulder does not travel normal to face A, the column traces are projected to a line vertical to the rock path and the total number of traces, as well as the average distance between them, are calculated, in order to use them in Eq. 2. Figure 10 presents scenarios 9 and 12, in which Eq. 13 gives the encounter probability P enc with any of columns 1, 2, and 3 (Fig. 9, scenario 9) and Eq. 14 the encounter probability P s with one specific column. The P enc and the P s for all basic hazard scenarios are reported in Table 2.

$$P_{{{\text{enc}}}} = \frac{{l_{{\text{c}}} + d}}{{a\sin \psi }}$$
(13)
$$P_{{\text{s}}} = \frac{1}{n}\frac{{l_{{\text{c}}} + d}}{{a\sin \psi }}$$
(14)

where

P enc :

is the probability of encounter with any exposed column,

P s :

is the probability of encounter with a specific column,

n :

is the number of projected columns on a line vertical to the rock path,

l c :

is the column width,

l w :

is the infill-wall width,

a :

is the distance between columns,

d :

is the boulder diameter, and

ψ :

is the angle between the rock path and the façade plane.

Fig. 10
figure 10

Projections of columns used for calculating P enc and P s

Full size image
Table 2 Penc and Ps for basic hazard scenarios (for lc = 0.35 m, d = 2 m, a = 5 m)
Full size table

In general, to evaluate the risk at a susceptible area, the probability of occurrence of the particular volume as well as the probability of the path have to be calculated as well.

Column capacity and required energy for each scenario

According to the Sezen (2008) model (Fig. 4), the energy that can be dissipated by a column is calculated by integrating the area under the curve in Fig. 11. An average axial compression force of 300 kN is assumed for all columns. The displacement represents the midspan deflection, due to the horizontal impact load. Two capacity curves are shown, with and without the dynamic increase factor (=1.3). For the former the calculated impact capacity of a column is 14 kJ.

Fig. 11
figure 11

The impact energy capacity E cap of a column

Full size image

The failure curves of Fig. 12 are developed for columns of this capacity. For a 2-m boulder, the speeds that are sufficient to collapse one, two, three, and four columns are 1.65, 2.31, 2.83, and 3.27 m/s, respectively. Please note that this analysis can be extended to different boulder sizes as shown in Fig. 12 and Table 3.

Fig. 12
figure 12

Impact properties sufficient to collapse one to four columns

Full size image
Table 3 Boulder speeds sufficient to collapse one or more columns (meters per second)
Full size table

Potential for progressive collapse and DI

The method of Fig. 6 is applied here to evaluate the potential for progressive collapse of the building. The member resistance is calculated according to Eurocode 2. In the supports, the moment resistance of beams (before considering ductility) is 85 kN·m and the shear resistance 100 kN. The moment resistance of the span is 75 kN.

For each scenario, the final state of the structural system is shown in Fig. 13, and the DI is calculated.

Fig. 13
figure 13

Remaining structure and DI for each scenario

Full size image

The results indicate that for the same kinetic energy, the damage extent varies significantly according to the rockfall path and impact location. The range of the DI for this particular structure and the considered impact properties is from 0.01 to 1 (Fig. 14). The smallest value corresponds to scenario 12, in which the structure is able to bridge over the damaged element. The greatest damage corresponds to scenarios 6 to 8. For the E k of 14 kJ (damage of one column), the maximum expected DI is 0.32, while for all higher energy levels, total collapse is possible.

Fig. 14
figure 14

DI versus kinetic energy, E k

Full size image

From the results obtained, damage to a single corner column can possibly cause partial collapse of the building in the neighborhood of the column and along the whole height of the building (scenario 1). On the other hand, damage of the first central column can be bridged over despite damage of beams on the façade, thus collapse is avoided. For single-column damage, the effect is higher if it is located in the corner than in the center. For multiple lateral and central column damages, the effect is greater (up to total collapse) if they are located in the center. Formation of a bridge over a damaged column without further collapse also may occur in scenario 12. This underlines the importance of impact location on the final response of the building.

In general, it can be observed that for kinetic energies sufficient to cause the damage of only one column, the damage is either local, at the vicinity of the column, or only partial collapse of the building ensues. The exception to this is scenario 13, in which the damage is more extensive, indicating that these specific columns are key elements in the impact vulnerability of the structure. If two, three, or four columns are damaged, in all cases apart from scenario 9, the damage is high enough that reconstruction may be preferable to repair.

The computational time for this step is proportional to the number of iterative analyses required to reach a new building equilibrium. When a bridge is formed over the damaged column (i.e., scenario 12) the time needed to develop the finite-element model and analyze it is relatively short. The computational time increases when further collapse occurs, and more iterative analyses have to be performed up to the new equilibrium state. In some cases, it was observed that after removal of the basement columns, collapse of the building was direct, and many members were damaged simultaneously. For example, for scenario 6, leading to total collapse, only five iterative analyses were needed. However, when the collapse is slow and members are not damaged concurrently, many analyses are required (i.e., 19 for scenario 10) and computational time increases significantly. The advantage of this approach is that once all the scenarios of a given structural system have been analyzed, the results can be used for all reinforced concrete buildings having the same structural-element pattern.

Conclusions

In this paper, a step-by-step method is presented to evaluate the response of reinforced concrete buildings, which are struck on their basement columns by a single large boulder. The method has four main steps: (a) calculation of the probability of a rock encountering a structural element, (b) evaluation of the response of one or more structural elements to the hit based on their capacity, (c) assessment of the robustness of the structure if any elements fail, calculating the potential for progressive collapse, and (d) calculation of the DI.

The method is applied to a simple two-story regular reinforced concrete building, assuming different scenarios of impact parameters and fall paths. The damage extent is calculated for scenarios representative of the possible impact locations. The DI levels are then correlated with the boulder kinetic energy.

The results reveal the importance of impact location and the trajectory on the structural damage to the structure. For kinetic energy E k sufficient to destroy only one column, the damage to the building is either local at the vicinity of the column or partial, and the collapse caused is repairable. On the other hand, for the collapse of more than one column, the damage is considerably higher, possibly making reconstruction preferable to repair.

In general, although the damage extent indicated by the investigated scenarios may range up to total collapse, given the generally low probability of impact with one or more structural elements, rockfall impact may be characterized as a phenomenon of low probability but high consequences.

Based on these conclusions, the quantified vulnerability of a building to rockfalls is a function of both the probability of occurrence of a given rock impact (with defined motion properties: mass, speed, and path) and the resulting damage index. The aim of this paper has been to propose a tool for quantifying these controlling factors at the building scale. Further investigation is necessary to provide a vulnerability value that could be directly included in the risk equation, for various ranges of rock size and motion properties.