Seismic probabilistic assessment of steel and reinforced concrete structures including earthquake-induced pounding

Abstract

Recent earthquakes demonstrate that prioritizing the retrofitting of buildings should be of the utmost importance for enhancing the seismic resilience and structural integrity of urban structures. To have a realistic results of the pounding effects in modeling process of retrofitting buildings, the present research provides seismic Probability Factors (PFs), which can be used for estimating collision effects without engaging in intricate and time-intensive analysis. To include the low-, to mid-rise buildings, the 3-Story, 5-Story, and 9-Story adjacent steel and Reinforced Concrete (RC) moment-resisting frames were modeled in OpenSees software capable to take into account the structure in a state of collapse during the analysis, which can provide the real condition of buildings under seismic excitations. Results of analysis confirmed that the impact force can considerably affect the moment–rotation curve of beams and columns, in which, it can affect the structural response of structures during earthquakes. Therefore, seismic PFs proposed to examine the possibility of changes in the performance levels and fragility assessments. Moreover, proposed PFs can be used as coefficient factors to facilitate the retrofitting process of buildings and improve the environmental effects.

1 Introduction

During decades, the knowledge of engineers about the response and designing process significantly increased, and structures with strong capabilities against severe earthquakes were constructed. Meanwhile, during the design process, the existence of adjacent structures was neglected. Seismic codes prescribed some formula to define minimum Separation Distance (SD_min) and should be considered during construction, while in many cities, SD_min between newly constructed adjacent buildings was neglected. Favvata [1] investigated the SD_min for adjacent pounding structures, and showed that the SD_min depends on the seismic limit state and level of seismic hazard. In addition, to fulfill the shortcomings, some formulas have been proposed for evaluating SD [2]. Kazemi et al. [3] showed that colliding can impose unexpected force in the level of the impact that significantly affects the response of adjacent structures (see Figs. 4–6). Although this impact force cannot be considered during the design process, it may result in extensive local damages or even total collapse of the structural members (see [4, 5]). To prevent this extensive damages, Sołtysik et al. [6] proposed polymer elements that can be implemented between adjacent structures to reduce the impact force. In addition, Kazemi et al. [7] enhanced the seismic performance of neighboring structures through the utilization of viscous dampers. Kandemir-Mazanoglu and Mazanoglu [8] proposed an optimal placement of viscous dampers in the inter-floor spaces of the adjoining pounding structures. Proposed approaches had good improvements in seismic limit states of adjacent structures. Karayannis and Favvata [9] investigated different level Reinforced Concrete (RC) structures, in which structural collision occurs when one structure impacts the columns of another. This type of collision can cause local damages or even destruction of columns in the impact area [10]. In addition, some characteristics of the constructed buildings such as irregular plans and lateral-load resisting systems (with and without assuming infill masonry walls) can alter the behavior of buildings [11] and may lead to torsional movements (see [12]), which is an important reason for local damages in buildings. Jankowski [13] investigated the structural response of two adjacent structures assuming different materials implemented on the shaking table. The steel structure witnessed the highest displacement response against concrete and ceramic material. In addition, the influence of materials on the dynamic properties was investigated by Favvata et al. [14]. Their results confirm that flexural and ductility demands in columns were affected by their location of them at the top of the structure.

For accurate seismic risk evaluation of adjacent colliding structures, seismic vulnerability assessment is a vital process. Although seismic risk assessment demands a precise estimation of the seismic hazard, outcomes of the vulnerability evaluation can be used for retrofitting structures and determining damages. Kazemi et al. [15] explored seismic collapse capacity and fragility curves of the adjacent pounding structures with different heights and floor weights. Zain et al. [16] proposed a framework for seismic fragility curve assessments of RC structures that reduces the computational efforts. Mohamed and Romão [17] investigated the seismic vulnerability assessment of RC structures that were not originally designed to withstand lateral forces considering the pounding phenomenon, assuming different conditions of collision such as floor-to-floor and floor-to-column. Tubaldi et al. [18] discussed the two major issues [i.e., appropriate Intensity Measure (IM) and selecting a regression model to explain the relation between Engineering Demand Parameter (EDP) and IM] in defining a probabilistic seismic demand model for collision risk assessment. While it mentions improvements in sufficiency obtained using certain IMs, it does not provide concrete data or analysis to substantiate these claims. However, a design methodology for determining the critical SD between adjacent buildings to prevent seismic collision including performing parametric analyses and developing efficient algorithms based on linear structural models have been done by Barbato and Tubaldi [19]. Ruggieri et al. [20] used a sample made by 90 masonry churches in Piemonte, Italy, as case study for a statistical basis seismic vulnerability analysis subjected to the Valle Scrivia earthquake. Seismic damage diagnosis plays a key role for vulnerability assessment of the structures.

Vulnerability evaluations can be projected as seismic fragilities, which can be sorted into four terms of empirical, analytical, hybrid, and judgmental. Surveys from previous seismic events as the major source of vulnerability evaluation can be employed for seismic performance assessment of colliding buildings in terms of empirical process, while judgmental process relies on the opinions of the expert. Ruggieri et al. [21] proposed a visual assessment process to evaluate the seismic risk of a school in Italy using a judgmental process. A hybrid process is a combination of two judgmental and empirical evaluations. Although these processes can be easily used by researchers, the precision of the outcomes is strongly contingent upon on expert judgment and the quality of previous seismic events. Therefore, using the analytical process to fragility curve assessment of the colliding structures applying nonlinear simulations is considered to be the most reliable process [11, 22,23,24,25]. It is worth mention that the nonlinear model should contain as possible as the actual condition of structures in collision. Kazemi et al. [26] investigated P-delta effect on seismic limit state capacities of adjacent frames and showed that the P-delta effect plays a crucial role in the seismic capacity level assessment. In addition, they developed a computational strategy to consider the effects of collapsed structure on the seismic response of the adjacent structure during the analysis, which is a real condition of damaged structures during severe earthquakes. Moreover, they proposed some retrofitting strategy to improve seismic performance of steel and RC structures [27, 28].

Recently, some studies have been carried out for seismic fragility curve assessment of structures. Miano et al. [29] evaluated seismic fragilities of the RC infilled buildings stock with a parallel plane frames assuming base differential displacement. They showed that the geometrical features had a crucial effect on the vulnerability measures. Wang and Sun [30] proposed self-centering columns with low-bond high-strength reinforcement to investigate the reparability of RC buildings. The seismic fragility curves of the residual story showed that using the self-centering columns significantly mitigated the residual deformation of damage states. Yazdanpanah et al. [31] introduced a novel methodology for assessing seismic fragilities in colliding adjacent structures, utilizing an enhanced wavelet-based refined feature. Their approach showed more efficient results to estimate seismic fragility curves based on Morlet and complex Morlet (cmorfb-fc) wavelets. Flenga and Favvata [31] proposed a method involving optimal SD and minimum collision risk to discuss the limitations of existing methods for assessing the risk associated with this phenomenon. They introduced probabilistic method to enhance the response prediction, and a novel methodology based on fragility analysis has been introduced to assess SD_min across various limit states. This approach considers localized demands, including shear, on structural members, as well as scenarios involving both floor-to-floor and floor-to-column collision. However, Flenga and Favvata [32] integrated the localized inelastic demands of a multi-story RC structure into the probabilistic assessment of seismic collision risk. One strength of the investigation is its recognition of the limited consideration given to local EDPs in probabilistic assessment. A novel approach has been developed for determining the optimal SD and assessing the acceptable risk of structural pounding in multi-story RC structures. Their findings suggest that the performance characteristics of the columns within the RC structure play a critical role as demand parameters in the probabilistic evaluation of collision risk. Moreover, they developed a risk-targeted decision model for verifying the seismic performance of a multi-story RC structure against collision, and assumed the lack of consideration for performance objectives, aseismic code-compliant design, and local inelastic demands of structural members. A novel decision framework, aimed at targeting risk, has been introduced to validate the seismic performance of RC structures concerning structural pounding [33]. Considering the impact effects and variations in geometric properties and material, Sinha and Rao [34] investigated displacement-based fragility for floor-to-floor and floor-to-column collision within an eight-story non-ductile RC frame adjacent to a three-story rigid RC frame with varying story levels. They emphasize the importance of accurately estimating structural integrity with respect to collision to prevent catastrophic failures. However, using machine-learning methods can be a useful preliminary tool for estimating performance levels and fragility curves of steel and RC buildings [35, 36].

The main purpose of this study is seismic performance and fragility curve assessment of adjacent RC and steel moment-resisting frames including the earthquake-induced collisions. Therefore, adjacent RC colliding with steel structures considering three SDs according to the seismic codes have been considered having a typical plan and connected with linear viscoelastic contact elements to assume collision phenomenon. The collapse state analyses were performed in numerical models of steel and RC structures with the possibility of destruction of one of the structures. To accurately simulate the real condition of steel and RC structures exposed to pounding, the structures were modeled in MATLAB [37] and OpenSees [38], a software application incorporating a crafted Tcl programming code, equipped with the capability to account for damages during the analysis. The executed program can accurately analyze a model under nonlinear conditions, employing innovative methods to incorporate damages and monitor structural responses throughout the analysis. This approach proves valuable in creating precise models that closely resemble the real conditions of buildings susceptible to earthquake-induced pounding. In addition, the developed Tcl algorithm possesses the capability to control engineering demands to capture the results of structural response of both structures to reduce the analysis time. Having a precise modeling approach for collision and considering the collapsed structure effects on the existing structure make this research a reliable investigation so far. Moreover, this study determines proper Probability Factors (PFs) for existing buildings or newly constructed ones to estimate the influence of collision phenomenon on the seismic performance and fragility curves based on the analytical process. Using PFs reduces the time of collision analysis and provides designers a preliminary estimation on how the collision would affect the structural performances.

2 Modeling methods

2.1 Modeling of structures

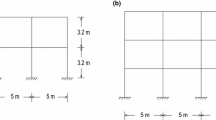
In this study, structures with 3-Story, 5-Story, and 9-Story steel and RC structures were investigated. Figure 1 shows the structural plan assumed for adjacent structures. To model these structures, soil class D with seismic parameters of SD_S = 1.0 g and SD₁ = 0.6 g were assumed. In this study, for both steel and RC structures, R = 8, Ω = 3, and C_d = 5.5, were selected according to ASCE/SEI 7–16 [39]. Moreover, live and dead loads of 2.39 kN/m² and 8.379 kN/m², respectively, were applied to all floor levels. All structures were modeled in ETABS 2016 based on ASCE 7–16 [39], AISC 360-16 [40], AISC 341-16 [41], and ACI 318-14 [42] provisions. Steel yield strength and concrete compressive strength equal to 345 MPa and 34.5 MPa were used, respectively. Figure 2 presents structural elements and geometry of the selected structures. To model two-dimensional steel and RC structures in OpenSees [38], all columns except those in the MRFs (see the red line for steel and blue line for RC in Fig. 1) were modeled as leaning column to consider P-Delta effects and connected to the main resisting frame with axially rigid links [43,44,45].

Fig. 1

Structural plan of the considered steel and RC structures

Fig. 2

Structural elements and geometry of the selected steel and RC structures

In the case of steel structures, two nonlinear springs located at the ends of beams and columns were employed to account for the modified Ibarra–Krawinkler model [26,27,28, 46] for assuming deteriorating moment–rotation hysteresis. To capture the deterioration modes of RC, an element model with the capability of considering deterioration modes (i.e., monotonic and cyclic) was used [47,48,49]. Tables 1 and 2 present design documentation of the structural elements of RC. h and b are the height and width of section, s is spacing of transverse reinforcement, $\rho_{tot}$ is longitudinal reinforcement ratio, $\rho^{\prime}$ is longitudinal reinforcement ratio in compression, and $\rho_{sh}$ is transverse reinforcement ratio near end of column (close spacing region).

Table 1 Detail of the column members of RC

Table 2 Detail of the beam members of RC

It worth mentioning that the structures have symmetric plan in both directions and regular weight distribution. Therefore, it is only possible that they collide in X-direction due to assumptions and there is no torsion impact during pounding. Due to these assumptions, it can be possible to model two-dimensional steel and RC structures with pounding effects [26,27,28, 46].

2.2 2.2. Impact element model

Seismic codes prescribed minimum SD regarding experimental and analytical models. In this study, SD prescribed by ASCE/SEI 7–16 [39] was used. According to this, Eq. (1) shows SD_min that can be calculated as follows:

$${\text{SD}}_{\min } = \sqrt {{\left( {\frac{{C_{\text{d}} .\delta_{\text{M}} }}{I}} \right)_1^2 + \left( {\frac{{C_{\text{d}} .\delta_{\text{M}} }}{I}} \right)_2^2 ,}}$$

(1)

where δ_M is maximum inelastic deformation, and I is importance factor. To calculate δ_M, base shear-roof displacement curves (pushover curve) based on the first mode lateral-load distribution for both categories of structures were obtained. In this research, the distance between two adjacent structures was selected as 0.0, 0.5, and 1.0 times of SD_min. Table 3 shows numerical models of structures used in this study with assumed SDs between them.

Table 3 SDs assumed between numerical models of steel and RC structures

There are many impact element models that can be used to model impact force due to colliding between adjacent structures. They can be sorted from the high accuracy of modeling this phenomenon such as linear and nonlinear viscoelastic model to the lower accuracy such as using spring element [50, 51]. The equation of linear viscoelastic element can be presented as follows:

$$F(t) = K_i \delta (t) + C_i \dot{\delta }(t),\quad C_i = \frac{ - 2 \times \ln (e)}{{\sqrt {\pi^2 + (\ln e)^2 } }}\sqrt {{K_i \frac{{m_{1 } m_{2} }}{m_1 + m_2 },}}$$

(2)

where the impact force, ${\text{F}}\text{(}{\text{t}}\text{)}$, can be calculated by the contact stiffness, K_i, and the damping coefficient of the contact model, C_i, having the amount of $\delta {\text{(t)}}$ and $\dot{\delta }(t)$, relative deformation and velocity of adjacent structures, respectively. In addition, m₁ and m₂ are the masses of structures in the level of implementing contact element. The coefficient of restitution, denoted as “e” signifies the ratio of the final relative velocity to the initial relative velocity of impacting bodies. It assumes a value between 0.0 and 1.0, representing fully elastic or fully plastic impacts, respectively. In the adopted models, the floor levels were treated as instances of concrete-to-concrete pounding, and a coefficient of restitution of 0.65 was presumed, aligning with findings from various other studies (for more details, see [5, 26,27,28, 31]).

The impact stiffness and damping coefficients of contact elements are contingent upon the material properties involved in the collision, and there is no singular relationship for their calculation. Nevertheless, Polycarpou et al. [52] proposed the methodology of three-dimensional colliding simulation that considers a simple approximation of the impact stiffness and damping coefficients assuming the plan geometry and material properties. This methodology prepares the requirements of this study for modeling of contact element. They proposed Eq. (3) to calculate the impact stiffness along the colliding side, K, as follows:

$$K = \left[ {\frac{1 - \nu_1^2 }{{E_{\text{Dynamic,1}} }} + \frac{1 - \nu_2^2 }{{E_{\text{Dynamic,2}} }}} \right]^{ - 1} ,\quad E_{{\text{Dynamic}}} = 5.82\left( {E_{{\text{Static}}} } \right)^{0.63}$$

(3)

where E_Dynamic is concrete dynamic elastic modulus that can be determined from static modulus of concrete, E_Static equal to 21 GPa. ν_i is Poisson's ratio and assumed equal to 0.2. Therefore, K can be calculated from Eq. (3) equal to K = 20.96 × 10⁶ kN/m². According to Fig. 1, the colliding length (9.15 m) multiplying by K can be used as K_i, which is 1.9185 × 10⁸ kN/m, and from then, the impact damping coefficient C_i equal to 7576 kN. s/m was obtained [26,27,28].

3 Results of analysis

3.1 Moment and rotation of hinges

In this section, the effects of colliding on the moment and rotation of hinges of beams and columns were investigated. Sudden impact force in the floor level can considerably affect response of adjacent structures, and then can cause damages in beams and columns. The damage state can be achieved by evaluation of moment and rotation curves of hinges. It should be noted that the collision time could vary during the analysis due to lateral behavior of the structures, while the collision occurs during lateral displacement more than the separation distance. In this part, a nonlinear time-history analysis was performed using Duzce Turkey record (11/12/1999, Duzce, RSN No. 1605) selected from Near-Fault Pulse Like (NF-PL) ground motion subset suggested by FEMA-P695 [53]. The 9-Story steel colliding with 3-Story RC was selected from models to use for nonlinear time-history analysis assuming S_a (T₁) = 1.27 g given SD of 0.0. Figures 3 and 4 compare moment curves of column and beam hinges of the third floor of the 9-Story steel in alone and colliding with the 3-Story RC assuming SD of 0.0, respectively. According to results, colliding can cause sudden changes in the moment curve compared to the excluding model. These changes in some time step of analysis can increase the amount of moment value suddenly, which causes damages in the structural element. According to Figs. 3 and 4, the maximum moment value of column and beam hinges increased by 37.96% (from 797.86 to 1100.75 kN. m) and 13.22% (from 1145 to 1296.4 kN. m), respectively.

Fig. 3

Comparison between the moments of the third-floor column hinge of 9-Story steel in collision with the 3-Story RC given SD = 0.0

Fig. 4

Comparison between the moments of the third-floor beam hinge of 9-Story steel in collision with the 3-story RC given SD = 0.0

Figures 5 and 6 compare rotation curves of column and beam hinges of the third floor of the 9-Story steel in alone and colliding with the 3-Story RC assuming SD of 0.0, respectively. It is obvious that in the same time step of increasing the moment values, the rotation values experienced sudden changes. This means that the hinges of the selected column and beam entered into a nonlinear state. In addition, according to the results, the maximum rotation value of column and beam hinges increased by 31.25% (from 0.0032 rad to 0.0043 rad) and 29.62% (from 0.0108 rad to 0.0140 rad), respectively. It is noteworthy that results concern all of the hinges of columns and beams in the considered analytical models.

Fig. 5

Comparison between the rotations of the third-floor column hinge of 9-Story steel in collision with the 3-Story RC given SD = 0.0

Fig. 6

Comparison between the rotations of the third-floor beam hinge of 9-story steel in collision with 3-story RC given SD = 0.0

3.2 Analysis procedure

Incremental Dynamic Analysis (IDA) method establishes a probabilistic framework for evaluating structural fragility through the creation of numerous response curves aligned with varying intensity levels. Gradually escalating the ground motion intensity enables IDA to encapsulate the nonlinear dynamics and eventual collapse mechanisms of structures, thereby facilitating the derivation of fragility curves that accommodate uncertainties in ground motion attributes and structural behavior [54]. Previous section emphasized that colliding structures may experience a sudden impact force in the colliding level and this force affected the moment and rotation of the structural members’ hinges. To extent the results, IDA is employed that uses IM to increase the intensity of records in each step until the total destruction of the structure, and in each step, EDP controls stability of structure. According to Kazemi et al. [55], various non-structure-specific IMs, including acceleration, velocity, and displacement-related IMs, were compared, revealing that the spectral-based IM, S_a (T₁), exhibited superior performance. Additionally, the analysis of the variations in standard deviation of natural logarithm of IMs indicated that S_a (T₁) demonstrated lower values, suggesting its efficiency as a scalar-valued IM for conducting IDA. Sufficiency, defined as the ability of an IM to render seismic response independent of other characteristics of seismic ground motion records, was evaluated by calculating the p value with respect to ground motion characteristics, such as M (magnitude), R (distance), and Vs30 (shear wave velocity). The results indicate that S_a (T₁) exhibits proper sufficiency, with p values ≥ 0.05, concerning M, R, and Vs30. For this purpose, spectral acceleration in the structure's period, S_a (T₁), is selected as IM, and maximum Interstory Drift Ratio (IDR) is selected as EDP. Therefore, in each step, IM and EDP values can be used for drawing the IDA curve. In this research, two ground motion sets of NF-PL and Near-Fault No Pulse (NF-NP) are considered regarding FEMA-P695 [53]. The NF records comprises 28 records (i.e., 56 individual components) sourced from the PEER NGA database, following the criteria outlined in Section A.7 in FEMA P-695 [53]. Among these, 14 records exhibit pulses (classified as NF-PL), while the remaining 14 records do not display pulses (classified as NF-NP). The selection of records is based on the maximum values of as-recorded Peak Ground Acceleration (PGA_max) and Peak Ground Velocity (PGV_max), which significantly influence the collision of adjacent structures. The mean spectrum of the chosen records aligns with the target spectrum specified for soil class D across the structural periods of colliding structures. Figure 7 presents the response spectrum of NF-PL and NF-NP record sets.

Fig. 7

Response spectrum of a NF-PL and b NF-NP records

It is obvious that the real condition of colliding structures should be considered during analysis. Regarding this, in this research, the real condition of colliding structures has been investigated. In the real colliding between two adjacent structures, differences between fundamental periods of adjacent structures (e.g., T_1,1 and T_1,2) can cause each of the structures to have different collapse IM. Therefore, one of them should be collapsed before the second one. Moreover, S_a (T_1,1) and S_a (T_1,2) should be assumed for selecting the IM. A Tcl algorithm improved in MATLAB [37] and OpenSees [38] software to assume these characteristics in the models, and capture the results of each structures separately with considering their effects on each other. Therefore, it is possible to capture both structure's IDA curves at the same time in one model, which reduces the analytical time and efforts. Figures 8 and 9 present IDA curves and the median of IDA curves (M-IDA) of selected steel and RC structures including NF-NP record subset, respectively.

Fig. 8

IDAs of a 3-, b 5-, and c 9-Story RC including NF-NP record subset

Fig. 9

IDAs of a 3-, b 5-, and c 9-Story steel including NF-NP record subset

3.3 Seismic performance level

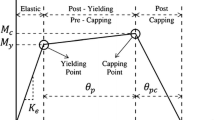
In accordance with the descriptions provided in the preceding section, it is feasible to concurrently evaluate IDA curves for both adjacent structures. In this section, seismic limit state capacities of the aforementioned structures were achieved from IDA curves. Four seismic performances of Immediate Occupancy (IO), Life Safety (LS), Collapse Prevention (CP), and Total Collapse (TC) were defined in accordance with FEMA 356 [56]. To determine these performance levels for steel structures, the allowable IDR of 0.7%, 2.5%, and 5.0% represented for primary members and performance levels of IO, LS, and CP, respectively, were considered. In addition, for RC, the allowable IDR of 1.0%, 2.0%, and 4.0% represented for primary members and performance levels of IO, LS, and CP, respectively, were assumed. Moreover, the seismic performance level of TC was selected in the flat part of IDAs of steel and RC structures. Table 4 presents performance levels of steel and RC structures in alone condition including NF-NP and NF-PL record subsets. According to Table 1, in all seismic performance levels, S_a (T₁) values for RC including NF-NP records were higher than those including NF-PL records, correspondingly. The same result can be seen for the 3-Story steel, while for the 5-Story and 9-Story steel, S_a (T₁) for performance levels including NF-PL record subset are higher.

Table 4 Seismic performance of steel and RC structures in alone state including NF-NP and NF-PL records

Tables 5 and 6 present seismic performance levels of colliding steel and RC structures including considered records for SD of 0.0 and 1.0SD_min, respectively. According to Table 5, in the colliding 3-Story steel with RC structures, the S_a (T₁) values in NF-PL record subsets are lower than those in NF-NP records, correspondingly. Except in performance level of IO for in collision with 3-, and 9-Story RC structures, the S_a (T₁) values in NF-PL record subsets are higher than in NF-NP record subsets. In addition, it can be seen that seismic performance level of TC in the 3-Story steel colliding with the 3-, 5-, and 9-Story RC structures decreased from 1.892 to 1.848, 1.812, and 1.861, respectively, in NF-PL record subset assuming 1.0SD_min. Therefore, the 3-Story steel is more vulnerable to structural damages in NF-PL record subsets. In the 5-Story steel colliding with RC structures, the S_a (T₁) values in the seismic performance levels of IO and LS in NF-PL record subsets are higher than those in NF-NP record subsets, while S_a (T₁) values in seismic performance levels of CP and TC in NF-PL record subsets are lower than those in NF-NP record subsets. It means that due to the seismic performance level, the seismic vulnerability of the 5-Story steel changes from NF-NP record subsets to NF-PL record subsets. Seismic TC performance in 5-Story steel colliding with 3-, 5-, and 9-Story RC structures decreased from 1.269 to 1.202, 1.216, and 1.245, respectively, in NF-PL record subset assuming 1.0SD_min. In the 9-Story steel colliding with 3-, and 9-Story RC structures, the S_a (T₁) values in NF-PL record subsets are higher than those in NF-NP record subsets correspondingly, while in the colliding with 5-Story RC structure, the S_a (T₁) values in NF-NP record subsets are higher than those in NF-PL record subsets correspondingly.

Table 5 Performance of steel structures in collision with RC structures including seismic records for SD of 0.0

Table 6 Performance of steel structures in collision with RC structures including seismic records for 1.0SD_min

The results showed that TC performance in 9-Story steel in collision with the 3-, 5-, and 9-Story RC structures increased from 0.547 to 0.626, 0.690, and 0.697, respectively, in NF-PL record subset assuming 1.0SD_min. Therefore, in the 9-Story steel, the kind of adjacent structures can change the seismic vulnerability from NF-NP record subsets to NF-PL record subsets.

According to Table 6, similar results were achieved for 3-, and 5-Story steel structures in collision with RC structures given 1.0SD_min. Therefore, increasing the distance between 3-, and 5-Story steel in collision with RC structures had no effects on their vulnerability according to the type of record subsets, while in the general view, the S_a (T₁) values in the 1.0SD_min were higher than those in 0.0, correspondingly. The comparison of results derived from contact elements under colliding conditions verifies that the acceleration response is influenced by the separation distance.

These variations in acceleration values have the potential to alter the extent of damage in structural elements. Consequently, as the separation distance increases to 1.0SD_min, the occurrences of pounding decrease accordingly. Therefore, the separation distance of 0.0 is more critical than 1.0SD_min. In 9-Story steel in collision with 3-, and 9-Story RC structures given SD of 1.0SD_min, similar results were obtained, while the S_a (T₁) values in the 1.0SD_min were higher than those in 0.0, correspondingly. For 9-Story steel colliding with 5-Story RC structure, the S_a (T₁) values in NF-PL record subsets are higher than those in NF-NP record subsets correspondingly. Tables 7 and 8 present seismic performance levels of RC in collision with steel structures including NF-NP and NF-PL records for SD of 0.0 and 1.0SD_min, respectively. According to Table 7, in 3-, and 5-Story RC structures colliding with steel structures, S_a (T₁) values in NF-PL record subsets are lower than those in NF-NP record subsets correspondingly. Thus, 3-, and 5-Story RC structures are more vulnerable to structural damages in NF-PL records. In 9-Story RC colliding with steel structures, S_a (T₁) values in NF-PL records are upper than NF-NP records.

Table 7 Seismic performance of RC in collision with steel structures including seismic records for SD of 0.0

Table 8 Seismic performance of RC in collision with steel structures including seismic records for 1.0SD_min

According to Table 8, similar results were obtained for selected RC colliding with steel structure given SD of 1.0SD_min. Therefore, increasing the distance between RC colliding with steel structures had no effects on their vulnerability according to the type of record subsets. In the general view, S_a (T₁) values of selected RC structures colliding with 3-Story steel witnessed an increase in both record subsets by changing the SD to 1.0SD_min. In addition, S_a (T₁) values of 3-Story RC in collision with 5-Story steel decreased in both record subsets by changing the SD from 0.0 to 1.0SD_min, while experienced an increase in colliding with 9-Story steel in both record subsets.

The S_a (T₁) values of 9-Story RC colliding with 9-Story steel decreased in both record subsets by changing the SD from 0.0 to 1.0SD_min. Therefore, the elevation and T₁ can significantly affect the performance levels of structures. This means that during the applied record subsets, the adjacent structure may collapse earlier and affect the response of the remained structure. It is important to highlight that due to some preliminary analysis on the pounding cases having 0.5SD_min, the results are approximately between those 0.0 and 1.0SD_min. Therefore, for brevity, only results of 0.0 and 1.0SD_min have been presented in the manuscript. Moreover, the outcomes of pounding for 0.5SD_min can be approximated through linear interpolation of the results as detailed in Tables 5–8. It should be added that these tables are comprehensive source for designers to predict the effects of the collision phenomenon regarding structures' type, record subsets, and seismic code prescribed distance.

3.4 Seismic fragility curve for SD of 0.0

Seismic fragility curves express the seismic vulnerability of structure for different damage states at different ground motion intensities. These curves are a typical tool for the physical understanding of functionally level of structures. The damage states play a pivotal role in illustrating the condition of a compromised structure and assessing the feasibility of retrofitting and repair options. In the Sect. 3.3, four seismic performances (e.g., IO, LS, CP, and TC) were defined that show the structural damage states prescribed in FEMA 356 [56]. Seismic fragility curves were derived for aforementioned performance levels for both adjacent colliding structures given two record subsets. Comparison was made between the structure in alone condition and colliding one to clearly show the pounding effect on the seismic fragility curves. Figure 10 illustrates the procedure done to determine fragility curve. It should be mentioned that fragility curves of colliding structures achieved considering the influence of collapsed structure into the analyses. Therefore, due to assuming the real conditions of buildings, these results can be used for buildings with similar structural characteristics.

Fig. 10

Analytical procedures of this study

According to the analytical procedure, the seismic fragility curves were generated from obtained IDA curves. Figures 11, 12, and 13 present fragilities of 3-Story steel in collision with 3-, 5-, and 9-Story RC structures for different drift thresholds given SD of 0.0, including NF-PL records, respectively. Capacity level probability of 3-Story steel increased in LS, CP, and TC performances, while it reached a reduction in IO performance. Therefore, adjacent RC structures have a negative effect on capacity level probability of 3-Story steel. On the other side of colliding structures, capacity level probability of 3-Story RC increased for all different drift thresholds. Capacity level probability of 5-Story and 9-Story RC structures experienced an improvement in IO and LS performances, while this value decreased in CP and TC performances.

Fig. 11

Seismic fragilities of a 3-Story steel, and b 3-Story RC for drift thresholds given SD of 0.0, including NF-PL records

Fig. 12

Seismic fragilities of a 3-Story steel, and b 5-Story RC for drift thresholds given SD of 0.0, including NF-PL records

Fig. 13

Seismic fragilities of a 3-Story steel, and b 9-Story RC for drift thresholds given SD of 0.0, including NF-PL records

Figures 14, 15, and 16 present the fragilities of 5-Story steel in collision with 3-, 5-, and 9-Story RC structures for different drift thresholds given SD of 0.0, including NF-PL record, respectively. Capacity level probability of 5-Story steel increased in IO, LS, CP, and TC performances. It is obvious that adjacent RC structures have a negative effect on capacity level probability of 5-Story steel.

Fig. 14

Seismic fragilities of a 5-Story steel, and b 3-Story RC for drift thresholds given SD of 0.0, including NF-PL records

Fig. 15

Seismic fragilities of a 5-Story steel, and b 5-Story RC for drift thresholds given SD of 0.0, including NF-PL records

Fig. 16

Seismic fragilities of a 5-Story steel, and b 9-Story RC for drift thresholds given SD of 0.0, including NF-PL records

Whereas, limit state probability of 3-Story RC increased in IO and LS performance levels, and remained unchanged in the CP and TC performance levels. It should be noted that limit state probability of 5-, and 9-Story RC were significantly decreased in CP and TC performance levels that shows the positive effects of being adjacent to 5-Story steel. Although 5-Story steel achieved a higher limit state probability, it helped the adjacent RC to achieve a lower limit state probability (e.g., 5-, and 9-Story RC).

Figures 17, 18, and 19 present the fragilities of 9-Story steel colliding with selected RC structures for different drift thresholds given SD of 0.0, including NF-PL subset, respectively. Figure 17 shows that limit state probability of 9-Story steel significantly reduced LS, CP, and TC performance levels, while the same reduction was observed in the adjacent 3-Story RC. The same results were observed from Fig. 18 for 9-Story steel colliding with 5-Story RC. According to Fig. 19, limit state probability of 9-Story steel reduced in IO, CP, and TC performances, while limit state probability of 9-Story RC significantly reduced in CP and TC performances. Therefore, 9-Story steel prevents adjacent RC from destruction during the seismic events and decreases their seismic limit state probabilities. According to the results, this phenomenon can be considered in the seismic evaluation of the adjacent structures.

Fig. 17

Seismic fragilities of a 9-Story steel, and b 3-Story RC for drift thresholds given SD of 0.0, including NF-PL records

Fig. 18

Seismic fragilities of a 9-Story steel, and b 5-Story RC for drift thresholds given SD of 0.0, including NF-PL records

Fig. 19

Seismic fragilities of a 9-Story steel, and b 9-Story RC for drift thresholds given SD of 0.0, including NF-PL records

3.5 Seismic fragility curve for SD of 1.0SD_min

Figures 20, 21, and 22 present fragilities of 3-Story steel colliding with selected RC structures for various drift thresholds given SD of 1.0SD_min, including NF-PL record subset, respectively. Fragilities of 3-Story steel in all performances were steeper than the colliding values and limit state probability of 3-Story steel can be achieved according to S_a (T₁) values. Limit state probability of 3-Story RC increased during the colliding in all performance levels, while limit state probability of 5-, and 9-Story RC structures significantly decreased in CP and TC performances. Although the slope of fragility curves of 3-Story steel reduced during collision, adjacent RC achieve a lower limit state probability (e.g., 5-, and 9-Story RC); thus, colliding effects can be considered in their seismic evaluation in the conservative way.

Fig. 20

Seismic fragilities of a 3-Story steel, and b 3-Story RC for drift thresholds given SD of 1.0SD_min, including NF-PL records

Fig. 21

Seismic fragilities of a 3-Story steel, and b 5-Story RC for drift thresholds given SD of 1.0SD_min, including NF-PL records

Fig. 22

Seismic fragilities of a 3-Story steel, and b 9-Story RC for drift thresholds given SD of 1.0SD_min, including NF-PL records

Figures 23, 24, and 25 present fragilities of 5-Story steel colliding with selected RC for different drift thresholds given SD of 1.0SD_min, including NF-PL record subset, respectively. According to results, limit state probability of 5-Story steel remained unchanged in IO performance, while decreasing in LS performance level. Limit state probability of 5-Story steel in collision with 3-, and 5-Story RC increased in CP and TC performances, and CP performance increased in colliding with 9-Story RC. On the other side, all performance levels of 3-Story RC affected by collision and 5-, and 9-Story RC-MRFs experienced a significant decrease in TC performance.

Fig. 23

Seismic fragilities of a 5-Story steel, and b 3-Story RC for drift thresholds given SD of 1.0SD_min, including NF-PL records

Fig. 24

Seismic fragilities of a 5-Story steel, and b 5-Story RC for drift thresholds given SD of 1.0SD_min, including NF-PL records

Fig. 25

Seismic fragilities of a 5-Story steel, and b 9-Story RC for drift thresholds given SD of 1.0SD_min, including NF-PL records

Figures 26, 27, and 28 present the fragilities of 9-Story steel colliding with selected RC structures for different drift thresholds given SD of 1.0SD_min, including NF-PL record subset, respectively. According to Fig. 26, limit state probability of 9-Story steel remained unchanged in IO performance, while significantly decreasing in LS, CP, and TC performances. Although seismic limit state probability of 3-Story RC decreased in IO and LS performances, values showed a reduction in CP and TC performances. Figure 27 shows that the seismic limit state probability of 9-Story steel and 5-Story RC significantly decreased. Therefore, these adjacent structures can help each other to remain more stable and achieve higher performance levels. Figure 28 shows that limit state probability of 9-Story steel and 9-Story RC increased during colliding and they have a negative effect on their performance levels.

Fig. 26

Seismic fragilities of a 9-Story steel, and b 3-Story RC for drift thresholds given SD of 1.0SD_min, including NF-PL records

Fig. 27

Seismic fragilities of a 9-Story steel, and b 5-Story RC for drift thresholds given SD of 1.0SD_min, including NF-PL records

Fig. 28

Seismic fragilities of a 9-Story steel, and b 9-Story RC for drift thresholds given SD of 1.0SD_min, including NF-PL records

Similar results hold true for aforementioned colliding cases, but due to brevity, seismic limit state fragility curves were presented for NF-PL record subset. In addition, Tables 9, 10, 11, 12, and 13 present the seismic limit state probability of RC and steel structures with and without colliding conditions for SDs of 0.0 and 1.0SD_min, including NF-NP and NF-PL record subsets. Then, it is possible to find out limit state probability in aforementioned performances for all types of models considered in this study. Then, it will be possible to compare limit state probability of a structure before and after colliding. For example, according to Table 9, 5-Story RC achieved probability of 0.503 in TC performance. Then, to find out the effects of colliding with SD of 0.0, the seismic probabilities presented in Table 12 can be used for any adjacent steel with all performance levels.

Table 9 Seismic limit state probability of for RC and steel structures in alone state including NF-NP and NF-PL records

Table 10 Seismic limit state probability of for steel in collision with RC including seismic records for SD of 0.0

Table 11 Seismic limit state probability of for steel in collision with RC including seismic records for 1.0SD_min

Table 12 Seismic limit state probability of for RC in collision with steel including seismic records for SD of 0.0

Table 13 Seismic limit state probability of for RC in collision with steel including seismic records for 1.0SD_min

3.6 Modification factors

Results confirm that colliding between structures even in the prescribed SD (i.e., seismic code) affects both performance levels of structures; however, the designer does not consider these effects in design process that can cause severe damages to structures. Therefore, it is hard for the structural designer to find out the external forces that can exert by colliding. To overcome this problem, researchers proposed modification factors that could be considered to estimate limit state capacities of adjacent structures (e.g., see [27, 28]). In this study, seismic Probability Factors (PFs) proposed to predict probability of colliding steel and RC structures in four performances. Figure 29 presents procedure used in this study for calculating the PF for the 9-Story steel including and excluding colliding with 5-Story RC in TC performance, given SD of 1.0SD_min including NF-PL record subset. In the first step, IO, LS, CP, and TC performances with the allowable IDR described in Sect. 3.3 were shown in M-IDA curve of the 9-Story steel (Fig. 29a). The S_a (T₁) values corresponding to IO, LS, CP, and TC performances were calculated by 0.079, 0.275, 0.459, and 0.547, respectively (these values are determined in Table 4). Then, these values can be assumed to determine seismic limit state probability. For instance, a value corresponding to the TC performance (i.e., 0.547) connected to limit state probability of 9-Story steel including and excluding collision with 5-Story RC (Fig. 29b), and the values of 0.248 and 0.486 were achieved, respectively. Comparing probability values of colliding and alone conditions show that colliding can decrease failure probability by 51%. Therefore, a seismic PF of 0.51 is obtained and can be easily used by designers to calculate the colliding effects on the seismic limit state probability.

Fig. 29

Procedure to calculate the seismic probability factors using a M-IDA curve of 9-Story steel, and b fragility curves of 9-Story steel including and excluding colliding with 5-Story RC in TC performance, given SD of 1.0SD_min, including NF-PL records

Seismic PFs proposed in this study significantly reduced the time and analysis efforts for designers, and help them to consider the colliding effect in their analyses. Tables 14, 15, 16, and 17 present seismic PFs for colliding steel and RC structures including NF-NP and NF-PL record subsets, given SD of 0.0 and SD_min. For example, to calculate colliding effects on limit state probability of 5-Story steel including NF-NP records given SD of 0.0, the values presented in Table 14 can be used. According to Table 14, adjacent 3-Story RC can improve limit state probability of 5-Story steel by a factor of 1.499 in IO performance. Therefore, designers can use these tables to find out about the effects of adjacent structures and take them into account.

Table 14 Seismic probability factors of steel structures in collision with RC including seismic records for SD of 0.0

Table 15 Seismic probability factors of steel structures in collision with RC including seismic records for 1.0SD_min

Table 16 Seismic probability factors of RC in collision with steel structures including seismic records for SD of 0.0

Table 17 Seismic probability factors of RC in collision with steel structures including seismic records for 1.0SD_min

4 Conclusions

This study aimed to evaluate the limit state probability of steel structures in collision with RC structures including NF-PL and NF-NP records introduced by FEMA-P695 [53] given SDs of 0.0, 0.5SD_min, and 1.0SD_min. According to developed analytical model, it is possible to perform IDAs for adjacent colliding structures with different fundamental periods (e.g., T_1,1 and T_1,2) assuming the effects of collapsed structure as it happens in real conditions. M-IDA curves and fragilities of selected structures have been determined and PFs have been proposed to estimate limit state probability of considered colliding structures. The results are summarized as follows:

• The findings validate that the S_a (T₁) values for RC structures, across various drift thresholds, including the NF-PL record subset, are lower compared to the NF-NP record subset. Consequently, it is evident that the NF-PL record subset has the potential to heighten the vulnerability of adjacent structures. Similar outcomes were observed for 3-story steel structure, while the S_a (T₁) values of 5-story and 9-story steel structures exhibited distinct trends across different drift thresholds.

• It is evident that structural collisions can exert external forces on the contact level of adjacent structures. These external forces may lead to sudden changes in the moment and rotation curves compared to the isolated condition of the structure. Examination of these external forces for 9-story steel structures colliding with 3-story RC structures, assuming a SD of 0.0, revealed that the maximum moment values of column and beam hinges increased by 37.96% and 13.22%, respectively. Additionally, the maximum rotation values of column and beam hinges increased by 31.25% and 29.62%, respectively.

• The analysis results indicate that structural pounding can affect performance levels. For instance, in 3-story and 5-story steel structures in collision with 5-story RC structures, the TC performance decreased by 4.22% and 4.17%, respectively, while the TC performance improved by 26.14% in 9-story steel structures in the NF-PL record subset under the assumption of 1.0SDmin. Thus, accounting for the effects of collisions on performance levels is deemed necessary.

• To apply the findings of this study, the authors propose seismic PFs to estimate the probability of capacity levels in various performance states such as IO, LS, CP, and TC, assuming 0.0 and 1.0SD_min, including both NF-PL and NF-NP record subsets. These proposed seismic PFs can significantly streamline the analysis process and reduce the modeling efforts required by designers to account for collision phenomena. Furthermore, the authors suggest that these PFs could be widely adopted for retrofitting existing buildings by considering the additional capacity that collisions might provide. In addition, for 0.5SD_min, the PFs can be approximated through linear interpolation.

Although this study tried to include a wide range of results, the findings are applicable for those low- to mid-rise adjacent structures including near-field records that present floor-to-floor collision. For future research, the authors suggested to include far-field records as well as more pounding cases having floor-to-column collision. In addition, it is suggest including different structural plan to see the influence of various floor weight.