On the effectiveness of a rod-like distributed piezoelectric controller in preventing the Hopf bifurcation of the visco-elastic Beck’s beam

Abstract

The linear stability of a piezo-electro-mechanical (PEM) system subject to a follower force is here discussed. The mechanical subsystem is constituted by a linear visco-elastic cantilever beam, loaded by a follower force at the free end. It suffers from the Hopf bifurcation, whose critical load is strongly affected by damping, according to the well-known Ziegler’s paradox. On the other hand, the electrical subsystem consists of a distributed array of piezoelectric patches attached to the beam and connected to a properly designed second-order analog circuit, aiming at possibly enhancing the stability of the PEM system. The partial differential equations of motion of the PEM system are discretized by the Galerkin method. Linear stability analysis is then carried out by numerically solving the associated eigenvalue problem, for different significant values of the electrical parameters. A suitable perturbation method is also adopted to detect the role of the electrical parameters and discuss the effectiveness of the controller.

1 Introduction

The use of piezoelectric materials has experienced a great increase in different fields of engineering applications [1,2,3,4,5,6,7,8,9,10,11]. In particular, several studies have been performed in the structural vibration mitigation context, e.g. [12,13,14,15,16,17,18], where distributed networks of piezoelectric devices have been adopted to propose alternative control approaches.

It has to be observed that most of the distributed piezoelectric-based control approaches have been formulated by enforcing the ‘principle of similarity’ [19,20,21,22,23,24,25,26,27,28,29], which is based on the concept that vibration mitigation can be successfully achieved when the controller resembles the behavior of the primary structure. Of course, this principle descends from more conventional, though successful, control strategies of mechanical nature: the tuned mass damper (TMD) [30,31,32,33,34,35,36,37,38,39,40,41,42,43] and the nonlinear energy sink (NES) [44,45,46,47,48,49,50].

However, while several efforts have been made in the literature to enhance the response of non-autonomous (i.e., externally excited) systems, the vibration control of structures, subject to non-conservative forces (e.g., follower forces) has not been yet extensively addressed. However, it has to be remarked that problems involving follower forces have triggered in the literature a controversial debate [51,52,53]. In particular, several works investigated the existence in the real-world applications of follower actions; some relevant examples in engineering applications can be found: (a) in aerospace [54,55,56]; (b) in vehicle brakes [57, 58], and in flexible pipes conveying a flowing fluid [59,60,61,62,63,64,65,66]. On the other hand, also experimental works have been performed to reproduce follower forces in order to demonstrate their existence and the theoretically derived findings, see e.g. [54, 67, 68]. Therefore, the development of suitable control strategies for this class of systems represents nowadays an interesting and challenging problem.

Another important remarkable aspect is that the above-mentioned mechanical systems, that are representative of real structures, e.g., aircrafts, wings, rocket motors, flexible pipes, suffer from Hopf bifurcation, triggered by follower forces; this bifurcation may occur in the presence of a very well-known and interesting, damping destabilization phenomenon. This is referred in the literature to as the Ziegler’s paradox [69,70,71,72,73,74,75,76,77,78,79], i.e., a detrimental effect of damping that causes a finite reduction of the Hopf critical load of a slightly damped system, with respect to that of the undamped one.

Recently, several studies have been performed on the stability of systems loaded by follower forces with the specific purpose of enhancing the Hopf critical load [29, 80,81,82,83,84,85]. In particular, it was discussed in [29] that similar piezoelectric controllers are actually detrimental in the case of autonomous systems, since the piezoelectric secondary system doubles the pair of the critical eigenvalues (which are on the imaginary axis) and the gyroscopic coupling splits them, generally causing instability. On the other hand, non-similar piezoelectric controllers were studied in [82] in the case of discrete autonomous systems, and it was also shown that they can enhance the linear stability as well as induce positive effects in the post-critical response [83, 84] of the Ziegler’s column [71], also when nonlinear damping is considered [85]. The beneficial/detrimental effects of non-similar piezoelectric controllers on the linear stability of continuous autonomous systems were investigated in [86], by adopting the zero-order network and zero-order dissipation (Z, Z) controller type driven from [28] and in [87] by adopting the second-order network and second-order dissipation (S, S) controller type, which in what follows will be referred to as "rod-like electric controller".

In this work, the linear stability of a piezo-electro-mechanical (PEM) system, constituted by the visco-elastic Beck’s beam [70, 75, 78, 79], i.e., a cantilever beam loaded at its free end by a follower force and here referred to as the primary structure, and by the rod-like controller, i.e., the secondary structure, coupled to the beam via distributed piezoelectric patches, is studied. The beam suffers from the Ziegler’s paradox, but the presence of the controller aims to enhance its stability. In addition to what was analyzed in [87], in this paper the focus is to deeply investigate how the mechanical and electrical eigenvalue spectra interact and, accordingly, how the controller is able to modify the beam response, thus possibly increasing the overall PEM stability. The main objective of this work is thus not actually the real design of the optimal control system, but it is to understand how the electrical parameters affect the PEM system stability. The partial differential equations governing the motion of the PEM system were derived in [87], and here, the associated eigenvalue problem is numerically solved after discretization by the Galerkin weighted residual approach. Moreover, a perturbation approach (first developed in [82]) is here suitably adapted to study the sensitivity of the PEM system to the electrical parameters. Finally, qualitative and quantitative interpretations of the interaction between primary and secondary subsystems are given for some case studies, through a projection of the modes of the coupled system onto the basis of those of the uncoupled one.

The paper is organized as follows. In Sect. 2, the PEM system equations of motion are presented. In Sect. 3, the control strategy is defined, and in Sect. 4 the perturbation approach for the sensitivity analysis of the eigenvalues is briefly recalled. In Sect. 5, preliminary numerical results are presented, while in Sect. 6 an extensive discussion on the PEM system linear stability is performed. In Sect. 7, the concluding remarks are summarized. Finally, two appendices, containing details on the discretization of the equations of motion and on the perturbation approach, respectively, close the paper.

2 The piezo-electro-mechanical model

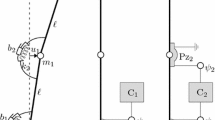
The piezo-electro-mechanical system here analyzed is the same as described in [87], to which the reader is referred to. The mechanical subsystem is a linear visco-elastic Euler–Bernoulli cantilever beam subject to a follower force at its free end. This represents the system that has to be controlled, i.e., its stability has to be enhanced for what concerns the Hopf bifurcation undergoing when the applied load exceeds the critical value. To this end, a piezoelectrical subsystem is coupled to the mechanical one, aiming to subtract and dissipate energy from it. This is possible thanks to the piezoelectric nature of the adopted controller. The schematic of the PEM system is represented in Fig. 1. The beam has length $\ell ,$ cross-section inertia I, and mass per unit-length $\rho$. The material obeys the Kelvin–Voigt visco-elastic law with an elastic modulus E and an internal damping coefficient $\eta$; moreover, external damping, as due to the interaction with the surrounding environment, is also modeled via a distributed layer of transversal external dashpots of viscous constant c.

Fig. 1

Piezoelectric-controlled visco-elastic Beck’s beam

The controller is composed by piezoelectric devices uniformly distributed along the beam, as sketched in Fig. 1. They are shunted to the electrical circuit represented by the light blue E.C. box, whose specific configuration was derived in [28] and adopted in [87] for similar controlling purposes: it is referred to as the rod-like controller, since the spatial derivatives of the damping- and stiffness-like terms in the flux-linkage equation resemble that of the rod, i.e., a linear elastic beam undergoing only axial displacements. According to the definition given in [28], the piezoelectric devices, shunted to the electrical circuit, are idealized as an array of infinite in-parallel RCL elements; in particular, the circuit is characterized by a linear density of piezoelectric capacitance C, of inductance L, and of resistances R, $r_{R}$, while has a piezoelectric coefficient $E_{em}$, that actually provides the coupling between the electrical and mechanical subsystems.

The partial-differential equations of motion, governing the linear dynamics of the PEM system [87], are discretized by a Galerkin approach, and in non-dimensional form, they read (see “Appendix A” for details):

$$\begin{aligned} \begin{aligned}&\mathbf {M}_{m}\ddot{\mathbf {q}}_{m}+\mathbf {B}_{m}\dot{\mathbf {q}}_{m}+\mathbf {K}_{m}\mathbf {q}_{m}+2\mu \mathbf {H}\mathbf {q}_{m}-\gamma \mathbf {G}^{T}\dot{\mathbf {q}}_{e}=\mathbf {0} ,\\&\nu _{e}\mathbf {M}_{e}\ddot{\mathbf {q}}_{e}+\mathbf {B}_{e}\dot{\mathbf {q}}_{e}+\kappa _{e}\mathbf {K}_{e}\mathbf {q}_{e}+\gamma \mathbf {G}\dot{\mathbf {q}}_{m}=\mathbf {0} \end{aligned} \end{aligned}$$

(1)

where the dot denotes differentiation with respect to the non-dimensional time t; $\mathbf {q}_{m},\mathbf {q}_{e}$ are the vectors collecting the modal coordinates of the mechanical and electrical subsystem, respectively; $\mathbf {M}_{\theta }$, $\mathbf {K}_{\theta }$ (with $\theta =m,e$) are the mass and stiffness matrices of the mechanical and electrical subsystem, respectively, $\mathbf {H}$ is the external action matrix, and $\mathbf {G}$ is the matrix associated with the gyroscopic nature of the electro-mechanical coupling. On the other hand, the damping operators are $\mathbf {B}_{\theta }=\alpha _{\theta }\mathbf {K}_{\theta }+\beta _{\theta }\mathbf {M}_{\theta }$ ($\theta =m,e$), where $\alpha _{\theta }$ and $\beta _{\theta }$ ($\theta =m,\,e$) represent the non-dimensional internal and external (mechanical and electrical) damping coefficients, respectively; $\nu _{e}$ and $\kappa _{e}$ are here referred to as the non-dimensional electrical mass and stiffness, respectively. Finally, $\gamma$ is the coupling parameter, and $\mu$ is the magnitude of the non-conservative force. All the coefficients are defined in “Appendix A.”

3 The control strategy

The linear stability of the PEM system is addressed by solving the eigenvalue problem associated with Eq. (1): the eigenvalues are actually a function of the electro-mechanical parameters, i.e., $(\mu ,\alpha _{m},\beta _{m},\gamma ,\nu _{e},\kappa _{e},\beta _{e},\alpha _{e})$, and the aim is to investigate how the capability of the rod-like controller affects the PEM behavior. By letting $\mathbf {q}_{m}=e^{\lambda t}\mathbf {u}_{m}$ and $\mathbf {q}_{e}=e^{\lambda t}\mathbf {u}_{e}$, the following eigenvalue problem associated with Eq. (1) is obtained:

$$\begin{aligned} \begin{aligned}&(\lambda ^2\mathbf {M}_{m}+\lambda \mathbf {B}_{m}+\mathbf {K}_{m}+2\mu \mathbf {H})\mathbf {u}_{m}-\lambda \gamma \mathbf {G}^T\mathbf {u}_{e}=\mathbf {0} ,\\&(\lambda ^2\nu _{e}\mathbf {M}_{e}+\lambda \mathbf {B}_{e}+\kappa _{e}\mathbf {K}_{e})\mathbf {u}_{e}+\lambda \gamma \mathbf {G}\mathbf {u}_{m}=\mathbf {0}. \end{aligned} \end{aligned}$$

(2)

When $\gamma =0$ and the load $\mu$ increases from zero, the uncontrolled system encounters a Hopf bifurcation, i.e., the first eigenvalue, namely the one with the lowest frequency, crosses from the left the imaginary axis of the complex plane, $\omega _d$, $\mu _d$ being the critical frequency and the corresponding critical load, respectively (subscript d means ‘damped’).

When $\gamma$ is larger than zero, a complex (and possibly beneficial in terms of stability) interaction between the mechanical and electrical subsystems occurs. Remarkably, and according to what discussed in [29, 86], the electro-mechanical coupling $\gamma$ is assumed to be small, i.e., $\gamma<<1$, to meet common practical applications requirements. However, as it was shown in [87], to significantly improve the controller performance, $\gamma$ should be the largest possible, within the situation of moderately largely coupled systems. However, when $\gamma$ is sufficiently small, the behavior of the PEM system can be synthesized as follows.

• The uncontrolled beam loses the stability at its critical load $\mu _d$ and thus oscillates at the corresponding frequency $\omega _d$.

• The gyroscopic coupling brings the mechanical response into the controller equation as a forcing term with frequency equal to $\omega _d$: the controller starts oscillating as well.

• Again the gyroscopic coupling returns the controller response back to the beam: its response is then modified.

Therefore, it is important to remark that the magnitude of the electrical response and thus its contribution to the overall stability of the PEM system depends on the coupling and on the electrical parameters. If they are correctly designed, the controller may enhance significantly the beam response. To achieve this goal, it is expected that the energy exchange between mechanical and electrical subsystems is maximized when the electrical frequency is close to $\omega _d$, thus giving rise to a so-called resonant controller, the SRC. However, as discussed in [29, 86], this may not be necessarily the best control approach, in fact non-resonant controllers, SNRC, may be more effective in a wider range of the electric parameter space. In particular, it has been observed in [86] that the best performance is obtained when the controller has small $\nu _e$, $\kappa _e$, and is away from resonance, and, in addition, when the electrical frequency is smaller than $\omega _d$. This aspect has also been confirmed when the controller has not only a single frequency (see [86]), but it becomes a multi (or infinite)-degree of freedom system (see [87]), as in the case at hand, where the controller is characterized by a multi-modal response whose (electrical) undamped natural frequencies are defined, thanks to the rod analogy, as:

$$\begin{aligned} \omega _{e,k}=\frac{\pi }{2}(2k-1)\sqrt{\frac{\kappa _{e}}{\nu _{e}}}\quad \text {with}\quad k=1,2,\dots \end{aligned}$$

(3)

Finally, it is worth noticing that the eigenvalue problem associated with the PDEs (A.1) may be also directly attacked by BVP solvers. However, in this work, a Ritz–Galerkin discretization approach of the equations of motion (A.1) has been preferred since, even if less accurate when compared to former solvers, it allows a more straightforward comprehension of the role played by each mode of the uncoupled subsystems on the whole PEM stability.

4 Sensitivity analysis

To investigate the role of the electrical parameters for both the resonant and non-resonant controllers, a sensitivity analysis based on a perturbation approach is carried out. The procedure is driven from the literature [82] (to which the reader is referred to) and here is briefly recalled (see also “Appendix B” for details).

When $0<\gamma<\!\!< 1$, the eigenvalue governing the PEM system stability can be sought as a perturbation of the critical eigenvalue at the Hopf bifurcation, which, due to the smallness of the coupling, is that of the mechanical subsystem, namely $\lambda _0=i\omega _d$. However, because two different control strategies are adopted, two separate perturbation schemes need to be defined, since for the SNRC the critical eigenvalue is simple, while for the SRC it is defective [82].

4.1 SRC

The small positive scaling parameter $0<\varepsilon \le 1$ (to be reabsorbed at the end of the procedure) is introduced to rescale the electrical parameters as follows: $\gamma \rightarrow \varepsilon \gamma$, $\nu _{e}\rightarrow \varepsilon \nu _{e}$, $\kappa _{e}\rightarrow \varepsilon \kappa _{e}$, $\beta _{e}\rightarrow \varepsilon ^{3/2}\beta _{e}$, and $\alpha _{e}\rightarrow \varepsilon ^{3/2}\alpha _{e}$. It is remarked that, here $\kappa _e$ and $\nu _e$ are fixed to enforce the resonance condition and thus tune a specific controller frequency (remember Eq. (3)) such that $\omega _{e,k}=\omega _d$. Therefore, $\lambda _0=i\omega _d$ is a double (defective) eigenvalue for the uncoupled PEM system. Accordingly, a Newton–Puiseux series is adopted:

$$\begin{aligned} \begin{aligned} \mu&=\mu _{0}+\varepsilon ^{1/2}\mu _{1/2}+\varepsilon \mu _{1}+\mathcal {O}\left( \varepsilon ^{3/2}\right) ,\\ \lambda&=\lambda _{0}+\varepsilon ^{1/2}\lambda _{1/2}+\varepsilon \lambda _{1}+\mathcal {O}\left( \varepsilon ^{3/2}\right) ,\\ \mathbf {u}_m&=\mathbf {u}_{m,0}+\varepsilon ^{1/2}\mathbf {u}_{m,1/2}+\varepsilon \mathbf {u}_{m,1}+\mathcal {O}\left( \varepsilon ^{3/2}\right) ,\\ \mathbf {u_e}&=\mathbf {u}_{e,0}+\varepsilon ^{1/2}\mathbf {u}_{e,1/2}+\varepsilon \mathbf {u}_{e,1}+\mathcal {O}\left( \varepsilon ^{3/2}\right) \end{aligned} \end{aligned}$$

(4)

where $\lambda _k$, $\mathbf {u}_{m,k}$, $\mathbf {u}_{e, k}$ ($k=1/2, 1, 3/2,\dots$) are the eigenvalue sensitivities evaluated at $\mu _0=\mu _d$, i.e., the Hopf critical load of the mechanical subsystem. It is worth noting that not only the eigenpairs, but even the load has been expanded around the critical value of the uncontrolled system. Thus, the value of $\mu$, which renders the controlled system marginally stable, is determined as an expansion from $\mu _0$. It is found that the sensitivity $\lambda _{1/2}$ governs the stability of the PEM system whose expression is derived from the solvability condition enforced at the $\varepsilon$-order problem, and it is the solution of the following second-order algebraic equation:

$$\begin{aligned} \lambda _{1/2}^2+c_1 \lambda _{1/2}+c_0=0 \end{aligned}$$

(5)

where the coefficients $c_0,c_1$ are defined in “Appendix B.” The latter equation admits two distinct roots $\lambda _{1/2}^{\pm }$ = $\lambda _{1/2}^{\pm }\left( \mu _{1/2},\nu _{e},\beta _{e}, \alpha _{e},\gamma \right)$ that do not explicitly depend on $\kappa _e$, since the ratio $\kappa _{e}/\nu _{e}$ has been fixed to enforce the resonance condition.

It is concluded that the PEM system endowed with the SRC controller is asymptotically stable when $\mathrm {Re}\left( \lambda _{1/2}^{\pm }\right) <0$. The boundary of the stability domain is thus defined by $\mathrm {Re}\left( \lambda _{1/2}^{\pm }\right) =0$, which, in a geometrical perspective, is a hyper-surface in the 5-D parameter space $\left( \mu _{1/2},\nu _{e},\beta _{e}, \alpha _{e},\gamma \right)$.

4.2 SNRC

The same rescaling of the electrical parameters of the SRC is taken, except for the electrical damping coefficients, that is: $\beta _{e}\rightarrow \varepsilon \beta _{e}$ and $\alpha _{e}\rightarrow \varepsilon \alpha _{e}$. Since $\lambda _0$ is a simple eigenvalue for the uncoupled PEM system, the following Mc Laurin series expansion is adopted:

$$\begin{aligned} \begin{aligned} \mu&=\mu _{0}+\varepsilon \mu _{1}+\mathcal {O}\left( \varepsilon ^{2}\right) ,\\ \lambda&=\lambda _{0}+\varepsilon \lambda _{1}+\mathcal {O}\left( \varepsilon ^{2}\right) ,\\ \mathbf {u}_{m}&=\mathbf {u}_{m,0}+\varepsilon \mathbf {u}_{m,1}+\mathcal {O}\left( \varepsilon ^{2}\right) ,\\ \mathbf {u}_{e}&=\mathbf {u}_{e,0}+\varepsilon \mathbf {u}_{e,1}+\mathcal {O}\left( \varepsilon ^{2}\right) . \end{aligned} \end{aligned}$$

(6)

Also in this case, the load $\mu$ is expanded around the critical value of the uncontrolled system $\mu _0=\mu _d$, and the value $\mu _1$ represents the sensitivity of the PEM critical load due to the presence of the controller. Under these assumptions, the perturbation algorithm is carried out, and the solvability conditions on the descending $\varepsilon$-order problem furnishes the first eigenvalue sensitivity, namely

$$\begin{aligned} \lambda _{1}=-\frac{\mu _{1}\nu _{e}h_{mm}+\gamma ^{2}\lambda _{0}^{2}g_{mm}\left( \nu _{e},\beta _{e},\alpha _e,\kappa _{e}\right) }{\nu _{e}\left( 2\lambda _{0}m_{mm}+b_{mm}\right) } \end{aligned}$$

(7)

where $g_{mm}\left( \nu _{e},\beta _{e},\alpha _e,\kappa _{e}\right) :=(\mathbf {v}_{m,0}^0)^{H}\mathbf {G}^{T}\mathbf {S}_{e}^{-1}\mathbf {G}\mathbf {u}_{m,0}^0$ and $\mathbf {S}_{e}$, $\mathbf {u}_{m}$, $\mathbf {v}_{m}$, $h_{mm}$, $b_{mm}$, $m_{mm}$ are defined in “Appendix B,” together with some details about the perturbation scheme.

It is concluded that the PEM system endowed with the SNRC controller is thus asymptotically stable when $\mathrm {Re}\left( \lambda _{1}\right) <0$. The boundary of the stability domain is identified by the equation $\mathrm {Re}\left( \lambda _{1}\right) =0$ which, from a geometrical point of view, represents a 6-D hyper-surface depending on the parameters $\left( \mu _{1},\nu _{e},\beta _{e}, \alpha _{e},\kappa _{e},\gamma \right)$.

5 Preliminary analysis on the controller frequency

In this Section, a preliminary sensitivity analysis on the PEM stability, with respect to the non-dimensional electrical stiffness and coupling coefficient $\gamma$ (keeping fixed the other electrical parameters), is carried out with the purpose of exploring the effects of the resulting interaction between the spectra of eigenvalues of the mechanical and electrical subsystems.

The beam parameters, here and in what follows, are taken as $\alpha _{m}=0.01$ and $\beta _{m}=0.1$, which correspond to a situation where the system suffers from a considerable detrimental effect due to the ‘Ziegler paradox’, entailing that damping reduces 30% of the critical load, i.e., $\mu _d = 6.46$ (being 10.02 that of the undamped beam) and $\omega _d = 5.92$.

The eigenvalue problem Eq. (2) is solved by adopting $N_{m}=N_{e}=9$ (see “Appendix A”), and the stability diagrams, namely the diagrams of the region of the parameter-space which characterize the PEM system stability, are obtained. These diagrams are represented in terms of percentage deviation of the load $\mu$ from $\mu _d$, namely $\Delta \mu =100(\mu -\mu _d)/\mu _d$. The eigenvalue problem is solved by varying two selected electrical parameters, namely $\kappa _e\in (0,5]$ and $\Delta \mu \in [-5,30]\%$, and for selected values of $\gamma$, namely $\gamma =0.125, 0.025, 0.05$. In particular, $\kappa _{e}$ is varied across a wide range (i.e., $\kappa _{e}\in [0,5]$) such that resonance can take place across the first nine electrical frequencies, i.e., $\omega _{e,k}=\omega _{d}$ with $k=1\dots ,9$. While the other electrical parameters are fixed at $\nu _e=0.1$, $\alpha _{e}=0$, $\beta _{e}=0.075$.

When $\gamma =0.0125$, it is sufficiently small such that the PEM system can be considered as weakly-coupled.

Fig. 2

Stability diagram of the discretized PEM system in the $\left( \kappa _{e},\Delta \mu \right)$-plane, when $\nu _e=0.1$, $\alpha _{e}=0$, $\beta _{e}=0.075$, $\kappa _{e}\in [0,5],$ and $\gamma =0.0125$. Stable regions are in light blue, denoted by S. Unstable regions are in white, denoted by U. The dashed gray lines indicate the values of $\kappa _{e}$ at which the kth electrical frequency $\omega _{e,k}$ equals $\omega _{d}$ (color figure online)

The results of the sensitivity analysis are illustrated in Fig. 2 where the stable regions of the stability diagram (i.e., all the eigenvalues have negative real part in these regions of the parameter-space) are denoted in blue, and the dashed lines identify the values of $\kappa _e$ that correspond to the resonance condition $\omega _{e,k}=\omega _d$ of the k-th electrical mode. It is observed that, when the first electrical mode is tuned to the beam frequency ($\omega _{e,1}=\omega _d$), the controller has a considerable detrimental effect since the system is stable for negative $\Delta \mu$. On the other hand, when $\kappa _e$ is larger, the controller effect is negligible ($\Delta \mu \simeq 0$), while if $\kappa _e$ is smaller significant stable regions can be detected, i.e., $\Delta \mu >0$, entailing that the controller is beneficial. In particular, the stability diagram exhibits multiple peaks when the resonance condition is attained on higher electrical modes, with the largest increase of critical load when $\omega _{e,2}=\omega _d$. It is then concluded that for small $\gamma$ the best control strategy, except for the resonance on the first electrical mode, corresponds to the SRC approach.

A second analysis is performed by increasing the coupling coefficient $\gamma$, so that the PEM system becomes moderately coupled. Analogously to what was shown before, the results are reported in Fig. 3 for the values of the coefficient: $\gamma =0.025$ in Fig. 3a and $\gamma =0.05$ in Fig. 3b.

Fig. 3

Stability diagrams of the discretized PEM system in the $\left( \kappa _{e},\Delta \mu \right)$-plane, when $\nu _e=0.1$, $\alpha _{e}=0$, $\beta _{e}=0.075$, $\kappa _{e}\in [0,5]$, and: a $\gamma =0.025$; b $\gamma =0.05$. Stable regions in light blue, denoted by S. Unstable regions in white, denoted by U. The dashed gray lines indicate the values of $\kappa _{e}$ at which the kth electrical frequency $\omega _{e,k}$ equals $\omega _{d}$. The ranges of $\kappa _e$ in which stability is governed by the mechanical mode are indicated by the white background, those where stability is governed by the electrical modes are denoted with a light gray background, and those where an interaction between them occurs is highlighted by a dark gray background (color figure online)

Also in this case, the tuning of the first electrical mode to the the beam frequency reveals to have a strong detrimental effect, and analogously if $\kappa _e$ increases, the controller effect becomes negligible. On the other hand, if $\kappa _e$ decreases, again a large stable region at positive $\Delta \mu$ appears showing multiple peaks for specific values of $\kappa _e$. However, it must be noted that, contrarily to the previous case, the largest increments of $\Delta \mu$ are attained when the electrical system is not in resonance with the beam. In particular, when $\gamma =0.025$ (see Fig. 3a), the largest peak is reached when $\kappa _e$ is slightly larger than that corresponding to $\omega _{e,2}=\omega _d$, i.e., in a nearly resonance condition. Whereas, when $\gamma =0.05$ (see Fig. 3b), the largest peak is reached when $\kappa _e$ is considerably far from that corresponding to $\omega _{e,2}=\omega _d$, as well as far from $\omega _{e,1}=\omega _d$: the SNRC strategy is then more effective. In addition, in both cases, the increase of critical load is considerably larger than that obtained at smaller $\gamma$.

By summarizing, the preliminary analysis revealed that when $\gamma$ is small SRC strategy is the best choice for improving the PEM stability, while if $\gamma$ is moderately large, SNRC strategy becomes more effective.

However, it is of interest to further shed light on the complex interaction taking place between the electrical spectrum and the mechanical one, as the controller parameters vary. An attempt to discuss this aspect can be made by carefully analyzing the stability diagrams shown in Fig. 3. Preliminarily, it is remarked that only the first mode of the uncontrolled beam, i.e., that at lowest frequency, participates to the PEM stability, the higher ones being passive, for the considered load values. On the other hand, more than one electrical mode is found to be involved the PEM stability depending on the adopted “tuning,” i.e., on the choice of the electrical stiffness $\kappa _e$: the lower $\kappa _e$, the higher the electrical mode possibly triggering instability. In addition, the stability of the PEM system is strongly affected by the choice of the coupling parameter $\gamma$ (having set $\alpha _e,\,\beta _e$), in particular: when $\gamma$ is small (see Fig. 3a), a weak interaction between the spectra of the uncoupled subsystems manifests itself, and the mode determining the Hopf bifurcation comes from the mechanical one (the background in the Figure is denoted in white); on the other hand, when $\gamma$ is larger (see Fig. 3b), a stronger spectra interaction takes place, since the stability is governed by the mechanical subsystem for large $\kappa _e$ (white background), but as $\kappa _e$ decreases the eigenvalue triggering the PEM instability comes from the electrical subsystem (light gray background). It is worth to note that in some regions (see the dark gray area) an interaction between the mechanical and electrical modes occurs for large $\kappa _e$, as well as for low $\kappa _e$ between electrical modes (not reported as gray scales region in the Figure). An in-depth discussion about this modal interaction will be given in Sect. 6.3.

6 Numerical results

In this Section, further sensitivity analyses are carried out to understand the role played by the electrical damping parameters. The linear stability analysis of the PEM system is here carried out via the previously discussed perturbation approach, whose results are compared with those obtained by the numerical analysis of the eigenvalue problem of the coupled PEM system.

6.1 Effects of the electrical damping

By exploiting the analytical expressions derived in Sect. 4, the sensitivity to the electrical damping is investigated for both the controllers: the SRC (see Sect. 4.1) and the SNRC (see Sect. 4.2). These are endowed with a source of electrical external, as well as internal damping represented by the parameters $\beta _e$ and $\alpha _e$, respectively. The stability diagrams are derived by fixing the electrical stiffness in correspondence of the largest peak appearing in Fig. 2 for the SRC and in Fig. 3a for the SNRC. The results are illustrated in Fig. 4, where the stability boundary is represented by a surface in the ($\beta _e,\alpha _e,\Delta \mu$)-space, the stable region being that below the surface. Moreover, the other electrical parameters are chosen according to the results derived in the previous Section, namely $\nu _e=0.1$ and $\gamma =0.0125$, $\kappa _e=0.157$ for the SRC (Fig. 4a), and $\gamma =0.025$, $\kappa _e=0.177$ for the SNRC (Fig. 4b).

Fig. 4

Stability diagrams of the discretized PEM system in the $\left( \beta _{e},\alpha _{e},\Delta \mu \right)$ space when $\nu _e=0.1$ and: a $\gamma =0.0125$ for the resonant controller tuned on its second mode, namely $\omega _{2,e}=\omega _d$; b $\gamma =0.025$ and $\kappa _e=0.177$ for the non-resonant controller

The obtained behavior is qualitatively similar for both the controllers: the increase of critical load is larger when both $\beta _e,\alpha _e$ are small; in particular, it is observed that the controllers are effective when $\beta _e\ne 0,\alpha _e=0$ or $\beta _e=0,\alpha _e\ne 0$. Thus, to improve the controller performance, the electrical external and internal damping should act separately.

Fig. 5

Stability diagrams of the discretized PEM system endowed with the SRC tuned on its second mode, namely $\omega _{2,e}=\omega _d$, when $\gamma =0.01,0.0125,0.15$, $\nu _e=0.1$, represented: a in the $\left( \Delta \mu ,\beta _{e}\right)$-plane with $\alpha _e=0$; b in the $\left( \Delta \mu ,\alpha _{e}\right)$-plane with $\beta _e=0$. The stable region is on the left of the blue lines for the PEM and on the left of the vertical axis ($\Delta \mu =0$) for the uncontrolled system (color figure online)

Then, slices of the surfaces shown in Fig. 4 are taken at the same $\kappa _e$, $\nu _e$ and slightly different $\gamma$, to further emphasize the effect of the coupling and electrical damping parameters on the PEM stability. Results relevant to the PEM endowed with the SRC are shown in Fig. 5, by taking $\nu _e=0.1$, $\kappa _e=0.157$, $\gamma =0.01,0.0125,0.15$; the stability diagram is represented: in the $\left( \Delta \mu ,\beta _{e}\right)$-plane with $\alpha _e=0$ (see Fig. 5a), and in the $\left( \Delta \mu ,\alpha _{e}\right)$-plane with $\beta _e=0$ (see Fig. 5a). Similarly, the results of the PEM endowed with the SNRC are shown in Fig. 6, by taking $\nu _e=0.1$, $\kappa _e=0.177$, $\gamma =0.02,0.025,0.03$, in the $\left( \Delta \mu ,\beta _{e}\right)$-plane with $\alpha _e=0$ (see Fig. 6a), and in the $\left( \Delta \mu ,\alpha _{e}\right)$-plane with $\beta _e=0$ (see Fig. 6b).

Fig. 6

Stability diagrams of the discretized PEM system endowed with the SNRC, when $\gamma =0.02,0.025,0.03$, $\nu _e=0.1$, $\kappa _e=0.177$, represented: a in the $\left( \Delta \mu ,\beta _{e}\right)$-plane with $\alpha _e=0$; b in the $\left( \Delta \mu ,\alpha _{e}\right)$-plane with $\beta _e=0$. The stable region is on the left of the blue lines for the PEM and on the left of the vertical axis ($\Delta \mu =0$) for the uncontrolled system (color figure online)

In both the cases, the behavior is qualitatively similar: when the electrical damping (analogously for $\beta _e$ and $\alpha _e$) is close to zero, the controller effect is negligible, i.e., the system is stable at $\Delta \mu \simeq 0$, then large stable regions (at the right of the boundary) are obtained until an optimum value is found above which $\Delta \mu$ decreases. Here, the small increase of $\gamma$ (close to the reference value) induces a shift of the stability boundaries toward higher $\Delta \mu$, thus confirming that, in order to improve the control performance, higher electrical coupling coefficients are preferred, but with the caveat that if $\gamma$ is strongly enlarged, the control strategy should change (remember Figs. 2, 3).

Fig. 7

Stability diagrams of the discretized PEM system endowed with the resonant controller tuned on its second mode, namely $\omega _{2,e}=\omega _d$, at $\gamma =0.0125$, represented in the: a $\left( \Delta \mu \,\beta _{e}\right)$-plane; b $\left( \Delta \mu ,\alpha _{e}\right)$-plane. The PEM stable regions are represented by the light blue regions (numerical solution) and by the area on the left of the blue lines (perturbation solution) (color figure online)

6.2 Analytical versus numerical results

Here, stability diagrams obtained via the perturbation approach are compared with those got by numerical analyses, directly carried out on the eigenvalue problem. This analysis aims to check the validity of the asymptotic approach and to confirm the qualitative findings previously discussed.

The first comparison is performed on the SRC ($\omega _{2,e}=\omega _d$). The stability diagrams are determined by taking $\nu _e=0.1$, $\kappa _e=0.157$, $\gamma =0.0125$, and they are shown: in the $\left( \Delta \mu \,\beta _{e}\right)$-plane with $\alpha _e=0$, in Fig. 7a; in the $\left( \Delta \mu ,\alpha _{e}\right)$-plane with $\beta _e=0$, in Fig. 7b. It can be observed that the behavior is qualitatively well captured by the asymptotic approach, though a discrepancy is quantitatively exhibited. This is due to the fact that the range of $\beta _e,\alpha _e$ actually slightly exceeds the parameters scaling grounding the perturbation method, introduced in Sect. 4. The ordering is respected in the insets of Fig. 7 that show a zoom in the region close to the origin: a better agreement is reached when the damping value is below the cusp of the domain, above which the ordering is violated (according to [82]).

Fig. 8

Stability diagrams of the discretized PEM system endowed with the non-resonant controller with $\nu _e=0.1$, $\gamma =0.025$, $\kappa _e=0.177$ represented in the: a $\left( \Delta \mu ,\beta _{e}\right)$-plane with $\alpha _e=0$; b $\left( \Delta \mu ,\alpha _{e}\right)$-plane $\beta _e=0$. The PEM stable regions are represented by the light blue regions (numerical solution) and by the area on the left of the blue lines (perturbation solution) (color figure online)

Fig. 9

Stability diagrams of the discretized PEM system endowed with the non-resonant controller with $\nu _e=0.1$,$\gamma =0.05$, $\kappa _e=0.2$ represented in the: a $\left( \Delta \mu ,\beta _{e}\right)$-plane with $\alpha _e=0$; b $\left( \Delta \mu ,\alpha _{e}\right)$-plane with $\beta _e=0$. The PEM stable region is represented by the light blue regions (numerical solution) and by the area on the left of the blue lines (perturbation solution) (color figure online)

An analogous comparison is performed at larger $\gamma$, thus entailing that the PEM is endowed with the SNRC. The results are illustrated with the same previous logic in Figs. 8 and 9. In Fig. 8, the stability diagrams are determined by taking $\gamma =0.025$, $\nu _e=0.1$, $\kappa _e=0.177$ and are shown: in the $\left( \Delta \mu \,\beta _{e}\right)$-plane with $\alpha _e=0$ (Fig. 8a); in the $\left( \Delta \mu ,\alpha _{e}\right)$-plane with $\beta _e=0$ (Fig. 8b). Contrarily to what was shown for the SRC, when the coupling become stronger, the analytical results are affected by a considerable discrepancy that is clear in terms of $\beta _e$, while is less evident in terms of $\alpha _e$. On the other hand, by evaluating the stability diagrams after a further increasing of gamma, namely $\gamma =0.05$ and by taking $\nu _e=0.1$, $\kappa _e=0.2$, a much more evident loss of accuracy of the perturbation approach is detected (see Fig. 9), but this is not only due to the fact that the electrical parameters are beyond the limit suggested by the ordering. In fact, it is expected that when the PEM is moderately coupled, the system response cannot be assumed as a small perturbation of the response of the beam alone. Thus, again confirming that the stronger the coupling is, the stronger the interaction between the spectra of electrical and mechanical subsystems is, and, accordingly, the instability of the PEM system is triggered by more than one mode (i.e., the first beam mode), and, in particular, that the electrical modes are no more passive.

To better emphasize these aspects, the solution of the discretized PEM system Eq. (1) (according to the adopted Galerkin projection, see Eq. (A.3)) is evaluated on the stability boundary in the correspondence of the black bullets placed in Figs. 8, 9 and denoted with $C_j$ with $j=1,2,3$. Since the results are qualitatively similar, only those relevant to the case of Fig. 9 are here reported. The critical eigenfunctions v(s, t) and $\psi (s,t)$ are rebuilt after numerically solving the eigenvalue problem Eq. (2) for the above-mentioned parameters values. In particular, they are normalized by taking $v(1,t)=1$ and $\psi (1,t)=1$, and their maximum amplitudes in time are represented in Fig. 10, namely $\underset{t}{\max }[v(s,t)]$ in Fig. 10a and $\underset{t}{\max }[\psi (s,t)]$ in Fig. 10b.

Fig. 10

Critical mode shape evaluated on the stability domain boundary when $\nu _{e}=0.1$, $\kappa _{e}=0.2$, $\alpha _{e}=0$, $\gamma =0.05$, and $\beta _{e}=0.03$ at the corresponding critical load denoted by $C_j$ (see the black bullets in Fig. 8c): a $\text {max}[v(s)]$ versus s; b $\text {max}[\psi (s)]$ versus s

It can be observed that the behavior of the mechanical subsystem qualitatively resembles the first mode of the cantilever beam (see Fig. 10a), even though quantitatively the solutions in $C_1,C_3$ are fully overlapped, while $C_2$ is slightly different. On the other hand, the behavior of the electrical subsystem resembles the second electrical mode (according to the choice of the parameters) in all the considered conditions; however, a significant quantitative difference can be observed, suggesting a different role of the electrical mode in the PEM stability.

6.3 Discussion

To further investigate the mechanical/electrical modal interaction on the stability of the PEM system, its eigenvalues are numerically evaluated by solving the eigenvalue problem Eq. (2) over the full range of $\mu \in [0.95,1.3]\mu _d$ and for the same parameters of Fig. 9a. The real and imaginary part of $\lambda$ are reported versus $\mu$ in Fig. 11a, b, respectively. As shown in Fig. 11a, it is clear that there is more than one eigenvalue crossing the horizontal axis, confirming the fact that the PEM instability can be triggered by two modes. The nature of such modes is easily recognized by analyzing the results illustrated in Fig. 11b: the first eigenvalue attaining the instability at a lower critical load (that corresponding to $C_1$) is related to the first beam mode ($\omega _{m,1}\simeq \omega _d$) and is the same determining the stability in $C_2$. On the contrary, the stability in $C_3$ is governed by the second electrical mode $\omega _{e,2}>\omega _d$ (here $\kappa _e=0.2$, remember Fig. 3b).

Fig. 11

Eigenvalues of the PEM system when $\nu _{e}=0.1$, $\kappa _{e}=0.2$, $\alpha _{e}=0$, $\gamma =0.05$, and $\beta _{e}=0.03$: a $\text {Re}(\lambda )$; b $\text {Im}(\lambda )$

A better understanding of these findings merges when a projection of the modes of the coupled system onto the basis of the eigenvectors of the uncoupled one is carried out. Indeed, the solution of Eq. (2) delivers the eigenvalues and the corresponding eigenvectors, namely $\lambda$ and $\mathbf {u}_{m},\mathbf {u}_{e}$, of the coupled PEM system. On the other hand, the eigenvalue problem of the uncoupled mechanical and electrical subsystems ($\gamma =0$) is governed by:

$$\begin{aligned} \begin{aligned}&(\lambda ^2\mathbf {M}_{m}+\lambda \mathbf {B}_{m}+\mathbf {K}_{m}+2\mu \mathbf {H})\mathbf {u}_{m}^0=\mathbf {0} ,\\&(\lambda ^2\nu _{e}\mathbf {M}_{e}+\lambda \mathbf {B}_{e}+\kappa _{e}\mathbf {K}_{e})\mathbf {u}_{e}^0=\mathbf {0} \end{aligned} \end{aligned}$$

(8)

where $\mathbf {u}_{m}^0,\mathbf {u}_{e,}^0$ are the eigenvectors of the uncoupled mechanical and electrical subsystems, respectively. Then, the eigenvectors of the coupled PEM system are written as a linear combination of the eigenvectors of the uncoupled subsystems, namely

$$\begin{aligned} \mathbf {u}_{m}=\sum _{j=1}^{N_m}a_j\mathbf {u}_{m,j}^0 ,\quad \mathbf {u}_{e}=\sum _{j=1}^{N_e}b_j\mathbf {u}_{e,j}^0 \end{aligned}$$

(9)

where $a_j$ and $b_j$ are the (unknown) coefficients of the linear combination.

Projection of the eigenvectors of the coupled PEM system onto the basis of those of the uncoupled subsystems calls for the left eigenvalue problems associated with Eq. (1) with $\gamma =0$, which read:

$$\begin{aligned} \begin{aligned}&(\lambda ^2\mathbf {M}_{m}+\lambda \mathbf {B}_{m}+\mathbf {K}_{m}+2\mu \mathbf {H})^H\mathbf {v}_{m}^0=\mathbf {0} ,\\&(\lambda ^2\nu _{e}\mathbf {M}_{e}+\lambda \mathbf {B}_{e}+\kappa _{e}\mathbf {K}_{e})^H\mathbf {v}_{e}^0=\mathbf {0} \end{aligned} \end{aligned}$$

(10)

where the superscript $()^H$ denotes the conjugate transpose and $\mathbf {v}_{m}^0,\,\mathbf {v}_{e}^0$ are the left eigenvectors of the uncoupled mechanical and electrical subsystems, respectively. Then, by premultiplying both members of Eq. (9) by the k-th corresponding left eigenvector, the projection reads:

$$\begin{aligned} \begin{aligned}&(\mathbf {v}_{m,k}^0)^H\mathbf {u}_{m}=\sum _{j=1}^{N_m}a_j(\mathbf {v}_{m,k}^0)^H\mathbf {u}_{m,j}^0=a_k(\mathbf {v}_{m,k}^0)^H\mathbf {u}_{m,k}^0, \\&(\mathbf {v}_{e,k}^0)^H\mathbf {u}_{e}=\sum _{j=1}^{N_e}b_j(\mathbf {v}_{e,k}^0)^H\mathbf {u}_{e,j}^0=b_k(\mathbf {v}_{e,k}^0)^H\mathbf {u}_{e,k}^0 \end{aligned} \end{aligned}$$

(11)

where use of the orthogonality between the left and the right eigenvectors (the scalar product in the sum is zero when $k\ne j$) has been made; moreover, by adopting the normalization criterion $(\mathbf {v}_{\theta ,k}^0)^H\cdot \mathbf {u}_{\theta ,k}^0=1$ ($\theta =m,e$), the $a_k,b_k$ coefficients can be obtained according to the following expressions:

$$\begin{aligned} a_k=(\mathbf {v}_{m,k}^0)^H\mathbf {u}_{m} ,\quad b_k=(\mathbf {v}_{e,k}^0)^H\mathbf {u}_{e}. \end{aligned}$$

(12)

According to the latter definitions, $a_k$, $b_k$ represent the participation factor of the k-th mode of the uncoupled subsystem to the response of the coupled PEM system.

Fig. 12

Participation factors evaluated on the stability domain boundary when $\nu _{e}=0.1$, $\kappa _{e}=0.2$, $\alpha _{e}=0$, $\gamma =0.05,$ and $\beta _{e}=0.03$ at the corresponding critical load denoted by $C_j$ (see the black bullets in Fig. 9a): a $\text {Re}(a_k)$; b $\text {Im}(a_k)$; c $\text {Re}(b_k)$; d $\text {Im}(b_k)$

The evaluation of the $a_k,b_k$ coefficients is performed on the points of the stability boundary denoted by $C_j$ with $j=1,2,3$ in Fig. 9. Since they are complex-valued coefficients, their real and imaginary parts are separately illustrated, namely $\text {Re}(a_k)$ and $\text {Re}(b_k)$ are shown in Fig. 12a, c, respectively, whereas $\text {Im}(a_k)$ and $\text {Im}(b_k)$ are reported in Fig. 12b, d, respectively. As expected, the larger modal participation factors are obtained on the first beam mode, see Fig. 12a, b, meaning that the mechanical part of the PEM response, $\mathbf {u}_m$, is mostly influenced by the first beam mode, though nonzero components of the second mode are also present. Similarly, it is observed that the electrical part of the PEM system response, $\mathbf {u}_e$, is mostly driven by the second mode of the controller, see Fig. 12c, d, with smaller but not negligible components of the first controller mode. This confirms that the PEM stability cannot only be evaluated as a small perturbation of the first beam mode, since, when $\gamma$ is moderately large, more than one mode may trigger the system instability.

7 Conclusions

The stability of a piezo-electro-mechanical (PEM) system has been investigated in this paper. The system is composed of a mechanical subsystem, i.e., a visco-elastic Beck’s beam, and a piezoelectric subsystem that is a rod-like controller. The beam suffers the detrimental effect of the Ziegler paradox on the Hopf bifurcation, triggered by a follower force; thus, the PEM system behavior has been investigated to evaluate the capability of the controller to improve its stability. The discretized equations of motion have been recalled from the literature, and the eigenvalue problem has been solved numerically as well as via an analytical perturbation approach based on the smallness of the coupling and electrical parameters. The sensitivity of the PEM system to the main electrical parameters has been discussed, and the contribution of the electrical modes to the system stability has been analyzed. The major outcomes are summarized below.

• 1. The most efficient control strategy depends on the magnitude of $\gamma$: if it is small, the SRC is more effective, while when it increases, an SNRC strategy is preferable. However, the larger $\gamma$, the larger is the beneficial effect of the controller in increasing the system Hopf critical load.

• 2. The electrical external and internal damping can be both beneficial, but should act separately to avoid detrimental effects on the stability.

• 3. The perturbation approach gives a good agreement for weakly-coupled systems, while, as it is expected, it loses accuracy when $\gamma$ grows toward moderately coupled systems. In that case only the numerical approach is able to well represent the PEM behavior.

• 4. In moderately coupled PEM systems, the stability is governed by the interaction of multiple modes: the first descends from the mechanical subsystem, while the other derives from the controller.

Further investigations may be performed on other types of controllers, i.e., different analog circuits, to analyze their effect on the system stability. Moreover, another interesting aspect which deserves to be investigated is the nonlinear response of the PEM system in the post-critical regime also in the presence of nonlinear electrical damping.

Appendices

Appendix A: Discretization of the PEM system

The assembly of the cantilever beam and the so-defined rod-like controller constitutes the piezo-electro-mechanical (PEM) system, whose governing equations of motions are derived in [87]. By introducing $\tilde{t}=\omega t$ as the non-dimensional time (with $\omega ^{2}=EI/\rho \ell ^{4}$), $\tilde{s}=s/\ell$ as the non-dimensional abscissa, $\tilde{v}(\tilde{s},\tilde{t})=v/v_{0}$ as the non-dimensional beam displacement, and $\tilde{\psi }(\tilde{s},\tilde{t})=\psi /\psi _{0}$ as the non-dimensional flux-linkage (with $\psi _{0}=v_{0}\sqrt{\rho /C_{0}}$), the non-dimensional form of the PEM equations can be expressed as follows:

$$\begin{aligned}&\ddot{v}+\beta _{m}\dot{v}+\alpha _{m}\dot{v}^{\prime \prime \prime \prime }+v^{\prime \prime \prime \prime }+2\mu v^{\prime \prime }-\gamma \dot{\psi }^{\prime \prime }=0,\end{aligned}$$

(A.1.1)

$$\begin{aligned}&\nu _{e}\ddot{\psi }+\beta _{e}\dot{\psi }-\alpha _{e}\dot{\psi }^{\prime \prime }-\kappa _{e}\psi ^{\prime \prime }+\gamma \dot{v}^{\prime \prime }=0,\end{aligned}$$

(A.1.2)

$$\begin{aligned}&v_{A}=v'_{A}=\psi _{A}=0,\end{aligned}$$

(A.1.3)

$$\begin{aligned}&-v_{B}^{\prime \prime \prime }-\alpha _{m}\dot{v}_{B}^{\prime \prime \prime }+\gamma \dot{\psi }_{B}^{\prime }=0,\end{aligned}$$

(A.1.4)

$$\begin{aligned}&v_{B}^{\prime \prime }+\alpha _{m}\dot{v}_{B}^{\prime \prime }-\gamma \dot{\psi }_{B}=0,\end{aligned}$$

(A.1.5)

$$\begin{aligned}&\kappa _{e}\psi _{B}^{\prime }+\alpha _{e}\dot{\psi }_{B}^{\prime }=0, \end{aligned}$$

(A.1.6)

where the dot denotes differentiation with respect to the non-dimensional time t and the prime with respect to the non-dimensional abscissa s. Accordingly, the non-dimensional parameters governing the PEM behavior are defined as:

$$\begin{aligned}&\beta _{m}=\frac{c}{\rho \omega }, \alpha _{m}=\frac{\eta I}{\rho \omega \ell ^{4}}, \mu =\frac{F\ell ^2}{2EI}, \gamma =\frac{\psi _{0}E_{em}}{v_{0}\rho \omega \ell ^{2}}, \end{aligned}$$

(A.2.1-4)

$$\begin{aligned}&\nu _{e}=\frac{C}{C_{0}}, \kappa _{e}=\frac{1}{LC_{0}\omega ^{2}\ell ^{2}}, \beta _{e}=\frac{1}{RC_{0}\omega }, \alpha _{e}=\frac{1}{r_{R}C_{0}\omega \ell ^{2}}. \end{aligned}$$

(A.2.5-8)

Equations (A.1. 1,2) represent the non-dimensional field equations, while Eqs. (A.1.3) and (A.1. 4–6) represent the corresponding geometrical and mechanical boundary conditions at the ends A and B, respectively.

The PEM equations of motion can be straightforwardly turned into a discretized form, by adopting a classical Galerkin projection approach. The beam transverse displacement v and the flux-linkage $\psi$ are thus expressed according to the following series:

$$\begin{aligned} \begin{aligned}&v(s,t)=\sum _{k=1}^{N_m}\phi _{k}^{(m)}(s)q_{k}^{(m)}(t)=\Phi _m^{T}(s)\,\mathbf {q}_m(t),\\&\psi (s,t)=\sum _{k=1}^{N_e}\phi _{k}^{(e)}(s)q_{k}^{(e)}(t)=\Phi _e^{T}(s)\,\mathbf {q}_e(t), \end{aligned} \end{aligned}$$

(A.3)

where the subscripts m, e denote the terms relative to the mechanical and electrical subsystems, respectively. The variables v and $\psi$ are thus expressed as a linear combination of $N_m$ and $N_e$ terms, respectively, each representing the product of the k-th shape function $\phi _{k}^{(\theta )}(s)$, collected in the vector $\Phi _{\theta }(s)$, and the corresponding time-depending amplitude $q_{k}^{(\theta )}(t)$, collected in the vector $\mathbf {q}_{\theta }(t)$, with $\theta =m,\,e$.

In [87], a variational approach is adopted to the derive the discretized PEM model, and to obtain Eqs. (1), the following operators are defined:

$$\begin{aligned} \begin{aligned}&\mathbf {M}_{m}=\int _{0}^{1}\Phi _m\Phi _m^{T}\mathrm {d}s,&\quad&\mathbf {K}_{m}=\int _{0}^{1}\Phi _m^{''}\Phi _m^{''T}\mathrm {d}s, ,&\quad&\mathbf {H}=\int _{0}^{1}\Phi _m\Phi _m^{''T}\mathrm {d}s, \\&\mathbf {M}_{e}=\int _{0}^{1}\Phi _e\Phi _e^{T}\mathrm {d}s,&\quad&\mathbf {K}_{e}=\int _{0}^{1}\Phi _e^{'}\Phi _e^{'T}\mathrm {d}s,&\quad&\mathbf {G}^{T}=\int _{0}^{1}\Phi _m^{''}\Phi _e^{T}\mathrm {d}s. \end{aligned} \end{aligned}$$

(A.4)

In the latter, the shape functions adopted for v are chosen as the eigenfunctions of an unloaded undamped Euler–Bernoulli beam undergoing flexural motion, while for $\psi$ the analogy with the rod is recalled; consequently, the eigenfunctions of an unloaded undamped rod undergoing axial motion are adopted.

Appendix B: Details on the perturbation sensitivity analysis

Details about the perturbation approach to the eigenvalue sensitivity analysis are given in the following. For the complete formulation of the asymptotic procedure here recalled, the reader is referred to [82]. Besides the different parameters scaling and the variable expansion, the leading-order problem possesses the same structure in both the cases of SRC and SNRC, namely

$$\begin{aligned} \varepsilon ^{0}: \left[ \begin{array}{cc} \mathbf {S}_{m}(\lambda _{0}) &{} \mathbf {0}\\ \frac{\gamma \lambda _{0}}{\nu _{e}}\mathbf {G} &{} \mathbf {S}_{e}(\lambda _{0}) \end{array}\right] \left( \begin{array}{c} \mathbf {u}_{m,0}\\ \mathbf {u}_{e,0} \end{array}\right) =\left( \begin{array}{c} \mathbf {0}\\ \mathbf {0} \end{array}\right) \end{aligned}$$

(B.5)

where

$$\begin{aligned} \mathbf {S}_{m}(\lambda _{0}):= \lambda _{0}^{2}\mathbf {M}_{m}+\lambda _{0}\mathbf {B}_{m}+\mathbf {K}_{m}+2\mu _{0}\mathbf {H} \end{aligned}$$

(B.6)

and:

$$\begin{aligned} \mathbf {S}_{e}(\lambda _{0}):={\left\{ \begin{array}{ll} \lambda _{0}^{2}\mathbf {M}_{e}+\frac{\kappa _{e}}{\nu _{e}}\mathbf {K}_{e} &{} \quad \text { for the } SRC\\ \lambda _{0}^{2}\mathbf {M}_{e}+\lambda _{0}\frac{1}{\nu _{e}}\mathbf {B}_{e}+\frac{\kappa _{e}}{\nu _{e}}\mathbf {K}_{e} &{} \quad \text { for the }SNRC. \end{array}\right. } \end{aligned}$$

(B.7)

When the mechanical and electrical subsystems are uncoupled ($\gamma =0$), system (B.5) admits as right eigenvector $\mathbf {u}_m^0: \mathbf {S}_m \mathbf {u}_m^0=0$ and $\mathbf {u}_e^0: \mathbf {S}_e \mathbf {u}_e^0=0$, respectively. Moreover, they admit as left eigenvectors $\mathbf {v}_m^0: \mathbf {S}_m^H \mathbf {v}_m^0=0$ and $\mathbf {v}_e^0: \mathbf {S}_e^H \mathbf {v}_e^0=0$ (where the superscript $()^H$ denotes the conjugate transpose) that are normalized according to $(\mathbf {v}_m^0)^H\cdot \mathbf {u}_m^0=1$ and $(\mathbf {v}_e^0)^H\cdot \mathbf {u}_e^0=1$. Accordingly, the following coefficients, which are useful for the analysis, can be defined:

$$\begin{aligned} \begin{alignedat}{2}m_{mm}&:=(\mathbf {v}_{m}^0)^{H}\mathbf {M}_{m}\mathbf {u}_{m}^0,&\quad m_{ee}&:=(\mathbf {u}_{e}^0)^{H}\mathbf {M}_{e}\mathbf {u}_{e}^0,\\ b_{mm}&:=(\mathbf {v}_{m}^0)^{H}\mathbf {B}_{m}\mathbf {u}_{m}^0,&\quad b_{ee}&:=(\mathbf {u}_{e}^0)^{H}\mathbf {B}_{e}\mathbf {u}_{e}^0,\\ g_{me}&:=(\mathbf {v}_{m}^0)^{H}\mathbf {G}^{T}\mathbf {u}_{e}^0,&\quad g_{em}&:=(\mathbf {u}_{e}^0)^{H}\mathbf {G}\mathbf {u}_{m}^0,\\ h_{mm}&:=(\mathbf {v}_{m}^0)^{H}\mathbf {H}\mathbf {u}_{m}^0. \end{alignedat} \end{aligned}$$

(B.8)

1.1 $\varvec{SRC}$

For the SRC the leading-order problem is expressed by Eq. (B.5), while the higher-order problems are defined by the following hierarchy:

$$\begin{aligned} \begin{alignedat}{2} \varepsilon ^{1/2}:&\left[ \begin{array}{cc} \mathbf {S}_{m}(\lambda _{0}) &{} \mathbf {0}\\ \frac{\gamma \lambda _{0}}{\nu _{e}}\mathbf {G} &{} \mathbf {S}_{e}(\lambda _{0}) \end{array}\right] \left( \begin{array}{c} \mathbf {u}_{m,1/2}\\ \mathbf {u}_{e,1/2} \end{array}\right) \\&= -\left( \begin{array}{c} \lambda _{1/2}\left( 2\lambda _{0}\mathbf {M}_{m}+\mathbf {B}_{m}\right) \mathbf {u}_{m,0}+\mu _{1/2}\mathbf {H}\mathbf {u}_{m,0}\\ \lambda _{1/2}\left( 2\lambda _{0}\mathbf {M}_{e}\mathbf {u}_{e,0}+\frac{\gamma }{\nu _{e}}\mathbf {G}\mathbf {u}_{m,0}\right) +\frac{1}{\nu _{e}}\lambda _{0}\mathbf {B}_{e}\mathbf {u}_{m,0} \end{array}\right) ,\\ \varepsilon ^{\mathrm {}}:&\left[ \begin{array}{cc} \mathbf {S}_{m}(\lambda _{0}) &{} \mathbf {0}\\ \frac{\gamma \lambda _{0}}{\nu _{e}}\mathbf {G} &{} \mathbf {S}_{e}(\lambda _{0}) \end{array}\right] \left( \begin{array}{c} \mathbf {u}_{m,1}\\ \mathbf {u}_{m,1} \end{array}\right) \\&= -\left( \begin{array}{c} \lambda _{1}\left( 2\lambda _{0}\mathbf {M}_{m}+\mathbf {B}_{m}\right) \mathbf {u}_{m,0}+\lambda _{1/2}^{2}\mathbf {M}_{m}\mathbf {u}_{m,0}\\ \lambda _{1}\left( 2\lambda _{0}\mathbf {M}_{e}\mathbf {u}_{m,0}+\frac{\gamma }{\nu _{e}}\mathbf {G}\mathbf {u}_{m,0}\right) +\lambda _{1/2}^{2}\mathbf {M}_{e}\mathbf {u}_{m,0} \end{array}\right) \\&-\left( \begin{array}{c} -\gamma \lambda _{0}\mathbf {G}^{T}\mathbf {u}_{e,0}+\lambda _{1/2}\left( 2\lambda _{0}\mathbf {M}_{m}+\mathbf {B}_{m}\right) \mathbf {u}_{m,1/2}\\ 2\lambda _{0}\lambda _{1/2}\mathbf {M}_{e}\mathbf {u}_{e,1/2}+\frac{\gamma }{\nu _{e}}\lambda _{1/2}\mathbf {G}\mathbf {u}_{m,1/2} \end{array}\right) \\&-\left( \begin{array}{c} \mu _{1}\mathbf {H}\mathbf {u}_{m,0}+\mu _{1/2}\mathbf {H}\mathbf {u}_{m,1/2}\\ \frac{1}{\nu _{e}}\left( \lambda _{0}\mathbf {B}_{e}\mathbf {u}_{e,1/2}+\lambda _{1/2}\mathbf {B}_{e}\mathbf {u}_{e,0}\right) \end{array}\right) . \end{alignedat} \end{aligned}$$

(B.9)

In the leading-order problem, it is observed that, because of the enforced tuning, $\lambda _{0}$ is a double eigenvalue, since $\mathrm {det}\left[ \mathbf {S}_{m}\right.$ $\left. (\lambda _{0})\right] =\mathrm {det}\left[ \mathbf {S}_{e}(\lambda _{0})\right] =0$; however, just one proper right eigenvector $\left\{ \mathbf {0},\mathbf {u}_{e}^0\right\} ^{T}$ exists, with $\mathbf {u}_{e}^0\mathrm {:}\,\mathbf {S}_{e}\mathbf {u}_{e}^0=\mathbf {0}$, so that $\lambda _{0}$ is defective. Similarly, there is just one proper left eigenvector, $\left\{ \mathbf {v}_{m}^0,\mathbf {0}\right\} ^{T}$. Therefore, the leading-order solution is:

$$\begin{aligned} \left( \begin{array}{c} \mathbf {u}_{m,0}\\ \mathbf {u}_{e,0} \end{array}\right) =\left( \begin{array}{c} \mathbf {0}\\ \mathbf {u}_{e}^0 \end{array}\right) . \end{aligned}$$

(B.10)

By substituting expressions (B.10) into the $\varepsilon ^{1/2}$-order problem, it is found that its solution is

$$\begin{aligned} \left( \begin{array}{c} \mathbf {u}_{m,1/2}\\ \mathbf {u}_{e,1/2} \end{array}\right) =\left( \begin{array}{c} -\frac{1}{\gamma g_{em}}\left( 2\lambda _{1/2}\nu _{e}m_{ee}+b_{ee}\right) \mathbf {u}_{m}^0\\ {\hat{\mathbf{u}}}_{e,1/2} \end{array}\right) \end{aligned}$$

(B.11)

where ${\hat{\mathbf{u}}}_{e,1/2}$ is a particular solution to the singular problem:

$$\begin{aligned} \begin{aligned}\mathbf {S}_{e}(\lambda _{0}){\hat{\mathbf{u}}}_{e,1/2}=&\frac{\lambda _{0}}{g_{em}}\left( 2\lambda _{1/2}m_{ee}+\frac{b_{ee}}{\nu _{e}}\right) \mathbf {G}\mathbf {\mathbf {u}}_{m}^0\\&-\lambda _{0}\left( 2\lambda _{1/2}\mathbf {M}_{e}+\frac{\mathbf {B}_{e}}{\nu _{e}}\right) \mathbf {u}_{e}^0 \end{aligned} \end{aligned}$$

(B.12)

rendered unique by a suitable normalization. It should be remarked that, at this order, $\lambda _{1/2}$ is still undetermined. The solvability condition must instead be invoked at the $\varepsilon$-order problem, which finally determines $\lambda _{1/2}$, according to Eq. (5), where the involved coefficients are defined as:

$$\begin{aligned} \begin{aligned}c_{1}:=&\frac{\mu _{1/2}h_{mm}}{2\lambda _{0}m_{mm}+b_{mm}}+\frac{b_{ee}}{2\nu _{e}m_{ee}},\\ c_{0}:=&\frac{\gamma ^{2}\lambda _{0}g_{em}g_{me}+\mu _{1/2}h_{mm}b_{ee}}{2\nu _{e}m_{ee}\left( 2\lambda _{0}m_{mm}+b_{mm}\right) }. \end{aligned} \end{aligned}$$

(B.13)

1.2 $\varvec{SNRC}$

For the SNRC, the leading-order problem takes again the expression given in Eq. (B.5), while the higher-order problem reads:

$$\begin{aligned} \begin{aligned} \varepsilon ^{1}:&\left[ \begin{array}{cc} \mathbf {S}_{m}(\lambda _{0}) &{} \mathbf {0}\\ \frac{\gamma \lambda _{0}}{\nu _{e}}\mathbf {G} &{} \mathbf {S}_{e}(\lambda _{0}) \end{array}\right] \left( \begin{array}{c} \mathbf {u}_{m,1}\\ \mathbf {u}_{e,1} \end{array}\right) \\&= \left( \begin{array}{c} \gamma \lambda _{0}\mathbf {G}^{T}\mathbf {u}_{e,0}-\lambda _{1}\left( 2\lambda _{0}\mathbf {M}_{m}+\mathbf {B}_{m}\right) \mathbf {u}_{m,0}-\mu _{1}\mathbf {H}\mathbf {u}_{e,0}\\ -\frac{\gamma }{\nu _{e}}\lambda _{1}\mathbf {G}\mathbf {u}_{m,0}-\lambda _{1}\left( 2\lambda _{0}\mathbf {M}_{e}+\frac{\mathbf {B}_{e}}{\nu _{e}}\right) \mathbf {u}_{e,0} \end{array}\right) . \end{aligned} \end{aligned}$$

(B.14)

In this case, $\lambda _{0}$ is a simple eigenvalue, since $\mathrm {det}\left[ \mathbf {S}_{m}\right.$ $\left. (\lambda _{0})\right] =0$ while $\mathrm {det}\left[ \mathbf {S}_{e}(\lambda _{0})\right] \ne 0$; therefore, the leading-order solution reads:

$$\begin{aligned} \left( \begin{array}{c} \mathbf {u}_{m,0}\\ \mathbf {u}_{e,0} \end{array}\right) =\left( \begin{array}{c} \mathbf {u}_{m}^0\\ -\frac{\gamma \lambda _{0}}{\nu _{e}}\mathbf {S}_{e}^{-1}\mathbf {G}\mathbf {u}_{m}^0 \end{array}\right) . \end{aligned}$$

(B.15)

Although the mechanical and electrical responses are of the same order, the electric oscillator behaves as passive, driven by the mechanical one. By substituting expressions (B.15) into the $\varepsilon$-order problem and enforcing its solvability the expression of $\lambda _1$ given in Eq. (7) is obtained.