Blast-Fragmentation Prediction Derived From the Fragment Size-Energy Fan Concept

Abstract

The size-energy fan concept formulation is developed into a prediction model of the fragment size distribution from blast design and rock mass variables. The fragment size is scaled with a characteristic size of the blast and the rock mass discontinuity spacing and orientation. The energy is scaled with the rock strength and the cooperation degree between adjacent holes. A cooperation function is introduced that modifies the energy with the in-row delay, non-dimensionalized with the P-wave velocity and the holes spacing. The cooperation increases as the delay increases up to a certain value, beyond which the cooperation decreases and the fragmentation is coarser. Several prediction models are presented, using the Swebrec-based fan slopes function of the percent passing as starting point, with subsequent improvements involving alternative formulations of that function, that encompass a non-Swebrec underlying distribution of the fragment size. The models include 12 to 14 parameters, controlling the effect on fragmentation of the variables describing the rock mass, the explosive and initiation sequence, and the blast geometry. The parameters are determined from fits to the data base that was used for the xP-frag model, expanded with seventeen additional blasts. All fragmentation data used are mass size distributions determined by sieving and weighing of blasted muckpiles. The different models are introduced sequentially and discussed. The models presented improve the performance of xP-frag, while including a much smaller number of parameters and, unlike xP-frag, keeping the physically sound size-energy fan pattern, effectively extending its nature from a descriptive frame of the fragmentation-energy relations, to a predictive tool.

Highlights

• A new fragmentation prediction model is developed from experimental, sieved data employing the fragment size – energy fan concept.

• The rock mass discontinuities and strength properties are incorporated to the model as modifiers of the fan focal coordinates.

• The cooperation between delayed holes is incorporated to the model as a modifier of the specific energy, a function of the delay.

• A 4-parameter distribution derived from the Swebrec function is introduced, that provides an excellent description of fragment size distributions.

• The accuracy of the predictions from the new model improves the existing state-of-the-art models of fragmentation from blasting.

1 Introduction

In hard rock, blasting is normally the most efficient way to create primary fragmentation. The properties of the more or less damaged fragments of rock and their distributions in size and space determine the efficiency of downstream operations such as digging, loading, hauling, crushing (mines and quarries) and grinding (mines). They also govern their use as e.g., aggregate for concrete or tarmac and in cement (quarries). Billions of tons of ore, waste and aggregate rock are annually excavated worldwide in bench blasts and often further fragmented on-site. The whole comminution chain ‘consumes’ a considerable part of the world’s energy production (Zhang et al. 2022), an amount that we need to rein in.

There is thus a clear incentive to be able to predict blast fragmentation, be it by experience, by compact formulas (equations) or by advanced computer codes (e.g., discrete element methods or combined finite/discrete element methods). Experience is always valuable on the local level but an extrapolation to different conditions is prone to error. Computer codes tend to be specific but far from all respect the laws of physics. They too are error prone because very few of the blast variables (rock conditions, geometry of the drilling and charging, detonation behavior, exact detonation times, etc.) are known with sufficient accuracy. Further, even today the finite element mesh of a blast model seldom provides a resolution beyond two magnitudes of fragment size.

The first international symposium on rock fragmentation by blasting (Holmberg and Rustan 1983) gave a boost to fragmentation equations. Of the many models presented the Kuz-Ram model by Cunningham (1983) became the most widespread one. Like most other models it assumed that the fragment size distribution follows the Rosin–Rammler function (Rosin and Rammler 1933; Weibull 1939, 1951). Cunningham (1983) provided formulas for how the median fragment size ${x}_{50}$ and the curve steepness parameter $n$ depend on the rock conditions, the blast geometry and the explosives used.

As experience with the Kuz-Ram model grew, Cunningham (1987, 2005) and many other people published improvements. An important example is the Crush Zone Model (CZM) (Kanchibotla et al. 1999) in which equations for a crushed zone around the blast hole are introduced to raise the underpredicted amount of fine fragments (‘fines’) to more realistic levels.

Ouchterlony and Sanchidrián (2019) review, in some detail, the development of prediction equations for blast fragmentation in bench blasting. They end up with two models. One is called xP-frag (Sanchidrián and Ouchterlony 2017a, 2017b). It uses dimensional analysis and is based on 169 sets of sieving data from full- and half-scale bench blasts. All model parameters are given explicitly as functions of $P$, the percentage of mass passing a given mesh size. The model is distribution-free, independent of any fragment size distribution function, as no specific distribution is assumed or used. The other recent fragmentation by blasting model is the so-called fragmentation-energy fan (Ouchterlony et al. 2017), to which we will devote some space in Sect. 2.

No model makes an exact prediction. When Sanchidrián and Ouchterlony (2017a) analyze the prediction errors of the Kuz-Ram model for their collected data sets, the interquartile ranges of the relative error of size prediction at different percentage passing are roughly + 50% and − 75%, respectively and for the CZM model surprisingly not much better. For the xP-frag, the interquartile ranges are ± 25%. More exactly, to obtain a total error estimate, the medians of the logarithmic errors of the size calculations at $P$ = 5, 10, …100% for each data set were calculated. The result was that the average median expected error of the size prediction for xP-frag is about 20%, whereas the corresponding number for the Kuz-Ram model and the CZM is about 60%.

Thus, the use of xP-frag instead of the Kuz-Ram or CZM models is for fragmentation predictions normally a considerable improvement. One reason is of course that there is more input data behind this model. A comparison of the variables of the models is made in Table 1.

Table 1 Input variables in fragmentation models for bench blasting

The variables that did not make a significant prediction improvement, or that were not possible to incorporate in the underlying model (non-dimensional parametrization of fragmentation in asteroid collisions, Holsapple and Schmidt 1987; Housen and Holsapple 1990) were left out in the final xP-frag model. One such variable was the detonation velocity (VOD) of the explosive, as it was found that incorporating it into a physically sound non-dimensional group was not straightforward. This has not been further pursued in the last developments of xP-frag (see e.g., Sanchidrián and Ouchterlony 2022; Sanchidrián et al. 2022) and neither is it in this paper. VOD is neither included in the Kuz-Ram system; it is in the CZM, used in the calculation of the detonation pressure for the estimation of the crush zone radius.

The functional dependence of most groups of variables in the xP-frag model are monotonically increasing or decreasing with changes in the underlying variables. The dependence of fragmentation on the initiation delay or on the rock mass jointing is more complex. Fragment size versus delay time in all probability has a minimum. Much effort is spent on this.

The joint orientation index, based in all models on Lilly’s blastability index definitions (Lilly 1986, 1992; Scott 1996), takes on the values 10, 20, 30 and 40 (or 0.25, 0.5, 0.75 and 1.0 in the xP-frag model) depending on relatively diffuse definitions. This means that a wrong choice would cause a distinct jump in the predicted ${x}_{P}$ value. It would seem natural to develop a better description of the influence of the rock mass jointing. A recent paper by Salmi and Sellers (2021) reviews methods to incorporate the geological and geotechnical characteristics of rock masses in blastability assessments for selective blast design, and it shows that this is far from trivial. Such task is under way but, in the present work, the joint orientation factor of xP-frag (Sanchidrián Ouchterlony 2017a, 2017b) is used nearly unchanged.

Of the three models compared in Sanchidrián and Ouchterlony (2017a), xP-frag uses fewer variables to obtain a much smaller median prediction error mainly because is based on a dimensional analysis in which the independent variables only appear once. This leaves xP-frag with the same number of variables as the first Kuz-Ram model, and fewer than those of the revisions of the Kuz-Ram and CZM. The number of parameters (i.e., constant factors) of the models has also grown from a relatively simple original Kuz-Ram model, with 10 constants, to 30 in the last version of Kuz-Ram and 33 in the xP-frag. In the latter, there are nine basic constants, functions of P, and their functional expressions of P need 33 numeric constants. This number in itself and the fact that they are just parameters of the fits of the basic constants with P, without any physical meaning, has been a strong incentive to improve xP-frag and make it a simpler and more transparent model.

The CZM and Kuz-Ram 2005 model developments were based on much fewer rounds and were not as systematic as xP-frag, which was optimized for a basic set of 169 high quality blasts; the model will change when a sufficient number of new blasts have been added to the data base. In this paper we add 17 blasts and extend the model, though this extension is not directly built on the existing xP-frag formulation but on a different paradigm —the fragmentation-energy fan—making the new model a significantly different, improved one from xP-frag.

The fan formulation is, like the xP-frag model, independent of any distribution function, though it was found, during its development and implementation, that a closed analytical form could be written for the fragment size distributions if these were Swebrec (Ouchterlony 2005a, b, 2009). The fan is inherent in the Swebrec function and its compactness makes it a sound feature for deriving a fragmentation model in ways similar to the development of xP-frag, where dimensional analysis was used. A step in this direction has been taken recently by Sanchidrián et al. (2022) and Sanchidrián and Ouchterlony (2022), and that is the starting point of this paper.

2 The Effect of Energy Input on Fragmentation: The Fragment Size-Energy Fan

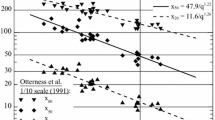
The powder factor or specific charge is the most influential blast design variable and all fragmentation prediction formulae include it as a significant blast descriptor (see e.g., Table 1). The effect of powder factor has been rationalized with the fragmentation-energy fan model (Ouchterlony et al. 2017), which is based on the fact that the percentiles of the size distribution (i.e., the sizes for a given percentage passing) are power functions of the powder factor of varying exponents such that, if plotted in log–log scale, form a set of straight lines that converge on a focal point. Figure 1 shows a conceptual scheme and Fig. 2 shows this pattern with the classical data by Otterness et al. (1991).

Fig. 1

Fragment size-energy fan concept graph. P₁ > P₂ > P₃

Fig. 2

Fan pattern in the Otterness et al. (1991) fragmentation by blasting data. Percentile lines shown are 80, 65, 50, 35 and 20%. The right plot has the axes extended away from the data range in order to show the convergence of the percentile lines in the typical fan shape

The slopes of the lines (i.e., the power exponents) grow monotonically in absolute value from percentile 100 towards the fine material. The fragment size may, therefore, be written as a function of the powder factor q, or the volume specific energy deposited in the rock, E as follows:

$${x}_{P}={x}_{0}{\left(\frac{q}{{q}_{0}}\right)}^{-\alpha (P)}$$

(1)

$${x}_{P}={x}_{0}{\left(\frac{E}{{E}_{0}}\right)}^{-\alpha (P)}$$

(2)

where the subscript P indicates that the size is a P percentile. E = q·e, where q is powder factor (mass of explosive per unit volume of blasted rock) and e is explosive energy (chemical energy per unit explosive mass); (q₀, x₀) or (E₀, x₀) are the focus coordinates in the powder factor or energy-size plane; $\alpha (P)\ge 0$.

This fan equation may be written in a convenient non-dimensional form by dividing the fragment size by a characteristic length of the blast, L_c:

$$\frac{{x}_{P}}{{L}_{c}}={x}_{P}^{\mathrm{^{\prime}}}=\frac{{x}_{0}}{{L}_{c}}{\left(\frac{E}{{E}_{0}}\right)}^{-\alpha (P)}={x}_{0}^{\mathrm{^{\prime}}}{\left(\frac{E}{{E}_{0}}\right)}^{-\alpha (P)}$$

(3)

It has been shown (Ouchterlony et al. 2017; Ouchterlony & Sanchidrián 2018) that when sieved size distributions are of the three-parameter Swebrec function type (Ouchterlony 2005a, b, 2009), i.e., are well-fitted by that function, then the percentile functions of the powder factor have the fan convergence pattern, and the function α(P) is fully determined by the slope exponents at the maximum and median sizes, and the Swebrec shape parameter, b (see Appendix):

$$\alpha \left(P\right)={\alpha }_{100}+({\alpha }_{50}-{\alpha }_{100}){\left(\frac{100}{P}-1\right)}^{1/b}$$

(4)

Size distributions of the underlying Swebrec type can be calculated analytically by solving Eqs. 1 or 2 for P with $\alpha$ determined from Eq. 4. The following $P(x,q)$ explicit form is obtained (see Appendix):

$$P(x,q)=\frac{100}{1+{\left[\frac{\frac{\mathrm{ln}x-\mathrm{ln}{x}_{0}}{\mathrm{ln}{q}_{0}-\mathrm{ln}q}-{\alpha }_{100}}{{\alpha }_{50}-{\alpha }_{100}}\right]}^{b}}$$

(5)

The exponent ${\alpha }_{100}$ expresses the dependence of the maximum size (x₁₀₀ = x_max) on the powder factor. In some cases, this dependence is weak and/or difficult to determine at moderate variations of the powder factor, resulting in ${\alpha }_{100}$ values insignificantly different from zero in the fits. If so Eq. 4 can be simplified to:

$$\alpha \left(P\right)\cong {\alpha }_{50}{\left(\frac{100}{P}-1\right)}^{1/b}$$

(6)

Note that with α₁₀₀ = 0, the higher percentile line (P = 100%) is horizontal, see e.g., Fig. 1, and the focus ordinate is the maximum size either dimensional if Eqs. 1 or 2 are used (${x}_{100}={x}_{max}={x}_{0}$), or non-dimensional if Eq. 3 is used, ${x}_{100}^{\mathrm{^{\prime}}}\equiv {x}_{max}^{\mathrm{^{\prime}}}={x}_{0}^{\mathrm{^{\prime}}}$.

In turn, the focus abscissa E₀ could be interpreted as the smallest specific energy required for fracturing. Besides, it also has an apparent character of strength since it ‘opposes’, in the denominator, the energy concentration of the explosive in the numerator, see Eqs. 2 or 3; note also that the energy concentration E is expressed in terms of energy per unit volume, dimensionally equal to pressure or strength. No relation has yet been established, however, of the actual E₀ value with any strength rating for a particular case. However, we will describe in the next section how the rock strength, and other influencing blasting variables other than the energy input, can be incorporated in the fragment-size energy fan formulation.

3 Fragmentation by Blasting: Influencing Variables Other Than The Energy Input

3.1 The Rock Strength

Let the rock mass strength be $\widetilde{\sigma }$, with which the focus abscissa E₀, being an obviously strength-related variable, should have a monotonically increasing relation. E₀ may also incorporate the power dependence of rock mass strength on size, with which E₀ should have a monotonically decreasing relation (Jaeger and Cook 1969; Hoek and Brown 1980; Scholz 1990) in order to jointly represent data from different blast sizes or, in lab tests, different specimen sizes. We may thus write a combined size and strength variable E₀ as:

$${E}_{0}={E}_{0}^{*} {\widetilde{\sigma }}^{\beta } {L}_{c}^{-\lambda }$$

(7)

where ${E}_{0}^{*}$ is the new focus abscissa that contains any relevant constant, reference size or strength; it has convenient dimensions so that the second member has the same dimensions as E₀, i.e., energy per unit volume; $\beta$ and $\lambda$ must be positive or zero. L_c, the general characteristic length for scaling the fragment sizes, see Eq. 3, is also used in Eq. 7 for the purpose of size-scaling the rock strength. The fan equation (Eq. 3) becomes:

$${x}_{P}^{\mathrm{^{\prime}}}={x}_{0}^{\mathrm{^{\prime}}}{\left[\frac{E {L}_{c}^{\lambda }}{{E}_{0}^{*} {\widetilde{\sigma }}^{\beta }}\right]}^{-\alpha (P)}$$

(8)

The size scaling of strength has also been used with success when incorporating the strength-size dependence in drop-weight test fragmentation (Ouchterlony and Sanchidrián 2018). In DWT testing the specimen size usually covers a broad range of values. However, size scaling does not necessarily contribute to a better representation of fragmentation by the fan formulation for blasting when the characteristic size (e.g., burden, spacing, bench height, etc.) does not show a significant variation in a data set (see e.g., Sanchidrián et al. 2022).

Equation 8 has a clear similarity with the energy-strength term of the non-dimensional analysis by Sanchidrián and Ouchterlony (2017a), based on work by Holsapple and Schmidt (1987) and Housen and Holsapple (1990) on fragmentation in high energy impact asteroid collisions, that led to the xP-frag model. The basic formulation in that case—a simplification of the asteroid work—was:

$$\frac{{x}_{P}}{{L}_{c}}=k{k}_{2}^{h}{\left(\frac{E {L}_{c}^{\lambda }}{\widetilde{\sigma }}\right)}^{-\alpha }$$

(9)

where the parameters k, h, $\lambda$ and $\alpha$ are functions of P; k₂ is a shape factor of the blast, equal to 1 for a cubic blast (B = S = H, B burden, S spacing and H bench height), decreasing as H and S are greater than B. The notation in Eq. 9 is otherwise the same as used here, see Eqs. 1–8. As characteristic length for strength scaling, the same general length L_c is used. Note, however, that Eq. 9 does not result in a fan scheme as it has no focal point since the leading factor $k{k}_{2}^{h}$ is P-dependent and so is $\lambda$.

3.2 The Rock Mass Structure

Going back to the focus ordinate ${x}_{0}^{\mathrm{^{\prime}}}$, the case of α₁₀₀ = 0 mentioned in Sect. 1, where ${x}_{100}\equiv {x}_{max}={x}_{0}$, offers an intuitive interpretation of x₀ as the maximum fragment size inherent to the rock which, for a jointed rock mass, is somewhat connected to the in-situ block size distribution of the rock mass, or the joint spacing. Using this interpretation of ${x}_{0}$, we could write a variable maximum size dependent on the joint spacing and orientation considering that such a maximum size should be a monotonic function of the joint spacing and the joint orientation factor, the latter as defined e.g., by Lilly (1986, 1992) and Scott (1996), and used in the Kuz-Ram and xP-frag models such that it grows as fragmentation becomes more difficult:

$${x}_{0}^{\mathrm{^{\prime}}}={x}_{0}^{*} {J}_{S}^{\xi } {J}_{O}^{\omega }$$

(10)

where ${x}_{0}^{*}$ is the new focus ordinate; J_S is the joint spacing factor and J_O the joint orientation factor; $\xi$ and $\omega$ are non-negative constant parameters. In general, J_S could be equal to the joint spacing S_J; for the case of a homogeneous, non-jointed rock mass, or one in which the discontinuity spacing is greater than the blast pattern, the joint spacing factor should be capped at some blast pattern length (for example, the burden) as the latter in fact constitutes an artificial discontinuity spacing, e.g., ${J}_{S}=\mathrm{min}({S}_{J},B)$.

Substituting in Eq. 8:

$${x}_{P}^{\mathrm{^{\prime}}}={x}_{0}^{*} {J}_{S}^{\xi } {J}_{O}^{\omega }{\left[\frac{E {L}_{c}^{\lambda }}{{E}_{0}^{*} {\widetilde{\sigma }}^{\beta }}\right]}^{-\alpha (P)}$$

(11)

Or, in a more fan-like form:

$$\frac{{x}_{P}^{\mathrm{^{\prime}}}}{{J}_{S}^{\xi } {J}_{O}^{\omega }}={x}_{0}^{*}{\left[\frac{E {L}_{c}^{\lambda }/{\widetilde{\sigma }}^{\beta }}{{E}_{0}^{*} }\right]}^{-\alpha (P)}$$

(12)

where the fan axes are not anymore specific energy and size (or non-dimensional size) but some scaled magnitudes, $E{L}_{c}^{\lambda }/{\widetilde{\sigma }}^{\beta }$ and ${x}_{P}^{\mathrm{^{\prime}}}/({J}_{S}^{\xi } {J}_{O}^{\omega })$, respectively.

3.3 The Delay

Besides the rock mass structural characteristics, a significant variable that affects fragmentation is the delay between consecutively fired holes. The detonation time of the next hole counted from the current detonating hole influences the interaction of the shock waves, the state of stress and the preconditioning of the rock in which the ensuing hole detonates. This interaction has been classically called cooperation between holes, and current fragmentation prediction formulae such as Kuz-Ram (Cunningham 2005, inspired in results by Bergmann et al. 1974) or xP-frag (Sanchidrián and Ouchterlony 2017a) include delay as a variable such that an optimum (finest) fragmentation is obtained at a certain, non-zero delay; both models include factors in the fragment size expression of the form:

$${x}_{P}={\left({x}_{P}\right)}_{0}{f}_{t}\left({\Pi }_{t}\right)$$

(13)

where ${\left({x}_{P}\right)}_{0}$ is the P-percentile (P = 50 only for Kuz-Ram) fragment size at zero delay and ${f}_{t}\left({\Pi }_{t}\right)$ is the delay correction factor, a function of a non-dimensional group ${\Pi }_{t}$ that contains the delay. ${f}_{t}$ is such that, for both models mentioned above, fragment sizes decrease from zero delay time (simultaneous initiation of holes or an instantaneous blast) up to an optimum delay at which the fragment size is minimal. Longer delays reduce the cooperation and increase the fragment size, see Fig. 3.

Fig. 3

Delay correction factors. Left: Kuz-Ram; right: xP-frag

The existing delay corrections are functions of a non-dimensional delay factor ${\Pi }_{t}$ that depends on the P-wave velocity and a characteristic length, the burden in Kuz-Ram and the spacing in xP-frag. For the Kuz-Ram (Fig. 3 left), in a rewritten form from Cunningham (2005):

$$f_{t} \left( {\Pi_{t} } \right) = 0.000174\Pi_{t}^{3} {-}0.000534\Pi_{t}^{2} {-}{ }0.1013\Pi_{t} { } + { }2.05{ };{ }\Pi_{t} \le 15.6$$

(14a)

$$f_{t} \left( {\Pi_{t} } \right) = 0.0064\Pi_{t} + { }0.9{ };{ }\Pi_{t} > 15.6,$$

(14b)

where ${\Pi }_{t}={c}_{P}\Delta t/B$, c_P being the P-wave velocity and $\Delta t$ the in-row delay. For the xP-frag (Fig. 3 right), from Sanchidrián & Ouchterlony (2017a):

$${f}_{t}\left({\Pi }_{t}\right)={\delta }_{1}+(1-{\delta }_{1}-{\delta }_{2}{\Pi }_{t}){e}^{-{\delta }_{3}{\Pi }_{t}}$$

(15)

where δ₁, δ₂, δ₃ are functions of the percentage passing $P$ (similar to the parameters k, h, $\lambda$ and $\alpha$ in Eq. 9, see Eqs. 51 and 52 in Table 8 of Sanchidrián and Ouchterlony 2017a);${\Pi }_{t}={c}_{P}\Delta t/S$, S being the hole spacing.

Both delay corrections predict that fragment sizes may be reduced significantly (approximately halved) if a certain (optimum) delay is used instead of a simultaneous initiation or a blast with very long delays. Different optimum delays follow from the two models though: the optimum non-dimensional delay (B-based) from the Kuz-Ram model is ${\Pi }_{t,B}$=${c}_{P}\Delta t/B=$ 15.6 that corresponds to a xP-frag delay (S-based) ${\Pi }_{t,S}={c}_{P}\Delta t/S={\Pi }_{t,B}/(S/B)=15.6/1.46=10.7$, where 1.46 is the mean S/B ratio of the blast data used. The optimum delay for xP-frag is in the range of 35–40 (variable with the percentile) which means that xP-frag favors a much slower initiation sequence than Kuz-Ram.

The inclusion of the delay effect in the fragmentation–energy fan was tested for the first time in a set of full-scale blasts in a quarry where fragmentation of the muckpile was measured by sieving (Sanchidrián et al. 2022). To incorporate the delay into the fragment size–energy fan formulation, the delay effect may be regarded as a modifier of the energy available for fragmentation from a single hole such that the cooperation between holes could be thought of as an increased effective energy; a cooperation function of the delay ${f}_{C\Delta }$, affecting the energy in Eq. 3, or any of its derived expressions, should increase up to an optimum and then decrease when cooperation no longer takes place efficiently, at a delay beyond optimum; inserting in Eq. 12 the cooperation function:

$$\frac{{x}_{P}^{\mathrm{^{\prime}}}}{{J}_{S}^{\xi } {J}_{O}^{\omega }}={x}_{0}^{*}{\left[\frac{E {f}_{C\Delta } {L}_{c}^{\lambda }/{\widetilde{\sigma }}^{\beta }}{{E}_{0}^{*} }\right]}^{-\alpha (P)}$$

(16)

A possible form for the cooperation function could be the reciprocal of the delay correction factor of the x_P-frag model, Eq. 15:

$${f}_{C\Delta }={\left[{\delta }_{1}+(1-{\delta }_{1}-{\delta }_{2}{\Pi }_{t}){e}^{-{\delta }_{3}{\Pi }_{t}}\right]}^{-1}$$

(17)

with ${\delta }_{1}$, ${\delta }_{2}$ and ${\delta }_{3}$, contrary to Eq. 15, not P-dependent; nothing inside the brackets in Eq. 16 depends on P. The function in Eq. 17 grows to a maximum cooperation at Π_t = 1/δ₂ + 1/δ₃–δ₁/δ₂ and then decreases towards an asymptotic value 1/δ₁ for long delays. The resulting delay correction factor, ${f}_{t}\left({\Pi }_{t}\right)$, is different for the different percentiles, as predicted in the xP-frag model; from Eq. 17:

$${f}_{t}\left({\Pi }_{t}\right)={f}_{C\Delta }^{-\alpha (P)}={\left[{\delta }_{1}+(1-{\delta }_{1}-{\delta }_{2}{\Pi }_{t}){e}^{-{\delta }_{3}{\Pi }_{t}}\right]}^{\alpha (P)}$$

(18)

Reverting to the initial simple fan formulation, Eqs. 2 or 3, we can write Eq. 16 as:

$${x}_{P}^{*}={x}_{0}^{*}{\left[\frac{{E}^{*}}{{E}_{0}^{*} }\right]}^{-\alpha (P)},$$

(19a)

with

$${x}_{P}^{*}=\frac{{x}_{P}/{L}_{c}}{{J}_{S}^{\xi } {J}_{O}^{\omega }}$$

(19b)

and

$${E}^{*}=E {f}_{C\Delta } {L}_{c}^{\lambda }/{\widetilde{\sigma }}^{\beta }$$

(19c)

4 Adjusting the Model with Fragmentation by Blasting Data

The xP-frag size calculation equation (Sanchidrián & Ouchterlony 2017a) was fitted to a data base of 169 bench blasts, all of them carried out in the field (i.e., no laboratory testing results were used), for which detailed blast design data and fragmentation from blasting existed; they were measured in very different environments, rock types, blast sizes, delays, etc. In all of them, fragmentation was measured by sieving of the muckpile. Tables 1 to 5 in Sanchidrián and Ouchterlony (2017a) give the references of the data and an overview of the rock and blast design variables of the blasts used there. The same data are used in this work. To that body of data, seventeen new sets have been added, with fragment size distributions derived from screened muckpile material data lately made available by Segarra et al. (2018) and Sanchidrián et al. (2022). With that, the data base now comprises 186 blasts. Table 2 gives the relevant properties of the new data.

Table 2 Blast and fragmentation data

Table 3 Parameters of the models and goodness-of-fit indicators

Equation 16, with ${f}_{C\Delta }$ from Eq. 17 and $\alpha (P)$ from Eq. 4, was fitted to the xP-frag extended body of data. The fit is carried out in log form so the function fitted is:

$$\mathrm{log}\frac{{x}_{P}}{{L}_{c}}=\xi \mathrm{log}{J}_{S}+\omega \mathrm{log}{J}_{O}+\mathrm{log}{x}_{0}^{*}-\alpha \left(P\right)\left[\mathrm{log}E+\mathrm{log}{f}_{C\Delta }\left({\delta }_{1},{\delta }_{2},{\delta }_{3},{\Pi }_{t}\right)+\lambda \mathrm{log}{L}_{c}-\beta \mathrm{log}\widetilde{\sigma }-\mathrm{log}{E}_{0}^{*}\right]$$

(20)

The variables have been chosen to be nearly the same as in xP-frag:

• ${J}_{S}$ is the joint spacing factor, equal to the mean joint spacing (m), capped at the burden value for homogeneous rock mass or very wide spacing, ${J}_{S}=\mathrm{min}({S}_{J},B)$.

• ${J}_{O}$ is Lilly’s (Lilly 1986, 1992; Scott 1996) joint orientation factor: 10 for sub-horizontal joints, 20 for joints of similar strike as the bench face, dipping out of the face, 30 for sub-vertical joints striking at large angle from the face and 40 for joints of similar strike as the bench face, dipping into the face.

• $E=qe$ (MPa) is the product of the explosive unit energy e (MJ/kg) times the powder factor q (kg/m³). x_P-frag uses total powder factor; however, in our fitting tests the powder factor above grade (meaning that the powder factor is calculated considering only the explosive inside the nominal breakage volume i.e., only the explosive above grade and not the explosive in the subdrill) gives slightly better fits. Cunningham (1983, 1987) already recognized that the powder factor above grade has a stronger relation with fragmentation than the total powder factor, as the explosive in the subdrill contributes less to the overall fragmentation, especially as the subdrill goes deeper.

• ${\Pi }_{t}={c}_{P}\Delta t/S$, where ${c}_{P}$ is P-wave velocity, $\Delta t$ in-row delay and S hole spacing. Any consistent units may be used so that ${\Pi }_{t}$ is non-dimensional.

• ${L}_{c}=\sqrt{HS}$ (m).

• $\widetilde{\sigma }={\sigma }_{C}^{2}/(2Y)$ (MPa), ${\sigma }_{c}$ being uniaxial compressive strength and Y Young’s modulus.

The parameters of the fit are 12: $\xi$, $\omega$, ${x}_{0}^{*}$, ${E}_{0}^{*}$, ${\delta }_{1},{\delta }_{2},{\delta }_{3}$, $\lambda$, $\beta$, ${\alpha }_{100}$, ${\alpha }_{50}$ and $b$.

The fragment sizes (percentiles ${x}_{P}$) for the fits are calculated by log–log linear interpolation of the size distributions. For those data sets in which the passing data range did not include the upper or lower percentiles, extrapolation was performed; in this case, the extrapolated points were penalized by a weight function increasing with the extrapolation ratio (i.e., the ratio of the extrapolated P over the closer data P_f); for example, if the lower size data of a fragment size distribution is at P_f = 20%, then the value extrapolated at P = 10% (extrapolation ratio = 2) has a weight 0.607 and the value at P = 5% (extrapolation ratio = 4) has a weight 10^–6 (Sanchidrián & Ouchterlony 2017a).

The percentage passing range used was 100 to 3%. In the fines end, the lower the minimum percentile used, the more points are censored by nearly zero weights due to extrapolation. About one-third of the x_P data at P = 3% have extrapolation weights less than 0.1 (extrapolation ratios greater than 2.66) so we set a lower limit for our fits at 3%. Besides the range of the sieved fragmentation data available, the use of the fragment size-energy fan formulation with a function for the exponents such as Eq. 4 cautions us not to go much below 5% passing, as this is the minimum passing that can be usually represented with limited errors by the Swebrec distribution (Sanchidrián 2015).

5 Results and Discussion

The fit of Eq. 20, with Eqs. 17 and 4 (here called model par-12, as 12 is the number of fitting parameters) was programmed in a MATLAB (Matlab 2021) environment using the function ‘nlinfit’. The goodness of the fit is measured by the determination coefficient (R²), the relative root mean squared error (RRMSE) and the median absolute relative error (MARE_y):

$$RRMSE=\frac{RMSE}{\left|\overline{y }\right|};RMSE=\sqrt{MSE};MSE=\frac{1}{n-p}\sum_{i=1}^{n}{\left({y}_{i}-{y}_{i}^{*}\right)}^{2}$$

(21)

$${MARE}_{y}=\mathrm{median}\left|\frac{{y}_{i}^{*}-{y}_{i}}{{y}_{i}}\right|$$

(22)

Here, ${y}_{i}=\mathrm{log}\left({x}_{Pi}/{L}_{ci}\right)$ are data, ${y}_{i}^{*}$ are predicted values and $\overline{y }$ is the mean of ${y}_{i}$; n is the number of cases (number of blasts times number of percentiles) and p the number of parameters of the fit.

The result of the 12-parameter fit is quite good in terms of determination coefficient and errors, see Table 3. The parameters of the model are also given in Table 3. All p-values for the parameters are < 0.05. Figure 4 shows the PDF-normalized histogram of the residuals, that has a normal distribution with near zero mean (3e-4), and the data vs. predicted plot, showing an unbiased fit with slope close to one and near-zero intercept.

Fig. 4

Left: PDF-normalized histogram of residuals. The red curve shows the normal distribution fit to the histogram. Right: data vs. predicted plot

The above goodness of the fit metrics refer to the straight data and predictions of the fit, made in log form. Hence, values of 11.8% or 8.0% for the relative root mean squared and the median absolute relative errors calculated on the fit variable $y=\mathrm{log}\left({x}_{P}/{L}_{c}\right)$ do not translate directly to an accuracy of the fit in absolute terms. This can be better illustrated by the relative error of the size prediction:

$${RE}_{{x}_{P}}=\frac{\left({x}_{Pi}^{*}-{x}_{Pi}\right)}{{x}_{Pi}}$$

(23)

The overall median absolute relative error of predicted sizes is ${MARE}_{{x}_{P}}=\mathrm{median}\left|{RE}_{{x}_{P}}\right|$ = 0.1855, see Table 3. This statistic can also be calculated for each blast, ${({\mathrm{MARE}}_{{x}_{P}})}_{blast}$, the median and extreme values are also given in Table 3.

Figures 5 shows the fragmentation-energy fan. The scaled percentile sizes and the scaled energies tend to collapse on straight lines that converge on a focus of coordinates (9.4e-7, 3434). This plot is in itself the fragmentation model, a kind of universal fragmentation chart, in which once the abscissa $E {f}_{C\Delta } {L}_{c}^{\lambda }/{\tilde{\sigma }}^{\beta }$ is evaluated, the scaled fragment size for a given percentage passing, $\left({x}_{P}/{L}_{c}\right)/\left({S}_{J}^{\xi } {J}_{o}^{\omega }\right)$, can be read in the ordinate of the corresponding ray, and the size ${x}_{P}$ derived from it. Doing this with different rays, the whole size distribution can be built. Of course, this can be done more conveniently with Eqs. 19 or 20. Note that the equivalent to Eq. 5 with scaled variables (see Appendix, Eq. A10), is actually a universal size distribution in the classical P(x) form.

Fig. 5

Fragmentation-energy fan for the par-12 model. In the right-hand plot, the rays have been extended to better show the convergent pattern. Shown percentiles are 90, 70, 50, 30 and 10

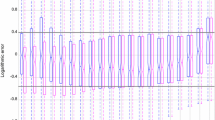
The relative error is assessed as function of the percent passing in the form of boxplots in Fig. 6. The blue band is the interquartile range. It indicates the range of errors expected half of the times at that passing; the tiny red dashes within the blue boxes are the median; the dashed lines (‘whiskers’) extend out to a 99% coverage and the red crosses are outliers. The overall performance is relatively good in a broad range (30–96% passing approximately), with errors less than ± 25%, and even lower in most of that range, increasing towards both ends, where negative-biased errors in the fine end exceed in the first quartile (lower end of the blue bars) -50% for P = 3%, and positive in the coarse end, close to 100% in the third quartile for P = 100%.

Fig. 6

Relative error as function of the percentage passing for the par-12 model. The blue bars are the interquartile range and the whiskers extend to a 99% coverage; points outside are plotted as red plus signs (crosses)

Although Fig. 4 shows that the fit is carried out properly and is statistically sound, with residuals normally distributed with zero mean, a remarkable feature of Fig. 6 is that the error is not zero-centered when plotted P-wise even in the central zone; instead the errors have a negative bias (predicted size smaller than the data) in the fines, shifting to positive from P = 6% up to P = 38%, then negative again up to P = 97%, and back to positive in the upper end. The reason for this behavior could be the shape of the underlying Swebrec distribution, linked to this model through the $\alpha (P)$ function, Eq. 4. A variant of this equation that would give some additional flexibility to the model, incorporating one more parameter, is the following:

$$\alpha \left(P\right)={\alpha }_{100}+({\alpha }_{{P}^{*}}-{\alpha }_{100}){\left[{\left(\frac{100}{P}\right)}^{\mu }-1\right]}^{1/b}$$

(24)

The new fitting parameter $\mu$ should in principle be positive; see Appendix for a discussion on this. Note that the second $\alpha$ parameter–previously denoted ${\alpha }_{50}$, now ${\alpha }_{{P}^{*}}$–is not any more the slope of the P = 50% line of the fan plot, but the slope of the line ${P}^{*}=100/{2}^{1/\mu }$ %.

The goodness-of-the-fit values of this 13-parameter model (par-13) are given in Table 3. They are better than the previous 12-parameter fit, as should be expected from the addition of one parameter. More relevant, however, is that the relative error vs. percent passing plot has a much better centered error band, see Fig. 7, even if the overall median absolute relative error ${MARE}_{{x}_{P}}$ is only a little smaller than the previous fit, see Table 3.

Fig. 7

Relative error as function of the percentage passing for the par-13 model. See the caption of Fig. 6

The fit in the fines region has a similar error, but better centered, and so is the error in the coarser end; especially the prediction of x_max has really improved, with an interquartile range of the error now confined to ± 25%, while the third quartile was close to 100% with par-12. The maximum and minimum median errors are 0.1105 at P = 7% and − 0.0569 at P = 100%, with a difference of 0.1674 and overall median 0.0017. The parameters of the model are given in Table 3; all p-values are < 0.05.

Note that b is very different from the par-12 b-value, as the defining equation is not anymore Eq. 4, but Eq. 24. The use of the latter for the $\alpha \left(P\right)$ function means that the underlying distributions are not anymore of Swebrec type but a modification of it with four parameters, see Appendix Eq. A17. The corresponding universal size distribution expression is Eq. A18. The size-energy plot is shown in Fig. 8.

Fig. 8

Fragmentation-energy fan for the par-13 model. See the caption of Fig. 5

The $\alpha \left(P\right)$ function, that represents the dependence of fragmentation on energy, is universal, which further means that the exponent of the functions ${q}^{\alpha }$ or ${E}^{\alpha }$ are the same, for a given percentage passing, in every blasting case. There are cases in which an energy dependence for the $\alpha \left(P\right)$ functions has been chosen, e.g., those where a wide range of energy values is covered. That is the case of fragmentation from breakage tests (Ouchterlony and Sanchidrián 2018; Ouchterlony et al. 2021); step functions of $\alpha \left(P\right)$ were used with two values for each percentage passing, one for low energy and another one for high energy, the transition energy determined from the fit. This could also be the case here, see Figs. 5 and 8, where the scaled energy varies nearly three orders of magnitude. Such a variable behavior, though in a continuous form, could be introduced simply by allowing the exponent b in Eq. 24 to vary with the scaled energy, for example:

$$b={b}_{0}{\left({E}^{*}/{E}_{0}^{*}\right)}^{\zeta }$$

(25)

${E}^{*}$ being scaled energy, as defined in Eq. 19c. Thus the expression for $\alpha$ becomes:

$$\alpha \left(P\right)={\alpha }_{100}+({\alpha }_{2}-{\alpha }_{100}){\left[{\left(\frac{100}{P}\right)}^{\mu }-1\right]}^{1/\left[{b}_{0}{\left({E}^{*}/{E}_{0}^{*}\right)}^{\zeta }\right]}$$

(26)

The dependence of b on the scaled energy makes this parameter–hence the slopes $\alpha \left(P\right)$–dependent on the powder factor, the degree of cooperation between holes and the rock strength, including its size dependence. This removes its universal, constant value, which is an important characteristic of the fan model as formulated with $\alpha \left(P\right)$ from Eq. 4, or its variant Eq. 24.

In practice, the 14-parameter model (par-14), at the cost of one more parameter, gives marginally better determination coefficient and errors, see Table 3. The parameters of the fit are given in Table 3. The error as function of P is plotted in Fig. 9, very similar to Fig. 7. The maximum positive and negative medians of the errors at each passing are 0.1049 at P = 6% and –0.0496 at P = 98% with a difference of 0.1545, so the undulation is just slightly less than for par-13. The overall median is 0.0055. In a blast per blast basis, the ${MARE}_{{x}_{P}}$ ranges from 0.030 for the best predicted data set to 0.555 for the worst, with median 0.1845, see Table 3.

Fig. 9

Relative error as function of the percentage passing for the par-14 model. See the caption of Fig. 6

The fan is plotted in Fig. 10; note that the lines are not straight although the curvature is small as the ${E}^{*}$ dependence of b is mild, given by the small exponent ζ = 0.0230, though this is also connected with the high values of ${E}^{*}/{E}_{0}^{*}$. b ranges, for the data used, from 1.46 to 1.70 (the constant-b model, par-13, yielded b = 1.61), leading to a small variation of the slope $\alpha$ e.g., for P = 50%, between 0.66 and 0.68. Figure 11 shows a plot of the $\alpha \left(P\right)$ functions for the three models. Note the small difference between the values from Eq. 4 (model par-12, blue line) and Eq. 24 (model par-13, red line), while the impact on the error at different P is very significant, compare Figs. 6 and 7. The gold and purple curves are the $\alpha$ functions in the par-14 case, for the minimum and maximum b value within the range of data.

Fig. 10

Fragmentation-energy fan for the par-14 model. See the caption of Fig. 5

Fig. 11

The exponents of the percentile lines

The effect of the delay is shown in Fig. 12. The cooperation function, Eq. 17, is plotted on the left graph for the par-12, -13 and -14 models; it happens to be nearly the same for all three. An optimum cooperation occurs at ${\Pi }_{t}$=35. This means an optimum delay of 7 ms per meter spacing for a rock mass of P-wave velocity 5000 m/s. The right graph shows the delay size correction (Eq. 18) for different percentiles of the par-14 models. Two lines are plotted for each percentile; they correspond to the range of $\alpha$ for the extreme values of ${E}^{*}$ of the data, see Eq. 26.

Fig. 12

Cooperation function (left) and resulting delay correction (right) for par-14 model

Figure 13 shows some size distributions for different cases, covering a broad range of errors and sizes, calculated with the par-14 model. Figure 14 shows the cases plotted in Fig. 13 lower right predicted with all three models, for comparison. The distributions from par-13 and par-14 are nearly undistinguishable except in some cases in the very upper end, while par-12 curves deviate especially in the fines and coarse ends; note especially that model par-12 curves bend towards sizes higher than the actual x_max, yielding the large positive errors shown in Fig. 6.

Fig. 13

Size distributions: comparison of data (circles and dashed lines) and calculated (solid lines) curves with par-14 model. Upper-left: distributions with highest ${({MARE}_{{x}_{P}})}_{blast}$ (worst fit cases). Upper-right: distributions with lowest ${({MARE}_{{x}_{P}})}_{blast}$ (best fit cases). Lower-left: distributions with ${({MARE}_{{x}_{P}})}_{blast}$ around percentiles 80, 60, 40 and 20. Lower-right: four distributions randomly selected in different size ranges

Fig. 14

Comparison of models. Circles and solid lines: data; dotted lines: par-12; dashed lines: par-13; dash-dotted lines: par-14. The right graph zooms in on the upper part of the curves

In the xP-frag model (Sanchidrián and Ouchterlony 2017a), where the same body of data was used (except for the 17 new blasts included here, see Table 2), the goodness of the fits (in xP-frag, fits for each percentile size x_P were done, then P-functions of the parameters were calculated) ranged from R² = 0.7813 to 0.9235, RRMSE = 0.3022 to 0.4693, MARE = 0.1651 to 0.2739. The lower R² value corresponded with ${x}_{100}$, not surprisingly according to the above discussion on model par-12, and the higher R² value with ${x}_{50}$.

Figure 15 shows the distributions of ${({MARE}_{{x}_{P}})}_{blast}$ for the three models presented in this work and, by way of comparison, for xP-frag. Some relevant values are included in Table 4.

Fig. 15

Distribution of median absolute relative errors ${({MARE}_{{x}_{P}})}_{blast}$ for all datasets (par-12, par-13, par-14: 186 cases; xP-frag: 169 cases). par-12: blue & red crosses (outliers); par-13: gold (no outliers); par-14: green (no outliers)

Table 4 Distribution of MARE per blast. Comparison with xP-frag

As explained above, the fits in xP-frag were carried out for each percentile independently; each fit had nine parameters, that were then expressed as functions of P by subsequent fitting equations with different numbers of parameters, resulting in a final number of 33 parameters for the whole model, see Table 1. Compared with this, the result obtained here with 12, 13 or 14 parameters is a substantial improvement. Even model par-12 performs very well in the overall prediction, although we do not recommend its use due to the P-wise undulating, non-centered error and the poor behavior in the extremes, particularly at P = 100%. This is overcome by par-13 that benefits from the modified $\alpha \left(P\right)$ expression. These results certainly speak of the soundness (that derives from its experimental realization) of the fan model.

Note that, although the original xP-frag formulation (Eq. 9) has some connection with Eq. 16, it did not originate from the fan concept, nor did the fragmentation obtained from it replicate a fan pattern.

The models presented here are, on average, able to predict the fragmentation outcome of a bench blast with much better accuracy than previous models. An application in a given mine or quarry to tell the relative effect of changing blast parameters would probably work even better as e.g., the loosely defined jointing factor can be back calibrated. The predictions will never be exact though, as variations in local conditions (anisotropy of the rock mass, jointing, water in blast holes, etc.) can sometimes have profound effects.

An important point is that all fragmentation data for the 186 bench blasting data sets, on which our model development rests, were obtained by classical sieving. We have not used data obtained with digital image-based methods. The latter are useful in production conditions since they do not interfere with production but they are not calibrated, they produce results that are not directly comparable between methods or even between different lighting conditions, and cover a much smaller range of fragment sizes. Unfortunately, many fragmentation prediction equations in the literature have been developed using digital image-based data, usually producing equations of limited precision with respect to the actual mass size distribution values. This means that a direct comparison of such prediction equations with our ${x}_{P}$ equations is a delicate matter, but of course, we welcome such comparisons.

The equations presented in this work are not the final word. Three factors that our equations leave out e.g., are the effect of VOD, the placement of the primer, see e.g., Zhang et al. (2022) and the number of rows. There are presently not sufficient sieved data to give these parameters a significant influence on the fits made to our entire group of bench blasting data sets.

6 Conclusions

The fragment size–energy fan description is used in this work to build an improved fragmentation prediction formula (model), a closed form expression from which the whole sieving curve may be computed for an arbitrary energy input (specific energy or powder factor). Some features relevant to fragmentation must be included as modifiers of the percentile size and of the energy input into the rock, in order to preserve the fan pattern. The size modifiers include the blast scale and the joints description, and the energy modifiers include the strength and its size correction, and the cooperation effect of neighboring boreholes, a function of the delay. Classic descriptions of these characteristics are used: joint spacing and orientation (the latter taken from Lilly’s rock mass description), characteristic size and rock strength as in the xP-frag model, ${L}_{c}=\sqrt{HS}$, $\widetilde{\sigma }={\sigma }_{c}^{2}/(2E)$, and a size-dependent strength correction. The energy concentration is described as the powder factor above grade times the explosive chemical energy per unit mass. The Swebrec-type function for the exponents of the energy (the log–log slopes of the percentile rays in the fan) is used. The resulting model (par-12) has 12 parameters and is fitted to a data base of 186 blasts (an extension of the 169 blasts data base used to fit the xP-frag model) with a determination coefficient R² = 0.9546.

The par-12 model, however, has non-centered relative errors for each percentile, with significant transitions from negative to positive median errors, and a relatively poor behavior in the extremes, particularly at P = 100%. This issue is solved with a modification of the exponent function of P including one more parameter, departing from the Swebrec-compatible function. With this (par-13) model, the error is more stable and smaller, significantly improving the prediction of the coarser sizes, especially the maximum, a shortcoming of the classical, Swebrec-related exponents function. It also improves, to a lesser degree, the prediction of the fines. The underlying distribution (ESP4), a 4-parameter function, is tested with some of the distribution data and its performance in fitting seems promising, with lesser error than the Swebrec distribution over a wider passing range.

The dependence of the slopes on rock properties has been tried through a scaled energy-dependent factor modifying the constant b of the slopes function, with marginal improvements of the model performance over the constant slopes one, at the cost of one more parameter of the fit. However, the fact that this model (par-14) has a slope function dependent on the scaled energy, hence on the rock strength properties embedded in it, is an interesting characteristic. The par-14 (a 14-parameter model) yields determination coefficient R² = 0.9583 and a median absolute relative prediction error per blast of 0.1845, improving the xP-frag (a 33-parameter model) value of 0.2026.

Appendix

$\boldsymbol{\alpha }\left({\varvec{P}}\right)$ Functions and underlying size distributions

From the fan expressions using e.g., Eq. 1 (see also Fig. 1):

$${\alpha }_{P}=\frac{\mathrm{ln}\left({x}_{P}/{x}_{0}\right)}{\mathrm{ln}\left({q}_{0}/q\right)}$$

(A1)

Let’s select two rays of the fan, the P = 100% and P = 50% for which ${x}_{P}={x}_{max}$ and ${x}_{P}={x}_{50}$ respectively. From Eq. A1:

$${\alpha }_{100}=\frac{\mathrm{ln}\left({x}_{max}/{x}_{0}\right)}{\mathrm{ln}\left({q}_{0}/q\right)};{\alpha }_{50}=\frac{\mathrm{ln}\left({x}_{50}/{x}_{0}\right)}{\mathrm{ln}\left({q}_{0}/q\right)}$$

(A2)

The following relations can be written:

$$\mathrm{ln}\left({x}_{P}/{x}_{0}\right)=\mathrm{ln}\left({x}_{P}/{x}_{\mathrm{max}}\right)+\mathrm{ln}\left({x}_{max}/{x}_{0}\right)=\mathrm{ln}\left({x}_{P}/{x}_{\mathrm{max}}\right)+{\alpha }_{100}\mathrm{ln}\left({q}_{0}/q\right)$$

(A3)

$$\mathrm{ln}\left({x}_{max}/{x}_{50}\right)=\mathrm{ln}\left({x}_{max}/{x}_{0}\right)+\mathrm{ln}\left({x}_{0}/{x}_{50}\right)={\alpha }_{100}\mathrm{ln}\left({q}_{0}/q\right)-{\alpha }_{50}\mathrm{ln}\left({q}_{0}/q\right)=\left({\alpha }_{50}-{\alpha }_{100}\right)\mathrm{ln}\left(q/{q}_{0}\right)$$

(A4)

Using A1 to A4:

$${\alpha }_{P}=\frac{\mathrm{ln}\left({x}_{P}/{x}_{\mathrm{max}}\right)}{\mathrm{ln}\left({q}_{0}/q\right)}+{\alpha }_{100}=\frac{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{P}\right)}{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{50}\right)}\left({\alpha }_{50}-{\alpha }_{100}\right)+{\alpha }_{100}$$

(A5)

Let us consider a size distribution that can be represented by a Swebrec distribution:

$$P({x}_{P})=\frac{100}{1+{\left[\frac{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{P}\right)}{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{50}\right)}\right]}^{b}}$$

(A6)

Solving for the quotient in brackets:

$$\frac{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{P}\right)}{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{50}\right)}={\left(\frac{100}{P}-1\right)}^{1/b}$$

(A7)

And, substituting in Eq. A5, Eq. 4 is obtained:

$${\alpha }_{P}={\alpha }_{100}+\left({\alpha }_{50}-{\alpha }_{100}\right){\left(\frac{100}{P}-1\right)}^{1/b}$$

(A8)

Note that the Swebrec distribution, Eq. A6, may be used to write the whole fragmentation-energy fan relation in a closed form, Eq. 5. The quotient in the denominator of the Swebrec can be written, using A5 and A1:

$$\frac{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{P}\right)}{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{50}\right)}=\frac{{\alpha }_{P}-{\alpha }_{100}}{{\alpha }_{50}-{\alpha }_{100}}=\frac{\frac{\mathrm{ln}\left({x}_{P}/{x}_{0}\right)}{\mathrm{ln}\left({q}_{0}/q\right)}-{\alpha }_{100}}{{\alpha }_{50}-{\alpha }_{100}}$$

(A9)

Inserting this result in Eq. A6, Eq. 5 is obtained:

$$P({x}_{P},q)=\frac{100}{1+{\left[\frac{\frac{\mathrm{ln}\left({x}_{P}/{x}_{0}\right)}{\mathrm{ln}\left({q}_{0}/q\right)}-{\alpha }_{100}}{{\alpha }_{50}-{\alpha }_{100}}\right]}^{b}}=\frac{100}{1+{\left[\frac{\frac{\mathrm{ln}{x}_{P}-\mathrm{ln}{x}_{0}}{\mathrm{ln}{q}_{0}-\mathrm{ln}q}-{\alpha }_{100}}{{\alpha }_{50}-{\alpha }_{100}}\right]}^{b}}$$

(A10)

Eq. A10 provides the size distribution at any powder factor. It may equally be written with an advanced formulation with scaled sizes and energies like Eqs. 19:

$$P({x}_{P}^{*},{E}^{*})=\frac{100}{1+{\left[\frac{\frac{\mathrm{ln}{x}_{P}^{*}-\mathrm{ln}{x}_{0}^{*}}{\mathrm{ln}{E}_{0}^{*}-\mathrm{ln}{E}^{*}}-{\alpha }_{100}}{{\alpha }_{50}-{\alpha }_{100}}\right]}^{b}}$$

(A11)

Let’s now not use the P = 50% slope ${\alpha }_{50}$ but a slope ${\alpha }_{{P}^{*}}$ corresponding to a percentile ${x}_{{P}^{*}}$, ${P}^{*}=100/{2}^{1/\mu }$, $\mu$ being in principle a positive number; the equivalent of Eq. A5 is readily obtained:

$${\alpha }_{P}=\frac{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{P}\right)}{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{{P}^{*}}\right)}\left({\alpha }_{{P}^{*}}-{\alpha }_{100}\right)+{\alpha }_{100}$$

(A12)

Let us further assume that the size distribution can be represented by the following function:

$$P({x}_{P})=\frac{100}{{\left\{1+{\left[\frac{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{P}\right)}{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{{P}^{*}}\right)}\right]}^{b}\right\}}^{1/\mu }}$$

(A13)

Solving for the quotient in brackets:

$$\frac{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{P}\right)}{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{{P}^{*}}\right)}={\left[{\left(\frac{100}{P}\right)}^{\mu }-1\right]}^{1/b}$$

(A14)

Hence Eq. A12 results in Eq. 24:

$$\alpha \left(P\right)={\alpha }_{100}+({\alpha }_{{P}^{*}}-{\alpha }_{100}){\left[{\left(\frac{100}{P}\right)}^{\mu }-1\right]}^{1/b}$$

(A15)

Note, from Eq. A13, that $P\left({x}_{{P}^{*}}\right)={P}^{*}=100/{2}^{1/\mu }$, consistent with the definition given above for ${P}^{*}$. Eq. A13, that we will call distribution ESP4 (expanded Swebrec – 4 parameters), may also be conveniently written as an explicit function of ${x}_{50}$; making P = 50% hence ${x}_{P}={x}_{50}$ in Eq. A13 and solving conveniently:

$$\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{{P}^{*}}\right)=\frac{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{50}\right)}{{\left[{2}^{\mu }-1\right]}^{1/b}}$$

(A16)

Substituting in Eq. A13, the size distribution is:

$$P=\frac{100}{{\left\{1+{\left[\frac{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{P}\right)}{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{50}\right)}\right]}^{b}\left({2}^{\mu }-1\right)\right\}}^{1/\mu }}$$

(A17)

where the parameters are now the more convenient two characteristic sizes, ${x}_{\mathrm{max}}$ and ${x}_{50}$, and the two exponents b and $\mu$. The fragment size-energy closed formula is now, inserting Eq. A9 in Eq. A17, using e.g., scaled sizes and energies:

$$P=\frac{100}{{\left\{1+{\left[\frac{\frac{\mathrm{ln}{x}_{P}^{*}-\mathrm{ln}{x}_{0}^{*}}{\mathrm{ln}{E}_{0}^{*}-\mathrm{ln}{E}^{*}}-{\alpha }_{100}}{{\alpha }_{50}-{\alpha }_{100}}\right]}^{b}\left({2}^{\mu }-1\right)\right\}}^{1/\mu }}$$

(A18)

And, for the b-variable case, par-14 model:

$$P=\frac{100}{{\left\{1+{\left[\frac{\frac{\mathrm{ln}{x}_{P}^{*}-\mathrm{ln}{x}_{0}^{*}}{\mathrm{ln}{E}_{0}^{*}-\mathrm{ln}{E}^{*}}-{\alpha }_{100}}{{\alpha }_{50}-{\alpha }_{100}}\right]}^{{b}_{0}{\left({E}^{*}/{E}_{0}^{*}\right)}^{\zeta }}\left({2}^{\mu }-1\right)\right\}}^{1/\mu }}$$

(A19)

Making $\zeta$=0 it reverts to model par-13, and further making $\mu$=1 it reverts to model par-12.

It still remains to be shown that the fragment size distributions can be well represented by the ESP4 function, Eq. A13. Taking as examples the four distributions chosen in Figs. 13 lower right and 14, their ESP4 fits are summarized in Table 5. The maximum size ${x}_{\mathrm{max}}$ is not calculated as a parameter of the fit but is fixed to the ${x}_{100}$ data value; when no data exists a P = 100, a log–log linear extrapolated value is used. Fits are 1/P-weighed least squares on plain (non-log-transformed) data. This type of fit results in distributions working better in the fines with little penalty in the coarse region, see e.g., Ouchterlony (2009), Sanchidrián et al. (2009, 2014). Table 5 also shows the Swebrec fits results for comparison. Figure 16 shows both Swebrec and ESP4 fits.

Table 5 Swebrec and ESP4 distribution fits

Fig. 16

Fits to some fragment size distributions. Blue lines and circles: data. Gold: Swebrec. Red: ESP4. Distribution case numbers are, from finer to coarser: 48, 151, 144 and 75

The plots give a possible explanation of the superior performance of par-13 model with respect to par-12, especially in what respects the wavy error pattern, as the Swebrec distribution has an undulatory shape so that errors in size shift from positive to negative across the distribution. This feature is not apparent in the ESP4 fits and may also transfer to the $\alpha \left(P\right)$ function, this way leading to a more consistent fragmentation-energy fan representation for all passing values. The goodness of the fit is clearly better with ESP4, at the cost of one more parameter; even if the determination coefficients of the Swebrec fits are high, note the substantial reduction in relative root mean squared error (RRMSE) of ESP4, in some cases less than half of the Swebrec error. It should be noted that the Swebrec distribution is one of the known 3-parameter distributions that best represent rock fragmentation (Sanchidrián et al. 2012, 2014). The better performance of ESP4 with the examples shown here is not a general proof of value of this distribution, still requiring a thorough assessment beyond the scope of this paper. However, the behavior shown in the trials made look definitely promising.

The parameter $\mu$ was introduced as a correction of the Swebrec expression for $\alpha \left(P\right)$ (Eqs. 24 and A15). From it, it appears that it should be restricted to positive numbers; for $\mu <0$ the term inside the brackets is negative and its power is generally not real. It should neither be zero since that would give a constant $\alpha \left(P\right)$ hence no fan pattern would exist. However, Table 5 shows a negative $\mu$ in the fit to B#151, which requires further assessment. Eq. A15 can be transformed by introducing ${\alpha }_{50}$; making P = 50 in A15:

$${\alpha }_{50}={\alpha }_{100}+\left({\alpha }_{{P}^{*}}-{\alpha }_{100}\right){\left[{2}^{\mu }-1\right]}^{1/b} ; {\alpha }_{{P}^{*}}-{\alpha }_{100}=\frac{({\alpha }_{50}-{\alpha }_{100})}{{\left[{2}^{\mu }-1\right]}^{1/b}}$$

(A20)

And the $\alpha \left(P\right)$ expression is, substituting Eq. A20 in Eq. A15:

$$\alpha \left(P\right)={\alpha }_{100}+({\alpha }_{50}-{\alpha }_{100}){\left[\frac{{\left(\frac{100}{P}\right)}^{\mu }-1}{{2}^{\mu }-1}\right]}^{1/b}$$

(A21)

This expression is always real for any $\mu$; for $\mu <0$, both the numerator and the denominator in the terms inside the brackets are negative so the quotient is positive; for $\mu =0$, the quotient converges to a positive number, $\mathrm{ln}\left(\frac{100}{P}\right)/\mathrm{ln}2$.

Regarding the size distribution ESP4, Eq. A17, some insight on it shows that it can also accept non-positive $\mu$ values. For negative $\mu$, the condition must be met (see Eq. A17):

$${\left[\frac{\mathrm{ln}\left({x}_{\mathrm{max}}/x\right)}{\mathrm{ln}\left({x}_{\mathrm{max}}/{x}_{50}\right)}\right]}^{b}\left({2}^{\mu }-1\right)>-1$$

(A22)

Or:

$$x>\frac{{x}_{max}}{\mathit{exp}{\left[\frac{\mathit{ln}\left({x}_{max}/{x}_{50}\right)}{\left|{2}^{\mu }-1\right|}\right]}^{1/b}}$$

(A23)

For the case B#151, this limit size is 0.004 mm, several orders of magnitude below the actual range of applicability of the distribution. For $\mu =0$, the distribution converges to:

$$P=\frac{100}{{2}^{{\left[\frac{\mathit{ln}\left({x}_{max}/{x}_{P}\right)}{\mathit{ln}\left({x}_{max}/{x}_{50}\right)}\right]}^{b}}}$$

(A24)