The Influential Role of Powder Factor vs. Delay in Full-Scale Blasting: A Perspective Through the Fragment Size-Energy Fan

Abstract

The fragmentation of 12 full-scale one-row blasts has been measured by sieving a large portion of the muckpiles. The procedure followed, the difficulties encountered and the solutions adopted to construct the fragment size distribution curves are described in detail; 11 curves were finally constructed as production constraints prevented the required measurements on one of the blasts. The blasts covered a powder factor range between 0.42 and 0.88 kg/m³, and were initiated with two significantly different delays, 4 and 23 ms between holes, to assess the influence of both powder factor and delay on fragmentation. The size distributions are well represented by the Swebrec function, which strongly suggests that the dependence of fragmentation with the powder factor can be analyzed by the fragmentation-energy fan. The result is excellent, and the frag-energy fan model in its simplest form (a four-parameter function) is able to predict sizes between percentage passings 92 to 8% with a mean error of 14.4% and a determination coefficient R² as high as 0.976. The powder factor above grade has been used, in its energy form obtained as the product of the mass powder factor by the explosive energy per unit mass. The incorporation of six more fragment size distributions, also obtained by sieving in a previous blasting project in the same rock mass, but with different layouts, explosives, delay and blast direction, only reduces R² to 0.968 and increases the mean error to 15.3%. A strength dependence with the size of the blasted block (burden, bench height, etc.) has been tested for inclusion in the fan formulation, with minor improvement compared with the powder factor alone, as the variation in size of the blasts was very limited. Some size descriptors as in-situ block size and fracture intensity have also been tested, though variations were also limited as all blasts were carried out in the same quarry site, not improving the prediction errors when other blast dimensions (e.g., burden) are used. Incorporating the effect of delay in the fragmentation-energy fan model has been attempted with a cooperation function modifying the powder factor, increasing from instantaneous to an optimum delay value, then decreasing as the delay further increases. The effect of such a function is noticeable in terms of improved prediction; the data analyzed, however, do not allow for a definitive statement on an optimum delay value as calculations with different fan characteristics and data result in different optimum values. The effect of the delay on the fragment size varies with the percentile, from about 10–15% for the high percentiles to somewhat more than 30% for the lower percentiles.

Highlights

• Fragmentation from full scale blasts has been determined by muckpile sieving.

• The Swebrec function represents well the fragmentation measured in the range 100% to 5% mass passing with error less than 12%.

• The fragmentation-energy fan concept is successfully applied to blasts with different characteristics in the same rock mass.

• The burden and other geometrical blast characteristics may be used as scaling factors of the fragment sizes and the rock strength, though their effect is limited, probably due to a limited variability in the data.

• The delay is successfully incorporated in the fragmentation-energy fan formulation by means of an energy cooperation function that varies with the delay.

1 Introduction

Rock fragmentation by blasting is the initial production operation of most mines and quarries. Mine and plant design and operational optimization require a reliable fragmentation prediction that can foresee changes in fragment sizes due to changes in rock or blasting parameters. As size distributions from blasting are input to crusher and mill models, their accuracy is instrumental for a realistic mine-to-mill modeling as part of the optimization. Likewise, a control of fragmentation caused by blasting may provide an early indication of issues in the excavation performance.

Fragmentation can only be measured by sieving if an absolute statement on sizes and percentage passing values is required; despite its difficulty, sieving provides reliability compared to the other fragment size distribution measurement methods (Şenyur 1998). However, due to the complication of carrying out such an operation on the muckpile of a blast, image analysis systems are often employed, see e.g., recent work by Azizi and Moomivand (2021) where fragmentation by blasting models are assessed with image analysis measurements, and Masumi-Nasab et al. (2019) where image-based fragmentation results obtained with different software are compared with sieved fragmentation data. Measuring fragmentation from images invariably entails segmentation and sizing errors (see e.g., Koh et al. 2009; Rosato et al. 2002; Wang 2008; Thurley 2011; Thurley and Ng 2008; Andersson and Thurley 2008). Added to these sizing errors is the fact that image analysis in any of its forms tries to determine the fragment size distribution of a pile of fragments (a three-dimensional structure) from measurements on the surface (a two-dimensional one). Stereological unfolding solutions, where random sampling in two-dimensional sections are used to derive quantitative information about a three-dimensional material based on statistics and geometrical principles, lead to generally unsatisfactory results in the case of muckpile imaging, as the section used when measuring rock fragmentation is the surface, not a random interior one, with a fragment size distribution intrinsically biased by the missing fines and the total or partial overlapping of particles in the second or third layer into the pile by particles in the first layer (Maerz 1996). Unfolding solutions heavily rely on calibration, which requires some a-priori knowledge of the actual fragment size distribution that can only be achieved by sieving. Ultimately, proper sieving measures the ‘waists’ of a stream of oriented particles and the third dimension influences the mass passing. The particles in an image of a muckpile surface are more likely to have different orientations and to be partially covered, and the analysis of 2D or 3D images does not have an information on the depth. The two methods do not measure the same thing.

The above is all too often overlooked by image analysis studies, that (1) most often lack a realistic error analysis or a statement on ranges of validity of the measurements, that (2) require an estimation (often out of reach) of how much material is not present in the delineated areas or beneath the working images, all of it requiring some knowledge about the actual size distribution (which can only be obtained by sieving). Still, image analysis may help to roughly detect large changes of fragmentation and that is often all that is needed to flag out rock changes, or drill and blast problems, e.g., drilling errors or poor explosives functioning. However, when fragment sizes are sought in an absolute, quantitative or predictive fashion, image analysis alone cannot provide a solution. Combinations of image analysis with on-site sieving, or derivation of rock cuts weights from crushing plant mass flows, have been used though to overcome the problem of sieving large rock blocks (Cho et al. 2003; Ouchterlony et al. 2006; Segarra et al. 2018).

This paper reports the measurement of fragmentation in a blasting campaign where quality experimental data on fragment sizes was obtained as a basis for the calibration of fragmentation models. Large scale (in excess of thousand tonnes) measurement of fragmentation from blasting was carried out by on-site sieving; the difficulties encountered in performing that task in a production environment, and how they were solved, are described. Though fragmentation cuts were made by sieving, a supplementary use was made of image analysis to resolve some uncertainties in the coarse fractions. The combination of both techniques provides some insight into their different reaches and limitations. A thorough discussion of the fragmentation obtained is conducted in light of the current knowledge on fragmentation by blasting, particularly how the results can be analytically described through the fragmentation-energy fan concept (Ouchterlony et al. 2017; Ouchterlony and Sanchidrián 2018). Some possible refinements of the fragmentation-energy fan formulation are pointed out.

2 Test Site and Blasts Description

The experimental work was carried out in the quarry El Aljibe as part of the EU-funded research project SLIM. El Aljibe is located in central Spain near the town of Almonacid de Toledo and mines mylonite to produce track ballast for high-speed and conventional trains and for sub-base and base course in road and rail track construction. The rock has an average density of 2721 ± 9 kg/m³.

Two test campaigns of six blasts each were carried out in the summer of 2017 and the autumn of 2018, respectively. These blasts are referred to as the ‘SLIM series’. Each blast consisted of a single row of seven blastholes with a mean bench height of 12 m. The blastholes had 89 mm diameter with an inclination of 16°, sub-drilled to a depth of up to 2.1 m, bottom initiated with a 400 g cast booster. The explosive used was a double salt straight emulsion; the velocity of detonation was measured in all blasts, ranging from 4956 to 5971 m/s. The burden times spacing grid employed in the first campaign was about 2.7 × 3.1 m, widened to 3.5 × 3.8 m in the second one to test lower powder factors. Two significantly different delay times with electronic initiation were employed, initiation progressing from one end of the row. Table 1 shows some relevant characteristics of the blasts; a Quarryman ALS Laser system (MDL) with a typical accuracy of 10 cm in distance and 0.02˚ in vertical and horizontal angles was used to scan the highwall faces and assess the position of the blastholes. The actual blasthole trajectory was measured with a Pulsar Micro Probe Mk3 (Geo-konzept) with a precision of 1° in the azimuth and 0.25° in the inclination.

Table 1 Blasting characteristics

3 Fragmentation Measurement

Figure 1 shows as an example the muckpiles from blasts B5 and B12. The mass of excavated rock, m_b lies in the range 1916–2342 t in the first campaign, and 3554–5580 t in the second one (Table 2). These figures were calculated with CloudCompare (2017) from the volume of the excavated void between pre- and post-blast highwall laser scans.

Fig. 1

Muckpiles from blast B5 (left) and B12 (right)

Table 2 Summary of sampled material

A significant amount (see Table 2, m_sp/m_b fraction) of material representative of the blasts was sampled to measure fragmentation. Relatively large fragments (that could not be sieved so as to preserve the integrity of the mobile screen) were first set aside. The mass of this fraction (column grueso, Spanish for coarse) and of the material fed to the mobile screen (column sieved) are given in Table 2; these data were provided by a front loader Liebherr 576 equipped with a weight scale in its bucket.

The aim of the grueso sorting was to remove fragments above 300–400 mm. However, the bucket had difficulty in loading the large fragments only (no screen bucket was available) and the resulting grueso stockpile included finer material entrained in the coarser rocks in the first campaign (see Fig. 2 left). In the second campaign (blasts B7 to B12), the selected material was hauled outside the pit and stacked in flat piles (see Fig. 3) 1–2 m high; their low profile aimed to reduce fines segregation and facilitate the sampling of grueso. The resulting grueso heaps contained less fine material than the first campaign (see right photo, Fig. 2). This effect is corrected for through the image analysis.

Fig. 2

Grueso stockpiles. Blast B2 (left, ground image; the diameter of the discs is 25 mm) and B7 (right, aerial image; the stripes of the pole in the upper left corner are 10 cm long)

Fig. 3

Truck-built stockpiles. Aerial view of material from blasts B7 and B8

3.1 Muckpile Sieving

A Kleemann MS 19D mobile screen was used to sieve the m_F material, see Fig. 4 left. It had a top deck of 1.52 × 6.1 m composed by a grizzly of parallel rods with an opening of 100 mm, and was equipped with three more screens of cut sizes 63, 30/25 (first and second campaign, respectively) and 8 mm. A cut size or effective aperture (i.e., square mesh equivalent) of 120 mm is assigned to the grizzly in order to account for the effect of flaky and elongated fragments (Colman 1985; Gluck 1965; Gupta and Yan 2006; Ouchterlony et al. 2006, 2015). Figure 4 right shows an example of the fractions obtained.

Fig. 4

Overview of the mobile screen at the beginning of processing blast B1 (left). The roll-off material, i.e., fragments not passing the grizzly, lies directly below it, while the fractions from the screens were dumped in heaps below the four conveyor belt booms. Right: stockpiles after sieving (blast B11)

Once sieving was completed, the front loader mucked and hauled the material in each stockpile, to weigh it. These data are shown in Table 3 for each blast.

Table 3 Results from in-situ sieving of m_F (sizes in mm and masses in kg)

3.2 Laboratory Sieving

For the second blast series (B7–B12), samples from fractions 63–25 mm, 25–8 mm and < 8 mm were taken for further laboratory sieving (7–13, 3–6 and 3–5 kg, respectively). The resulting partial size distributions are plotted in Fig. 5 left. For all fractions, the upper cut size is well defined, while the lower one is relatively poorly defined, with a passing fraction of 2–9% at 25 mm in the 63–25 mm fraction, and a passing fraction of 1–17% at 8 mm in the 25–8 mm fraction. These distributions are combined (Fig. 5 right) into single, total lab distributions using the amounts of muckpile material in each of the three fractions (see Table 3). They have been used to estimate intermediate points below 63 mm in the muckpile size distributions, and to extend them into the fines tail < 8 mm, as described below.

Fig. 5

Laboratory sieved size distributions of m_F. Left: fractions 63–25 mm, 25–8 mm and < 8 mm. Right: total lab distributions

Let $y(x)$ be the size distribution of material gone through the grizzly (i.e., actually sieved by the mobile screen). This variable is defined from the sieved weights in Table 3 at size ranges 120–63, 63–25, 25–8 and < 8 mm; $y\left(x=120 \mathrm{mm}\right)=100$. Let ${y}_{L}(x)$ be the size distributions of the laboratory sievings, defined at sizes 63, 50, 40, 31.5, 25, 22.4, 16, 11.2, 8, 4, 1, 0.5 and 0.063 mm, Fig. 5 right; ${y}_{L}\left(63 \mathrm{mm}\right)=100$. For a certain size $x$ in one of the intervals 63 < $x$  < 25, 25 < $x$  < 8, $x$ < 8 mm, $y(x)$ is calculated so that the mass fraction between the upper size limit of the interval and $x$ is equal to the same fraction in the laboratory curve; let ${y}^{S}$, ${y}^{I}$ be the percentage passing in the muckpile sieving below 120 mm at the upper and lower limits of one of the above intervals, ${y}_{L}^{S}$, ${y}_{L}^{I}$ the percentage passing of the laboratory distribution for those limits, and ${y}_{L}(x)$ the percentage passing at $x$ in the laboratory distribution; the following then applies:

$$\frac{{y}^{S}-y(x)}{{y}^{S}-{y}^{I}}=\frac{{y}_{L}^{S}-{y}_{L}(x)}{{y}_{L}^{S}-{y}_{L}^{I}}.$$

(1)

Hereby $y$ is obtained at the mesh sizes of the lab sievings. For sizes smaller than 8 mm, ${y}^{I}$ is estimated as:

$${y}^{I}={y}_{L}^{I}\cdot {y}^{S}/100,$$

(2)

where ${y}^{S}$ is the mobile screen mass fraction passing at 8 mm and ${y}_{L}^{I}$ the laboratory passing at 0.063 mm. With that, the size distributions below 120 mm (i.e., the material passing the mobile screen feeder grizzly) are as plotted in Fig. 6. For B1-B6, the fractions passing in Fig. 6 are directly calculated from Table 3 data, fractions 120–63, 63–30, 30–8 and < 8 mm.

Fig. 6

Size distributions of the m_F fractions passing the grizzly (< 120 mm). Solid lines: first campaign (B1–B6); dashed lines: second campaign (B7–B12). The first campaign distributions end at 8 mm since no lab sieving was performed. The right graph shows the enlarged upper parts of the distributions

From the masses of grueso m_G and sieved m_F in Table 2, the mass rolling-off the grizzly in Table 3 (> 120 mm) and the size distributions in Fig. 6, the complete size distributions of the muckpiles could be, in principle, calculated. However, in our case, due to the sorting method of the grueso and the material fed to the screen, additional data is required, namely: (1) the size distribution of the grueso, that includes some finer material entrained, and (2) the size distribution of the material rolling-off the grizzly for which the minimum size is assumed to be the opening of the grizzly, but the maximum size is not precisely known. These issues are addressed in the next section.

3.3 Image Analysis: Fragmentation of the Grueso and the Grizzly Roll-Off

To assess the fragmentation of the grueso and the grizzly roll-off, the heaps of both cuts were photographed and the resulting images analyzed with Split^® desktop (2016). The number of photos taken for each blast is given in Table 4. In the first campaign (blasts B1 to B6), 25 photos (14 of the grueso and 11 of the roll-off) were taken after placing the scaling objects on the stockpiles (see e.g., Fig. 2, left photo); the ground sampling distance (GSD) was 1.0–1.9 mm/px. Four more images taken by a PHANTOM 4 Pro Unmanned Aerial Vehicle System (UAV) were used in blasts B1 and B3 for the grizzly roll-off and in B4 for the grizzly roll-off and the grueso, see Table 4; their GSD was 20–33 mm/px. These flights were specifically made to scan the highwall face of the next blasts, and the stockpiles of gruesos and grizzly roll-off appeared partially in some images only, often near the limits of the surveyed area, so it was not possible to build a 3D model (nor to compute an orthophoto, i.e., a constant scale, geometrically corrected image) of them. They were used as single 2D images, conveniently scaled, for digital fragmentation analysis. Figure 7 shows one of these images for the grizzly roll-off; note the negligible amount of fine material or fragments smaller than the image resolution. No images of grueso were available for blast B3 as the heap was hauled out directly after weighing due to production requirements, before images could be taken. Since grueso represents 59% of the sampled material in this blast, the final size distribution would have been too speculative, as no estimation of the amount of finer material entrained in the grueso could be made, so it was decided not to use this blast for further fragmentation analysis and the size distribution was not calculated.

Table 4 Number and source of images analyzed with Split^® desktop

Fig. 7

Aerial image of the grizzly roll-off from blast B3; the circle diameter is 48 cm

In the second campaign, the stockpiles from sieving were systematically flown over, resulting in a GSD about 5 mm/px. From the images acquired, an orthophoto for each blast was generated and analyzed. The orthophotos were divided into the number of images shown in Table 4 for each blast, which allowed analyzing them without reducing their resolution (Split Desktop does not handle image files greater than 10 MB).

Images taken by the drone in the first campaign were directly delineated by hand for about 4 h each since the software had difficulty in properly identifying the edges of the rocks. The rest of the photos were automatically delineated and the resulting delineations manually edited for a total of around 4 h for grueso, and 1 h for the grizzly roll-off (which had an easier to segment fragmentation). Figure 8 illustrates this correction process; the central image is the result of the automatic delineation of the image on the left (the grizzly roll-off from blast B2) and the right image is the result of the manual edition. The main errors are a fusion of small particles into large ones and splitting of larger fragments. They are corrected by adding edges where they were missing and erasing the spurious lines that erroneously split larger fragments. Blue patches are non-delineated zones, either with fines (generic term for unresolved particles of size below a certain threshold called fines cutoff, FCO, related to the resolution of the image, see Table 5), or shadowed regions. The amount of material of size less than FCO is estimated as the sum of the blue areas multiplied by the fines factor (FF), that defines the percentage of non-delineated fragments in the patches. As result of the different sorting techniques for the grueso, it had either a significant amount of fines entrained between the coarser fragments in the first campaign, or almost none in the second (see Fig. 2). It was hence decided to use FF = 100% (i.e., all the blue pixels are considered fines) for the first campaign and FF = 0 (i.e., non-delineated areas are not fragments, but shadows, inter-particle spaces, etc.) for the second campaign. The grizzly roll-off (see Fig. 7) does not have fines patches to add to the segmented fines, so FF = 0 was used throughout.

Fig. 8

Digital image analysis. The lower images are zoomed from the square zones in the upper ones. Examples of the major errors in automatic delineation: fusion and sub-division of fragments (F and D respectively in the zoomed images). Left: original photograph. Center: automatic delineation. Right: after manual correction

Table 5 Fines cut-off for the image analysis (mm)

The areas that are not taken into account in the calculation of the distribution of sizes (scaling objects, partially censored fragments on the edges of the images, etc.) are marked in cyan.

The material of sizes below the FCO is assumed to have the general fragmentation characteristics of the sieved material (i.e., the size distributions in Fig. 6). The size distributions of the grueso and of the grizzly roll-off are as given in Fig. 9. White circles indicate the FCO points, below which the sieved distributions of Fig. 6 are grafted onto the Split Desktop data. Note the poor sorting of the grueso in the first campaign where about half of the material (e.g., up to sizes 200–250) mm could have probably been run safely to the grizzly. Also note the significant amount of material below the cut-size of the grizzly, 120 mm, due to some degree of overfeeding that resulted in grizzly choking, with the rolling-off of some of the material that should have otherwise passed the grizzly (see right graph, Fig. 9).

Fig. 9

Size distributions of the grueso (left) and the grizzly roll-off (right). White circles are the fines cut-off points

With the masses of grueso in Table 2, the roll-off from the grizzly in Table 3 (> 120 mm), the size distributions of grueso and grizzly roll-off (Fig. 9) and the size distributions below 120 mm of Fig. 6 (obtained from the muckpile screen weights in Table 2 and the laboratory sievings of Fig. 5), the size distributions are calculated. They are plotted in Fig. 10. The maximum sizes (Table 6) were measured with tape on the largest boulders found both in the muckpile and in the grueso heaps. The numeric data corresponding to Figs. 6, 9 and 10 are given as tables in the Appendix.

Table 6 Maximum sizes (mm)

Fig. 10

Size distributions of the muckpiles

4 Discussion

4.1 The Swebrec Function

Rock fragmentation, including (though not limited to) fragmentation by blasting, is generally well represented by the Swebrec function (Ouchterlony 2005, 2009), which nearly always provides a better fit to fragmentation data than other distributions of comparable complexity, see Sanchidrián et al. (2012, 2014) and Sanchidrián (2015). The Swebrec is a three-parameter distribution with cumulative probability function:

$$P\left( x \right) = \frac{100}{{1 + \left[ {\frac{{{\text{ln}}(x_{{{\text{max}}}} /x)}}{{{\text{ln}}(x_{{{\text{max}}}} /x_{50} )}}} \right]^{b} }}, \quad 0 < x \le x_{{{\text{max}}}} ,$$

(3)

where x_max is the maximum fragment size, x₅₀ is the median size and b is a shape parameter. The size distributions obtained for the first campaign ranged down to 8 mm in size, which corresponds to a passing of 7–14% (see Table 7), i.e., the curves span about one decade in relative mass passing and nearly two and a half decades in size. The second campaign distributions, with the fines tails determined from the lab sievings, span nearly three decades in passing in most cases (more than that in B9) and nearly five decades in size. Such wide range distributions cannot be generally well fitted with two- or three-parameter distributions as they often encompass some degree of bi-modality. Sanchidrián (2015), in a broad study of errors for several size distributions when fitted to fragmentation by blasting data, recommends the use of the three-parameter Swebrec for representing fragmentation from the upper end down to about 5% passing for an expected error in size prediction at a given passing of about 15% in the extremes of the range, lower in the central zone. As a reference, the Rosin–Rammler-Weibull distribution fits fragmentation with a similar expected error but in the narrower range 95–20%, or 90–10% passing. Wider size ranges require bi-modal or bi-component distributions, usually with five parameters such as the extended Swebrec (Ouchterlony 2005, 2009) or the bimodal Rosin–Rammler (e.g., Djordjevic 1999). These can extend their fidelity from the upper end down to about 1–2% passing (it can often be extended to 0.5% passing but then higher errors in the extremes of the range should be expected).

Table 7 Parameters and goodness of the Swebrec fits, R² and MAPE, to the constructed sieving curves

Fits of the Swebrec (Eq. 3; experimental x_max, see Table 6, are used, so the fit is carried out on x₅₀ and b) by an ordinary unweighted least squares method yield the determination coefficients (${R}^{2}$) given in Table 7, ranging from 0.9946 to 0.9995 with a mean of 0.9982 when only data from the size range greater or equal 8 mm are fitted. The percentages passing at 8 mm (given in Table 7) are 5–14%, lying well in the range of validity of the Swebrec. The functions fitted are plotted in Fig. 11. Fits have also been tried for the full range with, as expected, a worse performance in the fines region (dashed lines in Fig. 11 right), despite the seemingly good determination coefficients also in this case. This happens because the function values (percentage passing) in the fines zone are much smaller than in the upper zone so the large (relative) errors are still small compared with the small (relative) errors in the upper part; more so when they are squared. To make a more meaningful comparison, the mean absolute relative error (MARE, also called MAPE if expressed as percentage) has also been calculated. While mean errors in the ≥ 8 mm fits are a few percent (see Table 7), they become much higher when the fits are tried in a wide span of sizes and fractions passing due to the large errors in the lower end. Still, the range ≥ 8 mm is equally well fitted. Figure 12, where the absolute relative errors are plotted as function of the mesh size, clearly explains this behavior (MAPE in Table 7 are the mean of the error values plotted in Fig. 12 for each blast, expressed as percentage). Note that the errors grow towards the fines, and that at 8 mm (often not far from the 5% passing limit of accuracy of the Swebrec) they are in the range of 15%, as observed by Sanchidrián (2015).

Fig. 11

Swebrec function fits to the constructed size distribution data. Left: first campaign. Right: second campaign. In the latter, solid lines are the fits from 8 mm upwards, and the dashed lines are the fits to the full range of data. Circles are the experimental points

Fig. 12

Absolute relative errors (ARE) of the Swebrec function fits. Left: fits to x ≥ 8 mm data. Right: fits to the full range; the insert shows the errors in the coarse zone x ≥ 5 mm the same scale as the left plot. Gray lines are the mean absolute relative error (MARE) for a given mesh size

4.2 The Fragmentation-Energy Fan

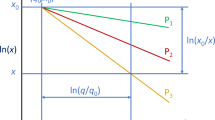
The powder factor is an influential blast design parameter and all fragmentation prediction formulae include it as a significant blast descriptor (e.g., the classical Kuz-Ram, Cunningham 1983, 1987, 2005 and more recently ${x}_{\mathrm{P}}-\mathrm{frag}$, Sanchidrián and Ouchterlony 2017). The effect of powder factor has been rationalized with the fragmentation-energy fan concept (Ouchterlony et al. 2017) that basically states that the percentiles of the size distribution (i.e., the sizes for a given percentage passing) are power functions of the powder factor of varying exponent value such that, if plotted in log–log scale, the data form a set of straight lines that converge to a focal point. The slopes of the lines (i.e., the power exponents) grow monotonically in absolute value from percentile 100 towards the fine material. The fragment size may therefore be written as a function of the powder factor, or the volume specific energy deposited in the rock, E as follows:

$${x}_{\text {P}}={x}_{0}{\left(\frac{E}{{E}_{0}}\right)}^{-\alpha (P)},$$

(4)

where the subindex P indicates that the size is a P percentile. E = q·e, where q is powder factor (mass of explosive per unit volume of blasted rock) and e is explosive energy (chemical energy per unit explosive mass); (E₀, x₀) are the focus coordinates in the energy-size plane and $\alpha (P)\ge 0$.

This fan equation may be written in a convenient non-dimensional form by dividing the fragment size by a characteristic length of the blast, L_c:

$$\frac{{x_{{\text{P}}} }}{{L_{{\text{c}}} }} = x_{\text {P}}^{^{\prime}} = \frac{{x_{0} }}{{L_{{\text{c}}} }}\left( {\frac{E}{{E_{0} }}} \right)^{ - \alpha \left( P \right)} = x_{0}^{^{\prime}} \left( {\frac{E}{{E_{0} }}} \right)^{ - \alpha \left( P \right)} .$$

(5)

It has been shown (Ouchterlony et al. 2017; Ouchterlony and Sanchidrián 2018) that when sieved size distributions are of Swebrec type (i.e., are well fitted by that function), then the percentile functions of the powder factor have the fan’s converging pattern, and the function α(P) is fully determined by the slope exponents at the maximum and median sizes, and the Swebrec shape parameter:

$$\alpha \left(P\right)={\alpha }_{100}+\left({\alpha }_{50}-{\alpha }_{100}\right){\left(\frac{100}{P}-1\right)}^\frac{1}{b}.$$

(6)

The exponent ${\alpha }_{100}$ expresses the dependence of the maximum size (x₁₀₀ = x_max) on the powder factor. Very often this dependence is weak at moderate variations of the powder factor, resulting in ${\alpha }_{100}$ values close to zero. If so Eq. 6 can be simplified to:

$$\alpha \left(P\right)\cong {\alpha }_{50}{\left(\frac{100}{P}-1\right)}^\frac{1}{b}.$$

(7)

Note that with α₁₀₀ = 0, the focus ordinate is the maximum non-dimensional size, ${x}_{100}^{^{\prime}}\equiv {x}_{\mathrm{max}}^{^{\prime}}={x}_{0}^{^{\prime}}$. Note also that (1) given the focal point coordinates E₀, ${x}_{0}^{^{\prime}}$, and $\alpha \left(P\right)$, one can always calculate x_P and (2) solving Eq. 5 for α, inserting it into Eq. 6 and then solving Eq. 6 for P, one retrieves the Swebrec distribution in a form that explicitly contains the energy dependence of the fragmentation. See Eq. 13 in Sect. 4.4.

Percentiles are calculated from the size distributions by interpolation at the passing values selected. Powder factors are given in Table 1; the explosive was rated by the manufacturer as having a relative weight strength 0.82, which corresponds to a mass specific energy of e = 3.19 MJ/kg. Since the explosive was the same in all tests, using mass of explosive per unit rock volume (powder factor, kg/m³) is equivalent in terms of functional fitting to using energy of explosive per unit rock volume (MJ/m³). The powder factor above grade is used as it yields a better determination with our data (powder factor above grade is used in the Kuz-Ram model, Cunningham (1983, 1987, 2005), and also in the fragmentation-energy fan model applied by Segarra et al. (2018).

If Eq. 5, with $\alpha \left(P\right)$ from Eq. 7, is fitted by an ordinary least squares algorithm, the four parameters E₀, ${x}_{0}^{^{\prime}}$, ${\alpha }_{50}$ and b are obtained. The result is as plotted in Fig. 13 left; it shows the percentile data points and the percentile fan lines of Eq. 5 for P = 80, 65, 50, 35, 20%.¹ The burden, $B$, is used as characteristic length ${L}_{\mathrm{c}}$; the determination coefficient and MAPE are shown in the figure. If the characteristic length is chosen as ${L}_{\mathrm{c}}={\sqrt{H\cdot S}}$, following the ${x}_{\text {P}}-frag$ suggestion (Sanchidrián and Ouchterlony 2017), the goodness of the fit is lower, R² = 0.9741, MAPE = 14.9%; all p-values of the parameters of the fits are less than 0.008. MAPE is affected by some outliers especially in the lower percentiles (see Fig. 13 right where absolute relative errors are plotted against the percentage passing, similarly to Fig. 12); the local MAPE is 10 to 12% in most of the range, growing towards the fines). Other blast characteristic lengths could be used (e.g., S or ${\sqrt{H\cdot B}}$), though the prediction error is slightly higher, in the present case, than with B. Note that the b value (see Table 8—SLIM series, first two rows) is related with the shape factors of the underlying size distributions, where b ranges from 2.4 to 4.2, average 3.2 for the fits ≥ 8 mm (see Table 7), which is generally the range used for building the fan (only 3% of the percentile sizes of the fan are less than 8 mm). The fits are statistically significant and unbiased, Fig. 14 shows the residuals plot, with zero mean, and the predicted versus data plot, of which the regression line has a slope of 1. The fits are done on logarithms of ${x}_{\text {P}}^{^{\prime}}$ and $E$.

Fig. 13

Left: Fragmentation-energy fan. Right: absolute relative error (ARE) of the prediction; the red line is the mean at each passing. The characteristic length is the burden

Table 8 Summary of fragmentation-energy fan results

Fig. 14

Residuals of the fragmentation-energy fan fit and predicted vs. data plot for the fit in Fig. 13 (Eqs. 5 and 7, ${L}_{\text {c}}=B$)

If the x_max slope, ${\alpha }_{100}$, is included (i.e., Eq. 6 is used instead of Eq. 7) the goodness of the fit increases marginally to R² = 0.9744, MAPE = 14.7 if ${L}_{\text {c}}={\sqrt{H\cdot S}}$, but the p values of the focus coordinates move above 0.15. Similarly with L_c = B, R² and MAPE are unchanged (0.9764 and 14.4) but in this case ${\alpha }_{100}$ is slightly negative, with p value 0.34, which confirms the non-significant dependence of x_max on the powder factor under the conditions of the blasts studied.

The focus abscissa E₀ could be interpreted as the smallest specific energy required for fracturing. It also has an apparent character of strength since it ‘opposes’ the energy concentration of the explosive (note that the energy concentration is energy per unit volume, dimensionally equal to pressure or strength). No relation has yet been established, however, of the actual E₀ value to any strength rating for a particular case. The fragmentation-energy fan in Eq. 5 can thus be supplemented with the classical power dependence of rock mass strength on size (Jaeger and Cook 1969; Hoek and Brown 1980; Scholz 1990) as follows:

$$x_{{\text{P}}}^{^{\prime}} = x_{0}^{^{\prime}} \left[ {\frac{E}{{E_{0} \left( {L_{{\text{s}}} /L_{{{\text{ref}}}} } \right)^{ - \lambda } }}} \right]^{ - \alpha \left( P \right)} = x_{0}^{^{\prime}} \left( {\frac{{EL_{{\text{s}}}^{\lambda } }}{{E_{0} L_{{{\text{ref}}}}^{\lambda } }}} \right)^{ - \alpha \left( P \right)} = x_{0}^{^{\prime}} \left( {\frac{{EL_{{\text{s}}}^{\lambda } }}{{E_{0}^{^{\prime}} }}} \right)^{ - \alpha \left( P \right)} .$$

(8)

Here L_s is a characteristic length of the blasted block and L_ref is an arbitrary reference size that, within the fan formulation, can be embedded in the focus abscissa, noted now ${E}_{0}^{^{\prime}}$; the strength size scaling exponent λ ≥ 0. Such a size-dependent strength term also appears in the non-dimensional analysis by Sanchidrián and Ouchterlony (2017), based on work by Holsapple and Schmidt (1987) and Housen and Holsapple (1990) on fragmentation in high energy impact asteroid collisions; it has also been used for the purpose of incorporating the strength-size dependence in drop-weight test fragmentation (Ouchterlony and Sanchidrián 2018). L_c, the general characteristic length may also be used for the purpose of size scaling the rock strength, e.g. ${L}_{\text {s}}={L}_{\text {c}}={\sqrt{H\cdot S}}$. The goodness of the fit is nearly unchanged, R² = 0.9742, MAPE = 15.0 (this one even gets worse). p values are nearly acceptable (the p value for λ is 0.08, with λ = 0.472, see Table 8). If burden is used, L_c = L_s = B, the results are not consistent (a large, negative λ value; a λ ≥ 0 constrained fit results in λ = 0). So the strength size-dependence implicated in Eq. 8 does not help in our case, which is not surprising as size variations are very moderate (for example, ${\sqrt{H\cdot S}}$ ranges from 6.0 to 7.1 m with our data).

This geometrical strength correction could be used to include a rock mass discontinuity description, which has a well-established effect on fragmentation. Joints were mapped in the bench faces from photogrammetry analysis using ShapeMetriX 3D software (3GSM 2010), and discrete fracture networks were built using the FracMan^® software (Golder Associates 2018), from which in-situ block size distributions (IBSD) were calculated with FracMan’s^® multi-dimensional spacing (MDS) algorithm (Bernardini et al. 2022). Two domains with distinct fracture characteristics were found for the two campaigns, as the second one was in the proximity of a major fault resulting in a more intense natural fracturing. Using the median size of the IBSD both as general characteristic length L_c and as strength-dependent reference length, L_c = L_s = (x₅₀)_IS (see Table 1) in Eq. 8, has a negative effect on the goodness of the fit: R² = 0.9724, MAPE = 16.9, though all p values are less than 0.05. Worse results are obtained if the reciprocal of fracture intensity (F_I, see Table 1), equivalent to an average fracture spacing, measured in borehole logs with optical televiewer (Bernardini et al., 2022), is used as scale, L_c = L_s = 1/F_I, R² = 0.9705, MAPE = 18.4, although all parameters are significant, see Table 8. In both IBSD and fracture intensity trials, the b parameter is inconsistently higher than all other functional tests.

The ratios ${\left({x}_{\text {P}}^{^{\prime}}\right)}_{\mathrm{data}}/{\left({x}_{\text {P}}^{^{\prime}}\right)}_{\mathrm{pred}}$ for the basic fit (Eqs. 5 and 7, fan result in Fig. 13) have been plotted against ${\sqrt{H\cdot S}}$, B and other possible strength scaling factors such as the median of the IBSD and the fracture intensity. Two of these plots are shown as an example in Fig. 15 for P = 80, 50 and 20%. The correlations are in all cases non-significant (the highest correlation coefficient is 0.32 and the lowest p value is 0.34). This explains why efforts to incorporate these variables were unfruitful. That the different fracture characteristics of the two regions did not result in different blastabilities is consistent with Lilly’s index (Lilly 1986, 1992; Scott 1996); the joint plane spacing factor in it is equal to 20 over the complete range of joint spacings of the different blasts (0.2–0.6 m, using as spacing the inverse of fracture intensity).

Fig. 15

Data/predicted ratio vs. size-related features

The orientation of joints with respect to the free face, an influential factor according to blasting practice, e.g., Lilly (1986, 1992), Scott (1996), and included in the rock mass description of the Kuz-Ram (Cunningham 1987, 2005) and xP-frag (Sanchidrián and Ouchterlony 2017) models, has not been tested. From the joints description available (Bernardini et al., 2022) five data sets were identified in the rock mass with dip orientations SW, SSE, SE, N and sub-horizontal, giving the rock face a blocky appearance. The average of Lilly’s joint orientation factor for the individual joints mapped ranges from 27.7 to 31.7 for the 12 blocks of the SLIM series blasts. This matter is revisited in Sect. 4.3.

One further source of variation in fragmentation by blasting is the delay between holes. We will discuss that in Sect. 4.4.

4.3 Previous Data Sets

A group of six blasts had been carefully monitored in the same quarry in 2012. These blasts will be referred to as the ‘2012 series’. Fragmentation was measured differently even though, as in the SLIM series, a combination of image analysis and material weighing was used. In the 2012 series, images were taken with a Split-Online^® system (Split Engineering 2010) mounted on the primary crusher’s feeder, after the feed had passed over a grizzly. The crusher bypass (i.e., the masses passing the grizzly) was sieved with a two-deck screen and the passing flows were weighed with belt scales. Thus two mass passing fractions were determined, at 120 and 25 mm, which, together with the coarse sizing obtained by image analysis allowed us to get reasonably accurate size distributions.

The 2012 blasts were done in the same rock formation, in an upper bench some 200 m from the SLIM blasts; the orientation of the 2012 blasts was different though, almost perpendicular, to the SLIM series, which may have led to a different behavior of the breakage, as mentioned in the previous section. However, assuming similar joint orientations in the 2012 series block as in the SLIM series, and considering a perpendicular orientation of the highwall faces, the average Lilly’s joint orientation factor becomes 28.3 for the 2012 series, very similar to the SLIM series range 27.7 to 31.7. This orientation factor value corresponds to strongly dipping joints with large strike angle with respect to the face direction. There are several such families, shaping a blocky structure, so that a 90° rotation of the face direction results also in strongly dipping discontinuities at a large angle hence yielding the same orientation factor value. In summary, the variation of blastability caused by joints orientation in the two series is very limited. This prevents from assessing the important effect of joints orientation, and is at the basis of the good results of the fragmentation-energy fan with merged data sets.

The explosives were different too and so were the delays, not only the delay times, but the detonators were non-electric in the 2012 series. The blasts had three rows, chevron initiated at midrow with 17 ms in-row and 42 ms inter-row delays. The multiple row character of the 2012 series is also a possible source of variability, as the SLIM series were one-row blasts, and preconditioning of the rock by the blasting of the previous rows may give finer fragmentation (Johansson and Ouchterlony 2013). A description of the 2012 series and the fragmentation measurements is made by Segarra et al. (2018). The main data are given in Table 9. Figure 16 shows the size distributions.

Table 9 2012 series blasts

Fig. 16

Size distributions of the 2012 series

The basic Eqs. 5 and 7 have been used for the merged set of the six size distributions of the 2012 series together with the eleven distributions of the SLIM series. The result is shown in Fig. 17. The parameters of the fit are given in the figure; all are strongly significant, see Table 8; ${L}_{\text {c}}={\sqrt{H\cdot S}}$ is used as characteristic length, using burden does not improve the fit in this case in terms of increased R² or reduced MAPE. The goodness of the fit is less than the ones obtained for the SLIM series alone. This is not surprising considering the differences between the two series, first different location (though similar rock masses, blastability-wise), then different detonators and delays, and finally the single vs. multiple row blasts. This should generate additional variability in the data when compared to the SLIM series. Nevertheless, the difference is small, a reduction of less than 0.01 in R² and an increase of 0.4–2.4% in MAPE, i.e. the fragmentation of both series can be described reasonably well by the same energy fan. Considering the uncertainties in the measurements, the different measuring techniques used and the differences in the blasts, this result is noteworthy.

Fig. 17

Fragmentation-energy fan of the merged 2012 and SLIM series. Crossed circles correspond to the 2012 series

The rock strength term in Eq. 8 behaves similarly for the merged test series as for the SLIM series alone, i.e., it generates a marginal improvement, better with L_s = L_c = B, R² = 0.9713, MAPE = 14.6, all parameters being significant. No joint mapping was done for the 2012 blasts though the rock mass conditions are probably similar to those of the closest blasts of the new series (the first campaign, blasts B1 to B6). Applying the IBSD median size of the first campaign to the 2012 series, R² = 0.9571, MAPE = 19.2, all p values low; results are worse with fracture intensity (mean of the first campaign holes for the 2012 blasts). In both cases, the parameter b is higher than for the other fit cases, as with the SLIM series alone. These numerical trials with the rock mass structure descriptors for the merged data sets are however speculative since no specific discontinuity mapping was performed in the 2012 series. Table 8 gives an overview of the main parameters and goodness of the fit indicators.

4.4 The Delay

Besides the powder factor and other less influential blast characteristics, the experimental design of the SLIM series was made to assess the impact of the delay on fragmentation. The delay affects the breakage cooperation between holes, and it is believed that an optimum (i.e., the finest) fragmentation is obtained at a certain, non-zero delay. Current fragmentation prediction formulae include delay as an influential variable; both the Kuz-Ram (Cunningham 2005) and the ${x}_{\text {P}}-frag$ (Sanchidrián and Ouchterlony 2017) include multiplicative delay factors in the fragment size expression so that fragment sizes decrease from zero delay (simultaneous initiation of holes or instantaneous blast) up to an optimum delay time at which fragment size is minimal. Longer delays reduce the cooperation and the fragment size increases, see Fig. 18. The delay factors are functions of a non-dimensional delay number ${\Pi }_{t}$ that depends on the p-wave velocity and a characteristic length, the burden in Kuz-Ram and the spacing in ${x}_{\text {P}}-frag$. For the Kuz-Ram (Cunningham 2005, Fig. 18 left):

$$f_{t} \left( {{\Pi }_{t} } \right) = 0.000174{\Pi }_{t}^{3} {-}0.000534{\Pi }_{t}^{2} {-}{ }0.1013{\Pi }_{t} { } + { }2.05,{\Pi }_{t} \le 15.6,$$

(9)

$$f_{t} \left( {{\Pi }_{t} } \right) = 0.0064{\Pi }_{t} { } + { }0.9,{\Pi }_{t} > 15.6$$

Fig. 18

Delay factors. Left: Kuz-Ram, right: ${x}_{\text {P}}-frag$

where ${\Pi }_{t}={c}_{\text {P}}\Delta t/B$, c_P being the p-wave velocity and $\Delta t$ the in-row delay. For the ${x}_{\text {P}}-frag$ (Sanchidrián and Ouchterlony 2017, Fig. 18 right):

$${f}_{t}\left({\Pi }_{t}\right)={\delta }_{1}+(1-{\delta }_{1}-{\delta }_{2}{\Pi }_{t}){e}^{-{\delta }_{3}{\Pi }_{t}}$$

(10)

where δ₁, δ₂, δ₃ are functions of the percentage passing $P$ (see Eqs. 51 and 52 shown in Table 8 of Sanchidrián and Ouchterlony 2017); ${\Pi }_{t}={c}_{\text {P}}\Delta t/S$, S being holes spacing.

If correct, both delay factors predict that fragment sizes may be reduced significantly if a certain (optimum) delay is used instead of a simultaneous initiation (approximately halved) or a blast with very long delays. Different optimum delays follow from each model though, ${\Pi }_{t}$ = 15.6 in the Kuz-Ram and in the range of 35–40 for ${x}_{\text {P}}-frag$, which means that ${x}_{\text {P}}-frag$ favors a slower initiation sequence than the Kuz-Ram. For the SLIM blast series studied here, with burdens, spacings and p-wave velocities given in Table 1, these numbers would result in optimum delays of about 9 ms and 22 ms for the Kuz-Ram and ${x}_{\text {P}}-frag$ models, respectively. The delays used in the SLIM blasts, 4 and 23 ms, were aiming at blasting one set of rounds in the low cooperation, short delay zone, with non-dimensional delay number Π_t = 6.5, and another set of rounds with a delay near the optimum value of the ${x}_{\text {P}}-frag$ delay factor, i.e., Π_t = 37.5. The ordinary production blasting in-row delay in the quarry was 17 ms (the nominal delay of the 2012 series), which corresponds to a delay number (using as c_P the average measured in blasts B1 to B6 of the SLIM series, see Table 1) of Π_t = 28.

In the fragmentation-energy fan formulation, the delay effect should preferably be incorporated as a blastholes cooperation function, ${f}_{cd}$, a modifier of the energy available for fragmentation from a single hole (energy concentration, or powder factor), in a way that it increases up to the optimum and then decreases when cooperation no longer takes place efficiently, at longer delays. This behavior can be obtained with a functional dependence as the reciprocal of Eq. 10 (with δ₁, δ₂ and δ₃ constant) so that, when raised to negative exponents, it results in delay factors of the type in Fig. 18:

$${x}_{\text {P}}^{^{\prime}}={x}_{0}^{^{\prime}}{\left(\frac{E {f}_{cd}}{{E}_{0}}\right)}^{-\alpha (P)},$$

(11a)

$${f}_{cd}={\left[{\delta }_{1}+(1-{\delta }_{1}-{\delta }_{2}{\Pi }_{t}){e}^{-{\delta }_{3}{\Pi }_{t}}\right]}^{-1}.$$

(11b)

Plotting the ratios of fragment sizes data over predicted with the plain fan, Eqs. 5 and 7, in a similar fashion as in Fig. 15, against the delay number, the graph in Fig. 19 left is obtained for the three percentiles 80, 50 and 20 as examples. Merged data from the SLIM and 2012 series have been used assuming that, despite the 2012 series were three-row blasts, the 42 ms inter-row delay was long enough not to affect substantially the in-row holes cooperation and that the additional breakage from fragments colliding is compensated by the front row(s) not moving out fast enough and preventing some of the tensile reflection. The ordinates of the plot are the relative factors, i.e., the numbers that the plain fan predictions should be multiplied by to get the data values. Functions of the type of Eq. 10 have been fitted, with the results shown in Fig. 19 left. The R² of the fits are less than 0.20, with δ₂ and δ₃ extremely non-significant in all cases. Still, there seems to be a tendency in the 80 and 20 percentiles to decrease with the delay (i.e., increased cooperation), with an indication of a possible minimum only in the 20 percentile curve.

Fig. 19

The delay effect: size reduction factors (delay factors) and cooperation functions. Left: data-to-predicted ratios for the plain fan, SLIM and 2012 series merged, as function of the non-dimensional delay number. Right: cooperation functions (magenta lines) and delay factors (color lines), SLIM series alone, fits with Eqs. 7, 10 and 11; solid lines: ${L}_{\text {c}}=B$; dashed lines: ${L}_{\text {c}}={\sqrt{H\cdot S}}$

When Eq. 11, with Eq. 7, are fitted to the SLIM series with ${L}_{\text {c}}={\sqrt{H\cdot S}}$, the goodness of the fit increases moderately with respect to the plain fan: R² = 0.9825, MAPE = 12.2. All p values are less than 0.05 except for one of the delay function parameters (δ₂, see Table 8). The cooperation function ${f}_{cd}$ is plotted in Fig. 19 right (dashed magenta line), together with the delay factors ${f}_{t}\left({\Pi }_{t}\right)={{f}_{cd}^{-{\alpha }_{\text {P}}}=\left[{\delta }_{1}+(1-{\delta }_{1}-{\delta }_{2}{\Pi }_{t}){e}^{-{\delta }_{3}{\Pi }_{t}}\right]}^{{\alpha }_{\text {P}}}$ for some percentile sizes (dashed color lines). The cooperation function has a maximum (hence the delay factors have minima) at ${\Pi }_{t}$=38.0 and then decreases to values below 1 when ${\Pi }_{t}$>42, which means less fragmentation cooperation between holes at long delays than if they were fired simultaneously. This could make sense as too long a delay effectively limits the interaction of the shock waves and of the stress fields from neighboring holes but it may be an artifact of the fit, especially the fast decline beyond the optimum point. The higher ${\Pi }_{t}$ value is 42.9 so this behavior takes place in the edge of the data range, with a questionable significance of one of the cooperation function parameters which makes the fast change from positive to negative cooperation unlikely. The main parameters of the fan fit are given in the fan plot, Fig. 20 left. If $B$ is used as the scale (${L}_{\text {c}}=B$) the goodness of the fit is lower (see Table 8 and Fig. 20 right), but the cooperation function has a shape similar to those shown in Fig. 18, with a maximum (mild though) at about ${\Pi }_{t}$=9, see Fig. 19 right (solid lines), and a slight decline in the cooperation at longer delays. The delay factors mirror the cooperation function and show an initial decline and beyond the minimum a slight growth towards a constant value.

Fig. 20

Fragmentation-energy fans for the SLIM series with delay factor. Left: ${L}_{\text {c}}={\sqrt{H\cdot S}}$; right: ${L}_{\text {c}}=B$. Percentiles shown are 80, 65, 50, 35 and 20%

If the SLIM and 2012 series are analyzed together, using ${L}_{\text {c}}={\sqrt{H\cdot S}}$, the delay improves very mildly the goodness of the fit (R² = 0.9703, MAPE = 15.0 compared to R² = 0.9676, MAPE = 15.3 of the plain fan), with one of the parameters of the cooperation function statistically non-significant (though not too severely). The appearance of the cooperation function is similar to that for the SLIM data alone with this scaling. The ${L}_{\text {c}}=B$ scaling does not converge to a sound solution.

Including the strength scale term in the model, the percentiles function becomes:

$${x}_{\text {P}}^{^{\prime}}={x}_{0}^{^{\prime}}{\left(\frac{E {L}_{\text {c}}^{\lambda } {f}_{cd}}{{E}_{0}^{^{\prime}}}\right)}^{-\alpha (P)}$$

(12)

with very similar result as Eqs. 11 for the SLIM series, i.e., slight improvement of the fit, see Table 8. In this case, the ${L}_{\text {c}}={\sqrt{H\cdot S}}$ scaling converges to a negative $\lambda$; if a condition $\lambda \ge 0$ is set, the fit converges to $\lambda =0$ i.e. no strength variation with scale (equivalent to using Eq. 11). The ${L}_{\text {c}}=B$ scaling gives sound results with altogether higher R² for the analysis of the two combined series. The fan, the delay cooperation function and the delay factors are shown in Fig. 21. The delay effect replicates the SLIM series behavior, see Fig. 19 right. The cooperation has a maximum at a similar delay (around ${\Pi }_{t}$=9) but the cooperation effect is somewhat milder.

Fig. 21

Fragmentation-energy fan fits with delay and size-dependent strength, Eq. 12, ${L}_{\text {c}}=B$. Left: the fan; crossed circles correspond to the 2012 series; percentiles shown are 80, 65, 50, 35 and 20%; the vertical lines and the labels indicate the size distributions shown in Fig. 22. Right: delay functions

Fig. 22

Examples of some distributions calculated from the fan constants for the combined SLIM and 2012 series blasts (Fig. 21 left); circle markers are the data points; the corresponding percentile points are labeled in the fan plot of Fig. 21 left

These results point towards (1) a cooperation maximum (i.e., a fragment size minimum) exists at a certain delay, but (2) the actual location of that optimum remains uncertain, and (3) the effect of the delay may not be as strong as what the ${x}_{p}-frag$ and Kuz-Ram models predict. The results for the SLIM series alone indicate a reduction of about 20% for high percentiles to about 50% for low percentiles but the combined two-series data limit that effect to a moderate 15–30% of size reduction—the higher value again obtained for the finer sizes.

The position of the maximum of the cooperation function (from which the optimum delay should be determined) has been a topic of debate in the blasting community; Kuz-Ram and ${x}_{\text {P}}-frag$ lead to different delay optimums, and also different values result from the work by different authors, e.g. Chung and Katsabanis (2000), Johansson and Ouchterlony (2013), Katsabanis et al. (2014), Petropoulos et al. (2014), Omidi (2015), Katsabanis and Omidi (2015), Yi et al. (2017) and Saadatmand Hashemi and Katsabanis (2020). Optimum delays are suggested at non-dimensional delay number as small as ${\Pi }_{t}$=1.5 (Petropoulos et al. 2014, experimental; authors discuss that the minimum may not be significant as the blast in which minimum size occurred had a slightly higher powder factor than others), ${\Pi }_{t}$=1.8 (Yi et al. 2017, numerical modeling; the discussion however concludes that the numerical results cannot support the hypothesis that very short delay time may improve fragmentation), ${\Pi }_{t}$=3 (Johansson and Ouchterlony 2013, experimental), ${\Pi }_{t}$=5 to 10 (Saadatmand Hashemi and Katsabanis 2020, numerical modeling), ${\Pi }_{t}$ around 30 (Katsabanis et al. 2014; Katsabanis and Omidi 2015; Omidi 2015, experimental) and even ${\Pi }_{t}$ in excess of 100 (Chung and Katsabanis 2000); Saadatmand Hashemi and Katsabanis do not observe a minimum for ${x}_{50}$ (or a very mild one, also compatible with an asymptotical-like behavior), but they do observe a minimum for ${x}_{80}$, quite similar to the delay functions in Fig. 19 right (solid lines) and Fig. 21 right. It is generally recognized that mechanisms other than shock wave interactions (that suggest optimum short delays) may be playing a role in fragmentation at longer delays (e.g., crack extension and gas penetration, Zhang et al. 2021) where shock waves from neighboring holes do not interact. Cunningham (2005) explains that the optimum delay corresponds to a window where stress waves and fracture growth operate optimally before movement within the rock mass interferes with these mechanisms. This remains a matter of discussion, for which additional analysis of quality fragmentation data would be very valuable. The fragmentation-energy fan offers an excellent analytic frame for such an analysis.

The size distributions can be calculated in an explicit form solving the fan equation for P; from Eqs. 12 and 6:

$$P\left( x \right) = \frac{100}{{1 + \left[ {\frac{{\frac{{\ln x_{0}^{^{\prime}} - \ln \left( {\frac{x}{{L_{\text {c}} }}} \right)}}{{\ln \left( {E L_{{\text{c}}}^{\lambda } f_{{{\text{cd}}}} } \right) - \ln E_{0}^{^{\prime}} }} - \alpha_{100} }}{{\alpha_{50} - \alpha_{100} }}} \right]^{b} }}.$$

(13)

Figure 22 shows some size distributions, which are in fact converted fan fits using Eq. 13. The fidelity is quite high, MAPE ranges from 0.7% (B1) to 14.5% (B12); both blasts B1 and B12 (best and worst fidelity to the experimental data) are included in the plot, together with other with intermediate errors. Median errors are used here as a more robust indicator than the mean, this one strongly affected by occasional large relative errors in the very fines (see Fig. 13 right).

4.5 An Overall Perspective

The fragmentation-energy fan formulation allows one to predict fragment sizes for a given rock mass at any powder factor with just four parameters, or five if we allow ${\alpha }_{100}\ne 0$ (a single size distribution for a given powder factor requires three parameters if the Swebrec function is used), with determination coefficients of 0.97 and prediction errors less than 15%—similar to what a size distribution fit for a single powder factor value often yields.

Obtaining quality fragmentation data in full scale blasts is a laborious and costly task, with many possibilities of errors and inaccuracies that have to be overcome, which makes it difficult to draw conclusions on fragmentation features that may stay hidden by the overriding influence of the powder factor. Sanchidrián (2015) compared size distributions measured by sieving from blasts with the same design parameters, and calculated an average dispersion of about 15% in sizes at equal percentages passing, a combined measure of the uncertainty of the fragmentation measurement (due to sampling, sieving and weighing), the variability of the phenomenon and the uncertainty of the rock and blasting data stemming from natural variations in rock conditions, drilling and charging. To all of this, the calculation of percentiles adds an interpolation error. Our opinion is that much of the dispersion observed e.g. in the fan plots of Figs. 13 (left), 17, 20 and 21 (left) and in the size distributions (Fig. 22), the errors in Fig. 13 (right) and the residuals in Fig. 14 are the results of that uncertainty, difficult to avoid.

5 Conclusions

In the SLIM project, the fragmentation of 12 full scale blasts was measured by sieving a significant fraction of the muckpiles, from about 50–100%. For one blast, the coarse cut measurement could not be made so its results were not used. The size distributions obtained are believed to be as accurate as can be measured with reasonable efforts, containing the inevitable errors caused by a mine’s production environment.

The size distributions are in the remaining eleven cases well fitted with the Swebrec function (within the usual percentage passing range of validity of that distribution, i.e., 100% to about 5%). This suggests that the fragmentation model of the quarry may be built primarily on the relation between the percentiles of the fragment size distributions and the explosive energy concentration in the rock (the powder factor), using the fragmentation-energy fan concept. The basic fan formulation can be expressed as a function of four parameters only: the coordinates of the fan’s focal point, E₀, ${x}_{0}^{^{\prime}}$, the slope ${\alpha }_{50}$ and b (Swebrec’s undulation parameter). These parameters can be determined by a non-linear least squares fit to the normalized percentile fragment sizes ${x}_{\text {P}}^{^{\prime}}$. Setting ${\alpha }_{100}$ equal to zero doesn’t seem to have a significant effect.

The fragmentation-energy fan formulation has been tested with a group of seventeen blasts comprising the eleven SLIM blasts monitored in this work, plus six more from previous work in the same quarry (the 2012 series), where fragmentation was also partly determined by sieving. This extended set of blasts, all carried out in essentially the same rock mass, included variation of characteristic sizes (burden, spacing), explosives, delays, detonator type and joints orientation with respect to the bench face. The simple fan formulation allows the prediction of the fragment size with an outstanding determination coefficient of nearly 0.9676 and a mean absolute percentage error just above than 15%, which lies in the range of the measurement error. This means that, if rock mass conditions do not change too much, the energy concentration or powder factor is the single variable that can explain most of the variance of fragmentation, even if other influential variables (like delay interval as tested in this work) have been made to vary as well; the fragmentation-energy fan is a convenient formulation for that dependency.

A size scaling of the rock strength, used with success in applications of the fragmentation-energy fan for drop weight test modeling and also employed in the ${x}_{\text {P}}-frag$ model, has been tested here without a clear improvement of the prediction error, that only takes place in some of the cases and formulations studied. This limited influence, that also applies to rock mass characterizations such as joint spacing and in-situ block size distribution median size, is explained by the limited variability of the rock mass in our data set, as all blasts were carried out in the same quarry and sector. Even the different orientation of the highwall face in some blasts (the 2012 series) does not seem to encompass a significant variation of blastability due to the blocky structure of the rock mass.

The effect of delay on the breakage cooperation between holes has been tested; delays of 4 and 23 ms (electronic) were employed in the SLIM blasts, while 17 ms (pyrotechnic) had been used in the older 2012 series. The incorporation of a cooperation function of the type used in ${x}_{\text {P}}-frag$ (i.e., increasing cooperation with delay time, starting from instantaneous initiation until a maximum is reached, then decreasing as the delay further increases) has a significant effect on the fragmentation-energy fan description of fragmentation, with a prediction error of 12% for the SLIM blasts alone and 14.5% for the merged series; further reductions of the prediction error are believed to be particularly difficult to achieve as the measurement error is estimated to be in that range. No definitive conclusion can be drawn on the existence of an optimum delay and its precise time from the data in this work, as different results have been obtained with merged and SLIM only data sets and using different scaling length. Some results would indicate an optimum time at ${\Pi }_{t}$ around 40, more in line with ${x}_{\text {P}}-frag$’s prediction, though the shape of the cooperation function in this case (both the slow initial growth and the fast decay beyond the maximum) is not strongly supported. Nor can a shorter optimum delay interval than predicted by Kuz-Ram or ${x}_{\text {P}}-frag$ (around ${\Pi }_{t}$=10) be ruled out by the data in this work. The results also show that the observed effect of the delay on fragmentation may not be as strong as existing fragmentation models predict; rather, in some cases, at most a moderate 15 to 30% of reduction in fragment size—the higher value occurring at the finer sizes—could be expected from an optimal choice of the delay time.

Appendix

1.1 Fragmentation data

See Tables 10, 11, 12 and 13.

Table 10 Size distributions of the m_F fractions passing the grizzly (< 120 mm, Fig. 6)

Table 11 Size distributions of grueso (Fig. 9 left)

Table 12 Size distributions of grizzly roll-off (Fig. 9 right)

Table 13 Final size distributions (Fig. 10)