A Distribution-Free Description of Fragmentation by Blasting Based on Dimensional Analysis

Abstract

A model for fragmentation in bench blasting is developed from dimensional analysis adapted from asteroid collision theory, to which two factors have been added: one describing the discontinuities spacing and orientation and another the delay between successive contiguous shots. The formulae are calibrated by nonlinear fits to 169 bench blasts in different sites and rock types, bench geometries and delay times, for which the blast design data and the size distributions of the muckpile obtained by sieving were available. Percentile sizes of the fragments distribution are obtained as the product of a rock mass structural factor, a rock strength-to-explosive energy ratio, a bench shape factor, a scale factor or characteristic size and a function of the in-row delay. The rock structure is described by means of the joints’ mean spacing and orientation with respect to the free face. The strength property chosen is the strain energy at rupture that, together with the explosive energy density, forms a combined rock strength/explosive energy factor. The model is applicable from 5 to 100 percentile sizes, with all parameters determined from the fits significant to a 0.05 level. The expected error of the prediction is below 25% at any percentile. These errors are half to one-third of the errors expected with the best prediction models available to date.

1 Introduction

The main goal of rock blasting is the fragmentation of the rock mass. Prediction of the size distribution of the fragmented rock from the rock mass characteristics, the blast design parameters (both in terms of the geometry and of the initiation sequence) and the explosive properties is a challenge that has been undertaken for decades, and is currently available to the blasting engineer in the form of formulae that relate the parameters of a given size distribution function to the rock properties and the blast design parameters.

One of the most relevant fragmentation by blasting formulae is the Kuznetsov (1973) one:

$$x_{m} = Aq^{ - 0.8} Q^{1/6}$$

(1)

where x _m is the mean fragment size in cm, A is a rock strength factor in the range 7–13, q is the powder factor (or specific charge, or charge concentration—explosive mass per unit rock volume) in kg/m³ and Q is the charge per hole in kg. These three factors comply essentially with the expected behavior of rock fragmentation by blasting. Essentially, the Kuznetsov formula means that (1) the harder the rock, the bigger the fragments; (2) the higher the specific amount (powder factor) of explosive, the smaller the fragments; and (3) the larger the scale (the charge per hole is used as scale factor, and larger charges per hole indicate larger drill patterns), the larger the fragments. In Eq. 1, the amounts of explosive in the powder factor and the charge per hole are given in TNT equivalent mass. Such equivalent mass can be calculated multiplying the mass of explosive by its relative strength with respect to TNT; if such strength is θ, Eq. 1 can be written as (Kuznetsov 1973, Eq. 12):

$$x_{m} = Aq^{ - 0.8} Q^{1/6} \theta^{ - 19/30}$$

(2)

in which q and Q refer to actual mass of explosive of relative strength θ. Equation 1 or its equivalent Eq. 2 is written originally for the mean size x _m of a Rosin–Rammler (RR) distribution (Rosin and Rammler 1933; Weibull 1939, 1951) that was assumed to accurately describe the fragmented rock. The Rosin–Rammler, or Weibull, cumulative distribution function is:

$$P\left( x \right) = 1 - \exp \left[ { - \left( {\frac{x}{{x_{\text{c}} }}} \right)^{n} } \right] = 1 - \exp \left[ { - \ln 2\left( {\frac{x}{{x_{50} }}} \right)^{n} } \right]$$

(3)

where x _c is the characteristic size (the size for which the passing fraction is 1 − 1/e, or 63.2%) and n is a shape factor, usually quoted as uniformity index; the expression on the right is written with the median size x ₅₀ instead of x _c. The use of the RR distribution for rock fragmented by blasting had been positively assessed by Baron and Sirotyuk (1967) and Koshelev et al. (1971), which is used by Kuznetsov (1973).

The Soviet literature of the time does not make it entirely clear whether Eqs. 1 or 2 refer to the mean or the characteristic size (which value is close to the mean if the shape index of the distribution is not much different than one). There has been some controversy (Spathis 2004, 2009, 2012, 2016; Ouchterlony 2016a, b) about the actual size that the Kuznetsov formula was addressing. For all practical purposes, it has been calibrated, tailored and used over the years to estimate the median size x ₅₀ (Cunningham 1987, 2005; Rollins and Wang 1990; Raina et al. 2002, 2009; Liu 2006; Cáceres Saavedra et al. 2006; Borquez 2006; Rodger and Gricius 2006; Vanbrabant and Espinosa Escobar 2006; Mitrovic et al. 2009; Engin 2009; Gheibie et al. 2009a, b; Bekkers 2009; McKenzie 2012; Sellers et al. 2012; Faramarzi et al. 2015; Jahani and Taji 2015; Singh et al. 2015; Adebola et al. 2016).

Kuznetsov derived his formula based on blasting tests in limestone specimens reported by Koshelev et al. (1971). These consisted of eleven small- to mid-scale shots in irregular limestone blocks, with RDX charges of 0.5–500 g. Kuznetsov then assessed the formula with some data from large-scale tests by Marchenko (1965), 6 blasts in limestone, 6 blasts in a medium-hard rock and 14 blasts in hard and very hard rock (the exact rock type is not reported, nor is the explosive used). A values recommended by Kuznetsov were 7, 10 and 13 for medium-to-hard, hard fissured and hard massive rocks, respectively. Kuznetsov mentions that the mean deviation of experimental data from the theoretical (i.e., predicted) data is ±15%; a detailed analysis of the data and the predictions by Eqs. 1 or 2 gives a mean error of 9%, with minimum and maximum errors of −42 and 55%, respectively (Ouchterlony 2016a). This matter will be re-assessed in this work.

About ten years after its publication, the Kuznetsov formula was popularized by Cunningham (1983), who wrote it so as to use the relative weight strength with respect to ANFO, the standard explosive in civil applications, instead of TNT, in what became the popular Kuz-Ram model. In his text, Cunningham uses the term ‘mean fragment size,’ but his mathematical definition of it implies the median; he in fact uses the symbol x ₅₀. In the Kuz-Ram papers that followed (Cunningham 1987, 2005), the term mean is also used but again contradicted by figures and equations that imply x ₅₀:

$$x_{50} = Aq^{ - 0.8} Q^{1/6} \left( {\frac{\text{RWS}}{115}} \right)^{ - 19/30}$$

(4)

Here RWS is the relative weight strength (heat of explosion, or energy in general, ratio with respect to ANFO, in percent; 115 is the relative weight strength of TNT). Cunningham (1987) adapted a blastability index proposed by Lilly (1986) to replace Kuznetsov’s numerical rock factor:

$$A = 0.06 \cdot \left( {{\text{RMD}} + {\text{JF}} + {\text{RDI}} + {\text{HF}}} \right)$$

(5)

The form of the rock mass description term (RMD) has had some changes over the years; in its final form (Cunningham 2005), it is:

• RMD = 10 (powdery/friable), JF (if vertical joints) or 50 (massive);

• JF (joint factor) = JPS (joint plane spacing) + JPA (joint plane angle);

• JPS = 10 (average joint spacing S _J  < 0.1 m), 20 (0.1 ≤ S _J  < 0.3 m), 80 (0.3 m ≤ S _J  < 0.95·(B·S)^1/2, B and S being burden and spacing), 50 (S _J  > (B·S)^1/2). Cunningham (2005) incorporates a joint condition correction factor that multiplies the joint plane spacing, with value 1, 1.5 and 2 for tight, relaxed and gouge-filled joints, respectively;

• JPA = 20 (dip out of face), 30 (strike perpendicular to face) or 40 (dip into face). Cunningham does not give a JPA value for horizontal planes but Lilly (1986) assigns them JPA = 10.

The rock density influence (RDI) is:

• RDI = 0.025·ρ − 50.

ρ being density (kg/m³). Finally, the hardness factor (HF) is:

• HF = E/3 if E < 50, or

• HF = σ _c/5 if E > 50.

σ _c and E being uniaxial compressive strength (MPa) and Young’s modulus (GPa).

The form of RMD implies that JF may enter twice in Eq. 5, directly and through RMD. The direct term in Eq. 5 Cunningham (1987) is in all probability a printing error and Cunningham (2005) removed it in later Kuz-Ram model updates, so that:

$$A = 0.06 \cdot \left( {{\text{RMD}} + {\text{RDI}} + {\text{HF}}} \right)$$

(6)

Cunningham (2005) also incorporated a delay-dependent factor in the central size formula, based on Bergmann et al. (1974) data:

$$\begin{aligned} A_{t} & = 0.66\left( {\frac{{\Delta T}}{{T_{\hbox{max} } }}} \right)^{3} \,-\, 0.13\left( {\frac{{\Delta T}}{{T_{\hbox{max} } }}} \right)^{2} \,-\, 1.58\left( {\frac{{\Delta T}}{{T_{\hbox{max} } }}} \right) + 2.1, \quad \frac{{\Delta T}}{{T_{\hbox{max} } }} < 1 \\ A_{t} & = 0.9 + 0.1\left( {\frac{{\Delta T}}{{T_{\hbox{max} } }} - 1} \right), \quad \frac{{\Delta T}}{{T_{\hbox{max} } }} > 1 \\ \end{aligned}$$

(7)

where $T_{\hbox{max} } = 15.6B/c_{P}$; ΔT is in-row delay (ms), B is burden (m) and c _P is P-wave velocity (m/ms). Note that A _t is not continuous at ΔT/T _max = 1, but replacing the constant term 2.1 by 2.05 would make it so.

As previously stated, the various factors (e.g., the rock description pre-factor 0.06) were tailored by Cunningham to fit the median. The final form of the Kuznetsov–Cunningham formula should be (Cunningham 2005):

$$x_{50} = AA_{t} q^{ - 0.8} Q^{1/6} \left( {\frac{\text{RWS}}{115}} \right)^{ - 19/30} C\left( A \right)$$

(8)

The factor C(A) is included in order to correct the predicted median size, to be determined experimentally from data in a given site; according to Cunningham, it would normally be within the range 0.5 < C(A) < 2.0. This suggests a prediction error expected of up to about 100%. This is larger than Kuznetsov’s (1973) error bounds, but while Kuznetsov’s A values lie in the range 7–13, Cunningham (1987) covers the much wider range 0.8–22.

Besides adapting Kuznetsov’s central size formula, Cunningham (1983) followed up the conclusion of the Soviet researchers that the fragmented rock could be described by the RR function and formulated an equation for the uniformity or shape index (n in Eq. 3); in its final form, after several corrections and refinements (Cunningham 1987, 2005), the shape index for the RR distribution of rock fragments is:

$$n = n_{s} \left( {2 - 0.03\frac{B}{d}} \right)^{0.5} \left( {\frac{1 + S/B}{2}} \right)^{0.5} \left( {1 - \frac{W}{B}} \right)\left( {\frac{{l_{\text{c}} }}{H}} \right)^{0.3} \left( {\frac{A}{6}} \right)^{0.3} C(n)$$

(9)

where W is drilling deviation, l _c is charge length, H is bench height and n _s is a factor that accounts for the delay precision:

$$n_{s} = 0.206 + \left( {1 - R_{s} /4} \right)^{0.8} ,\quad R_{s} = 6s_{t} /\Delta T$$

(10)

where s _t is the standard deviation of the initiation system. The factor C(n) is, again, a variable correction to match experimental data if available; no expected range is given to it.¹

The Kuznetsov–Cunningham formula is physically sound, as previously discussed. Similar forms may be obtained applying asteroid collision principles (Holsapple and Schmidt 1987; Housen and Holsapple 1990) as shown by Ouchterlony (2009b). However, the experimental data supporting the median size expression are, as mentioned above, extremely limited. Furthermore, no experimental data supporting the shape index formula seem to have been reported. The initial shape index dependence on geometry appears to originate in 2D blast modeling by Lownds (1983) (Cunninghan 1983, p. 441).²

The assessment of the Kuz-Ram model by, e.g., the JKMRC (Kanchibotla et al. 1999; Thornton et al. 2001; Brunton et al. 2001) and other publications (e.g., Ford 1997; Morin and Ficarazzo 2006; Gheibie et al. 2009a, b; Hafsaoui and Talhi 2009; Strelec et al. 2011; Tosun et al. 2014) seldom include hard experimental data and are often obscured by the lack of real knowledge of the resulting muckpile fragmentation, which hinders a reliable error assessment. A generally accepted weakness of the Kuz-Ram model is that it normally predicts too few fines in a muck pile. This led to model extensions involving one RR function for the coarse material and another for the fines, the crush zone model (CZM, Kanchibotla et al. 1999; Thornton et al. 2001; Brunton et al. 2001) and the two-component model (TCM, Djordjevic 1999) from the JKMRC. Of these, the CZM has become the one more used. The CZM rests on the assumption that the fines come from a volume around the borehole in which the rock may fail under compression (it is ‘crushed’); the radius of the crush zone is:

$$r_{\text{c}} = r_{\text{b}} \sqrt {\frac{{P_{\text{b}} }}{{\sigma_{\text{c}} }}}$$

(11)

where r _b is the borehole radius, P _b is the borehole pressure and σ _c is the uniaxial compressive strength. The crushed volume is a fraction F _c of the volume excavated by each borehole, BHS:

$$F_{\text{c}} = \frac{{\pi \left( {r_{\text{c}}^{2} - r_{\text{b}}^{2} } \right)\left( {H - l_{\text{s}} } \right)}}{\text{BHS}}$$

(12)

where l _s is the stemming length. The crushed zone maximum size of fragments is assumed to be 1 mm. The CZM uses the Kuz-Ram model³ for the coarse part (above 50% passing for competent rock, σ _c > 50 MPa, and 90% for soft rock, σ _c < 10 MPa), below which a second RR function is used, defined so as to include (for the competent rock case) the (x ₅₀, 0.5) and (1 mm, F _c) points; for the soft rock case, the grafting point is (x ₉₀, 0.9).⁴ Such a ‘fines’ RR function is defined by x ₅₀ and a uniformity index n _f :

$$n_{f} = \frac{{\ln \left[ { - \frac{{\ln \left( {1 - F_{c} } \right)}}{\ln 2}} \right]}}{{\ln \left[ {1/x_{50} \left( {\text{mm}} \right)} \right]}}$$

(13)

An analogous expression can be obtained for the soft rock case.

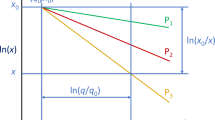
Both the Kuz-Ram model and its CZM extension have been assessed with the data set of 169 blasts that is described in Sect. 3. Figure 1 shows the logarithmic errors of the size prediction:

$$e_{L} = { \ln }\left( {\frac{{x^{*} }}{x}} \right)$$

(14)

where x* and x are predicted and data sizes, respectively.⁵

Fig. 1

Boxplots of the prediction error for the Kuz-Ram and crush zone models, based on the data set of 169 blasts. Blue boxes Kuz-Ram; magenta boxes CZM. Horizontal lines show the ln 1.5 and −ln 1.75 levels, equivalent to relative errors +50 and −75% (color figure online)

The error of the Kuz-Ram and crush zone predictions in about half of the cases (the interquartile range) lies within an approximate range [−0.6, 0.4], roughly equivalent to relative errors −75 to +50% in nearly the whole percentage passing range. The prediction is noticeably negative-biased (the sizes predicted are smaller than the data) in most of the range except the upper end. Other conclusions from Fig. 1 are that the largest bias occurs in the central zone, which suggests that (1) the median size formula has a limited predictive capability in terms of accuracy, with a systematic error of some −30%; the precision (i.e., the random error around the central value) is also limited, with the interquartile range of about [−75, +50%]; this prediction error is larger than the assessment by Ouchterlony (2016a) on the original Kuznetsov’s formula (−42 to 55% maximum error), though the number of blasts used in the present case more than quadruples the data set used by Kuznetsov; (2) the prediction in the extremes of the range analyzed is somewhat better than in the central range which means that also the uniformity (the overall slope in the size/passing plot in log–log) of the distribution is generally overestimated.

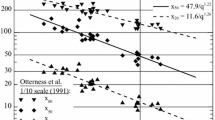
The data from the seminal small-scale (bench height of about 1 m) blasting tests by Otterness et al. (1991) underscore the above. Plotting some percentile sizes as a function of the powder factor from a selection of 10 blasts of nearly identical geometry gives the results shown in Fig. 2. Power laws fit each percentile size quite well (the determination coefficients are given in the figure; both the pre-factor and the exponent are significant in all the fits, and the maximum p values are 0.002 for the pre-factor and 0.003 for the exponent). Ouchterlony et al. (2016) show that such pattern requires that (1) the RR exponent would need to be variable at different percentiles (which would require a different function—e.g., a piecewise RR with variable exponent), and (2) its value should depend on the specific charge; only if the exponent of the power law $x_{P} = {\text{const}}/q^{\kappa }$ is constant in some percentile interval, then the RR exponent might not depend on q, but it would still need to vary at different percentiles. This fundamental discrepancy with the experimental evidence lies at the core that the RR function with a single n value is a poor description of the fragmentation data, and a severe hindrance for its use in state-of-the-art fragmentation prediction models.

Fig. 2

Log–log interpolated percentile size data x _P for rounds #1, 2, 5, 6, 13, 14, 18, 19, 25, 29 from Otterness et al. (1991) with P = 20, 35, 50, 65 and 80%. Fitted power laws x _P  = A/q ^κ are plotted (color figure online)

The x _P versus specific charge convergent lines pattern (which we call ‘fan’ plots) is a general characteristic of fragmentation by blasting. In fact, most of the groups of data that form the basis for this work show the same behavior as the data in Fig. 2; power laws fit the percentile size data to the powder factor quite well, and the exponent is a function of P. In well-controlled model-scale blasts, this behavior is extremely well developed; the consequences of that are discussed in Ouchterlony et al. (2016).

The facts above are not described by any known credible theory of blast fragmentation that favors a specific fragment size distribution. On the contrary, they speak in favor of developing prediction equations for blast fragmentation that do not depend on any specific size distribution function. Size and passing data have a clear physical meaning, whereas shape, or uniformity, indices are just a reduced interpretation of the data through some particular size distribution. A median, or a 20 percentile size, even a 63.2 percentile like x _c, have their full meaning without any additional statement; however, a shape index has no real meaning unless it is tied to a particular distribution—a RR, a Swebrec, a lognormal, a maximum-size-transformed RR one, etc.

2 The Model Foundations

Ouchterlony’s (2009b) blasting-related interpretation of Holsapple and coworkers’ work on asteroid collisions (Holsapple and Schmidt 1987; Housen and Holsapple 1990) has already been mentioned. From the dimensional analysis, Ouchterlony arrives at the following expression for the fraction P of fragments of mass less than m:

$$P = F_{1} \left( {\frac{m}{M},\Pi _{\text{s}} ,\Pi _{\text{g}} } \right)$$

(15)

where M is the total nominal mass fractured; Π_s and Π_g are strength- and gravity-related non-dimensional parameters; and F ₁ is an unspecified functional dependence.

The mass of a fragment is m = k ₁ ρx ³, x being size and k ₁ a particle shape factor. The nominal mass broken for each explosive charge, for the case of bench blast, is generally approximated as M = ρBHS/cos θ, θ being the holes inclination angle with respect to the vertical. Introducing a (as yet undetermined) characteristic blast size $L_{\text{c}} ,M = k_{2} rL_{\text{c}}^{3}$, with k ₂ a blast geometry or bench shape factor:

$$k_{2} = \frac{\text{BHS}}{{L_{\text{c}}^{3} \cos \theta }}$$

(16)

Equation 15 becomes:

$$P = F_{1} \left( {\frac{{k_{1} x^{3} }}{{k_{2} L_{\text{c}}^{3} }},\Pi _{\text{s}} ,\Pi _{\text{g}} } \right)$$

(17)

Neglecting the gravity parameter (that, for the case of asteroids, applies to bodies for which the material strength is less than the gravitational self-compressive strength which, obviously, does not apply to Earth) and solving Eq. 17 for x/L _c:

$$\frac{x}{{L_{\text{c}} }} = F_{2} \left( {P,\frac{{k_{1} }}{{k_{2} }},\Pi _{\text{s}} } \right)$$

(18)

The strength factor Π_s has the following expression (Ouchterlony 2009b, Eq. 7b, adapted from Housen and Holsapple 1990, Eq. 40):

$$\Pi _{\text{s}} = E_{M} \left( {\frac{{\sigma^{*} }}{\rho }} \right)^{{3\mu /\left( {\tau - 2} \right)}} L_{\text{s}}^{{ - 3\mu \left( {\lambda + \tau } \right)/\left( {\tau - 2} \right)}} {\text{e}}^{{\left( {3\mu - 2} \right)/2}} \left( {\frac{\rho }{{\rho_{e} }}} \right)^{1 - 3\nu }$$

(19)

where E _M is impact energy per target mass, clearly related to the powder factor in rock blasting; σ ^* is a rock strength quantity with dimension [stress][length]^λ[time]^τ; e is the explosive energy per unit mass;⁶ ρ _e is impactor density which is transposed in the blasting model as the explosive density;⁷ and L _s is a characteristic length (in the collision model, it is the target radius) that we will choose for simplicity equal to L _c.⁸ The constants μ, ν, λ and τ are to be determined experimentally. μ and ν describe the impactor coupling to the target; the two extremes of the coupling are energy-scaled impacts (μ = 2/3, ν = 1/3) and momentum-scaled ones (μ = 1/3, ν = 1/3). Holsapple and Schmidt (1987) show that the case of a point source explosion has μ = 2/3 and that collisions on non-porous targets, including rocks, are governed by μ close to 0.6, whereas porous targets (such as dry sand) have μ = 0.37–0.40, close to the momentum limit. Selecting thus the energy-scaled interaction for the blasting case analogy in Earth’s rock:

$$\Pi _{\text{s}} = E_{M} \left( {\frac{{\sigma^{*} }}{\rho }} \right)^{{2/\left( {\tau - 2} \right)}} L_{\text{c}}^{{ - 2\left( {\lambda + \tau } \right)/\left( {\tau - 2} \right)}}$$

(20)

λ and τ are material constants that describe the dependence of the strength on the scale of the target and the loading rate, respectively. Loading rate in blasting can, in principle, be described by the rise time of the pressure in the borehole, or the reaction time in the detonation front. This time is proportional to the ratio of the length of the reaction zone to the average sound speed of the detonation products in the reaction zone (Price 1981); in homogeneous explosives such as straight emulsions, it can range from less than 100 ns to about 1 μs, depending on the size of the sensitizing microspheres (Hirosaki et al. 2002); for heterogeneous explosives such as ANFO or ANFO/emulsion mixtures, rise times in the order of 10 μs have been reported (Onederra et al. 2011). Reaction time, or reaction zone thickness with which to estimate the reaction time using the reaction zone sonic velocity (that can be estimated from the detonation velocity), is never included in blasting reports so we have no way to assess its influence in the model. We are forced then, as a first approximation, to not consider the loading rate dependence, i.e., make τ = 0 in Eq. 20.

About the scale dependence, let us define $\bar{\sigma }$ as the strength (with dimensions of stress) of the rock mass of a certain size $\bar{R}$; we may write:

$$\sigma^{*} = \bar{\sigma }\bar{R}^{\lambda }$$

(21)

Assuming σ ^* invariant for a certain rock mass (which amounts to consider a classical power dependence of strength with size, Persson et al. 1994, quoting Weibull 1939; Jaeger and Cook 1969; Hoek and Brown 1980; Scholz 1990), the strength for a given size R is:

$$\sigma = \frac{{\bar{\sigma }}}{{\left( {R/\bar{R}} \right)^{\lambda } }}$$

(22)

Using Eq. 21 for σ ^* and making τ = 0 in Eq. 20 for a non-rate variable model:

$$\Pi _{s} = E_{M} \left( {\frac{{\bar{\sigma }\bar{R}^{\lambda } }}{\rho }} \right)^{ - 1} L_{c}^{\lambda }$$

(23)

Writing E _M (energy per unit rock mass) in terms of the powder factor q (mass of explosive per unit rock volume) and the explosive energy per unit mass e, E _M  = qe/ρ, the factor Π_s becomes:

$$\Pi _{\text{s}} = \frac{qe}{{\bar{\sigma }}}\left( {\frac{{L_{\text{c}} }}{{\bar{R}}}} \right)^{\lambda }$$

(24)

The size of fragments for a given fraction passing P, or size quantile P, becomes, from Eq. 18:

$$\frac{x}{{L_{\text{c}} }} = F_{2} \left[ {P,\frac{{k_{1} }}{{k_{2} }},\frac{qe}{{\bar{\sigma }}}\left( {\frac{{L_{\text{c}} }}{{\bar{R}}}} \right)^{\lambda } } \right]$$

(25)

The Kuznetsov formula and others that have been proposed for the calculation of the fragments size (Langefors and Kihlström 1963; Holmberg 1974; Larsson 1974; Kou and Rustan 1993; Rustan and Nie 1987) generally agree that the central fragment size is a power function of the powder factor; plots as the ones in Fig. 2 say the same for other percentile sizes so this will be attempted here. Assuming a power form also for the other parameters and writing Π_s and the k-ratio as the reciprocals in Eq. 25, this becomes:

$$\frac{x}{{L_{\text{c}} }} = P^{r} \left( {\frac{{k_{2} }}{{k_{1} }}} \right)^{h} \left( {\frac{{\bar{\sigma }\bar{R}^{\lambda } }}{{qeL_{\text{c}}^{\lambda } }}} \right)^{\kappa } = P^{r} \left( {\frac{{k_{2} }}{{k_{1} }}} \right)^{h} \left( {\frac{{\bar{\sigma }}}{qe }} \right)^{\kappa } \left( {\frac{{\bar{R}}}{{L_{\text{c}} }}} \right)^{\lambda \kappa }$$

(26)

The constants r, h, κ and λ are to be determined from experimental data. Note that they are not universal for all percentages passing since that would lead to a Gates–Gaudin–Schuhmann distribution (Gates 1915; Gaudin 1926; Schuhmann 1940), with exponent 1/r:

$$P = \left( {\frac{x}{{x_{\hbox{max} } }}} \right)^{1/r} ;\quad x_{\hbox{max} } = \left( {\frac{{k_{2} }}{{k_{1} }}} \right)^{h} \left( {\frac{{\bar{\sigma }}}{qe}} \right)^{\kappa } L_{\text{c}}^{1 - \lambda \kappa } \left( {\bar{R}} \right)^{\lambda \kappa }$$

(27)

The P-dependence of κ is already stated in Sect. 1 (Fig. 2), and the variation of r follows from the fact that the log–log slope of the cumulative size distribution is known to vary across the percentage passing range. In fact, Eq. 27 could be thought of as a piecewise log–log linear representation of the size distribution in which the top size and the slope vary constantly across the size range.

The fragments shape factor k ₁ is an experimental variable that is generally unknown so it will be considered as one more parameter (that, in principle, may also vary with the size of the fragments, hence with the percentile). Thus, for each percentage passing P, the group P ^r/k ^h₁ can be considered a single parameter, k (which should tend to zero with P). Assuming arbitrarily that the strength parameter $\bar{\sigma }$ corresponds to a unit size (in the same units as those used for L _c) of rock mass, $\bar{R}$ = 1, Eq. 26 is, finally:

$$\frac{{x_{P} }}{{L_{\text{c}} }} = kk_{2}^{h} \left( {\frac{{\bar{\sigma }}}{qe}} \right)^{\kappa } \frac{1}{{L_{\text{c}}^{\lambda \kappa } }}$$

(28)

The size has been written x _P to show that it is the percentile P size. This model requires the calibration of the four functions k(P), h(P), κ(P) and λ(P) which, together with the selection of the strength variable $\bar{\sigma }$ and the characteristic size L _c, will be accomplished from experimental data.

3 The Data

Fragmentation data from bench blasting have been gathered for a total of 169 blasts published in the literature. Some of them were small-scale (half to 1 m bench height) tests, and others were full-scale production blasts; all of them were carried out in the field on natural rock mass. For all of them, the fragmentation data were obtained by sieving and weighing of a sample of the muckpile, and the description of the blasts and the rock mass was reasonably detailed so that calculations of the Kuz-Ram type made in Sect. 1, and likewise of the model presented here, can be carried out. Table 1 lists the mine and quarry sites and the sources of the data; Table 2 gives a general description of the size distribution data; Tables 3, 4 and 5 give relevant rock and blast design variables.

Table 1 Blast and fragmentation data: blast sites, rock types and references

Table 2 Fragmentation data

Table 3 Rock properties

Table 4 Blast design data. Explosives and initiation systems

Table 5 Blast design data. Other dimensional and non-dimensional parameters

Elastic modulus is sometimes reported in the sources as from laboratory tests (static), and sometimes as calculated from P- and S-wave velocities, which results in somewhat different figures; the original value quoted in each case has been retained. This adds some uncertainty, or unwanted variability, to the data, that would probably not be overcome very much by the estimation of one from the other by grossly approximate formulae (e.g., Eissa and Kazi 1988). In some cases, some properties have been estimated from the data available using, e.g., elastic relations or properties of similar rocks. These are marked in Table 3.

The explosive energy is rated as the heat of explosion value, both for it being a well-defined magnitude, that does not depend much on the detonation thermodynamic code and on the products expansion assumptions, and for being a property commonly specified by the manufacturers; this is the same approach as the Kuz-Ram model in which the explosive energy is rated by means of the relative weight strength, a measure of the heat of explosion with respect to ANFO. Other explosive energy values such as the useful work could indeed be used, but the model would require a recalibration with them—a difficult task though, since useful work is often not given by the manufacturers and there is not a common ground for a standard calculation of it. When a heat of explosion value is not reported in the blast description, a value compatible with the type of explosive used has been assigned. In a few cases (9 blasts, their energies marked with b in Table 4), decoupled charges were used; for these, the explosive energy used is the energy remaining in an isentropic expansion point at the expansion ratio equal to the ratio of the borehole volume to the charge volume. This energy has been calculated from the JWL isentropes determined in Sanchidrián et al. (2015) from cylinder test data for ANFO and emulsion-type explosives. Figure 3 shows the ‘energy efficiency,’ or the ratio of the remaining energy at a given expansion (described as decoupling ratio, hole-to-charge diameter ratio) to the energy at expansion ratio equal one (the fully coupled case). Except for some outlier, most of the expansion energy ratio curves are packed in a fairly narrow band so that, as a first estimation, the mean curve has been used for all decoupled shots (even for the case of dynamite for which no experimental expansion data are available).

Fig. 3

Fraction of energy remaining in the detonation products along expansion

4 Model Fitting

For each blast, the fragmentation data have been interpolated to determine the size percentiles between 5 and 100. Linear interpolation in log–log space has been used. Extrapolation has been allowed whenever the range of data does not cover the 5–100% passing; however, a penalty has been applied to the extrapolated points in the fit so that their weight decreases as the extrapolation distance gets longer. The penalty function used is:

$$w_{e} = e^{{ - 0.5\left( {r_{P} - 1} \right)^{3} }}$$

(29)

r _P being the extrapolation ratio:

$$r_{P} = e^{{\left| {\ln \left( {P/P_{f} } \right)} \right|}}$$

(30)

where P is the percentage passing at which the size is being calculated and P _f is the lowermost (if P < P _f ) or uppermost (if P > P _f ) passing value with data.⁹ The minimum and maximum percentage passing for the different data groups that are listed (P _min and P _max) in Tables 2 and 6 gives the number of extrapolated points for each percentage passing; the large amount of extrapolated points below P = 5%, with long extrapolations required, prevent from analyzing any lower percentile size.

Table 6 Number of extrapolated points

Besides the extrapolation penalty, a size-dependent weight w _x  = 1/(x/L _c)^1/2 has been included in the least squares scheme, in order to allow a fair influence of the small data and to prevent the larger numbers to be too dominant in the overall error, while not penalizing the determination coefficient too much. The final weight of each point is the smaller of the size-dependent weight (normalized to one) and the extrapolation penalty factor:

$$w = { \hbox{min} }\left( {w_{e} ,w_{x} } \right)$$

(31)

Equation 28 is fitted to the x _P data values¹⁰ by means of a Levenberg–Marquardt (Seber and Wild 2003) nonlinear least squares method programmed in a MATLAB (2015) environment. Numerous minimizations (up to 1000 times the number of unknown parameters, and more than that in some particularly difficult cases) are run with variable starting parameters values until the minimum sum of squares is ensured, this way avoiding local minima as much as possible. The result for the 50 percentile sizes of the distributions data is a modest determination coefficient, R ² = 0.6413.

Since the determination coefficient may be a misleading value in nonlinear regression, the relative root-mean-squared error (RRMSE) and the median absolute log error (MALE) are also used as meaningful goodness-of-fit values, as they estimate the prediction capability of the model. The RRMSE is:

$${\text{RRMSE}} = \sqrt {\text{MSE}} /{\text{mean}}\left( {x_{P} /L_{c} } \right)$$

(32)

MSE being the mean-squared error:

$${\text{MSE}} = \frac{1}{{n_{\text{c}} - p}}\mathop \sum \limits_{i = 1}^{{n_{c} }} w_{ei} \left[ {\left( {x_{{P,{\text{pred}}}} /L_{\text{c}} } \right)_{i} - \left( {x_{{P,{\text{data}}}} /L_{\text{c}} } \right)_{i} } \right]^{2}$$

(33)

n _c being the number of data points (i.e., the number of blasts) and p the number of parameters. The extrapolation weights w _ei are applied so that only errors of long extrapolated (hence dubious) points are downsized; the fit weights w from Eq. 31 are not used so as not to give an unrealistic low value of the error. Let the logarithmic error of each predicted value be:

$$e_{Li} = w_{ei} \ln \frac{{\left( {x_{{P,{\text{pred}}}} } \right)_{i} }}{{\left( {x_{{P,{\text{data}}}} } \right)_{i} }}$$

(34)

where the extrapolation weights w _ei are also applied here. The median absolute log error, MALE, expressed as relative error for better interpretation, MALE _r , is:

$${\text{MALE}}_{r} = \exp \left( {{\text{median}}\left| {e_{Li} } \right|} \right) - 1$$

(35)

Both RRMSE and MALE indicate the relative deviation of the predicted values, MALE being more robust (since it is a median) and symmetric with respect to zero.¹¹ However, high RRMSE may indicate a large number of badly predicted cases (outliers) which may stay hidden with the MALE.

For the fit under study (Eq. 28, x ₅₀), RRMSE = 0.6730, MALE _r  = 0.4498. Although the determination coefficient and the errors are mediocre, the parameters of the model (k = 0.5932, h = 1.2029, κ = 0.2979, δ = 1.7740) are statistically significant with narrow confidence intervals, p values 8 × 10⁻⁷, 6 × 10⁻¹⁰, 1 × 10⁻⁴ and 2 × 10⁻⁴, respectively. Figure 4 shows the predicted values versus data plot and the distribution of residuals; the latter shows some positive skew, highlighted by the normal and t distributions fitted. The mean is 0.018 and the 95% coverage interval is [−0.119, 0.256]. In summary, the model, effectively, translates a significant relation between the variables, but there must be other factors of variation that are not accounted for.

Fig. 4

Four-parameter model (Eq. 28) for x ₅₀. Left data versus predicted values plot; the blue lines are the data versus predicted linear fit (dashed ordinary least squares, solid robust, least sum of absolute residuals); the orange line is the data = predicted values line. Right normalized histogram of residuals; the two PDF functions shown are normal (blue) and t (red), fitted to the distribution of residuals (color figure online)

At least two influential characteristics that are relevant to rock blasting are missing from Eq. 28, since they do not apply to asteroid collisions:

• 1. The rock mass discontinuities The important geotechnical information is neither included in the bench shape factor k ₂ nor in the fragments shape factor k ₁. Using a classical approach (Lilly 1986, 1992; Scott 1996), the discontinuities are described by means of a combination of a spacing J _s and an orientation J _o term:

  $$J_{\text{F}} = J_{\text{s}} + J_{\text{o}}$$

  (36)

  The joint spacing term is formulated as a non-dimensional ratio s _j /L _j , where s _j is the discontinuity mean spacing and L _j a characteristic size, selected as the variable (with dimensions of length) giving a higher determination for the model (see the end of this section). A limiting value a _s is required for large joint spacing:

  $$J_{\text{s}} = \hbox{min} \left( {\frac{{s_{j} }}{{L_{j} }},a_{\text{s}} } \right)$$

  (37)

  The joints orientation term J _o is defined as:

  $$J_{\text{o}} = a_{\text{o}} j_{\text{o}}$$

  (38)

  where j _o is Lilly’s joints orientation index normalized to one (listed in Table 3) in order to give it, in principle, a similar weight as the spacing term, though the relative importance of each one will be finally cast by the constant a _o, to be determined from the data. The joints orientation term describes the relative difficulty of the blast to break the toe for different joint orientations with respect to the face: j _o = 0.25 (horizontal), 0.5 (dipping out of the face), 0.75 (sub-vertical striking normal to the face) and 1 (dipping into the face or no visible jointing).

• 2. The delay Unlike asteroid collisions, rock blasting is carried out in multiple loadings taking place at successive times for neighboring shots so that there is wave and crack growth interference in the rock mass between two shots in the firing sequence. The general blasting knowledge, confirmed with experimental evidence, states that fragmentation improves (i.e., the size of the fragments decreases) when time is allowed for the cracks from a hole to propagate and damage the rock before the next hole detonates (Winzer et al. 1983; Katsabanis and Liu 1996; Cunningham 2005, referring data by Bergmann et al. 1974; Katsabanis et al. 2006, 2014; Johansson and Ouchterlony 2013). The time for the cracks to propagate is a function of their velocity and that is often normalized by dividing by the P-wave velocity c _P (Roberts and Wells 1954; Dulaney and Brace 1960). In linear elastic materials, the theoretical upper limit of the crack velocity is the Rayleigh wave velocity (Freund 1972), which lies around 90% of the shear wave velocity, though measured crack speeds in rock are hardly in excess of half that velocity (Daehnke et al. 1996; Fourney 2015). Physically, the P-wave velocity determines the time of the first wave arrival from a neighboring blast hole; its use is convenient since, unlike the Rayleigh wave velocity (or the more difficult to know crack velocity), it is a commonly available, easy to determine and often reported, property for a given rock mass. Thus, the non-dimensional delay factor is defined as:

  $$\Pi _{t} = \frac{{c_{P}\Delta t}}{{L_{t} }}$$

  (39)

  where Δt is the in-row delay and L _t is a characteristic length (to be selected with the same criterion as the other characteristic lengths, L _c and L _j , see the end of this section).¹² Π _t indicates how large the drill pattern (represented by the characteristic size L _t ) is with respect to the travel distance of the longitudinal waves during a delay period. With Π _t defined by Eq. 39, a power form for it cannot hold since it would lead to a zero size for an instantaneous blast if the exponent is positive, or infinite if negative (as should be since the fragment size diminishes with increasing delay). A suitable form of the Π _t function could be an exponential:

  $$f_{t} \left( {\Pi _{t} } \right) = e^{{ - \delta\Pi _{t} }}$$

  (40)

Inserting now the discontinuities term in Eq. 28:

$$\frac{{x_{P} }}{{L_{\text{c}} }} = k\left[ {\hbox{min} \left( {\frac{{s_{j} }}{{L_{j} }},a_{\text{s}} } \right) + a_{\text{o}} j_{\text{o}} } \right]k_{2}^{h} \left( {\frac{{\bar{\sigma }}}{qe}} \right)^{\kappa } \frac{1}{{L_{\text{c}}^{\lambda \kappa } }}$$

(41)

When Eq. 41, a six-parameter function, is fitted to x ₅₀, the determination coefficient grows to R ² = 0.8504, and the other two goodness-of-fit parameters reduce to RRMSE = 0.4270, MALE _r  = 0.1873, all coefficients significant (maximum p value 5 × 10⁻⁴). Inserting now the delay term, Eq. 40:

$$\frac{{x_{P} }}{{L_{\text{c}} }} = k\left[ {\hbox{min} \left( {\frac{{s_{j} }}{{L_{j} }},a_{\text{s}} } \right) + a_{\text{o}} j_{\text{o}} } \right]k_{2}^{h} \left( {\frac{{\bar{\sigma }}}{qe}} \right)^{\kappa } \frac{1}{{L_{\text{c}}^{\lambda \kappa } }}f_{t} \left( {\Pi _{t} } \right)$$

(42)

R ² = 0.8549, RRMSE = 0.4141, MALE _r  = 0.2116, all coefficients significant. The improvement of the quality figures is marginal considering the increase in one parameter of the model (MALE _r even increases). This, together with a moderately high p value for δ (though still within the 0.05 limit, p = 0.015), could indicate that the exponential may not be the right form for the delay factor.

If the ratios x _data/x _pred of Eq. 41 (the function without a delay term) are plotted against Π _t , the result is that of Fig. 5 (left graph); the aspect of this plot suggests a time function decreasing with the time factor down to a minimum, beyond which the function grows toward a constant value. Previous published work supports this behavior (Cunningham 2005, referring to data by Bergmann et al. 1974; Katsabanis et al. 2006, 2014; Johansson and Ouchterlony 2013; Katsabanis and Omidi 2015), though the existence of either a minimum or a lower asymptote is somewhat controversial (Katsabanis and Omidi 2015 suggest a minimum for the median size, though not so for the 20 percentile). Consequently, a time function has been sought that decreases with increasing delay with the possibility of having a minimum. Such function can be the following:

Fig. 5

Left error ratios of a model without delay factor (Eq. 41). Right Sample delay factors as in Eq. 43

$$f_{t} \left( {\Pi _{t} } \right) = \delta_{1} + \left( {1 - \delta_{1} - \delta_{2}\Pi _{t} } \right)e^{{ - \delta_{3}\Pi _{t} }}$$

(43)

δ ₁, δ ₂ and δ ₃ being constants to be determined from the fit; f(Π _t ) is 1 at Π _t  = 0 (the case of simultaneous initiation of holes), decreases to a minimum at Π _t  = 1/δ ₂ + 1/δ ₃ − δ ₁/δ ₂ and then grows toward an asymptotic value δ ₁ for long delays (see Fig. 5, right). Equation 43 can also represent a decay toward a lower asymptote at δ ₁ without a minimum if δ ₂ = 0, see Fig. 5 (right). Using this delay function leads to R ² = 0.9242, RRMSE = 0.2992, MALE _r  = 0.1840, the nine coefficients strongly significant: the highest p value is 2 × 10⁻⁴. Such low p values (lower than those for Eq. 41, having increased the number of parameters by three) are an outstanding result, a consequence of the narrow confidence intervals of the coefficients, and speak strongly in favor of the delay function in Eq. 43. Figure 6 (left) shows the predicted values versus data plot; Fig. 6 (right) shows the histogram of residuals with normal and t distributions superimposed. The distribution is nearly zero-centered and much narrower than the basic, four-parameter one in Fig. 4, with mean 0.0028, still slightly skewed with 95% coverage [−0.064, 0.093]. Figure 7 shows the delay function.

Fig. 6

Nine-parameter model (Eq. 41 with delay function Eq. 43) for x ₅₀. Left data versus predicted values plot; the blue lines are data versus predicted linear fits (dashed ordinary least squares, solid robust, least sum of absolute residuals); the orange line is the data = predicted values line. Right normalized histogram of residuals; the two PDF functions shown are normal (blue) and t (red), fitted to the distribution of residuals (color figure online)

Fig. 7

Delay function (Eq. 43) for x ₅₀

Many possible characteristic lengths L _c have been tested (burden, spacing, bench height, stemming length, charged length and geometric means of their pairs); the geometric mean of bench height and spacing has been observed to generally provide a best fit of the final model: L _c  = (H·S)^1/2. The shape factor k ₂ from Eq. 16 is then:

$$k_{2} = \frac{\text{BHS}}{{\left( {\text{HS}} \right)^{3/2} \cos \theta }} = \frac{B}{{\sqrt {\text{HS}} \cos \theta }}$$

(44)

The characteristic lengths for non-dimensionalizing the joints spacing and the delay have also been selected from tests with different lengths; the best fits are obtained with the burden for the joints spacing term and the holes spacing for the delay factor: L _j  = B, L _t  = S.

About the strength factor $\bar{\sigma }$, several rock properties have been tested, and the ratio σ ² _c /(2E)—the elastic strain energy at rupture per unit volume—has finally been chosen as the one giving the most favorable fits to the data. This energy appears in Griffith’s (1921) energy balance of linear elastic fracture mechanics, in which the strain energy released by a crack equals the elastic strain energy.

5 Results and Discussion

The function in Eq. 42 with the delay function f _t (Π _t ) in Eq. 43 has been fitted to percentiles from 100 to 5. The parameters are plotted in Fig. 8 as functions of the percentage passing. Table 7 summarizes some quality figures of the fits. Note that the p values are very low for all parameters and all percentiles, which indicate very tight confidence intervals, an outstanding result for a nine-parameter model fit.

Fig. 8

Parameters of the model. Left k, a _s, a _o, κ, h and λ. Right parameters of the delay function. Solid lines model fit results; dashed lines approximated functions

Table 7 Quality values of the fits

For ease of application of the model, approximating functional forms have been derived for the nine parameters as functions of P. The result is summarized in Table 8, and the P-functions are plotted in Fig. 8 as dashed lines. Note that not all the functions are direct fits to the parameters; functions for k, κ and the delay parameters are fitted first, and then, the model is adjusted again to the other parameters, for which analytic functions of P are finally obtained. This two-step procedure allows to correct the errors from the fits in the first step, which otherwise might combine to give, in some cases, odd results. k, being P ^r/k ^h₁ , has been chosen a monotonic function of P since the fragments shape factor is likely not to change much with P. In doing this, we assume that the observed decrease in k at high P is not a strong result (just as the mild increase below P = 10%) and is due to inaccuracies, always greater at high and low percentages passing. The functional form of κ(P) is also assumed a priori, and it will be revisited below.

Table 8 Functional forms of the parameters; P is fraction passing, 0.05 ≤ P ≤ 1

Figure 9 shows the resulting set of delay functions for the different percentages passing.

Fig. 9

Delay functions (Eq. 43, with coefficients from Eqs. 51–53)

The overall goodness of the fits is assessed in Fig. 10 where boxplots of logarithmic errors (as defined in Eq. 34) are plotted for the calculations using both the raw parameters from the fits and the functions of Table 8. The penalty for using Table 8 formulae with respect to using the raw parameter values is small. The prediction error is 50% of the times less than about 25% in nearly the whole range both with the raw parameters and with their fitting functions. The boxplots in Fig. 10 are equivalent to those in Fig. 1 for the Kuz-Ram and crush zone models (in fact, log errors in Fig. 1 are also w _e -corrected, as in Eq. 34). The comparison of both is self-explanatory.

Fig. 10

Boxplots of logarithmic errors (Eq. 34) of the calculated percentiles. Blue boxes are the errors using the raw parameters, and magenta boxes are the errors using the functions in Table 8. The gray horizontal lines are plotted at ±ln 1.25, equivalent to relative errors of 25% (color figure online)

Another way of assessing the errors is in terms of the median (used for robustness) error of the size calculation for each data set, in absolute value; for $i = 1, \ldots ,n_{c}$, n _c being the number of data sets (169):

$$e_{Li} = {\text{med}}\left| {e_{Lij} } \right| , \quad j = 1, \ldots ,20$$

(54)

where e _Lij are log errors (as in Eq. 34) of the size at passing P _j  = 5, 10 ,…, 100. The distribution of these errors, expressed as relative errors, exp(e _Li ) − 1, is given as boxplots in Fig. 11. This confirms an expected error of the percentile size prediction in the range of 20%. Plots are also shown for the Kuz-Ram and crush zone models, the median error of which (i.e., the expected error) is about 60%.

Fig. 11

Distributions of the medians of the absolute errors for all percentiles for each data set (Eq. 54, transformed to relative errors)

The 20–25% expected errors of the model should be viewed in the context of fragment size measurements. All data used were obtained by sieving and weighing samples of the muckpile—in many cases a large fraction of that, encompassing large amounts of material. Sampling, screen processing and weighing a large amount of rock fragments in field conditions is a hard task prone to errors. The sampling must be done on a significant fraction of the muckpile and from the different zones in it; loader sampling and dumping techniques, and end effects in the pile, are responsible for shifts in the size distributions (Stagg and Rholl 1987); the type of sieve (square, rectangular, grizzly, etc.) has an influence on the screening results; losses of material due to overweights (not loadable onto the screen), projections, fines, etc. also introduce errors. Since the data come from different sources, a general statement on the error of the data is difficult to give, nor is it usually assessed by the authors. Sanchidrián (2015) estimated the uncertainty of the data by calculating the differences of equal percentile sizes of pairs of similar blasts (i.e., blasts in the same mine or quarry with equal, or very close, blast design¹³) for which fragmentation should be (ideally) the same; such differences are a combined measure of the uncertainty of the fragmentation measurement (due to sampling, sieving and weighing), the variability of the phenomenon and the uncertainty of the blasting data. To all those, the calculation of sizes at some given percentages passing adds an interpolation error. The median differences for percentiles 5–100 was found to be between 8 and 22%. Even if this is only a rough estimation of the uncertainty, and does not include possible systematic measurement errors, it gives an idea of how much accuracy we should be prepared to demand from a fragmentation prediction model, as there is no way we can have a better knowledge of the actual fragmentation than what the measurements give us.

Figure 12 shows some sample size distribution curves calculated, compared with the data; the P-functions for the model parameters are used. Each graph shows distributions for which the relative errors are around the first quartile, the median and the third quartile, plus one more in which the three best and the three worst predicted distributions, as from the median absolute value of the log error, are plotted.

Fig. 12

Sample size distribution curves; dashed data, solid calculated. Median relative error of the curves plotted: upper left 11.0–12.6% (around the first quartile); upper right 19.4–21.0% (around the median); lower left 30.5–33.1% (around the third quartile); lower right 2.1–3.4% (the three best results), 88.3–107.6% (the three worst results)

One of the ideas that inspired this fragment size distribution model in which the exponent of the powder factor is variable with P was the ‘fan’ pattern we referred to in Sect. 1 (Ouchterlony et al. 2016). If extrapolated toward very low (away from the feasible range) powder factor, the different percentile lines often converge (more or less precisely) in a focal point. The data used for the fits happen to meet that ‘fan’ pattern more than well (see the upper graphs of Fig. 13; the energy concentration is used instead of the charge concentration used in Fig. 2). Even if the dispersion is very large (due to the great variation of scale, rock and shape factors, and delay), the coefficients of the fits (shown on the right plot) are significant, their p values below 10⁻²³ for the pre-factor and 0.03 for the exponent. The predicted results from the model also catch much of this behavior (Fig. 13, lower graphs; the P-functions for the parameters have been used for the calculation); the p values of the coefficients (shown in the right plot) are less than 10⁻²² for the pre-factor and 0.02 for the exponent. As an exercise to confirm this, without any cross-influence, a sample calculation with constant blast characteristics (Table 9) and with the powder factor only variable (implemented by varying the hole diameter) has been done; the results are shown in Fig. 14 for three delay times; the fanlike convergence is clearly visible.

Fig. 13

‘Fan plots’ of percentile sizes versus energy powder factor. Upper graphs data. Lower graphs predicted values. The right graphs show the extrapolation of the percentile power lines toward lower energy factors

Table 9 Blast data for sample calculation

Fig. 14

Sample fragmentation calculation. Left size distributions; right percentiles versus powder factor fan plots. In-row delay 30 ms (solid lines), 10 ms (dashed lines) and zero (dash-dotted lines)

The functional form of κ(P) (Table 8, Eq. 48) has been taken from the expression derived by Ouchterlony et al. (2016) for the exponent of the size versus powder factor power equations—i.e., the log–log slope of the fan-plot lines—following the hypothesis that the underlying distribution is a Swebrec function (Ouchterlony 2005a, b, 2009a) with shape parameter independent of the powder factor. The determination coefficient of the fit of Eq. 48 to the P-κ values of the model is 0.9772. This result provides an interesting link of the model presented here with the powder factor fan plots and the Swebrec distribution.

It is worth noting that the detonation velocity of the explosive is not among the variables of the model. The influence of detonation velocity in fragmentation is controversial: It appears only in the Kou and Rustan (1993) and Rustan and Nie (1987) formulae and is used in the crush zone model for the calculation of the borehole pressure; conversely, it is not present in the Kuz-Ram model (Cunningham 1983, 1987, 2005) and other fragmentation prediction formulae (Langefors and Kihlström 1963; Holmberg 1974; Larsson 1974; Chung and Katsabanis 2000).

In the present model, detonation velocity might influence the loading rate and the borehole pressure, both of which should in principle be relevant to fragmentation. Concerning the loading rate, the detonation velocity appears not to be the leading influence, since it varies in a relatively narrow range for most explosives used in rock blasting, while the reaction zone thickness appears to be much more important, as it varies in several orders of magnitude depending on the physical constitution and the sensitivity of the explosive. This is why explosives with not too different detonation velocity as, e.g., a straight emulsion and an emulsion/ANFO mixture have very different loading rates, as noted in Sect. 2.

About the borehole pressure, Boudet et al. (1996) gave the following expression of crack speed as function of the applied stress:

$$v_{\text{c}} /c_{\text{R}} = b\sqrt {1 - \frac{{\varDelta _{1} }}{\varDelta }}$$

(55)

where v _c is crack speed, c _R is Rayleigh wave speed and Δ strain, Δ = P _b /E; b and Δ ₁ are experimental constants, b < 1. The borehole pressure can be estimated, for a coupled explosive, as half of the detonation pressure, which can be approximated from the explosive density and detonation velocity squared. Thus, a non-dimensional delay factor to more correctly account for the time of arrival of the cracks to the proximity of the next hole in the firing sequence would be:

$$\Pi _{t} = \frac{{c_{\text{R}}\Delta t}}{{L_{t} }}\sqrt {1 - \frac{{\varDelta _{1} }}{{\rho_{e} D^{2} /E}}}$$

(56)

where Δ ₁, an unknown property of the rock, must, however, be left as a parameter of the fit. As pointed out in Sect. 4, the wave velocity reported in our data is the P-wave one, so that, in order to use Eq. 56, we must successively estimate the shear wave and the Rayleigh wave velocities. Tests with this delay factor were not satisfactory, perhaps due to the lack of precision of the Rayleigh wave velocity estimation or to the constant Δ ₁ assumption. A similar form to Eq. 56 but using directly the P-wave velocity instead of the Rayleigh wave one also failed. In summary, we have not been able to account for the two explosive/rock interaction processes on which detonation velocity could be influential. Perhaps better data, with a more detailed description of the detonation physics and the rock velocities, are required.

Other parameters that are not part of the model are:

• Number of rows Some of the variability in the data is probably due to this factor. Blasts used to fit the model were single and multi-row (see Table 5), with 3 or 4 rows and inter-row delays ranging from 24 to 120 ms, that correspond from 12 to 61 ms/m burden. Schimek et al. (2015) and Ivanova et al. (2015) reported the median size finer for the second and third rows of holes than for the first row, in tests with small-scale bench-like specimens (210 mm height, 70 × 95 mm burden × spacing, seven holes per row), where the first row was blasted in virgin material. This is seldom the case in mining or quarrying where, even if only one row is blasted, the burden has usually been damaged by the previous blasts in front of it. Error distributions for blasts with one and several rows have been compared by the Wilcoxon–Mann–Whitney test, and they are not different at a 0.05 significance in the range 40–95% passing, but they are below 40% and also at the maximum size. Attempts to incorporate the number of rows into a significant term yielding an improved predictive capability to the model have been unsuccessful. Two major difficulties have been encountered for it: (1) the amount of data for multi-row blasts is significantly smaller than the one row: only 35 blasts out of 169 are multiple row, and, more importantly, (2) there is a significant cross-correlation between the number of rows and the size of the blast in the data used. The results were in all cases a loss of significance (high p value) of some of the parameters of the model, or a marginal gain in the determination coefficient, or both. Be that as it may, the influence of both the number of rows and the row-to-row relief time remain a subject of further study.

• Detonator precision The amount of blasts with precise initiation (so considered if the time error is less than 1 ms) and non-precise initiation is fairly balanced: 78 precise (seismic, electronic and exploding bridge wire detonators) and 91 non-precise (pyrotechnic, both electric and non-electric). The error analysis for the two precision categories shows no difference in the error distributions for precise and non-precise initiated blasts in the whole 100–5 percentile range at a 0.05 significance.

6 Conclusions

A model for fragmentation by blasting has been built taking as starting point asteroid collisional fragmentation theory from which non-dimensional functional forms of the percentile sizes of the fragments distribution are derived. These functions include a scaling length and two non-dimensional factors: a rock strength-to-energy concentration ratio and a bench shape factor. The model is calibrated with data from 169 blasts for which the blast design variables were reported and the muckpile was sampled and sieved to determine the size distribution. Two additional factors are found to be required: one of them to account for the rock structure—the joints spacing and orientation—and the other for the delay between holes.

The scaling of the percentile sizes has been found to be optimum using the geometric mean of the bench height H and the spacing S. The bench shape factor is the ratio of the nominal volume excavated by a blasthole to the scaling length cubed.

The rock strength-to-explosive energy factor is the ratio of the resistance capacity (the strength) of the rock to the driving explosive force; the rock strength is described by the strain energy at rupture per unit volume σ ²_c /(2E), σ _c being the uniaxial compressive strength and E the Young’s modulus. The selection of this parameter has been done on a purely numerical screening of strength variables giving the best determination of the final model. The explosive yield is described as the energy concentration per unit volume, in a direct transpose of the asteroid collision that uses the impactor kinetic energy. Energy concentration is calculated as the powder factor times the explosive energy per unit mass; the explosive energy is rated with the common heat of explosion value.

The rock structure is accounted by a linear form of the joints spacing and the joint orientation descriptions. The joints spacing is written using its non-dimensional ratio to the burden. The joints orientation term is Lilly’s number normalized to one.

The influence of the delay is found to be a function of the non-dimensional factor c _P Δt/S; the function decreases as the delay factor increases, reaching a minimum at a certain value of the factor (in the range 30–40 for most percentiles), beyond which the function increases toward an asymptotic value.

The model is applied from 5 to 100 percentile sizes. All the parameters of the model have tight confidence intervals, which indicate a well-conditioned function and a robust model of the existing data with good predictive capability. The expected prediction error is about 20% across the 100–5 percentile range.