Time domain coupling of the boundary and discrete element methods for 3D problems

Abstract

This paper presents an extension of the authors’ previously developed interface coupling technique for 2D problems to 3D problems. The method combines the strengths of the Discrete Element Method (DEM), known for its adeptness in capturing discontinuities and non-linearities at the microscale, and the Boundary Element Method (BEM), known for its efficiency in modelling wave propagation within infinite domains. The 3D formulation is based on spherical discrete elements and bilinear quadrilateral boundary elements. The innovative coupling methodology overcomes a critical limitation by enabling the representation of discontinuities within infinite domains, a pivotal development for large-scale dynamic problems. The paper systematically addresses challenges, with a focus on interface compatibility, showcasing the method’s accuracy through benchmark validation on a finite rod and infinite spherical cavity. Finally, a model of a column embedded into the ground illustrates the versatility of the approach in handling complex scenarios with multiple domains. This innovative coupling approach represents a significant leap in the integration of DEM and BEM for 3D problems and opens avenues for tackling complex and realistic problems in various scientific and engineering domains.

1 Introduction

The study of wave propagation in elastic bodies has several applications in engineering [1]. Due to the complex geometries and loading conditions involved in real-life simulations, numerical methods are commonly employed [2, 3]. Among the numerical methods utilised in this field, the Discrete Element Method (DEM) and the BEM are particularly suitable to this research. These methods have been used to solve several simulations such as excavations [4, 5], blasting processes [6,7,8], tunnelling [9,10,11], rock cutting [12], slope stability analysis [13, 14], earthquakes [15, 16], ballistic impacts [17], soil-structure interaction [18, 19], and foundation design [20, 21].

The DEM is a well-known technique that can represent complex material behaviours and easily accommodate discontinuities and geometrical non-linearities [22]. The DEM discretises problems as assemblies of particles that interact through contact forces, making it appropriate for simulating granular materials [23]. The extension to cohesive materials, such as rock and concrete, was later introduced by incorporating new contact laws [24]. Nevertheless, DEM simulations face great difficulty modelling infinite domains [25]. Non-reflecting viscous boundaries [26] and the coupling with the Infinite Element Method (IEM) [27] are potential workarounds. However, these techniques cannot capture the wave propagation outside the computational domain.

In turn, the BEM is a numerical method that can accurately and efficiently simulate infinite domains [28]. Derived from continuum mechanics, the BEM employs fundamental solutions that satisfy the radiation condition. Its unique feature eliminates domain integrals [29], resulting in a lower order of discretisation within the limits of elasticity. The BEM can simulate wave propagation towards infinity in elastodynamics [30, 31] and solve a broader spectrum of problems using the Convolution Quadrature Method (CQM) [32], including viscoelasticity and poroelasticity. However, including physical or geometrical non-linearities in the method can cause significant computational costs and difficulties.

Combining different methods is a common practice to create comprehensive numerical models because no single method can capture all the physical phenomena required to simulate real-life problems efficiently [33]. For example, researchers have coupled the DEM with the Finite Element Method (FEM) to expand their modelling capabilities and increase efficiency. One of the earliest studies in this regard was conducted by Oñate and Rojek [34], who combined DEM with a continuum-based method by defining contact laws between DEM particles and finite elements. Later, Azevedo and Lemos [35] introduced an interface coupling between FEM and DEM. However, spurious wave reflections on the interface led [36] to propose an overlapping domain coupling, extending the work of Xiao and Belytschko [37]. At the same time, [38] developed a similar approach called the Arlequin coupling. More recently, efficient FEM-DEM frameworks have been developed [39,40,41,42,43].

The BEM has been combined with the FEM to expand modelling capabilities or increase performance [44]. Initially, the BEM-FEM coupling was developed for static applications [45, 46]. It was only after the work of Estorff and Prabucki [47] that dynamic problems started being considered within this framework. Later, the computational efficiency of this method was improved by truncating the time series [48]. An alternative approach to couple the BEM with the FEM was proposed by Moser et al. [19], which uses Duhamel integrals to obtain a dynamic stiffness matrix. Another interesting development in the coupling between these two methods is using non-conforming discretisations, which gives more modelling flexibility and facilitates accommodating a single time step for both methods [49]. Using staggered and iterative coupling schemes brought even more flexibility to the conception of the model regarding the time and spatial discretisation [50].

The BEM-DEM coupling was initially developed for quasi-static problems [51,52,53,54,55,56,57], but it cannot analyse wave propagation in the BEM infinite domain. Mirzayee et al. [58] used the coupled BEM-DEM for seismic analysis of dam reservoirs using the BEM formulation in the frequency domain. Malinowski et al. [59] attempted to couple the BEM and the DEM in the time domain, but their model relies on an overlapping FEM layer. An alternative approach uses the BEM to represent a particle, taking into account the deformability of the particle [60]. Barros et al. [61] successfully performed BEM-DEM coupling in the time domain for 1D wave propagation by rearranging the equations of the time integration scheme of the DEM to write a dynamic stiffness equilibrium equation. Later, Barros et al. [62] extended this formulation to 2D problems. Their formulation is based on conforming discretisations, i.e., the centre of the particles coincides with the BEM nodes, which generates particles outside the desired domain, disrupting the stiffness across the model. This is addressed by penalising the interaction between stiffnesses outside the domain. Another difficulty discussed by the authors is writing equilibrium equations between DEM point loads and BEM tractions. To write equilibrium, they suggested using Duhamel integrals to derive a stiffness matrix for the BEM, similar to the work of Moser et al. [19]. Both works Barros et al. [61, 62] use a monolithic time integration and report the difficulty of finding a time step size that grants numerical stability for both methods. In addition, the conforming discretisation renders a very fine BEM mesh, making it computationally expensive. To address these drawbacks, Barros et al. [63] developed a non-conforming staggered BEM-DEM coupling. Several approaches were examined in their work, and the Neumann–Dirichlet staggered approach is indicated as the most stable.

The current work extends the non-conforming Neumann–Dirichlet staggered approach previously developed by the authors for 2D [63] to 3D. To the authors’ knowledge, it is the first time that coupling of the BEM and DEM is proposed and validated for 3D problems. The BEM formulation becomes more complex due to the stronger singularities in the integrands [45, 64, e.g.]. Additionally, in the DEM, the number of degrees of freedom per particle increases from three to six, including three translations and three rotations. This results in more complex relative motions between interacting particles. Furthermore, the number of unknowns increases in both methods, leading to higher computational costs. In the coupling process, describing the motion of particles along the interface according to the motion of the boundary elements becomes more challenging, especially for 3D models where the BEM time-step requirements become more restrictive. The paper is structured as follows. Section 2 outlines the DEM and BEM formulations used in this coupled scheme. Section 3 describes how these formulations can be combined to provide a coupled model. Section 4 presents two benchmark examples used to validate the proposed method, and an application model is analysed to demonstrate the capabilities of the proposed approach. Finally, Sect. 5 summarises the paper, highlights its key findings, and poses challenges for future research in the field.

2 Numerical framework

2.1 DEM formulation

The DEM deals with discrete particles whose movement is governed by Newton’s law of motion

$$\begin{aligned} m_p\ddot{\varvec{u}} _p&=\varvec{f}_p\left( t\right) \,, \end{aligned}$$

(1)

$$\begin{aligned} \varvec{{\mathcal {J}}}_p\dot{\varvec{\omega }} _p&=\varvec{{\mathcal {M}}}_p\left( t\right) \,. \end{aligned}$$

(2)

where $m_p$ and $\varvec{{\mathcal {J}}}_p$ are the mass and inertia tensor of particle p, while $\ddot{\varvec{u}} _p$ and $\dot{\varvec{\omega }} _p$ are its linear and angular accelerations, respectively. The force and moment acting on particle p, $\varvec{f}_p$ and $\varvec{{\mathcal {M}}}_p$, are decomposed into externally applied and internal components, which depend on the contact with other particles. This decomposition can be written as

$$\begin{aligned} \varvec{f}_p\left( t\right)&=\varvec{f}_{\text {ext},p}\left( t\right) +\sum _{q\in {\mathcal {I}}_p}\varvec{f}_{\text {cont},pq}\left( t\right) \,, \end{aligned}$$

(3)

$$\begin{aligned} \varvec{{\mathcal {M}}}_p\left( t\right)&=\varvec{{\mathcal {M}}}_{\text {ext},p}\left( t\right) +\sum _{q\in {\mathcal {I}}_p}\varvec{{\mathcal {M}}}_{\text {cont},pq}\left( t\right) \,, \end{aligned}$$

(4)

where $\varvec{f}_{\text {ext},p}$ and $\varvec{{\mathcal {M}}}_{\text {ext},p}$ represent the external force and moment applied to particle prespectively. On the other hand, $\varvec{f}_{\text {cont},pq}$ and $\varvec{{\mathcal {M}}}_{\text {cont},pq}$ are the forces and moments arising from the contact between particles pand q. These contact forces and moments apply to each particle qin the set ${\mathcal {I}}_p$ of particles in contact with p. The contact force is calculated as

$$\begin{aligned} \varvec{f}_{\text {cont},pq}^{\left( i\right) }= f_{n,pq}^{\left( i\right) }\varvec{n}_{pq}^{\left( i\right) }+ f_{s,pq}^{\left( i\right) }\varvec{s}_{pq}^{\left( i\right) }, \end{aligned}$$

(5)

where $f_{n,pq}^{\left( i\right) }$ and $f_{s,pq}^{\left( i\right) }$ are the normal and shear contact forces in the normal and tangential directions, $\varvec{n}_{pq}^{\left( i\right) }$ and $\varvec{s}_{pq}^{\left( i\right) }$, shown in Fig. 1a. The normal direction is the direction that connects the centre of the two interacting particles. The shear direction lies in the plane defined by the normal direction and depends on the relative movement of the two contacting particles [65].

In the explicit DEM, the contact forces are calculated incrementally as a function of the relative displacements between particles as

$$\begin{aligned} f_{n,pq}^{\left( i\right) }&= f_{n,pq}^{\left( i-1\right) } + k_{n,pq}\Delta \delta _{n,pq}^{\left( i\right) }\,, \end{aligned}$$

(6)

$$\begin{aligned} f_{s,pq}^{\left( i\right) }&= f_{s,pq}^{\left( i-1\right) } + k_{s,pq}\Delta \delta _{s,pq}^{\left( i\right) }\,. \end{aligned}$$

(7)

where $k_{n,pq}$ and $k_{s,pq}$ are the normal and shear stiffnesses of the contact (see Fig. 1b), and $\Delta \delta _{n,pq}^{\left( i\right) }$ and $\Delta \delta _{s,pq}^{\left( i\right) }$ are the increments in the normal and tangential relative displacements respectively [62]. The stiffnesses are determined based on the micro-mechanical Young’s moduli $\tilde{E}_p$ and $\tilde{E}_q$, micro-mechanical Poisson’s ratios $\tilde{\nu }_p$ and $\tilde{\nu }_q$ and radii $r_p$ and $r_q$ as [65]

$$\begin{aligned} k_{n,pq}&= 4 \frac{\tilde{E}_pr_p\tilde{E}_qr_q}{\tilde{E}_pr_p+\tilde{E}_qr_q}\,, \end{aligned}$$

(8)

$$\begin{aligned} k_{s,pq}&= 4 \frac{\tilde{E}_pr_p\tilde{\nu }_p\tilde{E}_qr_q\tilde{\nu }_q}{\tilde{E}_pr_p\tilde{\nu }_p+\tilde{E}_qr_q\tilde{\nu }_q}\,. \end{aligned}$$

(9)

Fig. 1

Contact model in the DEM: a normal and shear direction of two interacting particles and b force–displacement relation of the contact law

Equations (1) and (2) are numerically solved using the “leapfrog” method, which is a second-order symplectic time integration scheme [65, 66, 67, e.g.]. In the DEM domain, time is discretised into a series of time steps so that $t^{\left( i+1\right) }=t^{\left( i\right) }+\Delta t_\text {DE}^{\left( i\right) }$. Here, $i\in {\mathbb {N}}$ refers to the number of steps, and $\Delta t_\text {DE}^{\left( i\right) }$ is the size of the i-th time step. All other variables are similarly discretised in time, e.g., $\varvec{u}_p\left( t^{\left( i\right) }\right) =\varvec{u}_p^{\left( i\right) }$. As per the “leapfrog” method, the translational velocities and displacements of particle pare updated as

$$\begin{aligned} \ddot{\varvec{u}} _p^{\left( i\right) }&=\frac{\varvec{f}_p^{\left( i\right) }}{m_p}\,, \end{aligned}$$

(10)

$$\begin{aligned} \dot{\varvec{u}} _p^{\left( i+\frac{1}{2}\right) }&=\dot{\varvec{u}} _p^{\left( i-\frac{1}{2}\right) }+\ddot{\varvec{u}} _p^{\left( i\right) }\Delta t_\text {DE}^{\left( i\right) }\,, \end{aligned}$$

(11)

$$\begin{aligned} \varvec{u}_p^{\left( i+1\right) }&=\varvec{u}_p^{\left( i\right) }+\dot{\varvec{u}} _p^{\left( i+\frac{1}{2}\right) }\Delta t_\text {DE}^{\left( i\right) }\,. \end{aligned}$$

(12)

In the case of spherical particles, the integration to obtain actual rotations is unnecessary because the relative tangential displacement, $\Delta \delta _{s,pq}^{\left( i\right) }$, can be calculated directly from the relative motion at the contact [65]. Moreover, The explicit time integration method used is conditionally stable, meaning that the time step size should not exceed the critical time step, i.e., $\Delta t_\text {DE}^{\left( i\right) }\le \Delta t_{\text {DE},\text {cr}}$, which depends on the local stiffnesses and masses [68, 69].

2.2 BEM formulation

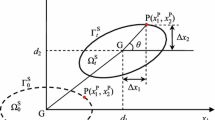
The BEM is a formulation derived from continuum mechanics theorems. One possible way to derive it is from Betti’s reciprocal theorem, as described by Dominguez [31]. This theorem establishes a correspondence between the real and virtual systems and observes reciprocity between them. The real system is the domain $\Omega \subset {\mathbb {R}}^3$ with tractions applied at the Neumann boundary $\Gamma ^\text {N}$ and displacements prescribed at the Dirichlet boundary $\Gamma ^\text {D}$, being $\Gamma ^\text {N}\cup \Gamma ^\text {D}=\Gamma =\partial \Omega$, as shown in Fig. 2. The virtual system, in turn, constitutes an infinite domain where a point load (Dirac delta) is applied at a specific point and time onto an infinite domain. The response of the infinite medium at the field point $\varvec{y}$, namely displacements $\varvec{u}^*:{\mathbb {R}}^3\longrightarrow {\mathbb {R}}^3$ and tractions $\varvec{t}^*:{\mathbb {R}}^3\longrightarrow {\mathbb {R}}^3$, under the point load applied at the source point $\varvec{x}$, are called fundamental solutions. Aside from $\varvec{y}$ and $\varvec{x}$, the fundamental solutions are also a function of the elapsed time $t$ after the load application.

Fig. 2

Sketch of a continuum body $\Omega$ with Neumann boundary $\Gamma ^\text {N}$ in blue and Dirichlet boundary $\Gamma ^\text {D}$ in cyan

The domain integrals in the reciprocal theorem vanish by utilising the properties of integration of a Dirac delta. This leads to the following Boundary Integral Equation (BIE) that needs to be solved,

$$\begin{aligned} \varvec{C}\varvec{u}= \int _{\Gamma ^{}}\varvec{U}^*\circledast \varvec{t}\,\text {d}\varvec{x} - \int _{\Gamma ^{}}\varvec{T}^*\circledast \varvec{u}\,\text {d}\varvec{x}, \end{aligned}$$

(13)

where the symbol $\circledast$ represents a convolution integral [31]. For 3D problems, $\varvec{C}$ is a $3\times 3$ matrix containing jump terms that arise from the Dirac delta integration properties. $\varvec{u}:\Omega \longrightarrow {\mathbb {R}}^3$ and $\varvec{t}:\Omega \longrightarrow {\mathbb {R}}^3$ are the displacement and traction vector fields, respectively. $\varvec{U}^*$ and $\varvec{T}^*$ are $3\times 3$ matrices containing the fundamental solutions of displacements and tractions for point loads applied to each direction, respectively, i.e., $\varvec{U}^*= \left[ \varvec{u}^*_x,\varvec{u}^*_y,\varvec{u}^*_z\right]$ and $\varvec{T}^*= \left[ \varvec{t}^*_x,\varvec{t}^*_y,\varvec{t}^*_z\right]$.

Note that the BIE in Eq. (13) is still exact, thus impossible to solve for most geometries and boundary conditions. Therefore, the numerical solution via the BEM introduces a discretisation of the displacement and traction fields over the boundary $\Gamma$. The boundary $\Gamma$ is discretised into $N_e$ elements and $N_\text {BE}$ nodes. Within each element, the coordinates are interpolated in the parametric space $\varvec{\xi }=\left( \xi ,\eta \right)$ as

$$\begin{aligned} x\left( \xi ,\eta \right)&= \sum _n^{n_e}\phi _n\left( \xi ,\eta \right) x_n\,, \end{aligned}$$

(14)

$$\begin{aligned} y\left( \xi ,\eta \right)&= \sum _n^{n_e}\phi _n\left( \xi ,\eta \right) y_n\,, \end{aligned}$$

(15)

$$\begin{aligned} z\left( \xi ,\eta \right)&= \sum _n^{n_e}\phi _n\left( \xi ,\eta \right) z_n\,, \end{aligned}$$

(16)

where the element $e$ has $n_e$ nodes and $\phi _n$ are the shape functions of the element. In this work, bilinear quadrilateral elements are used, which have the following shape functions:

$$\begin{aligned} \phi _1&= \frac{1}{4}\left( 1-\xi \right) \left( 1-\eta \right) \,, \end{aligned}$$

(17)

$$\begin{aligned} \phi _2&= \frac{1}{4}\left( 1+\xi \right) \left( 1-\eta \right) \,, \end{aligned}$$

(18)

$$\begin{aligned} \phi _3&= \frac{1}{4}\left( 1+\xi \right) \left( 1+\eta \right) \,, \end{aligned}$$

(19)

$$\begin{aligned} \phi _4&= \frac{1}{4}\left( 1-\xi \right) \left( 1+\eta \right) \,. \end{aligned}$$

(20)

The shape functions ultimately map the parametric space to a subset of the analysis space, i.e., $\varvec{x}\left( \varvec{\xi }\right) :\left[ -1,1\right] ^2\subset {\mathbb {R}}^2\longrightarrow \Gamma \subset {\mathbb {R}}^3$. In matrix form, the interpolation reads

$$\begin{aligned} \varvec{x}\left( \varvec{\xi }\right) = \varvec{\Phi }_e\left( \varvec{\xi }\right) \varvec{x}_e, \end{aligned}$$

(21)

where $\varvec{x}_e$ contains all three coordinates of all element nodes. The shape functions can be extended to the entire ${\mathbb {R}}^2$ evaluating zero everywhere outside the element. Therefore, the interpolation of all elements can be assembled in matrix form as

$$\begin{aligned} \varvec{x}\left( \varvec{\xi }\right) = \varvec{\Phi }\left( \varvec{\xi }\right) \varvec{x}_\text {BE}. \end{aligned}$$

(22)

In this work, the elements used are isoparametric, meaning displacement and geometry are interpolated using the same shape functions. Additionally, the BEM requires the discretisation of tractions over the boundary, which in this work is assumed to be the same as the discretisation for geometry and displacements. Therefore, the interpolated fields can be written as

$$\begin{aligned} \varvec{u}\left( \varvec{\xi },t\right)&= \varvec{\Phi }\left( \varvec{\xi }\right) \varvec{u}_\text {BE}\left( t\right) \quad \forall \varvec{x}\in \Gamma \,, \end{aligned}$$

(23)

$$\begin{aligned} \varvec{t}\left( \varvec{\xi },t\right)&= \varvec{\Phi }\left( \varvec{\xi }\right) \varvec{t}_\text {BE}\left( t\right) \quad \forall \varvec{x}\in \Gamma \,, \end{aligned}$$

(24)

where $\varvec{u}_\text {BE}$ and $\varvec{t}_\text {BE}$ contain the nodal values of displacements and the tractions. Thus their size is $3N_\text {BE}$, i.e., the number of Degrees of Freedom (DOFs) per node times the number of nodes in the boundary discretisation. Note that the interpolated fields are functions of the parametric value $\varvec{\xi }$ instead of the source point $\varvec{x}$ as in the BIE in Eq. (13). That allows for writing the boundary integrals in Eq. (13) in the parametric space such that

$$\begin{aligned} \varvec{C}\varvec{u}= \varvec{G}\circledast \varvec{t}_\text {BE}- \varvec{H}\circledast \varvec{u}_\text {BE}, \end{aligned}$$

(25)

with

$$\begin{aligned} \varvec{G}\left( \varvec{y},t\right)&=\sum _e^{N_e}\int _{\Gamma ^{e}}\varvec{U}^*\left( \varvec{y},\varvec{\xi },t\right) \varvec{\Phi }\left( \varvec{\xi }\right) |\varvec{J}\left( \varvec{\xi }\right) |\,\text {d}\varvec{\xi }\,, \end{aligned}$$

(26)

$$\begin{aligned} \varvec{H}\left( \varvec{y},t\right)&=\sum _e^{N_e}\int _{\Gamma ^{e}}\varvec{T}^*\left( \varvec{y},\varvec{\xi },t\right) \varvec{\Phi }\left( \varvec{\xi }\right) |\varvec{J}\left( \varvec{\xi }\right) |\,\text {d}\varvec{\xi }\,, \end{aligned}$$

(27)

where $\varvec{J}$ is the Jacobian matrix of the transformation to the parametric space.

To solve Eq. (25), one can use a time-marching time discretisation method, such as the one proposed by Mansur [70]. However, this method requires the fundamental solutions in the time domain, which are only available for a limited number of cases. Fortunately, the CQM provides an alternative solution that only necessitates the fundamental solution to be available in the Laplace domain. This allows for solving a broader range of problems with the BEM, including viscoelasticity and poroelasticity.

The CQM approximates the convolution integral in Eq. (25) utilising weighted summations. This results in a time-stepping numerical solution. Applying the CQM to Eq. (25) allows one to write [32, 71]

$$\begin{aligned} \varvec{C}\varvec{u}^{\left( j+1\right) } = \sum _{k=0}^{j+1}\varvec{G}^{\left( j+1-k\right) }\varvec{t}_\text {BE}^{\left( k\right) } - \sum _{k=0}^{j+1}\varvec{H}^{\left( j+1-k\right) }\varvec{u}_\text {BE}^{\left( k\right) } . \end{aligned}$$

(28)

Equation (28) allows the calculation of displacements at any internal point once the displacements and tractions of the boundary $\Gamma$ are known. To calculate the values of displacement and traction at the boundary, it is necessary to take the limit as this point tends to each of the boundary nodes. This process is known as collocation [45]. By doing so, one may find

$$\begin{aligned} \sum _{k=0}^{j+1}\varvec{H}_\text {BE}^{\left( j+1-k\right) }\varvec{u}_\text {BE}^{\left( k\right) }= \sum _{k=0}^{j+1}\varvec{G}_\text {BE}^{\left( j+1-k\right) }\varvec{t}_\text {BE}^{\left( k\right) }. \end{aligned}$$

(29)

The choice of the time step $\Delta t_\text {BE}$ is crucial to ensure the numerical stability of the method. While a too-large time step leads to significant numerical damping, a too-small one requires the computation of large numbers that may overflow the floating point precision [32]. Therefore, the time step must be within a range, i.e., $\Delta t_\text {BE}\in \left[ \alpha \Delta t_{\text {BE},\text {cr}},\beta \Delta t_{\text {BE},\text {cr}}\right]$, where $0<\alpha <1$ and $\beta >1$ are real numbers. [50] suggest that $\alpha =0.7$ and $\beta =1.2$, but these values might be problem-dependent. They also state that the critical time step $\Delta t_{\text {BE},\text {cr}}$ can be estimated by

$$\begin{aligned} \Delta t_{\text {BE},\text {cr}} = \frac{L_e}{c_s}, \end{aligned}$$

(30)

where $L_e$ is the minimum element length, and $c_s$ is the shear wave velocity of the material.

The BEM formulation relies on tractions whereas the DEM is based on forces. In order to couple the two methods, the forces acting from the discrete elements need to be transformed into tractions. The equilibrium between forces and tractions can be derived using the Principle of Virtual Work (pvw) such that

$$\begin{aligned} \left( \delta \varvec{u}_\text {BE}\right) ^{\textsf{T}}\varvec{f}_\text {BE}=\int _{\Gamma ^{}}\left( \delta \varvec{u}\right) ^{\textsf{T}}\varvec{t}\,\text {d}\varvec{x}, \end{aligned}$$

(31)

where $\delta \varvec{u}=\varvec{\Phi }\delta \varvec{u}_\text {BE}$ means the virtual displacement field interpolated by means of virtual nodal displacements $\delta \varvec{u}_\text {BE}$ in the same way that the real displacement field is interpolated. Substituting the interpolation of the traction and virtual displacement fields one gets

$$\begin{aligned} \left( \delta \varvec{u}_\text {BE}\right) ^{\textsf{T}}\varvec{f}_\text {BE}=\left( \delta \varvec{u}_\text {BE}\right) ^{\textsf{T}}\left[ \sum _e^{N_e}\int _{\Gamma ^{e}}\varvec{\Phi }\left( \varvec{\xi }\right) ^{\textsf{T}}\varvec{\Phi }\left( \varvec{\xi }\right) \,\text {d}\varvec{\xi }\right] \varvec{t}_\text {BE}.\nonumber \\ \end{aligned}$$

(32)

Therefore, the BEM nodal forces become

$$\begin{aligned} \varvec{f}_\text {BE}=\varvec{M}\varvec{t}_\text {BE}, \end{aligned}$$

(33)

where

$$\begin{aligned} \varvec{M}=\sum _e^{N_e}\int _{\Gamma ^{e}}\varvec{\Phi }\left( \varvec{\xi }\right) ^{\textsf{T}}\varvec{\Phi }\left( \varvec{\xi }\right) \,\text {d}\varvec{\xi }. \end{aligned}$$

(34)

Using Eq. (33) it is possible to derive an equation relating nodal forces to nodal displacements. In order to do so, one has to isolate all known tractions and displacements from the unknowns in Eq. (29) to write

$$\begin{aligned}{} & {} \varvec{H}_\text {BE}^{\left( 0\right) }\varvec{u}_\text {BE}^{\left( j+1\right) }+\sum _{k=0}^{j}\varvec{H}_\text {BE}^{\left( j+1-k\right) }\varvec{u}_\text {BE}^{\left( k\right) }\nonumber \\{} & {} \quad =\varvec{G}_\text {BE}^{\left( 0\right) }\varvec{t}_\text {BE}^{\left( j+1\right) }+\sum _{k=0}^{j}\varvec{G}_\text {BE}^{\left( j+1-k\right) }\varvec{t}_\text {BE}^{\left( k\right) }. \end{aligned}$$

(35)

Fig. 3

Sketch of a a boundary element and b discrete elements matching the shape of the boundary element at the interface

Fig. 4

Neumann–Dirichlet staggered coupling scheme. Empty and filled dots represent estimated and final values respectively

Then one can isolate the unknown tractions and substitute on Eq. (33) to write

$$\begin{aligned} \varvec{f}_\text {BE}^{\left( j+1\right) }+\varvec{h}_\text {BE}^{\left( j+1\right) } = \varvec{K}_\text {BE}\varvec{u}_\text {BE}^{\left( j+1\right) }, \end{aligned}$$

(36)

where $\varvec{K}_\text {BE}$ is the dynamic stiffness matrix of the BEM given by

$$\begin{aligned} \varvec{K}_\text {BE}=\varvec{M}\left( \varvec{G}_\text {BE}^{\left( 0\right) }\right) ^{-1}\varvec{H}_\text {BE}^{\left( 0\right) }\, \end{aligned}$$

(37)

and $\varvec{h}_\text {BE}^{\left( j+1\right) }$ is an inertial force vector that depends on the history of the analysis defined as

$$\begin{aligned}{} & {} \varvec{h}_\text {BE}^{\left( j+1\right) }=\varvec{M}\left( \varvec{G}_\text {BE}^{\left( 0\right) }\right) ^{-1}\nonumber \\{} & {} \quad \left[ \sum _{k=0}^{j}\varvec{G}_\text {BE}^{\left( j+1-k\right) }\varvec{t}_\text {BE}^{\left( k\right) }-\varvec{H}_\text {BE}^{\left( j+1-k\right) }\varvec{u}_\text {BE}^{\left( k\right) }\right] . \end{aligned}$$

(38)

Note that all matrices in Eq. (37) are precomputed before time-domain analysis. On the other hand, Eq. (38) contains precomputed matrices and known vectors from previous time steps.

3 Coupling

In the following, the efficient multi-scale staggered coupling strategy developed by the authors for 2D problems [63] is extended to 3D. It should be noted that, for 3D models, the BEM time-step requirements become more restrictive, making using the most stable coupling scheme compulsory.

The first step to implementing the staggered coupling is to define the compatibility of displacements at the interface. To do so, the interface displacement $\varvec{u}_\text {I}$ is defined as an independent variable. From there, the displacements of the BEM nodes and DEM particles incident at the interface are determined as dependent variables. For convenience, the interface displacements are chosen to be coincident with the BEM displacements, i.e.,

$$\begin{aligned} \varvec{u}_\text {BE}^{\left( j\right) } = \varvec{u}_\text {I}^{\left( j\right) }. \end{aligned}$$

(39)

Regarding the DEM, particle $p$ displacement depends on the element $e$ in which the particle lies. Since, in the 3D formulation, the shape functions are defined in the parametric space, one needs to solve a minimisation problem to encounter the parametric tuple $\varvec{\xi }_p= \left( \xi _p,\eta _p\right)$ corresponding to the particle’s reference position for each particle $p$ with coordinates $\varvec{x}_p$, i.e.,

$$\begin{aligned}{} & {} \min _{\xi ,\eta } \, \left( \varvec{x}_p- \varvec{\Phi }\left( \xi ,\eta \right) \varvec{x}_\text {BE}\right) ^2,\nonumber \\{} & {} \text {s.t.} \, -1 \le \xi \le 1 ,\quad -1 \le \eta \le 1. \end{aligned}$$

(40)

This is similar to the node-to-element contact used in FEM contact mechanics [72]. Therefore, the dependent displacement can be written as

$$\begin{aligned} \varvec{u}_p^{\left( i\right) } = \varvec{\Phi }_e\left( \varvec{\xi }_p\right) \varvec{u}_\text {I}^{\left( i\right) }. \end{aligned}$$

(41)

Fig. 3a shows the deformation of a boundary element as one of its nodes moves. In Fig. 3b it can be seen how the shape functions determine the motion of the particles lying on this boundary element. Although the figure shows a regular arrangement, the position and radius of the particles at the interface can vary freely, provided that their centre lies on the boundary element and there is no gap between the discrete elements. The displacement of all particles at the interface can be written together in vector form as

$$\begin{aligned} \varvec{u}_\text {DE}^{\left( i\right) }=\left( \varvec{u}^{\left( i\right) }_0, \dots , \varvec{u}^{\left( i\right) }_P\right) . \end{aligned}$$

(42)

By assembling the compatibility relation for all particles, it follows

$$\begin{aligned} \varvec{u}_\text {DE}^{\left( i\right) }=\varvec{T}\varvec{u}_\text {I}^{\left( i\right) }. \end{aligned}$$

(43)

where $\varvec{T}$ is a matrix that contains the values of the shape functions of the BEM elements evaluated at the position of each particle.

With Eqs. (39) and (43), the contributions of each method to the interface can be derived. The forces exerted from the BEM into the interface $\varvec{f}_{\text {I}\text {BE}}$ are derived straightforwardly using the reciprocity theorem as

$$\begin{aligned} \left( \varvec{u}_\text {I}^{\left( j\right) }\right) ^{\textsf{T}}\varvec{f}_{\text {I}\text {BE}}^{\left( j\right) } = \left( \varvec{u}_\text {BE}^{\left( j\right) }\right) ^{\textsf{T}}\varvec{f}_\text {BE}^{\left( j\right) }, \end{aligned}$$

(44)

which, substituting Eq. (39) gives

$$\begin{aligned} \varvec{f}_{\text {I}\text {BE}}^{\left( j\right) } = \varvec{f}_\text {BE}^{\left( j\right) }. \end{aligned}$$

(45)

Fig. 5

BEM-DEM coupled model of a finite rod subjected to a Heasiside load at the free end

Fig. 6

Analytical and numerical displacement at free-end using: a $D_\text {ave}={50}\,{cm}$, b $D_\text {ave}={20}\,{cm}$, and c $D_\text {ave}={10}\,{cm}$

Fig. 7

Absolute translational velocity at: a $t={0.08}\,\textrm{ms}$, b $t={0.38}\,\textrm{ms}$, c $t={0.61}\,\textrm{ms}$, d $t={0.99}\,\textrm{ms}$, e $t={1.36}\,\textrm{ms}$, f $t={1.89}\,\textrm{ms}$, g $t={2.27}\,\textrm{ms}$, and h $t={2.65}\,\textrm{ms}$. See online version for video

On the other hand, the forces at the interface arising from the DEM, $\varvec{f}_{\text {I}\text {DE}}$, can be derived from the reciprocity theorem as

$$\begin{aligned} \left( \varvec{u}_\text {I}^{\left( i\right) }\right) ^{\textsf{T}}\varvec{f}_{\text {I}\text {DE}}^{\left( i\right) } = \left( \varvec{u}_\text {DE}^{\left( i\right) }\right) ^{\textsf{T}}\varvec{f}_\text {DE}^{\left( i\right) }, \end{aligned}$$

(46)

and substituting Eq. (43) gives

$$\begin{aligned} \varvec{f}_{\text {I}\text {DE}}^{\left( i\right) } = \varvec{T}^{\textsf{T}}\varvec{f}_\text {DE}^{\left( i\right) }. \end{aligned}$$

(47)

The staggered coupling technique separates the boundary conditions at the interface. A schematic representation of the coupling scheme is represented in Fig. 4. In the Neumann–Dirichlet approach, a Neumann boundary condition is applied to the BEM, while a Dirichlet boundary condition is applied to the DEM. This means that the forces exerted by DEM particles on the interface are applied to the BEM. The calculated BEM displacements are then imposed on the interface and subsequently on the particles. However, the forces acting on the BEM and the DEM are known at different time instants. Typically, the DEM will take several steps within each BEM step. Therefore, the forces acting on the BEM are derived taking into account the impulses of the DEM force over each time step [73]. Then it is possible to determine the BEM displacements, and the DEM displacements are determined through time interpolation.

Fig. 8

BEM-DEM model for spherical cavity problem

Fig. 9

Spherical cavity displacements comparison between coupled BEM-DEM and pure BEM

In Fig. 4, there are seven distinct steps. Step 1 involves calculating the total force acting on each particle. This is done by considering both the external forces and contact forces that depend on the known position $\varvec{u}_\text {DE}^{\left( i\right) }$, as defined in Eqs. (6) and (7). For the sake of simplicity, it is assumed that the BEM and the DEM are synchronised at the beginning of the diagram, with the same displacement. Step 2 consists of incrementing the impulse using the calculated force as

$$\begin{aligned} \varvec{I}_\text {I}^{\left( i+1\right) } = \varvec{I}_\text {I}^{\left( i\right) } + \varvec{T}^{\textsf{T}}\varvec{f}_\text {DE}^{\left( i\right) }\Delta t_\text {DE}^{\left( i\right) }. \end{aligned}$$

(48)

In step 3, the force at the next BEM step can be extrapolated assuming the last known DEM force to stay constant until this time, i.e.,

$$\begin{aligned} \varvec{f}_{\text {I}\text {BE}}^{\left( j+1\right) } = \frac{\varvec{I}_\text {I}^{\left( i+1\right) } + \varvec{T}^{\textsf{T}}\varvec{f}_\text {DE}^{\left( i\right) }\left( t^{\left( j+1\right) }-t^{\left( i+1\right) }\right) }{\Delta t_\text {BE}}. \end{aligned}$$

(49)

Step 4 is simply the determination of the BEM displacements at $t^{\left( j+1\right) }$ through

$$\begin{aligned} \varvec{u}_\text {BE}^{\left( j+1\right) } = \varvec{K}_\text {BE}^{-1}\left( \varvec{f}_\text {BE}^{\left( j+1\right) }+\varvec{f}_{\text {I}\text {BE}}^{\left( j+1\right) }\right) . \end{aligned}$$

(50)

Then, in step 5, the displacement of the interface at $t^{\left( i+1\right) }$, the next DEM instant, can be interpolated via

$$\begin{aligned} \varvec{u}_\text {I}\left( t^{\left( i+1\right) }\right) = \varvec{u}_\text {BE}^{\left( j\right) } + \left( \varvec{u}_\text {BE}^{\left( j+1\right) }-\varvec{u}_\text {BE}^{\left( j\right) }\right) \frac{t^{\left( i+1\right) }-t^{\left( j\right) }}{t^{\left( j+1\right) }-t^{\left( j\right) }}, \end{aligned}$$

(51)

which allows for the determination of the DEM displacements through Eq. (43). Then $i$ is incremented. This process is repeated until the DEM advances further then the BEM, i.e., $t^{\left( i+1\right) }>t^{\left( j+1\right) }$. When this happens, steps 6 and 7 need to occur before step 3. Step 6 consists of removing the excess impulse to determine the final BEM force at $j+1$. This is done by using Eq. (49). Note that since $t^{\left( i+1\right) }>t^{\left( j+1\right) }$, the second term on the numerator becomes a subtraction. Then the accumulative impulse is reset, but to allow the new cycle to start with different positions for the BEM and the DEM, the excess impulse needs to be considered as the initial impulse value as

$$\begin{aligned} \varvec{I}_\text {I}^{\left( i+1\right) } = \varvec{T}^{\textsf{T}}\varvec{f}_\text {DE}^{\left( i\right) }\left( t^{\left( i+1\right) }-t^{\left( j+1\right) }\right) . \end{aligned}$$

(52)

Finally, step 7 consists of solving the final BEM at $j+1$ through Eq. (50) and incrementing $j$. Note that in Fig. 4, the black dots indicate final calculations, while the empty dots indicate estimates that will change in the next time step.

Fig. 10

Absolute translational velocity at: a $t={0.11}\,\textrm{ms}$, b $t={0.44}\,\textrm{ms}$, and c $t={0.59}\,\textrm{ms}$

Fig. 11

Absolute translational velocity of particles and BEM internal points along the plane $z=0$ at: a, b $t={0.59}\,\textrm{ms}$, c, d $t={1.22}\,\textrm{ms}$, and e, f $t={1.96}\,\textrm{ms}$. See online version of video

The current work assumes that particles at the interface have the freedom to rotate. A recent study by the authors found that the coupling of rotations had a negligible effect on the outcome in 2D analyses. This discovery is consistent with previous research on FEM-DEM coupling, demonstrating the possibility of free rotations in both 2D and 3D simulations [36, 38, 74]. Based on these findings, we can extrapolate that uncoupled rotations will also be effective in 3D BEM-DEM simulations. Additionally, it is assumed that the particles at the interface exhibit linear and elastic behaviour, while particles located deeper in the DEM region are allowed to have nonlinear behaviour.

It is crucial to understand how the size of particles relates to the length of boundary elements when making discretisation choices in the coupled BEM-DEM. Suppose the size of the particles is significantly larger than the length of the boundary elements. In that case, a single particle can cover multiple elements, causing a displacement field utterly incompatible with the motion of the particle. On the other hand, if the size of the particles is much smaller than the length of the boundary elements, multiple particles may lie on each boundary element. This presents no compatibility issue, but the difference in the time step between the methods would lead to instabilities in the Neumann–Dirichlet staggered approach.

In more typical scenarios, selecting the appropriate discretisation scale is crucial for balancing computational efficiency and accuracy. This is especially important in real-world applications where discretisation decisions heavily influence the accuracy of the simulation. A systematic procedure is recommended in defining the coupled model. Firstly, the particle size should be defined to represent the desired phenomena within the DEM region. Secondly, an appropriate time step is estimated for the particle assembly based on particle and contact properties. Thirdly, the BEM time step is defined, typically ten times larger than the DEM time step. Lastly, the boundary element length is determined via Eq. (30). This systematic procedure ensures a harmonised coupling between BEM and DEM while maintaining computational efficiency.

4 Results

4.1 Finite rod under Heaviside load

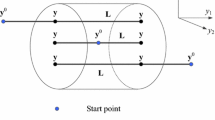
This problem is a classical benchmark in studying elastic wave propagation since it has an analytical solution. This benchmark is used to validate the coupling of BEM and DEM for 3D applications. The dimensions of the rod under consideration are a length of $2L={6}\,\textrm{m}$ (each domain is ${3}\,\textrm{m}$ long) and a square cross-section of $1\times {1}\,\textrm{m}$, i.e. $h=w={1}\,\textrm{m}$. The rod is subjected to Heaviside load $P\left( t\right) =P_0H\left( t\right)$ whose magnitude is $P_0={16}\,\hbox {kN}$. The rod is made out of a material with the following macroscopic parameters: Young’s modulus of $E={160}\,\hbox {GPa}$, Poisson’s ratio of $\nu =0.0$, and mass density of $\rho ={7850}{\hbox {kg/m}^{3}}$.

The fixed half of the rod is modelled with the BEM, while the loaded half is modelled with the DEM, as shown in Fig. 5. In order to study the sensibility of the coupled model to the diameter of the particle, three different average particle diameters are selected: $D_\text {ave}\in \{10,20,50\,\textrm{cm}\}$. In addition, due to the randomness of generating the initial particle assembly, three assemblies are generated for each average diameter. This allows for a stochastic analysis of the influence of the particle assembly. Each particle assembly is generated with a uniform particle size distribution varying from 75 to $125\%$ of the average diameter, i.e. $D\in \left[ 0.75D_\text {ave},1.25D_\text {ave}\right]$. Orthogonal regular assemblies, with all particles having the same diameter, are also considered. They serve as a reference as their microscopic Young’s moduli $\tilde{E}$ can be derived analytically. To render a null macroscopic value, the microscopic Poisson’s ratios were kept as $\tilde{\nu }=1.0$. GrainLearning [75] calibrated the microscopic Young’s modulus of irregular particle assemblies to match the analytical solution closely. A single calibration was performed for each assembly. The results reported in the sequel were obtained by averaging the parameter values for each particle size distribution.

In all simulations, the BEM discretisation consisted of square elements with a side length of 50 cm. This totalled 58 nodes and 56 elements. The time step size used in the BEM is $\Delta t_\text {BE}={2.0\times 10^{-5}}\,{s}$. The time step for the DEM is automatically adjusted by YADE [65]. Observed values ranged from 1.5$\times$10$^{-6}$ s to 7.9 $\times$ 10$^{-6}$s depending on particle size. Figures 6a–c show the results for average particle size of 50, 20, and 10 cm. The solid lines represent the average predictions obtained with irregular assemblies. The shaded areas around the solid lines indicate the range of numerical predictions. The dotted lines represent the predictions obtained with the regular assemblies. The dashed lines depict the analytical solutions. The blue colour corresponds to the end-node displacement, and the red colour corresponds to the mid-node displacement. As the average particle size decreases, the numerical predictions approach the analytical results, reducing their dispersions. Apart from the convergence, a slight decay can be observed throughout the model. This is a consequence of minor wave reflections that can be observed at the interface (see supplementary video in the online version). Although the effect of wave reflections is minor, it increases over time in finite models as the primary wave crosses the interface multiple times. This leads to a decay. In addition, an irregular particle assembly makes it difficult for the DEM to model plane waves due to imperfections. These imperfections, albeit small, amplify as the simulation proceeds because no damping is considered. This contributes to the wave reflection as well causing an increased decay. This decay can be seen, for instance in the mid-point displacement in Fig. 6c. Although the reflections seem to be greater compared to the 2D scenario [63, cf.], it is important to note that these reflections remain modest and do not influence the quality of the results.

Figure 7 displays a time series of the absolute translational velocities of the DEM particles and the BEM elements with $D_\text {ave}={10}\,\textrm{cm}$. In Fig. 7a, the velocities caused by applied forces propagate in the initial stage of wave propagation. As the wave traverses the DEM domain, in Fig. 7b, the imperfections of the particle assembly lead to an irregular velocity profile. In Fig. 7c, the wave approaches the interface while high local velocities can still be observed. The wavefront can be seen in the BEM domain in Fig. 7d, where the velocity profile appears uniform, and no significant wave reflections occur. The wave approaches the supported face in Fig. 7e from where it will reflect back. In Fig. 7f, the wave travels towards the interface after reflection and enters the BEM domain. In Fig. 7g, the wave crosses the interface again with no significant reflection and moves towards the loaded end of the rod. In Fig. 7h, the wave reaches back to the loaded end, and the velocities decrease close to zero along the rod at the moment of maximum displacement.

4.2 Spherical cavity in infinite space under uniform pressure

This problem is a well-established benchmark for wave propagation. It is used herein to further validate the 3D coupled BEM-DEM approach. Unlike the previous example, this problem occurs in an infinite domain. Moreover, while the previous example could be simulated in one dimension, this one demands a detailed 3D space depiction.

The example involves a spherical cavity in an infinite domain where an internal pressure is applied. The cavity has a radius of $r= {5.38}\,\textrm{m}$, and the surrounding medium has a Young’s modulus of $E={62}\,\textrm{GPa}$, a Poisson’s ratio of $\nu =0.25$, and a mass density of $\rho ={2670}{\hbox {kg/m}^{3}}$. The internal pressure is applied as a Heaviside function $p\left( t\right) =p_0H\left( t\right)$ with a magnitude of $p_0= {1}\,\textrm{kPa}$.

The DEM models the region between the cavity and a cube with a side length of 15 m. From this point on, the media is represented by the BEM. The coupled model is shown in Fig. 8. For better visualisation, only half of the BEM mesh and one-quarter of the DEM particle assembly with the cavity where the pressure is applied is shown.

The coupled analysis is carried out with DEM assemblies whose average diameter is $D_\text {ave}= {25}\,\textrm{cm}$ and vary uniformly within 25% of this value. Three different assemblies are considered to account for the variability of the particle assembly. This results in around 220,000 particles. The time-step of the DEM is automatically defined by YADE over the simulation with values close to 2.18 $\times$ 10$^{-3}$ ms. In the BEM, the time-step is 0.15 ms, and the element size is 1 m $\times$ 1 m rendering 1,350 bilinear quadrilateral boundary elements.

The displacements of three points are analysed: Point A $\left( 5.38,0,0\right)$, at the cavity; Point B $\left( 7.5,0,0\right)$, at the interface; and Point C $\left( 10,0,0\right)$, in the interior of the infinite domain. In Fig. 9, the displacements of these points are shown in blue, red, and green, respectively. The solid lines represent the average across all assemblies, while the shaded regions indicate the range of the observed values. The dashed lines depict the numerical predictions of the pure BEM.

The wave introduced by the internal pressure within the DEM propagates towards the interface with the BEM region. The analysis of particle velocity over a model section through the plane $z=0$, as illustrated in Fig. 10, provides insight into the wave propagation mechanism. To investigate the wave propagation within the BEM domain, velocities are computed at internal points along the same plane $z=0$. Figure 11 depicts the wave approach towards the interface and its transition into the BEM region. The velocities of each particle are shown alongside the coarse-grained velocity field (Appendix A). Although small wave reflections can be observed, they do not significantly affect the overall quality of the results. It can be seen that after crossing the interface the primary wave propagates into the infinite domain.

4.3 Cylindrical column embedded in infinite half-space

In this example, a cylindrical column is partially embedded in an infinite half-space and is subjected to a horizontal load on its top. The column is made out of a material with Young’s modulus of $E_c = {30}\,\textrm{GPa}$, Poisson’s ratio of $\nu _c=0.2$, and mass density of $\rho _c= {2400}\,{\hbox {kg/m}^{3}}$. The infinite half-space, in turn, is made out of a different material whose Young’s modulus is $E_s = {265}\,\textrm{MPa}$, Poisson’s ratio is $\nu _s=0.17$, and mass density is $\rho _s={1800}\,{\hbox {kg/m}^{3}}$. The load is suddenly applied as a Heaviside function, i.e., $P\left( t\right) =P_0H\left( t\right)$, at the top of the column. Its magnitude is $P_0={100}\,\textrm{kN}$, and it is distributed over the top area of the column.

A sketch of the model is shown in Fig. 12. The cylindrical column is modelled as a finite BEM domain. The surrounding region of the half-space is modelled using the DEM, while the remaining region is modelled as an infinite BEM domain. To better understand the embedment size, a section of the model across the plane of $z=0$ is shown in Fig. 13. The DEM domain is a rectangular prism 7 m by 7 m and 3.5 m deep, except for the space occupied by the column. The column is embedded 2 m into the DEM domain. The region in cyan across the plane $z=0$ indicates where internal point results are calculated to provide an insight into how the wave propagates within the BEM domain.

Fig. 12

BEM-DEM coupled model for the cylindrical column in a half-space

Fig. 13

Cross-section of the BEM-DEM coupled model for the cylindrical column in a half-space

The sizes of the particles in the DEM domain are uniformly distributed between 15 cm and 25 cm. The assembly consists of 28,945 particles. The DEM time-step is automatically defined by YADE, revolving around 2.55 $\times$ 10$^-2$ ms. The column is discretised using 544 bilinear quadrilateral boundary elements of size 25 cm $\times$ 25 cm. For modelling the column, a time-step of 0.1 ms is used. The surrounding soil is also modelled with the BEM, and the boundary mesh contains 1100 elements of size 70 cm $\times$ 70 cm. A time-step of 2 ms is used for this infinite region.

The horizontal displacement of the top of the column is shown in Fig. 14. The wave propagation is shown in Fig. 15. In Fig. 15a, it can be seen how the wave transitions from the column into the half-space. Figure 15b shows the moment the wave reaches the interface between the DEM domain and the BEM infinite half-space. A few milliseconds later, most of the wave travels within the BEM domain, which is depicted in Fig. 15c. In 15d, the wave dissipates as it travels towards infinity. The same instants are depicted in Fig. 16, where a section across the plane $z=0$ is shown. The depicted velocity is a coarse-grained approximated continuum field derived from the particles’ velocity. The Coarse-graining homogenisation is described in Appendix A. In Figs. 11a, c, and d, it can be seen a small region within the column where the velocity is close to zero. The centre of this region represents the centre of rotation of the column.

Fig. 14

Horizontal displacement at the top of the column

Fig. 15

Absolute translational velocity at: a $t={13}\,\textrm{ms}$, b $t={21}\,\textrm{ms}$, c $t={28}\,\textrm{ms}$, d $t={36}\,\textrm{ms}$, e $t={44}\,\textrm{ms}$, and f $t={54}\,\textrm{ms}$. See online version of video

Fig. 16

Absolute translational velocity of particles and BEM internal points along the plane $z=0$ at: a $t={13}\,\textrm{ms}$, b $t={21}\,\textrm{ms}$, c $t={28}\,\textrm{ms}$, d $t={36}\,\textrm{ms}$, e $t={44}\,\textrm{ms}$, and f $t={54}\,\textrm{ms}$. See online version of video

5 Conclusions

The present paper introduces a new framework for coupling the BEM and the DEM in the dynamic analysis of 3D problems. This is achieved by extending a previously developed 2D coupling strategy of the DEM and the BEM. The proposed approach combines the strengths of both methods, such as the representation of non-linearities and infinite domains. The extension from 2D to 3D modelling demonstrates the versatility and scalability of the coupled model, providing a comprehensive framework for real-life simulations.

The key findings of this research underscore the suitability of the coupled BEM-DEM model in capturing 3D wave propagation. As per the results, there is a seamless transition between the DEM and BEM domains, highlighting the adaptability of the framework across different dimensions. Another finding is that the assumption of free rotations at the interface, previously used in 2D, worked well in the 3D simulations. Despite the increased significance of spurious wave reflections in three dimensions, their impact remains negligible to the overall analysis. Moreover, introducing a staggered time-integration scheme is essential for 3D simulations, addressing restrictive time-step requirements for stable, accurate and efficient modelling.

Despite the slight increase in wave reflections at the interface compared to 2D, it must be emphasised that the impact of these reflections on the simulation outcomes remains minimal, underscoring the robustness of the proposed method. Future work will include the study of domain coupling approaches recently proposed in the context of FEM-DEM coupling to minimise wave reflections at the interface. Simultaneously, the incorporation of viscosity into the simulations is planned to enhance their fidelity. Another significant aspect of the future work involves addressing the challenge of calibrating microscopic damping parameters to align with macroscopic dynamic behaviour. Additionally, a more robust alternative is available to control the angular velocities of particles at the interface. The approach used in coupling 2D BEM-DEM can be extended to 3D. The components of the spin tensor, which is the unsymmetrical part of the velocity gradient tensor obtained from the BEM solution, can be used to constrain the angular velocities of the particles at the interface.

Appendices

Appendix

A Coarse-graining

Coarse-graining is a homogenisation technique that allows for establishing micro-to-macro relationships [76]. For this homogenisation to work, specific laws of physics must be obeyed, such as mass and momentum conservation. Therefore, the density field is defined as

$$\begin{aligned} \rho \left( \varvec{x}\right) = \sum _{p=0}^{N_p}{\mathcal {W}}\left( \varvec{x}-\varvec{x}_p\right) m_p, \end{aligned}$$

(53)

where ${\mathcal {W}}$ is a spatial smoothing kernel obeying the following conditions:

• it is normalised: $\int _{{\mathbb {R}}^\text {d}}{\mathcal {W}}\left( \varvec{x}\right) \,\text {d}\varvec{x}=1$;

• it is non-negative: ${\mathcal {W}}\left( \varvec{x}\right) \ge 0\,\forall \varvec{x}\in {\mathbb {R}}^\text {d}$; and

• it has compact support: $\exists c\in {\mathbb {R}}:{\mathcal {W}}\left( \varvec{x}\right) =0\,\forall \varvec{x}:\Vert \varvec{x}\Vert _{2}>c$.

Commonly used spatial smoothing kernels include the cut-off Gaussian and the Lucy polynomial [77]. In this study, the Lucy polynomial is used, and it is defined as:

$$\begin{aligned} {\mathcal {W}}\left( \varvec{x}\right) =\left\{ \begin{array}{lr} C_\text {L}\left( -3\left( \frac{\Vert \varvec{x}\Vert _{2}}{c}\right) ^4+8\left( \frac{\Vert \varvec{x}\Vert _{2}}{c}\right) ^3-6\left( \frac{\Vert \varvec{x}\Vert _{2}}{c}\right) ^2\right) &{} \text {if }\Vert \varvec{x}\Vert _{2}<c,\\ 0 &{} \text {otherwise}, \end{array}\right. \nonumber \\ \end{aligned}$$

(54)

where $C_\text {L}$ is a factor appropriately adjusted to meet the normalisation condition. A momentum field $\varvec{q}$ can be approximated by Coarse-graining (CG) analogously to the density field, i.e.,

$$\begin{aligned} \varvec{q}\left( \varvec{x}\right) = \sum _{p=0}^{N_p}{\mathcal {W}}\left( \varvec{x}-\varvec{x}_p\right) m_p\dot{\varvec{u}} _p. \end{aligned}$$

(55)

Hence, a velocity field can be defined as $\dot{\varvec{u}} \left( \varvec{x}\right) ={\varvec{q}\left( \varvec{x}\right) }/{\rho \left( \varvec{x}\right) }$. A displacement field whose time derivative corresponds to the derived velocity field can be written as

$$\begin{aligned} \varvec{u}\left( \varvec{x}\right) = \frac{\sum _{p=0}^{N_p}{\mathcal {W}}\left( \varvec{x}-\varvec{x}_p\right) m_p\varvec{u}_p}{\sum _{p=0}^{N_p}{\mathcal {W}}\left( \varvec{x}-\varvec{x}_p\right) m_p}. \end{aligned}$$

(56)