A simple FEM–DEM technique for fracture prediction in materials and structures

Abstract

This paper presents a new computational technique for predicting the onset and evolution of fracture in a continuum in a simple manner combining the finite element method (FEM) and the discrete element method (DEM). Onset of cracking at a point is governed by a simple damage model. Once a crack is detected at an element side in the FE mesh, discrete elements are generated at the nodes sharing the side and a simple DEM mechanism is considered to follow the evolution of the crack. The combination of the DEM with simple 3-noded linear triangular elements correctly captures the onset of fracture and its evolution, as shown in several examples of application in two and three dimensions.

1 Introduction

The development of a fracture within a continuous medium is a topic of much interest in the strength analysis of brittle and ductile materials. One of the most recent methodologies to simulate the fracture process is the discrete element method (DEM) [8, 13, 23–29]. However, the inherent difficulty for calibrating the material parameters in the DEM, as well as the need for a large number of discrete elements for solving practical problems, questions its effectiveness for large-scale fracture mechanics analysis, even though the qualitative results of the DEM for predicting fracture patterns are pretty good.

Much research has been invested in recent years in the development of the finite element method (FEM) for modeling the onset and propagation of cracks in frictional materials [4–6, 9, 11, 14–16, 18–20]. However, FEM procedures for crack prediction use sophisticated element formulations and often require to remesh in the vicinity of the possible cracks paths [7, 11, 16].

The approach followed in this paper uses the FEM to model a continuum whose fracture is described by means of discrete elements when it appears. The FEM–DEM transition is done without remeshing. Although several of the ideas on which this paper is based have been studied previously [12, 17, 30], the current development has enabled a new and promising approach to solving the problem of fracture propagation in a continuum.

Fig. 1

a Equivalence between a linear triangle and a cohesive link of three disks in the DEM. b Stiffness matrix for the linear triangle computed as the sum of three stiffness matrices involving the side nodes only

The paper describes the basis of the simple FEM–DEM procedure proposed. The method extends a well-defined crack opening methodology termed element elimination technique (EET) [12, 17, 30] that creates discrete elements at the crack lips. Onset of cracking at the midpoint of the element sides is governed by a standard single parameter damage model. This is followed by the removal of the side and the generation of a discrete element at the nodes sharing the side. Some important aspects inherent to the formulation here presented guarantee the good results obtained like a smoothed stress field, mass conservation, and the use of a simple algorithm to ensure the post-fracture contact. The FEM–DEM approach proposed is applied to a collection of benchmark problems in two (2D) and three (3D) dimensions which evidence the good performance of this numerical technique.

2 Analogy between dem and fem

The main feature of the DEM versus the FEM is its ability to generate a fracture in any direction by selectively breaking the bonds between the individual discrete elements. A time explicit integration scheme and the adequate definition of the DEM material parameters at the contact interface between the discrete elements are the key ingredients of most DEM procedures.

Despite the many advantages of the DEM, the material parameters used at the contact interface between discrete elements are not able to represent properly all the properties of a continuous domain. Additionally, and perhaps most importantly, the simple law that defines the crack appearance at the contact interface of discrete elements is not comparable to the sophisticated failure criteria used in fracture mechanics. As a consequence despite recent progress in this field [23], it is difficult to define the stress state on a continuum via the cohesive bonds of discrete elements.

On the other hand, the FEM defines correctly the stress state in a continuum, which facilitates the implementation of a variety of constitutive equations and failure criteria, allowing to model in a easy way the linear and non-linear behavior of a wide number of materials.

Fig. 2

Equivalence between the stiffness matrix of a linear triangle with a broken bond in a side and a cohesive link in the DEM

In view of above facts the question arises: Is there any way to define conditions at the particle interface in the DEM so that they yield the same displacement field as in the FEM?. Figure 1 shows that the answer is yes for 3-noded linear triangles. The stiffness matrix of a linear triangular element can be defined using Green’s theorem in terms of integrals along the element sides [10, 21, 22]. The integration over each element side ij yields the stiffness that each cohesive link must have in the DEM.

In this way, the stiffness required by a cohesive link in the DEM to represent a continuum via the FEM can be defined. However, if both approaches are identical, what is the advantage of using discrete elements?. Obviously, the finite element formulation is more complete and flexible. The displacement field is defined over the entire domain. Even more, the stress field in the FEM is more accurate and easier to obtain. It is also possible to prove convergence and stability for the numerical solution. However, there are distinct features in the DEM that make it a powerful numerical technique for modeling multifracture situations in materials and structures.

3 From fem to dem

The DEM is a very powerful tool when it is used for analysis of granular materials. Its main advantage when applied to a continuous domain is its capability for predicting random cracking paths, which is useful for reproducing correctly the fracture behavior of materials such as soils, rocks, ceramics, and concrete, among others [23–28]. Thus, the rationale of the FEM–DEM approach proposed in this work is to apply the DEM methodology for modeling the onset and evolution of a crack to the standard FEM formulation. The direct application of the FEM (or the DEM) using the stiffness matrix described in Figure 1 holds as long as no cohesive link is removed. The problem arises when there is a need to remove (or break) a cohesive link, coinciding with an element side. The stiffness matrix of a finite element is obtained as the balance of internal forces of the element. Hence by eliminating the stiffness contributed by a link, the forces between the two nodes involved are unbalanced which affects the entire finite element mesh, or all neighboring particles in the DEM. The right way to eliminate the cohesive bond is by calculating the stiffness loss associated to the removal area. In other words, the initial stiffness of the element is reduced by eliminating the area between the two nodes sharing the broken side and the centroid of the element, as shown in Figure 2.

The stiffness of the element zone to be eliminated is a function of the original element area (or volume in 3D) and is easily found in terms of the displacements of the element centroid (which coincides with the integration point in linear triangles). Thus, for a broken bond at a side ij, the stiffness matrix linking nodes i and j to be eliminated is

$$\begin{aligned} \varvec{K}_{ij} = \frac{1}{3}\varvec{K}^{(\mathrm e)} \end{aligned}$$

(3)

where $\varvec{K}^{(\mathrm e)}$ is the full stiffness matrix for the 3-noded triangle.

Once the side ij (and the corresponding element area) is removed, the remaining stiffness of the element is

$$\begin{aligned} \varvec{\hat{K}}^{(\mathrm e)} = \varvec{K}^{(\mathrm e)}-\varvec{K}_{ij} \end{aligned}$$

(4)

4 Failure due to accumulated damage

In order to eliminate properly a cohesive bond, it is necessary to define a failure criterion. Many references can be found on this subject [4–6, 9, 11, 14–16, 18–20]. However, it is important to note that cohesive bonds are assumed to be placed at the element sides and not at the integration point within the element. Recalling that the stress field is discontinuous between elements, a smoothing procedure is needed to evaluate the stresses at the element edges and, subsequently, the failure criteria chosen at the edges. The smoothing procedure selected is the key point to have an accuracy stress field. In our work, we have followed the superconvergent patch recovery (SPR) method proposed by Zienkiewicz, and Zhu [32] which overcomes the need to add stabilization terms to the stress field as in alternative procedures [4–6]. The failure criterion chosen is based on the standard single parameter damage model, typically used for predicting the onset of fracture in concrete and ceramic materials [6, 14, 15, 18–20]. The damage model is summarized below.

4.1 Computation of the remaining stiffness for an element

In this work, a standard single parameter damage model is used. The constitutive equation at the element center is therefore simply written as

$$\begin{aligned} \varvec{\sigma } = (1 - \tilde{d} ) \mathbf{D} \varvec{\varepsilon }, \end{aligned}$$

(5)

where

$$\begin{aligned} \tilde{d} = \frac{1}{3} (d_1 + d_2 + d_3) \end{aligned}$$

is the average damage parameter for the element, with $d_i$ $(i = 1,2,3)$ being the damage parameters at the midpoint of the ith element side.

The stiffness of a damaged 3-noded triangular element can be therefore be written as

$$\begin{aligned} \varvec{K}^{(\mathrm e)}=(1-\tilde{d})\varvec{K}_0^{(\mathrm e)}= \varvec{K}_0 - \hat{\varvec{K}}^{(\mathrm e)}, \end{aligned}$$

(6)

where $\varvec{K}^{(\mathrm e)}_0$ is the stiffness of the undamage element and the damaged stiffness matrix for an element $\hat{\varvec{K}}^{(\mathrm e)}$ is computed as

$$\begin{aligned} \hat{\varvec{K}}^{(\mathrm e)} = \frac{1}{3}(d_1+d_2+d_3)\varvec{K}_o^{(\mathrm e)}. \end{aligned}$$

(7)

Fig. 3

Three-noded triangle with two sides damaged. Effect on the adjacent triangles sharing the damaged sides

A key issue in this approach derives from analyzing in detail Eq. (7). As it can be seen in Fig. 3, when an element has two fully damaged edges according to Eq. (7), the damaged stiffness is one-third of the original one. However, the fact is that a crack has already appeared within the element and, therefore, when two sides of an element are fully damaged, the whole element can be considered to be as fully damaged as well.

Consequently, the remaining stiffness matrix for a damaged element is computed as

$$\begin{aligned} \hat{\varvec{K}}^{(\mathrm e)} = \frac{d_i+d_j}{2}\varvec{K}_o^{(\mathrm e)} \end{aligned}$$

(8)

where $d_i$ and $d_j$ are the two maximum values of the damage parameters for the three element sides.

4.2 Damage evolution model

In our model, damage is assumed to initiate at the element mid-sides once the stress field satisfies the Mohr–Coulomb criterion. This is schematically shown in Fig. 4 for a 2D stress state.

Fig. 4

Limit damage surface in the principal stress space ($\sigma _I$, $\sigma _{II}$) and uniaxial stress–strain curve for the damage model of Eqs. (5) and (9)

The evolution of the damage variable d at the midpoint of the element sides is defined by the following exponential function

$$\begin{aligned} d (\bar{\delta }) = 1 - \frac{1}{\bar{\delta }}\exp ~\{A (1 - \bar{\delta })\} \end{aligned}$$

(9)

where $\bar{\delta }= (1-\delta )$ and $\delta$ is the “distance” between a stress point and the yield function. Figure 4 shows an schematic representation of $\delta$ for three different stress points $S_1$, $S_2$, $S_3$. Note that for points laying on the yield surface $\delta =0$ and, hence, $\bar{\delta }= 1$, and $d (1) =0$. On the other hand, $d (\infty )=1$, as expected.

In Eq. (9), the parameter A is determined from the energy dissipated in an uniaxial tension test as [9, 18]

$$\begin{aligned} A=\left( \frac{G_f E}{\hat{l}(f_t)^2} -1/2\right) ^{-1} \end{aligned}$$

(10)

where $f_t$ is the tensile strength, $G_f$ is the specific fracture energy per unit area (taken as a material property), and $\hat{l}$ is the characteristic length of the fractured domain. This length defines the maximum finite element size [9, 18–21]. From the condition of A being positive, it is deduced that $\hat{l}\le {{2G_fE}\over {(f_t)^2}}$.

The damage model presented above is extremely simple in comparison to more sophisticated constitutive models for concrete and other frictional materials [4, 14, 15, 18–20].

The experimental characterization of the model is also simple, and the following material parameters are only required: Young modulus, tension, and compression limit strengths, and specific fracture energy per unit area obtained from uniaxial tests.

4.3 Definition of the characteristic length

In order to define properly the fracture energy consumed in breaking a side, the material volume assigned to the side ($V=\frac{1}{3}(A^\mathrm{e}+A^{\mathrm{e}^{\prime }})t$) can be made equal to a rectangular prism of dimensions $l \times h \times t$, where t is the prism thickness (Fig. 5). Considering that fracture is governed by a critical value of the maximum principal (tensile) stress $\sigma _\text {I}$, the prism volume is defined as $\hat{l} \times \hat{h} \times t$ where $\hat{l}$ lays on the principal stress direction. In this case, a smooth variation for $\hat{l}$ is proposed between $h \le \hat{l} \le l$. Therefore, $\hat{l}$ is defined in terms of the angle $\alpha$ given by the principal stresses direction and the side ij (Fig. 5) as

$$\begin{aligned} \hat{l}=l-\left[ 1-\cos (2\alpha )\right] \left[ {\frac{l-h}{2}}\right] \qquad \text {with}\qquad h = \frac{A^\mathrm{e}+A^{\mathrm{e}^{\prime }}}{3l} \end{aligned}$$

(11)

Fig. 5

Characteristic length definition at a side shared by two elements. Equivalent rectangular prism where fracture is localized

Note that when a side is damaged, it affects all the elements that share the side, as shown in Fig. 3.

Remark

The removal of a cohesive bond at a side does not give an indication of the cracking direction. The fracture patterns can be identified from the distribution of the broken bonds at the element sides, as it is usually done in damage models for frictional materials [9, 14–16, 18–20]

5 Generation of discrete particles

When a cohesive bond is fully removed (i.e., the side stiffness is neglected), two discrete elements (or particles) are created at the disconnected nodes. In our work, we have used circular disks (for 2D problems) and spheres (for 3D problems) for representing the discrete elements. The mass of each new discrete element corresponds to the nodal mass in the FEM and its radius will be the maximum one that guarantees the contact between the adjacent discrete elements without creating any overlappings between them. Indeed, this is not the only algorithm that can be used for generating discrete elements [13] but it has been proved to be a very effective procedure, as the main idea is to avoid that the new discrete elements created generate spurious contact forces.

Once a discrete element is created, the forces at the contact interfaces are used to define the interaction of the element with the adjacent ones. These forces are due only to the contact interaction in the normal and tangential directions. At the contact point, the minimum radius of the particles in contact are used to evaluate the contact forces [23].

In our work, we have used a local constitutive model for the normal and tangential forces at the contact interfaces between discrete elements as proposed in [23].

For 2D problems, the normal contact force $F_n$ at a contact point between two disks is given by

$$\begin{aligned} F_n=E_\mathrm{o}A\varepsilon _n=2E_\mathrm{o}\mathrm{rt}\left( \frac{u_n}{r_i+r_j}\right) \quad \text {with}\quad r=\min \left( r_i {,} r_j\right) \end{aligned}$$

(12)

where $u_n$ is the normal overlap between the two discrete elements.

The tangential force $F_s$ at the contact point is a function of the relative tangential displacement $u_s$ between the two particles in contact, and is defined in a regularized way as [23]

$$\begin{aligned} F_s= \min {\left\{ \begin{array}{ll} 2\mathrm{rt}\left( \frac{u_s}{r_i+r_j}\right) \frac{E_o}{2\left( 1+\nu \right) }\\ \mu F_n \end{array}\right. } \end{aligned}$$

(13)

where $\mu$ is the friction coefficient and $\nu$ is the Poisson’s ratio.

The extension of Eqs. (12) and (13) to the 3D case can be seen in [23, 31].

Some interesting facts are derived from this approach. Since the number of discrete elements generated in an analysis is only a fraction of the number of nodes in the mesh, the searching algorithm for evaluating the contact interactions between discrete elements does not consume much computational resources, as in the case of using discrete elements only. Additionally, the generated particles undergo relatively small displacements (due to the time increments used in the explicit integration scheme chosen here) so the list of possible contact points does not require a constant updating.

6 Examples

Four examples are presented to demonstrate the good behavior of the FEM–DEM approach described in the previous sections. The first example is the 2D study of a normalized tensile test in a concrete specimen. The second one is the 2D analysis of a mixed-mode fracture benchmark in a concrete beam. Next, an indirect tensile test widely used in concrete and rock mechanics is analyzed in 2D and 3D using the FEM–DEM technique proposed. Finally, we present an example of compressive failure of a concrete specimen.

All the examples have been solved using an explicit dynamic technique for the time integration of the governing equations for the FEM and for each individual particle, as it is typically done in the DEM [23–29].

Fig. 6

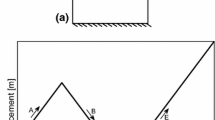
Normalized tensile test of a concrete specimen. Finite element meshes and dimensions according to the ASTM D638 norm [1]

Fig. 7

Normalized tensile test of a concrete specimen. Load–horizontal displacement curve at the specimen tip using $G_{f_1}=0.0 \times 10^{-3} \, \mathrm{J/m}^2$

6.1 Normalized tensile test

The first example corresponds to the fracture analysis of a flat concrete specimen under tensile stress. The geometry is defined according to the norm D638 of the American Section of the International Association for Testing Materials (ASTM) [1] as shown in Fig. 6 where the three meshes of 3-noded triangular elements used and the boundary conditions can be seen. A constant displacement field is imposed in the entire shadow area.

The study has been performed using the 2D FEM–DEM technique previously described. In order to localize the fracture, only one band of elements is allowed to break at the failure stress level corresponding to the tested material, using the linear damage model presented. The results obtained are analyzed by plotting the horizontal displacement of points PA and PB shown in Fig.  6.

The Young modulus, the Poisson ratio, and the density are, respectively, $E_0=30$ GPa, $\nu = 0.2$, and $\gamma = 1.0 \times 10^3 \, \mathrm{N/m}^3$. The tensile strength is $f_t = 10$ KPa. Two specific fracture energies per unit area have been considered $G_{f_1}=0.0 \, \mathrm{J/m}^2$ and $G_{f_2}=7.5 \times 10^{-3} \, \mathrm{J/m}^2$.

The specimen deforms by applying a constant velocity displacement of $0.5 \times 10^6 \, \mathrm{m/s}$. at the right tip of the specimen. Figure  7 shows the relationship between the imposed displacement and the load level for the brittle fracture case ($G_{f_1}=0.0 \, \mathrm{J/m}^3$). The behavior is exactly the same for the three meshes used and in agreement with the expected result. Figure 8 shows the damaged geometry. Note that where fracture appears, discrete elements are created at the crack lips as explained in the previous sections.

When the numerical experiments are carried out using a specific fracture energy of $G_{f_2}=7.5 \times 10^{-3} \, \mathrm{J/m}^2$, the displacement of points PA and PB situated at the right and the center of the specimen, respectively (Fig. 6), is tracked in order to evaluate the crack opening. Figure 9 shows the load–displacement relationship at these points. For the three meshes considered, the displacement evolution is very similar and in agreement with the expected results.

Fig. 8

Normalized tensile test of a concrete specimen. Cracked zone with the discrete particles generated for the three finite element meshes considered

Fig. 9

Normalized tensile test of a concrete specimen. Load–horizontal displacement curve at points PA and PB of the specimen using $G_2=7.5\times 10^{-3}$ J/m$^2$

Fig. 10

Double notched concrete beam. Dimensions and boundary conditions

Since the fractured elements have a different size for each mesh, the displacement of point PB in the elastic region becomes smaller as the element size is reduced. However, once the crack initiates, the displacement of point PB is ruled by the elastic energy stored in the specimen. Beyond the limit load value, the displacement of the point follows the continuous branch of the theoretical static problem. As the problem has been solved in a dynamic fashion, the change in slope progresses gradually and has small fluctuations around the theoretical result. The crack pattern for this case is very similar to that shown in Fig. 8.

6.2 Four-point bending beam

The next example is the failure test of a double notch concrete beam analyzed under plane stress conditions. This is a good example of mix-mode fracture. The beam is supported at two points and deforms in a bending mode by applying an imposed displacement at the two points depicted in Fig. 10 where the beam dimensions are also shown.

The beam has two singular points at the tip of the two notches where the tensile stresses are high and damage begins in this area. The material properties are $E_0=30$ GPa, $\nu =0.2$, $\gamma = 10^3\,$ N/m$^3$, $f_t =2$ MPa, and $G_f =100$ J/m$^2$. The problem has been solved with the 2D FEM–DEM technique explained. Figure 11 shows a detail of the three meshes used of 1165 nodes and 2202 linear triangular elements (coarse mesh), 1847 nodes and 3480 elements (intermediate mesh), and 5747 nodes and 11206 elements (fine mesh).

Fig. 11

Double notched concrete beam. Detail of the three meshes used in the vicinity of the two notches

Fig. 12

Double notched concrete beam. Displacement contours and crack path at the two notches regions using three different meshes: a Coarse mesh, b intermediate mesh, c Fine mesh. Detail of the discrete elements generated at the cracks

Fig. 13

Double notched concrete beam. Relationship between the force and the imposed displacement at any of the two points depicted in Fig. 10. FEM–DEM results are compared to those given in [7]

Fig. 14

BTS test on a concrete specimen. Dimensions, boundary conditions, and finite element meshes of three-noded triangles used for the analysis

Fig. 15

BTS test on a concrete specimen. Damage zone and discrete elements generated. a Coarse mesh, b intermediate mesh, c Fine mesh

Fig. 16

2D FEM–DEM analysis of BTS test on a concrete specimen. Force–displacement relationship for the three meshes used

Fig. 17

3D FEM–DEM analysis of BTS test on a concrete specimen. Damage zone and discrete elements generated. a Coarse mesh, b intermediate mesh, c Fine mesh

Fig. 18

3D FEM–DEM analysis of BTS test on a concrete specimen. Force–displacement relationship for the three meshes used

Fig. 19

Compressive failure analysis of a concrete specimen. Geometry and finite element meshes of 3-noded triangles

Fig. 20

Compressive failure analysis of concrete specimen. Stress–strain curve

Fig. 21

Compressive failure analysis of a concrete specimen using a structured mesh. a Theoretical result [2]. b Crack path. c Displacement distribution. d Damage distribution

Fig. 22

Compressive failure analysis of a concrete specimen using a unstructured mesh. a Theoretical result [2]. b Crack path. c Displacement distribution. d Damage distribution

Figure 12 shows the crack path for the three meshes analyzed which coincide with the numerical results of Cervera et al. [7]. Figure 13 shows the relationship between the vertical reaction at a force support and the imposed displacement at any of the two points depicted in Fig.  10. The graphs are in good agreement with the results obtained in [7].

6.3 Indirect tensile test

The Brazilian tensile strength (BTS) test is a very practical and simple experimental procedure to evaluate the tensile strength of brittle materials. The concrete sample analyzed is a cylinder of $0.2 \, \mathrm{m}$ diameter (D) and $0.1 \, \mathrm{m}$ thickness (t), which is diametrically loaded by a press. The tensile strength value is computed by the following relationship [3]:

$$\begin{aligned} f_t^\mathrm{num}=\frac{2P}{\pi tD} \end{aligned}$$

(14)

where P is the applied load.

The material properties are $E_0=21$ GPa, $\nu = 0.2$, $\gamma = 7.8 \times 10^3$  N/m$^3$, $f_t =10$  KPa, and $G_f =1\times 10^{-3}$  J/m$^2$. Using Eq. (14) this corresponds to a failure load of $P=314.16$  N.

Three meshes of 890, 1989, and 7956 linear triangular elements each were used for the analysis, as shown in Fig. 14. The sample is deformed by imposing a constant velocity displacement at the top of the sample.

Figure 15 depicts the damaged geometry, as well as the crack and the discrete elements generated at a certain instant of the analysis. The cracking pattern is similar for the three meshes and in agreement with the expected result. Figure 16 shows the evolution of the vertical load versus the horizontal displacement at the center of the specimen up to the failure load. The numerical values for the tensile strength obtained using Eq. (14) for each three meshes (coarse to fine) were 10587, 10506, and 10481 Pa, respectively, which yield a maximum of $5\,\%$ error versus the expected value of $f_t = 10$ KPa.

The same example with identical geometry and mechanical properties was solved in 3D using an extension of the FEM–DEM technique presented in this work [31]. Three meshes were used with 9338, 31455, and 61623 4-noded linear tetrahedra. Results of the crack pattern obtained for each of these meshes are depicted in Fig. 17. The numerical results for the load–displacement curve are presented in Fig. 18. The numerical values obtained for the tensile strength were (coarse to fine mesh) 10 693, 10 351, and 10 235 Pa which yielded a range of 6-2$\,\%$ error versus the expected value of $f_t = 10$  KPa.

6.4 Example of compressive failure

The usefulness of the FEM–DEM formulation is verified in the analysis of the compressive failure of a prismatic concrete specimen. The problem is analyzed in 2D. Figure 19 depicts the geometry of the specimen, the material properties, and the two meshes of 3-noded triangles used for the analysis.

The material properties are $E_0 = 30$ GPa, $\nu = 0.2$, $\gamma = 7.8 \times 103$ N/m$^3$, $f_t = 2.0$ MPa, $G_t = 100$ J/m$^2$, and $f_c/f_t = 10$. This corresponds to a maximum uniaxial compression stress of 20.0 MPa.

Figure 20 shows the stress–strain curve up to failure. The failure compressive stress is around $f_c =18.8$ MPa which agrees well with the expected value, taking into account the difficulty in modeling the correct boundary conditions.

Figure 21 shows the final failure pattern, displacements, and damage for the structured mesh. The fracture on the sample coincides with the theoretical case (Fig. 21a) [2] due to the symmetry of the mesh.

Figure 22 shows the final failure pattern, displacements, and damage for the unstructured mesh applying symmetry conditions. The fractures on the sample have a good agreement with the theoretical case [2] showing the bands of vertical cracks at $45^{\circ }$.

7 Conclusions

We have presented a simple FEM–DEM methodology for predicting the onset and evolution of the crack path in materials and structures. Some advantages and differences with similar procedures such as the EET [12, 17, 30] can be highlighted:

• The failure criterion is considered at the midpoint of the element sides using a smooth stress field which does not need any additional considerations such as stabilization, or complex mixed finite element formulations.

• Damaging the element sides implies that the two elements sharing the side reduce its stiffness simultaneously.

• There is no mass loss by eliminating the associated finite elements. This ensures the conservation of the domain mass during the fracturing process.

• The implementation of the FEM–DEM technique presented is quite simple and has yielded promising results, both qualitatively and quantitatively, for predicting the onset and propagation of fracture in concrete samples under tension, compression and mixed failure modes.