Abstract
Maximal lottery (\( ML \)) schemes constitute an interesting class of randomized voting rules that were proposed by Peter Fishburn in 1984 and have been repeatedly recommended for practical use. However, the subtle differences between different \( ML \) schemes are often overlooked. Two canonical subsets of \( ML \) schemes are
 schemes (which only depend on unweighted majority comparisons) and
schemes (which only depend on unweighted majority comparisons) and
 schemes (which only depend on weighted majority comparisons). We prove that
schemes (which only depend on weighted majority comparisons). We prove that
 schemes are the only homogeneous \( ML \) schemes that satisfy \( SD \)-efficiency and \( SD \)-participation, but are also among the most manipulable \( ML \) schemes. While all \( ML \) schemes are manipulable and even violate monotonicity, they are never manipulable when a Condorcet winner exists and satisfy a relative notion of monotonicity. We also evaluate the frequency of manipulable preference profiles and the degree of randomization of \( ML \) schemes via extensive computer simulations. In summary, \( ML \) schemes are rarely manipulable and often do not randomize at all, especially for few alternatives. The average degree of randomization of
schemes are the only homogeneous \( ML \) schemes that satisfy \( SD \)-efficiency and \( SD \)-participation, but are also among the most manipulable \( ML \) schemes. While all \( ML \) schemes are manipulable and even violate monotonicity, they are never manipulable when a Condorcet winner exists and satisfy a relative notion of monotonicity. We also evaluate the frequency of manipulable preference profiles and the degree of randomization of \( ML \) schemes via extensive computer simulations. In summary, \( ML \) schemes are rarely manipulable and often do not randomize at all, especially for few alternatives. The average degree of randomization of
 schemes is consistently lower than that of
schemes is consistently lower than that of
 schemes.
schemes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
When aggregating the preferences of multiple agents into one collective choice, it is easily seen that completely symmetric situations call for randomization. Moreover, it has been shown that—apart from guaranteeing impartiality—randomization allows the circumvention of well-known impossibility results that have plagued social choice theory for long (see, e.g., Gibbard 1977; Brandl et al. 2016, 2019b; Hoang 2017; Brandl and Brandt 2020). Two types of randomized voting rules that have been shown to be attractive from an axiomatic point of view are random (serial) dictatorships and maximal lottery (\( ML \)) schemes. While random dictatorships are renowned for being immune to strategic manipulation, \( ML \) schemes satisfy desirable consistency conditions (such as Condorcet-consistency, population-consistency, and composition-consistency) as well as a very strong version of Pareto efficiency.
Maximal lotteries were first conceived by Kreweras (1965) and independently proposed and studied in more detail by Fishburn (1984a). The basic idea is to circumvent the Condorcet paradox—which lies at the heart of many impossibility theorems—by introducing the concept of a randomized Condorcet winner whose existence is guaranteed by the minimax theorem. Interestingly, maximal lotteries have been rediscovered several times by economists (Laffond et al. 1993), mathematicians (Fisher and Ryan 1995), political scientists (Felsenthal and Machover 1992), and computer scientists (Rivest and Shen 2010). In particular, Laffond et al. (1993, 1996), Dutta and Laslier (1999), Laslier (2000) and Brandt et al. (2018) have extensively studied the support of maximal lotteries, called the bipartisan set or the essential set.Footnote 1 Felsenthal and Machover (1992) and Rivest and Shen (2010) also discuss whether \( ML \) schemes are suitable for real-world political elections. Rivest and Shen conclude that
[the maximal lotteries system] is not only theoretically interesting and optimal, but simple to use in practice; it is probably easier to implement than, say, [instant-runoff voting]. We feel that it can be recommended for practical use.
(Rivest and Shen 2010, p. 1)
More recently, Peyre (2013) and Hoang (2017) have popularized maximal lotteries in France under the name scrutin de Condorcet randomisé (randomized Condorcet voting system).Footnote 2 An easy-to-use web interface for computing various \( ML \) schemes (including
 and
and
 schemes) is available on the website voting.ml. Other online voting services that use
schemes) is available on the website voting.ml. Other online voting services that use
 and
and
 can be accessed through votation.ovh (in French) and pnyx.dss.in.tum.de, respectively.
can be accessed through votation.ovh (in French) and pnyx.dss.in.tum.de, respectively.
The literature on maximal lotteries often ignores the fact that there are different variants of maximal lottery schemes, which under certain circumstances may lead to entirely different outcomes (e.g., two lotteries with disjoint support). All these (infinitely many) variants are captured by Fishburn’s original classification of maximal lotteries (Fishburn 1984a). The two main candidates are
 schemes (which only depend on unweighted majority comparisons) and
schemes (which only depend on unweighted majority comparisons) and
 schemes (which only depend on weighted majority comparisons).
schemes (which only depend on weighted majority comparisons).
 schemes have, for example, been considered by Kreweras (1965), Felsenthal and Machover (1992), Laffond et al. (1993), Fisher and Ryan (1995), Peyre (2013) and Hoang (2017) while
schemes have, for example, been considered by Kreweras (1965), Felsenthal and Machover (1992), Laffond et al. (1993), Fisher and Ryan (1995), Peyre (2013) and Hoang (2017) while
 schemes have been considered by Dutta and Laslier (1999), Laslier (2000), Rivest and Shen (2010), Aziz et al. (2018), Brandl et al. (2016) and Brandl and Brandt (2020).
schemes have been considered by Dutta and Laslier (1999), Laslier (2000), Rivest and Shen (2010), Aziz et al. (2018), Brandl et al. (2016) and Brandl and Brandt (2020).
In this paper, we provide a detailed analytical and experimental comparison of all \( ML \) schemes in terms of economic efficiency, strategic manipulability, and the degree of randomization. Apart from clarifying the differences between \( ML \) schemes, we also aim at improving our understanding of two potential drawbacks of maximal lotteries. First, as already observed by Fishburn (1984a), maximal lotteries may violate monotonicity in the sense that improving an alternative in an individual preference ranking may reduce the probability that this alternative will be chosen. For the special case of three alternatives, Fishburn formally explains this behavior and essentially attributes the paradox to our lack of intuition when arguing about cyclic pairwise majorities. In this paper, we prove that all \( ML \) schemes satisfy a relative version of monotonicity, which further illuminates and alleviates this phenomenon. Secondly, like with any randomized voting procedure, there are persistent reservations whether randomization would be acceptable to the general public. For example, Felsenthal and Machover write that
“an inherent special feature of [maximal lotteries] is its extensive and essential reliance on probability in selecting the winner [...] Without sufficient empirical evidence it is impossible to say whether this feature of [maximal lotteries] makes it socially less acceptable than other majoritarian procedures. It is not at all a question of fairness, for nothing could be fairer than the use of lottery as prescribed by [maximal lotteries]. The problem is whether society will accept such an extensive reliance on chance in public decision-making. Different societies may have differing views about this. For example, it is well known that the free men of ancient Athens regarded it as quite acceptable to select holders of public office by lot. Clearly, before [the maximal lotteries system] can be applied in practice, public opinion must first be consulted, and perhaps educated, on this issue.” (Felsenthal and Machover 1992, pp. 268–269)
While we cannot give a definitive answer to this question, we ran extensive computer simulations which show that the average degree of randomization of maximal lotteries is surprisingly low. Even under very conservative assumptions about the distribution of preferences and up to 21 alternatives, the average support size of maximal lotteries lies below 4. When there are only 5 alternatives, maximal lotteries do not randomize at all in more than 75% of all considered cases.
2 Preliminaries
Let A be a finite set of m alternatives and \(N=\{1,\dots ,n\}\) be a set of n voters. A (weak) preference relation on A is a complete and transitive binary relation on A. The preference relation reported by voter i is denoted by \(\succsim _i\), and the set of all preference relations on A is denoted by \({\mathcal {R}}\). We write \(\succ _i\) for the strict part of \(\succsim _i\), i.e., \(x \succ _i y\) if \(x \succsim _i y\) but not \(y \succsim _i x\), and \(\sim _i\) for the indifference part of \(\succsim _i\), i.e., \(x \sim _i y\) if \(x \succsim _i y\) and \(y \succsim _i x\). A preference relation \(\succsim _i\) is called strict if it is anti-symmetric, i.e., either \(x \succ _i y\) or \(y\succ _i x\) for all distinct alternatives \(x,y \in A\). We will compactly represent a preference relation as a comma-separated list with all alternatives among which a voter is indifferent placed in a set. For example, \(x \succ _i y \sim _i z\) is represented by \({\succsim _i} :x, \{y,z\}\). A preference profile \(R = ({\succsim _1},\dots ,{\succsim _n})\) is an n-tuple containing a preference relation for each voter. The set of all preference profiles is thus given by \({\mathcal {R}}^N\). For a preference profile \(R\in {\mathcal {R}}^N\), we denote by \(n_{xy} = |\{i\in N:x\succ _i y\}|\) the number of voters who strictly prefer x to y. The majority margin of x over y is given by \(m_{xy} = n_{xy} - n_{yx}\). The majority margins between all pairs of alternatives can be represented by a skew-symmetric matrix (i.e., a matrix that equals the negative of its transpose), whose rows and columns are indexed by alternatives; the majority margin of x over y is given in the cell indexed by (x, y). Alternatively, majority margins can be illustrated by a weighted digraph with an edge from x to y with weight \(m_{xy}\) if \(m_{xy} > 0\). The majority relation \(\succsim _R\) on alternatives for a given preference profile R can be derived from the majority margins: \(x\succsim _R y\) if and only if \(m_{xy} \ge 0\). An alternative \(x\in A\) is a Condorcet winner in R if \(x\succ _R y\) for all \(y\in A\setminus \{x\}\) and a weak Condorcet winner in R if \(x\succsim _R y\) for all \(y\in A\setminus \{x\}\). The preceding definitions are illustrated in Fig. 1.
Illustration of the definitions given in Sect. 2. The table on the left represents a preference profile R for three alternatives a, b, c and 100 voters. The number on top of each column denotes the number of voters with the corresponding preference relation, e.g., there are 49 voters with the preference relation \({\succsim _i}:c,a,b\). The corresponding matrix of majority margins and the weighted digraph are displayed on the right. The majority relation of R is cyclic, i.e., \(a\succ _R b\succ _R c\succ _R a\). Hence, R does not admit a (weak) Condorcet winner
For our proofs, we will need that every skew-symmetric matrix with integer entries is the matrix of majority margins of some preference profile. This fact was observed by Debord (1987). We state it here for later use.
Lemma 1
(Debord 1987) For every skew-symmetric matrix \(M\in {\mathbb {Z}}^{A\times A}\), there are \(N = \{1,\dots , n\}\) and \(R\in {\mathcal {R}}^N\) such that M is the matrix of majority margins for R.
We consider voting rules that randomize over alternatives. The set of all lotteries over A is denoted by \(\Delta (A)\), i.e., \(\Delta (A) = \{p\in {\mathbb {R}}_{\ge 0}^A:\sum _{x\in A} p(x) = 1\}\), where p(x) is the probability that p assigns to x. By \(\mathrm {supp}(p)\) we denote the support of a lottery \(p\in \Delta (A)\), i.e., the set of all alternatives to which p assigns positive probability. A lottery p is degenerate if \(|\mathrm {supp}(p)| = 1\). We write lotteries as convex combinations of alternatives, e.g., the uniform lottery on \(\{a,b\}\) is denoted by \(\nicefrac {1}{2}\,a + \nicefrac {1}{2}\,b\). By \(\mathrm {uni}(X)\) we denote the uniform lottery over a set \(X\subset A\), i.e., \(\mathrm {uni}(X) = \nicefrac {1}{|X|}\sum _{x\in X}x\).
A social decision scheme (SDS) takes as input a preference profile \(R\in {\mathcal {R}}^N\) and returns a lottery over A. Two common symmetry conditions for SDSs are anonymity, i.e., invariance under renaming voters, and neutrality, i.e., equivariance under renaming alternatives. Furthermore, an SDS is majoritarian if it only depends on the majority relation, i.e., \(f(R)=f({\hat{R}})\) whenever \({\succsim _R} = {\succsim _{{\hat{R}}}}\), and pairwise if it only depends on the majority margins, i.e., \(f(R) = f({\hat{R}})\) whenever \(m_{xy} = {\hat{m}}_{xy}\) for all \(x,y\in A\).
3 Maximal lottery schemes
In this paper, we focus on maximal lottery schemes, a class of SDSs introduced by Fishburn (1984a). Every maximal lottery scheme is based on an odd and monotone function \(\tau :{\mathbb {Z}}\rightarrow {\mathbb {R}}\) with \(\tau (1) = 1\) and returns an optimal mixed strategy of the symmetric zero-sum game induced by \((\tau (m_{xy}))_{x,y\in A}\).Footnote 3 For every such function \(\tau \), we define the maximal lottery correspondence with respect to \(\tau \), denoted by \( ML ^\tau \), such that, for every \(R\in {\mathcal {R}}^N\),
When \(\tau \) is the identity function, the set of maximal lotteries \( ML ^\tau (R)\) thus corresponds to randomized weak Condorcet winners in the following sense: for \(p\in ML ^\tau (R)\) and any lottery \(q\in \Delta (A)\), the expected number of voters who prefer the outcome of p to that of q is larger than the expected number of voters who prefer the outcome of q to that of p. Maximal lotteries can be computed via linear programming and thus in polynomial time. An SDS f is a maximal lottery scheme based on \(\tau \) if, for all \(R,{\hat{R}}\in {\mathcal {R}}^N\), \(f(R)\in ML ^\tau (R)\) and \(f(R) = f({\hat{R}})\) whenever \( ML ^\tau (R) = ML ^\tau ({\hat{R}})\). The second condition ensures that \( ML \) schemes only depend on the underlying \( ML \) correspondence. Since \( ML \) correspondences only depend on the majority margins, all \( ML \) schemes are pairwise.
The function \(\tau \) describes how different sizes of majorities are traded off against each other. Roughly speaking, the steeper the function \(\tau \), the more emphasize is given to larger majorities. Two notable classes of \( ML \) schemes are obtained for particularly natural choices of \(\tau \). In accordance with Fishburn’s classification of deterministic voting rules, we call \( ML \) schemes based on the sign function
 schemes and also use
schemes and also use  to refer to the corresponding \( ML \) correspondence.
to refer to the corresponding \( ML \) correspondence.
 schemes are in fact the only \( ML \) schemes that are C1 functions, i.e., that only depend on the majority relation and thus treat all sizes of majorities equally. The \( ML \) correspondence based on the identity function will be referred to as
schemes are in fact the only \( ML \) schemes that are C1 functions, i.e., that only depend on the majority relation and thus treat all sizes of majorities equally. The \( ML \) correspondence based on the identity function will be referred to as
 and the corresponding \( ML \) schemes are called
and the corresponding \( ML \) schemes are called
 schemes. For an odd number of voters with strict preferences, both
schemes. For an odd number of voters with strict preferences, both
 and
and
 return a unique lottery, which follows from the fact that optimal mixed strategies are unique in symmetric zero-sum games with odd off-diagonal payoffs; moreover, the support of either lottery contains an odd number of alternatives (Laffond et al. 1997, Thm. 1). In these cases, we will simply refer to
return a unique lottery, which follows from the fact that optimal mixed strategies are unique in symmetric zero-sum games with odd off-diagonal payoffs; moreover, the support of either lottery contains an odd number of alternatives (Laffond et al. 1997, Thm. 1). In these cases, we will simply refer to
 and
and
 as SDSs, respectively. For the preference profile R from Fig. 1, we have that \( ML ^\tau (R) = \{1/(\tau (2) + \tau (4) + \tau (94))(\tau (2)\,a + \tau (4)\,b + \tau (94)\,c)\}\). In particular,
as SDSs, respectively. For the preference profile R from Fig. 1, we have that \( ML ^\tau (R) = \{1/(\tau (2) + \tau (4) + \tau (94))(\tau (2)\,a + \tau (4)\,b + \tau (94)\,c)\}\). In particular,

It may be instructive to compare these probabilities with the outcomes of classic voting rules. In the example, Borda’s rule would select alternative a while most other rules (plurality, Kemeny’s rule, maximin, Schulze’s rule, ranked pairs, and all runoff rules) would select alternative c. Perhaps the best studied SDS (for strict preferences) is random dictatorship, where one of the voters is chosen uniformly at random and this voter’s top choice is selected. The lottery returned by random dictatorship is \(\nicefrac {48}{100}\,a + \nicefrac {3}{100}\,b + \nicefrac {49}{100}\,c\).Footnote 4
Dutta and Laslier (1999, Prop. 4.2) illustrated that, perhaps surprisingly, the unique lottery returned by
 can have disjoint support from the unique lottery returned by
can have disjoint support from the unique lottery returned by
 . We generalize this statement to any pair of \( ML \) schemes.
. We generalize this statement to any pair of \( ML \) schemes.
Theorem 1
For any pair of \( ML \) schemes \( ML ^\tau \) and \( ML ^\sigma \), there is a preference profile \(R\in {\mathcal {R}}^N\) such that \( ML ^\tau (R)=\{p\}\) and \( ML ^\tau (R)=\{q\}\) and \(\mathrm {supp}(p)\cap \mathrm {supp}(q)=\emptyset \).
Proof
Consider two different \( ML \) schemes, \( ML ^\tau \) and \( ML ^\sigma \), based on the odd and monotone functions \(\tau \) and \(\sigma \). Since \(\tau \) and \(\sigma \) are not equal, we can find some number k such that \(\tau (k)\ne \sigma (k)\). Assuming that \(\tau (k) < \sigma (k)\), choose \(l,m\in {\mathbb {N}}\) such that m is odd and \(\tau (k)< \frac{m-l}{l} < \sigma (k)\). We construct a weighted majority graph, depicted in Fig. 3, for which \( ML ^\tau \) and \( ML ^\sigma \) both return a unique lottery and the supports of these lotteries are disjoint.
Let \(A = \{a_1,\dots , a_m,b_1,\dots ,b_m\}\) consist of 2m alternatives. (Indices will be treated as elements of \({\mathbb {Z}}/m{\mathbb {Z}}\).) We add an edge with weight 1 from \(a_i\) to \(a_{i+1}\) and from \(b_i\) to \(b_{i+1}\) for every \(i\in \{1,\dots ,m\}\). Moreover, for every \(b_i\), add edges with weight k to \(a_i,\dots , a_{i+l-1}\), and edges with weight 1 from the remaining \(a_j\) to \(b_i\). It follows from Lemma 1 that we can find a preference profile R which induces these majority margins.
Then the unique lotteries chosen by \( ML ^\tau \) and \( ML ^\sigma \) for the profile R are \(p = \mathrm {uni}(\{a_1,\dots , a_m\})\) and \(q = \mathrm {uni}(\{b_1,\dots , b_m\})\). To see that \(p\in ML ^\tau (R)\), observe that
by the choice of l and m. To prove uniqueness, let \(r\in ML ^\tau (R)\) be any maximal lottery. By the definition of a maximal lottery and the two equations above, we have
If follows that \(\sum _{i = 1}^m r(b_i) = 0\), that is, \(\mathrm {supp}(r)\subseteq \{a_1,\dots ,a_m\}\). In particular, r is a maximal lottery on the set \(\{a_1,\dots ,a_m\}\). Since m is odd, the unique maximal lottery on this set is p, and so \(r = p\) follows.
A similar argument shows that \( ML ^\sigma (R) = \{q\}\). \(\square \)
A potential advantage of
 schemes is that they require less information than other \( ML \) schemes. It suffices to only elicit the majority relation in order to compute the election outcome.
schemes is that they require less information than other \( ML \) schemes. It suffices to only elicit the majority relation in order to compute the election outcome.
A basic desideratum for SDSs is homogeneity, which prescribes that replacing every voter with a fixed number of clones, i.e., voters with the same preferences, does not change the outcome. It can be shown that an \( ML \) scheme is homogeneous if and only if it is based on \(\tau \) with \(\tau (k) = k^t\) for some \(t\ge 0\).
Theorem 2
\( ML ^\tau \) is homogeneous if and only if there is \(t\ge 0\) such that \(\tau (k) = k^t\) for all \(k\in {\mathbb {N}}\).
Proof
First we observe that \(\tau = k^t\) gives rise to a homogeneous \( ML \) scheme. Indeed, replacing every voter by a fixed number of say l clones results in multiplication of the matrix of majority margins by l. Thus, since \(\tau \) is homogeneous of degree t, this results in multiplication of the transformed matrix \((\tau (m_{xy}))_{x,y\in A}\) by \(l^t\). From the definition of maximal lotteries it is clear that two matrices that are equal up to multiplication by a positive constant admit the same maximal lotteries.
Now we prove that all homogeneous \( ML \) schemes are induced by \(\tau (k) = k^t\) for some \(t\ge 0\). Let f be a homogeneous \( ML \)-scheme based on \(\tau \); let \(A = \{a,b,c\}\). For all \(k,l\in {\mathbb {N}}\), let \(R^{kl}\in {\mathcal {R}}^N\) be such that \(m^{kl}_{ab} = m^{kl}_{ca} = k\) and \(m^{kl}_{bc} = kl\). We have that \(f(R^{kl}) = (2\tau (k) + \tau (kl))^{-1}(\tau (kl)a + \tau (k)b + \tau (k) c)\) for all \(k,l\in {\mathbb {N}}\). Since f is homogeneous, \(f(R^{kl}) = f(R^{1l})\) for all \(k,l\in {\mathbb {N}}\). Hence, \(\tau (kl)\tau (1) = \tau (k)\tau (l)\) for all \(k,l\in {\mathbb {N}}\). Recall that \(\tau (1) = 1\) by definition. Thus, \(\tau (kl) = \tau (k)\tau (l)\) for all \(k,l\in {\mathbb {N}}\). In particular, \(\tau (2^l) = \tau (2)^l\) for all \(l\in {\mathbb {N}}\). Let \(t = \log _2\tau (2)\), i.e., \(\tau (2) = 2^t\).
Now assume for contradiction that there is \({\bar{k}}\in {\mathbb {N}}\) such that \(\tau ({\bar{k}})\ne {\bar{k}}^t\). We first consider the case that \(\tau ({\bar{k}}) > {\bar{k}}^t\). Then, there is \(l\in {\mathbb {N}}\) such that \((\nicefrac {\tau ({\bar{k}})}{{\bar{k}}^t})^l > 2^t\). Let \(o\in {\mathbb {N}}\) such that \(2^{o-1} < {\bar{k}}^l \le 2^o\). From before, we know that
which contradicts monotonicity of \(\tau \).
The case that \(\tau ({\bar{k}}) < {\bar{k}}^t\) is analogous to the first case. \(\square \)
Theorem 2 implies that homogeneous \( ML \) schemes are completely defined by the value of \(\tau (2)\). Moreover, homogeneous \( ML \) schemes have a well-defined extension to fractional preference profiles, which for every preference relation, specify the fraction of voters with these preferences. The set of fractional preference profiles admits a canonical embedding into the unit simplex in \({\mathbb {Q}}^d\), where d is the number of possible preference relations. This embedding prompts a notion of continuity for correspondences mapping fractional preference profiles to sets of lotteries which requires that small changes to the preference profile can only lead to small changes in the set of returned lotteries (see Brandl et al. 2016). As a function on rational numbers, \(\tau (k) = k^t\) is continuous unless \(t = 0\), i.e., unless \(\tau \) is the sign function. As a result, the correspondence \( ML ^\tau \) is continuous whenever \(t > 0\).  is not continuous since arbitrarily small deviations from majority ties can lead to large changes in the set of maximal lotteries.Footnote 5
is not continuous since arbitrarily small deviations from majority ties can lead to large changes in the set of maximal lotteries.Footnote 5
4 Analytical results
In this section, we collect various analytical results about Pareto efficiency, strategyproofness, participation, and monotonicity of \( ML \) schemes. Figure 4 provides an overview of these results and shows the relationships between the considered properties.
Logical relationships between varying degrees of efficiency, strategyproofness, participation, and monotonicity. Relative monotonicity together with IUA, for example, implies set-monotonicity. The green labels indicate which \( ML \) schemes satisfy the corresponding property. (Cond) refers to strategyproofness on the domain of profiles with a Condorcet winner. The red label represents Theorem 4, while the two red connections refer to the impossibility theorems by Brandl et al. (2018, Thm. 3.1) and Brandl et al. (2020, Thm. 2). IUA and IIV are defined in Sect. 4.4
4.1 Lottery extensions
Defining properties such as efficiency and strategyproofness for SDSs requires to make assumptions about the voters’ preferences over lotteries. To this end, we consider lottery extensions, which map a preference relation on the set of alternatives A to a preference relation on the set of lotteries \(\Delta (A)\). For all examples we assume that the underlying preference relation of voter i is \(a\succ _i b \succ _i c\).
A very simple and crude lottery extension called deterministic dominance prescribes that p is preferred to q iff every alternative in the support of p is strictly preferred to every alternative in the support of q. Formally,

A variant of this extension can be defined using the weak preference relation rather than the strict one.

Hence, \(p\succ _i^ DD q\) if and only if every alternative returned by p is at least as good as every alternative returned by q with at least one strict preference. A voter may thus strictly prefer one lottery to another even though he is eventually indifferent between particular instantiations of the lotteries. \( DD '\) only allows the comparison of lotteries with disjoint supports whereas the supports may overlap for \( DD \) as long as the voter is indifferent between all alternatives contained in the intersection of both supports. For example, \(\nicefrac {2}{3}\,a + \nicefrac {1}{3}\,b\mathrel {\succ ^{ DD '}} c\) and \(\nicefrac {2}{3}\,a + \nicefrac {1}{3}\,b\mathrel {\succ ^{ DD }} \nicefrac {1}{2}\,b + \nicefrac {1}{2}\,c\).
We slightly generalize the definition of \( DD ' \) to lotteries p and q that assign the same probability to all alternatives that are contained in both supports and \((\mathrm {supp}(p) \setminus \mathrm {supp}(q)) \succ _i (\mathrm {supp}(p)\cap \mathrm {supp}(q)) \succ _i (\mathrm {supp}(q) \setminus \mathrm {supp}(p))\). Following Savage’s sure-thing principle, the resulting lottery extension is referred to as the sure-thing (\( ST \)) extension. Formally,

For example, \(\nicefrac {1}{2}\,a + \nicefrac {1}{2}\,b\succ _i^ ST \nicefrac {1}{2}\,b + \nicefrac {1}{2}\, c\).
The third extension we consider, called bilinear dominance (\( BD \)), requires that for every pair of alternatives the probability that p yields the more preferred alternative and q the less preferred alternative is at least as large as the other way round. Formally,

Apart from its intuitive appeal, the main motivation for \( BD \) is that p bilinearly dominates q iff p is preferable to q for every skew-symmetric bilinear (SSB) utility function consistent with \(R_i\) (cf. Fishburn 1984c; Aziz et al. 2015). For example, \(\nicefrac {1}{2}\,a + \nicefrac {1}{2}\,b\succ _i^ BD \nicefrac {1}{3}\,a + \nicefrac {1}{3}\, b + \nicefrac {1}{3}\, c\).
The most common lottery extension is stochastic dominance (\( SD \)), according to which a lottery p is preferred to another lottery q if for every alternative \(x\in A\), p is at least as likely to return an alternative that is at least as good as x as q. Formally,

For example, \(\nicefrac {1}{2}\,a + \nicefrac {1}{2}\,c \succ ^{ SD } \nicefrac {1}{2}\,b + \nicefrac {1}{2}\, c\). It is a well-known fact that \(p\mathrel {\succsim _i^{ SD }} q\) if and only if the expected utility of p is at least as large as that of q for every von Neumann Morgenstern utility function consistent with \(\succsim _i\).
An interesting strengthening of stochastic dominance is based on the pairwise comparisons of alternatives (see, e.g., Aziz et al. 2015; Brandl and Brandt 2020). A lottery p is preferred to another lottery q according to pairwise comparisons (\( PC \)) if p is more likely to return a more preferred alternative than q. Formally,

For example, \(\nicefrac {2}{3}\,a + \nicefrac {1}{3}\,c \succ ^{ PC } b\). While the \( PC \) extension results in preferences over lotteries that cannot be represented by any von Neumann-Morgenstern utility function, it represents a refinement of the \( SD \) extension, i.e., \({\succsim _i^{ SD }}\subseteq {\succsim _i^{ PC }}\) (Fishburn 1984c, Thm. 8). In contrast to all previous extensions, the \( PC \) extension yields a complete preference relation over lotteries.
The inclusion relationships between these lottery extensions are as follows (cf. Aziz et al. 2018; Brandt 2017). For any preference relation \(\succsim \),
The examples mentioned also show that these inclusions are strict if \(m\ge 3\).
4.2 Efficiency
A fundamental economic property is Pareto efficiency, which prescribes that no voter can be made better off without making another voter worse off. A weak interpretation of this principle for SDSs, known as ex post efficiency, is that, whenever there are two alternatives \(x,y\in A\) such that \(x\succsim _i y\) for all \(i\in N\) and \(x\succ _i y\) for at least one \(i\in N\), then y should receive probability 0. Fishburn (1984a, Prop. 3) has shown that all \( ML \) schemes satisfy ex post efficiency.
A stronger notion of efficiency can be obtained by comparing lotteries via stochastic dominance. Formally, a lottery \(p\in \Delta (A)\) is \( SD \)-efficient for a preference profile \(R\in {\mathcal {R}}^N\) if there is no lottery \(q\in \Delta (A)\) such that \(q\succsim _i^{ SD } p\) for all \(i\in N\) and \(q\succ _j^{ SD } p\) for some \(j\in N\). An SDS f is \( SD \) -efficient if f(R) is \( SD \)-efficient for all \(R\in {\mathcal {R}}^N\). In a similar vein, one can define \( PC \) -efficiency, which results in an efficiency notion that is stronger than \( SD \)-efficiency. Aziz et al. (2018) have shown that every
 scheme is \( PC \)-efficient. Here, we prove that every other \( ML \) scheme violates even the weaker notion of \( SD \)-efficiency.
scheme is \( PC \)-efficient. Here, we prove that every other \( ML \) scheme violates even the weaker notion of \( SD \)-efficiency.
Theorem 3
Every
 scheme is \( PC \)-efficient. No other \( ML \) scheme is \( SD \)-efficient for all values of m and n.
scheme is \( PC \)-efficient. No other \( ML \) scheme is \( SD \)-efficient for all values of m and n.
Proof
The proof that every
 scheme is \( PC \)-efficient is due to Aziz et al. (2018, Thm. 3).
scheme is \( PC \)-efficient is due to Aziz et al. (2018, Thm. 3).
It is left to show that no other \( ML \) scheme is \( SD \)-efficient for all values of m and n. To this end, let f be an \( ML \) scheme based on \(\tau \) with \(\tau \ne id \). First consider the case that \(\tau (k^*) > k^*\) for some \(k^*\in {\mathbb {N}}\). Then, there are \(s,t\in {\mathbb {N}}\) such that \(k^*+ \frac{1}{t} < \tau (k^*)\), \(s = tk^*+ 1\), and \(s+t\) is odd. We now construct a preference profile R such that every lottery in \( ML ^\tau (R)\) is \( SD \)-inefficient, which implies that f is \( SD \)-inefficient. Let \(A = \{a_1,\dots a_{s+t},b_1,\dots ,b_{s+t}\}\) and \(|N| = 2(s+t)s\). In the following, all indices that are equal modulo \((s+t)\) are treated as equivalent. For \(k,k',l\in \{1,\dots ,s+t\}\), let \(R^{kk'l}\) be the following preference profile.

Observe that \(m^{kk'l}_{a_ka_{k'}} = m^{kk'l}_{a_kb_{l+1}} = m^{kk'l}_{b_la_{k'}} = m^{kk'l}_{b_lb_{l+1}} = 1\), \(m^{kk'l}_{a_kb_l} = m^{kk'l}_{a_{k'}b_{l+1}} = 0\), and \(m^{kk'l}_{xy} = 0\) for all \(\{x,y\}\not \subseteq \{a_k,a_{k'},b_l,b_{l+1}\}\). Now, for every \(l\in \{1,\dots ,s+t\}\), \(k'\in \{l+1,\dots ,l+t\}\), and \(k\in \{l-k^*(k'-l),\dots ,l-k^*(k'-l) + k^*- 1\}\), we add the preference profile \(R^{kk'l}\) to R. This requires \(2(s+t)(s-1)\) voters. Now for every \(l \in \{1,\dots ,s+t\}\), the following hold: first, we have added \(k^*\) profiles \(R^{kk'l}\), where \(k'\) is one of the t indices proceeding l; second, we have added one profile \(R^{kk'l}\), where k is one of the \(k^*t = s - 1\) indices preceding l. We have obtained the weighted majority graph in Fig. 5, except for the edges from \(a_l\) to \(b_l\) of weight 1. We get those by adding one additional preference profile for every l.
For \(l\in \{1,\dots ,s+t\}\), let \(R^l\) be the following preference profile.

Observe that \(m^l_{a_lb_l} = 1\) and \(m^l_{xy} = 0\) for all \(\{x,y\}\not \subseteq \{a_l,b_l\}\). For every \(l\in \{1,\dots ,s+t\}\), we add the preference profile \(R^l\) to R. This requires an additional \(2(s+t)\) voters and completes the construction of R. In total, there are \(2(s+t)(s-1) + 2(s+t) = 2(s+t)s\) voters in R. The corresponding weighted majority graph is displayed in Fig. 5.
Weighted majority graph of the preference profile R constructed in the proof of Theorem 3. The label of an edge gives the corresponding majority margin, e.g., \(m_{b_la_{l+1}} = k^*\). Unlabeled edges have weight 1
Then, we have that, for every \(l\in \{1,\dots ,s+t\}\), \(k\in \{l-s+1,\dots ,l\}\), and \(k'\in \{l+1,\dots ,l+t\}\), \(m_{b_lb_{l+1}} = k^*t = s-1\), \(m_{b_la_k} = -1\), and \(m_{b_la_{k'}} = k^*\).
Let \(p = \nicefrac {1}{(s+t)}\,(b_1 + \dots + b_{s+t})\). Since \(t\tau (k^*) > s\), we have that
for all \(y\in \{a_1,\dots ,a_{s+t}\}\). Moreover, since \(m_{b_{l-1}b_l} = -m_{b_{l+1}b_{l}} = k^*t\) for all \(l\in \{1,\dots ,s+t\}\), we have that
for all \(y\in \{b_1,\dots ,b_{s+t}\}\). Hence, \(p\in ML ^\tau (R)\). Now let \(p'\in ML ^\tau (R)\). Since \(\sum _{x\in A} p(x)\tau (m_{xy})>0\) for all \(y\in \{a_1,\dots ,a_{s+t}\}\), it follows that \(\mathrm {supp}(p')\subseteq \{b_1,\dots ,b_{s+t}\}\). Since \(m_{b_{l-1}b_l} = -m_{b_{l+1}b_{l}}\) for all \(l\in \{1,\dots ,s+t\}\), it follows that \(p'(b_{l-1}) = p'(b_{l+1})\) for all \(l\in \{1,\dots ,s+t\}\). Since \(s+t\) is odd by assumption, the previous conclusion implies that \(p'(b_{l-1}) = p'(b_{l})\) for all \(l\in \{1,\dots ,s+t\}\). Hence, \(p' = p\), which shows that \( ML ^\tau (R) = \{p\}\).
Finally, let \(q = \nicefrac {1}{(s+t)}\,(a_1 + \dots + a_{s+t})\) and observe that \(q\succsim _i^{ SD } p\) for all voters i in R and \(q\succ _j^{ SD } p\) for the voters j in R with a preference relation of the form \({\succsim _l}:a_l, b_l, A\setminus \{a_l,b_l\}\) for some \(l\in \{1,\dots ,s+t\}\). This shows that p is not \( SD \)-efficient and completes the proof for the case \(\tau (k^*) > k^*\).
The proof for the case that \(\tau (k^*) < k^*\) for some \(k^*\in {\mathbb {N}}\) is analogous to the proof for the first case. \(\square \)
Theorem 3 implies that no
 scheme is \( SD \)-efficient.Footnote 6 This raises the question whether there is any \( SD \)-efficient majoritarian SDS. In Theorem 4 we show that the answer to this question is negative when also assuming neutrality. The proof of this statement was found with the help of a computer.
scheme is \( SD \)-efficient.Footnote 6 This raises the question whether there is any \( SD \)-efficient majoritarian SDS. In Theorem 4 we show that the answer to this question is negative when also assuming neutrality. The proof of this statement was found with the help of a computer.
The preference profile R used in the proof of Theorem 4 is depicted on the left. The corresponding matrix of majority margins is illustrated on the right
Theorem 4
Every majoritarian and neutral SDS violates \( SD \)-efficiency for \(m\ge ~9\) (and \(n=5\), \(n=7\), or \(n\ge 9\)), even when preferences are strict.Footnote 7
Proof
We first prove the statement for \(m = 9\) and \(n = 5\). Let \(A = \{a,b,c,d,e,f,g,h,i\}\) and consider the preference profile \(R\in {\mathcal {R}}^N\) and the corresponding matrix of majority margins depicted in Fig. 6. Every majoritarian and neutral SDS f yields the uniform lottery  over all alternatives in A for R due to the symmetrical structure of the majority relation of R, i.e., for any pair of alternatives \(x,y\in A\), there is an automorphism of \(\succsim _R\) that maps x to y. However, shifting all the probabilities from the “red” alternatives g, h, and i to the “green” alternatives d, e, and f yields another lottery
over all alternatives in A for R due to the symmetrical structure of the majority relation of R, i.e., for any pair of alternatives \(x,y\in A\), there is an automorphism of \(\succsim _R\) that maps x to y. However, shifting all the probabilities from the “red” alternatives g, h, and i to the “green” alternatives d, e, and f yields another lottery  , which is \( SD \)-preferred to p by all voters, i.e., \(q\succ _i^{ SD }p\) for all \(i\in N\). This can be checked by looking at R, because there is always a “green” alternative directly above a “red” alternative for each voter. Additional alternatives can be added at the bottom of each preference relation. These alternatives will then be Pareto dominated and do not break the symmetry among the first 9 alternatives. If f assigns positive probability to a Pareto dominated alternative, it is \( SD \)-inefficient. Otherwise, f is \( SD \)-inefficient with the same argument as for the case \(m = 9\). For more than 5 voters, analogous proofs can be obtained by duplication and combination of profiles that induce the same majority graph as R. \(\square \)
, which is \( SD \)-preferred to p by all voters, i.e., \(q\succ _i^{ SD }p\) for all \(i\in N\). This can be checked by looking at R, because there is always a “green” alternative directly above a “red” alternative for each voter. Additional alternatives can be added at the bottom of each preference relation. These alternatives will then be Pareto dominated and do not break the symmetry among the first 9 alternatives. If f assigns positive probability to a Pareto dominated alternative, it is \( SD \)-inefficient. Otherwise, f is \( SD \)-inefficient with the same argument as for the case \(m = 9\). For more than 5 voters, analogous proofs can be obtained by duplication and combination of profiles that induce the same majority graph as R. \(\square \)
This impossibility is somewhat surprising since ex post efficient, majoritarian SDSs do exist. In fact, there is an elegant characterization of such SDSs in terms of the McKelvey uncovered set (see Brandt et al. 2016). This characterization can be used to show that neutrality is required for Theorem 4 since every SDS that puts probability 1 on an ex post efficient alternative satisfies \( SD \)-efficiency. Theorem 4 can be understood as an argument against neutral majoritarian SDSs in general as the majority relation does not contain enough information to guarantee \( SD \)-efficiency.
Theorem 4 implies Theorem 1 by Aziz et al. (2013) who showed that no neutral, majoritarian, \( SD \)-efficient, and \( SD \)-strategyproof SDS exists (although their result already holds when \(m=4\)).
4.3 Strategyproofness
In this section, we derive analytic results about the vulnerability of \( ML \) schemes to strategic manipulation. Just like in Sect. 4.2, we consider manipulability when preferences over lotteries are derived using a lottery extension. For example, an SDS f is \( SD \)-manipulable for a preference profile \(R\in {\mathcal {R}}^N\) if there is a preference profile \({\hat{R}}\in {\mathcal {R}}^N\) and \(j\in N\) such that \({\succsim }_i={{\hat{\succsim }}}_i\) for all \(i \ne j\) and \(f({\hat{R}}) \succ _j^{ SD } f(R)\). An SDS f is \( SD \)-strategyproof if it is not \( SD \)-manipulable for any preference profile \(R\in {\mathcal {R}}^N\). Our definition of \( SD \)-strategyproofness is often called weak \( SD \)-strategyproofness, because it is possible to definer a stronger version which requires that \(f(R) \succsim _j^{ SD } f({\hat{R}})\) for all \(R,{\hat{R}}\in {\mathcal {R}}^N\) and \(j\in N\) such that \({\succsim }_i={{\hat{\succsim }}}_i\) for all \(i \ne j\). This stronger notion is largely prohibitive in the context of voting and is, for example, leveraged in the random dictatorship theorem, which shows that only random dictatorships satisfy strong \( SD \)-strategyproofness and ex post efficiency (Gibbard 1977). The weaker notion employed here was introduced by Postlewaite and Schmeidler (1986) and popularized by Bogomolnaia and Moulin (2001).
In analogy to \( SD \)-strategyproofness, one can define manipulability and strategyproofness for all the other lottery extensions proposed in Sect. 4.1. The logical relationships between these varying notions of strategyproofness (and some monotonicity properties to be introduced in Sect. 4.4) are depicted in Fig. 4.
For any \(\tau \) and any lottery extension, an \( ML \) scheme may be manipulable simply because ties between maximal lotteries are broken in an unfavorable way (see Aziz et al. 2018, pp. 8–9). This problem can be avoided by restricting attention to the subclass of \( ML \) schemes that return maximal lotteries with maximal support, so-called strict maximal lotteries. Since \( ML ^\tau (R)\) is convex for any \(\tau \) and R, the relative interior of \( ML ^\tau (R)\) is non-empty and yields a well-defined correspondence \( SML ^\tau \) that refines \( ML ^\tau \). An SDS f is a strict maximal lottery scheme based on \(\tau \) if, for all \(R,{\hat{R}}\in {\mathcal {R}}^N\), \(f(R)\in SML ^\tau (R)\) and \(f(R) = f({\hat{R}})\) whenever \( SML ^\tau (R) = SML ^\tau ({\hat{R}})\).
Aziz et al. (2018) have shown that all strict
 schemes satisfy \( ST \)-strategyproofness. Their proof can be straightforwardly extended to all strict \( ML \) schemes by applying \(\tau \) to all majority margins. Aziz et al. also gave an example showing that all
schemes satisfy \( ST \)-strategyproofness. Their proof can be straightforwardly extended to all strict \( ML \) schemes by applying \(\tau \) to all majority margins. Aziz et al. also gave an example showing that all
 schemes violate \( BD \)-strategyproofness. Their example does not work for all \( ML \) schemes and we generalize their statement in the following theorem.
schemes violate \( BD \)-strategyproofness. Their example does not work for all \( ML \) schemes and we generalize their statement in the following theorem.
Theorem 5
All strict \( ML \) schemes are \( ST \)-strategyproof. All \( ML \) schemes violate \( DD \)-strategy proofness when \(m\ge 3\) and \(n\ge 3\). For strict preferences, all \( ML \) schemes violate \( BD \)-strategyproofness when \(m\ge 7\) and \(n\ge 5\) is odd.
Proof
The proof that all strict \( ML \) schemes are \( ST \)-strategyproof can be obtained by replacing every occurrence of \(m_{xy}\) (g(x, y) in their notation) with \(\tau (m_{xy})\) in the proof of Theorem 4 by Aziz et al. (2018).
The second statement, which relies on weak preferences, directly follows from Theorem 2 by Brandt et al. (2020) who have shown that no neutral and pairwise SDS can be ex post efficient and \( DD \)-strategyproof for \(m\ge 3\) and \(n\ge 3\). Nevertheless, we give a shorter and self-contained proof for an arbitrary \( ML \) scheme \( ML ^\tau \) for the case \(m = 3\) and \(n = 3\). Let \(A = \{a,b,c\}\) and consider the following preference profile \(R\in {\mathcal {R}}^N\), where voter i in the last column is indifferent between a and c, and the corresponding matrix of majority margins.

By the definition of \( ML \) schemes, we have that \(\tau (1) = 1\) independently of the choice of \(\tau \). Then, \( ML ^\tau (R) = \{\lambda \,a + (1-\lambda )\,c : \nicefrac {1}{2} \le \lambda \le 1\}\). Now assume that the voter i changes his preference relation to \({{\hat{\succsim _i}}}:b,c,a\), i.e., he breaks the tie between a and c. For the resulting preference profile \({\hat{R}}\) we have \( ML ^\tau ({\hat{R}}) = \{q\}\), where \(q = \nicefrac {1}{3}\,a + \nicefrac {1}{3}\,b + \nicefrac {1}{3}\,c\). Note that \(q\mathrel {\succ }_i^{ DD } p\) for all \(p \in ML ^\tau (R)\). Thus, voter i can manipulate \( ML ^\tau \) at R, which shows that no \( ML \) scheme based on \(\tau \) is \( DD \)-strategyproof.
The third statement, which even holds for strict preferences, already holds when there are only three alternatives for all \( ML \) schemes except those with \(\tau (3) = 1\) (which is the case for
 ). Thus, we first prove the case \(m = 3\) and \(n = 5\) and then show how to adapt the construction to prove the statement for the remaining \( ML \) schemes. Let \(A = \{d, e, f\}\) and \( ML ^\tau \) be an arbitrary \( ML \) scheme with \(\tau (3) > 1\). Consider the following preference profile \(R'\in {\mathcal {R}}^N\) and the corresponding matrix of majority margins.
). Thus, we first prove the case \(m = 3\) and \(n = 5\) and then show how to adapt the construction to prove the statement for the remaining \( ML \) schemes. Let \(A = \{d, e, f\}\) and \( ML ^\tau \) be an arbitrary \( ML \) scheme with \(\tau (3) > 1\). Consider the following preference profile \(R'\in {\mathcal {R}}^N\) and the corresponding matrix of majority margins.

By the definition of \( ML \) schemes, we have that \(\tau (1) = 1\) independently of the choice of \(\tau \). Then, \( ML ^\tau (R') = \{p\}\), where \(p = \nicefrac {1}{3}\,d + \nicefrac {1}{3}\,e + \nicefrac {1}{3}\,f\). Now assume that the voter i in the last column changes his preference relation to \({{\hat{\succsim _i}}}:d,e,f\), i.e., he strengthens the majority of e over f. For the resulting preference profile \({\hat{R}}'\) we have \( ML ^\tau ({\hat{R}}') = \{q\}\), where \(q = \nicefrac {\tau (3)}{s}\,d + \nicefrac {1}{s}\,e + \nicefrac {1}{s}\,f\) with \(s=\tau (3)+2\). Note that \(q\mathrel {\succ }_i^{ BD } p\) for all \( ML ^\tau \) with \(\tau (3) > 1\). Thus, voter i can manipulate \( ML ^\tau \) at \(R'\), which shows that no \( ML \) scheme based on \(\tau \) with \(\tau (3) > 1\) is \( BD \)-strategyproof.
Extending this result to \( ML \) schemes with \(\tau (3) = 1\) requires more alternatives, e.g., by replacing the alternatives e and f in \(R'\) with three new alternatives respectively which copy the majority margins of \(R'\) as their internal structure. Hence, we finally consider the case \(m = 7\) and \(n = 5\) with an arbitrary \( ML \) scheme \( ML ^\tau \). Let \(A = \{a,b,c,d,e,f,g\}\) and consider the following preference profile \(R''\in {\mathcal {R}}^N\), mimicking an extension of \(R'\), and the corresponding matrix of majority margins with the internal structure of the replaced alternatives marked in blue and red.

By the definition of \( ML \) schemes, we have that \(\tau (1) = 1\) independently of the choice of \(\tau \). Then, \( ML ^\tau (R'') = \{p\}\), where \(p = \nicefrac {1}{3}\,a + \nicefrac {1}{9}\,(b + c + d + e + f + g)\). Now assume that the voter i in the last column changes his preference relation to \({{\hat{\succsim _i}}}:e, b, f, c, g, d, a\), i.e., he swaps e and b, c and f, and d and g, respectively. For the resulting preference profile \({\hat{R}}''\) we have \( ML ^\tau ({\hat{R}}'') = \{q\}\), where \(q = \nicefrac {1}{7}\,(a+b+c+d+e+f+g)\). Note that \(q\mathrel {\succ }_i^{ BD } p\). Thus, voter i can manipulate \( ML ^\tau \) at \(R''\), which shows that no \( ML \) scheme based on any \(\tau \) is \( BD \)-strategyproof.Footnote 8
The proofs for the second and third statement can be generalized to larger profiles by adding completely indifferent voters and letting all additional alternatives be last-ranked by all voters. When preferences are assumed to be strict, pairs of voters with opposing preferences instead of completely indifferent voters can be used. \(\square \)
When there are only few alternatives,
 fares comparatively well in terms of strategyproofness because of the limited influence that voters have on the outcome. For example, when \(m=3\) and there no majority ties,
fares comparatively well in terms of strategyproofness because of the limited influence that voters have on the outcome. For example, when \(m=3\) and there no majority ties,
 randomizes uniformly whenever there is a majority cycle and returns a Condorcet winner otherwise. The strategyproofness of this simple three-alternative SDS was already observed by Potthoff (1970). However, once there are at least four alternatives,
randomizes uniformly whenever there is a majority cycle and returns a Condorcet winner otherwise. The strategyproofness of this simple three-alternative SDS was already observed by Potthoff (1970). However, once there are at least four alternatives,
 is \( SD \)-manipulable, even when preferences are strict.
is \( SD \)-manipulable, even when preferences are strict.
The proof of Theorem 5 crucially relies on the fact that Condorcet winners may fail to exist. Empirical studies have however observed that the vast majority of preferences profiles that appear in real-world elections admit a Condorcet winner (see Footnote 12), in which case every \( ML \) scheme chooses the Condorcet winner with probability 1. As it turns out, no \( ML \) scheme can be \( PC \)-manipulated whenever there is a Condorcet winner (not even to a profile without a Condorcet winner), which mitigates the seemingly severe implications of Theorem 5 for most real-world settings. Peyre (2013) and Hoang (2017) have shown this statement for
 schemes. In particular, it implies that choosing the Condorcet winner on the domain of preference profiles that admit a Condorcet winner is a strategyproof voting rule (see, e.g., Campbell and Kelly 2003; Moulin 1988, Lem. 10.3).
schemes. In particular, it implies that choosing the Condorcet winner on the domain of preference profiles that admit a Condorcet winner is a strategyproof voting rule (see, e.g., Campbell and Kelly 2003; Moulin 1988, Lem. 10.3).
Theorem 6
Let R be a preference profile that admits a Condorcet winner. Then, no \( ML \) scheme is \( PC \)-manipulable at R.
Proof
Let \(R\in {\mathcal {R}}^N\) be a preference profile with Condorcet winner \(c\in A\) and let f be some \( ML \) scheme based on \(\tau \), where \(\tau \) is arbitrary. Assume for contradiction that some voter \(j\in N\) can manipulate f at R. Then, there is \({\hat{R}}\in {\mathcal {R}}^N\) such that \({{\hat{\succsim }}}_i = {\succsim _i}\) for all \(i\ne j\), \(f(R) = p\), and \(f({\hat{R}}) = q\) with \(q\succ _j^{ PC } p\). Without loss of generality, \({\succsim _j}\) takes the following form for some \(B,C,D\subseteq A\setminus \{c\}\).
Observe that \({\hat{m}}_{xc} \le -1\) for all \(x\in B\), \({\hat{m}}_{xc} \le 0\) for all \(x\in C\cup \{c\}\), and \({\hat{m}}_{xc} \le 1\) for all \(x\in D\), since \(m_{xc} \le -1\) for all \(x\in A\setminus \{c\}\) by the assumption that c is a Condorcet winner in R. Let \(X = \{x\in A:{\hat{m}}_{xc} > 0\}\) be the set of alternatives that have a positive majority margin compared to c in \({\hat{R}}\). By the previous observation, we have \(X\subseteq D\). Since \(q\in ML ^\tau ({\hat{R}})\) by definition of f, we have that
where the inequalities follow from the fact that \(\tau (0) = 0\) (implied by the assumption that \(\tau \) is an odd function), \(\tau (1) = 1\), and \(\tau \) is odd and monotonic. Hence, the probability that \(q = f({\hat{R}})\) assigns to alternatives that \(\succsim _j\) prefers strictly more than c is at least as large as the probability that it assigns to alternatives that \(\succsim _j\) prefers strictly less than c. So we get \(p\succsim _j^{ PC } q\). This contradicts our assumption and shows that f is not \( PC \)-manipulable at R. \(\square \)
Theorem 6 shows that voters cannot manipulate from a Condorcet profile to another profile. Similarly, it can be shown that it is impossible to manipulate from an arbitrary profile to a Condorcet profile. Since for all \(\tau \), \( SML ^\tau (R)\) only contains degenerate lotteries if R admits a Condorcet winner, all \( SML \) schemes are strategyproof for an artificial weakening of the \( PC \) extension in which one of the two lotteries to be compared has to be degenerate.
Note that Theorem 6 does not contradict Theorem 3 by Hoang (2017), who showed that every pairwise SDS that satisfies their Condorcet proofness condition agrees with some
 scheme on all preference profiles that are close to a profile with a Condorcet winner. Condorcet proofness prescribes that, for all profiles that admit a Condorcet winner, no group of voters with identical preferences can \( PC \)-manipulate. Condorcet proofness is thus stronger than the strategyproofness requirement of Theorem 6 and, among \( ML \) schemes, is only satisfied by
scheme on all preference profiles that are close to a profile with a Condorcet winner. Condorcet proofness prescribes that, for all profiles that admit a Condorcet winner, no group of voters with identical preferences can \( PC \)-manipulate. Condorcet proofness is thus stronger than the strategyproofness requirement of Theorem 6 and, among \( ML \) schemes, is only satisfied by
 . When not insisting that manipulating voters have to have the same preferences, all \( ML \) schemes can be \( BD \)-manipulated by groups of voters. Formally, an SDS f is \( BD \)-group-manipulable for a preference profile \(R\in {\mathcal {R}}^N\) if there is a preference profile \({\hat{R}}\in {\mathcal {R}}^N\) and \(S\subseteq N\) such that \({\succsim }_i={{\hat{\succsim }}}_i\) for all \(i\in N\setminus S\) and \(f({\hat{R}}) \succ _j^{ SD } f(R)\) for all \(j\in S\).
. When not insisting that manipulating voters have to have the same preferences, all \( ML \) schemes can be \( BD \)-manipulated by groups of voters. Formally, an SDS f is \( BD \)-group-manipulable for a preference profile \(R\in {\mathcal {R}}^N\) if there is a preference profile \({\hat{R}}\in {\mathcal {R}}^N\) and \(S\subseteq N\) such that \({\succsim }_i={{\hat{\succsim }}}_i\) for all \(i\in N\setminus S\) and \(f({\hat{R}}) \succ _j^{ SD } f(R)\) for all \(j\in S\).
Theorem 7
All \( ML \) schemes are \( BD \)-group-manipulable even on a profile with a Condorcet winner when \(m\ge 4\) and \(n\ge 5\).
Proof
Let \(A = \{a,b,c,d\}\) and f be an arbitrary \( ML \) scheme. Consider the following preference profile R and the corresponding matrix of majority margins.

Since d is a Condorcet winner in R, we have that \(f(R) = d\). Now consider the preference profile \(R'\), that result from R if the first three voters change their preferences.

We have that \(f(R') = p\), where \(p = \nicefrac 13\,a + \nicefrac 13\,b + \nicefrac 13\,c\). Since \(p\succ _i^ BD d\) for \(i\in \{1,2,3\}\), f is \( BD \)-group-manipulable at R. \(\square \)
We have seen that all \( ML \) schemes are strategyproof for single voters in profiles that admit a Condorcet winner. For the remaining profiles, the situation is almost the exact opposite: whenever a diverse profile, i.e., a profile in which every preference relation is represented by at least one voter, does not admit a weak Condorcet winner, every \( ML \) scheme based on a strictly monotonic function can be manipulated by some voter. Theorems 6 and 8 leave open the cases of profiles with a weak rather than a strict Condorcet winner and \( ML \) schemes based on non-strictly increasing functions \(\tau \). A closer look reveals that some \( ML \) schemes are manipulable for some profiles with a weak Condorcet winner but others are not. Similarly, \( ML \) schemes based on non-strictly increasing functions \(\tau \) are manipulable in some but not all diverse profiles without a weak Condorcet winner. But neither case seems amenable to a unified treatment of all combinations of profiles and \( ML \) schemes.
Theorem 8
Let R be a preference profile that does not admit a weak Condorcet winner and in which every preference relation appears at least once. Then every \( ML \) scheme based on a strictly monotone function \(\tau \) can be \( SD \)-manipulated at R.
Proof
Let \(R\in {\mathcal {R}}^N\) be a preference profile that does not admit a weak Condorcet winner and in which every preference relation appears at least once. Let f be an \( ML \) scheme based on a strictly monotonic function \(\tau \) and let \(p = f(R)\). Since R does not admit a weak Condorcet winner, for every \(x\in A\), there is \(y\in A\) such that \(m_{yx} > 0\). We distinguish two cases: either all majority margins between alternatives in the support of p are 0 or one of them is non-zero.
First consider the former case, i.e., \(m_{xy} = 0\) for all \(x,y\in \mathrm {supp}(p)\). Let \(j\in N\) be a voter who prefers all alternatives outside the support of p to all alternatives in the support, i.e.,
Let \(a\in \mathrm {supp}(p)\) and \({\hat{R}}\) be a preference profile such that \({\succsim _i} = {{\hat{\succsim _i}}}\) for all \(i\ne j\) and
so voter j breaks the tie between alternatives in the support of p in favor of a. (The set \(\mathrm {supp}(p)\setminus \{a\}\) may be empty if \(p = a\).) Let \(q = f({\hat{R}})\). If \(q = a\), then, since a is not a weak Condorcet winner, there is \(b\in A\setminus \mathrm {supp}(p)\) such that \({\hat{m}}_{ba} > 0\), which contradicts \(q = f({\hat{R}})\in ML ^\tau ({\hat{R}})\). If \(q\ne a\) and \(\mathrm {supp}(q)\subseteq \mathrm {supp}(p)\), then
which again contradicts \(q = f({\hat{R}})\in ML ^\tau ({\hat{R}})\). Thus, \(\mathrm {supp}(q)\not \subseteq \mathrm {supp}(p)\), which implies that \(q\mathrel {\succsim _j^{ SD }}p\), i.e., voter j can successfully manipulate f at R by reporting \({\hat{\succsim _j}}\).
Secondly, consider the complementary case that there are \(a,b\in \mathrm {supp}(p)\) such that \(m_{ab} > 0\). We show that increasing the weight of the edge between a and b while not changing any of the other weights must change the probability of at least one other alternative. Knowing the lottery q resulting from this change allows us to construct a preference relation for which q is \( SD \)-preferred to p along with a manipulation of this relation which increases the weight of the edge between a and b. From the diversity assumption about R we know that there is some voter with these preferences and thus f is manipulable at R.
Let \({\bar{R}}\in {\mathcal {R}}^N\) be a preference profile such that \({\bar{m}}_{ab} = m_{ab} + 1\) and \({\bar{m}}_{xy} = m_{xy}\) for all \(\{x,y\}\ne \{a,b\}\) and \(q = f({\bar{R}})\). We show that \(q(x)\ne p(x)\) for some \(x\in A\setminus \{a,b\}\).
Assume for contradiction that \(q(x) = p(x)\) for all \(x \in A\setminus \{a,b\}\). If \(q(b) > p(b)\), we have
where the first inequality uses that \(q = f({\bar{R}})\in ML ({\bar{R}})\), the first equality uses \({\bar{m}}_{aa} = 0\), and the final inequality uses \(a \in \mathrm {supp}(p)\) and \(p = f(R)\in ML (R)\). Since this gives a contradiction, we conclude that \(q(b) \le p(b)\) and \(q(a) \ge p(a) > 0\).
We distinguish two cases. If \(q(b) = 0\), then
The equality uses \({\bar{m}}_{aa} = m_{aa} = 0\) and the inequality under the first brace follows from \(b \in \mathrm {supp}(p)\). This contradicts \(a\in \mathrm {supp}(q)\).
If \(q(b) > 0\), i.e., \(b\in \mathrm {supp}(q)\), then
where the first and second (in)equality use \({\bar{m}}_{bb} = m_{bb} = 0\). This contradicts \(b\in \mathrm {supp}(q)\).
Since both cases yield a contradiction, we conclude that there is \(x\in A\setminus \{a,b\}\) such that \(q(x)\ne p(x)\).
Let \(A^> = \{x\in A\setminus \{a,b\}:q(x) > p(x)\}\), \(A^= = \{x\in A\setminus \{a,b\}:q(x) = p(x)\}\), and \(A^< = \{x\in A\setminus \{a,b\}:q(x) < p(x)\}\). By the previous argument, either \(A^>\ne \emptyset \) or \(A^<\ne \emptyset \). We use the sets \(A^>\) and \(A^<\) to construct a preference relation for which q is \( SD \)-preferred to p and which is manipulable so that the majority margin between a and b increases by 1. Consider a voter \(j\in N\) who has the following preference relation in R.
Such a voter exists, since every preference relation appears at least once in R by assumption. Let \({\hat{R}}\in {\mathcal {R}}^N\) be the preference profile that is identical to R except that voter j breaks the tie between a and b in favor of a, i.,e.,
Observe that \({\hat{m}}_{xy} = {\bar{m}}_{xy}\) for all \(x,y\in A\). Hence, since \( ML ^\tau ({\hat{R}}) = ML ^\tau ({\bar{R}})\), it follows that \(f({\hat{R}}) = f({\bar{R}}) = q\). However, we have that \(q\succ _j^{ SD } p\), i.e., voter j can manipulate f at R by reporting \({\hat{\succsim _j}}\). \(\square \)
A particularly simple variant of strategic manipulation occurs when a voter obtains a more preferred outcome by abstaining from the election. In analogy to strategyproofness, an SDS is said to satisfy participation if no voter is better off by abstaining from an election. Each of the lottery extensions proposed in Sect. 4.1 yields a corresponding notion of participation. Brandl et al. (2019b, Cor. 1) have shown that
 satisfies \( PC \)-participation, the strongest notion of participation considered in this paper.
satisfies \( PC \)-participation, the strongest notion of participation considered in this paper.
Theorem 9
Every
 -scheme satisfies \( PC \)-participation. No other homogeneous \( ML \) scheme satisfies \( SD \)-participation when \(m\ge 4\) and n is sufficiently large.
-scheme satisfies \( PC \)-participation. No other homogeneous \( ML \) scheme satisfies \( SD \)-participation when \(m\ge 4\) and n is sufficiently large.
Proof
See Brandl et al. (2019b, Cor. 1) for the proof that
 satisfies \( PC \)-participation.
satisfies \( PC \)-participation.
Any other homogeneous \( ML \) scheme is based on a function \(\tau (k) = k^t\) which is not the identity function on \({\mathbb {N}}\), hence \(t \ne 1\). We split the proof into three cases.
Case
(\(t > 1\)) For the following preference profile R, we get \( ML ^{\tau }(R) = \{p\}\) with \(p(c) = 1/(3^t + 2)\).

If a voter i with preference relation \(\succsim _i: \{a,b\},c\) joins, the new preference profile \(R'\) yields \( ML ^{\tau }(R') = \{p'\}\) with \(p'(c) = 1/(2\cdot 2^t+1) > p(c)\) due to \(t > 1\).

Thus, this new voter prefers to abstain because \(p \succ ^{ SD }_i p'\).
Case
(\(0< t < 1\)) Again, for the preference profile \(R'\), we get \( ML ^{\tau }(R') = \{p'\}\) with \(p'(c) = 1/(2\cdot 2^t + 1)\). If another voter j with preference relation \(\succsim _j: \{a,b\},c\) joins, the new preference profile \({\tilde{R}}\) yields \( ML ^{\tau }({\tilde{R}}) = \{{\tilde{p}}\}\) with \({\tilde{p}}(c) = 1/(3^t + 2) > p'(c)\) due to \(0< t < 1\).

Thus, this new voter prefers to abstain because \(p' \succ ^{ SD }_j p''\).
Case
(\(t=0\)) For \(t=0\) we have that every homogeneous \( ML \) scheme is a  scheme. Hence, for the following preference profile \({\hat{R}}\), we get
scheme. Hence, for the following preference profile \({\hat{R}}\), we get  .
.

If the first voter \({{\hat{\imath }}}\) with preference relation \(\succsim _{{\hat{\imath }}}: a,b,c,d\) abstains, the new preference profile \({\hat{R}}'\) yields  .
.

Thus, this new voter prefers to abstain because \({\hat{p}}' \succ ^{ SD }_{{\hat{\imath }}} {\hat{p}}\) and \({\hat{p}}' \succ ^{ SD }_{{\hat{\imath }}} {\hat{q}}\) and thus \({\hat{p}}' \succ ^{ SD }_{{\hat{\imath }}} \lambda \,{\hat{p}} + (1-\lambda )\,{\hat{q}}\) for every \(0 \le \lambda \le 1\).
\(\square \)
4.4 Monotonicity
Monotonicity describes the idea that an alternative should not be worse off if it rises in the voters’ preferences. On the surface, monotonicity-type conditions seem to be related to strategyproofness. While there is a connection between these two concepts (which we make precise below), it is only a loose one. In order for strategyproofness to imply any kind of monotonicity, one either has to assume a very strong notion of strategyproofness or to restrict the class of SDSs. Contrary to strategyproofness, the normative appeal of monotonicity is not clear from the voters’ point of view. If however, the alternatives are viewed as candidates that seek to be represented in the outcome, it is natural to demand that a rise of a candidate in the voters’ preferences should be rewarded in the outcome. When the outcome is a single alternative (or a set of alternatives), it is fairly unambiguous what it means to not be “worse off”: if an alternative is chosen, it should still be chosen when it rises in the voters preferences (see, e.g., Sen 1970; Fishburn 1973). But with lotteries as outcomes, there are various reasonable ways to define monotonicity; we will consider four different notions here.
Perhaps the most straightforward definition for social decision schemes is that the probability assigned to an alternative should not decrease if it rises in some voter’s preferences. To make this formal, we say that for two profiles \(R,{\hat{R}}\) and two alternatives \(x,y\in A\), \({\hat{R}}\) is an (x, y)-improvement over R if there is a voter i such that \(y\succsim _i x\), \(x\mathrel {{\hat{\succsim _i}}} y\), and for all \(v,w\in A\) with \(\{v,w\}\ne \{x,y\}\), \(v\succsim _i w\) if and only if \(v\mathrel {{\hat{\succsim _i}}} w\), and for all \(j\ne i\), \({\succsim _j} = {{\hat{\succsim _j}}}\). Hence, \({\hat{R}}\) is an (x, y)-improvement over R if voter i weakly prefers y to x in the profile R, weakly prefers x to y in the profile \({\hat{R}}\), and his preferences over the remaining pairs of alternatives as well as the preferences of the remaining voters are unchanged. We say that \({\hat{R}}\) is an x-improvement over R if \({\hat{R}}\) is an (x, y)-improvement over R for some \(y\in A\). Then, an SDS f satisfies absolute monotonicity if for \(p = f(R)\) and \(q = f({\hat{R}})\), we have \(q(x) \ge p(x)\) whenever \({\hat{R}}\) is an x-improvement over R. The specification “absolute” refers to the fact that the absolute probability of x should not decrease.Footnote 9
Our second notion of monotonicity, which we call relative monotonicity, prescribes that the probability of x relative to that of y does not decrease when x is improved over y. Formally, f satisfies relative monotonicity if for \(p = f(R)\) and \(q = f({\hat{R}})\), \(q(x) p(y)\ge p(x)q(y)\) whenever \({\hat{R}}\) is an (x, y)-improvement over R. The rationale underlying relative monotonicity is that a rise of x in some voter’s preferences compared to y only allows us to draw conclusions about the probability of x relative to the probability of y; while the probability of x might decrease, this can only be if the probability of y decreases by at least the same fraction. Observe that absolute monotonicity implies relative monotonicity, since when x is improved over y and absolute monotonicity holds, the probability of x can only increase and the probability of y can only decrease, where the latter follows from an application of absolute monotonicity to the same pair of profiles but in reverse order.
Third, we consider set-monotonicity, which was introduced by Brandt (2015) for set-valued social choice functions and in that context prescribes that the set of chosen alternatives should not change when an unchosen alternative is weakened. We adapt set-monotonicity to SDSs by requiring that the support of the chosen lottery should not change in such a situation. Formally, f satisfies set-monotonicity if \(\mathrm {supp}(f(R)) =\mathrm {supp}(f({\hat{R}}))\) whenever \({\hat{R}}\) is an (x, y)-improvement over R and \(y\not \in \mathrm {supp}(f(R))\). Set-monotonicity is not implied by absolute monotonicity (and thus relative monotonicity), since absolute monotonicity has no relevant implications for the probability of \(z\not \in \{x,y\}\) when improving x over \(y\not \in \mathrm {supp}(f(R))\). However, relative monotonicity implies set-monotonicity when assuming independence of unchosen alternatives (Brandt 2015, Def. 2). An SDS f satisfies independence of unchosen alternatives (IUA) if for all \(R,{\hat{R}}\in {\mathcal {R}}^N\) such that \(R_i|_{\{x,y\}}={\hat{R}}_i|_{\{x,y\}}\) for all \(x\in \mathrm {supp}(f(R))\), \(y\in A\), and \(i\in N\), it holds that \(f(R)=f(R')\). IUA is implied by set-monotonicity and all strict \( ML \) schemes satisfy set-monotonicity and thereby IUA. Set-monotonicity has some interesting connections to strategyproofness and participation. Every set-monotonic SDS is \( DD '\)-strategyproof (Brandt 2015, Rem. 6). Moreover, every set-monotonic SDS that satisfies independence of indifferent voters also satisfies \( DD \)-participation (Brandl et al. 2019a, Thm. 3). Independence of indifferent voters (IIV) is weaker than pairwiseness and merely requires that the outcome of the SDS is unaffected by voters who are completely indifferent between all alternatives.
Finally, the weakest monotonicity property we consider requires that an alternative should stay in the support if it rises in some voter’s preferences. We say that f satisfies support-monotonicity if \(x\in \mathrm {supp}(f({\hat{R}}))\) whenever \(x\in \mathrm {supp}(f(R))\) and \({\hat{R}}\) is an x-improvement over R. Support-monotonicity is weaker than set-monotonicity, which we can see by considering an instance where a set-monotonic SDS violates support-monotonicity, e.g., \(x\in \mathrm {supp}(f(R))\) and \({\hat{R}}\) is an (x, y)-improvement over R but \(x\not \in \mathrm {supp}(f({\hat{R}}))\). Since R is an (y, x)-improvement over \({\hat{R}}\) and \(x\not \in \mathrm {supp}(f({\hat{R}}))\), set-monotonicity yields \(\mathrm {supp}(f({\hat{R}})) = \mathrm {supp}(f(R))\), which contradicts \(x\in \mathrm {supp}(f(R))\). It is easy to see that absolute monotonicity implies support monotonicity. To the contrary, relative monotonicity does not: improving \(x\in \mathrm {supp}(f(R))\) over y may lead to probability 0 for both x and y, which is in accordance with relative monotonicity. The logical relationships between the monotonicity properties are depicted in Fig. 4.
For pairwise SDSs, absolute monotonicity is weaker than \( SD \)-strategyproofness.
Theorem 10
Every \( SD \)-strategyproof pairwise SDS satisfies absolute monotonicity.
Proof
We show the contrapositive. Let f be a pairwise SDS and \(x,y\in A\). Assume there are profiles \(R,R'\) so that \(R'\) is an (x, y)-improvement over R, \(p = f(R)\), and \(q = f(R')\) and \(q(x) < p(x)\). So we can find a voter \(i\in N\) as in the definition of an (x, y)-improvement with \(y\succsim _i x\) and \(x\succsim _i' y\) where at least one of these two comparisons is strict. There are three cases: either the first comparison is strict, or the second, or both. We consider the case \(y\sim _i x\) and \(x\succ _i' y\); the other cases are similar.
We split up the set of alternatives other than x and y depending on whether their probability increases or decreases from p to q. Let
We construct a new profile \({\bar{R}}\) which consists of R and two additional voters \(i_1,i_2\) with the preferences
Notice that the preferences of \(i_1\) and \(i_2\) are completely opposed so that the majority margins in R and \({\bar{R}}\) are the same. Since f is pairwise, it follows that \(f({\bar{R}}) = f(R) = p\). Moreover, if \(i_1\) changes his preferences to \({{\bar{\succsim }}'}_{i_1}:A^+, \{x,y\}, A^-\), then the resulting profile \({\bar{R}}'\) has the same majority margins as \(R'\) and so \(f({\bar{R}}') = f(R') = q\). From the definition of \(A^+\) and \(A^-\) and the assumption that \(q(x) < p(x)\), it follows that \(q\mathrel {{\bar{\succ }}_{i_1}^ SD } p\). So we have shown that f is not \( SD \)-strategyproof, which concludes the proof. \(\square \)
Laffond et al. (1993, Prop. 5) and Dutta and Laslier (1999, Thm. 4.3) have shown that every
 scheme satisfies support-monotonicity. Laslier (2000, Prop. 4) has shown the same statement for
scheme satisfies support-monotonicity. Laslier (2000, Prop. 4) has shown the same statement for
 schemes.
schemes.
Perhaps the least intuitive phenomenon of \( ML \) schemes is their failure of absolute monotonicity. It was already observed by Fishburn (1984a) that
 violates absolute monotonicity. It is easily seen that Fishburn’s example extends to all \( ML \) schemes except
violates absolute monotonicity. It is easily seen that Fishburn’s example extends to all \( ML \) schemes except
 . An example for
. An example for
 and \(m=7\) was later given by Laslier (1997, Ex. 6.2.9).Footnote 10 For
and \(m=7\) was later given by Laslier (1997, Ex. 6.2.9).Footnote 10 For
 schemes, the conflict goes even deeper: we are not aware of a diverse preference profile without a weak Condorcet at which some
schemes, the conflict goes even deeper: we are not aware of a diverse preference profile without a weak Condorcet at which some
 scheme satisfies absolute monotonicity. If this turns out to be a general fact, it would generalize Theorem 8, since every violation of absolute monotonicity allows us to construct a successful manipulation (possibly by a different voter). Clearly, all \( ML \) schemes satisfy absolute monotonicity in profiles that admit a Condorcet winner.
scheme satisfies absolute monotonicity. If this turns out to be a general fact, it would generalize Theorem 8, since every violation of absolute monotonicity allows us to construct a successful manipulation (possibly by a different voter). Clearly, all \( ML \) schemes satisfy absolute monotonicity in profiles that admit a Condorcet winner.
While absolute monotonicity is irreconcilable with \( ML \) schemes, all of them satisfy relative monotonicity as we show in Theorem 11.
 schemes meet an even stronger form of relative monotonicity, which requires that the probability of a set of alternatives X relative to that of alternatives in Y does not decrease when improving all alternatives in X over all alternatives in Y (without changing the order within X or Y).
schemes meet an even stronger form of relative monotonicity, which requires that the probability of a set of alternatives X relative to that of alternatives in Y does not decrease when improving all alternatives in X over all alternatives in Y (without changing the order within X or Y).
Theorem 11
Every \( ML \) scheme satisfies relative monotonicity.
Proof
For two profiles \(R,{\hat{R}}\) and two alternatives \(x^*,y^*\), assume that \({\hat{R}}\) is an \((x^*,y^*)\) improvement over R. Let \(M,{\hat{M}}\in {\mathbb {R}}^{A\times A}\) be the matrices holding the majority margins of R and \({\hat{R}}\). Let f be some \( ML \) scheme based on \(\tau \), where \(\tau \) is arbitrary, and \(f(R) = p\) and \(f({\hat{R}}) = q\). Then, we have that for all alternatives x, y with \(\{x,y\}\ne \{x^*,y^*\}\), \(\tau (M_{xy}) = \tau ({\hat{M}}_{xy})\) and, \(\tau ({\hat{M}}_{x^*y^*}) - \tau (M_{x^*y^*}) = \epsilon \ge 0\), since \(\tau \) is monotonic. We have that
where the first equality follows from the fact that \(q = f({\hat{R}})\in ML ^\tau ({\hat{R}})\) and the second inequality follows from \(p = f(R)\in ML ^\tau (R)\) and \(q^t \tau (M) p = - p^t \tau (M) q\). If \(\epsilon = 0\), then \({\hat{M}} = M\), which implies that \( ML ^\tau ({\hat{R}}) = ML ^\tau (R)\) and thus, \(q = f({\hat{R}}) = f(R) = p\). In this case, relative monotonicity trivially holds. If \(\epsilon > 0\), (1) implies that \(q(x^*) p(y^*) - q(y^*) p(x^*)\ge 0\), and relative monotonicity also holds. \(\square \)
Theorem 11 also follows from Theorem 1 of Brandl et al. (2019b), which shows that welfare-maximizing mechanisms on so-called skew-symmetric bilinear (SSB) utility functions (see, e.g., Fishburn 1984b) entice voters to participate, i.e., voters weakly prefer participating to abstaining. SSB utility functions allow a voter to express certain intransitive preferences, such as being indifferent between all alternatives except for preferring x to y. If such a voter joins the electorate, it leads to the same change of the majority margins as if a voter improves x over y. Moreover, enticing this voter to participate is equivalent to the inequality that defines relative monotonicity. Since we can view \( ML \) schemes as welfare maximizing mechanisms, relative monotonicity follows.
Our study of maximal lottery schemes can be viewed more generally in the context of zero-sum games. Consider a zero-sum game given by a matrix M with matrix entries representing monetary payoffs. Say we have a monotone function \(\tau \) which expresses how much utility the players derive from a given monetary payoff. Then the strategy that maximizes the minimal expected utility of a player is his maximin strategy in the game \(\tau (M)\), where \(\tau \) is applied to each matrix entry. One can then ask how the maximin strategy changes for different functions \(\tau \).
For example, Theorem 1 shows that different choices of \(\tau \) can result in maximin strategies with disjoint supports, even if M is skew-symmetric. Theorem 11 has a similarly natural interpretation for zero-sum games. Consider two zero-sum games M and \({\hat{M}}\) which only differ in that the row player’s payoff is higher in \({\hat{M}}\) than in M when the players choose the actions x and y, respectively. If (p, q) and \(({\hat{p}},{\hat{q}})\) are pairs of maximin strategies for M and \({\hat{M}}\), then relative monotonicity requires that \({\hat{p}}(x) q(y) \ge p(x) {\hat{q}}(y)\), so the row player’s relative increase in playing x is at least as large as the column player’s relative increase in playing y. This is indeed true for arbitrary zero-sum games, with or without applying \(\tau \).Footnote 11
5 Experimental results
We have conducted various computer simulations concerning the multiplicity, the support size, the degree of randomization, and the manipulability of \( ML \) schemes. The stochastic preference model used for our experiments is called impartial anonymous culture (IAC). Under IAC, preference profiles are partitioned into equivalence classes with two profiles belonging to the same class if they are identical up to permuting the voters. Every equivalence class is assumed to be equally likely. Impartial culture models are known to significantly underestimate the likelihood of Condorcet winners (see, e.g., Regenwetter et al. 2006).Footnote 12 Our results on all four of the above-mentioned quantities under IAC can thus be interpreted as upper bounds. In real-world settings, one would expect lower numbers.
5.1 Multiplicity
First, we checked the frequencies of profiles with an even number of voters for which the
 and the
and the
 correspondence are single-valued. Figure 7 shows the results of these simulations. They confirm the intuition that these frequencies quickly tend to 1 when the size of the electorate increases. There are profiles for which the
correspondence are single-valued. Figure 7 shows the results of these simulations. They confirm the intuition that these frequencies quickly tend to 1 when the size of the electorate increases. There are profiles for which the
 correspondence is single-valued and the
correspondence is single-valued and the
 correspondence is not and vice versa. Interestingly, profiles of the first type are more common (under the IAC model). This effect is more pronounced for larger numbers of alternatives.
correspondence is not and vice versa. Interestingly, profiles of the first type are more common (under the IAC model). This effect is more pronounced for larger numbers of alternatives.
For all further experiments, we confined ourselves to profiles with an odd number of voters with strict preferences. Recall that for every such profile, both the  and the
and the  correspondence are single-valued and the unique maximal lottery has odd support size. Hence, on this domain, all
correspondence are single-valued and the unique maximal lottery has odd support size. Hence, on this domain, all
 schemes coincide and all
schemes coincide and all
 schemes coincide. For the remainder of this section, we thus simply refer to
schemes coincide. For the remainder of this section, we thus simply refer to
 and
and
 as the unique
as the unique
 and
and
 scheme, respectively.
scheme, respectively.
5.2 Support size
For an odd number of voters with strict preferences, an \( ML \) scheme returns a degenerate lottery if and only if there is a Condorcet winner. Hence, the frequency of cases where maximal lotteries do not randomize can be directly obtained by looking at the number of profiles that admit a Condorcet winner (see, e.g., Gehrlein 2002; Regenwetter et al. 2006; Laslier 2010; Gehrlein and Lepelley 2011; Brandt and Seedig 2016).
Figure 8 shows the distribution of small supports of the two canonical \( ML \) schemes under IAC for different numbers of alternatives and voters, e.g., for \(m=21\) and \(n=501\),
 and
and
 randomize over 5 or more alternatives in \(31.4\%\) and \(21.3\%\) of the cases, respectively. The average support sizes for these parameters are still relatively low (3.18 and 2.87, respectively). As an alternative to IAC, we have also conducted simulations for a spatial model where alternatives and voters are represented as uniformly distributed points in the 10-dimensional unit cube. A voter then ranks alternatives according to the Euclidian distance between him and the alternatives, with closer alternatives being more preferred. In this more realistic model, the average support size was less than 1.8 for \(m\le 21\) and any number of voters. In general,
randomize over 5 or more alternatives in \(31.4\%\) and \(21.3\%\) of the cases, respectively. The average support sizes for these parameters are still relatively low (3.18 and 2.87, respectively). As an alternative to IAC, we have also conducted simulations for a spatial model where alternatives and voters are represented as uniformly distributed points in the 10-dimensional unit cube. A voter then ranks alternatives according to the Euclidian distance between him and the alternatives, with closer alternatives being more preferred. In this more realistic model, the average support size was less than 1.8 for \(m\le 21\) and any number of voters. In general,
 results in slightly lower average support sizes than
results in slightly lower average support sizes than
 .
.
The extreme case of disjoint
 and
and
 supports (see Theorem 1) turns out to be extremely rare. We have found only a handful of these examples in millions of tested profiles. Moreover, the supports of
supports (see Theorem 1) turns out to be extremely rare. We have found only a handful of these examples in millions of tested profiles. Moreover, the supports of
 and
and
 almost always coincide (largely due to the fact that Condorcet winners are likely to exist). We have not encountered a single
almost always coincide (largely due to the fact that Condorcet winners are likely to exist). We have not encountered a single
 \( SD \)-efficiency violation (see Theorem 3) during our simulations.
\( SD \)-efficiency violation (see Theorem 3) during our simulations.
Distributions of the support sizes of
 (left) and
(left) and
 (right) based on 100, 000 samples according to the IAC model for every combination of parameters. The bars represent the frequency of a support with size 1, 3, 5, and 7 or more stacked from bottom to top. Frequencies lower than \(4\%\) are not labeled
(right) based on 100, 000 samples according to the IAC model for every combination of parameters. The bars represent the frequency of a support with size 1, 3, 5, and 7 or more stacked from bottom to top. Frequencies lower than \(4\%\) are not labeled
5.3 Degree of randomization
The support size is a rather crude value to measure the degree of randomization because it ignores the values of non-zero probabilities. We therefore evaluate the degree of randomization of a lottery \(p\in \Delta (A)\) in terms of Shannon entropy  . We set the basis of the logarithm \(b=m\) to normalize the maximal entropy to 1, which is attained for the uniform lottery.
. We set the basis of the logarithm \(b=m\) to normalize the maximal entropy to 1, which is attained for the uniform lottery.
Figure 9 shows a considerable disparity between the average degree of randomization for
 and
and
 , which widens as the number of voters or the number alternatives increases.Footnote 13 This behavior is also reflected when plotting the average distance between
, which widens as the number of voters or the number alternatives increases.Footnote 13 This behavior is also reflected when plotting the average distance between
 and
and
 according to the \(L^1\)-norm or Manhattan distance, which is defined as the sum of differences of probabilities. Somewhat surprisingly, the average degree of randomization of
according to the \(L^1\)-norm or Manhattan distance, which is defined as the sum of differences of probabilities. Somewhat surprisingly, the average degree of randomization of
 tends to slightly decrease for large n. For
tends to slightly decrease for large n. For
 , no consistent trend for all plotted numbers of alternatives can be identified.
, no consistent trend for all plotted numbers of alternatives can be identified.
Average normalized Shannon entropies of \( ML \) schemes with the lower boundary of each colored area corresponding to
 and the upper boundary corresponding to
and the upper boundary corresponding to
 . Additionally, the average distances between the outcomes of both \( ML \) schemes according to the \(L^1\)-norm are displayed as solid lines. Each point is based on 100,000 samples according to the IAC model
. Additionally, the average distances between the outcomes of both \( ML \) schemes according to the \(L^1\)-norm are displayed as solid lines. Each point is based on 100,000 samples according to the IAC model
In order to get a better intuition for how to interpret these numbers, Fig. 10 compares the average degree of randomization of
 with those of random dictatorship and an interpretation of plurality that returns a uniform lottery over all alternatives that are top-ranked by the largest number of voters. As expected, the degree of randomization of
with those of random dictatorship and an interpretation of plurality that returns a uniform lottery over all alternatives that are top-ranked by the largest number of voters. As expected, the degree of randomization of
 is lower than that of random dictatorship and, for reasonable numbers of voters, higher than that of the plurality rule. This comparison underlines how little randomization is required by
is lower than that of random dictatorship and, for reasonable numbers of voters, higher than that of the plurality rule. This comparison underlines how little randomization is required by
 .
.
5.4 Strategyproofness
\( SD \)-manipulability of
 (solid lines) with confidence intervals for a confidence level of 95% (in color) and manipulability of
(solid lines) with confidence intervals for a confidence level of 95% (in color) and manipulability of
 for \(m=5\) (dotted line). Each point is based on 2000 preference profiles sampled according to the IAC model and on testing all possible deviations for each type of voter. The dashed lines show the limit probabilities that no Condorcet winner exists for \({n\rightarrow \infty }\) derived by Gehrlein (2002)
for \(m=5\) (dotted line). Each point is based on 2000 preference profiles sampled according to the IAC model and on testing all possible deviations for each type of voter. The dashed lines show the limit probabilities that no Condorcet winner exists for \({n\rightarrow \infty }\) derived by Gehrlein (2002)
The analytic results we obtained in Sect. 4.3 suggest a strong connection between the existence of Condorcet winners and manipulability of
 schemes. When the number of voters is large compared to the number of alternatives, there is a high probability that every preference relation appears at least once in a randomly chosen profile under the IAC model. Moreover, when there is an odd number of voters with strict preferences, which implies that the majority relation is strict, the notions of weak and strict Condorcet winners coincide. Hence, one would expect the probability that
schemes. When the number of voters is large compared to the number of alternatives, there is a high probability that every preference relation appears at least once in a randomly chosen profile under the IAC model. Moreover, when there is an odd number of voters with strict preferences, which implies that the majority relation is strict, the notions of weak and strict Condorcet winners coincide. Hence, one would expect the probability that
 is \( SD \)-manipulable for a random profile to converge to the probability that no Condorcet winner exists as the number of voters grows. Figure 11 shows the empirical frequency that
is \( SD \)-manipulable for a random profile to converge to the probability that no Condorcet winner exists as the number of voters grows. Figure 11 shows the empirical frequency that
 is \( SD \)-manipulable in a randomly chosen profile under the IAC model for various numbers of alternatives and voters (solid lines). For a fixed number of alternatives, this frequency converges relatively quickly to the probability that no Condorcet winner exists (dashed lines), which confirms the above intuition. In addition, Fig. 11 displays the frequency of profiles at which
is \( SD \)-manipulable in a randomly chosen profile under the IAC model for various numbers of alternatives and voters (solid lines). For a fixed number of alternatives, this frequency converges relatively quickly to the probability that no Condorcet winner exists (dashed lines), which confirms the above intuition. In addition, Fig. 11 displays the frequency of profiles at which
 is \( SD \)-manipulable for 5 alternatives (dashed line). It is significantly lower than for
is \( SD \)-manipulable for 5 alternatives (dashed line). It is significantly lower than for
 for the same number of alternatives and decreases as the number of voters increases. This can be explained by observing that the absolute values of majority margins are unlikely to be 1 for large numbers of voters, which renders it improbable that a single voter can affect the majority relation, and thus the returned lottery, at all.
for the same number of alternatives and decreases as the number of voters increases. This can be explained by observing that the absolute values of majority margins are unlikely to be 1 for large numbers of voters, which renders it improbable that a single voter can affect the majority relation, and thus the returned lottery, at all.
6 Conclusions and discussion
We have carried out an extensive comparison of \( ML \) schemes. Our analytical findings and related results from the literature are summarized in Fig. 4 while our experimental results are illustrated in Figs. 7, 8, 9, 10 and 11. These results can be used to guide the decision whether to use
 or
or
 schemes. We showed that
schemes. We showed that
 schemes are the only \( SD \)-efficient \( ML \) schemes (and even satisfy the stronger notion of \( PC \)-efficiency). Moreover, we proved that all majoritarian and neutral SDSs violate \( SD \)-efficiency, a statement that may be of independent interest.
schemes are the only \( SD \)-efficient \( ML \) schemes (and even satisfy the stronger notion of \( PC \)-efficiency). Moreover, we proved that all majoritarian and neutral SDSs violate \( SD \)-efficiency, a statement that may be of independent interest.
 efficiency failures are, however, extremely rare and may not appear in actual use. We also showed that, while all \( ML \) schemes are \( SD \)-manipulable, they are \( PC \)-strategyproof whenever a Condorcet winner exists (which is the case for most real-world preference profiles) and satisfy relative monotonicity. Moreover,
efficiency failures are, however, extremely rare and may not appear in actual use. We also showed that, while all \( ML \) schemes are \( SD \)-manipulable, they are \( PC \)-strategyproof whenever a Condorcet winner exists (which is the case for most real-world preference profiles) and satisfy relative monotonicity. Moreover,
 schemes are the only homogeneous \( ML \) schemes that satisfy \( SD \)-participation (and even satisfy the stronger notion of \( PC \)-participation). Unsurprisingly,
schemes are the only homogeneous \( ML \) schemes that satisfy \( SD \)-participation (and even satisfy the stronger notion of \( PC \)-participation). Unsurprisingly,
 is less manipulable then
is less manipulable then
 , simply because single voters are often unable to affect the outcome of majoritarian SDSs. This observation is connected to another potential drawback of
, simply because single voters are often unable to affect the outcome of majoritarian SDSs. This observation is connected to another potential drawback of
 : it is less responsive than
: it is less responsive than
 . When there are three alternatives and no majority ties,
. When there are three alternatives and no majority ties,
 will randomize with equal probabilities whenever there is no Condorcet winner. While uniform lotteries may be easier to implement in the real world and perhaps be more acceptable to the general public, this rigidity comes at a cost. Consider, for example, the profile given in Fig. 1. Here,
will randomize with equal probabilities whenever there is no Condorcet winner. While uniform lotteries may be easier to implement in the real world and perhaps be more acceptable to the general public, this rigidity comes at a cost. Consider, for example, the profile given in Fig. 1. Here,
 selects b with probability \(\nicefrac {1}{3}\) even though 97 of 100 voters prefer a to b and no reasonable (deterministic) voting rule would select b.
selects b with probability \(\nicefrac {1}{3}\) even though 97 of 100 voters prefer a to b and no reasonable (deterministic) voting rule would select b.
 , on the other hand, puts probability 0.04 on alternative b.
, on the other hand, puts probability 0.04 on alternative b.
Finally, we evaluated the degree of randomization of \( ML \) schemes via computer simulations. For few alternatives, Condorcet winners are likely to exist in which case \( ML \) schemes do not randomize at all. The average degree of randomization (in terms of Shannon entropy) of
 schemes is lower than that of
schemes is lower than that of
 schemes and significantly lower than that of random dictatorship.
schemes and significantly lower than that of random dictatorship.
Notes
The term bipartisan set was proposed by Nobel Prize Laureate Roger Myerson (Laffond et al. 1993, Footnote 1).
Two French YouTube videos about maximal lotteries by Lê Nguyên Hoang have gathered more than 100,000 views (youtu.be/wKimU8jy2a8 and youtu.be/vAdGZkXhlNM).
\(\tau \) is odd if \(\tau (-k) = -\tau (k)\) for all \(k\in {\mathbb {Z}}\). Thus, \(\tau (0) = 0\) and \(\tau \) is completely defined by its values on positive integers.
One can find other examples where an alternative with
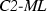 probability almost 1 is not selected by the mentioned classic rules except Baldwin’s rule. It can be shown that, when \(m=3\), a unique Baldwin winner always receives a
probability almost 1 is not selected by the mentioned classic rules except Baldwin’s rule. It can be shown that, when \(m=3\), a unique Baldwin winner always receives a
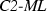 probability of at least \(\nicefrac 13\).
probability of at least \(\nicefrac 13\).The other extreme would be “\( ML ^{\infty }\)”, i.e., \(\limsup _{t\rightarrow \infty } ML ^{\tau }\) with \(\tau (k)=k^t\).
An example where
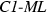 violates \( PC \)-efficiency can be constructed for \(m=n=5\).
violates \( PC \)-efficiency can be constructed for \(m=n=5\).The theorem also holds for \(m=7\) using a similar proof, which requires more voters.
Notably, the proof for the statement about \( BD \)-manipulability does not only hold for \( ML \) schemes, but for any pairwise SDS that satisfies composition-consistency and that returns the uniform lottery in all regular profiles (see Brandl et al. 2016, for definitions).
For strict preferences, absolute monotonicity is equivalent to Gibbard’s (1977) “non-perverseness”, which prescribes that the probability of x should not decrease if it is swapped with the alternative immediately above it in the preference ranking of a single voter. A natural strengthening of absolute monotonicity requires not only that \(q(x)\ge p(x)\), but also that \(p(z)=q(z)\) for all \(z\in A\setminus \{x,y\}\). For strict preferences, the resulting condition is equivalent to strong \( SD \)-strategyproofness and the only ex post efficient SDSs satisfying this property are random dictatorships (Gibbard 1977).
The smallest example of this kind requires \(m=6\).
To see that this statement holds, consider two zero-sum games M and \({\hat{M}}\) that only differ in that \({\hat{M}}_{xy} > M_{xy}\). Then \(0\le {\hat{p}}^t{\hat{M}} q - p^t{\hat{M}} {\hat{q}} = {\hat{p}}^t M q - p^t M{\hat{q}} + ({\hat{M}}_{xy} - M_{xy}) ({\hat{p}}(x)q(y) - p(x){\hat{q}}(y))\). The first equality holds since the row player’s expected payoff is at least the value of \({\hat{M}}\) when playing the maximin strategy \({\hat{p}}\) and at most the value of \({\hat{M}}\) when the column player plays \({\hat{q}}\). Similarly, we get \({\hat{p}}^t M q - p^t M{\hat{q}}\le 0\). So we conclude that \({\hat{p}}(x)q(y) - p(x){\hat{q}}(y)\ge 0\) as desired.
Feld and Grofman (1992) analyze election data from 36 real-world elections, all of which admitted a Condorcet winner. Gehrlein and Lepelley (2011) summarize 37 empirical studies from 1955 to 2009 and concluded that “there is a possibility that Condorcet’s Paradox might be observed, but that it probably is not a widespread phenomenon.” Similar conclusions were drawn by Regenwetter et al. (2007), Mattei et al. (2012) and Tideman and Plassmann (2012). Laslier (2010) and Brandt and Seedig (2016) report concrete probabilities for the existence of Condorcet winners under various distributional assumptions using computer simulations.
The high degree of randomization exhibited by
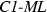 can also be backed by formal arguments. For example, we showed that—when preferences are strict, n is odd, and there is no Condorcet winner—the highest probability that
can also be backed by formal arguments. For example, we showed that—when preferences are strict, n is odd, and there is no Condorcet winner—the highest probability that
 assigns to any alternative is \(\nicefrac 13\).
assigns to any alternative is \(\nicefrac 13\).
References
Aziz H, Brandt F, Brill M (2013) On the tradeoff between economic efficiency and strategy proofness in randomized social choice. In: Proceedings of the 12th International Conference on Autonomous Agents and Multiagent Systems (AAMAS), pp 455–462
Aziz H, Brandl F, Brandt F (2015) Universal Pareto dominance and welfare for plausible utility functions. J Math Econ 60:123–133
Aziz H, Brandl F, Brandt F, Brill M (2018) On the tradeoff between efficiency and strategyproofness. Games Econ Behav 110:1–18
Bogomolnaia A, Moulin H (2001) A new solution to the random assignment problem. J Econ Theory 100(2):295–328
Brandl F, Brandt F (2020) Arrovian aggregation of convex preferences. Econometrica 88(2):799–844
Brandl F, Brandt F, Seedig HG (2016) Consistent probabilistic social choice. Econometrica 84(5):1839–1880
Brandl F, Brandt F, Eberl M, Geist C (2018) Proving the incompatibility of efficiency and strategyproofness via SMT solving. J ACM 65(2):1–28
Brandl F, Brandt F, Geist C, Hofbauer J (2019a) Strategic abstention based on preference extensions: positive results and computer-generated impossibilities. J Artif Intell Res 66:1031–1056
Brandl F, Brandt F, Hofbauer J (2019b) Welfare maximization entices participation. Games Econ Behav 14:308–314
Brandt F (2015) Set-monotonicity implies Kelly-strategyproofness. Soc Choice Welf 45(4):793–804
Brandt F (2017) Rolling the dice: recent results in probabilistic social choice. In: Endriss U (ed) Trends in computational social choice. AI access, chapter 1, pp 3–26
Brandt F, Seedig HG (2016) On the discriminative power of tournament solutions. In: Selected papers of the International Conference on Operations Research, OR2014, Operations Research Proceedings. Springer, pp 53–58
Brandt F, Geist C, Harrenstein P (2016) A note on the McKelvey uncovered set and Pareto optimality. Soc Choice Welf 46(1):81–91
Brandt F, Brill M, Seedig HG, Suksompong W (2018) On the structure of stable tournament solutions. Econ Theory 65(2):483–507
Brandt F, Saile C, Stricker C (2020) Strategyproof social choice when preferences and outcomes may contain ties. Working paper
Campbell DE, Kelly JS (2003) A strategy-proofness characterization of majority rule. Econ Theory 22(3):557–568
Debord B (1987) Caractérisation des matrices des préférences nettes et méthodes d’agrégation associées. Mathématiques et sciences humaines 97:5–17
Dutta B, Laslier J-F (1999) Comparison functions and choice correspondences. Soc Choice Welf 16(4):513–532
Feld SL, Grofman B (1992) Who’s afraid of the big bad cycle? Evidence from 36 elections. J Theor Polit 4(2):231–237
Felsenthal DS, Machover M (1992) After two centuries should Condorcet’s voting procedure be implemented? Behav Sci 37(4):250–274
Fishburn PC (1973) The Theory of Social Choice. Princeton University Press, Princeton
Fishburn PC (1977) Condorcet social choice functions. SIAM J Appl Math 33(3):469–489
Fishburn PC (1984a) Probabilistic social choice based on simple voting comparisons. Rev Econ Stud 51(4):683–692
Fishburn PC (1984b) SSB utility theory: an economic perspective. Math Soc Sci 8(1):63–94
Fishburn PC (1984c) Dominance in SSB utility theory. J Econ Theory 34(1):130–148
Fisher DC, Ryan J (1995) Tournament games and positive tournaments. J Graph Theory 19(2):217–236
Gehrlein WV (2002) Condorcet’s paradox and the likelihood of its occurrence: different perspectives on balanced preferences. Theory Decis 52(2):171–199
Gehrlein WV, Lepelley D (2011) Voting paradoxes and group coherence. Studies in choice and welfare. Springer
Gibbard A (1977) Manipulation of schemes that mix voting with chance. Econometrica 45(3):665–681
Hoang LN (2017) Strategy-proofness of the randomized Condorcet voting system. Soc Choice Welf 48(3):679–701
Kreweras G (1965) Aggregation of preference orderings. In: Mathematics and social sciences I: Proceedings of the seminars of Menthon-Saint-Bernard, France (1–27 July 1960) and of Gösing, Austria (3–27 July 1962), pp 73–79
Laffond G, Laslier J-F, Le Breton M (1993) The bipartisan set of a tournament game. Games Econ Behav 5(1):182–201
Laffond G, Lainé J, Laslier J-F (1996) Composition-consistent tournament solutions and social choice functions. Soc Choice Welf 13(1):75–93
Laffond G, Laslier J-F, Le Breton M (1997) A theorem on symmetric two-player zero-sum games. J Econ Theory 72(2):426–431
Laslier J-F (1997) Tournament solutions and majority voting. Springer, Berlin
Laslier J-F (2000) Aggregation of preferences with a variable set of alternatives. Soc Choice Welf 17(2):269–282
Laslier J-F (2010) In silico voting experiments. In: Laslier J-F, Sanver MR (eds) Handbook on approval voting, chapter 13, pp 311–335. Springer
Mattei N, Forshee J, Goldsmith J (2012) An empirical study of voting rules and manipulation with large datasets. In: Proceedings of the 4th International Workshop on Computational Social Choice (COMSOC)
Moulin H (1988) Axioms of cooperative decision making. Cambridge University Press, Cambridge
Peyre R (2013) La quête du graal électoral. CNRS, Images des Mathématiques
Postlewaite A, Schmeidler D (1986) Strategic behaviour and a notion of ex ante efficiency in a voting model. Soc Choice Welf 3(1):37–49
Potthoff RF (1970) The problem of the three-way election. In: Rose RC, Chakravarti IM, Mahalanobis PC, Rao CR, Smith KJC (eds) Essays in probability and statistics. The University of North Carolina Press
Regenwetter M, Grofman B, Marley AAJ, Tsetlin IM (2006) Behavioral social choice: probabilistic models, statistical inference, and applications. Cambridge University Press, Cambridge
Regenwetter M, Kim A, Kantor A, Ho M-HR (2007) The unexpected empirical consensus among consensus methods. Psychol Sci 18(7):629–635
Rivest RL, Shen E (2010) An optimal single-winner preferential voting system based on game theory. In: Proceedings of the 3rd International Workshop on Computational Social Choice (COMSOC), pp 399–410
Sen AK (1970) Collective choice and social welfare. North-Holland
Tideman N, Plassmann F (2012) Modeling the outcomes of vote-casting in actual elections. In: Felsenthal DS, Machover M (eds) Electoral systems: paradoxes, assumptions, and procedures, Studies in Choice and Welfare. Springer
Acknowledgements
This material is based on work supported by the Deutsche Forschungsgemeinschaft under grants BR 2312/11-1 and BR 5969/1-1. Preliminary results of this paper were presented at the 27th International Joint Conference on Artificial Intelligence (Stockholm, July 2018). The authors thank Johannes Hofbauer for contributing the third case in the proof of Theorem 9 and the anonymous reviewers for constructive feedback.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Brandl, F., Brandt, F. & Stricker, C. An analytical and experimental comparison of maximal lottery schemes. Soc Choice Welf 58, 5–38 (2022). https://doi.org/10.1007/s00355-021-01326-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-021-01326-x











 (solid lines) and
(solid lines) and  (dotted lines), respectively. Each point is based on 100,000 samples according to the IAC model
(dotted lines), respectively. Each point is based on 100,000 samples according to the IAC model


 (solid line) compared to random dictatorship (dashed line) and the plurality rule (dotted line). Each point is based on 100, 000 samples according to the IAC model
(solid line) compared to random dictatorship (dashed line) and the plurality rule (dotted line). Each point is based on 100, 000 samples according to the IAC model
 probability almost 1 is not selected by the mentioned classic rules except Baldwin’s rule. It can be shown that, when
probability almost 1 is not selected by the mentioned classic rules except Baldwin’s rule. It can be shown that, when 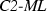 probability of at least
probability of at least 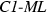 violates
violates 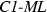 can also be backed by formal arguments. For example, we showed that—when preferences are strict, n is odd, and there is no Condorcet winner—the highest probability that
can also be backed by formal arguments. For example, we showed that—when preferences are strict, n is odd, and there is no Condorcet winner—the highest probability that
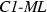 assigns to any alternative is
assigns to any alternative is