Set-monotonicity implies Kelly-strategyproofness

Abstract

This paper studies the strategic manipulation of set-valued social choice functions according to Kelly’s preference extension, which prescribes that one set of alternatives is preferred to another if and only if all elements of the former are preferred to all elements of the latter. It is shown that set-monotonicity—a new variant of Maskin-monotonicity—implies Kelly-strategyproofness in comprehensive subdomains of the linear domain. Interestingly, there are a handful of appealing Condorcet extensions—such as the top cycle, the minimal covering set, and the bipartisan set—that satisfy set-monotonicity even in the unrestricted linear domain, thereby answering questions raised independently by Barberà (J Econ Theory 15(2):266–278(1977a)) and Kelly (Econometrica 45(2):439–446 (1977)).

Appendix

For the domain of transitive and complete (but not necessarily antisymmetric) preference relations $\fancyscript{R}^N$, we show that all Condorcet extensions are Kelly-manipulable. This strengthens Theorem 3 by Gärdenfors (1976) and Theorem 8.1.2 by Taylor (2005), who showed the same statement for a weaker notion of manipulability and a weaker notion of Condorcet winners, respectively. When assuming that pairwise choices are made according to majority rule, this also strengthens Theorems 1 and 2 by MacIntyre and Pattanaik (1981). However, our construction requires that the number of agents is linear in the number of alternatives.

Theorem 2

No Condorcet extension is Kelly-strategyproof in domain $\fancyscript{R}^N$ when there are more than two alternatives.

Proof

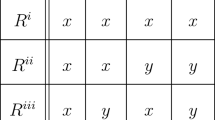
Let $A=\{a_1,\dots ,a_m\}$ with $m\ge 3$ and consider the following preference profile $R$ with $3m$ agents. In the representation below, sets denote indifference classes of the agents.

For every alternative $a_i$, there are two agents who prefer every alternative to $a_i$ and are otherwise indifferent. Moreover, for every alternative $a_i$ there is one agent who prefers every alternative except $a_{i+1}$ to $a_i$, ranks $a_{i+1}$ below $a_i$, and is otherwise indifferent.

Since $f(R)$ yields a nonempty choice set, there has to be some $a_i\in f(R)$. Due to the symmetry of the preference profile, we may assume without loss of generality that $a_2\in f(R)$. Now, let

$$\begin{aligned} R_3^\prime ,R_4^\prime :a_1, \{a_3,\ldots ,a_m\},a_2 \end{aligned}$$

and define $R^\prime =(R_{-3},R^\prime _3)$ and $R^{\prime \prime }=(R^\prime _{-4},R^\prime _4)$. That is, $R^\prime$ is identical to $R$, except that agent 3 lifted $a_1$ on top and $R^{\prime \prime }$ is identical to $R^\prime$, except that agent 4 lifted $a_1$ on top. Observe that $f(R^{\prime \prime })=\{a_1\}$ because $a_1$ is the Condorcet winner in $R^{\prime \prime }$.

In case that $a_2\not \in f(R^\prime )$, agent 3 can manipulate as follows. Suppose $R$ is the true preference profile. Then, the least favorable alternative of agent 3 is chosen (possibly among other alternatives). He can misstate his preferences as in $R^\prime$ such that $a_2$ is not chosen. Since he is indifferent between all other alternatives, $f(R^\prime ) \mathrel {\widehat{P}_3} f(R)$.

If $a_2\in f(R^\prime )$, agent 4 can manipulate similarly. Suppose $R'$ is the true preference profile. Again, the least favorable alternative of agent 4 is chosen. By misstating his preferences as in $R^{\prime \prime }$, he can assure that one of his preferred alternatives, namely $a_1$, is selected exclusively because it is the Condorcet winner in $R^{\prime \prime }$. Hence, $f(R^{\prime \prime }) \mathrel {\widehat{P}^\prime _4} f(R^\prime )$.$\square$