Study of the wavelength dependence of the absorption function of diesel soot by LII modeling integrating the effect of multiple scattering within aggregates

Abstract

This work represents a first attempt at proposing a refined LII model suitable for simulating signals collected with excitation wavelengths (EWs) of 266, 355, 532 and 1064 nm. In this context, we implemented a comprehensive version of laser-irradiated soot heat and mass balance equations integrating terms representing the saturation of linear, single- and multi-photon absorption processes, cooling by sublimation, conduction, radiation and thermionic emission, as well as mechanisms depicting soot oxidation and annealing, non-thermal photodesorption of carbon clusters and corrective factors accounting for the shielding effect and multiple scattering (MS) within aggregates. This simulation tool was fully parameterized, by coupling design of experiments with a genetic algorithm-based solver, against data collected at different heights above the burner (HAB) in a diesel spray flame. This allowed to assess values of different model parameters involved in absorption and sublimation terms, which, to date, have never been reported in LII modeling studies for UV EWs (e.g., multi-photon absorption cross sections for C₂ photodesorption and saturation coefficients for linear- and multi-photon absorption). The simulation work proposed herein then enabled to infer information regarding the evolution of the absorption function of soot ($E\left(m,\lambda \right)$). $E\left(m,266\right)$, $E(m,355)$ and $E(m,532)$ ranging from 0.25 to 0.51, 0.20 to 0.38 and 0.18 to 0.30, respectively, were notably estimated as a function of the HAB. Alternatively, values ranging from 0.31 to 0.53, 0.26 to 0.44 and 0.22 to 0.38 were assessed while neglecting the effect of MS and provided constant $E(m,266)$/$E(m,1064)$, $E(m,355)$/$E(m,1064)$ and $E(m,532)$/$E(m,1064)$ ratios of 1.4, 1.2 and 1.0, regardless of the HAB. In addition, the obtained results showed that the wavelength dependence of the soot absorption function was quite negligible for EWs higher than 532 nm, irrespective of whether the effect of MS was considered or neglected. On the other hand, aggregate properties were proven to substantially influence the $E(m,\lambda )$/$E(m,1064)$ ratios for decreasing $\lambda$ and increasing HAB, thus illustrating the significant effect of aggregation on the optical properties of soot. Finally, the results issued from the different analyses we conducted on the diesel flame investigated in this paper led to the conclusion that values of $E\left(m,\lambda \right),$ falling within the 0.38 ± 0.15 and 0.29 ± 0.11 range at 266 and 355 nm, versus 0.25 ± 0.09 at 532 and 1064 nm could be considered as suitable for simulating LII signals of progressively aging aggregated particles.

1 Introduction

Soot particles issued from the high-temperature fuel-rich incomplete combustion of hydrocarbons are subject to increasingly stringent regulations due to their harmful impacts on climate and human health [1, 2]. Indicated as a major factor in global warming [3, 4], soot also drastically impacts air quality, and, as such, causes serious public health and safety issues [5, 6]. Technological avenues in the fields of fuel formulation and combustion chamber design are, therefore, more than ever required to limit the production of this particulate pollutant in combustion devices. In this context, diesel technology is particularly pinpointed, as it intrinsically tends to produce more particles (whose toxicity is widely documented [2]) than spark-ignition engines. A detailed characterization of the physical properties of soot (including optical ones) is thus imperative, notably to better assess its interaction with the environment. It is, moreover, worth noting that the development of advanced combustion technologies aimed at limiting the formation of fine carbonaceous particles requires addressing the current deficiencies hindering our understanding of soot inception and growth. Despite the major progress that has been realized in this field for over a half century [7,8,9,10], additional work is still required, as highlighted in [11], emphasizing the need for advanced optical diagnostics allowing to probe complex reacting media.

Over the last decades, laser-induced incandescence (LII) has come to represent a reference diagnostic tool for the in situ measurement of soot volume fractions in combustion environments [12]. It involves heating particles to their incandescence temperature by means of a high-power pulsed laser source before collecting the Planck radiation emitted above the flame emission using an adapted detector (a photomultiplier tube or an intensified camera). Although LII is also commonly used to infer the soot diameter by coupling a time-resolved detection approach (TiRe-LII) with LII signal modeling [13,14,15,16], it is still mostly implemented for the qualitative and quantitative analysis of spatial and temporal soot distributions in flames and exhaust gases. In fact, ever since Melton [17] showed that the intensity of the radiative emission from laser-heated soot could be considered as proportional to its volume fraction in the probed medium for detection wavelengths in the visible spectral range, LII has been extensively coupled with single- or multi-pass light extinction techniques to assess absolute soot concentrations [18, 19]. A full knowledge of the optical properties of soot particles (including their refractive index ($m$) or absorption function ($E\left(m\right)= -Im\left[\left({m}^{2}-1\right)/\left({m}^{2}+2\right)\right]$)) is, however, crucial for a quantitative interpretation of optical measurements performed by LII or extinction. This thus justifies the emphasis on assessing the soot absorption function (which is the primary property of direct interest for LII [20]), as illustrated in Sect. 2, which consists of an overview of $E(m)$ values reported in the literature, along with discussions regarding the factors influencing this parameter and its estimation.

2 Review of ${\varvec{E}}({\varvec{m}})$ values and assessment approaches

2.1 ${\varvec{E}}({\varvec{m}})$ values issued from the literature

Different reviews, including those by Sorensen [21], Bond and Bergstrom [22], and more recently, Liu et al. [23], illustrate the significant discrepancies characterizing the values of $E(m)$ reported in the literature. That variability, as well as its effect on LII signals, is illustrated in [24], where the predictions issued from different LII models were compared. $E(m,532)$ values between 0.179 and 0.4 were notably selected therein depending on the authors who contributed to this benchmark, which partly explains the widely divergent results obtained. Prior to that, [20] proposed an average $E(m)$ of 0.3 ± 0.06 for a visible to near-infrared (IR) wavelength range based on an extensive set of data derived from light extinction measurements [25,26,27,28,29,30]. While being in good agreement with the above-mentioned $E(m)$ range [24], as well as with the results by [31], among other things, this soot absorption function value, however, contrasts somewhat with data reported in other studies, including those by [32] or [33]. Although a consensus seems to emerge on the fact that the $E(m)$ of mature soot would be comprised between 0.2 and 0.4 in the visible spectrum, with an uncertainty of about a factor of 2, many works undertaken over the last 30 years still highlight a more or less marked dependence of the absorption function on the particle maturation stage and on the wavelength ($\lambda$).

Regarding the first aspect, an increase of the $E(m)$ with soot growth is globally admitted. This was observed by [34,35,36,37] in premixed ethylene/air flames, by [38] in co-flow diffusion ethylene–air flames, by [39] in a premixed methane/oxygen/nitrogen flat flame, and more recently by [40] in a diesel spray flame. This behavior can be traced to the properties of partially mature and mature soot, which differ significantly. The former is characterized by a more transparent liquid-like structure, while the latter exhibits a lower H/C ratio, more sp²-bonded carbon atoms, and consequently, a more ordered graphitic structure [22] prone to enhancing the particle absorption capacity according to [41]. This explanation is, moreover, supported by the results of [31] and [33], which showed that decreasing the H/C ratio of soot by burning fuels having widely varying hydrogen-to-carbon ratios (acetylene and propane, in [31], versus methane, propane or ethylene, in [33]) induces a significant increase of the complex refractive index. In a review of recent literature on soot optical properties [23], Liu et al. reported $E(m)$ values for freshly emitted and aged black carbon (also referred to as mature soot) in the visible and near-infrared between 0.29 [42] and 0.52 [43], with a more likely range of values falling between 0.35 and 0.45. Based on the average value of recently measured mass absorption cross sections (MAC) of mature soot, the authors also proposed a lower $E(m)$ limit between 0.29 and 0.35, as derived from the Rayleigh–Debye–Gans approximation applied to fractal aggregates (RDG-FA). After summarizing a selected range of refractive indexes ($m$) reported in recent studies, Liu et al. placed them in the context of absorption measurements using a contour plot of $E(m)$ on the $n$–$k$ plane (with $n$ and $k$ denoting the real and imaginary parts of $m$). They also reported therein measured MAC values using the RDG-FA theory integrating a correction factor which notably accounts for the particle morphology as well as for the size of primary particles and aggregates (see [44,45,46]). In doing so, Liu et al. concluded that $E(m)$ of mature soot should be greater than 0.32 in the visible and near infrared.

On the other hand, uncertainties persist with respect to the spectral dependence of the soot absorption function. For instance, [47] concluded that the $E(m)$ function was constant (or at least did not increase by more than 20%) over a spectral range extending from 500 to 945 nm, which agrees with the observation in [48], thus supporting the fact that the $E(m)$ of mature soot displays a negligible variation with the wavelength in the visible and near infrared as concluded in [23]. As for [29, 49], they reported increases of $E(m)$ with the wavelength in the visible, while for their part, [31, 32] showed a decrease of the soot absorption function between 400 and 600 nm, followed by an opposite trend for longer wavelengths. By analyzing experimentally monitored data available in the literature, greatly varying expressions have been proposed to account for the spectral dependence of the soot refractive index. This includes functions depicting an inverse wavelength dependence, as suggested by [49, 50], and then considered in [51], relations accounting for a linear dependence of $E(m)$ with the wavelength, as proposed by [52] based on the results from [29], or specific parameterized equations derived from data-fitting procedures, as is the case in [53].

2.2 LII-based ${\varvec{E}}({\varvec{m}})$ assessment approaches used in the literature

The fact that widely varying results emerge from past studies clearly illustrates that assessing the absorption function of soot while characterizing its dependence on the wavelength is far from straightforward. The complexity herein relates in particular to the implementation of sophisticated measurement approaches and to difficulties in selecting adapted models to interpret experimentally assessed optical data [21, 23]. For example, soot sampling procedures represent a significant source of uncertainty likely to impact obtained results when performing ex situ analyses. This partly explains why the use of optical diagnostics (including LII) has been gaining in currency.

In this context, the two-excitation wavelength LII (TEW-LII) has proven to be a fitting approach for evaluating the relative wavelength dependence of the soot absorption function [12]. The principle of this technique consists in heating soot in the same way, but using laser sources at two different wavelengths (${\lambda }_{1}$ and ${\lambda }_{2}$). This allows to infer the relative variation of $E(m)$ between ${\lambda }_{1}$ and ${\lambda }_{2}$ based on the ratio of the fluences required to ensure that soot absorbs the same amount of energy at the two selected wavelengths. When applied to flames burning diesel [53, 54], a diesel/rapeseed methyl ester mixture [53], methane [54] and ethylene [38, 55, 56], the TEW-LII technique has led to the determination of values of around 1, 1.1 and 1.4 for the $E(m,532)$/$E(m,1064)$, $E(m,355)$/$E(m,1064)$ and $E(m,266)$/$E(m,1064)$ ratios, respectively. However, the TEW-LII only provides the relative evolution of $E\left(m\right)$ as a function of λ. Indeed, inferring its absolute value implies implementing more sophisticated procedures based on a comparison of measured and simulated LII signals [34, 35, 37,38,39,40, 52, 57]. The major difficulty with such an approach stems from the implementation of a proper LII model. Although a wide variety of simulation tools have been proposed in the literature (see [12, 20, 24, 51, 58, 59] and references therein), their predictive capabilities still vary significantly, depending on the nature of the energy fluxes integrated within the energy and mass balance equations accounting for the temporal evolution of the soot temperature and diameter during the laser heating and cooling stages, as well as on the governing equations related to these fluxes.

In the majority of recent works covering the inference of soot optical properties through LII modeling, relatively standard model formulations (solely integrating laser absorption and cooling by conduction, evaporation and radiation) were selected [35, 37]. More simple models which neglect sublimation and radiation rates have even sometimes been preferred [34, 52]. Even though the selection of simple model formulations can be considered quite acceptable in the context of analyses focusing on the rate of change of the energy stored by soot particles during their laser heating, [37] still recalled that inferring information on the evolution of soot properties (especially at relatively high fluences) using simplified LII models should be addressed with caution. A more comprehensive treatment incorporating advanced sub-model formulations, together with additional physical processes (such as internal multiple scattering (MS) within soot aggregates) is indeed a must if consistent information on soot physical properties is to be derived. This fact is especially at the root of recent investigations focusing on $E(m)$ assessments using more refined LII models derived from the formulations proposed by Michelsen [24, 51], which integrate mechanisms accounting for soot melting and annealing, saturation of linear, single- and multi-photon absorption leading to the photodesorption of C₂ clusters, in addition to oxidation and thermionic emission. Using this kind of model to study the soot maturity and absorption cross sections of particles generated in ethylene flames, [38] obtained an excellent agreement between measured and simulated LII time decays while drawing conclusions consistent with those reported in [53, 55, 56] regarding the evolution of the soot absorption cross section as a function of the wavelength. Later, [39] simulated LII signals measured in a premixed methane/oxygen/nitrogen flat flame using a model derived from the one proposed in [24, 51]. $E(m)$ values in line with those reported in [34] were then obtained (i.e., between ⁓0.2 and ⁓0.4, depending on the soot maturation degree). None of these works, however, considered the influence of MS, which can strongly impact the values of the absorption function estimated by LII modeling, depending on the excitation wavelength (EW) considered.

It is indeed commonly assumed in LII studies that soot aggregates behave similarly to clusters of identical non-interacting spherical primary particles in point contact. Due to their specific spatial layout, these aggregates can be described as fractal-like structures with a number of primary particles in each aggregate, ${N}_{p}$, which can be expressed as a function of a fractal prefactor ${k}_{f}$, a fractal dimension ${d}_{f}$, the diameter of the primary particles forming the aggregate ${D}_{p}$ and the gyration diameter ${D}_{g}$, so that:

$${N}_{p}={k}_{f}\cdot {\left(\frac{{D}_{g}}{{D}_{p}}\right)}^{{d}_{f}}.$$

(1)

Based on the RDG-FA approximation, one can consider that the light absorption of soot aggregates corresponds to the product of the absorption cross section of a single primary particle by the number ${N}_{p}$ of individual primary particles composing the aggregates. The validity of the RDG-FA approximation must, however, be considered with caution due to the different hypotheses underlying this theory [60, 61]. First, the RDG-FA model applies when the following inequalities are satisfied: |m-1|≪ 1, 2·π·${D}_{p}$·|m-1|⁄${\lambda }_{l}$ < 1 and π·${D}_{p}$⁄${\lambda }_{l}$ ≪ 1 (where ${\lambda }_{l}$ denotes the wavelength of the incident light source). Furthermore, each primary particle is supposed to be exposed to the incident light, while the effect of MS induced by the presence of several primary particles joined together within an aggregate is considered as negligible, as is the self-interaction of the primary particle itself. Despite these important assumptions, many numerical and experimental works [62,63,64,65,66] have demonstrated that the RDG-FA theory could be considered a reasonable approach to account for the absorption behavior of soot aggregates under conditions typical of those encountered during LII measurements. According to [20], comparisons between the RDG-FA approximation and more exact numerical models would lead to errors of less than 10% for soot aggregates containing up to 500 primary particles when $\pi \cdot {D}_{p}/{\lambda }_{l}<0.5$. That being said, other studies have still reported higher errors (up to 30%) in the prediction of soot absorption and scattering properties [21, 67,68,69]. For MS, it is commonly assumed that this phenomenon can be neglected as long as ${d}_{f}$ < 2 (a condition often verified for soot aggregates) [70]. Liu et al. still demonstrated that for ${\lambda }_{l}$ of 532 and 1064 nm, the RDG-FA theory may lead to an underprediction of the absorption capability of soot aggregates by nearly 10–15% (depending on their size), in comparison with predictions issued from the use of the generalized multi-sphere Mie-solution method (GMM), which is said to be more accurate for the characterization of aggregate radiative properties as it strictly accounts for the multiple scattering between primary particles [70, 71]. Using the RDG-FA theory while neglecting internal MS can thus have significant consequences on the interpretation of optical measurements, as highlighted in [71], where the above-mentioned underpredictions of soot aggregate absorption cross sections were considered as unacceptable for LII applications. To address this issue, [45] recently proposed an extended form of the RDG-FA theory integrating a generalized structure factor function accounting for the scattering behavior of fractal aggregates. The parameterization of this structure factor, which was carried out based on calculations relying on the discrete dipole approximation (DDA) and on the GMM method, led to a proper simulation of the effect of MS on aggregate absorption and scattering properties, while still retaining the simplicity of the RDG-FA approach. Considering this correction factor in reanalyzing TEW-LII data from [39, 54], [72] showed that the values of the $E(m,\lambda )$/$E(m,1064)$ ratio remain highly unchanged for $\lambda$ > 532 nm with respect to data issued from the use of the classical RDG-FA theory on which the original TEW-LII approach was developed. For $\lambda$ < 532 nm, the values of the above ratio alternatively increase with decreasing wavelengths when the effect of MS is considered. Reference [41] then also implemented the improved RDG-FA theory from [45] to evaluate the optical properties of nanoparticle aggregates issued from different sources by analyzing specific extinction spectra obtained in the near-UV spectrum. Here again, the major impact of multiple scattering on the proper estimation of the wavelength-dependent absorption function of soot was demonstrated. Notwithstanding these important findings, with the exception of [40, 57], none of the above-cited LII modeling works dealing with soot absorption function assessment (i.e., [34, 35, 37,38,39, 52]), however, considered the MS effect.

2.3 E(m) assessment by advanced LII modeling

Following the conclusions drawn in [59, 73] pinpointing the need to integrate photolytic mechanisms to simulate soot LII over an extended range of operating conditions, [40] proposed a refined model formulation derived from the one developed by [24, 51] integrating, for the first time, the generalized structure factor from [45, 72] to account for the scattering behavior of fractal aggregates. Using an advanced parameterization procedure coupling design of experiments with a genetic algorithm-based solver, the proposed model was fully parameterized and allowed estimating the values taken by different factors influencing soot LII at 1064 nm, including the multi-photon absorption cross section for C₂ photodesorption, the empirical saturation coefficients for linear and multi-photon absorption, the enthalpy required to photodesorb carbon clusters, the thermal accommodation coefficient, and the soot absorption function [40]. In this context, $E(m)$ values between 0.18 and 0.31 were inferred for soot generated in a turbulent spray flame of diesel, depending on the particle maturation stage. Similarly, $E(m)$ values between 0.20 and 0.34 were estimated in [40] by simulating signals collected by [39] in an atmospheric methane/oxygen/nitrogen premixed flat flame. However, no estimation of the wavelength dependence of the soot absorption function was carried out therein, notwithstanding the crucial need for additional data regarding this aspect, as clearly pointed out in Sect. 2.1. To contribute to the resolution of this issue, the present work, which is a continuation of a recent study presented at a conference [74], and whose proceedings was published in [57], aims at implementing the modeling approach proposed in [40] to simulate a series of LII signals generated with different EWs and collected at different heights above the burner (HAB) in the diesel flame studied in [40, 53, 54, 57]. To that end, measurements were carried out in the low-to-intermediate fluence regime with excitation wavelengths of 266, 355 and 532 nm. To the best of the authors’ knowledge, this work represents the first attempt at modeling LII signals measured with UV EWs of 266 or 355 nm using a refined model, which notably integrates terms representing the saturation of linear, single- and multi-photon absorption processes, cooling by thermionic emission, as well as corrective factors allowing to consider the shielding effect and multiple scattering (MS) within aggregates. In addition to inferring soot properties (e.g., multi-photon absorption cross section and saturation coefficients for linear- and multi-photon absorption) whose values are not available in the literature for EWs of 266 and 355 nm, $E(m)$ values determined for each considered wavelength will be reported and commented on. In that respect, the emphasis will be on the impact of MS, soot maturation and wavelength on the soot absorption function, noting that obtained results will be systematically compared with previously published data.

3 Experiment

Both the experimental setup and the measurement procedure implemented in this work are identical to those detailed in [40]. As a consequence, only a short description of their main characteristics will be given below.

3.1 Flame generation system

The Lemaire spray burner configuration, which was described and characterized in detail in [75], was used to generate a turbulent diesel flame similar to the one extensively studied in [40, 53, 54, 76,77,78]. In brief, this setup consists of a McKenna hybrid flat flame burner composed of a 60-mm-diameter bronze porous plate on which a lean premixed methane–air flat flame is stabilized. A central 6.35-mm-diameter tube allows the introduction of a direct injection high-efficiency nebulizer (DIHEN model 170-AA) for the atomization of the liquid fuel, which almost quite immediately ignites when crossing the hot gases produced by the flat flame. A low sulfur diesel similar to the one used in [40] was burned. Furthermore, the setup flow rates were set as in [40] (i.e., 2.4 × 10^–5 Nm³·s⁻¹ of methane and 2.9 × 10^–4 Nm³·s⁻¹ of air for the flat flame against 5.3 × 10^–6 Nm³·s⁻¹ for the nebulization gas (nitrogen) and 46 g·h⁻¹ for diesel). These operating conditions allow generating an 18-cm height and 2-cm width spray flame with a peak soot concentration measured at a 92-mm height above the burner (HAB) [76], where a temperature of 1850 K is reached [40, 78]. The size distributions of primary particles and soot aggregates measured at this HAB by coupling transmission electron microscopy (TEM) and scanning mobility particle sizer (SMPS) analyses are detailed in [53], whereas results issued from measurements performed at other HAB are reported in [40].

3.2 LII setup and procedure

The LII analytical chain, which is schematized in [78], is composed of an Nd:YAG laser generating a fundamental wavelength of 1064 nm. It is equipped with frequency doubling, tripling and quadrupling crystals, allowing generating laser pulses at 532, 355 and 266 nm, respectively. For each wavelength, the central part of the unfocussed near-Gaussian laser beams was selected using a 1-mm diaphragm to generate Airy diffraction profiles, which were then propagated through the flame. As was previously done in [53, 54], the distance between the diaphragm and the center of the burner was adapted for each wavelength to obtain identical beams having a section of 0.0021 cm² at 1/e², as monitored using a Gentec Beamage-CCD12 beam profiling camera (typical spatial profiles of the laser beam energy being provided in [53] as examples). Since the soot volume fractions in the studied flame are very low (below 200 ppb [79]), the attenuation of the laser through the flame (as well as signal trapping) is negligible. The laser energy was thus continuously measured during experiments using a Gentec power detector located behind the flame. Time-resolved LII signals were collected perpendicularly to the laser propagation direction, as depicted in the diagram reported in [78], by imaging a thin part of the measurement volume on a 300 µm horizontal slit placed in front of a Hamamatsu R2257 photomultiplier tube (see [40, 53, 78] for more details concerning the signal collection procedure). An OG-550 long pass filter was used, as in [40], to limit photochemical interferences attributable to C₂ Swan band emission and C₃ Swings band emission for instance [80], further reiterating that measurements herein mainly cover the low-to-intermediate fluence regime for which these interferences should be relatively negligible. As for the laser-induced fluorescence measurements reported in Sect. 5.2, they were carried out using a WG280 filter placed in front of the detector along with 355-nm and 532-nm notch filters to suppress radiation at 266, 355 and 532 nm. 200 LII temporal profiles were averaged for each measurement on a Teledyne Lecroy oscilloscope (500 MHz bandwidth, 20 Gs/s) triggered by the signal from a Thorlabs photodiode having a spectral range between 200 and 1100 nm. Finally, a Princeton Instruments Acton 2300i spectrograph was coupled with a PI-MAX 4 camera for flame temperature assessment [40, 78] through a Planck function fitting procedure [47]. To that end, the calibration of the detection chain was achieved as was previously done in [54, 77], using a Gamma Scientific integrating sphere. Signals were processed following the procedure detailed in [47, 81, 82], thus leading to an estimation of the flame temperature at each investigated position in the diesel flame [40, 78].

4 LII signal modeling

4.1 Model description

The LII model is described in Appendix 1 of [40]. Only its main features will therefore be presented and discussed below (the reader is indeed referred to [40] for more details on the equations underlying the terms integrated within the heat and mass balance equations of laser-heated soot).

In short, the core of the model is based on the following system of coupled differential equations depicting the variations of the internal energy rate ($\frac{{dU}_{int}}{dt}$) and mass ($\frac{d{M}_{p}}{dt}$) of the particles composing soot aggregates as a function of time:

$$\left\{\begin{array}{l}\frac{{dU}_{int}}{dt}={\dot{Q}}_{abs}+{\dot{Q}}_{ann}+{\dot{Q}}_{ox}-{\dot{Q}}_{rad}-{\dot{Q}}_{th}-{\dot{Q}}_{sub}-{\dot{Q}}_{cond}\\ \\ \frac{d{M}_{p}}{dt}=\sum_{j=1}^{5} {\left(\frac{d{M}_{p}}{dt}\right)}_{sub, j}+{\left(\frac{d{M}_{p}}{dt}\right)}_{ox} , \\ \end{array}\right.$$

(2)

where t represents the time, ${\dot{Q}}_{abs}$ stands for the rate of energy gained by absorption of the laser energy, ${\dot{Q}}_{ann}$ and ${\dot{Q}}_{ox}$ depict the rates of energy production by soot annealing and oxidation, respectively, while ${\dot{Q}}_{rad}$, ${\dot{Q}}_{th}$, ${\dot{Q}}_{sub}$ and ${\dot{Q}}_{cond}$ represent the rates of energy loss by radiation, thermionic emission, sublimation and conduction. For the subscripts ‘sub’ and ‘ox’, they, respectively, denote the contributions of the sublimation and oxidation mechanisms to the mass loss, while ‘j’ stands for the contribution of each vaporized carbon cluster C_j to the particle mass loss. The governing equations standing for each of these energy rates will be briefly presented in the following. It should, however, be noted that although the expressions accounting for the different terms integrated in Eq. (2) depend on the spatial domain (x,y) delimited by the dimensions of the laser beam, the time t and the number ${N}_{p}$ of primary particles contained in soot aggregates, for the sake of clarity, the actual identification of this dependence through a “(x,y,t,${N}_{p}$)” notation will not be realized.

4.1.1 Internal energy

The rate of change of energy stored by the particles during LII is expressed considering both unannealed (subscript ‘s’) and annealed (subscript ‘a’) soot fractions (see Eq. (3)) while neglecting the possible melted fraction whose contribution has been demonstrated to be rather insignificant [51]:

$$\frac{{dU}_{int}}{dt}={N}_{p}\cdot \frac{\pi }{6}{{\cdot D}_{p}}^{3}\cdot \frac{d{ T}_{p}}{dt}\cdot \left[{\rho }_{s}{\cdot c}_{s}\cdot \left(1-{X}_{a}\right)+{\rho }_{a}\cdot {c}_{a}{\cdot X}_{a}\right].$$

(3)

The term ${X}_{a}$ in Eq. (3) denotes the soot annealed fraction (see Sect. 4.1.3), while $\rho$ and $c$ represent the particle density and specific heat, respectively, whose variation as a function of the temperature is calculated using the equations proposed in [83] for graphite, as done in [15, 51, 84].

4.1.2 Absorption

Following [51], the rate of energy change by absorption of the laser pulse was expressed as the sum of the contributions of unannealed and annealed soot fractions while considering the saturation of linear, single-photon and multi-photon absorption processes [24], as well as the effect of multiple scattering within aggregates [45]:

$${\dot{Q}}_{abs}={C}_{abs, s}^{multi}\cdot \frac{{f}_{1,s}\cdot {B}_{\lambda 1,s}}{\underset{0}{\overset{{t}_{l}}{\int }}{q}_{exp}dt}\cdot \left\{1-exp\left[-\frac{F\cdot {q}_{exp}}{{B}_{\lambda 1,s}}\right]\right\}+{C}_{abs, a}^{multi}\cdot \frac{{f}_{1,a} \cdot {B}_{\lambda 1,a}}{\underset{0}{\overset{{t}_{l}}{\int }}{q}_{exp}dt}\cdot \left\{1-exp\left[-\frac{F\cdot {q}_{exp}}{{B}_{\lambda 1,a}}\right]\right\} +{N}_{p}\cdot \frac{n\cdot h\cdot c_{l}}{{\lambda }_{l}}\cdot \left({k}_{\lambda n,s}+{k}_{\lambda n,a}\right),$$

(4)

with ${C}_{abs}^{multi}$ being the absorption cross section, ${f}_{1}$ and ${B}_{\lambda 1}$ the empirical factors related to the single-photon absorption process, ${q}_{exp}$ the normalized laser irradiance, ${t}_{l}$ and $F$ the laser pulse duration and energy density, respectively, $n$ the number of photons to be adsorbed to photodesorb C₂ clusters, $h$ the Planck constant, $c_{l}$ the speed of light and ${k}_{\lambda n}$ the rate constant for removal of C₂ clusters by photodesorption. For the absorption cross sections of unannealed and annealed soot, they were computed by integrating the MS corrective factor from [45] so that:

$${C}_{abs,s}^{multi}= {N}_{tot}\cdot \left(1-{X}_{a}\right)\cdot \frac{{\pi }^{2} {{\cdot D}_{p}}^{3} }{{\lambda }_{l}}\cdot E(m)\cdot {h}_{\lambda {,N}_{p}}{\cdot N}_{p}\cdot p\left({N}_{p}\right),$$

(5)

and

$${C}_{abs,a}^{multi}= {N}_{tot}\cdot {X}_{a}\cdot \frac{{\pi }^{2} {{\cdot D}_{p}}^{3} }{{\lambda }_{l}}{\cdot {f}_{a}\cdot E}_{a}\left(m\right)\cdot {h}_{\lambda {,N}_{p}}{\cdot N}_{p}\cdot p\left({N}_{p}\right),$$

(6)

with ${N}_{tot}$ being the aggregate number density, ${f}_{a}$ an empirical scaling factor for annealed soot [51], ${h}_{\lambda {,N}_{p}}$ the MS corrective factor whose calculation procedure is detailed in [40], and $p\left({N}_{p}\right)$ the probability density function of the aggregate size, while $E(m)$ and ${E}_{a}(m)$ stand for the absorption functions of unannealed and annealed particle fractions, respectively (the subscript ‘s’ being intentionally omitted for unannealed soot to allow consistency with the formalism generally adopted in the literature). As for the rate constants related to the photodesorption of C₂ clusters from unannealed and annealed soot fractions, they were calculated based on the following expressions:

$${k}_{\lambda n,s}=\left(1-{X}_{a}\right)\cdot \frac{{\lambda }_{l}}{n\cdot h\cdot c_{l}}\cdot \frac{{\sigma }_{\lambda n,s}\cdot \pi {{\cdot D}_{p}}^{3}{\cdot N}_{ss}}{6}\cdot \frac{{\left({B}_{\lambda n,s}\right)}^{n}}{\underset{0}{\overset{{t}_{l}}{\int }}{\left({q}_{exp}\right)}^{n}dt}\cdot \left\{1-exp\left[-{\left(\frac{F\cdot {q}_{exp}}{{B}_{\lambda n,s}}\right)}^{n}\right]\right\}$$

(7)

and

$${k}_{\lambda n,a}={X}_{a}\cdot \frac{{\lambda }_{l}}{n\cdot h\cdot c_{l}}\cdot \frac{{\sigma }_{\lambda n,a}\cdot \pi {{\cdot D}_{p}}^{3}\cdot {N}_{sa}}{6}\cdot \frac{{\left({B}_{\lambda n,a}\right)}^{n}}{\underset{0}{\overset{{t}_{l}}{\int }}{\left({q}_{exp}\right)}^{n}dt}\cdot \left\{1-exp\left[-{\left(\frac{F\cdot {q}_{exp}}{{B}_{\lambda n,a}}\right)}^{n}\right]\right\},$$

(8)

in which ${\sigma }_{\lambda n}$ stands for the multi-photon absorption cross section related to the photodesorption of C₂ clusters, ${N}_{ss}$ and ${N}_{sa}$ are the density of carbon atoms on the surface of the unannealed and annealed particle fractions, respectively, and ${B}_{\lambda n}$ denotes the saturation coefficient for multi-photon absorption.

4.1.3 Annealing

With the exception of a few works [38, 40, 51], and as highlighted in [12], annealing has seldom been considered in LII model formulations despite the significant impact that such an exothermic process may have on simulated signals, especially near and above the sublimation threshold. In short, soot particles are typically composed of graphite crystallites comprising three to ten flat graphene sheets (each of which is around 2- to 5-nm long and wide) aligned parallel to the particle surface at the outer edge and more randomly oriented near the core [85,86,87,88,89,90]. When being laser heated to temperatures above ~ 2500 K [51], primary particles may experience an exothermic annealing process, leading to significant structure modifications, including the formation of hollow carbon onions corresponding to spherical multi-shell fullerenes [85, 91,92,93,94]. These specific structures tend to result from the loss of carbon atoms from the soot surface, which enables interstitial atom and vacancy migration [51]. Furthermore, the introduction and migration of five- and seven-membered ring structures into the flat hexagonal ring structure of graphene sheets at high temperatures also contributes to the rearrangement of the primary particle structure by enhancing the curvature of the graphitic layers, thus allowing the formation of carbon onion structures with hollow cores [12]. Such a restructuration process is therefore likely to impact the soot properties (including optical ones) governing the LII phenomenon [12, 51]. This thus justifies the embedding of annealing within the simulation tool implemented herein, noting that the latter was tailored to enable the modeling of LII signals collected under widely varying experimental conditions. As such, it should thus be greatly beneficial for future works to be undertaken in the high fluence regime. Following the expression proposed in [51], the rate of energy increase by annealing was presented in equation form as follows:

$${\dot{Q}}_{ann}={N}_{p}\cdot \frac{-\Delta {H}_{imig} {\cdot k}_{imig} {\cdot N}_{d}-\Delta {H}_{vmig} \cdot {k}_{vmig} {\cdot N}_{d}}{{N}_{A}},$$

(9)

where $\Delta {H}_{imig}$ and $\Delta {H}_{vmig}$ represent the enthalpy for interstitial [95] and vacancy [96, 97] migrations, respectively, ${k}_{imig}$ and ${k}_{vmig}$ account for the interstitial and vacancy migration rates, respectively, and ${N}_{A}$ is the number of Avogadro. As for ${N}_{d}$, it stands for the number of Frenkel or Schottky defects. It is calculated by solving the following ordinary differential equation:

$$\frac{d{N}_{d}}{dt}={X}_{a}\cdot \frac{{N}_{c}}{2}{\cdot k}_{diss}-{k}_{imig}\cdot {N}_{d}-{k}_{vmig} {\cdot N}_{d},$$

(10)

where ${k}_{diss}$ represents the rate constant of pyrolysis of annealed soot, while the annealed fraction ${X}_{a}$ can be calculated as per Eq. (11):

$${X}_{a}=1-\frac{{N}_{d}}{{X}_{d} {\cdot N}_{c}},$$

(11)

with ${X}_{d}$ being the initial defect density [98] and ${N}_{c}$ the number of atoms in primary particles.

4.1.4 Oxidation

Oxidation of soot by the oxygen-containing species present in flame gases may lead to changes in the internal energy and mass of soot. Following the formulation proposed in [99], the energy rate associated with this exothermic process was expressed using the relation:

$${\dot{Q}}_{ox}={N}_{p}\cdot \frac{1 }{ {W}_{1}}\cdot \left[{\int }_{{T}_{ref}}^{{T}_{f}^{CO}}{C}_{p}^{CO}\left(T\right)dT-\frac{1}{2}\cdot {\int }_{{T}_{ref}}^{{T}_{g}}{C}_{p}^{{O}_{2}}\left(T\right)dT+\frac{R}{2}\cdot \left({T}_{f}^{CO}-{T}_{g}\right)+\Delta {H}_{ox}\right]{\cdot \left(\frac{d{M}_{p}}{dt}\right)}_{ox},$$

(12)

where ${T}_{ref}$ is a reference temperature, ${T}_{f}^{CO}$ corresponds to the temperature at which CO molecules exit from oxidizing particles, $R$ stands for the universal gas constant, and ${T}_{g}$ represents the temperature of the gaseous species surrounding soot. As far as the integrals of the heat capacities of CO (${C}_{p}^{CO}$) and O₂ (${C}_{p}^{{O}_{2}}$) are concerned, they were calculated using polynomial functions fitted based on the NIST-JANAF database [100], as was also done for the enthalpy of formation of CO ($\Delta {H}_{ox}$). For the variation of the particle mass as a function of time ${\left(\frac{d{M}_{p}}{dt}\right)}_{ox}$, it was calculated following Eq. (13):

$${\left(\frac{d{M}_{p}}{dt}\right)}_{ox}=\frac{-2\cdot \pi \cdot {{D}_{p}}^{2}\cdot {W}_{1}\cdot \left({k}_{ox,s}+{k}_{ox,a}\right)}{{N}_{A}},$$

(13)

where ${k}_{ox,s}$ and ${k}_{ox,a}$ are the oxidation rate constants of the unannealed and annealed soot fractions, respectively, whose calculation procedure is detailed in [40].

4.1.5 Radiation

The radiative emission from laser-heated soot was calculated by integrating the Planck function over the wavelength while considering the reabsorption of background emission (as done by Charwath, Michelsen or Will in [24]) and the effect of MS, through the formulation of the ${C}_{abs, a}^{multi}$ and ${C}_{abs, s}^{multi}$ terms:

$${\dot{Q}}_{rad}=8\cdot \pi \cdot h\cdot {c_{l}}^{2}\cdot \underset{0}{\overset{{\lambda }_{\infty }}{\int }}\frac{{ C}_{abs,s}^{multi}+{ C}_{abs,a}^{multi} }{{\lambda }^{5} }\cdot \left[\frac{1}{exp\left(\frac{h\cdot c_{l}}{\lambda \cdot {k}_{B}{\cdot T}_{p}}\right)-1}-\frac{1}{exp\left(\frac{h\cdot c_{l}}{\lambda \cdot {k}_{B}\cdot {T}_{g}}\right)-1}\right]d\lambda,$$

(14)

with ${k}_{B}$ being the Boltzmann constant.

4.1.6 Thermionic emission

The energy loss induced by the thermal ejection of electrons from heated particles was expressed according to the formulation proposed in [101]:

$${\dot{Q}}_{th}={N}_{p}\cdot \frac{4\cdot \left(\phi +\Delta \phi \right)\cdot {m}_{el}\cdot {\left(\pi \cdot {D}_{p}\cdot {k}_{B}\cdot {T}_{p}\right)}^{2}}{{h}^{3}}\cdot exp\left[-\frac{\left(\phi +\Delta \phi \right)}{{k}_{B}\cdot {T}_{p}}\right],$$

(15)

where $\phi$ represents a work function and m_el stands for the mass of an electron. As for $\Delta \phi$, which describes the increased barrier to further electron emission due to a positive charge buildup, it was obtained by solving the following equation at each time step $t$:

$$\Delta \phi \left(t\right)=8\cdot \pi \cdot {m}_{el}\cdot {k}_{el}\cdot {D}_{p}\cdot {\int }_{0}^{t}\frac{{\left(\pi \cdot {c}_{el}\cdot {k}_{B}\cdot {T}_{p}\right)}^{2}}{{h}^{3}}\cdot exp\left[-\frac{\left(\phi +\Delta \phi \right)}{{k}_{B}\cdot {T}_{p}}\right]dt,$$

(16)

with ${k}_{el}$ and ${c}_{el}$ being the Coulomb constant and the charge of an electron, respectively.

4.1.7 Sublimation

When being heated to temperatures around 4400 K [102], soot sublimes to produce carbon clusters including C₁ to C₅ species [24]. The loss of C_j clusters induced by the excitation of localized electronic states of soot at high fluences can, moreover, also occur through a non-thermal photodissociation of covalent bonds within primary particles [51]. These phenomena were therefore considered in the implemented sublimation sub-model which integrates the contributions of both unannealed and annealed soot fractions in the calculation of the thermal (sublimation) and non-thermal (photodesorption) vaporization rates:

$${\dot{Q}}_{sub}=-{N}_{p}\cdot \sum_{j=1}^{5} \frac{1}{{W}_{j}}\cdot {\left(\frac{d{M}_{p}}{dt}\right)}_{sub, j}\cdot \left[\frac{\Delta {H}_{j} \cdot \left({P}_{sat}^{{C}_{j}}-{P}_{\lambda s}-{P}_{diss}-{P}_{\lambda a}\right)+\Delta {H}_{\lambda n,s}\cdot {P}_{\lambda s}+\Delta {H}_{diss}\cdot {P}_{diss}+\Delta {H}_{\lambda n,a}\cdot {P}_{\lambda a}}{{P}_{sat}^{{C}_{j}}}\right],$$

(17)

where ${W}_{j}$ and $\Delta {H}_{j}$ stand for the molecular weight and the enthalpy of formation of each cluster C_j, ${P}_{sat}^{{C}_{j}}$ refers to the partial saturation pressure of vaporized carbon clusters C_j, ${P}_{\lambda s}$ and ${P}_{\lambda a}$ represent the effective pressures calculated based on the rate of non-thermal photodesorption of C_j clusters from the unannealed and annealed particle fractions, respectively, ${P}_{diss}$ denotes the effective pressure issued from the rate of thermal photodesorption from annealed soot, $\Delta {H}_{\lambda n,s}$ and $\Delta {H}_{\lambda n,a}$ are the energies required to photodesorb C_j clusters from the unannealed and annealed fractions of the particles, and $\Delta {H}_{diss}$ is the enthalpy of formation of C_j clusters by thermal sublimation of annealed soot. As far as the mass loss rate ${\left(\frac{d{M}_{p}}{dt}\right)}_{sub, j}$ is concerned, it was expressed independently for each C_j species as follows:

$${\left(\frac{d{M}_{p}}{dt}\right)}_{sub, j}=\frac{-\pi \cdot {{D}_{p}}^{2} {\cdot W}_{j} \cdot {\alpha }_{j}\cdot {B}_{j}}{{R}_{p}\cdot {T}_{p}}\cdot \sqrt{\frac{{R}_{m}{ \cdot T}_{p}}{2\cdot \pi \cdot {W}_{j}}},$$

(18)

where ${\alpha }_{j}$ stands for the mass accommodation coefficient of the C_j clusters, ${R}_{p}$ and ${R}_{m}$ correspond to the universal gas constant expressed in effective pressure and mass units, respectively, while ${B}_{j}$ allows accounting for the convective contributions to heat and mass transfers from primary particles to their surrounding atmosphere, as approximated based on the works by Bukatyi et al. [103,104,105] (see [40] for more information regarding the calculation procedures of the different terms listed above).

4.1.8 Conduction

The rate of energy loss at the surface of soot particles through collisions with surrounding gas molecules was calculated considering a Fuchs equivalent sphere modeling approach [106, 107]. This latter allows calculating the conduction rates in the free molecular (FM) and continuum (C) regimes based on the following equations:

$${\dot{Q}}_{cond,FM}=\frac{1}{8}\cdot \pi \cdot {\alpha }_{T}\cdot {{D}_{HC}}^{2}\cdot {P}_{g}\cdot \sqrt{\frac{8\cdot {k}_{B}\cdot {T}_{\delta }}{\pi \cdot {M}_{g}}}\cdot \frac{{\gamma }^{*}+1}{{\gamma }^{*}-1}\cdot \left(\frac{{T}_{p}}{ {T}_{\delta }}-1\right),$$

(19)

$${\dot{Q}}_{cond,C}=4\cdot \pi \cdot \left(\frac{{D}_{HC}}{2}+\delta \right)\cdot {\int }_{{T}_{g}}^{{T}_{\delta }}{k}_{g}\left(T\right)dT,$$

(20)

where ${\alpha }_{T}$ is the thermal accommodation coefficient, ${P}_{g}$ stands for the ambient pressure, ${M}_{g}$ represents the average mass of the gas molecules, ${\gamma }^{*}$ denotes the mean value of the heat capacity ratio, $\delta$ and ${T}_{\delta }$ correspond to the distance and temperature related to the limiting sphere separating the free molecular from the continuum regimes, ${T}_{g}$ is the surrounding gas temperature and ${k}_{g}$ stands for the heat conduction coefficient of the surrounding gas, while ${D}_{HC}$ is the equivalent heat conduction diameter [108, 109] allowing to consider the so-called shielding effect [52, 110] induced by the presence of several primary particles within aggregates. As explained in [40], heat conduction mainly operates in the free molecular regime in the diesel flame investigated herein. The Fuchs sub-model was still considered to propose a comprehensive model formulation having the potential to be easily adapted for studies conducted in high-pressure media, for instance.

4.2 Numerical procedure

The solving of the system of coupled differential equations summarized in Eq. (1) leads to an inference of the evolution of ${T}_{p}$ and ${D}_{p}$ as a function of space and time. Knowing the space- and time-dependent temperature and diameter of soot particles, theoretical LII signals were then generated by integrating the Planck function over the spectral range of the detection system, including its spectral response, as explained in [40]. For proper comparisons with measured data, simulated LII signals were also integrated over a spatial domain corresponding to the dimensions of the collection area. To that end, the experimentally monitored spatial distribution of the laser irradiance was numerically reproduced and discretized using 17 × 17 elements as validated through a grid sensitivity analysis. Theoretical signals calculated over all the dimensions of the laser beam were subsequently integrated over a 300-μm height corresponding to the dimension of the slit placed in front of the photomultiplier tube during experiments (see Sect. 3.2).

The coupled differential equations depicting the evolution of the soot temperature and mass as a function of time and space were solved using the ‘ode15s’ multistep variable order solver of MATLAB® [111]. This solver, which is particularly efficient at resolving stiff problems, was indeed found to be well adapted, considering the operating conditions investigated herein (i.e., low and intermediate fluences). The ‘ode45’ solver was also used to determine the rate of defects and annihilation needed to obtain the annealed fraction of the particles, while the ‘fsolve’ function incorporating the default ‘trust-region-dogleg’ algorithm [112] was selected to compute $\Delta \phi$ in the thermionic flux as well as the distance ($\delta$) and temperature (${T}_{\delta }$) related to the Fuchs equivalent sphere in the heat conduction term.

4.3 Model parameterization and uncertainties

The values of the parameters integrated within the governing equations accounting for the different energy fluxes described in Sect. 4.1 were set as detailed in [40]. A few variables, however, were required to be adjusted, depending on the considered excitation wavelength. These variables include the multi-photon absorption cross section for C₂ photodesorption (${\sigma }_{\lambda n,s}$), the empirical saturation coefficients for linear (${B}_{\lambda 1,s}$) and multi-photon (${B}_{\lambda n,s}$) absorption, the enthalpy required to photodesorb carbon clusters (${\Delta H}_{\lambda n,s}$) and the absorption function ($E(m)$). In fact, ${\sigma }_{\lambda n,s}$, ${B}_{\lambda 1,s}$, ${B}_{\lambda n,s}$ and ${\Delta H}_{\lambda n,s}$, which are involved in the formulations of the absorption and sublimation sub-models derived from [24, 51], were originally proposed for measurements conducted using a 532-nm laser source. Although an advanced parameterization procedure was recently proposed in [40] to estimate the values taken by these factors for a wavelength of 1064 nm, no data on the matter have been reported to date to enable the modeling of LII signals issued from the use of laser sources at 266 and 355 nm. Based on the methodology detailed in [40, 78], a model parameterization was conducted to identify adequate parameters allowing to obtain simulated signals matching measured ones for 266 and 355-nm excitation wavelengths, as well as for a 532-nm one, since the model implemented herein significantly diverges from the formulations proposed in [24, 51]. It, moreover, also differs from the model used in [57], where a different expression of the thermionic flux was used. Following [40, 57, 78], a full central composite design of experiments (DoE) was coupled with a genetic algorithm-based optimizer (the ga function of MATLAB® [112]) to identify parameter values minimizing an objective function defined as a least square sum between experimental and numerical data at different fluences. A detailed analysis of the possible uncertainties inherent in this optimization approach was proposed in [40]. Its overall consistency was nonetheless demonstrated with a view to parameterizing refined LII simulation tools, as exemplified through validations conducted against data obtained for a 1064-nm EW in methane [39], diesel [40] and ethylene [102] flames. It should finally be noted that uncertainty ranges related to each optimized parameter were estimated by considering variations of ± 23 K, ± 2.7 nm and ± 5% for ${T}_{g}$, ${D}_{p}$ and measured LII signals, respectively, as explained and commented on in [40].

5 Results and discussion

5.1 Model parameterization against data acquired at 110-mm HAB in the diesel flame

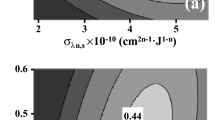
The model parameterization was realized based on data acquired at 110-mm HAB in the diesel flame. This height was selected to avoid any interference with signals originating from polycyclic aromatic hydrocarbons (PAHs), which can fluoresce upon UV and visible excitations at lower HAB in this flame [76, 77]. As far as the soot aggregate properties and thermal accommodation coefficient are concerned, they were derived from [40] (mean ${D}_{p}$ and ${N}_{p}$ of 20 nm and 139 with a ${\alpha }_{T}$ of 0.49). Following the approach proposed in [57], DoEs were first built to find suitable $E(m)$ and ${\sigma }_{\lambda n,s}$ values by defining an objective function based on a minimization of the least square sum between numerical and experimental fluence curves below the sublimation thresholds (i.e., the threshold above which the LII response tends to show a lack of fluence dependence). Other unknown parameters were not considered at this stage as they do not truly impact the increasing section of the fluence curves (see [40]). Obtained DoE response surfaces, plotted in Fig. 1, show that optimized $E(m)$ of ⁓0.52, ⁓0.36 and ⁓0.31 and ${\sigma }_{\lambda n,s}$ of ⁓7.8 × 10^–9, ⁓4.8 × 10^–9 and ⁓8.6 × 10^–10 cm²ⁿ⁻¹·J¹⁻ⁿ can be estimated for EWs of 266, 355 and 532 nm, respectively (results obtained for a 1064-nm laser source not represented as they are already detailed in [40]).

Fig. 1

DoE response surfaces for $E\left(m\right)$ and ${\sigma }_{\lambda n,s}$ in the case of EWs of: a 266 nm, b 355 nm and c 532 nm. Values depicted on the graphs (expressed in arbitrary unit (a.u.)) are representative of the least square sum between experimental and numerical LII signals

The parameterization was then completed by running the genetic algorithm-based optimizer while defining a minimization function based on a least square sum between experimental and numerical data, considering the whole lifetime of the LII time decays obtained at each investigated fluence for each wavelength (see [40] for more details regarding the optimization procedure). To that end, intervals of ± 15% around the optimum values found above for $E(m)$ and ${\sigma }_{\lambda n,s}$ were set. As for the other parameters (i.e., ${B}_{\lambda 1,s}$, ${B}_{\lambda n,s}$ and ${\Delta H}_{\lambda n,s}$), preliminary results issued from DoEs based on the above objective function (i.e., minimization of the least square sum between numerical and experimental LII time decays) led to the identification of the following global constraints: 0.2 J·cm⁻² < ${B}_{\lambda 1,s}$  < 0.8 J·cm⁻², 0.1 J·cm⁻² < ${B}_{\lambda n,s}$  < 0.8 J·cm⁻², and 6.1 × 10⁵ J·mol⁻¹ < ${\Delta H}_{\lambda n,s}$  < 15.0 × 10⁵ J·mol⁻¹ at 266 nm, 3.4 × 10⁵ J·mol⁻¹ < ${\Delta H}_{\lambda n,s}$  < 10.0 × 10⁵ J·mol⁻¹ at 355 nm and 1.7 × 10⁵ J·mol⁻¹ < ${\Delta H}_{\lambda n,s}$  < 5.0 × 10⁵ J·mol⁻¹ at 532 nm. By considering a population of 20 individuals, it was found that around 150 generations was sufficient to reach the tolerance constraint set to 10^–4 as in [40, 57]. As such, the optimized parameters summarized in Table 1 were assessed. Results previously obtained in [40] for a 1064-nm wavelength are also reported therein for comparison and completeness.

Table 1 Optimized values of $E(m)$, ${\sigma }_{\lambda n,s}$, ${B}_{\lambda 1,s}$, ${B}_{\lambda n,s}$ and ${\Delta H}_{\lambda n,s}$ inferred for wavelengths of 266, 355, 532 and 1064 nm with their respective uncertainties

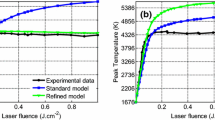
As can be seen from Fig. 2, the use of the parameters listed in Table 1 allows obtaining modeled fluence curves that adequately reproduce their experimental counterparts, regardless of the considered excitation wavelength.

Fig. 2

Measured and simulated fluence curves obtained at 110-mm HAB in the diesel flame for 266-, 355-, 532- and 1064-nm excitation wavelengths. Note that ‘Peak LII signal’ refers to the maximum of the LII temporal profiles

For LII time decays, predicted and measured signals are compared in Fig. 3 for EWs of 266, 355 and 532 nm (data obtained at 1064-nm not reported as they are already provided in [40]). To obtain plotted curves, laser fluences allowing to obtain roughly identical measured and simulated LII signals at the three considered wavelengths were selected (e.g., 0.018 J·cm⁻² at 266 nm for 0.029 J·cm⁻² at 355 nm and 0.05 J·cm⁻² at 532 nm, as exemplified by the arrows plotted in Fig. 2). Here again, obtained results illustrate that the refined model integrating the optimized parameters summarized in Table 1 allows predicting LII signals matching measured ones.

Fig. 3

Measured and simulated LII time decays obtained at 110-mm HAB in the diesel flame for different laser fluences using excitation wavelengths of a 266, b 355 and c 532 nm. For clarity, only a few points are plotted in measured LII time decays

We still performed complementary analyses to rule on the validity of inferred parameters. First, and looking further at the obtained results, it is noteworthy that identical $E(m)$ are obtained at 532 and 1064 nm, which agrees with the overall trend reported in Sect. 2 [23, 47, 53, 54, 72]. Furthermore, and although being discussed more particularly in Sect. 5.3, the fact that the $E(m)$ increases when decreasing the excitation wavelength from 532 to 266 nm is also in line with the results reported in previous works [31,32,33, 53, 54, 72]. As can be seen from the ${B}_{\lambda 1,s}$, ${B}_{\lambda n,s}$ values reported in Table 1, the lower the wavelength, the lower the empirical saturation coefficients for linear and multi-photon absorption, which is consistent with the fact that the lower the wavelength, the lower the fluence for which the LII response plateaus (above ⁓0.04, ⁓0.06, ⁓0.11 and ⁓0.22 J·cm⁻² at 266, 355, 532 and 1064 nm, respectively (see Fig. 2)). This is, moreover, consistent with the fact that the shorter the wavelength, the higher the absorption cross section, as confirmed by the values of ${C}_{abs}^{multi}$ calculated in the present work based on Eqs. (5) and (6). Since the absorption cross section is integrated in ${\dot{Q}}_{abs}$, as is ${\sigma }_{\lambda n,s}$, which increases with decreasing excitation wavelengths, the parameters reported in Table 1 therefore seem to be physically relevant as they coherently explain why the plateau region of the fluence curves is reached sooner when decreasing the EW. One can further add that the fact that the saturation coefficients estimated at 532 nm are lower than their counterparts assessed for a 1064-nm EW is in line with the observations in [85]. As far as ${\Delta H}_{\lambda n,s}$ is concerned, the value inferred for a 532-nm laser source diverges somewhat from those previously reported in [24, 57]. This can be explained by the fact that we used the formulation from Mitrani et al. [101] for the thermionic flux instead of the one proposed by Michelsen in [24], as was done in [57]. As a consequence, and as explained in [40], a reduced thermionic flux is computed. Consequently, fulfilling the energy balance allowing to reproduce measured signals implies compensating for the ${\dot{Q}}_{th}$ reduction through the intensification of other energy losses originating from sublimation (through the contribution of non-thermal photodesorption of C₂ clusters) and conduction (through an increase of the thermal accommodation coefficient, which was set to 0.49 (as in [40]), versus 0.47 in [57]).

In a bid to further validate the consistency of the inferred parameters, the values reported in Table 1 for ${\sigma }_{\lambda n,s}$, ${B}_{\lambda 1,s}$, ${B}_{\lambda n,s}$ and ${\Delta H}_{\lambda n,s}$ were also implemented to simulate LII fluence curves issued from another experimental database. To that end, the comprehensive dataset from Goulay et al. [102] was used as was previously done in [40, 73]. These LII signals were measured in a laminar diffusion flame of ethylene using the 1064- or 532-nm output from an injection-seeded Nd:YAG laser providing pulses with a smooth temporal profile, together with spatially homogeneous beams. As shown in Fig. 4, a good agreement between measured and simulated fluence curves is obtained at both 1064 nm and 532 nm when setting the soot absorption function to 0.31, as was done in [40]. The good match between simulated and measured data for the IR EW was already presented and commented on in [40]. On the other hand, it is noteworthy that the parameterized model implemented in this work still allows predicting signals measured by Goulay et al. when using a 532-nm laser source, although no effort was expended on trying to adjust the model inputs to better fit experimental results from [102]. Here again, reproducing measured data implies setting identical $E(m)$ values at 532 and 1064 nm, which is consistent with the trend reported in Sect. 2, as well as with the above results obtained during the analysis of the diesel flame. No further validations were, however, possible at 266 and 355 nm due to a relative lack of available datasets for such EWs.

Fig. 4

Comparison of model predictions with LII fluence curves measured in [102]. Note that ‘Peak LII signal’ refers to the maximum of the LII temporal profiles

In conclusion, the refined model which has been parameterized herein allowed to properly simulate LII signals measured at 266, 355, 532 and 1064 nm in a diesel flame as well as fluence curves experimentally monitored with 532- and 1064-nm EWs in the ethylene flame characterized in [102]. While being encouraging, it is important to note that this research does not claim to propose a model as well as parameters that should be considered as universally valid. This was notably explained in [40], where a critical analysis dealing with the uncertainties encompassing the implemented model formulation and the related parameterization procedure was proposed. As an example, it is noteworthy that the effect of aggregation was considered solely within the absorption and conduction terms. The absence of adapted sub-models integrating these effects in the other energy fluxes embedded within the energy and mass balance equations thus represents a potential limitation of the proposed simulation tool. Furthermore, in this work, the emphasis is mainly on the low and intermediate fluence regimes (as exemplified in Fig. 3). We thus did not put any specific effort into optimizing parameters embedded within the governing equations representing the annealing flux, as explained in [40]. It was especially noted therein that the annealed soot fraction for an EW of 1064 nm was relatively limited at low and intermediate fluences (less than 0.1 over the laser pulse duration when considering a fluence of the order of 0.1 J·cm⁻² for instance), thus inducing limited impacts on the temporal evolution of ${T}_{p}$ and ${D}_{p}$. Of course, the values considered for the absorption function of annealed soot at each EW (issued from the wavelength-dependent expression provided in [51]), are likely to impact the results obtained, especially for LII signals generated at high fluences. This would thus prompt the need for complementary investigations aimed at extending the validity domain of the proposed model, although being out of the scope of this preliminary study. Among the other uncertainty sources likely to impact the results obtained in this paper, there are the values considered in order to represent some soot properties. For instance, selecting the particle density and specific heat issued from [113] instead of those proposed in [83] is likely to modify the direct model predictions and in turn the values of the parameters inferred by inverse calculations. A rapid comparison of the soot absorption functions derived for EWs of 532 and 1064 nm, whether taking into account the parameters from [83] or [113], however, led to estimated variations in the inferred $E(m)$ globally falling within the mean uncertainty range related to this parameter (i.e., ± 5% on average, based on the values reported in Table 1 for each EW). As a consequence, and although the selection of $\rho$ and $c$ values needs to be further assessed in our future works, the above observation tends to illustrate that the assumption we made in Sect. 4.1.1 with respect to these soot properties should not induce major errors in the results reported throughout this section. Finally, one should add that the use of the extended RDG-FA formulation from [45] is also subject to certain limitations, as the parameters proposed therein were set on the basis of typical combustion-generated soot characterized by a fractal dimension of ⁓1.7 and refractive indexes derived from measurements carried out at a relatively high HAB in the diesel flame studied in the present paper [53]. Consequently, and although the generalized structure factor function from [45] was used in [72] to process data obtained at low HAB in the methane/oxygen/nitrogen premixed flat flame from [39], where soot was considered as “immature” [72], caution should nonetheless be exercised when interpreting the $E\left(m\right)$ values assessed at low HAB in the diesel flame. Indeed, the refractive index of young soot typically differs from that of more mature particles, which can affect the magnitude of the MS effect [46]. With these restrictions in mind, the consistency of the parameterization achieved in this work was further assessed against data collected at other HAB in the diesel flame.

5.2 Modeling LII signals measured at different HAB in the diesel flame with 266-, 355-, 532- and 1064-nm excitation wavelengths

As explained at the beginning of Sect. 5.1, laser-induced fluorescence (LIF) signals can coexist with soot LII at low HAB in the diesel flame due to the presence of PAHs [53, 54, 76, 77]. The duration of the LIF signals is, however, of the order of ⁓40 ns, while LII time decays typically extend over several hundreds of ns [53]. As a consequence, laser-induced emissions (LIE) collected using UV or visible EWs can correspond to the superposition of both soot LII and PAH LIF during the first 40 ns following laser irradiation. Alternatively, LIE above 40 ns will be solely assignable to soot LII. Based on these temporal features, LII signals obtained using an IR laser source can be compared with signals issued from the use of UV or visible EWs, for instance, even in the presence of PAHs, by considering the portions of the LIE time decays measured above 40 ns, as was done in [53]. Following a similar approach, the consistency of our parameterized model was assessed by comparing simulated LII signals with measured LIE for t > 40 ns at HAB of 55 and 92 mm when using EWs of 266, 355 and 532 nm. To perform the calculations, all the parameters listed in Table 1 were kept constant, with the exception of the soot absorption function, which was adjusted as a function of the HAB (i.e., the soot maturation stage). It was indeed demonstrated in [40] that the $E(m)$ was the sole parameter needing to be adjusted as a function of the HAB for heights between 55 and 116 mm in the diesel flame. Of course, the values reported in [40] for the soot size and the number of primary particles in the aggregates at 55- and 92-mm HAB were considered as inputs. As shown in Fig. 5, which compares modeled signals with LIE experimentally monitored at 55-mm HAB using laser sources of 355 and 532 nm as examples, an excellent fit is obtained between measured and predicted signals for t > 40 ns, provided that the $E(m)$ is set to 0.20 and 0.18 at 355 and 532 nm, respectively.

Fig. 5

Measured LIE and simulated LII time decays obtained at 55-mm HAB in the diesel flame using excitation wavelengths of: a 355 and b 532 nm with fluences of 0.029 and 0.05 J·cm⁻², respectively. The insets correspond to a zoom-in on the time domain extending from 40 to 400 ns

In a bid to find suitable $E(m)$ values for each investigated HAB and EW, the genetic algorithm-based optimizer implemented in Sect. 5.1 was used. To that end, an objective function aimed at minimizing the least square sum between experimental and numerical LII time decays for 50 ns < t < 400 ns and fluences between 0 and 0.2 J·cm⁻² was defined. $E(m)$ values of 0.25, 0.20 and 0.18 were then inferred at 55-mm HAB for EWs of 266, 355 and 532 nm, respectively, against 0.36, 0.28 and 0.23 at 92-mm HAB. Parameterizing the model with these $E(m)$ together with the values reported in Table 1 for the other parameters led to the obtention of the simulated fluence curves reported in Fig. 6 (data previously obtained in [40] with an EW of 1064 nm also being depicted for completeness). Theoretical signals are compared therein with their experimental counterparts where feasible (i.e., in the absence of PAH LIF). In addition, the evolution of the LII intensity 50 ns after the first photons of the laser are emitted (i.e., delayed detection) is also plotted as a function of the fluence and compared with measured results for each EW in the insets of Fig. 6. It is reiterated here that the emphasis is on the increasing section of the fluence curves since the present work only focuses on the low-to-intermediate fluence regime, as explained in Sects. 2.3 and 5.1.

Fig. 6

Comparison between simulated (curves) and measured (symbols) evolution of the maximum of the LII temporal profiles (referred to as “peak LII signal”) as a function of the fluence at: a 55 mm-HAB and b 92-mm HAB in the diesel flame for 266- (light gray), 355- (middle gray), 532- (dark gray) and 1064-nm (black) excitation wavelengths. The insets depict the evolution of simulated and measured LII intensity assessed 50 ns after the first photons of the laser are emitted (i.e., delayed detection) for each investigated excitation wavelength

As can be seen, simulated fluence curves reproducing their experimental counterparts are obtained for a 1064-nm EW regardless of the HAB, as already shown in [40]. In addition, Fig. 6b also shows that a good match is obtained for a 266-nm EW at 92-mm HAB (where no more PAHs capable of fluorescing at this EW are present, as exemplified in [53, 76]). Looking at the insets of Fig. 6, which compare the intensity of LIE obtained with a 50-ns delayed detection (thus corresponding to LII signals free of PAH LIF), a good agreement is, here again, obtained between simulated and measured data. All these observations thus tend to corroborate the overall validity of our parameterized model formulation, whose use especially allowed inferring $E(m)$ values at different HAB in the diesel flame and for different EWs, as will be discussed in Sect. 5.3. The obtained results must, however, be considered with caution due to the assumptions made during the modeling process. For instance, and in addition to the possible limitations identified in Sect. 5.1, the fact that the multi-photon absorption cross sections for C₂ photodesorption were kept constant for HAB between 55- and 110 mm-HAB could be questioned since we notably demonstrated in [40] that it was necessary to adjust this parameter in order to properly reproduce LII signals measured at 1064 nm in the atmospheric methane/oxygen/nitrogen premixed flat flame from [39]. This was particularly true at low HAB, where soot typically undergoes significant internal structural changes as a function of its growing stage. On the other hand, it was still demonstrated in [40] that a constant multi-photon absorption cross section was assessed above 11-mm HAB in this methane flame, where soot exhibits ${D}_{p}$ values close to 10 nm. The ${\sigma }_{\lambda n,s}$ value estimated above 11-mm HAB was, moreover, identical to that inferred for HAB ≥ 55 mm in the diesel flame studied in the present work, for which ${D}_{p}$ ≥ 8 nm. This trend could thus be traced to the fact that soot then reaches a relatively similar aging stage, thus corroborating the relevance of considering constant absorption cross sections at 55- and 110-mm HAB, as we did. To delve deeper into the validity of the results obtained, an analysis of the effect of the aggregate properties, soot maturity and the wavelength on inferred $E(m)$ values is proposed below based on comparisons with results from the literature.

5.3 Evolution of the soot absorption function as a function of aggregate properties, soot maturity and wavelength

5.3.1 Evolution of the ${\varvec{E}}({\varvec{m}})$ and ${\varvec{E}}({\varvec{m}},{\varvec{\lambda}})$/${\varvec{E}}({\varvec{m}},1064)$ ratio values as a function of aggregate properties

The $E(m)$ estimated in the present work for each EW and HAB are summarized in Table 2, together with the values of the ensuing $E(m,\lambda )$/$E(m,1064)$ ratios. Reported values notably include results obtained from calculations performed whether considering (‘MS’) or neglecting (‘${N}_{p}$ = 1’) the multiple scattering within aggregates to highlight the impact of MS on the estimated $E(m,\lambda )$. As can be seen, on average, ⁓25% higher $E(m)$ values are obtained at 55-mm HAB when neglecting the multiple scattering within soot aggregates. This trend is in line with the observation in [40], where the effect of MS on the $E(m)$ assessment was evaluated for an EW of 1064 nm. It is, however, noteworthy that the orders of magnitude of the $E(m)$ variation due to the effect of multiple scattering are relatively close, regardless of the wavelength at 55-mm HAB, which is consistent with the values of the MS corrective factor (${h}_{\lambda {,N}_{p}}$) computed at this specific height, for which ${N}_{p}$ = 60 [40] (see Fig. 7a).

Table 2 $E(m,\lambda )$ and $E(m,\lambda )$/$E(m,1064)$ ratios obtained for HAB of 55, 92 and 110 mm whether neglecting (${N}_{p}$ = 1) or considering (MS) the multiple scattering within aggregates

Fig. 7

Evolution of the multiple scattering corrective factor (${h}_{\lambda {,N}_{p}}$) as a function of the number of particles per aggregate (${N}_{p}$) and wavelength at HAB of: a 55 mm, b 92 mm, and c 110 mm

Furthermore, the effect of MS also remains globally similar, regardless of the HAB for EWs of 532 and 1064 nm, with a mean reduction of the $E(m)$ values of ⁓25%. Alternatively, the impact of MS significantly decreases as a function of the height in the flame for EWs of 266 and 355 nm. The $E(m)$ drop indeed goes from ⁓14 to ⁓4% at 266 nm, versus ⁓21 to ⁓16% at 355 nm when the HAB goes from 92 to 110 mm, respectively. Here again, this trend is in line with the evolution of the ${h}_{\lambda {,N}_{p}}$ values for ${N}_{p}$ > 100, which are significantly reduced for UV EWs, as depicted in Fig. 7b and c.

Looking at the $E(m,\lambda )$/$E(m,1064)$ ratios in Table 2, one can first note that neglecting the effect of MS leads to the estimation of constant $E(m,266)$/$E(m,1064)$, $E(m,355)$/$E(m,1064)$ and $E(m,532)$/$E(m,1064)$ values (i.e., 1.4, 1.2 and 1.0, respectively), regardless of the HAB. The obtained results are, moreover, globally similar to those previously estimated by TEW-LII in [53, 54], where no variation of the $E(m,\lambda )$/$E(m,1064)$ ratios as a function of the HAB was reported as well. Furthermore, it was shown in [53, 54] that the $E(m,\lambda )$/$E(m,1064)$ ratios could be estimated by multiplying the values of the fluences used to plot the fluence curves at any given wavelength $\lambda$ by a translation factor (TF = $1064/\lambda \cdot E(m,\lambda )/E(m,1064)$ [53]) in order to obtain identical evolutions of the peak LII signals as a function of the fluence for EWs of $\lambda$ and 1064 nm. Proceeding as such with the fluence curves simulated herein leads to the results reported in Fig. 8 for HAB of 55 and 92 mm, as examples. As can be seen, setting TF to 5.6, 3.5 and 2.0 for $\lambda$ = 266, 355 and 532 nm, respectively, allows obtaining fluence curves matching the one obtained for a 1064-nm EW, considering a ± 5% uncertainty range, as depicted by the error bars plotted in Fig. 8. Values of 1.4, 1.2 and 1.0 can thus be inferred for the $E(m,266)$/$E(m,1064)$, $E(m,355)$/$E(m,1064)$ and $E(m,532)$/$E(m,1064)$ ratios, in agreement with the results gathered in Table 2. This is actually consistent with what would be anticipated since the theoretical background underlying the TEW-LII technique does not take the effect of MS into account. Applying the translation factor approach proposed in [53, 54] therefore logically leads to results in line with those obtained by LII modeling when neglecting multiple scattering. On the other hand, the $E(m,\lambda )$/$E(m,1064)$ ratios tend to increase significantly with the HAB for UV EWs when considering the effect of MS (see Table 2). The ratios obtained notably increase from 1.4 to 1.7 and from 1.1 to 1.3 for $\lambda$ = 266 and 355 nm, respectively, when the HAB goes from 55 to 110 mm. This thus illustrates the importance of thoroughly considering the aggregate properties when attempting to derive the evolution of the wavelength-dependent absorption function of soot. The results summarized in Table 2 finally show that for EWs in the UV, the $E(m,\lambda )$/$E(m,1064)$ ratio increases with decreasing wavelengths, while for visible and IR EWs, the wavelength dependence of the $E(m,\lambda )$/$E(m,1064)$ ratios vanishes, in agreement with the conclusions drawn in [72] (see Sect. 5.3.3 for related complementary information).

Fig. 8

Simulated evolution of the peak LII signal as a function of the fluence at: a 55-mm HAB and b 92-mm HAB in the diesel flame for 266-, 532-, 355- and 1064-nm excitation wavelengths. The values of the fluence used to plot the curves obtained at 266, 355 and 532 nm were multiplied by the translation factors TF, whose values are specified in the chart legends. Note that ‘Peak LII signal’ refers to the maximum of the LII temporal profiles

5.3.2 Evolution of the ${\varvec{E}}({\varvec{m}})$ and ${\varvec{E}}({\varvec{m}},{\varvec{\lambda}})$/${\varvec{E}}({\varvec{m}},1064)$ ratio values as a function of soot maturity

In a previous work dealing with LII signal modeling, we plotted the evolution of the $E(m,1064)$ of diesel soot as a function of an adimensional normalized flame height (HAB/HAB_max) used to account for soot aging [40]. In a bid to complement the preliminary analysis proposed in [40], in Fig. 9, we plotted the variation of the $E(m,\lambda )$ inferred considering or neglecting the effect of MS as a function of the HAB/HAB_max ratio for EWs of 266, 355, 532 and 1064 nm. The results obtained were, moreover, compared with a series of $E(m,\lambda )$ values issued from [34, 35, 37, 39, 40, 72, 114, 115] for different soot maturation stages.

Fig. 9

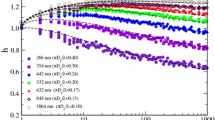
$E(m,\lambda )$ evolution as a function of soot maturity. Comparison of results obtained in the present work with data issued from [34, 35, 37, 39, 40, 72, 114, 115]. Of note, the $E(m,\lambda )$ from Henriksen et al. were derived from the values of the real and imaginary parts of the refractive index reported in [114], while results from Johansson et al. were calculated by integrating the ξ and β depicted in Fig. 2a of [115] into the wavelength-dependent formulation of $E(m,\lambda )$ proposed in Eq. (2) therein

The variation of the $E\left(m,1064\right)$ of diesel soot as a function of the adimensional normalized flame height has already been commented on in [40]. That said, it should still be noted that the data plotted in Fig. 9 show a continuous increase of the $E\left(m,1064\right)$ as a function of soot aging, regardless of the considered study, with values ranging from ⁓0.16 [114] to ⁓0.24 [115], for young particles, versus ⁓0.37 [39] to ⁓0.48 [115], for more mature ones. Relatively widely varying $E\left(m,1064\right)$ values are thus derived from one study to another, depending on the soot maturation level. It is nonetheless noteworthy that the upper range of $E\left(m,1064\right)$, which globally matches the soot absorption functions assessed in [34, 37, 115], corresponds to results issued from calculations performed without considering the effect of MS [40]. Alternatively, the lower range of $E\left(m,1064\right)$ values (with the exception of the data from [35, 114]) mainly includes values obtained from simulations conducted while considering the multiple scattering within aggregates [40, 72]. Here again, this illustrates the crucial role played by the aggregate properties, which may tend to account for a large part of the discrepancies reported in published studies with respect to the soot absorption function.

As for $E\left(m,532\right)$ and $E\left(m,1064\right)$ estimated in Sect. 5.3.1 (see Table 2), they are superimposed in Fig. 9, in agreement with the results from [72]. Alternatively, the soot absorption functions assessed in [115] for EWs of 532 and 1064 nm are higher than those calculated herein and in [40], respectively, when neglecting the effect of MS. The data from [115], moreover, show a slight increase (⁓6.5% on average) of the $E(m,\lambda )$ values when the EW goes from the visible (i.e., 532 nm) to the IR (i.e., 1064 nm) for HAB/HAB_max > 0.45. This contrasts with the results we obtained, as well as with data and conclusions from [23, 53, 54, 72], who evidenced no significant variation of the soot absorption function for EWs between 532 and 1064 nm. Furthermore, Fig. 9 also shows that the evolution of the $E\left(m,532\right)$ and $E\left(m,1064\right)$ values as a function of the soot maturation stage is quite similar in [72] and in our works (the effect of MS being considered in each case), although in [72], methane, not diesel, was considered as a fuel. Similarly, [34, 37, 40] depict identical $E\left(m,1064\right)$ evolutions as a function of HAB/HAB_max when neglecting the multiple scattering within aggregates, although ethylene, methane and diesel were considered as fuels in these different studies. This therefore tends to highlight the importance of the soot maturity stage over the nature of the burned fuel, as previously suspected in [40]. It is, however, noteworthy that we inferred an $E\left(m\right)$ of 0.30 at 110-mm HAB for EWs of 532 and 1064 nm (see Table 2) although [23] concluded that the absorption function of freshly emitted and aged black carbon should be between 0.32 and 0.40 in the visible and near infrared (see Sect. 2.1). While being quite close to this specific range of values, the $E\left(m,532\right)$ and $E\left(m,1064\right)$ we found still fall below the lower limit recommended in [23]. In an attempt to interpret this discrepancy, we explored different avenues, in addition to the potential influence of the uncertainty sources and model limitations already discussed in Sect. 5.1. First, it is noteworthy that the range of plausible $E\left(m\right)$ values from [23] was derived from the processing of a series of data issued from the literature. With the exceptions of the work from [43], who analyzed soot issued from a laminar flame of kerosene and [116], who investigated kerosene and diesel flames generated by means of a wick lamp, the majority of the studies considered in [23] are based on experiments conducted in laminar flames of gaseous fuels. The combustion conditions encountered in the turbulent spray flame of diesel studied herein therefore differ significantly from those associated with the reacting media from which the data used in [23] are taken. Soot may have thus experienced a different aging process influencing its properties, including optical ones, noting that the refractive index of different soot samples can indeed vary substantially due to variations in the microstructure and composition of the particles. Furthermore, it should be noted that soot produced at low HAB in the diesel flame (below 92 mm) is quite young. It then undergoes a growth process that extends beyond 110 mm HAB, as illustrated in [40] where an $E\left(m,1064\right)$ of 0.31 was inferred for a HAB/HAB_max of ⁓0.6 (no higher HAB having been probed to assess the optical properties of more mature soot, however). As a consequence, and considering the uncertainty of ± 5% related to the estimation of the soot absorption function (see Sect. 5.1), an upper plausible value of 0.33 is obtained for $E\left(m,1064\right)$, which is consistent with the range of $E\left(m\right)$ recommended in [23]. It can finally be noted that the soot absorption functions assessed for EWs of 266 and 355 nm increase with increasing HAB/HAB_max ratios, as was the case for $\lambda$ = 532 and 1064 nm. $E\left(m,266\right)$ and $E\left(m,355\right)$ values are, however, significantly higher than those inferred at 532 and 1064 nm, notably when neglecting the effect of MS, as shown in Fig. 9. It can further be observed that the results obtained herein and in [72] depict a similar evolution of the soot absorption functions at 266 and 355 nm as a function of HAB/HAB_max, with identical $E\left(m,266\right)$ and $E\left(m,355\right)$ values for young (HAB/HAB_max < ⁓0.4) and more mature (HAB/HAB_max > ⁓0.5) soot. The fact that the results we obtained by LII modeling are consistent with the main trends reported in the literature contributes to illustrate the overall consistency of the $E(m,\lambda )$ values listed in Table 2 as well as the relevance of the methodology we implemented for assessing the soot absorption function.

5.3.3 Evolution of the ${\varvec{E}}({\varvec{m}})$ and ${\varvec{E}}({\varvec{m}},{\varvec{\lambda}})$/${\varvec{E}}({\varvec{m}},1064)$ values as a function of the wavelength

To conclude this study, the relative and absolute evolutions of the soot absorption function are reported as a function of $\lambda$ in Fig. 10. To that end, $E(m,\lambda )$ values estimated in Sect. 5.3.1 are plotted alongside results issued from [29, 31,32,33, 40, 47,48,49, 53, 54, 72, 115] for comparison.

Fig. 10

Evolution of: a the relative and b the absolute $E(m,\lambda )$ values as a function of wavelength. Comparison of results obtained in the present work with data issued from [29, 31,32,33, 40, 47,48,49, 53, 54, 72, 115]. Note that when different $E(m,\lambda )$ are proposed for a given $\lambda$ depending on the soot maturity level, the range of reported values is highlighted by error bars ([72, 115] in a and b as well as in the present work for ${N}_{p}$ = 1 in b) and/or a gray area (this work for MS). Note that the gray area and the thick black error bars in b include the $E(m,\lambda )$ values inferred, whether considering or neglecting the effect of MS, at 116-mm HAB in [40]. These values are considered constant in the visible and near infrared, and their plot in b includes the ± 5% uncertainty range related to the estimation of the soot absorption function

Contrary to the results from [29, 49], which indicate a continuous increase of the $E(m,\lambda )$/$E(m,1064)$ ratio from the UV to the IR (see Fig. 10a), the values estimated in Sect. 5.3.1 decrease for 266 nm < $\lambda$  < 532 nm, in agreement with the trend reported in [31,32,33, 48, 53, 54, 72], before plateauing between the visible and the IR, which agrees with the results from [23, 33, 47, 48, 53, 54, 72]. The wavelength for which the soot absorption function peaks, as well as the absolute $E(m,\lambda )$ values, however, diverge significantly from one study to another, as exemplified in Fig. 10. In that regard, the results obtained in the present work, whether considering or neglecting the effect of MS, fall in the middle range of $E(m,\lambda )$ values commonly reported in the literature, as shown in Fig. 10b. It is, moreover, noteworthy that the gray region, which encompasses the soot absorption functions we assessed for EWs between 266 and 1064 nm as a function of the soot maturation stage, globally covers the $E(m,\lambda )$ reported in [31, 32, 48, 53], while also being in line with the data from [72], despite the use of widely varying fuels (methane [72], acetylene [31], propane [31, 48], diesel [40, 53]). To conclude, the gray area depicted in Fig. 10b (which includes the ± 5% uncertainty range estimated in Sect. 5.1) indicates that considering $E(m,\lambda )$ values of 0.38 ± 0.15 and 0.29 ± 0.11 at 266 and 355 nm, versus 0.25 ± 0.09 at 532 and 1064 nm, can be regarded as a reasonable option for modeling LII signals from diesel soot particles ranging from young to more mature ones.

6 Conclusion

This work covered the modeling of an extensive set of LII signals measured in a diesel spray flame with EWs of 266, 355 and 532 nm. To that end, we implemented a refined model integrating terms representing the saturation of linear, single- and multi-photon absorption processes, cooling by sublimation, conduction, radiation and thermionic emission, in addition to mechanisms depicting soot oxidation and annealing, non-thermal photodesorption of carbon clusters, together with corrective factors allowing to consider the shielding effect and multiple scattering (MS) within aggregates. A complete parameterization of this simulation tool was realized using an advanced optimization procedure coupling design of experiments with a genetic algorithm-based solver. Doing so allowed deriving soot optical properties and empirical factors (including the multi-photon absorption cross sections for C₂ photodesorption and the saturation coefficients for linear- and multi-photon absorption, among others), whose values have never been reported for UV EWs in LII modeling studies, to the best of the authors’ knowledge. While satisfactorily reproducing measured data at each considered wavelength for different HAB in the diesel flame, the proposed model also proved to be well suited to simulate LII fluence curves measured with EWs of 532 and 1064 nm in a diffusion ethylene flame previously characterized in [102]. To summarize, the following findings were highlighted:

• The implemented parameterization procedure led to the inference of ${\sigma }_{\lambda n,s}$ values ranging from 8.78 × 10^–9 to 7.60 × 10^–10 cm²ⁿ⁻¹·J¹⁻ⁿ, ${B}_{\lambda 1,s}$ and ${B}_{\lambda n,s}$ falling between 0.27 and 0.58 versus 0.18 and 0.35 J·cm⁻², respectively, and ${\Delta H}_{\lambda n,s}$ between 8.49 × 10⁵ and 2.21 × 10⁵ J·mol⁻¹ for EWs going from 266 to 532 nm. As far as the soot absorption function is concerned, $E\left(m,266\right)$, $E(m,355)$ and $E(m,532)$ values ranging from 0.25 to 0.51, 0.20 to 0.38 and 0.18 to 0.30, respectively, were estimated for HAB between 55- and 92-mm HAB (i.e., depending on the particle maturation degree).

• Neglecting the effect of multiple scattering within aggregates enabled inferring significantly higher absorption functions, with values ranging from 0.31 to 0.53, 0.26 to 0.44 and 0.22 to 0.38 for $E\left(m,266\right)$, $E(m,355)$ and $E(m,532)$, respectively.

• By comparing the results obtained in this work with a series of $E\left(m,\lambda \right)$ values issued from past studies, it was shown that the lower and upper ranges of absorption functions commonly reported in the literature globally match results issued from calculations performed either considering or neglecting the effect of MS. This observation illustrated the importance of thoroughly taking aggregate properties into account when assessing soot optical properties, as these latter are likely to account for a large part of the $E\left(m,\lambda \right)$ variability observed in the literature.

• As previously noted in [40], the $E\left(m,\lambda \right)$ evolution as a function of soot maturity was found to be relatively similar in the present work and in [34, 37] when neglecting the effect of MS, despite the use of different fuels (diesel, methane and ethylene). Similarly, we noted an $E\left(m,\lambda \right)$ evolution quite close to that reported in [72] for EWs of 266, 355, 532 and 1064 nm, when considering the multiple scattering within aggregates, although methane was used in [72] instead of diesel. These results therefore tends to show the greater significance of the soot maturity level over the nature of the burned fuel.

• Neglecting MS led to an estimation of constant $E(m,266)$/$E(m,1064)$, $E(m,355)$/$E(m,1064)$ and $E(m,532)$/$E(m,1064)$ ratios, regardless of the HAB, with values of 1.4, 1.2 and 1.0, respectively, which agrees with the results reported in [53, 54]. Alternatively, considering the effect of MS significantly increased the $E(m,\lambda )$/$E(m,1064)$ ratios for EWs in the UV at high HAB (i.e., when particles are more mature), as observed in [72].

• As for the wavelength dependence of the soot absorption function, a decrease of the $E(m,\lambda )$ for 266 nm < λ < 532 nm was noted, in agreement with the results from [31,32,33, 48, 53, 54, 72], followed by a plateau extending from the visible to the IR, as reported in [23, 33, 47, 48, 53, 54, 72]. Furthermore, the $E(m,\lambda )$ values inferred by LII modeling were found to be well consistent with those issued from [31, 32, 48, 53, 72].

• Finally, when considering the data previously obtained in [40] at high HAB while taking into account a ± 5% uncertainty range, it was concluded that $E(m,\lambda )$ values of 0.38 ± 0.15 and 0.29 ± 0.11 at 266 and 355 nm, versus 0.25 ± 0.09 at 532 and 1064 nm were appropriate to simulate the LII signals we measured in the diesel flame for particles going from young to more mature ones.

The present work, which is part of broader research [40, 57, 78], allowed to propose for the first time a fully parameterized LII model suitable for simulating signals collected with EWs of 266, 355, 532 and 1064 nm in the low-to-intermediate fluence regime. As clearly stated in [40], it is, however, not claimed that this simulation tool should be preferred to other more classical formulations or considered as universally valid. Indeed, although being quite promising, this attempt to propose a refined LII model valid over an extended wavelength range still needs to be trained against data obtained with higher fluences and in other flames. Furthermore, complementary sensitivity analyses focusing on parameters likely to more or less significantly influencing the LII phenomenon (which includes the density and specific heat of unannealed soot as well as the physical and optical properties of annealed particles), are required, thus paving the way for future works to be undertaken.

7 Appendix

${B}_{j}$	Parameter representing the influence of diffusive and convective mass and heat transfer during sublimation	$\left[\mathrm{bar}\right]$
${B}_{\lambda 1,a}$	Empirically determined saturation coefficient for linear absorption of annealed soot	$\left[J\cdot {cm}^{-2}\right]$
${B}_{\lambda 1,s}$	Empirically determined saturation coefficient for linear absorption of unannealed soot	$\left[J\cdot {cm}^{-2}\right]$
${B}_{\lambda n,a}$	Empirically determined saturation coefficient for multi-photon absorption of annealed soot particles	$\left[J\cdot {cm}^{-2}\right]$
${B}_{\lambda n,s}$	Empirically determined saturation coefficient for multi-photon absorption of unannealed soot particles	$\left[J\cdot {cm}^{-2}\right]$
$c$	Specific heat	$\left[J\cdot {g}^{-1}{\cdot K}^{-1}\right]$
$c_{l}$	Speed of light (2.998 × 1010)	$\left[cm\cdot {s}^{-1}\right]$
${c}_{a}$	Specific heat of annealed soot [51]	$\left[J\cdot {g}^{-1}{\cdot K}^{-1}\right]$
${c}_{el}$	Charge of an electron (1.60218 × 10–19)	$\left[C\right]$
${c}_{s}$	Specific heat of unannealed soot [51]	$\left[J\cdot {g}^{-1}{\cdot K}^{-1}\right]$
${C}_{p}^{CO}$	Molar heat capacity of CO fitted from the NIST-JANAF database [100]	$\left[J\cdot {mol}^{-1}\cdot {K}^{-1}\right]$
${C}_{p}^{{O}_{2}}$	Molar heat capacity of O2 fitted from the NIST-JANAF database [100]	$\left[J\cdot {mol}^{-1}\cdot {K}^{-1}\right]$
${C}_{abs,a}^{multi}$	Absorption cross section of the annealed fraction of aggregated soot particles	$\left[{cm}^{2}\right]$
${C}_{abs,s}^{multi}$	Absorption cross section of the unannealed fraction of aggregated soot particles	$\left[{cm}^{2}\right]$
${d}_{f}$	Fractal dimension	$\left[-\right]$
${D}_{g}$	Soot particle gyration diameter	$\left[cm\right]$
${D}_{HC}$	Equivalent heat conduction diameter	$\left[cm\right]$
${D}_{p}$	Primary particle diameter	$\left[cm\right]$
$E(m)$	Dimensionless refractive index function of unannealed soot	$\left[-\right]$
Ea(m)	Dimensionless refractive index function of annealed soot	$\left[-\right]$
$F$	Laser fluence	$\left[J\cdot {cm}^{-2}\right]$
${f}_{1,a}$	Empirical scaling factor for linear absorption of annealed soot	$\left[-\right]$
${f}_{1,s}$	Empirical scaling factor for linear absorption of unannealed soot	$\left[-\right]$
${f}_{a}$	Absorption empirical scaling factor related to annealed soot [51]	$\left[-\right]$
$h$	Planck constant (6.626 × 10–34)	$\left[J.s\right]$
${h}_{\lambda {,N}_{p}}$	Correction factor for multiple scattering within soot aggregates	$\left[-\right]$
${k}_{B}$	Boltzmann constant (1.381 × 10–23)	$\left[J\cdot {K}^{-1}\right]$
${k}_{diss}$	Rate constant for pyrolysis of annealed particles ${k}_{diss}=1\times {10}^{18}\cdot exp\left[-9.6\times {10}^{5}/\left(R \cdot {T}_{p}\right)\right]$ [51]	$\left[{s}^{-1}\right]$
${k}_{el}$	Coulomb constant (8.987 × 109)	$\left[N\cdot {m}^{2}\cdot {C}^{-2}\right]$
${k}_{f}$	Fractal prefactor	$\left[-\right]$
${k}_{g}$	Heat conduction coefficient of surrounding gas	$\left[W\cdot {cm}^{-1}\cdot {K}^{-1}\right]$
${k}_{imig}$	Rate constant for interstitial migrations within annealed particles: ${k}_{imig}=1\times {10}^{8}\cdot exp\left[-8.3\times {10}^{4}/\left(R\cdot {T}_{p}\right)\right]$ [51]	$\left[{s}^{-1}\right]$
${k}_{ox,a}$	Oxidation rate constant of annealed soot	$\left[{s}^{-1} {\cdot cm}^{-2}\right]$
${k}_{ox,s}$	Oxidation rate constant of unannealed soot	$\left[{s}^{-1} {\cdot cm}^{-2}\right]$
${k}_{vmig}$	Rate constant for vacancy migrations within annealed particles: ${k}_{vmig}=1.5\times {10}^{17}\cdot exp\left[-6.7\times {10}^{5}/\left(R\cdot {T}_{p}\right)\right]$ [51]	$\left[{s}^{-1}\right]$
${k}_{\lambda n,a}$	Rate constant for removal of C2 from annealed soot by photodesorption	$\left[{s}^{-1}\right]$
${k}_{\lambda n,s}$	Rate constant for removal of C2 from unannealed by photodesorption	$\left[{s}^{-1}\right]$
${M}_{g}$	Average mass of gas molecules	$\left[g\right]$
${M}_{p}$	Primary particle mass	$\left[g\right]$
$m$	Optical index	$\left[-\right]$
${m}_{el}$	Mass of an electron (9.1095 × 10–35)	$\left[J\cdot {s}^{2}\cdot {cm}^{-2}\right]$
$n$	Estimated number of photons needing to be absorbed to photodesorb C2 clusters	$\left[-\right]$
${N}_{A}$	Avogadro constant (6.02214 × 1023)	$\left[{mol}^{-1}\right]$
${N}_{c}$	Number of atoms in the primary particles:${N}_{c}={M}_{p}{\cdot N}_{A}/{W}_{1}$	$\left[-\right]$
${N}_{d}$	Number of lattice defects in the particles	$\left[-\right]$
${N}_{p}$	Number of primary particles in an aggregate	$\left[-\right]$
${N}_{sa}$	Density of carbon atoms on the surface of annealed soot particles (3.8 × 1015 [51])	$\left[{cm}^{-2}\right]$
${N}_{ss}$	Density of carbon atoms on the surface of unannealed soot particles (2.8 × 1015 [51])	$\left[{cm}^{-2}\right]$
${N}_{tot}$	Aggregate number density	$\left[-\right]$
$p\left({N}_{p}\right)$	Probability density function of aggregate size	$\left[-\right]$
${P}_{diss}$	Effective pressure issued from the rate of thermal photodesorption from annealed particles	$\left[bar\right]$
${P}_{g}$	Ambient pressure	$\left[bar\right]$
${P}_{sat}^{{C}_{j}}$	Saturation partial pressure of vaporized carbon clusters Cj	$\left[bar\right]$
${P}_{\lambda a}$	Effective pressure calculated based on the rate of non-thermal photodesorption of Cj clusters from annealed particles	$\left[bar\right]$
${P}_{\lambda s}$	Effective pressure calculated based on the rate of non-thermal photodesorption of Cj clusters from unannealed particles	$\left[bar\right]$
${q}_{\mathrm{exp}}$	Normalized laser irradiance	$\left[-\right]$
${\dot{Q}}_{abs}$	Rate of energy increase by laser absorption	$\left[W\right]$
${\dot{Q}}_{ann}$	Rate of energy increase by annealing	$\left[W\right]$
${\dot{Q}}_{cond,FM}$	Rate of energy loss by conduction in the free molecular regime	$\left[W\right]$
${\dot{Q}}_{cond,C}$	Rate of energy loss by conduction in the continuum regime	$\left[W\right]$
${\dot{Q}}_{ox}$	Rate energy increase by particle oxidation	$\left[W\right]$
${\dot{Q}}_{rad}$	Rate of energy loss by radiative emission	$\left[W\right]$
${\dot{Q}}_{sub}$	Rate of energy loss by sublimation	$\left[W\right]$
${\dot{Q}}_{th}$	Rate of energy loss by thermionic emission	$\left[W\right]$
$R$	Universal gas constant (8.3145)	$\left[J\cdot {mol}^{-1}\cdot {K}^{-1}\right]$
${R}_{m}$	Universal gas constant expressed in effective mass units (8.3145 × 107)	$\left[g\cdot {cm}^{2}\cdot {mol}^{-1}\cdot {K}^{-1}\cdot {s}^{-2}\right]$
${R}_{p}$	Universal gas constant in expressed effective pressure units (83.145)	$\left[bar\cdot {cm}^{3}\cdot {mol}^{-1}\cdot {K}^{-1}\right]$
$t$	Time	$\left[s\right]$
${t}_{l}$	Laser pulse duration	$\left[s\right]$
${T}_{f}^{CO}$	Temperature at which CO molecules are emitted from oxidizing soot (790 [99])	$\left[K\right]$
${T}_{g}$	Ambient gas temperature	$\left[K\right]$
${T}_{p}$	Particle temperature	$\left[K\right]$
${T}_{ref}$	Reference temperature (0)	$\left[K\right]$
${T}_{\delta }$	Limiting sphere temperature within the Fuchs heat conduction model	$\left[K\right]$
${U}_{int}$	Internal energy of soot particles	$\left[J\right]$
${W}_{1}$	Molecular weight of atomic carbon ($12.011$)	$\left[g\cdot {mol}^{-1}\right]$
${W}_{j}$	Molecular weight of Cj species $\left(\mathrm{j}\times 12.011\right)$	$\left[g\cdot {mol}^{-1}\right]$
$x$	Spatial coordinate	$\left[cm\right]$
Xa	Primary particle annealed fraction	$\left[-\right]$
${X}_{d}$	Initial defect density (1 × 10–2 [98])	$\left[{\mathrm{atom}}^{-1}\right]$
$y$	Spatial coordinate	$\left[cm\right]$
${\alpha }_{j}$	Mass accommodation coefficient of vaporized species Cj (with α1 = α2 = 0.5, α3 = 0.1 and α4 = α5 = 0.0001 [51])	$\left[-\right]$
${\alpha }_{T}$	Thermal accommodation coefficient	$\left[-\right]$
${\beta }$	Empirical scaling factor [115]	$\left[cm^{\xi-1}\right]$
$\delta$	Distance between the equivalent heat conduction radius and the limiting sphere of the Fuchs heat conduction model	$\left[cm\right]$
${\gamma }^{*}$	Mean heat capacity ratio	$\left[-\right]$
$\Delta {H}_{diss}$	Enthalpy of formation of Cj clusters by thermal sublimation of annealed soot	$\left[J\cdot {mol}^{-1}\right]$
$\Delta {H}_{imig}$	Enthalpy related to interstitial migrations (-1.9 × 104 as estimated in [51] based on the data from [95])	$\left[J\cdot {mol}^{-1}\right]$
$\Delta {H}_{j}$	Enthalpy of formation of carbon vapor species Cj [51]: ${\Delta H}_{1}=-5.111\cdot {T}_{p}+7.266\times {10}^{5}$, ${\Delta H}_{2}=-12.326\cdot {T}_{p}+8.545\times {10}^{5}$, ${\Delta H}_{3}=-26.921\cdot {T}_{p}+8.443\times {10}^{5}$, ${\Delta H}_{4}=-2.114\times {10}^{-3}\cdot {{T}_{p}}^{2}-7.787\cdot {T}_{p}+9.811\times {10}^{5}$ and ${\Delta H}_{5}=-2.598\times {10}^{-3}\cdot {{T}_{p}}^{2}-7.069\cdot {T}_{p}+9.898\times {10}^{5}$	$\left[J\cdot {mol}^{-1}\right]$
${\Delta H}_{ox}$	Enthalpy of the reaction 2C + O2 → 2CO: ${\Delta H}_{ox}=2.8901$×${10}^{-14}\cdot {{T}_{p}}^{5}-4.9868\times {10}^{-10}\cdot {{T}_{p}}^{4}+3.2206\times {10}^{-6}\cdot {{T}_{p}}^{3}-1.0307{\times 10}^{-2}\cdot {{T}_{p}}^{2}+7.9303\cdot {T}_{p}-1.1221\times {10}^{5}$	$\left[J\cdot {mol}^{-1}\right]$
$\Delta {H}_{vmig}$	Enthalpy related to vacancy migrations (-1.4 × 105 as derived from the works of [96, 97])	$\left[J\cdot {mol}^{-1}\right]$
${\Delta H}_{\lambda n,a}$	Enthalpy required to photodesorb Cj clusters from annealed particles	$\left[J\cdot {mol}^{-1}\right]$
${\Delta H}_{\lambda n,s}$	Enthalpy required to photodesorb Cj clusters from unannealed particles	$\left[J\cdot {mol}^{-1}\right]$
$\Delta \phi$	Positive charge buildup	$\left[J\right]$
$\lambda$	Wavelength	$\left[cm\right]$
λ l	Laser-excitation wavelength	$\left[cm\right]$
ξ	Dispersion exponent [115]	$\left[-\right]$
ρ	Density	$\left[g\cdot {cm}^{-3}\right]$
${\rho }_{a}$	Density of annealed soot:${\rho }_{a}=2.6-1\times {10}^{-4}\cdot {T}_{p}$	$\left[g\cdot {cm}^{-3}\right]$
${\rho }_{s}$	Density of unannealed soot:${\rho }_{s}=2.3031-7.3106\times {10}^{-5}\cdot {T}_{p}$	$\left[g\cdot {cm}^{-3}\right]$
${\sigma }_{\lambda n,a}$	Empirically determined cross section for removal of C2 clusters by photodesorption from annealed soot particles	$\left[{cm}^{2n-1}\cdot {J}^{1-n}\right]$
${\sigma }_{\lambda n,s}$	Empirically determined cross section for removal of C2 clusters by photodesorption from unannealed soot particles	$\left[{cm}^{2n-1}\cdot {J}^{1-n}\right]$
$\Phi$	Equivalence ratio	$\left[-\right]$
$\phi$	Work function (7.37 × 10–19)	$\left[J\right]$