Modeling laser-induced incandescence of Diesel soot—Implementation of an advanced parameterization procedure applied to a refined LII model accounting for shielding effect and multiple scattering within aggregates for ${\varvec{\alpha}}_{{\varvec{T}}}$ and ${\varvec{E}}\left( {\varvec{m}} \right)$ assessment

Abstract

An extensive set of LII signals measured in a Diesel spray flame has been simulated using a refined LII model built upon a comprehensive version of soot heat- and mass-balance equations. This latter includes terms standing for saturation of linear, single- and multi-photon absorption processes, cooling by sublimation, conduction, radiation and thermionic emission in addition to mechanisms depicting soot oxidation and annealing, non-thermal photodesorption of carbon clusters as well as corrective factors allowing considering shielding effect and multiple scattering (MS) within aggregates. A complete parameterization of the so-proposed model has been achieved by means of an advanced optimization procedure coupling design of experiments with a genetic algorithm-based solver. Doing so, the values of different factors involved in absorption and sublimation terms have been assessed for a 1064-nm laser excitation wavelength including the multi-photon absorption cross section for C₂ photodesorption and the saturation coefficients for linear- and multi-photon absorption, among others. This parameterized model has then been demonstrated to effectively reproduce signals measured in different combustion media including a CH₄/O₂/N₂ premixed flat flame and a diffusion ethylene flame. As a result of the data derived from the analysis of the Diesel flame, a thermal accommodation coefficient value of 0.49 has been assessed against 0.34 when neglecting the shielding effect. In addition, values of the soot absorption function ($E\left( m \right)$) comprised between 0.18 and 0.31 have been inferred depending on the particle maturation stage. On the other hand, $E\left( m \right)$ 24% higher on average have been estimated when neglecting MS thus illustrating the importance of aggregate characteristics on soot properties derived through LII modeling. Eventually, the $E\left( m \right)$ evolution observed herein has been compared with results issued from studies conducted with varied hydrocarbons which led to highlight the crucial role played by the soot maturity level over the nature of the burnt fuel as far as optical properties are concerned.

1 Introduction

Due to the increasing concern regarding the impact of soot emissions on human health and on the environment, continuous efforts have been devoted to the development of advanced diagnostics allowing the formation of combustion-generated nanoparticles to be studied [1]. Within this context, laser-induced incandescence (LII) has proven to be one of the most powerful techniques for soot characterization in flames and at the exhaust of combustion devices [2]. It briefly consists in heating particles up to their incandescence temperature by means of a high-power pulsed laser source while collecting the quasi-blackbody radiation emitted above the flame emission through gated or time-resolved detection approaches for spatially resolved soot concentration measurement or primary-particle size assessment [2]. Since the early works from [3, 4], many developments have been achieved to increase the potential of this technique which is commonly combined with a variety of diagnostics including extinction for the quantitative measurement of soot volume fractions [5, 6], laser-induced fluorescence for coupled detection of polycyclic aromatic hydrocarbons and soot [7], transmission electron microscopy for soot size assessment [8], transmittance measurements to infer information on soot optical properties [9], or elastic light scattering for the characterization of soot aggregate properties [10] and volatile coating fractions on exhaust particles [11]. In parallel, major progress has been achieved in the application of the LII technique itself by taking advantages of a firm examination of the theoretical background underlying the laser-induced incandescence phenomenon. This includes the development of the auto-compensating approach [12] enabling the soot volume fraction to be quantified without requiring any coupling with extinction techniques, advances made in the field of soot diameter assessment by time-resolved LII [8, 13], as well as the development of the so-called two-excitation wavelength LII approach [14, 15] which is particularly valuable to evaluate the relative wavelength dependence of the soot absorption function.

In all the above applications, the correct analysis of the radiative emission from laser-heated soot, however, requires a thorough understanding of the physical mechanisms governing the LII process thus explaining why considerable efforts have also been devoted to the development of theoretical models capable of predicting LII signals over a wide range of conditions. With the exception of the early work from [3] that only considers an energy balance to compute the light emission issued from laser-irradiated particles, all the models from the literature predict the radiation from heated soot by introducing the temporal evolution of the soot temperature ($T_{p}$) and diameter ($D_{p}$) in a Planck function. To do so, $T_{p}$ and $D_{p}$ variations are typically calculated by solving a couple of differential equations standing for particle energy and mass balances during heating and cooling stages. The main differences between existing models actually lie in the nature of the fluxes considered within the energy and mass balances as well as on their governing equations. Within this framework, major achievements have been made since the pioneer works from [3, 4] to improve the predictive character of LII models. One can cite, for instance, the formulation of advanced sublimation sub-models depicting the effects of multiple carbon clusters evaporating from the soot surface [16, 17], the refinement of conduction sub-models through the implementation of an extended Fuchs two-layer approach allowing taking the so-called shielding effect into account [18] likewise advances made in the precise integration of the spatial energy distribution when using non-uniform laser sources [19, 20]. That being said, the most significant contributions to LII model refinement probably remain those proposed by Michelsen who integrated mechanisms accounting for soot melting and annealing, non-thermal photodesorption of carbon clusters from the particle surface, saturation of the linear, single- and multi-photon absorption leading to the photodesorption of C₂ clusters at high fluences in addition to oxidation and thermionic emission [17, 21]. The use of such a type of refined model particularly led to simulated signals merging on a single curve with experimentally monitored ones in [22] though no detailed description of model equations and parameterization was provided therein. Alternatively, predicted signals diverging from measured ones were reported in [23] when using a model derived from the formulations proposed in [17, 21]. The absence of explicit contribution of the multi-photon absorption within the expression standing for the absorption flux (despite the integration of both thermal and non-thermal desorption in the sublimation sub-model) together with the selection of a two-photon mechanism to account for the C₂ photodesorption at 1064 nm may possibly explain the so-observed gaps while illustrating the difficulties related to the selection and parameterization of adapted LII model formulations. More recently, a powerful open-source software has been proposed to the LII community so as to process and analyze measured and simulated LII signals [24]. No photolytic process such as those described in [17, 21] has been embedded within this code, however, despite the importance of integrating such mechanisms to reproduce LII signals over a wide range of conditions as demonstrated in [25] by means of inverse techniques.

To contribute improving the predictive capability of LII simulation tools, the present study aims at proposing a refined and fully parameterized LII model allowing reproducing a new and extensive set of LII signals obtained in a turbulent diffusion flame of Diesel previously investigated in [7, 26]. The choice of Diesel as a fuel has been motivated by the fact that compression ignition engines are known to produce a large amount of particulate pollutant noting that the toxicity of Diesel soot is well documented now [27]. Investigations aiming at describing the characteristics of such combustion-generated fine carbonaceous particles, including their optical properties, are, therefore, quite required to better apprehend their interactions with the environment. The relatively limited number of studies pertaining to the determination of Diesel soot absorption function [14, 15], especially as a function of the particle maturation stage, however, clearly prompts the need for additional investigations which justifies the interest of the current research. Within this context, an extended LII model built upon a comprehensive version of soot heat- and mass-balance equations has been implemented. It includes an absorption term accounting for saturation of the linear, single- and multi-photon absorption, expressions depicting cooling processes by sublimation, conduction, radiation and thermionic emission in addition to mechanisms standing for soot oxidation and annealing as well as non-thermal photodesorption of carbon clusters (i.e., processes that have been evidenced as being likely to influence the LII phenomenon in the low-to-high fluence regime this paper focuses on [17, 25]). Besides, corrective terms accounting for the shielding effect [18] and the multiple scattering (MS) within aggregates [28, 29] have also been considered due to their influence on conduction and absorption rates, thus making the proposed model the most refined ever implemented so far to the best of the authors’ knowledge. Of course, there is no basic evidence that the more the intrinsic complexity of a given model, the more the reliability of its predictions. It has, however, been clearly demonstrated in numerous works that neglecting some important mechanisms including the above-mentioned shielding and MS effects as examples is likely to lead to biased estimates of important factors driving the LII process thus supporting the approach adopted herein. To address this research, a procedure coupling design of experiments (DoE) and genetic algorithm-based optimization has been implemented to obtain simulated data merging on a single curve with measured ones while allowing the values of some soot properties and empirical factors to be estimated including the cross section and saturation coefficients for multi-photon absorption whose values have never been reported in the literature for a 1064-nm wavelength (except in the first-approach work presented in [30]). To rule on the consistency of the so-derived parameter values while estimating the uncertainties surrounding their assessment, a critical analysis has been conducted to discuss the impact of various factors prone to influence obtained results including the experimental error associated to the measurement of the surrounding gas temperature or the possible variations of LII signals induced by measurement noise. Furthermore, the validity of the proposed model has been further verified by accurately simulating an extensive set of LII signals collected in an atmospheric CH₄/O₂/N₂ premixed flat flame characterized in [23]. Finally, additional model predictions have been compared with signals measured at different HAB in the Diesel flame so as to infer and discuss the values taken by some parameters of interest in LII studies such as the thermal accommodation coefficient driving the conductive cooling process and the maturity-dependent absorption function of soot.

2 Experimental and modeling approaches

2.1 Experiment

The experimental setup, likewise the LII measurement procedure implemented in this work, has already been extensively described in previous works [30,31,32]. As a consequence, they will be only briefly presented in the following.

Concerning the Diesel flame first, it has been generated using the Lemaire’s spray burner configuration (previously characterized in detail in [31]) with operating conditions similar to those implemented in [14, 15, 26, 30]. The flame generation system consists of a McKenna hybrid flat flame burner composed of a 60-mm diameter porous plate with a central 6.35-mm diameter tube allowing the introduction of a direct injection high efficiency nebulizer. A lean premixed methane–air flat flame stabilized on the porous plug produces the hot gases ensuring the ignition of the low-sulfur Diesel spray exiting from the injector tip. A turbulent diffusion flame is then obtained at atmospheric pressure with a peak soot concentration located at 92-mm height above the burner (HAB) [33] where a temperature of 1850 K has been measured [30]. Besides, soot samples collected at each studied HAB have been characterized by scanning mobility particle sizer (SMPS) as previously described in [14].

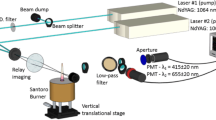
The implemented LII setup is identical to the one previously used in [30] where a diagram of the whole experimental configuration can be found. It is composed of a Continuum Nd:YAG laser operating at 1064 nm. The central part of the Gaussian laser beam has been selected using a 1-mm diaphragm to obtain a beam section of 0.0021 cm² at 1/e² at the center of the burner as monitored using a Gentec CCD beam profiler. The time-resolved LII signals have been collected perpendicularly to the laser propagation direction using a 300-µm horizontal slit placed in front of a Hamamatsu R2257 photomultiplier tube. An OG-550 long pass filter has, moreover, been used to reduce the measurement noise caused by the flame emission. Broadband signals have then been digitized and stored by means of a Teledyne Lecroy oscilloscope (see [14] for more details regarding the measurement procedure). Eventually, a Princeton Instruments acton spectrograph has been coupled to a gated ICCD PI-MAX camera for flame temperature assessment through a Planck function fitting procedure [34]. To do so, the calibration of the detection chain has been achieved as done in [15, 26] using an optical sphere noting that the optical setup, as well as the solid angle, has been kept constant during the calibration and the flame emission measurements. Signals have then been processed based on the procedure detailed in [34,35,36] to assess the flame temperature at the investigated HAB [30].

2.2 LII signal modeling

2.2.1 Model description

For brevity purposes and following the formalism adopted in [19] or [23], only the main features of the implemented model will be given in this section noting that the detail of the governing equations is provided in Appendix 1. In short, the system of coupled differential equations depicting the variations of the internal energy rate ($\frac{{{\text{d}}U_{{\text{int}}} }}{{{\text{d}}t}}$) and mass ($\frac{{{\text{d}}M_{p} }}{{{\text{d}}t}}$) of the particles composing a soot aggregate as a function of time has been built upon mechanisms standing for heating by absorption of the laser energy ($\dot{Q}_{{{\text{abs}}}}$), soot annealing ($\dot{Q}_{{{\text{ann}}}}$) and oxidation ($\dot{Q}_{ox}$) as well as cooling by radiation ($\dot{Q}_{{{\text{rad}}}}$), thermionic emission ($\dot{Q}_{{{\text{th}}}}$), sublimation ($\dot{Q}_{{{\text{sub}}}}$) and conduction ($\dot{Q}_{{{\text{cond}}}}$):

$$\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}U_{{\text{int}}} }}{{{\text{d}}t}} = \dot{Q}_{{{\text{abs}}}} + \dot{Q}_{{{\text{ann}}}} + \dot{Q}_{ox} - \dot{Q}_{{{\text{rad}}}} - \dot{Q}_{{{\text{th}}}} - \dot{Q}_{{{\text{sub}}}} - \dot{Q}_{{{\text{cond}}}} } \hfill \\ \hfill \\ {\frac{{{\text{d}}M_{p} }}{{{\text{d}}t}} = \sum\limits_{j = 1}^{5} \left( {\frac{{{\text{d}}M_{p} }}{{{\text{d}}t}}} \right)_{{{\text{sub}}, j}} + \left( {\frac{{{\text{d}}M_{p} }}{{{\text{d}}t}}} \right)_{ox} } \hfill \\ \hfill \\ \end{array} } \right.$$

(1)

where the subscripts ‘sub’ and ‘ox’ denote the contributions of the sublimation and oxidation mechanisms to the mass loss, respectively, while ‘j’ stands for the contribution of each vaporized carbon cluster C_j to the particle mass loss. The rate of change of energy stored by the particles has been put into equation based on the formulation proposed in [17] to differentiate between the contributions of the unannealed and annealed soot fractions. Similarly, $\dot{Q}_{{{\text{abs}}}}$ has been expressed as a sum of the energy rates absorbed by the unannealed (subscript ‘s’) and annealed (subscript ‘a’) particles (i.e., $\dot{Q}_{{{\text{abs}}}} = \dot{Q}_{{{\text{abs}},s}} + \dot{Q}_{{{\text{abs}},a}}$), each of these terms accounting for saturation of the linear, single- and multi-photon absorption processes [21], so that:

$$\begin{aligned} \dot{Q}_{{{\text{abs}},r}} & = C_{{{\text{abs}},r}}^{{{\text{multi}}}} \left( {\lambda_{l} ,N_{p} } \right) \,\cdot\, \frac{{f_{1,r} \,\cdot\, B_{\lambda 1,r} }}{{\mathop \smallint \nolimits_{0}^{{t_{l} }} q_{\exp } \left( t \right){\text{d}}t}} \\ & \quad \,\cdot\, \left\{ {1 - \exp \left[ { - \frac{{F \,\cdot\, q_{\exp } \left( t \right)}}{{B_{\lambda 1,r} }}} \right]} \right\} + N_{p} \,\cdot\, \frac{n \,\cdot\, h \,\cdot\, c}{{\lambda_{l} }} \,\cdot\, k_{\lambda n,r} \\ \end{aligned}$$

(2)

where the subscript ‘r’ stands for either ‘s’ or ‘a’, while $h$ is the Planck constant, $c$ is the speed of light, $\lambda_{l}$ denotes the laser-excitation wavelength, $f_{1,r}$ and $B_{\lambda 1,r}$ are empirical factors related to the single-photon absorption process, $q_{\exp } \left( t \right)$ is the normalized laser irradiance, $t_{l}$ and $F$ stand for the laser pulse duration and energy density, respectively, $k_{\lambda n,r}$ is the rate constant for removal of C₂ clusters by photodesorption, $N_{p}$ corresponds to the number of primary particles per aggregate and $n$ is the number of photons to be adsorbed to photodesorb C₂ clusters. As far as $C_{{{\text{abs}},r}}^{{{\text{multi}}}}$ is concerned, it corresponds to the absorption cross section, whose expression integrates, in an original way, the MS corrective factor from [28], so that:

$$C_{{{\text{abs,}}r}}^{{{\text{multi}}}} \left( {\lambda , N_{p} } \right) = N_{{{\text{tot}}}} \,\cdot\, C_{{{\text{abs}},r}}^{{{\text{mono}}}} \,\cdot\, h_{{\lambda ,N_{p} }} \,\cdot\, N_{p} \,\cdot\, p\left( {N_{p} } \right)$$

(3)

where $N_{{{\text{tot}}}}$ is the aggregate number density, $p\left( {N_{p} } \right)$ stands for the probability density function of the aggregate size and $h_{{\lambda ,N_{p} }}$ corresponds to the corrective factor proposed by Yon et al. whose calculation procedure is detailed in [29]. Regarding the absorption cross section of primary particles ($C_{{{\text{abs}},r}}^{{{\text{mono}}}}$), it has been equated as a function of the annealed fraction $X_{a}$ following:

$$\begin{gathered} C_{{{\text{abs}},s}}^{{{\text{mono}}}} = \left( {1 - X_{a} } \right) \,\cdot\, \frac{{\pi^{2} \,\cdot\, D_{p}^{3} }}{{\lambda_{l} }} \,\cdot\, E\left( m \right)\quad {\text{and}} \hfill \\ C_{{{\text{abs}},a}}^{{{\text{mono}}}} = X_{a} \,\cdot\, \frac{{\pi^{2} \,\cdot\, D_{p}^{3} }}{{\lambda_{l} }} \,\cdot\, f_{a} \,\cdot\, E_{a} \left( m \right) \hfill \\ \end{gathered}$$

(4)

where $D_{p}$ is the primary particle diameter, $f_{a}$ denotes an empirical scaling factor for annealed soot [17], while $E\left( m \right)$ and $E_{a} \left( m \right)$ stand for the refractive index functions of unannealed and annealed particle fractions, respectively. As for $k_{\lambda n,r}$, it has been calculated based on the following equation:

$$\begin{aligned} k_{\lambda n,r} & = X_{s/a} \,\cdot\, \frac{{\lambda_{l} }}{n \,\cdot\, h \,\cdot\, c} \,\cdot\, \frac{{\sigma_{\lambda n,r} \,\cdot\, \pi \,\cdot\, D_{p}^{3} \,\cdot\, N_{sr} }}{6} \\ & \quad \,\cdot\, \frac{{\left( {B_{\lambda n,r} } \right)^{n} }}{{\mathop \smallint \nolimits_{0}^{{t_{l} }} \left[ {q_{\exp } \left( t \right)} \right]^{n} {\text{d}}t}} \,\cdot\, \left\{ {1 - \exp \left[ { - \left( {\frac{{F \,\cdot\, q_{\exp } \left( t \right)}}{{B_{\lambda n,r} }}} \right)^{n} } \right]} \right\} \\ \end{aligned}$$

(5)

in which $X_{s/a}$ is equal to either $1 - X_{a}$ or $X_{a}$ for unannealed and annealed soot, $\sigma_{\lambda n,r}$ represents the multi-photon absorption cross section for the photodesorption of C₂ clusters, $N_{sr}$ is the density of carbon atoms on the surface of primary particles, while $B_{\lambda n,r}$ is an empirical saturation coefficient for multi-photon absorption. As far as the annealing ($\dot{Q}_{{{\text{ann}}}}$) and oxidation ($\dot{Q}_{ox}$) fluxes are concerned, they have been implemented based on the formulations proposed in [17, 37], respectively. Besides, the governing equations standing for the cooling processes by radiation ($\dot{Q}_{{{\text{rad}}}}$) and thermionic emission ($\dot{Q}_{{{\text{th}}}}$) have been formulated using the expressions provided in [17, 38]. Concerning the sublimation sub-model, it has been derived from the one extensively presented in [17] so as to integrate the contribution of the annealed fraction within both thermal and non-thermal mechanisms. According to [21], only C₁ to C₅ species have been considered, while the rate constants for the photodesorption of C₂ clusters from unannealed and annealed particles have been estimated based on Eq. (5). Finally, a Fuchs equivalent sphere modeling approach [18] has been selected to compute the conductive cooling rate $\dot{Q}_{cond}$. This latter allows calculating the conduction rates in the free-molecular (FM) and continuum (C) regimes based on the following relations:

$$\dot{Q}_{{{\text{cond}},{\text{FM}}}} = \frac{1}{8} \,\cdot\, \pi \,\cdot\, \alpha_{T} \,\cdot\, D_{HC}^{2} \,\cdot\, P_{g} \,\cdot\, \sqrt {\frac{{8 \,\cdot\, k_{B} \,\cdot\, T_{\delta } }}{{\pi \,\cdot\, M_{g} }}} \,\cdot\, \frac{{\gamma^{*} + 1}}{{\gamma^{*} - 1}} \,\cdot\, \left( {\frac{{T_{p} }}{{ T_{\delta } }} - 1} \right)$$

(6)

$$\dot{Q}_{{{\text{cond}},C}} = 4 \,\cdot\, \pi \,\cdot\, \left( {\frac{{D_{HC} }}{2} + \delta } \right) \,\cdot\, \mathop \smallint \limits_{{T_{g} }}^{{T_{\delta } }} k_{g} \left( T \right){\text{d}}T$$

(7)

where $\alpha_{T}$ is the thermal accommodation coefficient, $P_{g}$ stands for the ambient pressure, $k_{B}$ corresponds to the Boltzmann constant, $M_{g}$ represents the average mass of the gas molecules, $\gamma^{*}$ denotes the mean value of the heat capacity ratio, $\delta$ and $T_{\delta }$ correspond to the distance and temperature related to the limiting sphere separating the free-molecular from the continuum regimes, $T_{p}$ and $T_{g}$ are the particle and surrounding gas temperatures, $k_{g}$ stands for the heat conduction coefficient of the surrounding gas, while $D_{HC}$ is the equivalent sphere diameter related to the shielding corrective factor defined in [18]. Though heat conduction in the studied flame mainly operates in the free-molecular regime as supported by Knudsen numbers higher than ~ 30, the Fuchs sub-model has still been considered so as to propose a model formulation as generic as possible to allow conducting further studies involving wide range of operating conditions. Besides, and since in the free molecular regime, the Fuchs modeling approach reduces to an expression similar to the one related to the more straightforward McCoy and Cha formulation [42] commonly used in LII studies (see [30]), the selection of the Fuchs conduction sub-model, therefore, absolutely does not challenge the consistency of the simulation results presented in the following.

2.2.2 Numerical procedure

Solving the coupled differential equations summarized in (1) allows estimating the variations of $T_{p}$ and $D_{p}$ as a function of space and time. Obtained $T_{p}$ and $D_{p}$ values can then be introduced into a Planck function which is integrated over the spectral range of the detection system including its spectral response as done in [20]. To do so, the measured spatial distribution of the laser energy has been numerically reproduced and discretized using 17 × 17 elements as validated through a grid-sensitivity analysis. The simulated LII signals have then been calculated over the entire laser beam dimensions before being integrated over the spatial domain corresponding to the 300-µm slit experimentally used for proper comparisons with measured data.

2.2.3 Model parameterization

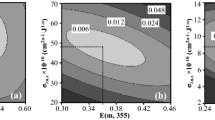
The model parameterization has been achieved based on the data acquired at 92 mm HAB in the Diesel flame. Calculations have been conducted using the normal law derived from the measurements reported in [14] leading to a mean $D_{p}$ of 16.4 nm, a standard deviation $\sigma_{p}$ of 3.3 and a mean $N_{p}$ of 125. The values of the parameters integrated within the governing equations accounting for the different energy fluxes have been set as detailed in the references listed in Sect. 2.2.1 as well as in Appendices 1 and 2. On the other hand, a few variables still required to be adjusted including $\alpha_{T}$ and other factors whose values have never been reported in the literature for a 1064-nm laser excitation wavelength (except in [30] where a model similar to the one implemented herein (except for $\dot{Q}_{{{\text{abs}}}}$ and $\dot{Q}_{{{\text{th}}}}$) has been used). Among the parameters needing to be adjusted, one can list those involved in the absorption and sublimation sub-models from [17, 21] whose formulations have been validated against data acquired with a 532-nm laser source. An advanced parameterization procedure has, therefore, been implemented to define the values of the multi-photon absorption cross section for C₂ photodesorption ($\sigma_{\lambda n,s}$), the empirical saturation coefficients for linear ($B_{\lambda 1,s}$) and multi-photon ($B_{\lambda n,s}$) absorption, the enthalpy required to photodesorb carbon clusters from unannealed soot $\Delta H_{\lambda n,s}$ ($\Delta H_{\lambda n,a}$ being set as suggested in [17]), the absorption function of unannealed soot $E\left( m \right)$ (the $E_{a} \left( m \right)$ value being issued from [17]) and the thermal accommodation coefficient ($\alpha_{T}$). Finally, and supported by the results from [30] that showed that the effect of the soot annealed fraction is quite low in the fluence range this work more particularly focuses on (i.e., below and near the LII fluence curve plateau region), $\sigma_{\lambda n,a}$, $B_{\lambda 1,a}$ and $B_{\lambda n,a}$ have been set equal to $\sigma_{\lambda n,s}$, $B_{\lambda 1,s}$ and $B_{\lambda n,s}$, respectively. Following the methodology introduced and described in [30], a full central composite design of experiments (DoE) has been coupled to a genetic algorithm-based optimizer (the ga function of MATLAB®) to identify a set of parameters allowing obtaining simulated signals identical to measured ones. Examples of DoE response surfaces obtained by defining an objective function corresponding to a least square sum between experimental and numerical LII time decays obtained at each investigated fluence are depicted in Fig. 1.

Fig. 1

Examples of DoE response surfaces for $E\left( m \right)$ and $\sigma_{\lambda n,s}$ (a) as well as for $\alpha_{T}$ and $B_{\lambda n,s}$ (b). Values depicted on the graphs (expressed in arbitrary unit (a.u.)) are representative of the least square sum between experimental and numerical LII signals

As one can see by looking at Fig. 1(a), optimized $E\left( m \right)$ and $\sigma_{\lambda n,s}$ around ~ 0.25 and ~ 4.5 × 10^–10 cm²ⁿ⁻¹·J¹⁻ⁿ, respectively, can be determined. Similarly, $\alpha_{T}$ and $B_{\lambda n,s}$ values around ~ 0.44 and ~ 0.45 J·cm⁻² can be assessed as shown in Fig. 1(b). Regarding $B_{\lambda 1,s}$ and $\Delta H_{\lambda n,s}$, broader ranges of values have been identified as being suitable (i.e., between 0.8 and 1.5 J·cm⁻² for $B_{\lambda 1,s}$ and between 1 × 10⁵ and 3.4 × 10⁵ J·mol⁻¹ for $\Delta H_{\lambda n,s}$). A second optimization procedure has consequently been conducted to refine the obtained solution using the ga solver while fixing the above-mentioned ranges of values for $B_{\lambda 1,s}$ and $\Delta H_{\lambda n,s}$ against intervals of ± 15% around the optimum values defined by the DoE for the other parameters. By doing so, the following results have then been derived: $E\left( m \right)$ = 0.23, $\sigma_{\lambda n,s}$ = 4.2 × 10^–10 cm²ⁿ⁻¹·J¹⁻ⁿ, $B_{\lambda 1,s}$ = 1.15 J·cm⁻², $B_{\lambda n,s}$ = 0.41 J·cm⁻², $\Delta H_{\lambda n,s}$ = 1.02 × 10⁵ J·mol⁻¹ and $\alpha_{T}$ = 0.49. These parameters are in the end relatively close to those estimated in [30] though some discrepancies emerge as far as the values of $E\left( m \right)$, $\Delta H_{\lambda n,s}$ or $\alpha_{T}$ are concerned, due to the inclusion of the MS corrective factor from [28] in $\dot{Q}_{{{\text{abs}}}}$ and to the selection of the thermionic sub-model from Mitrani et al. [38] instead of the formulation proposed in [21]. As illustrated in Fig. 2, the use of the above-listed parameters allows obtaining predicted LII fluence curves and time decays matching their experimental counterparts.

Fig. 2

Comparison of simulated LII fluence curves (a) and time decays (b) with data measured at 92 mm HAB in the Diesel flame

On the other hand, and even though obtained results tend to confirm the relevance of the procedure proposed in [30] to assess parameters enabling an excellent agreement between measured and simulated LII signals to be obtained, further validations (detailed in the following section) are still required prior to consider these factor values as being consistent.

3 Critical analysis and model validation

3.1 Uncertainties related to model formulation and parameterization

One of the issues that may be raised concerning the implementation of sophisticated LII models lies in the somewhat complex formulations of this type of simulation tool. This would hence increase the uncertainty associated with recovered parameters [43] and justifies, under certain circumstances, using simpler models such as those involving equations issued and/or derived from the basic formulation proposed by Melton [4]. While being a wise approach in the context of analyses limited to the examination of a specific energy flux or to the modeling of signals collected on very narrow fluence regimes, it has, however, been shown in numerous studies that too simplistic model formulations were clearly inadequate to simulate LII responses on an extended range of operating conditions [17, 23, 25, 44, 45]. Such a conclusion has been particularly supported by the inverse-technique-based analysis reported in [25] which demonstrated that modeling soot LII considering solely $\dot{Q}_{{{\text{abs}}}}$, $\dot{Q}_{{{\text{rad}}}}$, $\dot{Q}_{{{\text{sub}}}}$ and $\dot{Q}_{{{\text{cond}}}}$, as these fluxes are commonly expressed and computed in Melton-derived models, is unsuitable to properly capture the soot heating and cooling mechanisms particularly near and above the soot sublimation threshold. This has been lately confirmed in a sensitivity analysis [45] dealing with the ability of different model formulations and parameterizations to simulate the extensive set of data gathered in [23]. In addition, the results from [25] also led to infer the temporal and fluence dependences of energy rates needing to be integrated to fulfill the particle energy and mass balances while correctly reproducing the LII fluence curves and time decays measured up to 1 J·cm⁻² in [46]. The analysis of the so-derived energy rates showed that their governing equations were similar to those proposed by Michelsen to represent multi-photon absorption and non-thermal photodesorption of carbon clusters. This, therefore, justifies why such important processes have been embedded within the refined model formulation implemented herein. Similarly, the inclusion of corrective terms accounting for MS [28, 29] and shielding [18] effects within aggregates have been considered due to their significant influence on absorption and conduction rates. It should, however, be noted that the absence of established sub-models allowing taking the effects of aggregation on other processes into account represents a limitation of the developed modeling tool. That being said, and even if physical and chemical phenomena such as sublimation or oxidation are likely to be affected to different degrees by aggregation, this issue has still been neglected due to the lack of available information evidencing and quantifying the relative impact of aggregate properties on the energy rates (other than $\dot{Q}_{{{\text{abs}}}}$ and $\dot{Q}_{{{\text{cond}}}}$) governing the LII response.

As far as the parameterization process is concerned, it has been recalled in Sect. 2.2.3 that the factors (including empirical ones) introduced in the governing equations accounting for the photolytic processes listed above have been initially set to reproduce data obtained using a 532-nm laser excitation source [17, 21]. Though far from being trivial, adjusting their values for other wavelengths is quite required to avoid unsatisfactory results to be obtained as exemplified in [23]. Addressing this critical step may, however, raise questions concerning the unicity of the solution arising from the fitting procedure as well as regarding the possible interactions between assessed parameters. The advanced optimization procedure introduced in [30] and extended in the present work has, therefore, been chosen to tackle such an issue. This latter indeed relies on the minimization of an objective function defined as a least square sum between experimental and numerical results considering the whole lifetime of the LII signals at each investigated fluence. The definition of such a criterion has been dictated by the fact that some parameters are known to mainly influence the LII phenomenon during the heating stage, while others essentially act during the subsequent cooling of the particles. Similarly, some mechanisms have quite a negligible role at low fluences, while they inversely significantly impact the processes underlying the incandescence of laser-heated soot at higher fluences. In this regard, it is particularly worthy to note that the factors listed in Sect. 2.2.3 do not influence soot LII the same way as shown in [45]. For instance, while increasing $E\left( m \right)$ or $\sigma_{\lambda n,s}$ may tend to similarly increase the value of the peak LII signals below the sublimation threshold, a drastic reduction of the LII response at high fluences (i.e., > 0.2 J·cm⁻²) can be drawn when increasing $\sigma_{\lambda n,s}$ which contrasts with the effect of $E\left( m \right)$ that remains relatively moderate in comparison. In addition, while modifying $B_{\lambda n,s}$ has logically almost no impact on the increasing section of the fluence curves, it significantly influences the threshold above which the LII response tends to show a lack of fluence dependence. Consequently, operating a parameterization procedure considering solely the peak of the LII signal or a portion of the decay time while taking a limited range of fluences into account, as sometimes achieved, will inevitably lead to neglect, overestimate and/or underestimate the impact of some important mechanisms governing soot LII. This will in turn lead to biased parameter values thus prompting the need for implementing a comprehensive, though time consuming, optimization approach that takes the whole time and fluence dependence of the LII responses into account as done herein. The use of a DoE in the preliminary optimization stage is, moreover, of high interest as it allows identifying local optimum, as shown in Fig. 1 which tends to illustrate the unicity of the so-assessed solution. Indeed, if two factors ($E\left( m \right)$ and $\sigma_{\lambda n,s}$ for instance) would have similar effects on the LII responses regardless of the time and fluence, it would be impossible to identify a local optimum as an infinity of parameter couples ($E\left( m \right)$;$\sigma_{\lambda n,s}$) could suit to minimize the defined objective function.

To conclude, it is noteworthy that the reliability of obtained estimates has to be analyzed with caution, since parameters such as the measured surrounding gas temperature $T_{g}$, the initial soot diameter $D_{p}$ or the signal measurement noise are prone to strongly influence the modeling of LII signals likewise the results of the fitting process. An error analysis has, therefore, been conducted considering the uncertainties encompassing the measurement of $T_{g}$ (± 23 K) and $D_{p}$ (set equal to ± 2.7 nm based on the variations reported in [8, 47, 48] when determining the size of soot particles formed in a premixed ethylene/air flame). Besides and though a LII signal variation of the order of ± 1% has been derived at 92 mm HAB (in agreement with the value determined at the same height in a kerosene flame stabilized using the same burner and the same operating conditions [49]), a variation of ± 5% has still been taken into account to maximize the errors associated to the estimation of $E\left( m \right)$, $\sigma_{\lambda n,s}$, $B_{\lambda 1,s}$, $B_{\lambda n,s}$, $\Delta H_{\lambda n,s}$ and $\alpha_{T}$. By doing so, one obtains the following uncertainty ranges: ± 0.007 for $E\left( m \right)$, ± 6.0 × 10^–11 cm²ⁿ⁻¹·J¹⁻ⁿ for $\sigma_{\lambda n,s}$, ± 0.3 J·cm⁻² for $B_{\lambda 1,s}$, ± 0.09 J·cm⁻² for $B_{\lambda n,s}$, ± 3.05 × 10⁴ J·mol⁻¹ for $\Delta H_{\lambda n,s}$ and ± 0.07 for $\alpha_{T}$. Though some values may seem somewhat high (close to 30% for $\Delta H_{\lambda n,s}$ for instance), such results are, however, not truly surprising especially, since some experimental errors have been increased on purpose. Besides, the more complex a LII model, the more difficult the optimization problem to be solved and the more the uncertainties related to the estimation of the parameters embedded within its governing equations. Such errors, however, remain perfectly consistent with the uncertainties commonly reported in the literature regarding the values of important factors, such as $E\left( m \right)$ or $\alpha_{T}$ [2, 21, 50]. Furthermore, it is worthy to note that the parameterization procedure conducted herein allowed obtaining results physically meaningful as exemplified by the estimated $E\left( m \right)$ and $\alpha_{T}$ which are comprised within the classical range of considered values as extensively discussed in Sect. 4. Similarly, the derived $B_{\lambda 1,s}$ is well in line with the experimental observations from [51], while the orders of magnitude of other parameters are coherent with expected ones [21].

3.2 Model validation against data from the literature

To further validate the ability of the proposed model to simulate LII signals collected in wide varied conditions, a complementary modeling work has been carried out to reproduce the LII fluence curves and time decays measured by Bejaoui et al. at different HAB in an atmospheric CH₄/O₂/N₂ premixed flat flame [23]. These signals have been obtained using a 1064-nm nearly top-hat laser beam and a detection wavelength of 610 nm. This comprehensive work, moreover, provides the spatial- and temporal profiles of the laser energy, NO-LIF thermometry-derived flame temperatures likewise information regarding primary particle and aggregate sizes determined by transmission electron microscopy. All these input data have, therefore, been considered to perform the calculations leading to the agreement between measured and simulated signals depicted in Figs. 3 and 4.

Fig. 3

Comparison of model predictions with LII fluence curves measured in [23, 46]

Fig. 4

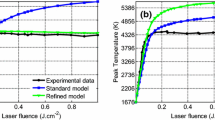
Comparison of model predictions with LII time decays obtained at 12 mm HAB in [23]

The parameters defined in Sect. 2.2.3 have been used as a first stage before applying the above-described multi-parameter optimization procedure. In the end, only the values of $E\left( m \right)$ and $\sigma_{\lambda n,s}$ did require to be adjusted (as specified in the legend of Fig. 3) to reproduce the LII fluence curves measured at each HAB. The fact that the value of the absorption function has been found to increase with the HAB (i.e., with the soot maturation stage) is quite consistent with the observations made in different works [8, 14, 23, 52,53,54] noting that the so-inferred $E\left( m \right)$ are, moreover, in very good agreement with those reported in [29] (see Sect. 4). Concerning the increase of $\sigma_{\lambda n,s}$ at low HAB (i.e., in the early soot formation stage), this latter can be traced to the internal structure changes undergone by the particles as a function of their maturation level. This observation is all the more strengthened by the fact that a constant $\sigma_{\lambda ns}$ of 4.2 × 10^–10 cm²ⁿ⁻¹·J¹⁻ⁿ is found at high HAB (i.e., where soot is mature) noting that such a value is identical to the one assessed in the case of the Diesel flame in which particles rapidly reach a mature-like structure.

Concerning LII time decays, Fig. 4 reports simulated and measured signals at a HAB of 12 mm as an example. To obtain modeled signals merging on a single curve with experimental ones, the selection of a $\alpha_{T}$ of 0.30 has been found to be the most suited. The fact that such a value differs from the one estimated in the Diesel flame can be explained by various factors including the probing of different combustion media leading to far different oxidation products prone to influence $\alpha_{T}$ which largely depends on the chemical structure and molecular mass of the surrounding gases (see [30] and references therein).

Eventually and to complement this set of results that already illustrates the ability of the proposed model to correctly reproduce LII signals collected in different combustion environments, a simulation of the LII fluence curve experimentally monitored by Goulay et al. in a laminar diffusion flame of ethylene [46] is shown in Fig. 3. Signals measured therein have been obtained using the 1064-nm output from an injection-seeded Nd:YAG laser providing pulses with a smooth temporal profile together with spatially homogeneous beams. Additional details regarding this database can be found in [46] as well as in [25] where an attempt to model measured signals had already been undertaken. Here again, using the parameterization proposed in Sect. 2.2.3, while simply adjusting the $E\left( m \right)$ value to 0.31 allows perfectly reproducing measured LII peak intensities as a function of the fluence, as depicted in Fig. 3.

The parameterized model proposed in the present work (with $\sigma_{\lambda n,s}$ = 4.2 × 10^–10 cm²ⁿ⁻¹·J¹⁻ⁿ, $B_{\lambda 1,s}$ = 1.15 J·cm⁻², $B_{\lambda n,s}$ = 0.41 J·cm⁻² and $\Delta H_{\lambda n,s}$ = 1.02 × 10⁵ J·mol⁻¹ for mature soot) thus efficiently simulates signals measured in different combustion media going from laminar gaseous to turbulent spray flames. To the best of the authors’ knowledge, this is probably one of the first times that a given LII model allows reproducing with such an accuracy data measured in wide varied flames characterized by different research groups. This consequently tends to attest the relative reliability of the so-built modeling tool that will, therefore, be used in the next section to infer information regarding the evolution of the optical properties of Diesel soot as a function of their maturation stage. Nevertheless, one still has to note that this research does not pretend to propose a model with parameters that should be considered as universally valid. Additional investigations are indeed more than ever required especially at very high fluences for which additional processes, including annealing, are much more important. Results reported at this stage, however, remain encouraging, while the proposed optimization routine clearly contributes to paving the road for the effective parameterization of refined LII models.

4 Modeling of LII signals at different HAB in the Diesel flame and analysis of assessed thermal accommodation coefficient and soot absorption function

4.1 Simulation of data obtained at 55 and 110 mm HAB in the Diesel flame

To model signals obtained at different HAB in the Diesel flame, the parameterization set in Sect. 2.2.3 and validated in Sect. 3 has been retained except for the maturity-dependent absorption function of soot whose value has been quite logically adjusted as a function of the flame height (see the text labels in Fig. 5). Obviously, measured $T_{g}$ have been considered for the calculations likewise the soot size distribution parameters (including $D_{p}$ of 8 and 20 nm and $N_{p}$ of 60 and 139 at 55 and 110 mm HAB, respectively) which have been derived from the processing of measurements carried out at such specific heights using the equations provided in [14, 55]. Doing so led to obtain the results plotted in Figs. 5 and 6.

Fig. 5

Comparison of simulated and measured LII fluence curves at 55 mm HAB (a) and 110 mm HAB (b)

Fig. 6

Comparison of simulated (lines) and measured (symbols) LII time decays at 55 mm HAB (a) and 110 mm HAB (b). The legend in (a) also applies to (b). Black and gray lines in (a) and (b) denote signals modeled using the thermionic emission sub-models from [38] and [21], respectively

As one can see by looking at Fig. 5, using $E\left( m \right)$ values of 0.18 and 0.30 at 55 and 110 mm HAB, respectively, allows obtaining simulated fluence curves that perfectly match measured ones. Since a $E\left( m \right)$ of 0.23 had been previously assessed at 92 mm HAB (see Sect. 2.2.3), the so-obtained evolution of the soot absorption function as a function of the particle maturation stage is, therefore, well consistent with the trends reported in [8, 14, 23, 52,53,54] (see Sect. 4.3). Furthermore, the fact that no other parameter required to be modified to get the agreement depicted in Fig. 5 once more supports the intrinsic validity of the parameterization proposed in Sect. 2.2.3.

As far as LII time decays are concerned, the results gathered in Fig. 6 clearly show that the model predicts signals merging on a single curve with experimentally monitored ones for each HAB and reported fluence. Besides and for the sake of completeness, a series of additional calculation has been performed using the formulation of the thermionic flux initially suggested by Michelsen in [21] instead of the one developed by Mitrani et al. [38] (see Appendix 1 for more details regarding the corresponding equations). Doing so still allows obtaining an excellent agreement between measured and simulated data provided that $\Delta H_{\lambda n,s}$ and $\alpha_{T}$ are set to 1.70 × 10⁵ J·mol⁻¹ and 0.47, respectively, noting that identical values have been found at 92-mm HAB (though the corresponding curves have not been reported in Fig. 6 for brevity purposes). Such variations of $\Delta H_{\lambda n,s}$ and $\alpha_{T}$ are in fact correlated with the reduced thermionic flux issued from the use of the Mitrani et al. sub-model. To fulfill the energy balance allowing measured signals to be reproduced by the model, the ensuing $\dot{Q}_{{{\text{th}}}}$ reduction thus needs to be compensated by the intensification of other sources of energy loss such as conduction and sublimation through the contribution of non-thermal photodesorption of C₂. In the light of these explanations and even though obtained trends are, in the end, not drastically impacted by the expression selected to account for $\dot{Q}_{{{\text{th}}}}$, the formulation proposed in [38] has been retained for the subsequent analyses as it has been demonstrated therein to be more adapted within the context of LII modeling studies.

4.2 Influence of the shielding effect on ${\varvec{\alpha}}_{{\varvec{T}}}$

The analyses conducted within the Diesel flame led to estimate a $\alpha_{T}$ of 0.49 at 55, 92 and 110 mm HAB. While such a value may seem somewhat high as compared to the usual range of thermal accommodation coefficients used in the literature (from 0.23 to 0.37 according to [21]), it remains consistent with results reported in other studies [8, 47, 54, 56]. One has, moreover, to remind that the so-derived $\alpha_{T}$ value is issued from a model based on a conduction term that incorporates a corrective factor allowing taking the shielding effect [18] into account. This process indeed tends to reduce the conduction flux of aggregates as compared to the rate of energy dissipation calculated considering isolated primary particles. Consequently, for a given conductive cooling rate, considering the aggregate properties and thus the shielding phenomenon will intrinsically lead to derive a higher $\alpha_{T}$ as illustrated in [57]. Neglecting such a process will, on the other hand, translate into an inferred thermal accommodation coefficient of 0.34 (i.e., ~ 31% lower) which is closer to the range of values usually reported. As a majority of the works conducted to estimate $\alpha_{T}$ based on LII modeling neglects the shielding process (see [2] and references therein), the results issued from the present study thus illustrate the particular attention that has to be devoted to the aggregate characteristics so as to estimate $\alpha_{T}$. The fact that a constant thermal accommodation coefficient has been inferred regardless of the HAB in the Diesel flame is, moreover, consistent with the conclusions from [58] who reported no modification of such a parameter for incipient and mature soot. Such an observation is all the more justified by the fact that particles rapidly reach a soot-mature-like structure in the type of atmospheric flame investigated herein [59] in addition to the absence of clear-cut conclusion regarding the possible dependence of $\alpha_{T}$ towards soot maturity [2]. Eventually, one can note that the thermal accommodation coefficient of 0.30 found in Sect. 3.2 when modeling the data collected in the CH₄/O₂/N₂ premixed flat flame from [23] is logically much less impacted by the shielding effect (whose inclusion only modifies the $\alpha_{T}$ value of ~ 7%), since the aggregate size is in this case much lower than in the Diesel flame [23, 29]. In conclusion, and even though it is not claimed that the thermal accommodation coefficients determined in this work should be considered as better than previously proposed ones, they have still been assessed by taking the shielding effect into account. As such, they are thus more likely to correctly account for the impact of the aggregate features on the conduction process while giving insights for the selection of such an important parameter for future LII modeling studies.

4.3 Evaluation of the maturity-dependent absorption function of soot

To analyze the evolution of the absorption function of soot particles as a function of their maturity, the series of $E\left( m \right)$ values previously assessed at 55, 92 and 110 mm HAB have been completed with data acquired at 72, 100 and 116 mm HAB in the Diesel flame. To do so, fluence curves measured at these specific heights have been simulated using the model formulation and parameterization defined in Sect. 2.2, as illustrated in Fig. 7.

Fig. 7

Comparison of simulated and measured LII fluence curves at 72 (a), 100 (b) and 116 (c) mm HAB in the Diesel flame

Obtained results have then been plotted in Fig. 8 as a function of the soot maturation stage represented by means of an adimensional normalized flame height (HAB/HAB_max). For comparison purposes, $E\left( m \right)$ variations reported in other works focusing on the analysis of soot generated during the combustion of different fuels have also been plotted [8, 29, 54]. Finally, data obtained by modeling the signals measured in the Diesel flame while neglecting the effect of MS have also been represented in Fig. 8 so as to better highlight the impact of aggregate properties on inferred $E\left( m \right)$ values.

Fig. 8

$E\left( {m,1064} \right)$ variation as a function of the soot maturity

On the whole, the data depicted in Fig. 8 clearly illustrate that the more the maturity level, the more the soot absorption function as stated in Sects. 3.2 and 4.1. Such an observation can be exemplified by referring to the $E\left( m \right)$ of Diesel soot that rises from 0.18 to 0.31 (0.23 to 0.39 when neglecting multiple scattering) with increasing HAB/HAB_max. It is, moreover, interesting to note that eluding the effect of MS leads to estimate soot absorption function values in the Diesel flame that agree with those determined by Bladh et al. [8] or Olofsson et al. [54] in premixed ethylene/air flat flames of equivalence ratios 2.1 and 2.3, respectively. Such a trend is first consistent with the fact that the LII models used by these authors for $E\left( m \right)$ assessment did not take the effect of MS into account. Besides, it tends to complement the observation made in [15] regarding the marginal impact of the nature of the burnt fuel on the relative evolution of the soot absorption function. It is finally noteworthy that the $E\left( m \right)$ of 0.29 assessed at 92 mm HAB in the Diesel flame when neglecting MS is perfectly coherent with the 0.288 value determined based on the parameterized equation from [14] that is derived from analyses conducted at the same height in the same flame.

On the other hand, integrating the generalized structure factor function from [28, 29] to account for MS results in lower $E\left( m \right)$ values (as observed in Fig. 8) which is in line with the effect of aggregation on the absorption capability of soot [28, 29]. It is, moreover, highly interesting to find in this case a soot maturity-dependence of $E\left( m \right)$ for Diesel soot that fits the results from [29] which are based on a reprocessing of the data acquired in [23] while integrating the effect of MS. Here again, the similar evolution of the absorption function observed for different fuels (i.e., Diesel and methane) tends to illustrate the fundamental importance of the soot maturity stage over the nature of the burnt fuel. Eventually, the data gathered within this study also clearly demonstrate that using the classical Rayleigh-Debye-Gans approximation applied to Fractal Aggregates (RDG-FA), while neglecting internal MS can have significant consequences on the interpretation of optical measurements as well as on the assessment of $E\left( m \right)$ values through LII modeling (a deviation of the order of 24% on average being indeed determined between data assessed with or without integrating the MS effect).

5 Conclusion

The present work pertained to the simulation of an extensive set of LII signals measured in a Diesel flame by implementing a comprehensive model allowing taking the main phenomena known to influence soot laser-induced incandescence into account. In addition to integrating mechanisms standing for saturation of the linear, single- and multi-photon absorption, soot oxidation and annealing likewise cooling by sublimation, conduction, radiation and thermionic emission, the proposed model also combines corrective factors allowing shielding effect and multiple scattering (MS) within aggregates to be considered. A complete parameterization of the so-built model has been achieved by coupling DoE with a genetic algorithm-based solver which allowed deriving soot properties and empirical factors whose values are quite rare for a 1064-nm wavelength. The validity of the developed modeling tool has eventually been verified by satisfactorily simulating LII responses measured in 3 different combustion environments including a CH₄/O₂/N₂ premixed flat flame [23] and two diffusion flames of Diesel [30] and ethylene [46]. Based on obtained results, the following conclusions can be drawn:

• The parameterization procedure implemented herein allowed estimating the following values of absorption and sublimation factors: $\sigma_{\lambda n,s}$ = 4.2 × 10^–10 ± 6.0 × 10^–11 cm²ⁿ⁻¹·J¹⁻ⁿ, $B_{\lambda 1,s}$ = 1.15 ± 0.3 J·cm⁻², $B_{\lambda n,s}$ = 0.41 ± 0.09 J·cm⁻² and $\Delta H_{\lambda n,s}$ = 1.7 × 10⁵ ± 3.05 × 10⁴ J·mol⁻¹. The use of these parameters has been shown to be well suited to reproduce data obtained at different HAB in the Diesel flame investigated herein as well as to properly simulate the LII fluence curves and time decays measured in [23, 46] at HAB for which soot particles can be considered as being mature. Concerning LII signals collected at low HAB in the CH₄/O₂/N₂ flame from [23], an increase of $\sigma_{\lambda n,s}$ from 1.3 × 10^–10 to 4.2 × 10^–10 cm²ⁿ⁻¹·J¹⁻ⁿ has been found to be necessary to perfectly fit measured data and has been traced to the internal structure changes undergone by the particles as a function of their maturation stage.

• The inclusion of the shielding effect within the conduction sub-model led to estimate $\alpha_{T}$ of 0.49 and 0.30 in the Diesel and methane flames, respectively. Such values have been found to be 31% and 7% higher than those determined when neglecting the influence of the aggregate properties. These results thus corroborate previous findings regarding the strong effect of aggregate morphology and size on conductive cooling rates [60, 61]. They, moreover, illustrate that assessing $\alpha_{T}$ through LII modeling without taking the shielding effect into account is likely to induce large biases especially in the case of complex reacting media burning highly sooting fuels (such as Diesel) which are prone to generate large soot aggregates.

• $E\left( m \right)$ values comprised between 0.18 and 0.31 for Diesel soot have been assessed depending on the particle maturation stage. Such a result represents an important finding as data regarding the evolution of the optical properties of Diesel soot is quite rare in the literature as recalled in [14]. Regarding methane soot, the $E\left( m \right)$ determined by modeling the data from [23] led to values comprised between 0.2 and 0.34 which are perfectly in line with those reported in [29].

• Integrating the effect of MS within the absorption process led to estimate $E\left( m \right)$ values for Diesel soot 24% lower on average than when considering the classical RDG-FA theory. This, therefore, supports the importance of thoroughly considering aggregate properties to be able to derive consistent information on soot optical properties by LII modeling.

• The observed $E\left( m \right)$ evolution as a function of the soot maturity stage has been found to be well consistent with trends reported in other studies conducted using wide varied fuels. This consequently tends to illustrate the fundamental importance of the soot maturity level over the nature of the burnt fuel.

In the end, this research contributed to improving the predictive capability of simulation tools used to account for laser-induced incandescence of soot while proposing an advanced approach allowing parameterizing refined LII models. Besides and even though it is not claimed that the properties assessed in the present work should be preferred as compared to values classically found in the literature, they have at least the merit of being issued from analyses conducted by considering important processes (such as shielding and MS) that are known to influence soot LII. That being said, and despite its established effectiveness, the fully parameterized model that has been developed does not intend to be considered as universally valid. Additional validations and improvements are indeed required to rule on its consistency in the very high fluence regime where annealing will be quite active for instance while considering other phenomena (such as soot coating [60, 62]) which can significantly impact the energy balance of heated particles.

6 Appendix 1: Detailed description of the LII model

The governing equations underlying the phenomena integrated within the model used in this study are detailed in the present appendix. The nomenclature defining the different functions and parameters introduced below together with their related values is provided in Appendix 2.

As briefly explained in Sect. 2.2.1, the core of the proposed model draws on a system of coupled differential equations depicting the variations of the soot internal energy rate ($\frac{{{\text{d}}U_{{\text{int}}} }}{{{\text{d}}t}}$) and mass ($\frac{{dM_{p} }}{dt}$) as a function of time (see Eq. (1)). To do so, mechanisms standing for absorption ($\dot{Q}_{{{\text{abs}}}}$), annealing ($\dot{Q}_{{{\text{ann}}}}$), oxidation ($\dot{Q}_{ox}$), radiation ($\dot{Q}_{{{\text{rad}}}}$), thermionic emission ($\dot{Q}_{{{\text{th}}}}$), sublimation ($\dot{Q}_{sub}$) and conduction ($\dot{Q}_{cond}$) have been considered.

Concerning the mass of the primary particle $M_{p}$, it has been expressed as a function of $D_{p}$ following:

$$M_{p } = \frac{{\pi \,\cdot\,D_{p}^{3} }}{6}/\left( {\frac{{1 - X_{a} }}{{\rho_{s} }} + \frac{{X_{a} }}{{\rho_{a} }}} \right)$$

(8)

According to [17], the rate of change of the energy stored by the particles during the LII process has been put into equation based on a relation accounting for both the contributions of unannealed (subscript ‘s’) and annealed (subscript ‘a’) soot fractions:

$$\frac{{{\text{d}}U_{{\text{int}}} }}{{{\text{d}}t}} = N_{p} \,\cdot\, \frac{\pi }{6} \,\cdot\, D_{p}^{3} \,\cdot\, \frac{{{\text{d}}T_{p} }}{{{\text{d}}t}} \,\cdot\, \left[ {\rho_{s} \,\cdot\, c_{s} \,\cdot\, \left( {1 - X_{a} } \right) + \rho_{a} \,\cdot\, c_{a} \,\cdot\, X_{a} } \right]$$

(9)

Besides and as specified in Sect. 2.2.1 the absorption term that has been implemented is derived from the one proposed by Michelsen in [17, 21] so as to account for saturation of linear, single- and multi-photon absorption processes. Its detailed expression follows an equation of the type:

$$\begin{aligned} \dot{Q}_{{{\text{abs}}}} & = C_{{{\text{abs}}, s}}^{{{\text{multi}}}} \,\cdot\, \frac{{f_{1,s} \,\cdot\, B_{\lambda 1,s} }}{{\mathop \smallint \nolimits_{0}^{{t_{l} }} q_{\exp } \left( t \right){\text{d}}t}} \,\cdot\, \left\{ {1 - \exp \left[ { - \frac{{F \,\cdot\, q_{\exp } \left( t \right)}}{{B_{\lambda 1,s} }}} \right]} \right\} \\ & \quad + C_{{{\text{abs}}, a}}^{{{\text{multi}}}} \,\cdot\, \frac{{f_{1,a} \,\cdot\, B_{\lambda 1,a} }}{{\mathop \smallint \nolimits_{0}^{{t_{l} }} q_{\exp } \left( t \right){\text{d}}t}} \,\cdot\, \left\{ {1 - \exp \left[ { - \frac{{F \,\cdot\, q_{\exp } \left( t \right)}}{{B_{\lambda 1,a} }}} \right]} \right\} \\ & \quad + N_{p} \,\cdot\, \frac{n \,\cdot\, h \,\cdot\, c}{{\lambda_{l} }} \,\cdot\, \left( {k_{\lambda n,s} + k_{\lambda n,a} } \right) \\ \end{aligned}$$

(10)

noting that the generalized structure factor function proposed by [29] to represent the effect of multiple scattering within aggregates has been integrated in the expressions standing for the absorption cross section of unannealed and annealed soot, so that:

$$C_{{{\text{abs}},s}}^{{{\text{multi}}}} = N_{{{\text{tot}}}} \,\cdot\, \left( {1 - X_{a} } \right) \,\cdot\, \frac{{\pi^{2} \,\cdot\, D_{p}^{3} }}{{\lambda_{l} }} \,\cdot\, E\left( m \right) \,\cdot\, h_{{\lambda ,N_{p} }} \,\cdot\,N_{p} \,\cdot\,p\left( {N_{p} } \right)$$

(11)

and

$$C_{{{\text{abs}},a}}^{{{\text{multi}}}} = N_{{{\text{tot}}}} \,\cdot\, X_{a} \,\cdot\, \frac{{\pi^{2} \,\cdot\, D_{p}^{3} }}{{\lambda_{l} }} \,\cdot\, f_{a} \,\cdot\, E_{a} \left( m \right) \,\cdot\, h_{{\lambda ,N_{p} }} \,\cdot\,N_{p} \,\cdot\,p\left( {N_{p} } \right)$$

(12)

with

$$h_{{\lambda , N_{p} }} = h_{{\lambda , N_{p} }}^{\infty } + \left( {1 - h_{{\lambda , N_{p} }}^{\infty } } \right) \,\cdot\, \exp \left( { - \frac{2}{3} \,\cdot\, \sqrt {N_{p} - 1} } \right)$$

(13)

where

$$h_{{\lambda , N_{p} }}^{\infty } = 1.11 \,\cdot\, \alpha_{1}^{\prime 2} \,\cdot\, N_{p}^{{2 \,\cdot\, \left( {\alpha_{2}^{^{\prime}} - 1} \right)}}$$

(14)

with

$$\alpha_{1}^{\prime } = \left( {1.0209 - 24.0657 \,\cdot\, \frac{{\ln \left( {{\raise0.7ex\hbox{$\lambda $} \!\mathord{\left/ {\vphantom {\lambda {\lambda_{0} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\lambda_{0} }$}} \,\cdot\, {\raise0.7ex\hbox{${D_{{\text{p,ref}}} }$} \!\mathord{\left/ {\vphantom {{D_{{\text{p,ref}}} } {D_{p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{p} }$}}} \right)}}{{{\raise0.7ex\hbox{$\lambda $} \!\mathord{\left/ {\vphantom {\lambda {\lambda_{0} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\lambda_{0} }$}} \,\cdot\ {\raise0.7ex\hbox{${D_{{p,{\text{ref}}}} }$} \!\mathord{\left/ {\vphantom {{D_{{p,{\text{ref}}}} } {D_{p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{p} }$}}}} + 2244.37 \,\cdot\, \left( {{\raise0.7ex\hbox{$\lambda $} \!\mathord{\left/ {\vphantom {\lambda {\lambda_{0} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\lambda_{0} }$}} \,\cdot\, {\raise0.7ex\hbox{${D_{{p,{\text{ref}}}} }$} \!\mathord{\left/ {\vphantom {{D_{{p,{\text{ref}}}} } {D_{p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{p} }$}}} \right)^{ - 1.5} } \right)^{ - 1}$$

(15)

and

$$\alpha_{2}^{\prime } = \left( {0.9871 + 2.4878 \,\cdot\, \frac{{ln\left( {{\raise0.7ex\hbox{$\lambda $} \!\mathord{\left/ {\vphantom {\lambda {\lambda_{0} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\lambda_{0} }$}} \,\cdot\, {\raise0.7ex\hbox{${D_{{p,{\text{ref}}}} }$} \!\mathord{\left/ {\vphantom {{D_{{p,{\text{ref}}}} } {D_{p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{p} }$}}} \right)}}{{{\raise0.7ex\hbox{$\lambda $} \!\mathord{\left/ {\vphantom {\lambda {\lambda_{0} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\lambda_{0} }$}} \,\cdot\, {\raise0.7ex\hbox{${D_{{p,{\text{ref}}}} }$} \!\mathord{\left/ {\vphantom {{D_{{p,{\text{ref}}}} } {D_{p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{p} }$}}}}} \right)^{ - 1}$$

(16)

Concerning the rate constants related to the photodesorption of C₂ clusters from unannealed and annealed soot fractions, they have been expressed as follows:

$$\begin{aligned} k_{\lambda n,s} & = \left( {1 - X_{a} } \right) \,\cdot\, \frac{{\lambda_{l} }}{n \,\cdot\, h \,\cdot\, c} \,\cdot\, \frac{{\sigma_{\lambda n,s} \,\cdot\, \pi \,\cdot\, D_{p}^{3} \,\cdot\, N_{ss} }}{6} \\ & \quad \,\cdot\, \frac{{\left( {B_{\lambda n,s} } \right)^{n} }}{{\mathop \smallint \nolimits_{0}^{{t_{l} }} \left[ {q_{\exp } \left( t \right)} \right]^{n} dt}} \,\cdot\, \left\{ {1 - \exp \left[ { - \left( {\frac{{F \,\cdot\, q_{\exp } \left( t \right)}}{{B_{\lambda n,s} }}} \right)^{n} } \right]} \right\} \\ \end{aligned}$$

(17)

and

$$\begin{aligned} k_{\lambda n,a} & = X_{a} \,\cdot\, \frac{{\lambda_{l} }}{n \,\cdot\, h \,\cdot\, c} \,\cdot\, \frac{{\sigma_{\lambda n,a} \,\cdot\, \pi \,\cdot\, D_{p}^{3} \,\cdot\, N_{sa} }}{6} \\ & \quad \,\cdot\, \frac{{\left( {B_{\lambda n,a} } \right)^{n} }}{{\mathop \smallint \nolimits_{0}^{{t_{l} }} \left[ {q_{\exp } \left( t \right)} \right]^{n} {\text{d}}t}} \,\cdot\, \left\{ {1 - \exp \left[ { - \left( {\frac{{F \,\cdot\, q_{\exp } \left( t \right)}}{{B_{\lambda n,a} }}} \right)^{n} } \right]} \right\} \\ \end{aligned}$$

(18)

As far as the rate of energy increase by annealing is concerned, its governing equation is of the type:

$$\dot{Q}_{{{\text{ann}}}} = N_{p} \,\cdot\, \frac{{ - \Delta H_{{{\text{imig}}}} \,\cdot\, k_{{{\text{imig}}}} \,\cdot\, N_{d} - \Delta H_{{{\text{vmig}}}} \,\cdot\, k_{{{\text{vmig}}}} \,\cdot\, N_{d} }}{{N_{A} }}$$

(19)

where the number of Frenkel Schottky defects $N_{d}$ can be estimated by solving the ordinary differential equation:

$$\frac{{{\text{d}}N_{d} }}{{{\text{d}}t}} = X_{a} \,\cdot\, \frac{{N_{c} }}{2} \,\cdot\, k_{{{\text{diss}}}} - k_{{{\text{imig}}}} \,\cdot\, N_{d} - k_{{{\text{vmig}}}} \,\cdot\, N_{d}$$

(20)

in which the annealed fraction $X_{a}$ computes as:

$$X_{a} = 1 - \frac{{N_{d} }}{{X_{d} \,\cdot\, N_{c} }}$$

(21)

The radiative emission from laser-heated soot has been calculated for its part by integrating the Planck function over the wavelength while taking the re-absorption of background emission likewise the effect of multiple scattering within aggregates into account through the formulation of the $C_{{{\text{abs}}, a}}^{{{\text{multi}}}}$ and $C_{{{\text{abs}}, s}}^{{{\text{multi}}}}$ terms:

$$\dot{Q}_{{{\text{rad}}}} = 8 \,\cdot\, \pi \,\cdot\, h \,\cdot\, c^{2} \,\cdot\, \mathop \smallint \limits_{0}^{{\lambda_{\infty } }} \frac{{ C_{{{\text{abs}},s}}^{{{\text{multi}}}} + C_{{{\text{abs}},a}}^{{{\text{multi}}}} }}{{\lambda^{5} }} \,\cdot\, \left[ {\frac{1}{{\exp \left( {{\raise0.7ex\hbox{${h \,\cdot\, c}$} \!\mathord{\left/ {\vphantom {{h \,\cdot\, c} {\lambda \,\cdot\, k_{B} \,\cdot\, T_{p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\lambda \,\cdot\, k_{B} \,\cdot\, T_{p} }$}}} \right) - 1}} - \frac{1}{{\exp \left( {{\raise0.7ex\hbox{${h \,\cdot\, c}$} \!\mathord{\left/ {\vphantom {{h \,\cdot\, c} {\lambda \,\cdot\, k_{B} \,\cdot\, T_{g} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\lambda \,\cdot\, k_{B} \,\cdot\, T_{g} }$}}} \right) - 1}}} \right]{\text{d}}\lambda$$

(22)

According to [37], the oxidation rate of soot can be expressed based on a relation of the type:

$$\dot{Q}_{ox} = N_{p} \,\cdot\, \frac{1 }{{ W_{1} }} \,\cdot\, \left[ {\mathop \smallint \limits_{{T_{ref} }}^{{T_{f}^{CO} }} C_{p}^{CO} \left( T \right){\text{d}}T - \frac{1}{2} \,\cdot\, \mathop \smallint \limits_{{T_{ref} }}^{{T_{g} }} C_{p}^{{O_{2} }} \left( T \right){\text{d}}T + \frac{R}{2} \,\cdot\, \left( {T_{f}^{CO} - T_{g} } \right) + \Delta H_{ox} } \right] \,\cdot\, \left( {\frac{{{\text{d}}M_{p} }}{{{\text{d}}t}}} \right)_{ox}$$

(23)

where the variation of the particle mass during the oxidation process is calculated as follows:

$$\left( {\frac{{{\text{d}}M_{p} }}{{{\text{d}}t}}} \right)_{ox} = \frac{{ - 2 \,\cdot\, \pi \,\cdot\, D_{p}^{2} \,\cdot\, W_{1} \,\cdot\, \left( {k_{ox,s} + k_{ox,a} } \right)}}{{N_{A} }}$$

(24)

with

$$k_{ox,s} = 12 \,\cdot\, P_{{O_{2} }} \,\cdot\, \left[ {\frac{{k_{a} \,\cdot\, \chi_{A} }}{{1 + k_{Z} \,\cdot\, P_{{O_{2} }} }} + k_{b} \,\cdot\, \left( {1 - \chi_{A} } \right)} \right] \,\cdot\, \left( {1 - X_{a} } \right)$$

(25)

and

$$k_{ox,a} = \frac{{2.8 \,\cdot\, Z_{ox} }}{{\sqrt {T_{g} } }} \,\cdot\, \exp \left( {\frac{{ - 1.4 \times 10^{5} }}{{R \,\cdot\, T_{p} }}} \right) \,\cdot\, X_{a}$$

(26)

noting that the $\chi_{A}$ and $Z_{ox}$ terms expresses as:

$$\chi_{A} = \frac{1}{{1 + \frac{{k_{T} }}{{k_{b} \,\cdot\,P_{{O_{2} }} }}}}$$

(27)

$$Z_{ox} = \frac{{P_{{O_{2} }} }}{{k_{p} \,\cdot\, T_{g} }} \,\cdot\, \sqrt {\frac{{R_{m} \,\cdot\, T_{g} }}{{2 \,\cdot\, \pi \,\cdot\, W_{{O_{2} }} }}}$$

(28)

Concerning the energy loss induced by the thermal ejection of electrons from the heated particles, it has been expressed according to the formulation recently proposed by Mitrani et al. in [38]:

$$\dot{Q}_{th, \phi + \Delta \phi } = N_{p} \,\cdot\, \frac{{4 \,\cdot\, \left( {\phi + \Delta \phi } \right) \,\cdot\, m_{el} \,\cdot\, \left( {\pi \,\cdot\, D_{p} \,\cdot\, k_{B} \,\cdot\, T_{p} } \right)^{2} }}{{h^{3} }} \,\cdot\, \exp \left[ { - \frac{{\left( {\phi + \Delta \phi } \right)}}{{k_{B} \,\cdot\, T_{p} }}} \right]$$

(29)

where ${\Delta }\phi$ that describes the increased barrier for further electron emission due to the positive charge buildup can be obtained by solving the following equation at each time step $t$:

$$\Delta \phi \left( t \right) = 8 \,\cdot\, \pi \,\cdot\, m_{el} \,\cdot\, k_{el} \,\cdot\, D_{p} \,\cdot\, \mathop \smallint \limits_{0}^{t} \frac{{\left( {\pi \,\cdot\, c_{el} \,\cdot\, k_{B} \,\cdot\, T_{p} } \right)^{2} }}{{h^{3} }} \,\cdot\, \exp \left[ { - \frac{{\left( {\phi + \Delta \phi } \right)}}{{k_{B} \,\cdot\, T_{p} }}} \right] \, {\text{d}}t$$

(30)

It is noteworthy that the Mitrani et al.’s formulation of the thermionic fluxes has been demonstrated in [38] to be more adapted than the one used by Michelsen [21] based on the Richardson–Dushman equation [39] as it allows, as illustrated above, correcting the values of emitted current due to the accumulation of positive charge in laser-heated nanoparticles that increase the energy barrier for further emission of electrons. That being said, the formulation of $\dot{Q}_{th}$ proposed in [21] has still been considered for comparison purposes within the framework of the discussion proposed in Sect. 4. To do so, the equation below has been implemented:

$$\dot{Q}_{th} = N_{p} \,\cdot\, \frac{{4 \,\cdot\, \phi \,\cdot\, m_{el} \,\cdot\, \left( {\pi \,\cdot\, D_{p} \,\cdot\, k_{B} \,\cdot\, T_{p} } \right)^{2} }}{{h^{3} }} \,\cdot\, \exp \left( { - \frac{\phi }{{k_{B} \,\cdot\, T_{p} }}} \right)$$

(31)

The selected sublimation sub-model is derived from the one proposed in [17]. It especially allows the contributions of both the unannealed and annealed soot fractions to be considered as depicted in the equation:

$$\begin{aligned} \dot{Q}_{{{\text{sub}}}} & = - N_{p} \,\cdot\, \mathop \sum \limits_{j = 1}^{5} \frac{1}{{W_{j} }} \,\cdot\, \left( {\frac{{{\text{d}}M_{p} }}{{{\text{d}}t}}} \right)_{{{\text{sub}}, j}} \\ & \quad \,\cdot\, \left[ {\frac{{\Delta H_{j} \,\cdot\, \left( {P_{{{\text{sat}}}}^{{C_{j} }} - P_{\lambda s} - P_{{{\text{diss}}}} - P_{\lambda a} } \right) + \Delta H_{\lambda n,s} \,\cdot\, P_{\lambda s} + \Delta H_{{{\text{diss}}}} \,\cdot\, P_{{{\text{diss}}}} + \Delta H_{\lambda n,a} \,\cdot\, P_{\lambda a} }}{{P_{{{\text{sat}}}}^{{C_{j} }} }}} \right] \\ \end{aligned}$$

(32)

where the rate of mass loss computes independently for each C_j-specie following:

$$\left( {\frac{{{\text{d}}M_{p} }}{{{\text{d}}t}}} \right)_{{{\text{sub}}, j}} = \frac{{ - \pi \,\cdot\, D_{p}^{2} \,\cdot\, W_{j} \,\cdot\, \alpha_{j} \,\cdot\, B_{j} }}{{R_{p} \,\cdot\, T_{p} }}\,\cdot\,\sqrt {\frac{{R_{m} \,\cdot\, T_{p} }}{{2 \,\cdot\, \pi \,\cdot\, W_{j} }}}$$

(33)

with

$$B_{j} = \left\{ {\begin{array}{*{20}l} {\frac{{2 \,\cdot\, {\mathcal{D}}_{{{\text{eff}}}} \,\cdot\, P_{sat}^{{C_{j} }} }}{{D_{p} \,\cdot\, \alpha_{j} \,\cdot\, \sqrt {\frac{{R_{m} \,\cdot\, T_{p} }}{{2 \,\cdot\, \pi \,\cdot\, W_{j} }}} + 2 \,\cdot\, {\mathcal{D}}_{{{\text{eff}}}} }},} \hfill & {{\text{if}} \frac{{P_{{{\text{sat}}}}^{{C_{j} }} }}{{P_{g} }} < 0.003} \hfill \\ {P_{{{\text{sat}}}}^{{C_{j} }} - P_{{{\text{surf}}}}^{{C_{j} }} ,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$

(34)

and

$${\mathcal{D}}_{{{\text{eff}}}} = {\mathcal{D}}_{{{\text{eff}}}}^{{C_{3} }} \,\cdot\,\left( {1 - X_{a} } \right) + {\mathcal{D}}_{{{\text{eff}}}}^{{C_{2} }} \,\cdot\,X_{a}$$

(35)

noting that the values of the effective diffusion coefficients of C₂ and C₃ clusters (i.e., ${\mathcal{D}}_{{{\text{eff}}}}^{{C_{2} }}$ and ${\mathcal{D}}_{{{\text{eff}}}}^{{C_{3} }}$) can be estimated using temperature-dependent expressions of the type:

$${\mathcal{D}}_{{{\text{eff}}}}^{{C_{j} }} = \frac{{3 \,\cdot\, f \,\cdot\, k_{P} \,\cdot\, T_{p} }}{{4 \,\cdot\, \sigma_{j} \,\cdot\, P_{g} }} \,\cdot\, \sqrt {\frac{{R_{m} }}{{\pi \,\cdot\, W_{j} }}} \,\cdot\, \frac{{\left[ {\left( {T_{p} + \frac{{A_{0} }}{{A_{1} }}} \right)^{2} - \left( {T_{g} + \frac{{A_{0} }}{{A_{1} }}} \right)^{2} } \right]}}{{\left[ {\sqrt {T_{p} } \,\cdot\, \left( {T_{p} + \frac{{3 \,\cdot\, A_{0} }}{{A_{1} }}} \right) - \sqrt {T_{g} } \,\cdot\, \left( {T_{g} + \frac{{3 \,\cdot\, A_{0} }}{{A_{1} }}} \right)} \right]}}$$

(36)

The calculation of the saturation partial pressure $P_{sat}^{{C_{j} }}$ can be achieved for its part based on the equation:

$$P_{{{\text{sat}}}}^{{C_{j} }} = \left\{ {\begin{array}{*{20}l} {P_{{{\text{phot}}}}^{{C_{j} }} = P_{\lambda s} + P_{{{\text{diss}}}} + P_{\lambda a} ,} \hfill & {{\text{if}}\;j = 2\;{\text{and}}\;P_{{{\text{eq}}}}^{{C_{j} }} < P_{{{\text{phot}}}}^{{C_{j} }} } \hfill \\ {P_{{{\text{eq}}}}^{{C_{j} }} = P_{{{\text{ref}}}} \,\cdot\, \exp \left[ {\frac{{ - \Delta H_{j} }}{R} \,\cdot\, \left( {\frac{1}{{T_{p} }} - \frac{1}{{T_{{{\text{ref}}}}^{{C_{j} }} }}} \right)} \right],} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$

(37)

in which the effective pressures calculated based on the rate of non-thermal photodesorption of C_j clusters from the unannealed $P_{\lambda s}$ and annealed $P_{\lambda a}$ particles are expressed as follows:

$$P_{\lambda ,k} = \left\{ {\begin{array}{*{20}l} {\frac{{k_{p} \,\cdot\, T_{p} \,\cdot\, k_{\lambda n,k} }}{{\pi \,\cdot\, D_{p}^{2} \,\cdot\, \alpha_{j} }} \,\cdot\, \sqrt {\frac{{2 \,\cdot\, \pi \,\cdot\, W_{j} }}{{R_{m} \,\cdot\, T_{p} }},} } \hfill & {{\text{if}}\;j = 2 } \hfill \\ {0,} \hfill & {\text{otherwise }} \hfill \\ \end{array} } \right.$$

(38)

where the subscript ‘k’ stands for either ‘s’ or ‘a’.

Regarding the relation accounting for the effective pressure issued from the rate of thermal photodesorption from the annealed soot fraction, it is calculated using the relation:

$$P_{{{\text{diss}}}} = X_{a} \,\cdot\, \frac{{k_{p} \,\cdot\, T_{p} \,\cdot\, N_{c} }}{{2 \,\cdot\, \pi \,\cdot\, D_{p}^{2} \,\cdot\, \alpha_{j} }} \,\cdot\, \sqrt {\frac{{2 \,\cdot\, \pi \,\cdot\, W_{j} }}{{R_{m} \,\cdot\, T_{p} }}} \,\cdot\, k_{{{\text{diss}}}}$$

(39)

while the partial pressure of C_j at the particle surface is put into equation following:

$$P_{{{\text{surf}}}}^{{C_{j} }} = \frac{{P_{g} }}{\eta } \,\cdot\, \left[ {1 - \frac{{2 \,\cdot\, {\mathcal{D}}_{{{\text{eff}}}} }}{{D_{p} \,\cdot\, \alpha_{j} }} \,\cdot\, \sqrt {\frac{{2 \,\cdot\, \pi \,\cdot\, W_{j} }}{{R_{m} \,\cdot\, T_{p} }}} \,\cdot\, J\left( \xi \right)} \right]$$

(40)

with

$$\eta = \frac{1}{{P_{{{\text{sat}}}}^{{C_{j} }} }} \,\cdot\, \left( {P_{g} + \mathop \sum \limits_{j = 1}^{5} P_{{{\text{sat}}}}^{{C_{j} }} } \right)$$

(41)

and

$$\xi = \frac{{D_{p} \,\cdot\, \alpha_{j} }}{{2 \,\cdot\, {\mathcal{D}}_{{{\text{eff}}}} }} \,\cdot\, \sqrt {\frac{{R_{m} \,\cdot\, T_{p} }}{{2 \,\cdot\, \pi \,\cdot\, W_{j} }}} \,\cdot\, \exp \left[ {\frac{{D_{p} \,\cdot\, \alpha_{j} }}{{2 \,\cdot\, {\mathcal{D}}_{{{\text{eff}}}} }} \,\cdot\, \sqrt {\frac{{R_{m} \,\cdot\, T_{p} }}{{2 \,\cdot\, \pi \,\cdot\, W_{j} }}} \,\cdot\,\left( {1 - \frac{{\eta \,\cdot\, P_{{{\text{sat}}}}^{{C_{j} }} }}{{P_{g} }}} \right)} \right]$$

(42)

where

$$J\left( \xi \right) = \left\{ {\begin{array}{*{20}l} {\xi ,} \hfill & {{\text{if}}\;\xi \le 0.003} \hfill \\ {0.92267 \,\cdot\, \xi^{0.98535} , } \hfill & {{\text{for}}\;0.003 < \xi < 0.05} \hfill \\ {5.815 \times 10^{ - 1} + 3.496 \times 10^{ - 1} \,\cdot\, \ln \left( \xi \right) + 6.516} \hfill & {} \hfill \\ { \times 10^{ - 2} \,\cdot\, \left( {\ln \left( \xi \right)} \right)^{2} + 1.667 \times 10^{ - 3} \,\cdot\, \left( {\ln \left( \xi \right)} \right)^{3} - 6.031} \hfill & {} \hfill \\ { \times 10^{ - 4} \,\cdot\, \left( {\ln \left( \xi \right)} \right)^{4} - 4.161 \times 10^{ - 5} \,\cdot\, \left( {\ln \left( \xi \right)} \right)^{5} , } \hfill & {{\text{for}}\;0.05 \le \xi \le 300} \hfill \\ { - 1.189 + 9.187 \times 10^{ - 1} \,\cdot\, \left( {\ln \left( \xi \right)} \right)} \hfill & {{\text{if}}\;\xi > 300} \hfill \\ \end{array} } \right.$$

(43)

To compute the energy loss at the surface of soot particles through collisions with the surrounding gas molecules, a Fuchs conduction sub-model [40, 41] has been implemented. This latter actually relies on the estimation of the temperature $T_{\delta }$ and distance $\delta$ of a delimiting sphere separating the free molecular (FM) from the continuum (C) conduction regimes. In the first case, the rate of energy dissipation by conduction can be expressed as:

$$\dot{Q}_{{{\text{cond,}}FM}} = \frac{1}{8} \,\cdot\, \pi \,\cdot\, \alpha_{T} \,\cdot\, D_{HC}^{2} \,\cdot\, P_{g} \,\cdot\, \sqrt {\frac{{8 \,\cdot\, k_{B} \,\cdot\, T_{\delta } }}{{\pi \,\cdot\, M_{g} }}} \,\cdot\, \frac{{\gamma^{*} + 1}}{{\gamma^{*} - 1}} \,\cdot\, \left( {\frac{{T_{p} }}{{ T_{\delta } }} - 1} \right)$$

(44)

where

$$\frac{1}{{\gamma^{*} - 1}} = \frac{1}{{T_{p} - T_{\delta } }} \,\cdot\, \mathop \smallint \limits_{{T_{\delta } }}^{{T_{p} }} \frac{{{\text{d}}T}}{\gamma - 1}$$

(45)

while $D_{HC}$ stands for the equivalent heat conduction diameter [18] allowing taking the shielding effect into account:

$$D_{HC} = \left\{ {\begin{array}{*{20}l} {D_{p} ,} \hfill & {{\text{if}}\;N_{p} = 1} \hfill \\ {D_{p} \,\cdot\, \left( {\frac{{N_{p} }}{{k_{h} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {D_{h} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${D_{h} }$}}}} ,} \hfill & {{\text{if}}\;N_{p} > 1} \hfill \\ \end{array} } \right.$$

(46)

On the other hand, when the conduction occurs in the continuum regime, the rate of energy dissipation then expresses:

$$\dot{Q}_{{{\text{cond}},C}} = 4 \,\cdot\, \pi \,\cdot\, \left( {\frac{{D_{HC} }}{2} + \delta } \right) \,\cdot\, \mathop \smallint \limits_{{T_{g} }}^{{T_{\delta } }} k_{g} \left( T \right){\text{d}}T$$

(47)

Since $\dot{Q}_{{{\text{cond}},{\text{FM}}}}$ and $\dot{Q}_{{{\text{cond}},C}}$ must be equal at the interface of the delimiting sphere, the distance δ can be estimated based on the equality:

$$\frac{{2 \,\cdot\, \delta + D_{HC} }}{{D_{HC} }} = \frac{{D_{HC}^{2} }}{{4 \,\cdot\, \lambda_{\delta }^{2} }} \,\cdot\, \left( {\frac{1}{5} \,\cdot\, {\Lambda }_{1}^{5} - \frac{1}{3} \,\cdot\, {\Lambda }_{2} \,\cdot\, {\Lambda }_{1}^{3} + \frac{2}{15} \,\cdot\, {\Lambda }_{2}^{5/2} } \right)$$

(48)

where

$${\Lambda }_{1} = 1 + \frac{{2 \,\cdot\, \lambda_{\delta } }}{{D_{HC} }}$$

(49)

$${\Lambda }_{2} = 1 + \left( {\frac{{2 \,\cdot\, \lambda_{\delta } }}{{D_{HC} }}} \right)^{2}$$

(50)

and

$$\lambda_{\delta } = \frac{{k_{g} \left( {T_{\delta } } \right) \,\cdot\, \sqrt {T_{\delta } } \,\cdot\, \left[ {\gamma \left( {T_{\delta } } \right) - 1} \right]}}{{k_{g} \left( {T_{g} } \right) \,\cdot\, \sqrt {T_{g} } \,\cdot\, \left[ {\gamma \left( {T_{g} } \right) - 1} \right]}} \,\cdot\, \frac{{f\left( {T_{g} } \right)}}{{f\left( {T_{\delta } } \right)}} \,\cdot\, \lambda_{g}$$

(51)

in which the mean free path of the gas molecules $\lambda_{g}$ is given by:

$$\lambda_{g} = \frac{{k_{g} \left( {T_{g} } \right)}}{{f\left( {T_{g} } \right) \,\cdot\, P_{g} }} \,\cdot\, \left[ {\gamma \left( {T_{g} } \right) - 1} \right] \,\cdot\, \sqrt {\frac{{\pi \,\cdot\, M_{g} \,\cdot\, T_{g} }}{{2 \,\cdot\, k_{B} }}}$$

(52)

Eventually, the generation of theoretical LII signals has been achieved by integrating a Planck function over the spectral range of the detection system, so that:

$$\begin{aligned} S_{{{\text{LII}}}} \left( {\Omega_{\exp } ,D_{p} ,N_{p} ,t} \right) & = 8 \,\cdot\, \pi \,\cdot\, h \,\cdot\, c^{2} \\ & \quad \,\cdot\, \mathop \smallint \limits_{{\Delta \lambda_{\det } }}^{{}} \frac{{ C_{{{\text{abs}},s}}^{{{\text{multi}}}} + C_{{{\text{abs}},a}}^{{{\text{multi}}}} }}{{\lambda^{5} }} \,\cdot\, \left\{ {\frac{{{\mathcal{R}}_{\det } }}{{\left[ {\exp \left( {\frac{h \,\cdot\, c}{{\lambda \,\cdot\, k_{B} \,\cdot\, T_{p} }}} \right) - 1} \right]}} - \frac{{{\mathcal{R}}_{\det } }}{{\left[ {\exp \left( {\frac{h \,\cdot\, c}{{ \lambda \,\cdot\, k_{B} \,\cdot\, T_{g} }}} \right) - 1} \right]}}} \right\} \\ & \quad \,\cdot\, p\left( {D_{p} } \right) \,\cdot\, p\left( {N_{p} } \right) {\text{d}}\lambda \\ \end{aligned}$$

(53)

and

$$S_{{{\text{LII}}}} \left( t \right) = \mathop \smallint \limits_{{{\Omega }_{\exp } }}^{{}} \mathop \smallint \limits_{{D_{p} }}^{{}} \mathop \smallint \limits_{{N_{p} }}^{{}} S_{{{\text{LII}}}} \left( {{\Omega }_{\exp } ,D_{p} ,N_{p} ,t} \right) {\text{d}}\Omega_{\exp } {\text{ d}}D_{p} {\text{d}}N_{p}$$

(54)

7 Appendix 2: Nomenclature

$A_{0}$	Parameter used for the determination of the effective diffusion constant of Cj clusters (9.0235 × 10–4 W·cm−1·K−1 for C2 and 5.7683 × 10–4 W·cm−1·K−1 for C3)
$A_{1}$	Parameter used for the determination of the effective diffusion constant of Cj clusters (3.8475 × 10–7 W·cm−1·K−2 for C2 and 1.8429 × 10–7 W·cm−1·K−2 for C3)
$B_{j}$	Parameter representing the influence of diffusive and convective mass and heat transfers during sublimation (bar)
$B_{\lambda 1,a}$	Empirically determined saturation coefficient for linear absorption of annealed soot (J·cm−2)
$B_{\lambda 1,s}$	Empirically determined saturation coefficient for linear absorption of unannealed soot (J·cm−2)
$B_{\lambda n,a}$	Empirically determined saturation coefficient for multi-photon absorption of annealed soot (J·cm−2)
$B_{\lambda n,s}$	Empirically determined saturation coefficient for multi-photon absorption of unannealed soot (J·cm−2)
$c$	Speed of light (2.998 × 1010 cm·s−1)
$c_{a}$	Specific heat of annealed soot [17] (J·g−1·K−1)
$c_{el}$	Charge of an electron (1.60218 × 10–19 C)
$c_{s}$	Specific heat of unannealed soot [17] (J·g−1·K−1)
$C_{abs,a}^{multi}$	Absorption cross section of the annealed fraction of aggregated soot particles (cm2)
$C_{abs,s}^{multi}$	Absorption cross section of the unannealed fraction of aggregated soot particles (cm2)
$C_{p}^{CO}$	Molar heat capacity of CO (J·mol−1·K−1)
$C_{p,m}$	Temperature-dependent molar heat capacity (J·mol−1·K−1)
$C_{p}^{{O_{2} }}$	Molar heat capacity of O2 (J·mol−1·K−1)
${\mathcal{D}}_{{{\text{eff}}}}$	Total effective diffusion constant (cm2·s−1)
${\mathcal{D}}_{{{\text{eff}}}}^{{C_{j} }}$	Effective diffusion constant of Cj clusters (cm2·s−1)
$D_{h}$	Scaling factor involved in the estimation of $D_{HC}$: $D_{h} = 1.99345 + 0.30224 \,\cdot\, \alpha_{T} - 0.11276 \,\cdot\, \alpha_{T}^{2}$ (–)
$D_{HC}$	Equivalent heat conduction diameter (cm)
$D_{p}$	Primary particle diameter (cm)
$D_{{p,{\text{ref}}}}$	Reference diameter used in Eqs. (15) and (16) (34 × 10–7 cm)
$E\left( m \right)$	Dimensionless refractive-index function of unannealed soot (–)
$E_{a} \left( m \right)$	Dimensionless refractive-index function of annealed soot (–)
exp	Experimental
F	Laser fluence (J·cm−2)
f	Dimensionless Eucken correction to the thermal conductivity of polyatomic gas: $\left( {9 \,\cdot\, \gamma_{j} - 5} \right)/4$ (–)
$f_{1,a}$	Empirical scaling factor for linear absorption of annealed soot (–)
$f_{1,s}$	Empirical scaling factor for the linear absorption of unannealed soot (–)
$f_{a}$	Absorption empirical scaling factor related to annealed soot [17] (–)
h	Planck constant (6.626 × 10–34 J·s)
$h_{{\lambda ,N_{p} }}$	Correction factor for multiple scattering within soot aggregates (–)
$h_{{\lambda , N_{p} }}^{\infty }$	Asymptotic form of the correction factor for multiple scattering within large aggregates (–)
$J\left( \xi \right)$	Parameter used for the calculation of the partial pressure of Cj clusters at the surface of soot particles (–)
$k_{a}$	Rate constants for oxidation reactions involving active sites: $k_{a} = 4.935 \times 10^{23} \,\cdot\, \exp \left[ { - 1.255 \times 10^{5} /\left( {R \,\cdot\, T_{p} } \right)} \right]$ (s−1·cm−2·bar−1)
$k_{b}$	Rate constants for oxidation reactions involving less active sites: $k_{b} = 4.935 \times 10^{21} \,\cdot\, \exp \left[ { - 6.352 \times 10^{4} /\left( {R \,\cdot\, T_{p} } \right)} \right]$ (s−1·cm−2·bar−1)
$k_{B}$	Boltzmann constant (1.381 × 10–23 J·K−1)
$k_{{{\text{diss}}}}$	Rate constant for pyrolysis of annealed particles $k_{diss} = 1 \times 10^{18} \,\cdot\, \exp \left[ { - 9.6 \times 10^{5} /\left( {R \,\cdot\, T_{p} } \right)} \right]$ (s−1)
$k_{g}$	Heat conduction coefficient of surrounding gas: $k_{g} = 1.0811 \times 10^{ - 4} + 5.1519 \times 10^{ - 7} \,\cdot\, T_{g}$ (W·cm−1·K−1)
$k_{h}$	Scaling factor involved in the estimation of $D_{HC}$: $k_{h} = 1.04476 + 0.22329 \,\cdot\, \alpha_{T} + 7.14286 \times 10^{ - 3} \,\cdot\, \alpha_{T}^{2}$ (–)
$k_{{{\text{imig}}}}$	Rate constant for interstitial migrations within annealed particles: $k_{{{\text{imig}}}} = 1 \times 10^{8} \,\cdot\, \exp \left[ { - 8.3 \times 10^{4} /\left( {R \,\cdot\, T_{p} } \right)} \right]$ (s−1)
$k_{ox,a}$	Oxidation rate constant of annealed soot (s−1·cm−2)
$k_{ox,s}$	Oxidation rate constant of unannealed soot (s−1·cm−2)
$k_{p}$	Boltzmann constant expressed in effective pressure units (1.38065 × 10–22 bar·cm3·K−1)
$k_{T}$	Rate constant related to the annealing of A sites to form B sites: $k_{T} = 3.79 \times 10^{27} \,\cdot\, \exp \left[ { - 4.06 \times 10^{5} /\left( {R \,\cdot\, T_{p} } \right)} \right]$ (s−1·cm−2)
$k_{{{\text{vmig}}}}$	Rate constant for vacancy migrations within annealed particles: $k_{{{\text{vmig}}}} = 1.5 \times 10^{17} \,\cdot\, \exp \left[ { - 6.7 \times 10^{5} /\left( {R \,\cdot\, T_{p} } \right)} \right]$ (s−1)
$k_{Z}$	Rate constant for oxide formation at the surface of A sites: $k_{Z} = 21.02 \,\cdot\, \exp \left[ {1.713 \times 10^{4} /\left( {R \,\cdot\, T_{p} } \right)} \right]$ (bar−1)
$k_{\lambda n,a}$	Rate constant for removal of C2 from annealed soot by photodesorption (s−1)
$k_{\lambda n,s}$	Rate constant for removal of C2 from unannealed soot by photodesorption (s−1)
$m_{el}$	Mass of an electron (9.1095 × 10–35 J·s2·cm−2)
$M_{g}$	Average mass of gas molecules (g)
$M_{p}$	Primary particle mass (g)
n	Estimated number of photons needing to be absorbed to photodesorb C2 clusters (–)
$N_{A}$	Avogadro constant (6.02214 × 1023 mol−1)
$N_{c}$	Number of atoms in the primary particles: $N_{c} = M_{p} \,\cdot\, N_{A} /W_{1}$ (–)
$N_{d}$	Number of lattice defects in the particles (–)
$N_{p}$	Number of primary particles in an aggregate (–)
$N_{sa}$	Density of carbon atoms on the surface of annealed soot [17] (3.8 × 1015 cm−2)
$N_{ss}$	density of carbon atoms on the surface of unannealed soot [17] (2.8 × 1015 cm−2)
$N_{tot}$	Aggregate number density (–)
$p\left( {D_{p} } \right)$	Probability density function of primary particle size (–)
$p\left( {N_{p} } \right)$	Probability density function of aggregate size (–)
$P_{{{\text{diss}}}}$	Effective pressure issued from the rate of thermal photodesorption from annealed particles (bar)
$P_{{{\text{eq}}}}^{{C_{j} }}$	Thermal equilibrium partial pressure of Cj clusters (bar)
$P_{g}$	Ambient pressure (bar)
$P_{{O_{2} }}$	O2 partial pressure [21]: $0.21 \,\cdot\, P_{g}$ (bar)
$P_{{{\text{phot}}}}^{{C_{j} }}$	Instantaneous partial pressure of Cj produced by photodesorption (bar)
$P_{{{\text{ref}}}}$	Reference pressure [17] (1.01325 bar)
$P_{{{\text{sat}}}}^{{C_{j} }}$	Saturation partial pressure of vaporized carbon clusters Cj (bar)
$P_{{{\text{surf}}}}^{{C_{j} }}$	Partial pressure of Cj at the particle surface (bar)
$P_{\lambda a}$	Effective pressure calculated based on the rate of non-thermal photodesorption of Cj clusters from annealed particles (bar)
$P_{\lambda s}$	Effective pressure calculated based on the rate of non-thermal photodesorption of Cj clusters from unannealed particles (bar)
$q_{{{\text{exp}}}}$	Normalized laser irradiance (–)
$\dot{Q}_{{{\text{abs}}}}$	Rate of energy increase by laser absorption (W)
$\dot{Q}_{{{\text{ann}}}}$	Rate of energy increase by annealing (W)
$\dot{Q}_{{{\text{cond}}}}$	Rate of energy loss by conduction (W)
$\dot{Q}_{{{\text{cond}},C}}$	Rate of energy loss by conduction in the continuum regime (W)
$\dot{Q}_{{{\text{cond}},{\text{FM}}}}$	Rate of energy loss by conduction in the free molecular regime (W)
$\dot{Q}_{ox}$	Rate of energy increase by particle oxidation (W)
$\dot{Q}_{{{\text{rad}}}}$	Rate of energy loss by radiative emission (W)
$\dot{Q}_{{{\text{sub}}}}$	Rate of energy loss by sublimation (W)
$\dot{Q}_{{{\text{th}}}}$	Rate of energy loss by thermionic emission (W)
R	Universal gas constant (8.3145 J·mol−1·K−1)
${\mathcal{R}}_{det}$	Spectral characteristics of the detection system
$R_{m}$	Universal gas constant expressed in effective mass units (8.3145 × 107 g·cm2·mol−1·K−1·s−2)
$R_{p}$	Universal gas constant expressed in effective pressure units (83.145 bar·cm3·mol−1·K−1)
$S_{LII}$	Calculated LII signal (a.u.)
$t$	Time (s)
$t_{l}$	Laser pulse duration (s)
$T_{f}^{CO}$	Temperature at which CO molecules are emitted from oxidizing soot (i.e., 790 K according to [37])
$T_{g}$	Ambient gas temperature (K)
$T_{p}$	Particle temperature (K)
$T_{{{\text{ref}}}}$	Reference temperature (0 K)
$T_{{{\text{ref}}}}^{{C_{j} }}$	Reference temperature for each Cj cluster [21]: $T_{{{\text{ref}}}}^{{C_{1} }} = 4603.48\,{\text{K}}$, $T_{{{\text{ref}}}}^{{C_{2} }} = 4456.59\,{\text{K}}$, $T_{{{\text{ref}}}}^{{C_{3} }} = 4136.78\,{\text{K}}$, $T_{{{\text{ref}}}}^{{C_{4} }} = 4949.74\,{\text{K}}$ and $T_{{{\text{ref}}}}^{{C_{5} }} = 4772.87\,{\text{K}}$
$T_{\delta }$	Limiting sphere temperature within the Fuchs heat conduction model (K)
$U_{{\text{int}}}$	Internal energy of soot particles (J)
$W_{j}$	Molecular weight of Cj species: $W_{j} = 12.011\,\cdot\,j$ (g·mol−1)
$W_{{O_{2} }}$	Molecular weight of O2 (31.99 g·mol−1)
X a	Primary particle annealed fraction (–)
$X_{d}$	Initial defect density (1 × 10–2 atom−1)
$Z_{ox}$	Collision rate of O2 molecules with the surface of oxidizing particles (s−1·cm−2)
$\alpha_{1}^{^{\prime}}$	Parameter involved in the calculation of $h_{{\lambda , N_{p} }}^{\infty }$ (–)
$\alpha_{2}^{^{\prime}}$	Parameter involved in the calculation of $h_{{\lambda , N_{p} }}^{\infty }$ (–)
$\alpha_{j}$	Mass accommodation coefficient of vaporized species Cj [21]: α1 = α2 = 0.5, α3 = 0.1 and α4 = α5 = 0.0001 (–)
$\alpha_{T}$	Thermal accommodation coefficient (–)
$\gamma$	Specific heat capacity ratio: $C_{p,m} /\left( {C_{p,m} - R} \right)$ (–)
$\gamma_{j}$	Heat capacity ratio of desorbing species Cj [17] (–)
$\gamma^{*}$	Mean heat capacity ratio (–)
$\delta$	Distance between the equivalent heat conduction radius and the limiting sphere of the Fuchs heat conduction model (cm)
$\Delta H_{{{\text{diss}}}}$	Enthalpy of formation of Cj clusters by thermal sublimation of annealed soot: $\Delta H_{diss} = - 12.326\,\cdot\,T_{p} + 8.545\,\times\,10^{5}$ (J·mol−1)
$\Delta H_{{{\text{imig}}}}$	Enthalpy related to interstitial migrations (-1.9 × 104 J·mol−1)
$\Delta H_{j}$	Enthalpy of formation of carbon vapor species Cj [17]: $\Delta H_{1} = - 5.111\,\cdot\,T_{p} + 7.266\times10^{5}$ (J·mol−1), $\Delta H_{2} = - 12.326\,\cdot\,T_{p} + 8.545\times10^{5}$ (J·mol−1), $\Delta H_{3} = - 26.921\,\cdot\,T_{p} + 8.443\times10^{5}$ (J·mol−1), $\Delta H_{4} = - 2.114 \times 10^{ - 3} \,\cdot\,T_{p}^{2} - 7.787\,\cdot\,T_{p} + 9.811 \times 10^{5}$ (J·mol−1) and $\Delta H_{5} = - 2.598 \times 10^{ - 3} \,\cdot\,T_{p}^{2} - 7.069\,\cdot\,T_{p} + 9.898 \times 10^{5}$ (J·mol−1)
$\Delta H_{ox}$	Enthalpy of the reaction 2C + O2 → 2CO: $\Delta H_{ox} = 2.8901 \times 10^{ - 14} \,\cdot\, T_{p}^{5} - 4.9868 \times 10^{ - 10} \,\cdot\, T_{p}^{4} + 3.2206 \times 10^{ - 6} \,\cdot\, T_{p}^{3} - 1.0307 \times 10^{ - 2} \,\cdot\, T_{p}^{2} + 7.9303 \,\cdot\, T_{p} - 1.1221 \times 10^{5}$(J·mol−1)
$\Delta H_{{{\text{vmig}}}}$	Enthalpy related to vacancy migrations (-1.4 × 105 J·mol−1)
$\Delta H_{\lambda n,a}$	Enthalpy required to photodesorb Cj clusters from annealed particles (3.4 × 105 J·mol−1 for C2)
$\Delta H_{\lambda n,s}$	Enthalpy required to photodesorb Cj clusters from unannealed particles (J·mol−1)
$\Delta \lambda_{\det }$	Spectral range of the detection system (cm)
${\Delta }\phi$	Positive charge buildup obtained by solving Eq. (30)
$\eta$	Stoichiometric coefficient used in the calculation of the convective transport of sublimed species (–)
$\lambda$	Wavelength (cm)
$\lambda_{0}$	Arbitrary wavelength (1 cm)
$\lambda_{\infty }$	Wavelength defined as upper boundary in Eq. (22) (cm)
λ l	Laser-excitation wavelength (cm)
$\lambda_{g}$	Mean free path of gas molecules (cm)
$\lambda_{\delta }$	Mean free path of the gas inside the limiting sphere of the Fuchs heat conduction model (cm)
$\Lambda_{1}$	Function used in the Fuchs heat conduction model (–)
$\Lambda_{2}$	Function used in the Fuchs heat conduction model (–)
$\xi$	Dimensionless parameter used for the calculation of the partial pressure of Cj clusters at the surface of soot particles (–)
$\rho_{a}$	Density of annealed soot: $\rho_{a} = 2.6 - 1\times10^{ - 4} \,\cdot\,T_{p}$ (g·cm−3)
$\rho_{s}$	Density of unannealed soot: $\rho_{s} = 2.3031 - 7.3106\times10^{ - 5} \,\cdot\,T_{p}$ (g·cm−3)
$\sigma_{j}$	Molecular cross section of sublimed species Cj [17] (cm2)
$\sigma_{\lambda n,a}$	Empirically determined cross section for removal of C2 clusters by photodesorption from annealed soot (cm2n−1·J1−n)
$\sigma_{\lambda n,s}$	Empirically determined cross section for removal of C2 clusters by photodesorption from unannealed soot (cm2n−1·J1−n)
$\phi$	Work function (7.37 × 10–19 J)
$\chi_{A}$	Fraction of available A sites (–)
$\Omega_{\exp }$	Laser spatial domain (cm2)