3D large-scale forward modeling of gravitational fields using triangular spherical prisms with polynomial densities in depth

Abstract

To take the sphericity of the Earth into account, tesseroids are often utilized as grid elements in large-scale gravitational forward modeling. However, such elements in a latitude–longitude mesh suffer from degenerating into poorly shaped triangles near poles. Moreover, tesseroids have limited flexibility in describing laterally variable density distributions with irregular boundaries and also face difficulties in achieving completely equivalent division over a spherical surface that may be desired in a gravity inversion. We develop a new method based on triangular spherical prisms (TSPs) for 3D gravitational modeling in spherical coordinates. A TSP is defined by two spherical surfaces of triangular shape, with one of which being the radial projection of the other. Due to the spherical triangular shapes of the upper and lower surfaces, TSPs enjoy more advantages over tesseroids in describing mass density with different lateral resolutions. In addition, such an element also allows subdivisions with nearly equal weights in spherical coordinates. To calculate the gravitational effects of a TSP, we assume the density in each element to be polynomial along radial direction so as to accommodate a complex density environment. Then, we solve the Newton’s volume integral using a mixed Gaussian quadrature method, in which the surface integral over the spherical triangle is calculated using a triangle-based Gaussian quadrature rule via a radial projection that transforms the spherical triangles into linear ones. A 2D adaptive discretization strategy and an extension technique are also combined to improve the accuracy at observation points near the mass sources. The numerical experiments based on spherical shell models show that the proposed method achieves good accuracy from near surface to a satellite height in the case of TSPs with various dimensions and density variations. In comparison with the classical tesseroid-based method, the proposed algorithm enjoys better accuracy and much higher flexibility for density models with laterally irregular shapes. It shows that to achieve the same accuracy, the number of elements required by the proposed method is much less than that of the tesseroid-based method, which substantially speeds up the calculation by more than 2 orders. The application to the tessellated LITHO1.0 model further demonstrates its capability and practicability in realistic situations. The new method offers an attractive tool for gravity forward and inverse problems where the irregular grids are involved.

1 Introduction

Forward computation of the gravity effects induced by a 3D mass density distribution is one of the crucial issues in geodesy and geophysics. The gravitational signal of mass bodies (e.g., gravitational potential, gravity acceleration, and gravity gradients) is expressed as the volume integral of Newton’s kernel and its derivatives. A commonly used method for evaluating these volume integrals is to divide the topographic mass model into elementary bodies of different geometric shapes, such as rectangular prisms (e.g., Nagy et al. 2000; Tsoulis 2000; Wild-Pfeiffer 2008; Wu and Chen 2016; Chen and Liu 2019), polyhedrons (e.g., D’Urso and Trotta 2017; Ren et al. 2018a, b; Chen et al. 2019; Wu et al. 2019), tesseroids (e.g., Kuhn 2003; Asgharzadeh et al. 2007; Heck and Seitz 2007; Grombein et al. 2013; Uieda et al. 2016; Zhao et al. 2019; Deng 2023), and triangles (e.g., Zhang and Chen 2018; Zhang et al. 2018). Then, the gravitational effects of each elementary mass are solved by numerical or analytical integration, and the overall gravity field is obtained as a cumulative contribution of all building blocks.

Among these mass elements, the rectangular prism is the most widely used one, due to its simplicity and the readily available analytical solutions (Nagy et al. 2000; Heck and Seitz 2007). But it is restricted only to local applications where the flat Earth approximation is sufficient. In contrast, polyhedral elements are more applicable to both local and global scales and are endowed with great flexibility in approximating mass sources with complex geometries (Benedek et al. 2018; Zhang and Chen 2018). Moreover, various closed-form solutions of the gravity potential, gravity vector, and gravity gradient tensor are available for a polyhedral body with constant, linear, or higher-order polynomial densities (e.g., Barnett 1976; Okabe 1979; Holstein 1996; Petrović 1996; Werner and Scheeres 1997; Tsoulis and Petrović 2001; Hamayun et al. 2009; Tsoulis 2012; D’Urso 2014a, b; Conway 2015; D’Urso and Trotta 2017; Ren et al. 2017; Werner 2017). However, in regional and global forward modeling, a large number of polyhedral elements may be required to take the curvature of the Earth into account. In addition, the analytical solutions for the polyhedral body are often expressed in Cartesian coordinates, and hence, coordinate transforms are required to compute the gravitational effects in a local tangential coordinate system. Considering the sphericity of the Earth, a tesseroid (or spherical prim) bounded by pairs of latitude, longitude, and radial surfaces is the most advantageous choice for continental and global applications. It is a natural presentation to link to the curvature of the Earth in geocentric spherical coordinates and can also integrate certain geographical model data easily, such as the global model ETOPO1 (Amante 2009), CRUST5.1, CRUST2.0, and CRUST1.0 (Mooney et al. 1998; Chulick et al. 2002; Laske et al. 2013). Compared with the prism and polyhedron, analytical solutions for a tesseroid only exist when the observation points are located along the polar axis (Lafehr 1991; Mikuška et al. 2006; Grombein et al. 2013; Marotta and Barzaghi 2017; Lin and Li 2022; Deng and Sneeuw 2023). In more general cases, the volume integral must be solved numerically or semi-numerically.

Over the past years, various numerical methods were developed to calculate the gravity effects of a tesseroid, such as Taylor series expansion (e.g., Heck and Seitz 2007; Grombein et al. 2013; Deng et al. 2016; Zeng et al. 2022), the Gauss–Legendre quadrature (GLQ) (e.g., Li et al. 2011; Uieda et al. 2016; Lin and Denker 2019; Soler et al. 2019; Zhao et al. 2019; Zhong et al. 2019; Lin et al. 2020; Qiu and Chen 2020), and the mixed methods that use analytical integration in radial dimension and apply numerical evaluation in horizontal directions (e.g., Wild-Pfeiffer 2008; Fukushima 2018; Lin and Denker 2019; Ouyang et al. 2022). In addition, 2D (Lin and Denker 2019) and 3D (Li et al. 2011; Uieda et al. 2016) adaptive discretization strategies were also developed to help achieve satisfactory accuracy and to retain acceptable computational efficiency at near-source points. These adaptive strategies divide a tesseroid when the distance to the computation point is smaller than a constant times the size of the element, so that only elements close to the observation point require a larger number of subdivisions. However, tesseroids have their intrinsic limitations. In a standard latitude–longitude grid, tesseroids vary significantly in size and shape with the increase in latitudes. They become distorted as moving away from the equator and degenerate into increasingly triangular shapes near the poles. This makes it difficult to achieve constant resolution all over the spherical surface using tesseroids. Note that a uniform grid is often preferred in the gravity inversion. Furthermore, tesseroids also have limited flexibility in describing laterally variable density distributions with irregular boundaries and face difficulties in handling geographical models with irregular data points, such as LITHO1.0 (Pasyanos et al. 2014).

One way to solve the problem is to use triangular elements instead of tesseroids. Different from the latitude–longitude mesh, a triangular grid enjoys higher flexibility in describing variable-resolution density models. Using spherical triangular tessellation, Zhang and Chen (2018) developed a tetrahedron-based forward modeling method to evaluate spherical and ellipsoidal topographic effects. They decomposed a spherical surface into a set of planar triangular regions (i.e., tetrahedrons) and solved the Newton’s integral using the analytical solutions derived by Werner and Scheeres (1996) for a polyhedron. Therefore, Zhang and Chen (2018)’s method is in fact a polyhedron-based method with all facets of the polyhedron being planar triangles. Due to the planar facets of the element, it may take a great number of elements to approximate a curved surface with specific curvature. Another method to deal with irregular data points is that proposed by Sebera et al. (2018). To achieve the triangular parameterization used in LITHO1.0, Sebera et al. (2018) adopted triangular grids with densities given for nodes and evaluated the gravity effects with respect to the center of mass of the spherical triangular elements. They defined a volume for each node according to the average solid angle from all spherical triangles that contains the node. The total gravitational effects were then approximated with a sum over all layers and nodes in a geocentric Earth-fixed equatorial reference frame and transferred into the local tangential coordinate system by Euler rotation. Sebera et al. (2018)’s approach is essentially a node-based method. The key problem of the method is that the numerical results are systematically affected by the triangular patterns and can only achieve desired accuracy with uniform triangular grids (Root et al. 2022). For spherical triangles with different areas, however, unequal weights may be introduced to data in the numerical integration. In addition, the method of Sebera et al. (2018) is limited only to large observation heights.

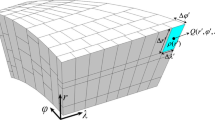
This study goes beyond the previous studies in that we perform large-scale gravitational forward modeling using elementary bodies of a geometric shape called triangular spherical prism (TSP). A triangular spherical prism is defined by two spherical triangles with one of which being the radial projection of the other (see Fig. 1). It is similar to a tesseroid, but the difference lies in that its top and bottom surfaces are in a spherical triangular shape. In comparison with the tesseroids commonly used in large-scale modeling, such a volume element enjoys both the natural feasibility of tesseroids in accounting for the effects of Earth’s curvature and also the high flexibility of triangles in describing laterally variable density distributions. In the proposed method, the gravitational effects of a TSP are calculated by decomposing the volume integral into a 1D integral with a polynomial density in the radial direction and a 2D surface one. The 1D integration is numerically evaluated by the GLQ method, while the 2D integral over the spherical triangular surface is solved using a triangle-based Gaussian quadrature rule (Dunavant 1985) via a radial projection from spherical triangles to linear ones following the work of Li and Jiao (2022). A 2D adaptive discretization strategy is also constructed for spherical triangles to obtain accurate results at near-source points.

The remainder of the paper is organized as follows: In Sect. 2, we introduce the theoretical aspects. We first derive the gravitational potential, gravitational vector, and Marussi tensor for a TSP in Sect. 2.1. Then, the numerical implementation of the Gaussian quadrature rule is described in Sect. 2.2 and the 2D adaptive discretization strategy is constructed in Sect. 2.3. Section 3 tests the performance of the proposed method based on spherical shell models and carries out numerical investigations, including the determination of key parameter (Sect. 3.1), analysis on the influence of the observation height and the TSP dimension (Sect. 3.2), accuracy verification of polynomial density models (Sect. 3.3), and a comparison study with existing methods (Sect. 3.4). The application of the proposed method to the LITHO1.0 model is presented in Sect 4. Finally, conclusions are drawn from the work in Sect 5.

Fig. 1

A triangular spherical prism (TSP) with inner radius $r'_1$ and outer radius $r'_2$ in the geocentric Earth-fixed equatorial reference system defined by (X, Y, Z). P and $Q'$ denote the observation point and the running integration point in the TSP, respectively. The local tangential coordinate system (North/East/Up) is represented by (x, y, z)

2 Methodology

2.1 Gravitational effects of a TSP with arbitrary-order polynomial density

In this section, the formulas of the gravitational potential, gravitational vector, and Marussi tensor are derived for a TSP with a polynomial density up to an arbitrary degree in depth. According to Heiskanen and Moritz (1967), the Newton’s integral for the gravitational potential of an arbitrary solid body $\Omega ' \subset {\mathrm{{R}}^\mathrm{{3}}}$ can be expressed as

$$\begin{aligned} V( \mathbf{{r}} ) = G \iiint _{\Omega '}\frac{{\rho (\mathbf{{r'}})}}{\ell }\mathrm{{d}} \Omega ' \end{aligned}$$

(1)

where G is the Newton’s gravitational constant, $\rho (\mathbf {r'})$ the location-dependent density, and $\ell$ the distance between the computation point $P\in {\mathrm{{R}}^\mathrm{{3}}}$ and the running mass point $Q'\in {\Omega '}$.

A TSP is defined by two triangular spherical surfaces with $r=r'_1$ and $r=r'_2$ in geocentric spherical coordinates (see Fig. 1). By introducing a infinitesimal solid angle $\mathrm{{d}}s'$, the volume element of the TSP can be expressed as

$$\begin{aligned} \mathrm{{d}}\Omega '=r'^2\mathrm{{d}}r'\mathrm{{d}}s' \end{aligned}$$

(2)

Based on the Newton’s integral Eq. (1), the gravitational potential for a TSP with a Nth-order polynomial density $\rho (r') ={\rho _0} + {\rho _1}r' + {\rho _2}{r'^2} + \cdots {\rho _N}{r'^N}$ can then be specified by decomposing the volume integral into a one-dimension integral in the radial direction and a surface integral in the horizontal direction, that is,

$$\begin{aligned} V(r,\varphi ,\lambda ) = G\sum \limits _{n = 0}^N {\rho _n}\iint _{S'} {\int \limits _{{r'_1}}^{{r'_2}} \underbrace{{\frac{{{1}}}{\ell }{r'}^{n + 2}}}_{{K_V^n}}\mathrm{{d}}r'} \mathrm{{d}}s' \end{aligned}$$

(3)

where $S'$ is the projected surface area of the TSP onto a unit sphere, $K_V^n$ denotes the nth integration kernel of V, and

$$\begin{aligned} \ell \mathrm{{ = }}\sqrt{{r^2} + {{r'}^2} - 2rr'\cos \psi } \end{aligned}$$

(4)

is the distance between the computation point P and the mass point $Q'$, with

$$\begin{aligned} \cos \psi = \sin \varphi \sin \varphi ' + \cos \varphi \cos \varphi '\cos (\lambda ' - \lambda ) \end{aligned}$$

(5)

As useful for most practical applications, we restrict the computation point P to be located outside the TSP in this study.

Following Grombein et al. (2013) and Lin et al. (2020), we can also express the gravitational vector and the Marussi tensor into the following form:

$$\begin{aligned}{} & {} {g_i}(r,\varphi ,\lambda ) = G\sum \limits _{n = 0}^N {{\rho _n}}\iint _{S'}{ {\int \limits _{{r'_1}}^{{r'_2}} \underbrace{{\frac{{{{\Delta _i}}}}{\ell ^3 }{r'}^{n + 2}}}_{K_i^n}\mathrm{{d}}r' }\mathrm{{d}}s'} \end{aligned}$$

(6)

$$\begin{aligned}{} & {} {M_{ij}}(r,\varphi ,\lambda ) = G\sum \limits _{n = 0}^N {{\rho _n}}\iint _{S'}{ \int \limits _{{r'_1}}^{{r'_2}} \underbrace{{\left( {\frac{{3{\Delta _i}{\Delta _j}}}{{{\ell ^5}}} - \frac{{{\delta _{ij}}}}{{{\ell ^3}}}} \right) }{r'}^{n + 2}}_{K_{ij}^n}\mathrm{{d}}r' }\mathrm{{d}}s' \nonumber \\ \end{aligned}$$

(7)

where $i,j = x,y,z, K_i^n$ and $K_{ij}^n$ denote the nth integration kernel of $g_i$ and $M_{ij}$, respectively, $\delta _{ij}$ is the Kronecker delta with

$$\begin{aligned} {\delta _{ij}} = \left\{ \begin{array}{l} 1,\;\;\;i = j\\ 0,\;\;\;i \ne j \end{array} \right. \end{aligned}$$

(8)

and

$$\begin{aligned}&{\Delta _x} = r'\left[ {\cos \varphi \sin \varphi ' - \sin \varphi \cos \varphi '\cos \left( {\lambda ' - \lambda } \right) } \right] \nonumber \\&{\Delta _y} = r'\cos \varphi '\sin \left( {\lambda ' - \lambda } \right) \nonumber \\&{\Delta _z} = r'\cos \psi - r \end{aligned}$$

(9)

Due to the fact that the surface integration over $S'$ comprises elliptical integrals, Eqs. (3), (6) and (7) must be solved numerically.

2.2 Mixed Gaussian quadrature method

Next, we evaluate the numerical integration in Eqs. (3), (6) and (7) using a mixed Gaussian quadrature method.

In the method, the integration of $K_V^n, K_i^n$ and $K_{ij}^n$ with respect to $r'$ is solved by the GLQ approach (Asgharzadeh et al. 2007). According to the GLQ, the radial integral can be approximated by a weighted sum of the integration kernel, that is,

$$\begin{aligned} \int \limits _{{r'_1}}^{{r'_2}} {K(r',\varphi ',\lambda ')\mathrm{{d}}r'} \approx \frac{{\Delta r'}}{2}\sum \limits _{k = 1}^{N_G^r} {{A_k}K({{{\hat{r}}'}_k},\varphi ',\lambda ')} \end{aligned}$$

(10)

with

$$\begin{aligned} {{\hat{r}}'_k} = \frac{{{r'_1} + {r'_2}}}{2} + \frac{{\Delta r'}}{2}{t_k} \end{aligned}$$

(11)

where ${\Delta r'} = r'_2 - r'_1$ and K represents $K_V^n, K_i^n$ or $K_{ij}^n$. $A_k$ and $t_k$ are the GLQ weights and quadrature nodes for the radial integration, and $N_G^r$ is the number of GLQ points used.

Fig. 2

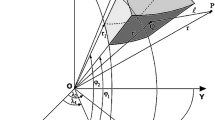
Transformation from a linear triangle $T'$ to a spherical triangle $S'$ via radial projection. The vertices $\textbf{x}_1, \textbf{x}_2, \textbf{x}_3$ of the triangle are located on a sphere. $\textbf{x}$ denotes a Gaussian point in $T'$, and ${\tilde{\textbf{x}}}$ is its radial projection onto the surface area $S'$ of the sphere

On this basis, we then solve the surface integrals in Eqs. (3), (6) and (7) using a radially projected Gaussian quadrature method (Li and Jiao 2022). The key point of the method is that it utilizes a simple and efficient radial projection to transform the spherical triangle to its corresponding linear triangle (see Fig. 2), and hence, Gaussian quadrature rules on linear triangles can be adopted to integrate over spherical triangle directly. By applying a pth-degree Gaussian quadrature rule, the numerical integration over a spherical triangle is approximated as Li and Jiao (2022):

$$\begin{aligned}{} & {} \iint _{S'}f(\varphi ',\lambda ')\mathrm{{d}}s' \approx {R^2}\det \left[ {{\mathbf{{x}}_1},{\mathbf{{x}}_2},{\mathbf{{x}}_3}} \right] \sum \limits _{l = 1}^{{N_G^h(p)}} \nonumber \\{} & {} \quad {\frac{{{\omega _l}}}{{{{\left\| {\mathbf{{x}}({\mathbf{{\xi }}_l})} \right\| }^3}}}f\left( {R\frac{{\mathbf{{x}}({\mathbf{{\xi }}_l})}}{{\left\| {\mathbf{{x}}({\mathbf{{\xi }}_l})} \right\| }}} \right) } \end{aligned}$$

(12)

where $f(\varphi ',\lambda ')$ is the kernel function of the surface integral for the gravitational potential, gravitational vector, or Marussi tensor. The vertices of the triangle denoted by $\textbf{x}_1, \textbf{x}_2, \textbf{x}_3$ are located on a sphere with radius of R, and hence, $R=\Vert {\mathbf{{x}}_1}\Vert =\Vert {\mathbf{{x}}_2}\Vert =\Vert {\mathbf{{x}}_3}\Vert$. ${\omega _l}$ and ${\xi }_l$ are the quadrature weights and nodes for the linear triangle $T'$. $\mathbf{{x}}({\mathbf{{\xi }}_l})$ denotes the lth quadrature point, where $l=1,2,\ldots ,N_G^h$, and $N_G^h$ is the number of quadrature points depending on the degree p of the Gaussian quadrature rule. The expression $R$ $\mathbf{{x}}(\xi _l)/\Vert \mathbf{{x}}(\xi _l)\Vert$ in Eq. (12) suggests a radial projection from a point in $T'$ to a point on $S'$. Note that $\mathbf{{x}}$ are Cartesian coordinates, that is, $\mathbf{{x}} = (X,Y,Z)$, which can be obtained by its spherical coordinates through

$$\begin{aligned}&X = r'\mathrm{{cos}}\varphi '\mathrm{{cos}}\lambda ' \nonumber \\&Y = r'\mathrm{{cos}}\varphi '\sin \lambda '\nonumber \\&Z = r'\sin \varphi ' \end{aligned}$$

(13)

In our context, the integration domain $S'$ is a triangular surface area on the unit sphere, and thus, R in Eq. (12) can be replaced with 1. Further, to make it easier to understand, we rewrite Eq. (12) into a form similar to Eq. (10):

$$\begin{aligned} \iint _{S'} f(\varphi ',\lambda ')\mathrm{{d}}s' \approx \sum \limits _{l = 1}^{{N_G^h(p)}} {{{\tilde{\omega }}_l}f({{{{\tilde{\textbf{x}}}}}_l})} \end{aligned}$$

(14)

with

$$\begin{aligned}&{{\tilde{\omega }}_l} = \frac{{\det \left[ {{\mathbf{{x}}_1},{\mathbf{{x}}_2},{\mathbf{{x}}_3}} \right] }}{{{{\left\| {\mathbf{{x}}({\mathbf{{\xi }}_l})} \right\| }^3}}}{\omega _l} \nonumber \\&{{{{\tilde{\textbf{x}}}}}_l} = \frac{{\mathbf{{x}}({\mathbf{{\xi }}_l})}}{{\left\| {\mathbf{{x}}({\mathbf{{\xi }}_l})} \right\| }} \end{aligned}$$

(15)

where ${{{\tilde{\textbf{x}}}}_l}$ denote the quadrature points in the projected surface area of the spherical triangle onto the unit sphere and $\tilde{\omega }_l$ are the corresponding quadrature weights. As can be seen, both ${{{\tilde{\textbf{x}}}}_l}$ and $\tilde{\omega }_l$ can be obtained directly from the Gaussian nodes $\xi _l$ and weights $\omega _l$ of the linear triangle.

Substituting Eqs. (10) and (14) into Eqs. (3), (6) and (7), the gravitational potential, gravitational vector and Marussi tensor become

$$\begin{aligned}&V(r,\varphi ,\lambda ) \approx \frac{{\Delta r'}}{2}G\sum \limits _{n = 0}^N {{\rho _n}} \left[ {\sum \limits _{k = 1}^{N_G^r} {\sum \limits _{l = 1}^{N_G^h(p)} {{A_k}{{\tilde{\omega }}_l}K_V^n({{{\hat{r}}'}_k},{{{{\tilde{\textbf{x}}}}}_l})} } } \right] \nonumber \\&{g_i}(r,\varphi ,\lambda ) \approx \frac{{\Delta r'}}{2}G\sum \limits _{n = 0}^N {{\rho _n}} \left[ {\sum \limits _{k = 1}^{N_G^r} {\sum \limits _{l = 1}^{N_G^h(p)} {{A_k}{{\tilde{\omega }}_l}K_i^n({{{\hat{r}}'}_k},{{{{\tilde{\textbf{x}}}}}_l})} } } \right] \nonumber \\&{M_{ij}}(r,\varphi ,\lambda ) \approx \frac{{\Delta r'}}{2}G\sum \limits _{n = 0}^N {{\rho _n}} \left[ {\sum \limits _{k = 1}^{N_G^r} {\sum \limits _{l = 1}^{N_G^h(p)} {{A_k}{{\tilde{\omega }}_l}K_{ij}^n({{{\hat{r}}'}_k},{{{{\tilde{\textbf{x}}}}}_l})} } } \right] \end{aligned}$$

(16)

Finally, by dividing the target region into a number of TSPs, the overall gravitational effects can then obtained by adding the contribution of each elementary TSP (given by Eq. (16)) together in terms of superposition.

2.3 2D adaptive discretization

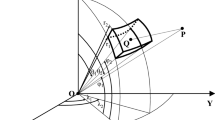
To ensure the accuracy at near-source points, we construct a 2D adaptive discretization strategy for the TSP based on the work of Lin and Denker (2019). The adaptive strategy satisfies a criterion that the TSP is divided into two parts along the median line from the midpoint of the largest edge of the upper spherical triangle to the opposite vertex if the distance to the computation point is smaller than a constant (D) times the maximum size of the triangle. Therefore, the stop condition of the 2D adaptive discretization is

$$\begin{aligned} {{{\ell _0}}\big / {\max ({L_1 },{L_2 },{L_3 })}} \ge D \end{aligned}$$

(17)

where D is called the distance–size ratio and $L_1, L_2$, and $L_3$ are the dimensions of the upper spherical triangle determined by

$$\begin{aligned}&{L_1} = 2{r'_2}\arcsin \left( {{{0.5\left\| {{\mathbf{{x}}_1} - {\mathbf{{x}}_2}} \right\| } \big /{{r'_2}}}} \right) \nonumber \\&{L_2} = 2{r'_2}\arcsin \left( {{{0.5\left\| {{\mathbf{{x}}_2} - {\mathbf{{x}}_3}} \right\| } \big /{{r'_2}}}} \right) \nonumber \\&{L_3} = 2{r'_2}\arcsin \left( {{{0.5\left\| {{\mathbf{{x}}_3} - {\mathbf{{x}}_1}} \right\| } \big / {{r'_2}}}} \right) \end{aligned}$$

(18)

Here $r'_2=\Vert \textbf{x}_1\Vert =\Vert \textbf{x}_2\Vert =\Vert \textbf{x}_3\Vert$ is the radius of the upper spherical triangle, and $\mathbf{{x}_1},\mathbf{{x}_2}, \mathbf{{x}_3}$ are position vectors of the three vertices in the Cartesian coordinates. ${\ell _0}$ is the distance between the computation point P and the geometric center C of the upper spherical triangle:

$$\begin{aligned} {\ell _0} = \left\| {{\mathbf{{x}}_C} - {\mathbf{{x}}_P}} \right\| \end{aligned}$$

(19)

with

$$\begin{aligned} {\mathbf{{x}}_C} = {r'_2}{{({\mathbf{{x}}_1} + {\mathbf{{x}}_2} + {\mathbf{{x}}_3})} \big / {\left\| {{\mathbf{{x}}_1} + {\mathbf{{x}}_2} + {\mathbf{{x}}_3}} \right\| }} \end{aligned}$$

(20)

where $\mathbf{{x}}_P$ and $\mathbf{{x}}_C$ are Cartesian coordinates of P and C (Fig. 3).

Fig. 3

Illustration of the 2D adaptive discretization of a TSP. C is the geometric center of the upper spherical triangle, and ${L_1},{L_2},{L_3}$ (${L_3}>{L_1}>{L_2}$ is assumed here) are the dimensions. P is the observation point. If inequality (17) is not satisfied, the TSP will be split up into two parts along the median formed on the maximum edge of the upper spherical triangle. This process is recursively implemented

3 Numerical tests

In this section, the performance of the proposed method is tested using several spherical shell models and a regional irregular density model.

Fig. 4

Spherical shell (a) and the polynomial density models (b) used in the numerical tests. $N=0,1,2,3$ correspond to the constant, linear, quadratic, and cubic density model, respectively

Table 1 Polynomial coefficients of the density models shown in Fig. 4b

For numerical experiments based on shell models, we choose the spherical shell with a variable density in depth as the reference model, since its closed-form solution is readily available (e.g., Soler et al. 2019; Ouyang et al. 2022; Deng 2023). The shell models are set to have a fixed outer radius of $R=6371$ km, a thickness $\Delta R$, and a Nth-degree polynomial density $\rho (r') ={\rho _0} + {\rho _1}r' + {\rho _2}{r'^2} + \cdots {\rho _N}{r'^N}$ (see Fig. 4; Table 1). To build a shell model with TSPs, we use the open-source codes SPHERETRI (https://github.com/pgagarinov/spheretri) and SPHERE_DELAUNAY (Renka 1997; Goodman and O’Rourke 2004) to perform the uniform and non-uniform triangulation of a unit sphere (e.g., Fig. 5), and then map the triangulation of points to the upper and bottom surfaces of the shell. If not differently specified, a uniform triangular grid is applied. In the tests, four nonzero components of $V, g_z, M_{xx}$ and $M_{zz}$ are investigated, and $180\times 360=64{,}800$ observation points, which are evenly distributed along the latitudinal and longitudinal directions on a spherical surface at a height of H above the shell surface, are considered. In addition, because of the large difference of the magnitudes of the gravitational effects, we prefer to use the relative root mean square (RRMS) to measure the overall misfits between the analytical solutions and numerical results at a given observation height H:

$$\begin{aligned} \mathrm{{RRMS}}[\chi ] = \Big \vert {\frac{{\mathrm{{RMS[}} \chi - \chi _\textrm{ana}]}}{{\mathrm{{RMS}}[\chi _\textrm{ana}]}}} \Big \vert \times 100\% \end{aligned}$$

(21)

where $\chi$ can be any component of $V, {g_i}$ and $M_{ij}$ calculated by the proposed method and $\chi _\textrm{ana}$ is the corresponding analytical solution.

Fig. 5

Diagrammatic sketch of the uniform (a) and non-uniform (b) triangulation on a unit sphere. By mapping the triangulation of points to the upper and lower spherical surfaces of a shell, the corresponding discretized model consisting of TSPs can be established

Table 2 Relation between $N_G^h$ and p

3.1 Determination of the number of Gaussian quadrature nodes and the distance–size ratio

The computational accuracy and efficiency of the proposed method depend basically on two parameters: the number of Gaussian quadrature nodes ($N_G^r / N_G^h$ or $N_G^r / p$) and the distance–size ratio (D). The number of quadrature nodes determines the accuracy of the numerical integration over the TSP, and the distance–size ratio controls the number of subdivisions for each TSP. Therefore, to ensure the accuracy while retaining acceptable efficiency of the algorithm, it is important to determine the optimal values for $N_G^r / N_G^h$ and D. It is also noteworthy that $N_G^h$ is a function of the degree p and their relation is listed in Table 2. Therefore, using $N_G^r / p$ instead of $N_G^r / N_G^h$ is more straightforward in the following analysis.

3.1.1 Optimal selection of $N_G^r / p$

We adopt the spherical shell model with a thickness of $\Delta R=10$ km to investigate the influence of $N_G^r / p$. To generate a TSP-based model, the shell is uniformly discretized into a triangular grid of roughly $1^\circ$ that consists of 81,920 TSPs with one layer in the radial direction. The observation points are located at a height of $H=10$ km under a latitude–longitude grid of $1^\circ$. To analyze the influence of the variable density on the accuracy, four polynomial density models given in Fig. 4 are taken into consideration.

Fig. 6

RRMS in the p—$N_G^r$ space for shell models with constant, linear, quadratic, and cubic densities in depth. The points within the dashed lines are the ones whose RRMS present a very slight difference

Figure 6 shows the RRMS deviation of $V, g_z,M_{xx}$ and $M_{zz}$ in the case of different combinations of p and $N_G^r$ for spherical shell models with constant, linear, quadratic, and cubic densities in depth. It is clear that the RRMS value exhibits a general decrease trend with the increase in p and $N_G^r$. The numerical error versus $N_G^r$ is closely related to the radial density variation of the shell model. In the constant case, the increase in $N_G^r$ does not improve the accuracy significantly and $N_G^r=1$ is sufficient for all gravity components. For shell models with a higher-degree polynomial density (i.e., $N=1,2,3$), however, the RRMS first declines and then becomes stable at $N_G^r\ge 2$. In contrast, the RRMS as a function of p shows different trends for different gravity components, while the density variation has almost no influence. For the gravitational potential, the numerical error reaches its minimum at $p=2$ when $N_G^r$ is fixed, while for $g_z, M_{xx}$ and $M_{zz}$, the RRMS deviation decreases rapidly first and then remains stable for $p\ge 4$. Therefore, in regard of the accuracy and efficiency, the optimal values can be determined as $p/N_G^r=4/2$ or $N_G^h/N_G^r=6/2$ (see Table 2).

3.1.2 Optimal selection of D

Next, we choose the optimal value for the distance–size ratio D. In this numerical test, the spherical shell with a homogeneous density is employed. The computation points are situated on a spherical surface, and different observation heights including $H=1$ m, 65 km, 130 km, 195 km, and 260 km are considered.

Fig. 7

RRMS of a V, b $g_z$, c $M_{xx}$ and d $M_{zz}$ as a function of the distance–size ratio D at different observation heights. In the figures, $D=0$ indicates that no adaptive discretization is adopted. $N_G^h=6$ and $N_G^r=2$ are used in the calculation

Figure 7 presents the RRMS deviation versus D at different observation heights. In general, the increase in D improves the numerical accuracy significantly, especially at lower altitudes. The height of observation also imposes an important impact on the RRMS deviation. Moreover, the accuracy of the gradient components $M_{xx}$ and $M_{zz}$ seems to be more sensitive to the computation heights as compared with V and $g_z$. On the other hand, we also observe that the RRMS curves do not change with D at first, but then decrease rapidly as D increases to a certain value, and finally become stable again. The inflection points of the curves from which the RRMS begins to decrease are also different for different H. The reason for this is that the 2D adaptive discretization (see Eq. (17)) only works when $D\ge D_0$, where $D_0=\ell _0/\max ({L_1},{L_2},{L_3})$ is the inflection point of D. Therefore, the change of D does not affect the accuracy at first when $D< D_0$. But with the further increase in D, the RRMS begins to decrease rapidly and then hold constant after reaching its minimum value. Therefore, the optimal value of D can be selected as the one larger than which the RRMS deviation becomes unchanged, that is, $D=1.5$ for $V, D=2$ for $g_z$, and $D=3$ for $M_{xx}$ and $M_{zz}$.

3.2 Influence of the observation height and the TSP dimension

In the previous tests, the thickness of the TSP is assumed to be $\Delta R=10$ km and its horizontal size $\Delta _h$ is roughly $1^\circ$. Here we take a deeper insight into the performance of the proposed method. In the following tests, we keep the outer radius of the shell models constant (i.e., $R=6371$ km) and calculate the gravitational effects at different observation heights using TSPs with different vertical and horizontal dimensions.

Fig. 8

RRMS of a V, b $g_z$, c $M_{xx}$ and d $M_{zz}$ as a function of the height of observation in the cases of different $\Delta _h$ varying from 0.5$^\circ$ to 9$^\circ$. $N_G^h=6, N_G^r=2$, and $D=3$ are used in the calculation

In the first test, the thickness of the shell is fixed as 10 km, and different triangular grids with equivalent angles of $\Delta _h$ varying from 0.5$^\circ$ to 9$^\circ$ are considered. The number of elements used in these cases is found in Table 5. Figure 8 shows the RRMS deviation of $V, g_z, M_{xx}$ and $M_{zz}$ versus the observation height in different cases of $\Delta _h$. As can be seen, the RRMS for all gravity components exhibits a decline trend with increasing altitude of observation. In addition, the gravitational potential seems the least affected by the observation height. We also observe that the decrease in $\Delta _h$ can improve the computation accuracy of V and $g_z$. But for $M_{xx}$ and $M_{zz}$, this only happens at large observation heights. The reason is that the RRMS deviations at lower heights are also affected by the adaptive discretization. Note that different $\Delta _h$ indicates different triangular meshes, and thus, the final grid after the adaptive discretization is also different, which consequently leads to fluctuations in the accuracy at different $\Delta _h$. Overall, the proposed method has a good performance across the altitudes from near surface to a satellite height under different triangular grids.

Fig. 9

RRMS of a V, b $g_z$, c $M_{xx}$ and d $M_{zz}$ as a function of the shell thickness $\Delta R$ at different observation heights varying from 1 m to 260 km. $N_G^h=6, N_G^r=2$ and $D=3$ are used in the calculation

Next, we hold $\Delta _h \approx 1^\circ$ and investigate the influence of $\Delta R$. The RRMS deviation as a function of the thickness $\Delta R$ is shown in Fig. 9. It can be seen that the accuracy generally increases as $\Delta R$ and H become larger. For the gravitational potential, high accuracy is achieved in all the cases, and its maximum deviation is lower than 0.01%. The maximum RRMS of $g_z$ is larger than that of V but still of good accuracy (about 0.1%). In contrast, the gravitational gradient components seem to be quite sensitive to the variation in the observation height as well as the shell thickness and exhibit deceasing accuracy when $\Delta R$ and H are reduced. We notice that the RRMS of $M_{xx}$ and $M_{zz}$ is larger than 10% in the range of $\Delta R \le$100 m and $H \le$1 km.

The main reason for the poor accuracy of $M_{xx}$ and $M_{zz}$ is the singularity caused by the numerical integration. From Eqs (3), (6) and (7), one can find that the amplitudes of $V, g_i$, and $M_{ij}$ are proportional to ${\ell }^{-1}, {\ell } ^{-3}$, and ${\ell }^{-5}$, respectively, and ${\ell }=0$ is an obvious singularity. It indicates that when the observation point is near the TSP surface, a small $\ell$ may occur and cause rounding off error affecting the computational accuracy. In addition, the error effect of the singularity of $V, g_i$, and $M_{ij}$ from weak to strong follows $V< g_i < M_{ij}$. In fact, even if $(\varphi ,\lambda )\approx (\varphi ',\lambda ')$, the kernel functions of $M_{ij}$ also have a sharp peak or a steep kink at the point of angular coincidence when $\vert r-r'\vert$ is small. In such case, it is difficult to describe the behavior of the integrand accurately by standard numerical integration methods (Fukushima and Toshio 2017). Moreover, the decrease in the thickness will further make the situation worse because there may exist more quadrature nodes located close to the computation points. Therefore, the proposed method should be improved for the evaluation of the TSPs with a small thickness.

Fig. 10

RRMS of a $M_{xx}$ and b $M_{zz}$ as a function of the shell thickness $\Delta R$ at $H=1$ m, 1 km, and 10 km before and after applying the extension technique

To improve the accuracy of computation points at lower altitudes, we combine the extension technique developed by Lin et al. (2020) into the proposed algorithm. The basic idea of the technique is to expand a TSP (A) along the radial direction to obtain an extending TSP (B) and an extended TSP (AB), and then calculate the gravitational effects of the original TSP A as the difference between those due to AB and B. The technique works because the TSP with a larger thickness could be better approximated. More details of the extension technique can be found in Lin et al. (2020).

We employ the extension technique to evaluate the RRMS of $M_{xx}$ and $M_{zz}$ at $H=1$ m, 1 km and 10 km again. Figure 10 compares the results before and after applying the extension technique. V and $g_z$ are not calculated since their accuracy is sufficient for most applications. From Fig. 10, it is observed that the numerical errors are significantly reduced as compared with the former results, and the maximum RRMS is now about 0.1$\%$ for $M_{xx}$ and $M_{zz}$. Moreover, the difference caused by the observation height also becomes negligible after the extension technique is applied. The cost is that the computation time will be also increased.

3.3 Gravitational effects of polynomial density models

Using the optimal values of $N_G^h, N_G^r$ and D, we can now calculate the gravitational effects of a shell with a variable density in depth. Here, the polynomial density models shown in Fig. 4b are considered. The thickness of the shell is set as $\Delta R=10$ km, and the observation height ranges from 1 m to 260 km above the 6371 km surface of the shell.

Fig. 11

RRMS as a function of the observation height H based on shell models with a constant, b linear, c quadratic, and d cubic densities

Table 3 Statistics of the numerical solutions calculated by the proposed method in terms of V (m$^2$/s$^2$), $g_z$ (mGal = $10^{-5}$m/s$^2$), $M_{zz}$ and $M_{xx}$ ($E=10^{-9}$s$^{-2}$) for shell models with constant (A), linear (B), quadratic (C), and cubic (D) densities

Figure 11 presents the RRMS values for the shell models with different polynomial densities. The corresponding statistic properties of the results in the case of $H=1$ km are provided in Table 3. It is clear that the proposed method obtains accurate results for all four polynomial density models. The gravitational potential has the highest precision, then $g_z$, and finally $M_{zz}$ and $M_{xx}$, and the numerical errors of the gravity components are all lower than 0.1$\%$. In addition, there is little difference between the RRMS values of the constant, linear, and quadratic density models. For the cubic model, the errors of V and $g_z$ show a slight increase as compared with the lower-degree density models, but still of high precision (approximately 10$^{-4}\%$). In general, the proposed method achieves good accuracy for different polynomial density models, which demonstrates the correctness and effectiveness of the method.

3.4 Comparison with existing methods

In the following, we carry out a benchmark study by comparing the proposed method with existing methods in terms of accuracy and efficiency so as to verify the superiority of the new algorithm.

3.4.1 Computational accuracy

The computational accuracy of different methods, including the proposed method, the classical tesseroid-based 3D GLQ method (Uieda et al. 2016), and the node-based integration method of Sebera et al. (2018) and Root et al. (2022), are compared in this section. In the node-based integration method, the Newton’s kernel is computed with respect to the nodes of the spherical triangles, since the density values in published tessellated models (like LITHO1.0) are given for the nodes of the triangular grid instead of the triangle themselves. This also results in an ambiguity in the way the volume element can be set up around each node. To simplify the situation and take the spherical geometry into account, Root et al. (2022) calculated the distance between the grid nodes and the area of each element by assuming triangular sides to be great circles. They built up an alternative area–volume element around each node as a local mean of the surrounding triangles (see Fig. 12) and then scaled the value of the local area to the number of triangles because the number of nodes is not equal to that of the triangles. Therefore, the spherical triangle is not really used in the calculation. One challenge of the method is that the nodes associated with larger triangles make greater contributions to gravitational effects so that the results will be systematically affected by the triangular patterns, especially a non-uniform triangular grid (Root et al. 2022). In addition, this method is limited only to large observation heights.

Fig. 12

Volume element built up around each node in the node-based integration method (modified after Sebera et al. 2018; Root et al. 2022)

For a fair comparison, we adopt the same homogeneous shell model used in Root et al. (2022) and set the altitude of observation at a large distance of 250 km above the shell surface. The shell is located at a mean depth of 100 km with respect to the Earth ($R_{Earth}=6371$ km) and has a density of 3300 $\mathrm{{kg/}}{\mathrm{{m}}^\mathrm{{3}}}$. Different thicknesses of 2, 5, 10 km are considered for comparison. In the test, we did not repeat the work of Sebera et al. (2018) and Root et al. (2022), but directly cited their results. For the proposed method, $N_G^h=6, N_G^r=2$ and $D=2$ are used. To further demonstrate the superiority of our algorithm over the traditional methods, we also compute the gravitational fields from a non-uniform triangular grid with 19,996 triangles and 10,000 nodes in which case the traditional methods face challenges. The results are summarized in Table 4.

Table 4 Comparison of the results obtained by the proposed method, the tesseroid-based method, and the node-based integration method of Root et al. (2022) at $H=250$ km for a homogeneous shell model

We observe that all three methods can produce a root mean square (RMS) value similar to the analytical solution. The tesseroid-based method slightly underestimates the gravity fields with approximately 0.1 mGal difference with respect to the analytical values. This may be related to the small volume loss due to the degenerated tesseroid shape approaching the poles. The method of Root et al. (2022) seems to perform slightly better, but shows different behavior at different lateral resolution of the triangular grid. At a roughly 2$^\circ$ grid, it obtains accurate RMS values but with larger variations. The finer 1$^\circ$ grid can reduce this variation to some extent, but produces larger differences in RMS. Furthermore, for a fixed lateral resolution, the increase in the shell thickness also leads to higher variation. In comparison, the proposed method performs much better than the traditional methods across all the shell thicknesses at both 1$^\circ$ and 2$^\circ$ grids, and only a slight difference in RMS value and a small variation are observed. Moreover, the proposed method also performs well when a completely non-uniform triangular grid is applied. In this case, a precision at about 0.01 mGal is achieved, which verifies the advantages of the new algorithm in computational accuracy over the traditional methods.

3.4.2 Computational efficiency

Next, we verify the computational efficiency of the proposed method based on a shell model and a regional irregular density model. All numerical experiments in this section are carried out on a PC with i9-12900K CPU and 64 GB RAM.

Fig. 13

Comparison of the computation time and numerical accuracy of $g_z$ obtained by the proposed method and the classical tesseroid-based method in the case of one observation point. The computation time is an averaged value by repeating the calculation 100 times. $N_G^h=6, N_G^r=2$ and $D=3$ are used for the proposed method, and $N_G^\varphi =N_G^\lambda =3, N_G^r=2$ and $D=3$ for the tesseroid-based 3D GLQ method

The first model is a homogeneous shell with $\Delta$R=10 km and $\rho =2300$ kg/m$^3$. The observation point is located at $(H,\varphi ,\lambda )=(100\,\hbox {km},0^\circ ,0^\circ )$. Since the computation cost of the gravitational potential, vector, and gradient tensor is close to each other, here we only take $g_z$ as an example. Figure 13 shows the calculation time of the proposed method and the tesseroid-based method for different horizontal mesh intervals ranging from 0.07$^\circ$ to 36$^\circ$. The corresponding number of elements in these cases is listed in Table 5. As can be seen, the computation time and accuracy of the two methods are generally comparable. The proposed method is only slightly faster than the tesseroid-based method. It suggests that the computation time required by the two methods to calculate the gravity effects generated by one mass element at a certain observation point is basically the same. However, this result does not mean that the proposed method has no significant advantage in efficiency for all cases, since the calculation time is highly dependent on the complexity of the density model used, or in other words, the number of elements used to describe the density model.

Table 5 Number of elements used to construct a shell model in the proposed method and the tesseroid-based method

Fig. 14

Illustration of the laterally irregular artificial density model with an outer radius of 6050 km, a thickness of 50 km and a density of 3300 kg/m$^3$. a 3D perspective of the artificial model; b discretization of the model based on TSPs; c discretization of the model based on tesseroids. Note that only the tesseroids with nonzero densities in c are considered in the calculation

Fig. 15

Comparison of the computation time and RRMS deviation of $g_z$ obtained by the proposed method and the classical tesseroid-based method in different cases for the laterally irregular density model. The integers marked in a denote the number of tesseroids (blue) and TSPs (red) for the eight cases. The open circles in the figures suggest the case that the two methods reach a similar accuracy (i.e., RRMS=0.02%). $N_G^h=6, N_G^r=2$ and $D=3$ are used for the proposed method, and $N_G^\varphi =N_G^\lambda =3, N_G^r=2$ and $D=3$ for the tesseroid-based 3D GLQ method

Fig. 16

Numerical results and differences of $V, g_z, M_{zz}$ for the laterally irregular density model. a–c The reference solutions of $V, g_z, M_{zz}$; d–f the differences between the reference solutions and the numerical results calculated by the proposed method in Case 3 (Fig. 15); g–i the differences between the reference solutions and the numerical results calculated by the tesseroid-based method in Case 7 (Fig. 15)

To further demonstrate the superiority of the proposed method in flexibility and efficiency, a regional artificial density model with laterally irregular boundaries is constructed. The model has an outer radius of 6050 km, a thickness of 50 km and a density of 3300 kg/m$^3$. By using mass elements of different shapes (i.e., TSPs and tesseroids), the irregular density model can be discretized in different ways (see Fig. 14). For the proposed method, TSPs with variable sizes can be used, while in the tesseroid-based method the grid must be refined under a longitude–latitude mesh. For example, to generate a grid of 0.5$^\circ$, 14,484 tesseroids with 142 in latitude and 102 in longitude are required. It is also noteworthy that among the tesseroids, only the ones with nonzero densities (5892 tesseroids) are considered in the calculation. In this test, there are $161\times 121=19{,}481$ observation points evenly distributed along the latitudinal and longitudinal directions on a spherical surface at a height of 250 km above the surface of the model. Their latitude ranges from 5$^\circ$ to 85$^\circ$ and the longitude varies from 5$^\circ$ to 65$^\circ$. For such a density model, no analytical solution is available and hence we take the numerical results obtained based on a dense triangular grid of 975,961 elements as the reference solution. Eight cases with the grid from coarse to fine are considered in the test. The computation time and RRMS deviation of $g_z$ obtained by the two methods in these cases are compared in Fig. 15. Figure 16 shows the differences between the reference solutions and the numerical results when the RRMS values of both methods approximate 0.02$\%$. The results of other gravitational components are listed in Table 6.

Table 6 Calculation time and RRMS deviation obtained by the proposed method and the tesseroid-based method for Case 3 and Case 7 specified in Fig. 15

From Fig. 15, we can see that owing to the high flexibility of TSPs, the number of elements required in the proposed method to accurately describe the irregular density model is much less than that of the tesseroid-based method. For example, to achieve an accuracy of 0.02$\%$, only 1978 TSPs are needed in our algorithm while for the classical method, 590,013 elements are required (see Case 3 and Case 7 specified in Fig. 15). In that case, the calculation time of the proposed method is 4 s, which is less than that of the tesseroid-based method (1011 s) by more than 2 orders. It indicates that using TSPs instead of tesseroids for irregular density models can substantially improve the computational efficiency. Figure 16 and Table 6 further confirm the high efficiency and good accuracy of the proposed TSP-based method.

4 Application

In this section, we apply the method in the computation of the gravitational effects for the LITHO1.0 model (Pasyanos et al. 2014). The LITHO1.0 is a 1$^\circ$ tessellated model of the crust and upper mantle of the Earth, parameterized laterally by triangular nodes and vertically as a set of geophysically identified layers, including water, ice, sediments, crystalline crust, lithospheric lid, and asthenosphere. The LITHO1.0 consists of 40,962 nodes and 81,920 triangles, and each node has its own number of layers that are equipped with the volumetric mass density, upper radius $R_1$, lower radius $R_2$, thickness ($\Delta R = R_2-R_1$), and other parameters. Figure 17 shows the density and thickness distributions of the upper crust in the LITHO1.0 model. It is also noteworthy that the spherical 1D Earth model ak135 located at the lowest layers of the LITHO1.0 model is neglected in our calculation.

Fig. 17

Density and thickness distribution of the upper crust in the LITHO1.0 model. a Density distribution and b thickness distribution

To evaluate the gravitational effects of the LITHO1.0 model with the proposed method, special treatment is required since the density values of the model are given for the nodes and not for the triangles. In other words, the vertices of the triangle may have different density values. Therefore, for the sake of simplicity, we take an average of the three nodal density values so that a single density can be obtained for each element. In addition, to take the spherical geometry into account, the vertices of each triangle are assumed to be situated on a spherical surface whose radius is an average of those of the vertices. In our implementation, the LITHO1.0 model is divided into ten parts, that is, water, ice, upper sediments, middle sediments, lower sediments, upper crust, middle crust, lower crust, lithospheric lid, and asthenosphere. The observation points are placed on a $1^\circ \times 1^\circ$ global grid at a GOCE altitude of 250 km above the mean Earth radius. Then, the gravitational effects of each part of the LITHO1.0 model are calculated separately. Figure 18 shows the gravity fields produced by the ten parts of the LITHO1.0 model, and Fig. 19 presents the overall gravitational effects of the Earth crust that adds the contributions of water, ice, upper sediments, middle sediments, lower sediments, upper crust, middle crust, and lower crust together. We also provide the statistics of the numerical results in Table 7, including the minimum value, the maximum value, and the RMS. Although there is no exact formula to validate the results, the magnitudes and spatial distribution of the numerical solutions correspond with other authors (e.g., Fig. 2b in Sebera et al. 2018, and Fig. 16 in Ouyang et al. 2022 for the CRUST1.0 model).

Fig. 18

Vertical component $g_z$ of the gravitational vector calculated using the proposed method for different parts of the LITHO1.0 model at the altitude of 250 km. The sign of $g_z$ is reversed since the positive direction of Z axis is pointing upward

Fig. 19

Total gravitational effects due to the crust part of the LITHO1.0 model (excluding the contributions of the lithospheric lid and the asthenosphere) at the altitude of 250 km. The sign of the gravity components is reversed since the positive direction of Z axis is pointing upward in the proposed method

Table 7 Numerical values of the gravitational potential (m$^2$/s$^2$), gravitational vector (mGal) and Marussi tensor (E) for different parts of the LITHO1.0 model

5 Conclusions and outlook

In the present work, we developed a triangular spherical prism (TSP) based method for 3D large-scale gravitational forward modeling. The TSP is defined by two spherical triangles with one of which being the radial projection of the other. Compared with the commonly used tesseroid, such a element not only has the capability to describe the curvature of the Earth, but also enjoys high flexibility in dealing with laterally variable density distributions. By dividing the source region into a number of TSPs, we numerically calculate the gravitational effects of each TSP using the mixed Gaussian quadrature method, that is, the GLQ method for the radial integration and the triangle-based Gaussian quadrature rule for the surface integration. A 2D adaptive discretization strategy and a well-established extension technique are also combined to ensure the accuracy for near-source computation points.

From the numerical experiments based on spherical shell models, we found that the computational accuracy and efficiency of the proposed method are closely related to two parameters: the number of Gaussian nodes ($N_G^h/N_G^r$) and the distance–size ratio (D). $N_G^r$ and $N_G^h$ determine the numerical accuracy of the radial integration and the surface integration over the spherical triangle, respectively, while D controls the number of subdivisions. Generally, the increase in these parameters can improve the computational accuracy, but also increase the computation cost. Therefore, the optimal selection on these parameters is important. Our numerical tests showed that when different polynomial density models are used, the optimal value of $N_G^r$ is different. In the case of constant density, $N_G^r=1$ is sufficient for all the gravity components to achieve a good accuracy, while for higher-order polynomial density models, the best choice of $N_G^r$ is 2. In contrast, the optimal values of $N_G^h$ for different polynomial densities are almost the same, that is, $N_G^h=3$ for V, and $N_G^h=6$ for $g_z,M_{xx}$ and $M_{zz}$. Therefore, $N_G^h/N_G^r=6/2$ is finally recommended. As for the parameter D, it plays an important role at lower observation heights, but stops to work when the altitude is larger than D times the maximum lateral size of the TSP. According to the numerical results, to achieve an RRMS value lower than 0.1$\%$, the best value of D is 1.5 for V, 2 for $g_z$, and 3 for $M_{xx}$ and $M_{zz}$.

The height of observation and the dimension of the TSP also have an influence on the computational accuracy. The RRMS generally decreases as the observation height and the shell thickness increase. The influence of the horizontal size of the TSP is negligible owing to the use of the adaptive discretization. For V and $g_z$, good accuracy can be always achieved and their RRMS values are also less affected by the observation height and the shell thickness. In comparison, $M_{xx}$ and $M_{zz}$ are quite sensitive to the variation in the altitude and exhibit decreasing accuracy when the observation height and the thickness of the TSP are reduced. This is mainly caused by the complex behavior of the kernel functions. When the observation point is near the TSP, small $\ell$ may occur and result in singularity. In fact, even if $(\varphi ,\lambda )\approx (\varphi ',\lambda ')$, the kernel functions will also have a sharp peak at the point of angular coincidence, leading to difficulties in approximating the behavior of the integrand. To improve the accuracy in this case, the extension technique can be combined into the proposed algorithm for the calculation of $M_{xx}$ and $M_{zz}$ at lower altitudes. Numerical tests illustrated that the maximum RRMS values of $M_{xx}$ and $M_{zz}$ were significantly reduced from above $1\%$ to approximately $0.1\%$ after applying the extension technique. On the whole, the combination of the adaptive discretization and the extension technique strategy can help ensure the accuracy at lower altitudes.

The comparison analysis with the existing methods further verified the superiority of the new algorithm. The results suggested that the proposed method calculates RMS values more closer to the analytical signal than the classical methods (including the tesseroid-based and node-based integration methods), regardless of the shell thickness and the lateral resolution of the triangular grid. The maximum variations obtained from the new method are also more than one order of magnitude lower than those calculated by the node-based integration method. Moreover, for a completely non-uniform triangular grid in which case the traditional methods face challenges, the proposed method can also obtain a precision at about 0.01 mGal. On the other hand, for shell models with an equivalent-angle grid, the number of required TSPs is larger than that of tesseroids, and hence, the corresponding computation cost for the TSP-based method is also theoretically larger. However, owing to the high flexibility of TSPs, the number of elements required in our algorithm to accurately describe a complex irregular density model is much less than that needed for the tesseroid-based method, which as a result substantially speeds up the forward calculation by more than 2 orders. The application of the new method to the tessellated LITHO1.0 model further demonstrated its capability and flexibility in real applications.

In conclusion, the newly developed TSP-based method can use the least number of mass elements to achieve good accuracy and efficiency for complex density models with varying lateral resolutions and hence offers an attractive and flexible alternative for large-scale gravity forward and inverse problems with irregular grids. However, the current method calculates the total gravitational fields by adding the contribution of each TSP together through pure summation, which is simple but still time-consuming. Therefore, suitable acceleration technique for the TSP-based method needs to be developed. This is also the focus of our future work.