Skip to main content
SpringerLink
Log in

A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling

  • Original Article
  • Published:
Journal of Geodesy Aims and scope Submit manuscript

A Comment to this article was published on 13 May 2016

Abstract

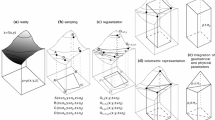
The calculation of topographic (and iso- static) reductions is one of the most time-consuming operations in gravity field modelling. For this calculation, the topographic surface of the Earth is often divided with respect to geographical or map-grid lines, and the topographic heights are averaged over the respective grid elements. The bodies bounded by surfaces of constant (ellipsoidal) heights and geographical grid lines are denoted as tesseroids. Usually these ellipsoidal (or spherical) tesseroids are replaced by “equivalent” vertical rectangular prisms of the same mass. This approximation is motivated by the fact that the volume integrals for the calculation of the potential and its derivatives can be exactly solved for rectangular prisms, but not for the tesseroids. In this paper, an approximate solution of the spherical tesseroid integrals is provided based on series expansions including third-order terms. By choosing the geometrical centre of the tesseroid as the Taylor expansion point, the number of non-vanishing series terms can be greatly reduced. The zero-order term is equivalent to the point-mass formula. Test computations show the high numerical efficiency of the tesseroid method versus the prism approach, both regarding computation time and accuracy. Since the approximation errors due to the truncation of the Taylor series decrease very quickly with increasing distance of the tesseroid from the computation point, only the elements in the direct vicinity of the computation point have to be separately evaluated, e.g. by the prism formulas. The results are also compared with the point-mass formula. Further potential refinements of the tesseroid approach, such as considering ellipsoidal tesseroids, are indicated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Anderson EG (1976) The effect of topography on solutions of Stokes’ problem. Unisurv S-14, Rep, School of Surveying. University of New South Wales, Kensington

    Google Scholar 

  • Forsberg R (1984) A study of terrain reductions, density anomalies and geophysical inversion methods in gravity field modelling. Rep 355, Department of Geodetic Science. The Ohio State University, Columbus

    Google Scholar 

  • Forsberg R (1985) Gravity field terrain effect computations by FFT. Bull Géod 59:342–360

    Article  Google Scholar 

  • Forsberg R, Sideris MG (1989) On topographic effects in gravity field approximation. In: Kejlsø E, Poder K, Tscherning CC (eds) Festschrift to Torben Krarup. Geodaetisk Institut Meddelelse No 58, København, pp 129–148

    Google Scholar 

  • Forsberg R, Tscherning CC (1997) Topographic effects in gravity field modelling for BVP. In: Sansò F, Rummel R (eds) Geodetic boundary value problems in view of the one centimetre geoid. Lecture Notes in Earth Sciences, vol 65. Springer, Berlin Heidelberg New York, pp 241–272

    Google Scholar 

  • Grüninger W (1990) Zur topographisch-isostatischen Reduktion der Schwere. PhD Thesis, Universität Karlsruhe

  • Hackney RI, Featherstone WE (2003) Geodetic versus geophysical perspective of the ‘gravity anomaly’. Geophys J Int 154(1):35–43, erratum in 154(2):596

    Google Scholar 

  • Hammer S (1939) Terrain corrections for gravimeter stations. Geophysics 4:184–194

    Article  Google Scholar 

  • Harrison JC, Dickinson M (1989) Fourier transform methods in local gravity field modelling. Bull Géod 63:149–166

    Article  Google Scholar 

  • Heck B (2003a) On Helmert’s methods of condensation. J Geod 77(3–4):155–170, DOI: 10.1007/s00190-003-0318-5

    Article  Google Scholar 

  • Heck B (2003b) Rechenverfahren und Auswertemodelle der Landesvermessung. Klassische und moderne Methoden, 3rd edn. Wichmann, Heidelberg

    Google Scholar 

  • Heiskanen WA, Moritz H (1967) Physical geodesy. Freeman, San Francisco

    Google Scholar 

  • Heiskanen WA, Vening Meinesz FA (1958) The Earth and its gravity field. McGraw-Hill, New York

    Google Scholar 

  • Jekeli C, Serpas JG (2003) Review and numerical assessment of the direct topographical reduction in geoid determination. J Geod 77(3–4):226–239, DOI: 10.1007/s00190-003-0320-y

    Article  Google Scholar 

  • Jung K (1961) Schwerkraftverfahren in der Angewandten Geophysik. Akademische Verlagsgesellschaft. Geest& Portig, Leipzig

    Google Scholar 

  • Klose U, Ilk KH (1993) A solution to the singularity problem occurring in the terrain correction formula. Manuscr Geod 18:263–279

    Google Scholar 

  • Koch KR (1965) Die topographische Schwere- und Lotabweichungsreduktion für Aufpunkte in geneigtem Gelände. Allg Vermess.-Nachr 11:438–441

    Google Scholar 

  • Kuhn M (2000) Geoidbestimmung unter Verwendung verschiedener Dichtehypothesen. Reihe C, Heft Nr 520. Deutsche Geodätische Kommission, München

    Google Scholar 

  • Kuhn M, Seitz K (2005) Comparison of Newton’s integral in the space and frequency domains. In: Sansò F (ed) A window on the future of geodesy. Proceedings of the IAG General Assembly, Sapporo, Japan 2003. IAG Symposia, vol 128. Springer, Berlin Heidelberg New York, pp 386–391

    Google Scholar 

  • LaFehr TR (1991a) Standardization in gravity reduction. Geophysics 56(8):1170–1178

    Article  Google Scholar 

  • LaFehr TR (1991b) An exact solution for the gravity curvature (Bullard B) corrections. Geophysics 56 (8):1179–1184

    Article  Google Scholar 

  • Lemoine FG, Kenyon SC, Factor JK, Trimmer RG, Pavlis NK, Chinn DS, Cox CM, Klosko SM, Luthcke SB, Torrence MH, Wang YM, Williamson RG, Pavlis EC, Rapp RH and Olson TR (1998) The development of the joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) geopotential model EGM96. Report TP-1998–206861, NASA Goddard Space Flight Center, Greenbelt, 575 pp

  • Li YC, Sideris MG (1994) Improved gravimetric terrain corrections. Geophys J Int 119:740–752

    Article  Google Scholar 

  • MacMillan WD (1930) Theoretical Mechanics, vol 2: the Theory of the potential. McGraw-Hill, New York (reprinted by Dover Publications, New York 1958)

    Google Scholar 

  • Mader K (1951) Das Newtonsche Raumpotential prismatischer Körper und seine Ableitungen bis zur dritten Ordnung. Österr Z Vermess Sonderheft, vol 11

  • Martinec Z (1998) Boundary value problems for gravimetric determination of a precise geoid. Lecture notes in Earth Sciences, vol 73. Springer, Berlin Heidelberg New York

    Google Scholar 

  • Martinec Z, Vanicěk P, Mainville A and Véronneau M (1996) Evaluation of topographical effects in precise geoid computation from densely sampled heights. J Geod 70(11):746–754, DOI: 10.1007/BF00867153

    Google Scholar 

  • Moritz H (1968) On the use of the terrain correction in solving Molodensky’s problem. Rep 108, Department of Geodetic Science. The Ohio State University, Columbus

    Google Scholar 

  • Moritz H (1980) Advanced physical geodesy. Wichmann, Karlsruhe

    Google Scholar 

  • Nagy D (1966) The gravitational attraction of a right rectangular prism. Geophysics 31:362–371

    Article  Google Scholar 

  • Nagy D, Papp G, Benedek J (2000) The gravitational potential and its derivatives for the prism. J Geod 74(7–8):552–560, DOI: 10.1007/s001900000116

    Article  Google Scholar 

  • Nagy D, Papp G, Benedek J (2002) Corrections to “The gravitational potential and its derivatives for the prism”. J Geod 76(8):475, DOI: 10.1007/s00190-002-0264-7

    Article  Google Scholar 

  • Novák P, Grafarend EW (2005) Ellipsoidal representation of the topographical potential and its vertical gradient. J Geod 78(11–12):691–706, DOI: 10.1007/s00190-005-0435-4

    Article  Google Scholar 

  • Novák P, Vaniček P, Martinec Z, Véronneau M (2001) Effects of the spherical terrain on gravity and the geoid. J Geod 75(9–10):491–504, DOI: 10.1007/s001900100201

    Google Scholar 

  • Nowell DAG (1999) Gravity terrain corrections – an overview. J Appl Geophys 42:117–134

    Article  Google Scholar 

  • Papp G, Wang ZT (1996) Truncation effects in using spherical harmonic expansions for forward local gravity field modelling. Acta Geod Geoph Hung 31(1–2):47–66

    Google Scholar 

  • Paul MK (1974) The gravity effect of a homogeneous polyhedron for three-dimensional interpretation. Pure Appl Geophys 112:553–561

    Article  Google Scholar 

  • Petrović S (1996) Determination of the potential of homogeneous polyhedral bodies using line integrals. J Geod 71(1):44–52, DOI: 10.1007/s001900050074

    Article  Google Scholar 

  • Rodriguez E, Morris CS, Belz JE, Chapin EC, Martin JM, Daffer W, Hensley S (2005) An assessment of the SRTM topographic products. Technical Report JPL D-31639, Jet Propulsion Laboratory, Pasadena, 143 pp

  • Schwarz K-P, Sideris MG, Forsberg R (1990) The use of FFT techniques in physical geodesy. Geophys J Int 100:485–514

    Article  Google Scholar 

  • Seitz K, Heck B (2001) Tesseroids for the calculation of topographic reductions. Abstracts “Vistas for Geodesy in the New Millenium”, IAG 2001 Scientific Assembly 2–7 September 2001, Budapest, Hungary, 106

  • Sideris MG (1985) A fast Fourier transform method for computing terrain corrections. Manuscr Geod 10:66–73

    Google Scholar 

  • Smith DA (2000) The gravitational attraction of any polygonally shaped vertical prism with inclined top and bottom faces. J Geod 74(5): 414–420, DOI: 10.1007/s001900000102

    Article  Google Scholar 

  • Smith DA (2002) Computing components of the gravity field induced by distant topographic masses and condensed masses over the entire Earth using the 1-D FFT approach. J Geod 76(3):150–168, DOI: 10.1007/s00190-001-0227-4

    Article  Google Scholar 

  • Smith DA, Robertson DS, Milbert DG (2001) Gravitational attraction of local crustal masses in spherical coordinates. J Geod 74(11–12):783–795, DOI: 10.1007/s001900000142

    Article  Google Scholar 

  • Talwani M, Ewing M (1960) Rapid computation of gravitational attraction of three-dimensional bodies of arbitrary shape. Geophysics 25:203–225

    Article  Google Scholar 

  • Tsoulis D (1999) Analytical and numerical methods in gravity field modelling of ideal and real masses. Reihe C, Heft Nr 510. Deutsche Geodätische Kommission, München

    Google Scholar 

  • Tsoulis D, Tziavos IN (2002) A comparison of some existing methods for the computation of terrain correction in local gravity field modelling. In: Tziavos IN (ed) Gravity and Geoid 2002. Proceedings of the 3rd meeting of the international gravity and geoid commission, Thessaloniki, pp 156–160

  • Tsoulis D, Wziontek H, Petrović S (2003) A bilinear approximation of the surface relief in terrain correction computations. J Geod 77(5–6):338–344, DOI: 10.1007/s00190-003-0332-7

    Article  Google Scholar 

  • Vaniček P, Novák P, Martinec Z (2001) Geoid, topography, and the Bouguer plate or shell. J Geod 75(4):210–215, DOI: 10.1007/s001900100165

    Article  Google Scholar 

  • Vaniček P, Tenzer R, Sjöberg LE, Martinec Z, Featherstone WE (2004) New views of the spherical Bouguer gravity anomaly. Geophys J Int 159:460–472

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Geodetic Institute, University of Karlsruhe, Englerstraße 7, 76128, Karlsruhe, Germany

    B. Heck & K. Seitz

Authors
  1. B. Heck
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. Seitz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to B. Heck.

Additional information

A comment to this article is available at http://dx.doi.org/10.1007/s00190-016-0907-8.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Heck, B., Seitz, K. A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling. J Geod 81, 121–136 (2007). https://doi.org/10.1007/s00190-006-0094-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00190-006-0094-0

Keywords

Search

Navigation