Fast calculation of gravitational effects using tesseroids with a polynomial density of arbitrary degree in depth

Abstract

Fast and accurate calculation of gravitational effects on a regional or global scale with complex density environment is a critical issue in gravitational forward modelling. Most existing significant developments with tessroid-based modelling are limited to homogeneous density models or polynomial ones of a limited order. Moreover, the total gravitational effects of tesseroids are often calculated by pure summation in these methods, which makes the calculation extremely time-consuming. A new efficient and accurate method based on tesseroids with a polynomial density up to an arbitrary order in depth is developed for 3D large-scale gravitational forward modelling. The method divides the source region into a number of tesseroids, and the density in each tesseroid is assumed to be a polynomial function of arbitrary degree. To guarantee the computational accuracy and efficiency, two key points are involved: (1) the volume Newton’s integral is decomposed into a one-dimensional integral with a polynomial density in the radial direction, for which a simple analytical recursive formula is derived for efficient calculation, and a surface integral over the horizontal directions evaluated by the Gauss–Legendre quadrature (GLQ) combined with a 2D adaptive discretization strategy; (2) a fast and flexible discrete convolution algorithm based on 1D fast Fourier transform (FFT) and a general Toepritz form of weight coefficient matrices is adopted in the longitudinal dimension to speed up the computation of the cumulative contributions from all tesseroids. Numerical examples show that the gravitational fields predicted by the new method have a good agreement with the corresponding analytical solutions for spherical shell models with both polynomial and non-polynomial density variations in depth. Compared with the 3D GLQ methods, the new algorithm is computationally more accurate and efficient. The calculation time is significantly reduced by 3 orders of magnitude as compared with the traditional 3D GLQ methods. Application of the new algorithm in the global crustal CRUST1.0 model further verifies its reliability and practicability in real cases. The proposed method will provide a powerful numerical tool for large-scale gravity modelling and also an efficient forward engine for inversion and continuation problems.

1 Introduction

With the advent of satellite gravimetry, high-quality gravity measurements with global-scale coverage become available (Soler et al. 2019). To estimate the density distribution from observed data sets by a regularized inversion, an efficient and accurate forward engine is of great importance. The gravitational forward modelling primarily focuses on solving the volumetric integral of Newton’s kernel and its derivatives. A common method for evaluating these integrals is to firstly decompose the source region into small elementary mass bodies of various geometrical shapes, such as rectangular prism and polyhedral body in Cartesian coordinates (e.g. Anderson 1976; Pohanka 1988; Holstein and Ketteridge 1996; Tsoulis 2012; D’Urso 2014a; Conway 2015; Wu and Chen 2016; Benedek et al. 2018; Zhang and Chen 2018; Chen and Liu 2019; Wu et al. 2019), and tesseroid (spherical prism) in spherical coordinates (e.g. Heck and Seitz 2007; Grombein et al. 2013; Uieda et al. 2016; Zhao et al. 2019, 2021). Then, the overall gravitational effect is calculated by adding all contributions of each individual element together. For regional and global applications, the effect of the Earth’s curvature is significant. Hence, the forward modelling are often implemented in geocentric spherical coordinates and use tesseroids, bounded by pairs of latitude, longitude, and radial surfaces, as building blocks.

Generally, the forward calculation in spherical coordinates consists of two parts: the evaluation of gravitational effects produced by a single tesseroid and the computation of cumulative contribution from all elementary cells. In contrast to the most common rectangular prism (Nagy et al. 2000; Wild-Pfeiffer 2008), the closed-form solution for a general tesseroid is not available. Due to the fact that it is an “elliptical integral”, the volumetric integral for a tesseroid must be solved numerically or semi-analytically. The literature offers three main approaches: Taylor series expansion, Gauss–Legendre quadrature (GLQ), and mixed integration. The Taylor series expansion approach solves the elliptic integral using a Taylor series expansion of the triple integral and a subsequent analytical integration of the expansions (Heck and Seitz 2007; Grombein et al. 2013; Marotta et al. 2019). This approach has high accuracy at low latitudes, but exhibits decreasing accuracy towards the polar as the tesseroid gradually degenerates into an approximately triangular shape (Uieda et al. 2016). For the GLQ approach, the gravitational effects of a tesseroid are numerically calculated by a weighted sum of the contribution of Gaussian points (Li et al. 2011; Uieda et al. 2016; Lin and Denker 2019; Soler et al. 2019; Zhao et al. 2019, 2021; Qiu and Chen 2020). The accuracy of GLQ is predominantly controlled by the number of Gaussian nodes (Ku 1977). In general, the more the Gaussian nodes, the better the accuracy of GLQ, while the lower the computational efficiency. To reduce the computational cost and retain satisfactory accuracy at the same time, the idea of adaptive discretization is proposed. The adaptive discretization strategies, whether 2D (Lin and Denker 2019; Soler et al. 2019) or 3D (Li et al. 2011; Uieda et al. 2016), adopt a similar criterion that a tesseroid is divided if the distance to the computation point is smaller than a constant times the size of the tesseroid. This means that only the tesseroid close to the computation point requires a greater number of subdivisions, which as a result significantly shortens the computation time.

As an alternative, the mixed integration approach solves the volumetric integrals for a tesseroid using a 2D spherical integration in the horizontal directions and a 1D analytical integration in the radial dimension. To solve the 2D spherical integral, various numerical methods can be utilized, such as Taylor series expansion (e.g. Smith 2002), GLQ (e.g. Wild-Pfeiffer 2008; Lin and Denker 2019; Zhong et al. 2019), and double exponential quadrature rule (e.g. Fukushima 2018). Compared to the former volume integral approaches, this mixed method using a combination of the numerical calculation of a surface integral and the analytical integration over the radial coordinate can generate more accurate solutions with less computation cost. Another significant advantage lies in that the mixed method can be naturally extended to the case of a general tesseroid with a radially varying density, especially a polynomial one. In fact, most existing volume integral approaches limit their applications only to homogeneous mass bodies. However, the constant density assumption is not realistic for most geological structures. In real media, the subsurface density must increase with increasing depth, due to the compression of the material composing the crust (Kumagai 1933; Maxant 1980; Rao et al. 1993; Kennett 1998). Therefore, considering the density variation with depth is of great practical significance (Chai and Hinze 1988; Holstein 2003; Hamayun et al. 2009; D’Urso 2014b; Wu and Chen 2016; D’Urso and Trotta 2017; Ren et al. 2017, 2018). Recently, some studies based on tesseroids generalize the constant density assumption to the linear (Lin and Denker 2019) and nonlinear cases (Fukushima 2018; Soler et al. 2019; Lin et al. 2020) so as to meet the requirements of depth variable density. However, most of these methods only consider a polynomial density up to an limited order.

The aforementioned methods provide desired solutions for the triple integral of an individual tesseroid. Actually, these solutions are weight coefficients, because the density term is usually pulled outside of the triple integral. Hence, the gravitational potential and its derivatives for a tesseroid can always be expressed as the products of the densities and the corresponding weight coefficients. Once the gravitational effects for a tesseroid are obtained, the overall effects of the whole source region can then be computed as a cumulative contribution of all individual tesseroids in terms of the principle of superposition. Although this process looks very simple, the computational cost substantially increases with the complexity of the model. Therefore, a precise evaluation is extremely time-consuming in practical applications, especially for the regional and global large-scale forward modelling.

To speed up the forward calculation, some attempts to apply the well-known fast Fourier transform (FFT) to gravity problems have been made. Smith (2002) adopted series expansions and 1D FFT to compute the gravity fields induced by distant global masses. He manipulated the integrals for the gravitational potential and acceleration into convolution integrals in longitude, and used 1D FFT techniques to efficiently compute the convolutions. Recently, Zhao et al. (2021) combined the 1D FFT into a 3D GLQ-based forward modelling method. Similar to Smith (2002), they accelerated the modelling by using the FFT techniques in discrete convolution along longitude. In the method of Zhao et al. (2021), however, the FFT-based fast algorithm is achieved using a square and symmetric Toeplitz form of the weight coefficient matrices. This requires that the number and location of the observation points must be consistent with those of the tesseroids in the longitudinal direction, which as a result may lead to undesirable computation cost and makes the method not that flexible in real cases. Moreover, these methods are established under the assumption of constant density in each tesseroid and hence face difficulties in practical applications with complex density environment.

Fig. 1

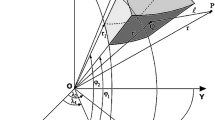
Source region with irregular tesseroids in spherical coordinates $(r,\varphi ,\lambda )$. $\Delta {r'}$, $\Delta {\varphi '}$, and $\Delta \lambda '$ denote the mesh interval of a tesseroid with a polynomial density $\rho (r')$. $Q(r',\varphi ',\lambda ')$ is the geometric centre of the tesseroid. In the proposed method, $\Delta \lambda '$ is required to be constant along the longitudinal direction

In this work, we propose a new efficient and accurate method for 3D large-scale forward modelling that can be applied to the case of a general tesseroid with a polynomial density up to an arbitrary degree and with variable intervals in latitude and depth (see Fig. 1). Firstly, a combination of 1D analytical integration in the radial direction and 2D GLQ with an adaptive discretization in horizontal directions is introduced to calculate the gravitational effects of an individual tesseroid. The radial analytical integration here can be applicable to a polynomial density up to an arbitrary order by using a simple recursive relation. Next, a flexible and efficient discrete convolution algorithm based on 1D FFT and a general Toeplitz form of weight coefficient matrices is presented to compute the overall effects from all combined tesseroids. Then, the influence of some key parameters are discussed, and several shell models are established to verify the computational efficiency and accuracy of the proposed method. Finally, we apply the method to the global crustal model CRUST1.0 to further verify its flexibility and practicability.

2 Gravitational effects of a tesseroid with a polynomial density

In this section, a mixed method is presented to evaluate the gravitational potential, the gravitational vector and the Marussi tensor for a tesseroid with a polynomial density function up to an arbitrary degree.

Fig. 2

A tesseroid in spherical coordinates $(r,\varphi ,\lambda )$. The spherical coordinates are referred to the geocentric Earth-fixed equatorial reference system defined by (X, Y, Z). $P(r,\varphi ,\lambda )$ and $Q(r',\varphi ',\lambda ')$ denote the observation point and the centre of a tesseroid in the source region, respectively. The topocentric local Cartesian coordinate system (north/east/up) is represented by (x, y, z)

2.1 Gravitational potential

A tesseroid in geocentric spherical coordinates is defined by three pairs of boundaries: a pair of concentric spheres (${r'_1}=\,\,$constant, ${r'_2}=\,\,$constant), a pair of parallels (${\varphi '_1}=\,\,$constant, ${\varphi '_2}=\,\,$constant), and a pair of meridians (${\lambda '_1}=\,\,$constant, ${\lambda '_2}=\,\,$constant (see Fig. 2). According to the Newton’s integral (Heiskanen and Moritz 1967; Grombein et al. 2013), the gravitational potential of a tesseroid with a radially varying density $\rho (r')$ can be expressed as

$$\begin{aligned} V(r,\varphi ,\lambda ) = G\int \limits _{{\lambda '_1}}^{{\lambda '_2}} {\int \limits _{{\varphi '_1}}^{{\varphi '_2}} {\int \limits _{{r'_1}}^{{r'_2}} {\frac{{{{r'}^2}}}{\ell }\rho (r'){\hbox {cos}}\varphi '{\hbox {d}}r'{\hbox {d}}\varphi '{\hbox {d}}\lambda '}} } \end{aligned}$$

(1)

where G is the gravitational constant, $\rho$ the depth-dependent density, and $\ell$ the distance between the computation point $P(r,\varphi ,\lambda )$ and the mass point $Q(r',\varphi ',\lambda ')$ with the following form

$$\begin{aligned}{} & {} \ell = \sqrt{{r^2} + {{r'}^2} - 2rr'\cos \psi } \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \cos \psi = \sin \varphi \sin \varphi ' + \cos \varphi \cos \varphi '\cos (\lambda ' - \lambda ) \end{aligned}$$

(3)

We assume that the density variation in depth for such a tesseroid follows an Nth-order polynomial function,

$$\begin{aligned} \rho (r') = \sum \limits _{k = 0}^N {{l_k}(r'){\rho _k}} \end{aligned}$$

(4)

with

$$\begin{aligned} {l_k}(r')&= \sum \limits _{p = 0}^{N} {L_p^k{{r'}^p}} \nonumber \\&= \frac{{(r' - {r'_0})(r' - {r'_1}) \cdots (r' - {r'_{k - 1}})(r' - {r'_{k + 1}}) \cdots (r' - {r'_N})}}{{({r'_k} - {r'_0})({r'_k} - {r'_1}) \cdots ({r'_k} - {r'_{k - 1}})({r'_k} - {r'_{k + 1}}) \cdots ({r'_k} - {r'_N})}}\nonumber \\ \end{aligned}$$

(5)

where $L_p^k$ is the polynomial coefficient, and ${r'_k}$ and ${\rho _k}$ are the kth node and nodal density along the radial direction in the tesseroid, respectively.

Using (1), (4), and (5), the gravitational potential over a tesseroid becomes

$$\begin{aligned} V(r,\varphi ,\lambda ) = \sum \limits _{k = 0}^N {\sum \limits _{n = 0}^N {L_n^k} {I_{n + 2}}{\rho _k}} = \sum \limits _{k = 0}^N {w_k{\rho _k}} \end{aligned}$$

(6)

where

$$\begin{aligned}{} & {} {w_k} = \sum \limits _{n = 0}^N {L_n^k} {I_{n + 2}} \end{aligned}$$

(7)

$$\begin{aligned}{} & {} {I_{n+2}} = G\int \limits _{{\lambda '_1}}^{{\lambda '_2}} {\int \limits _{{\varphi '_1}}^{{\varphi '_2}} {{\hbox {cos}}\varphi '\left( \left. {{\xi _{n+2}}} \right| _{{r'_1}}^{{r'_2}}\right) {\hbox {d}}\varphi '{\hbox {d}}\lambda '} } \end{aligned}$$

(8)

$$\begin{aligned}{} & {} {\xi _{n + 2}} = \int {\frac{{{{r'}^{n + 2}}}}{\ell }{\hbox {d}}r'} \end{aligned}$$

(9)

with

$$\begin{aligned} {\xi _0}&= \left\{ \begin{array}{ll} {\hbox {sign}}(r' - r)\ln \vert {r' - r} \vert ,&{}\quad \cos \psi = 1\\ \ln (r' + r),&{}\quad \cos \psi = - 1\\ \ln \left| {\ell + r' - r\cos \psi } \right| ,&{}\quad \cos \psi \ne \pm 1 \end{array} \right. \nonumber \\ {\xi _m}&= \frac{1}{m}\Bigg ( {{r'}^{m - 1}}\ell + (2m - 1)r\cos \psi {\xi _{m - 1}} \nonumber \\&\quad - (m - 1){r^2}{\xi _{m - 2}} \Bigg )\nonumber \\&\quad {m=1,2,...,n+2} \end{aligned}$$

(10)

where $n=0,1,...,N$, and $w_k$ denotes the weight coefficient for the gravitational potential. ${\xi _{n+2}}$ is the radial integration over ${r'}$, which is solved analytically in a recursive way. By doing this, the original triple integral in (1) degenerates into several surface integrals given by ${I_{n+2}}$, and these double integrals can then be numerically evaluated using the 2D GLQ integration. Note that in (6), only ${I_{n+2}} = {I_{n+2}}(r,\varphi ,\lambda )$ is related to the location of the computation point, while ${L_n^k}$ and ${\rho _k}$ are constants independent of $r,\varphi ,\lambda$.

2.2 Gravitational vector fields

According to Wild-Pfeiffer (2008), the gravitational vector can be obtained using the first-order partial derivatives of the gravitational potential V by

$$\begin{aligned} {g_x} = \frac{1}{r}{\partial _\varphi }V,\quad {g_y} = \frac{1}{{r\cos \varphi }}{\partial _\lambda }V,\quad {g_z} = {\partial _r}V \end{aligned}$$

(11)

where ${\partial _j}\;(j=\varphi ,\lambda ,r)$ denotes the first-order partial differentiation with respect to a spatial variable. Using (6), we have

$$\begin{aligned} {\partial _j}V = \sum \limits _{k = 0}^N {\sum \limits _{n = 0}^N {L_n^k} {I_{n + 2,j}}{\rho _k}} = \sum \limits _{k = 0}^N {w_k^j{\rho _k}} \end{aligned}$$

(12)

with

$$\begin{aligned}{} & {} w_k^j = \sum \limits _{n = 0}^N {L_n^k} {I_{n + 2,j}} \end{aligned}$$

(13)

$$\begin{aligned}{} & {} {I_{n+2,j}} = G\int \limits _{{\lambda '_1}}^{{\lambda '_2}} {\int \limits _{{\varphi '_1}}^{{\varphi '_2}} {{\hbox {cos}}\varphi '\left. {({\partial _j}{\xi _{n+2}})} \right| _{{r'_1}}^{{r'_2}}{\hbox {d}}\varphi '{\hbox {d}}\lambda '} } \end{aligned}$$

(14)

The recursive analytical expressions for ${\partial _j}{\xi _{n+2}}$ are given in Appendix A.

2.3 Gravitational gradient tensor

The components of the symmetric Marussi tensor can be expressed as follows (Tscherning 1976):

$$\begin{aligned} {M_{xx}}&= \frac{1}{r}\left( {\frac{{\partial _{\varphi \varphi }^2V}}{r} + {g_z}} \right) \nonumber \\ {M_{yy}}&= \frac{1}{r}\left( {\frac{{\partial _{\lambda \lambda }^2V}}{{r{{\cos }^2}\varphi }} - {g_x} \tan \varphi + {g_z}} \right) \nonumber \\ {M_{zz}}&= \partial _{rr}^2V \nonumber \\ {M_{xy}}&= \frac{1}{r}\left( {\frac{{\partial _{\varphi \lambda }^2V}}{{r\cos \varphi }} + {g_y}\tan \varphi } \right) \nonumber \\ {M_{xz}}&= \frac{1}{r}\left( {\partial _{\varphi r}^2V - {g_x}} \right) \nonumber \\ {M_{yz}}&= \frac{1}{r}\left( {\frac{{\partial _{\lambda r}^2V}}{{\cos \varphi }} - {g_y}} \right) \end{aligned}$$

(15)

where $\partial _{ij}^2\;\left( {i,j = \varphi ,\lambda ,r} \right)$ denotes the second-order partial differentiation with respect to the spatial variables. According to Eq. (6), we also have

$$\begin{aligned} {\partial _{ij}}V = \sum \limits _{k = 0}^N {\sum \limits _{n = 0}^N {L_n^k} {I_{n + 2,ij}}{\rho _k}} = \sum \limits _{k = 0}^N {w_k^{ij}{\rho _k}} \end{aligned}$$

(16)

with

$$\begin{aligned}{} & {} w_k^{ij} = \sum \limits _{n = 0}^N {L_n^k} {I_{n + 2,ij}} \end{aligned}$$

(17)

$$\begin{aligned}{} & {} {I_{n+2,ij}} = G\int \limits _{{\lambda '_1}}^{{\lambda '_2}} {\int \limits _{{\varphi '_1}}^{{\varphi '_2}} {{\hbox {cos}}\varphi '\left. {(\partial _{ij}^2{\xi _{n+2}})} \right| _{{r'_1}}^{{r'_2}}{\hbox {d}}\varphi '{\hbox {d}}\lambda '} } \end{aligned}$$

(18)

The recursive expressions for ${\partial _{ij}^2}{\xi _{n+2}}$ are provided in Appendix A. Note that in the case of the computation point being located on the polar axis ($\varphi =\pm 90^\circ$, i.e. cos$\varphi =0$), Eqs (11) and (15) will lead to indeterminate values. Therefore, our method cannot calculate the gravitational effects for observation points on the polar axis.

2.4 2D GLQ integration

After the analytical integration along the radial direction, the resultant surface integrals ${{I_p},{I_{p,j}},{I_{p,ij}}}$ in the above equations are then evaluated using the 2D GLQ that approximates the double integral using a weighted sum of the integration kernel,

$$\begin{aligned}{} & {} \int \limits _{{\lambda '_1}}^{{\lambda '_2}} {\int \limits _{{\varphi '_1}}^{{\varphi '_2}} {f(\varphi ',\lambda '){\hbox {d}}\varphi '\mathrm{{d}}\lambda '} }\nonumber \\{} & {} \quad \approx \frac{{\Delta \varphi '\Delta \lambda '}}{4}\sum \limits _{n = 1}^{{{\bar{N}}}} {\sum \limits _{m = 1}^{{{\bar{M}}}} {{A_n}{A_m}f({{{\bar{\varphi }} '}_n},{{{\bar{\lambda }} '}_m})} } \end{aligned}$$

(19)

with

$$\begin{aligned} {{{\bar{\varphi }}'}_n}&= \frac{{{\varphi '_1} + {\varphi '_2}}}{2} + \frac{{\Delta \varphi '}}{2}{t_n},\quad \Delta \varphi ' = {\varphi '_2} - {\varphi '_1}\;\nonumber \\ {{{\bar{\lambda }}'}_m}&= \frac{{{\lambda '_1} +{\lambda '_2}}}{2} + \frac{{\Delta \lambda '}}{2}{t_m},\quad \Delta \lambda ' = {\lambda '_2} - {\lambda '_1} \end{aligned}$$

(20)

where ${A_n,A_m}$ and ${t_n},{t_m}$ are the Gaussian weights and nodes along the latitudinal and longitudinal directions, respectively. ${{\bar{N}},{\bar{M}}}$ are the number of Gaussian points.

3 Numerical implementation

Next, we introduce the fast algorithm based on the Toeplitz structure of the weight coefficient matrix to improve the computational efficiency and the 2D adaptive discretization strategy that ensures the accuracy at observation points near the tesseroids.

3.1 Fast algorithm based on a general Toeplitz

We divide the source region into ${N_{r'}} \times {N_{\varphi '}} \times {N_{\lambda '}}$ tesseroids in the radial, latitudinal and longitudinal directions, respectively. For each tesseroid, its geometric centre is $({r'_E},{\varphi '_I},{\lambda '_J})$ with a mesh interval $\Delta r',\Delta \varphi ',\Delta \lambda '$, respectively. According to (6), (12), and (16), the gravitational potential V and its derivatives ${\partial _j}V,\;{\partial _{ij}}V$ produced by all mass tesseroids can be expressed as

$$\begin{aligned}&V(r,\varphi ,\lambda )\nonumber \\&\quad = \sum \limits _{E = 1}^{{N_{r'}}} {\sum \limits _{I = 1}^{{N_{\varphi '}}} {\sum \limits _{J = 1}^{{N_{\lambda '}}} {\left( {\sum \limits _{k = 0}^N {w_k^E(r,\varphi ,\varphi '_I,{\lambda '_J} - \lambda )\rho _k^E({\varphi '_I},{\lambda '_J})} } \right) } } } \nonumber \\&{\partial _j}V(r,\varphi ,\lambda ) \nonumber \\&\quad = \sum \limits _{E = 1}^{{N_{r'}}} {\sum \limits _{I = 1}^{{N_{\varphi '}}} {\sum \limits _{J = 1}^{{N_{\lambda '}}} {\left( {\sum \limits _{k = 0}^N {w_k^{E,j}(r,\varphi ,{\varphi '_I},{\lambda '_J} - \lambda )\rho _k^E({\varphi '_I},{\lambda '_J})} } \right) } } } \nonumber \\&{\partial _{ij}}V(r,\varphi ,\lambda )\nonumber \\&\quad = \sum \limits _{E = 1}^{{N_{r'}}} {\sum \limits _{I = 1}^{{N_{\varphi '}}} {\sum \limits _{J = 1}^{{N_{\lambda '}}} {\left( {\sum \limits _{k = 0}^N {w_k^{E,ij}(r,\varphi ,{\varphi '_I},{\lambda '_J} - \lambda )\rho _k^E({\varphi '_I},{\lambda '_J})} } \right) } } } \end{aligned}$$

(21)

where $\rho _k^E$ denotes the kth nodal density in the Eth element along the radial direction. $w_k^E,w_k^{E,j}$, and $w_k^{E,ij}$ are the weight coefficients given by (7), (13), and (17), respectively. As can be seen, in the longitudinal direction, the gravitational potential and its derivatives are discrete convolutions of the weight coefficient and the density. Since the expressions for $V,{\partial _j}V,{\partial _{ij}}V$ have a similar form, we will focus only on V henceforth for simplicity, and ${\partial _j}V,{\partial _{ij}}V$ can finally be obtained by replacing $w_k^E$ with $w_k^{E,j},w_k^{E,ij}$.

Assume that there are ${N_\lambda }$ observation points distributed along the longitudinal direction at $(r,\varphi ) = ({r_O},{\varphi _L})$ with an equal mesh interval $\Delta \lambda =\Delta \lambda '$. Then, we have ${\lambda '_J} = {\lambda '_0} + J\Delta \lambda$, ${\lambda _P} = {\lambda _0} + P\Delta \lambda$, and ${\lambda '_J} - {\lambda _P} = {{{\hat{\lambda }} }_0} + (J - P)\Delta \lambda$ where ${{{\hat{\lambda }} }_0} = {{\lambda '}_0} - {\lambda _0}$, ${\lambda '_0},{\lambda _0}$ are the starting points of $\lambda '$ and $\lambda$, and J, P are integers. Thus, the gravitational potential in Eq. (21) can be rewritten as

$$\begin{aligned} \mathbf{{V}}({r_O},{\varphi _L}) = \sum \limits _{E = 1}^{{N_{r'}}} {\sum \limits _{I = 1}^{{N_{\varphi '}}} {\sum \limits _{k = 0}^N {\mathbf{{W}}_k^E({r_O},{\varphi _L},{\varphi '_I}){\varvec{\rho }}_k^E({\varphi '_I})} } } \end{aligned}$$

(22)

where $\mathbf{{V}} = {[V({\lambda _1}), \ldots ,V({\lambda _{{N_\lambda }}})]^{\mathrm{{T}}}}$, ${\varvec{\rho }}_k^E = {[\rho _k^E({\lambda '_1}), \ldots ,}{\rho _k^E({{\lambda '}_{{N_{\lambda '}}}})]^{\mathrm{{T}}}}$, and

$$\begin{aligned} \mathbf{{W}}_k^E = \left[ {\begin{array}{*{20}{c}} {w_k^E({{{\hat{\lambda }} }_0})}&{}{w_k^E({{{\hat{\lambda }} }_0} + \Delta \lambda )}&{} \cdots &{}{w_k^E({{{\hat{\lambda }} }_0} + ({N_{\lambda '}} - 1)\Delta \lambda )}\\ {w_k^E({{{\hat{\lambda }} }_0} - \Delta \lambda )}&{}{w_k^E({{{\hat{\lambda }} }_0})}&{} \cdots &{}{w_k^E({{{\hat{\lambda }} }_0} + ({N_{\lambda '}} - 2)\Delta \lambda )}\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ {w_k^E({{{\hat{\lambda }} }_0} + (1 - {N_\lambda })\Delta \lambda )}&{}{w_k^E({{{\hat{\lambda }} }_0} + (2 - {N_\lambda })\Delta \lambda )}&{} \cdots &{}{w_k^E({{{\hat{\lambda }} }_0} + ({N_{\lambda '}} - {N_\lambda })\Delta \lambda )} \end{array}} \right] \end{aligned}$$

(23)

where $\textbf{W}_k^E$ is the weight coefficient matrix. According to Vogel (2002), a matrix in a form of $\mathbf{{W}}_k^E$, which is constant along diagonals, is called Toeplitz. Here, $\mathbf{{W}}_k^E$ has a general Toeplitz form that can be either symmetrical or non-symmetrical and square or non-square. For such a Toeplitz matrix, a product like $\mathbf{{W}}_k^E{\varvec{\rho }}_k^E$ can be efficiently computed by FFTs (Sansó and Sampietro 2022):

$$\begin{aligned} \mathbf{{v}} = {\hbox {IFFT}}\left\{ {{\hbox {FFT}}[\mathbf{{c}}].*\hbox {FFT}[\mathbf{{s}}]} \right\} \end{aligned}$$

(24)

where $\mathbf{{v}}$, $\mathbf{{c}}$, and $\mathbf{{s}}$ are matrices with a length of ${N_\lambda +N_\lambda '}$, and

$$\begin{aligned} \mathbf{{c}}&= \Big [w_k^E({{{\hat{\lambda }} }_0}), \ldots ,w_k^E({{{\hat{\lambda }}}_0} - ({N_\lambda } - 1)\Delta \lambda ),0,\nonumber \\&\qquad w_k^E({{{\hat{\lambda }} }_0} + ({N_{\lambda '}} - 1)\Delta \lambda ), \ldots ,w_k^E({{{\hat{\lambda }} }_0} + \Delta \lambda )\Big ]^{\mathrm{{T}}} \nonumber \\ \mathbf{{s}}&= \Big [\rho _k^E({{\lambda '}_1}), \ldots ,\rho _k^E({{\lambda '}_{{N_{\lambda '}}}}),0, \ldots ,0\Big ]^{\mathrm{{T}}} \end{aligned}$$

(25)

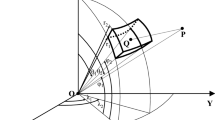
By extracting the first ${{N_\lambda }}$ components of $\mathbf{{v}}$, the results of $\mathbf{{W}}_k^E{\varvec{\rho }}_k^E$ are obtained. It is noteworthy that only the elements in the first row and column of $\mathbf{{W}}_k^E$ are required in implementing the algorithm, and thus, the computational cost and memory occupation are significantly reduced as compared to conventional purely summation methods (e.g. Uieda et al. 2016). In fact, the above fast FFT-based calculation is a general version of the method of Zhao et al. (2021). More exactly, the weight coefficient matrix they used is a special case of Eq. (23). In Zhao et al. (2021)’s algorithm, $\textbf{W}_k^E$ is required to be symmetrical and square. It means that the number of the observation points must be equal to that of the tesseroids and their longitudinal coordinates must coincide with the centres of the tesseroids, i.e. $N_{\lambda }=N_{\lambda '}$ and $\lambda =\lambda '$ (as shown in Fig. 3a). In practical applications, this may result in undesirable computation and inflexibility. Here, we extend $\textbf{W}_k^E$ to a general form (see Eq. (23)), which makes the placement of the observation points independent of the discretization of the source region. Our fast algorithm only requires $\Delta \lambda =\Delta \lambda '$ and puts no other constraints on $N_{\lambda }$, $N_{\lambda '}$ and $\lambda$, $\lambda '$ (see Fig. 3b). Hence, it enjoys higher flexibility than the method of Zhao et al. (2021).

Fig. 3

Comparison of the observation points and mesh grids in the longitudinal dimension used by Zhao et al. (2021)’ method (a) and our method (b). In the method of Zhao et al. (2021), the number of the observation points is required to be equal to that of the tesseroids along the longitudinal direction ($N_{\lambda }=N_{\lambda '}$) and the observation points should align with the centres of the tesseroids in the horizontal directions (${\lambda }={\lambda '}$). In our fast algorithm, only $\Delta \lambda = \Delta \lambda '$ is required, and one can take $N_{\lambda } \ne N_{\lambda '}$ and ${\lambda } \ne {\lambda '}$

Also we notice from Eq. (1) that, if the observation points align with the source points in the longitudinal direction (${{\hat{\lambda }} }_0 = 0$ and $N_\lambda =N_{\lambda '}$, as shown in Fig. 3a), $\mathbf{{W}}_k^E$ degenerates to those used by Zhao et al. (2021). In this case, the forward modelling can be further speeded up by utilizing the parity of the gravitational components, that is, $V,{g_x},{g_z},{M_{xx}},{M_{yy}},{M_{zz}}$ are even functions of ($\lambda '-\lambda$), while ${g_y},{M_{xy}},{M_{yz}}$ are odd functions. For even functions, $\mathbf{{W}}_k^E$ in Eq. (23) can be reduced to

$$\begin{aligned} \mathbf{{W}}_k^E = \left[ {\begin{array}{*{20}{c}} {w_k^E(0)}&{}{w_k^E(\Delta \lambda )}&{} \cdots &{}{w_k^E(({N_{\lambda }} - 1)\Delta \lambda )}\\ {w_k^E(\Delta \lambda )}&{}{w_k^E(0)}&{} \cdots &{} \vdots \\ \vdots &{} \vdots &{} \ddots &{}{w_k^E(\Delta \lambda )}\\ {w_k^E(({N_\lambda } - 1)\Delta \lambda )}&{} \cdots &{}{w_k^E(\Delta \lambda )}&{}{w_k^E(0)} \end{array}} \right] \nonumber \\ \end{aligned}$$

(26)

Similarly, for the case of odd functions, we have

$$\begin{aligned} \mathbf{{W}}_k^E = \left[ {\begin{array}{*{20}{c}} {0}&{}{w_k^E(\Delta \lambda )}&{} \cdots &{}{w_k^E(({N_{\lambda }} - 1)\Delta \lambda )}\\ { - w_k^E(\Delta \lambda )}&{}{0}&{} \cdots &{} \vdots \\ \vdots &{} \vdots &{} \ddots &{}{w_k^E(\Delta \lambda )}\\ { - w_k^E(({N_\lambda } - 1)\Delta \lambda )}&{} \cdots &{}{ - w_k^E(\Delta \lambda )}&{}{0} \end{array}} \right] \nonumber \\ \end{aligned}$$

(27)

As can be seen, only the elements in the first row of $\mathbf{{W}}_k^E$ are required in this case, which can further reduce the computational cost.

3.2 2D adaptive discretization

A 2D adaptive discretization strategy based on Uieda et al. (2016) and Lin and Denker (2019) is also combined in our algorithm to improve the accuracy at points close to the mass sources. The 2D adaptive discretization follows a criterion that a tesseroid is divided along the latitudinal or longitudinal direction when the distance to the computation point is smaller than a constant (D) times the maximum size of the tesseroid (see Fig. 4), that is,

$$\begin{aligned} {{{\ell _0}}/{\max ({L_\varphi },{L_\lambda })}} \ge D \end{aligned}$$

(28)

where D is called the distance–size ratio. A larger D means a finer division of the tesseroid close to the computation point. ${\ell _0}$ is the distance between the computation point $P(r,\varphi ,\lambda )$ and the geometric centre of the upper horizontal surface of the tesseroid $({r'_2},{\varphi '_0},{\lambda '_0})$:

$$\begin{aligned}&\ell _0 = \sqrt{{r^2} + {r'_2}^2 - 2r{r'_2}\cos {\psi _0}} \nonumber \\&\cos {\psi _0} = \sin \varphi \sin {\varphi '_0} + \cos \varphi \cos {\varphi '_0}\cos ({\lambda '_0} - \lambda )\nonumber \\&{\varphi '_0} = \left( {\varphi '_1} + {\varphi '_2}\right) /2,\quad {\lambda '_0} = \left( {\lambda '_1} + {\lambda '_2}\right) /2 \end{aligned}$$

(29)

Here the division criterion is slightly different from those used in Uieda et al. (2016) and Lin and Denker (2019), but all these adaptive discretizaion strategies work in a similar way. ${L_\varphi }$ and ${L_\lambda }$ are the dimensions of the tesseroid in the latitude and longitude:

$$\begin{aligned} {L_\varphi } = {r_2'}\left( \varphi '_2-\varphi '_1\right) ,\quad {L_\lambda } = {r_2'}\cos {\varphi _1}\left( \lambda '_2-\lambda '_1\right) \end{aligned}$$

(30)

Fig. 4

Illustration of the 2D adaptive discretization. $({r'_2},{\varphi '_0},{\lambda '_0})$ is the geometric centre of the top surface of the tesseroid, and ${L_\varphi },{L_\lambda }$ are the dimensions of the tesseroid in the latitude and longitude. P is the observation point

By checking the inequality given by Eq. (28) for each tesseroid, the algorithm judges whether the tesseroid needs to be discreticized. Following the criterion, the tesseroid is divided in half along the dimension that failed the relation in a recursive way until Eq. (28) holds for all sub-elements. However, it should be noted that if the observation point coincides with the centre of the top surface of the tesseroid, i.e. ${\ell _0}=0$, the criterion given by Eq. (28) will lead to a “dead circulation”. To avoid this problem, we use the following inequality as the stop condition of the discretization when the observation point is located on the surface of the tesseroid:

$$\begin{aligned} {\max ({L_\varphi },{L_\lambda })} < {\max \left( {L_\varphi ^0 },{L_\lambda ^0 }\right) }/\alpha \end{aligned}$$

(31)

where $L_\varphi ^0$ and $L_\lambda ^0$ are the dimensions of the original tesseroid without subdivision, and $\alpha$ is a parameter empirically determined based on numerical tests. The inequality indicates that the adaptive discretization will stop once the maximum horizontal dimension of the current tesseroid is less than that of the original one.

Fig. 5

Relative errors of V (a–d), $g_z$ (e–h), $M_{zz}$ (i–l), and $M_{yy}$ (m–p) as a function of the latitude at different observation heights. Different combinations of the Gauss nodes (${{\bar{M}} / {\bar{N}}} = 1/1, 2/2, 3/3, 4/4$) are tested

Compared with the 3D adaptive scheme that is implemented along all three dimensions, this 2D adaptive discretization requires a smaller number of sub-elements due to the removal of a dimension from the discretizaion (see Fig. 4). Consequently, it is more computationally efficient.

4 Numerical verification

In this section, we test the performance of the proposed method and determine the optimal values of some key parameters, including the number of GLQ nodes, the distance–size ratio D, and the parameter $\alpha$. Several spherical shell models with different density variations in depth are used to verify the correctness and accuracy of the proposed method. These shells have a density model $\rho (r')$ and are located on a spherical Earth with inner radius $R_1$ and outer radius $R_2$. The closed-form expressions of the gravitational effects for shell models with a polynomial density of arbitrary degree and a exponential density are provided in Appendix B. The codes for the new algorithm are freely available at https://github.com/Yonfou/gravity-modelling-with-polynomial-density.

4.1 Optimal selection of key parameters

The number of GLQ nodes ${{\bar{M}} / {\bar{N}}}$, the distance–size ratio D, and the parameter $\alpha$ are three important parameters that have a significant influence on the computational accuracy and efficiency. The number of GLQ nodes controls the accuracy of the surface integration over a single tessseroid, while D determines how many times each tesseroid will be divided. Besides, $\alpha$ works when the observation point is located on the surface of the tesseroid. It determines the minimum horizontal size of the mesh and hence also indirectly influences the performance of the method. In order to ensure both acceptable numerical accuracy and computation efficiency for the proposed algorithm, it is necessary to find the optimal values for these parameters.

Fig. 6

Relative errors of V (a), $g_z$ (b), $M_{zz}$ (c), and $M_{yy}$ (d) as a function of the observation height at different D varying from 0 (corresponding to the case of no adaptive division) to 5.5

Fig. 7

Relative errors of $g_z$ varying with mesh intervals for observation points located on the shell surface. Different values of D are used

We start with a homogeneous shell model with $R_1 =6271\,\hbox {km}$, $R_2 =6371\,\hbox {km}$, and $\rho = 1000\,\hbox {kg}/\hbox {m}^3$. In the numerical experiments, four nonzero independent gravitational components V, $g_z$, $M_{zz}$, and $M_{yy}$ are considered to investigate the influence of the three parameters. The whole shell is discreticized into $180 \times 360 = 64,800$ tesseroids of size ${1^ \circ } \times {1^ \circ }$ along the latitudinal and longitudinal directions with one layer in depth. The observation points are located on a spherical surface at a constant height above the top of the shell, having consistent coordinates $(\varphi ,\lambda )$ with the centres of the tesseroids. In addition, because the magnitudes of the gravitational effects of the spherical shells vary largely, we use the relative errors to measure the computational accuracy instead of the absolute errors here. Moreover, a maximum tolerated relative error of 0.1% is established as a error threshold in the optimal selection of ${{\bar{M}} / {\bar{N}}}$ and D considering the trade-off between accuracy and computation time.

Figure 5 shows the maximum relative errors between the numerical and analytical solutions calculated using different combinations of the GLQ nodes (i.e., ${{\bar{M}}/{\bar{N}}}=1/1,\ 2/2,\ 3/3,\ 4/4$) at different observation heights ranging from 10 m to 250 km. As can be seen, the relative errors of the gravitational effects generally decrease as the number of GLQ nodes increases. To achieve an error level of 0.1% for all gravitational components, ${{\bar{M}}/{\bar{N}}}=2/2$ is the best choice in terms of accuracy and efficiency. Figure 5 clearly shows that the latitude of the observation point has an impact on the numerical results. We can notice that oscillations occur in the relative errors, especially for the gradient components. This phenomenon is caused by the inherent singularity of the integral kernels for the tesseroids near the observation points and the rounding error for those in the far zone (Lin and Denker 2019). The gravitational effects of an observation point are usually calculated by superposing the contributions of all tesseroids over the source region. The tesseroids at different latitudes have different geometrical shapes and consequently may give rise to different approximation errors, causing numerical oscillations.

Fig. 8

Spherical shell model with radial density variation. a Density distribution of PREM, b exponential density. N marked in a denotes the order of the polynomial density

Next, we select the optimal value for D by investigating the gravitational effects at different observation heights varying from 0.01 to 1000 km. Figure 6 presents the maximum difference between the shell and tesseroid fields with different D that ranges from 0 (i.e., no adaptive division) to 5.5 at each height. We can observe that the computational accuracy improves with increasing observation heights. To be more specific, the relative errors first decrease slowly with the increase of the altitude. Then, after reaching a critical height (denoted as $h_c$), the error curves for $D>0$ coincide with the one for $D=0$ and exhibit a much more rapid decline trend. The critical height $h_c$ for different D can be estimated using the adaptive criterion Eq. (28). It means that the adaptive discretization strategy only works at observation heights lower than $h_c$. At a fixed observation height, the relative errors decrease as D increases and then become stable. Figure 6 shows that the minimum value for D to achieve a relative error lower than 0.1% is 0 for the gravitational potential, 1.5 for the gravitational acceleration, and 4 for the gravitational gradient, respectively. These optimal values of D are different for different gravitational components due to the different complexity of their integral kernels.

Besides the number of GLQ nodes and the distance–size ratio D, the parameter $\alpha$ also plays a role in the forward modelling when the observation points are located on the surface of the shell. Here, we take $g_z$ as an example to analyse the influence of $\alpha$, because it is one of the gravitational components continuous on the shell surface. Figure 7 shows the relative errors of $g_z$ as a function of the mesh interval at different $\alpha$ and D. We can see that the relative errors decrease in general as $\alpha$ goes up. At lower D, the errors decline first and then remain almost unchanged when $\alpha$ increases to a value higher than $10^3$. The reason is that the minimum size of the tesseroid is larger than $1/\alpha$ times the original dimension without subdivision, and thus, the stop condition is not activated in this situation. When D becomes larger, the stop condition begins to work and the errors exhibit an obvious decrease with the increase of $\alpha$. For the case of D=1.5 (the optimal value for $g_z$), $\alpha =10^3$ is shown to be the best choice for all mesh intervals ranging from 0.5$^\circ$ to 10$^\circ$. This value of $\alpha$ is also the optimal one to achieve an error level of $0.1\%$ at higher D (see Fig. 7c, d).

4.2 Validation tests

Next, we validate the correctness and capability of the proposed algorithm using the preliminary reference Earth model (PREM) with different polynomial densities in different layers and a spherical shell model with an exponential density (see Fig. 8).

Fig. 9

Relative errors between the numerical and analytical solutions for PREM. a Relative errors varying with the latitude at a constant height of 1 km. b Maximum relative errors varying with the height of observation. The distance–size ratio D of 0 is used for V, 1.5 for $g_z$, and 4.0 for $M_{zz}$, $M_{xx}, M_{yy}$. The number of GLQ nodes is ${{\bar{M}} / {\bar{N}}}=2/2$

Table 1 Statistics of the errors of V (in $\hbox {m}^2/\hbox {s}^2$), $g_z$ (in mGal), $M_{xx}$, $M_{yy}$ and $M_{zz}$ (in E) at a observation height of 1 km for the PREM model

4.2.1 Polynomial density model

One significant advantage of the new method is its ability to deal with density models in a form of a polynomial up to an arbitrary order along the radial direction. To demonstrate this capability of the method, we construct a shell model composed by eight layers that have different density variations and thicknesses in depth using the well-known preliminary reference Earth model (PREM) developed by Dziewonski and Anderson (1981). Figure 8a presents the radial density distribution of the model, in which the influence of the core is neglected. The total thickness of the eight-layered shell is 2221 km ranging from $R_1=3480~\hbox {km}$ to $R_2=5701~\hbox {km}$ (Dziewonski and Anderson 1981). In each layer, the density variation follows a polynomial function of N degree, the value of which is marked in Fig. 8a. In this PREM model, the mean radius of the Earth is set to be $R_E=6371~\hbox {km}$.

For polynomial density variations, the proposed algorithm can achieve radial integration analytically by setting N in Eq. (4) equal to the order of the real polynomial density, without the requirement of further subdivision along the radial direction. Therefore, we divide the PREM into $180 \times 360$ regular meshes along the latitudinal and longitudinal directions with eight layers in the vertical dimension. The observation surface has the same mesh grids as the shell in horizontal directions. Its elevation ranges from 0.01 to 1000 km above the top surface of the spherical shell. The optimal values for the distance–size ratio D and the number of GLQ nodes are used in the calculation of V, $g_z$, $M_{xx}$, $M_{yy}$ and $M_{zz}$.

Figure 9 shows the maximum relative errors varying with the latitude and the height of observation. It can be seen from the figure that the maximum relative errors of the nonzero gravitational components are all blow 0.01% at different latitudes and observation heights. We also provide the statistical properties of the misfits, including the maximum, minimum, and mean absolute errors (AE), the root-mean-square (RMS) error, and the relative root-mean-square (RRMS) error (see Table 1). Obviously, the proposed method works well for all gravitational components. The RMS errors are approximately $280.86~\hbox {m}^2/\hbox {s}^2$ for V, 5.60 mGal for $g_z$, 0.01E for $M_{xx}$ and $M_{yy}$, and 0.018E for $M_{zz}$. The RRMS errors for the gravitational components are generally less than 0.001%. These results demonstrate the good accuracy of the proposed method in the case of polynomial density variations.

Fig. 10

Maximum relative errors (a) and computation time (b) varying with N obtained by Method A for the spherical shell model with an exponential density. The distance–size ratio D of 0 is used for V, 1.5 for $g_z$, and 3.5 for $M_{zz}$

Fig. 11

Maximum relative errors and computation time varying with $N_{r'}$ obtained by Method B for the spherical shell model with an exponential density. a and b Constant density assumption in each layer. c and d Quadratic density assumption in each layer. The distance–size ratio D of 0 is used for V, 1.5 for $g_z$, and 3.5 for $M_{zz}$

4.2.2 Exponential density model

Besides the polynomial density models, the new method is also well suited to other kinds of density variations. To test the performance of the algorithm in this aspect, we consider a spherical shell with an exponential density defined as follows (Soler et al. 2019):

$$\begin{aligned} \rho (r') = A{e^{ - b\frac{{r' - {R_1}}}{{{R_2} - {R_1}}}}} + C \end{aligned}$$

(32)

with

$$\begin{aligned} A = \frac{{\rho ({R_1}) - \rho ({R_2})}}{{1 - {e^{ - b}}}},\quad C = \rho ({R_1}) - A \end{aligned}$$

(33)

The thickness of the spherical shell is assumed to be 140 km ranging from $R_1=6151$ to $R_2=6291$ km. We set the values of $\rho ({R_1})=3300\,\hbox {kg}/\hbox {m}^3$, $\rho ({R_2})=2700\,\hbox {kg}/\hbox {m}^3$, and $b=7$ (see Fig. 8b). The shell model is discretized into $180 \times 360$ regular meshes in the horizontal directions with $N_{r'}$ layer in the radial dimension. The observation points are on a regular grid that aligns with the spherical shell, and its elevation is 1 km.

For such a non-polynomial density model, two approaches can be utilized to achieve desirable accuracy. The first one (Method A) is to apply high-degree polynomial functions to approximate the real density variation and use only one layer in the radial dimension, i.e.,

$$\begin{aligned} {\rho _A}(r') = \sum \limits _{ n = 0}^N {{a_n}{{r'}^n}} \end{aligned}$$

(34)

where $a_n$ is the polynomial coefficient and N is the order of the polynomial function. The second one (Method B) lies in the combined use of the low-degree polynomial functions and the radial subdivision. We divide the shell into $N_{r'}$ layers in the radial direction and describe the density in each layer using a low-order polynomial function, that is,

$$\begin{aligned} {\rho _B}(r') = \sum \limits _{n = 0}^{{N^m}} {{a_n^m}{{r'}^n}},\quad {r'_1}(m) \le r' \le {r'_2}(m) \end{aligned}$$

(35)

where $N^m$ is the order of the polynomial function in the mth layer, ${a_n^m}$ is the corresponding polynomial coefficient, ${r'_1}(m)$ and ${r'_2}(m)$ are the radial coordinates of the bottom and top of the layer, respectively, and $m = 1,2, \ldots ,{N_{r'}}$. To investigate the computational accuracy and efficiency of the two approaches, we choose D equal to a fixed value, and only explore the errors caused by the radial integration. Here, the gravitational components V, $g_z$, and $M_{zz}$ are used as examples to investigate the performance of the method in the case of a non-polynomial density.

Fig. 12

Comparison of a the maximum relative errors at different observation heights and b the relative computation time of $g_z$ with different mesh intervals. The computation time is normalized by the slowest calculation time (890,964.72 s)

Table 2 Comparison of the computation time and the memory occupation of the proposed method and the 3D GLQ algorithms developed by Uieda et al. (2016), Zhao et al. (2019), and Zhao et al. (2021)

By applying Nth-order polynomial interpolation to the exponential density, we obtain the relative errors and the computation time of V, $g_z$, and $M_{zz}$ for Method A (see Fig. 10). As can be seen, a low-degree polynomial function with $N\le 3$ is not sufficient to describe the exponential density variation well, and a polynomial of very high order also results in inaccurate solutions, due to its oscillation properties. To achieve an accuracy with a maximum error of 0.1% in this case, a fourth-order or fifth-order polynomial density assumption is the best for V and $g_z$, and a fourth-order assumption for $M_{zz}$. It is also shown that the computation time exhibits a linear increase with increasing N. The calculation of $M_{zz}$ takes the longest time, then followed by $g_z$ and V. Moreover, the difference in time consumption for the three gravity components becomes larger and larger with the increase of N.

Figure 11 shows the relative errors and the computation time as a function of $N_{r'}$ (the number of layers used in the radial direction) for Method B based on the same model. By assuming that the density is constant in each layer, a minimum number of $N_{r'}=10$ is required to achieve an acceptable accuracy (0.1%) and the corresponding computation time is 93.21 s for V, 119.6 s for $g_z$ and 172.4 s for ${M_{zz}}$. For a quadratic density assumption, however, $N_{r'}=2$ is adequate. In comparison with the constant density model, less calculation time is required in this case, that is, 32.33 s for V, 44.84 s for $g_z$ and 59.82 s for ${M_{zz}}$. Therefore, the quadratic density assumption is more appropriate than the constant one in terms of both accuracy and efficiency for the exponential density variation considered.

Comparing Method A with Method B, the former is superior in computational efficiency in this example. It takes only 22.72 s for V, 31.99 s for $g_z$ and 42.72 s for $M_{zz}$ to reach an accuracy of 0.1%. However, for highly variable density variations, Method B will be more beneficial, since the use of high-degree polynomial functions may cause oscillation and result in unstable results. On the whole, although our method considers up only to polynomial density models, its application to non-polynomial density models is also straightforward.

4.3 Comparison with the 3D GLQ methods

This section is aimed at comparing the proposed method with the commonly used tesseroid-based 3D GLQ methods in terms of accuracy and efficiency. Based on the same homogeneous shell model used in Sect. 4.1, we calculate the vertical component of the gravity acceleration $g_z$ using the traditional 3D GLQ method (no adaptive division), Uieda et al. (2016)’s method, Zhao et al. (2019)’s method, Zhao et al. (2021)’s method, and the proposed method, respectively. A same distance–size ratio of $D=1.5$ is used for the 3D GLQ methods and the proposed method in this comparison analysis. The observation surface is located on a regular grid at an elevation ranging from 1 to 250 km (observation height of GOCE satellite (Cesare et al. 2010)) above the top surface of the shell.

Fig. 13

CRUST1.0 gloabal crustal model. a Global density distribution at 10 m below mean Earth radius. b Density section along the latitude of $32.5^\circ$ N

Figure 12a compares the maximum relative errors obtained by the 3D GLQ methods and the proposed method as a function of the height of observation. It is observed that the results obtained by Uieda et al. (2016), Zhao et al. (2019), and Zhao et al. (2021) are exactly the same. In contrast, the proposed method achieves better accuracy at the near zone as compared to the 3D GLQ methods. In the far zone, the relative errors for all methods are almost the same and less than 0.01%. Therefore, the advantage of the proposed method in accuracy is verified.

We also compare the computational efficiency of both methods for different horizontal mesh intervals ranging from $0.5^ \circ$ to $10^ \circ$. We divide the spherical shell into 10 layers in depth, and place the observation surface at a height of 10 km above the top surface of the shell. The relative computation time normalized by the slowest calculation varying with the mesh interval is presented in Fig. 12b. The results show that at small mesh intervals less than $2^ \circ$, the calculation speed of the proposed algorithm is sped up by 3 orders of magnitude compared with Uieda et al. (2016)’s method, 1.5 order of magnitude compared with Zhao et al. (2019)’s method, and more than half compared with Zhao et al. (2021)’s improved method. Table 2 lists the computation time and memory occupation for a discretization size of $360 \times 720 \times 10$ with $D=1.5$. Compared with the fast algorithm developed by Zhao et al. (2021), the calculation time of the proposed method is further decreased by more than half, and the memory requirement is significantly reduced to 0.1 GB by seven times.This comparison further demonstrates the capability of the proposed method in fast calculation.

5 Application

In this section, we apply the new algorithm in the calculation of gravitational effects of the CRUST1.0, a global model of Earth crust on a 1 by 1 degree grid (Laske et al. 2013), so as to illustrate the reliability and flexibility of the method in practice. The CRUST1.0 incorporates the global sediment thickness and consists of eight-layered crustal profile, including water, ice, upper sediments, middle sediments, lower sediments, upper crust, middle crust, and lower crust. The model has the latitude ranging from ${-89.5^\circ }$ to ${89.5^\circ }$ and the longitude from ${-179.5^\circ }$ to ${179.5^\circ }$ with an equal interval of $1^{\circ }$. Its elevation ranges from $-74.81~\hbox {km}$ below mean Earth radius to 5.41 km above mean Earth radius. The density distribution of the CRUST1.0 global crustal model is shown in Fig. 13. Note that the influence of the mantle below the Moho is neglected here.

Fig. 14

Illustration of the model discretization at different latitudes. $N_{r'}$ denotes the number of elements in the radial direction and varies with latitudes

In order to evaluate the gravitational effects of the CRUST1.0 model efficiently and accurately, we use different mesh grids at different latitudes (Fig. 14). According to the CRUST1.0 model, the latitude ranges from $-89.5^\circ$ to $89.5^\circ$ and the longitude ranges from $-179.5^\circ$ to $179.5^\circ$ with $\Delta \varphi '=\Delta \lambda '=1^\circ$. Therefore, only the radial subdivision needs to be considered. To exactly describe the density variation in the radial direction, we obtain the sampling points for each $r-\lambda$ plane using the union of the layer boundaries given by the CRUST1.0 model (as shown in Fig. 15a). Note that for this model, the density is constant within each layer. Because the density distribution of the CRUST1.0 model is quite different on different $r-\lambda$ planes, the number of layers ($N_{r'}$) varies with latitudes. Figure 15$\textrm{b}$ shows the $N_{r'}$ we used along the vertical direction at different latitudes for the CRUST1.0 model. As can be seen, $360 \times \sum \nolimits _{I = 1}^{180} {{N_{r'}}({\varphi '_I})}$ tesseroids are required to build up the global crustal model.

Fig. 15

Radial discretization for the CRUST1.0 model. a Determination of the sampling points in depth. b Number of radial elements ($N_{r'}$) varying with latitude

The observation points are located at a height of 10 km above mean Earth radius and align with the geometric centres of the top horizontal surface of the tesseroids. Figures 16 and 17 show the numerical results for the gravitational vector fields and the Marussi tensor components calculated by the proposed method. To verify the correctness of the results, we also compare our solutions with those obtained by the 3D GLQ method based on a refined regular discretization of $180\times 360\times 8022$ (with a interval of 10m in depth). In the GLQ method, the distance–size ratio D is set to be 8 for all gravitational components, and in the proposed algorithm, $D=4$ is used. The statistics of the forward results calculated by the two methods are listed in Table 3. It is observed that the maximum RRMS error between the two methods is $1.3\times 10^{-5}\%$ for V, 0.001% for the gravitational vector, and 0.022% for the gravitational gradient. This result further demonstrates the reliability and practicability of the proposed method.

Table 3 Statistics of the forward results of the gravitational potential (in $\hbox {s}^2/\hbox {m}^2$), vector (in mGal) and Marussi tensor (in E) for the CRUST1.0 global crustal model

Fig. 16

Gravitational vector calculated by the proposed method for the CRUST1.0 global crustal model. Since the positive direction of the z axis is pointing upward, we use ${-\textbf{g}}$ instead of $\textbf{g}$

Fig. 17

Gravitational gradient calculated by the proposed method for the CRUST1.0 global crustal model. Since the positive direction of the z axis is pointing upward, we use ${-\textbf{M}}$ instead of $\textbf{M}$

6 Conclusions

An accurate and efficient method for 3D large-scale gravitational forward modelling is developed on the basis of tesseroids with a polynomial density up to an arbitrary order. The new method achieves high computational accuracy and efficiency by taking advantage of the recursive analytical expressions for the radial integration with a polynomial density and a fast discrete convolution algorithm based on the general Toeplitz form of the weight coefficient matrix. The proposed method first transformed the triple integral into a surface integral through analytical integration along the radial direction and then numerically evaluated the surface integral by GLQ with a 2D adaptive discretization. A stop condition controlled by a scalar $\alpha$ is introduced into the adaptive strategy to avoid it from entering a dead circulation in the case of observation points located on the surface of the tesseroid. This also allows more control over errors when too many divisions are necessary for surface observation points. Next, the FFT-based fast algorithm is adopted to speed up the forward modelling and to reduce the memory in the computation of the discrete convolution between the density and the weight coefficient along the longitudinal dimension. Comparing with existing FFT-based convolution methods used in gravity modelling, this algorithm has a more general form that can be applicable for symmetric or non-symmetric and square or non-square weight coefficient matrices. It only requires $\Delta \lambda =\Delta \lambda '$ and puts no other constraints on the position and number of observation points, which means that one can take $\lambda \ne \lambda '$ and $N_\lambda \ne N_\lambda '$. However, $\Delta \lambda =\Delta \lambda '$ is also to some extent a limitation resulting from the fast calculation. Another limitation of the proposed method is that the explicit forms of the gravitational vector and tensor suffer from the polar singularity induced by the spherical coordinate system, and hence, our method cannot calculate the gravitational effects at observation points with $\varphi =\pm 90^\circ$.

In the proposed method, the numerical accuracy and efficiency are mainly determined by three parameters: the number of GLQ nodes ${\bar{M}} / {\bar{N}}$, the distance–size ratio D, and the parameter $\alpha$. To guarantee a satisfying accuracy while maintaining the computational efficiency, we carried out an optimal selection on ${\bar{M}} / {\bar{N}}$, D, and $\alpha$ based on a homogeneous shell model. The numerical experiments showed that to achieve a maximum relative error of 0.1%, ${\bar{M}} / {\bar{N}}=2/2$ is often sufficient, while the optimal value of D is 0 for the gravitational potential, 1.5 for the gravitational vector, and 4 for the Marussi tensor. For the parameter $\alpha$, which controls the accuracy of surface observation points, $10^3$ is generally a good choose.

One significant advantage of the proposed method is its ability to deal with a polynomial density up to an arbitrary degree. It can obtain accurate results for a tesseroid with a Nth-order polynomial density using only one layer in the radial direction. Our numerical examples showed that for the PREM model with a polynomial density of different order in different layers, the proposed method can achieve an accuracy with a relative error lower than 0.01% for an observation height of 1 km. For a shell model with a non-polynomial exponential density, the method still works well. The results showed that by using a fourth-order polynomial function to fit the exponential density, the relative errors between the numerical and analytical solutions are about 0.05%. It also showed that increasing the number of layers in the radial dimension and using a lower-degree polynomial density in each layer can also achieve good results, but require more calculation time. The application to the global CRUST1.0 model with undulating topography further demonstrated the reliability and applicability of the new method in real cases. For the CRUST1.0 model, the numerical results obtained from the proposed method and the 3D GLQ method with a dense mesh are nearly the same and the RRMS error between the two methods is lower than 0.002%.

The comparison analysis of the proposed method and the existing tesseroid-based 3D GLQ methods also verified the good accuracy and efficiency of the new algorithm. The numerical results showed that the new method has higher precision than the 3D GLQ methods at the near zone and exhibits the same accuracy at the far zone. In addition, the computational efficiency of the proposed algorithm is significantly improved by 3 orders of magnitude as compared to Uieda et al. (2016)’s method, by 1.5 order of magnitude as compared to Zhao et al. (2019), and by more than half as compared to Zhao et al. (2021)’s improved method. Further, the memory occupation for the proposed algorithm is also substantially decreased by seven times.

In conclusion, the newly developed method is more advantageous over the tesseroid-based 3D GLQ methods in both accuracy and efficiency, and also in its capability in dealing with polynomial and non-polynomial density models. Therefore, we believe that our method could have more potentials in large-scale gravity forward and inverse problems.

Appendices

Appendix A: Analytical expressions for ${\xi _p}$, ${\partial _j}{\xi _p}$, and ${\partial _{ij}^2}{\xi _p}$

The radial integrals ${\partial _j}{\xi _{n+2}}\;({n=0,1,...,N},\;j = \varphi ,\lambda ,r)$ in Eq. (14) can be analytically expressed as

$$\begin{aligned} {\partial _\varphi }{\xi _{n + 2}}&= r{\eta _{n + 3}}{\partial _\varphi }\cos \psi \nonumber \\ {\partial _\lambda }{\xi _{n + 2}}&= r{\eta _{n + 3}}{\partial _\lambda }\cos \psi \nonumber \\ {\partial _r}{\xi _{n + 2}}&= {\eta _{n + 3}}\cos \psi - {\eta _{n + 2}}r \end{aligned}$$

(A1)

where

$$\begin{aligned} {\eta _k} = \int {\frac{{{{r'}^k}}}{{{\ell ^3}}}dr'} ,\quad k = 0,1, \ldots ,n + 3 \end{aligned}$$

(A2)

with

$$\begin{aligned} {\eta _0}&= \left\{ \begin{array}{ll} - \frac{{\mathrm{{sign}}(r' - r)}}{{2{{(r' - r)}^2}}},&{}\quad \cos \psi = 1\\ - 0.5{(r' + r)^{ - 2}},&{}\quad \cos \psi = - 1\\ \frac{{({{r'} r} - \cos \psi )}}{{r(1 - {{\cos }^2}\psi )\ell }},&{}\quad \cos \psi \ne \pm 1 \end{array} \right. \nonumber \\ {\eta _2}&= - \frac{{r'}}{\ell } + r\cos \psi \cdot {\eta _1} + {\xi _0}\nonumber \\ {\eta _k}&= \frac{1}{{k - 2}}\Bigg ( \frac{{{{r'}^{k - 1}}}}{\ell } + (2k - 3)r\cos \psi {\eta _{k - 1}}\nonumber \\&\quad - (k - 1){r^2}{\eta _{k - 2}} \Bigg ) \nonumber \\&\quad k > 0\quad \hbox {and}\quad k \ne 2 \end{aligned}$$

(A3)

The radial integrals ${\partial _{ij}^2}{\xi _{n+2}}\;({n=0,1,\ldots ,N},\;i,j = \varphi ,\lambda ,r)$ in Eq. (18) have the following analytical form:

$$\begin{aligned} \partial _{\varphi \varphi }^2{\xi _{n + 2}}&= r\partial _{\varphi \varphi }^2\cos \psi {\eta _{n + 3}} + 3{r^2}{\left( {{\partial _\varphi }\cos \psi } \right) ^2}{\zeta _{n + 4}}\nonumber \\ \partial _{\lambda \lambda }^2{\xi _{n + 2}}&= r\partial _{\lambda \lambda }^2\cos \psi {\eta _{n + 3}} + 3{r^2}{\left( {{\partial _\lambda }\cos \psi } \right) ^2}{\zeta _{n + 4}}\nonumber \\ \partial _{rr}^2{\xi _{n + 2}}&= 2{\eta _{n + 2}} - 3\left( {1 - {{\cos }^2}\psi } \right) {\zeta _{n + 4}}\nonumber \\ \partial _{\varphi \lambda }^2{\xi _{n + 2}}&= r\partial _{\varphi \lambda }^2\cos \psi {\eta _{n + 3}} + 3{r^2}\left( {{\partial _\varphi }\cos \psi {\partial _\lambda }\cos \psi } \right) {\zeta _{n + 4}}\nonumber \\ \partial _{\varphi r}^2{\xi _{n + 2}}&= {\partial _\varphi }\cos \psi \left( {{\eta _{n + 3}} - 3r(r{\zeta _{n + 3}} - \cos \psi {\zeta _{n + 4}})} \right) \nonumber \\ \partial _{\lambda r}^2{\xi _{n + 2}}&= {\partial _\lambda }\cos \psi \left( {{\eta _{n + 3}} - 3r(r{\zeta _{n + 3}} - \cos \psi {\zeta _{n + 4}})} \right) \end{aligned}$$

(A4)

where

$$\begin{aligned} {\zeta _k} = \int {\frac{{{{r'}^k}}}{{{\ell ^5}}}dr'} ,\quad k = 0,1, \ldots ,n + 4 \end{aligned}$$

(A5)

with

$$\begin{aligned} {\zeta _0}&= \left\{ \begin{array}{ll} - \frac{{\mathrm{{sign}}(r' - r)}}{{4{{(r' - r)}^4}}},&{}\quad \cos \psi = 1\\ - 0.25{(r' + r)^{ - 4}},&{}\quad \cos \psi = - 1\\ \frac{{{{r'} r} - \cos \psi }}{{3r(1 - {{\cos }^2}\psi )}}\left( {\frac{1}{{{\ell ^3}}} + \frac{2}{{\ell (1 - {{\cos }^2}\psi ){r^2}}}} \right) ,&{}\quad \cos \psi \ne \pm 1 \end{array} \right. \nonumber \\ {\zeta _4}&= - \frac{{{{r'}^3}}}{{3{\ell ^3}}} + r\cos \psi {\zeta _3} + {\eta _2} \nonumber \\ {\zeta _k}&= \frac{1}{{k - 4}}\Bigg ( \frac{{{{r'}^{k - 1}}}}{{{\ell ^3}}} + (2k - 5)r\cos \psi {\zeta _{k - 1}}\nonumber \\&\quad - (k - 1){r^2}{\zeta _{k - 2}} \Bigg )\nonumber \\&\quad k> 0\quad \hbox {and}\quad k \ne 4 \end{aligned}$$

(A6)

and

$$\begin{aligned} {\partial _\varphi }\cos \psi&= \cos \varphi \sin \varphi ' - \sin \varphi \cos \varphi '\cos (\lambda ' - \lambda )\nonumber \\ {\partial _\lambda }\cos \psi&= \cos \varphi \cos \varphi '\sin (\lambda ' - \lambda )\nonumber \\ \partial _{\varphi \varphi }^2\cos \psi&= - \cos \psi \nonumber \\ \partial _{\lambda \lambda }^2\cos \psi&= - \cos \varphi \cos \varphi '\cos (\lambda ' - \lambda )\nonumber \\ \partial _{\varphi \lambda }^2\cos \psi&= - \sin \varphi \cos \varphi '\sin (\lambda ' - \lambda ) \end{aligned}$$

(A7)

Appendix B: Analytical solutions for spherical shell

For a spherical shell with a radially varying density $\rho (r')$, the analytical expressions for the gravitational potential V, vector $\mathbf{{g}}$, and Marussi tensor $\mathbf{{M}}$ on any point with a radial distance r above the shell can be expressed as

$$\begin{aligned}{} & {} V = \frac{{4\pi G}}{\ell }\gamma \end{aligned}$$

(B8)

$$\begin{aligned}{} & {} {g_i} = 4\pi G\gamma \frac{{{\Delta _i}}}{{{\ell ^3}}} \end{aligned}$$

(B9)

$$\begin{aligned}{} & {} {M_{ij}} = 4\pi G\gamma \left( {\frac{{3{\Delta _i}{\Delta _j}}}{{{\ell ^5}}} - \frac{{{\delta _{ij}}}}{{{\ell ^3}}}} \right) \end{aligned}$$

(B10)

with

$$\begin{aligned}&\ell = \sqrt{\Delta _x^2 + \Delta _y^2 + \Delta _z^2} \nonumber \\&{\Delta _x} = {r_0}\left[ {\cos \varphi \sin {\varphi _0} - \sin \varphi \cos {\varphi _0}\cos \left( {{\lambda _0} - \lambda } \right) } \right] \nonumber \\&{\Delta _y} = {r_0}\cos {\varphi _0}\sin \left( {{\lambda _0} - \lambda } \right) \nonumber \\&{\Delta _z} = {r_0}\cos \psi - r \nonumber \\&\cos \psi = \sin \varphi \sin {\varphi _0} + \cos \varphi \cos {\varphi _0}\cos \left( {{\lambda _0} - \lambda } \right) \end{aligned}$$

(B11)

where $i,j=x,y,z$, ${\delta _{ij}}$ is the Kronecker delta function, $(r_0,\varphi _0,\lambda _0)$ is the geometrical centre of the spherical shell, and

$$\begin{aligned} \gamma = \int \limits _{{R_1}}^{{R_2}} {{{r'}^2}\rho (r')} \mathrm{{d}}r' \end{aligned}$$

(B12)

where $R_1$ and $R_2$ are the inner and outer radius of the shell. When the geometrical centre of the shell is located at the origin, i.e. $(r_0,\varphi _0,\lambda _0)=(0,0,0)$, Eqs (B8) to (B10) further reduce to

$$\begin{aligned} V= & {} \frac{{4\pi G}}{\ell }\gamma \end{aligned}$$

(B13)

$$\begin{aligned} {g_z}= & {} - \frac{{4\pi G}}{{{\ell ^2}}}\gamma \end{aligned}$$

(B14)

$$\begin{aligned} {M_{xx}}= & {} {M_{yy}} = - \frac{{4\pi G}}{{{\ell ^3}}}\gamma ,\quad {M_{zz}} = \frac{{8\pi G}}{{{\ell ^3}}}\gamma \end{aligned}$$

(B15)

with ${g_x} = {g_y} =0$, and ${M_{xy}} = {M_{xz}} = {M_{yz}} = 0$.

For a polynomial density function of N degree, $\rho (r') = \sum \nolimits _{n = 0}^N {{A_n}{{r'}^n}}$, $\gamma$ is given by

$$\begin{aligned} \gamma = \sum \limits _{n = 0}^N {\frac{{{A_n}}}{{n + 3}}\left( {R_2^{n + 3} - R_1^{n + 3}} \right) } \end{aligned}$$

(B16)

For a exponential density function $\rho (r') = A{e^{ - B(r' - {R_1})}} + C$, $\gamma$ is as follows:

$$\begin{aligned}&\gamma = \frac{C}{3}(R_2^3 - R_1^3) + \frac{A}{{{B^3}}}\left[ {\left( {R_1^2{B^2} + 2{R_1}B + 2} \right) } \right. \nonumber \\&\;\;\;\;\;\left. { - \left( {R_2^2{B^2} + 2{R_2}B + 2} \right) {e^{ - B({R_2} - {R_1})}}} \right] \end{aligned}$$

(B17)

with

$$\begin{aligned} A= & {} \frac{{{\rho (R_1)} - {\rho (R_2)}}}{{1 - {e^{ - b}}}},\quad B = \frac{b}{{{R_2} - {R_1}}},\nonumber \\ C= & {} {\rho (R_1)} - A \end{aligned}$$

(B18)

where $R_1$ is the inner radius of the shell and $R_2$ the outer radius.

The analytical solutions for the gravitational effects of PREM are obtained by summing the contributions of the spherical shells that form it.