Geodetic VLBI for precise orbit determination of Earth satellites: a simulation study

Abstract

Recent efforts of tracking low Earth orbit and medium Earth orbit (MEO) satellites using geodetic very long baseline interferometry (VLBI) raise questions on the potential of this novel observation concept for space geodesy. Therefore, we carry out extensive Monte Carlo simulations in order to investigate the feasibility of geodetic VLBI for precise orbit determination (POD) of MEO satellites and assess the impact of quality and quantity of satellite observations on the derived geodetic parameters. The MEO satellites are represented in our study by LAGEOS-1/-2 and a set of Galileo satellites. The concept is studied on the basis of 3-day solutions in which satellite observations are included into real schedules of the continuous geodetic VLBI campaign 2017 (CONT17) as well as simulated schedules concerning the next-generation VLBI system, known as the VLBI Global Observing System (VGOS). Our results indicate that geodetic VLBI can perform on a comparable level as other space-geodetic techniques concerning POD of MEO satellites. For an assumed satellite observation precision better than 14.1 mm (47 ps), an average 3D orbit precision of 2.0 cm and 6.3 cm is found for schedules including LAGEOS-1/-2 and Galileo satellites, respectively. Moreover, geocenter offsets, which were so far out of scope for the geodetic VLBI analysis, are close to the detection limit for the simulations concerning VGOS observations of Galileo satellites, with the potential to further enhance the results. Concerning the estimated satellite orbits, VGOS leads to an average precision improvement of 80% with respect to legacy VLBI. In absolute terms and for satellite observation precision of 14.1 mm (47 ps), this corresponds to an average value of 17 mm and 7 mm concerning the 3D orbit scatter and precision of geocenter components, respectively. As shown in this study, a poor satellite geometry can degrade the derived Earth rotation parameters and VLBI station positions, compared to the quasar-only reference schedules. Therefore, careful scheduling of both quasar and satellite observations should be performed in order to fully benefit from this novel observation concept.

Introduction

Geodetic very long baseline interferometry (VLBI) is a space-geodetic technique with a long tradition of realizing terrestrial (Bachmann et al. 2016) and celestial reference systems (Fey et al. 2009), and uniquely providing the full set of Earth orientation parameters (EOP) that relate those two systems (Nothnagel et al. 2017). Observations of radio emission from very distant natural radio sources, objects commonly referred to as quasars, are the basis of geodetic VLBI. Due to the great distances, a catalog of well-defined quasars realizes a quasi-inertial reference frame. While using these radio sources provides a unique capability of simultaneous determination of a full set of EOP, other Earth-based parameters, commonly accessible by satellite techniques like satellite laser ranging (SLR), Global Navigation Satellite Systems (GNSS) or Doppler Orbitography and Radio positioning Integrated by Satellite (DORIS), cannot be derived from standard geodetic VLBI analysis. In particular, this implies that VLBI does not provide a direct access to information that relates to the gravity field or to geocenter motion.

Driven by recent efforts to track Earth-orbiting satellites with geodetic VLBI, several technical (McCallum et al. 2017) and theoretical (e.g., Hase 1999; Duev et al. 2012) questions arose concerning the use of such observations for the benefit of the geodetic community (Dickey 2010) and the Global Geodetic Observing System (GGOS, Plag and Pearlman 2009). Since the latter aims to combine all space-geodetic techniques in a consistent manner for a very stable and precise reference frame, the question of the performance of geodetic VLBI for satellite tracking needs to be also addressed before observation concepts for GGOS can be designed. The simultaneous use of several space-geodetic techniques is beneficial for overcoming the technique-specific weaknesses while providing the highest quality and homogeneity of global geodetic parameters (Rothacher et al. 2011; Artz et al. 2012; Sośnica et al. 2019). The inclusion of a dedicated VLBI transmitter on board of future GNSS satellites would thus create a great opportunity for the multi-technique analysis of space-geodetic data. Such a concept is realized nowadays with SLR observations of GNSS satellites that are equipped with laser retroreflector arrays. This allows, for instance, validation of microwave-based GNSS orbits with SLR (Otsubo et al. 2001; Montenbruck et al. 2015; Hackel et al. 2015).

Observations of both satellites and quasars with VLBI could bring several benefits along with some challenges. As the very same instruments (i.e., reference points) are used to observe both quasars and Earth-orbiting satellites, technique-specific coordinate frame solutions (Plank et al. 2016) can be derived in order to investigate technique-specific systematic effects and the quality of local ties. The latter refers to vectors connecting the reference points of geodetic instruments at co-location sites. The insufficient quality of local ties (Ray and Altamimi 2005; Altamimi et al. 2016) limits the accuracy of today’s ITRF realizations, besides inhomogeneous network configurations or technique-specific errors. Observations of satellites with VLBI telescopes would allow to include this technique in co-location on board of spacecrafts and realize the concept of space ties. With VLBI, the positions of satellites can be connected directly to the reference frame defined by extragalactic radio sources and those estimates can be compared with positions determined by other space-geodetic techniques. In this case, the technique ties are realized together by all instruments that can observe the co-location satellite, enhancing in this way the quantity of tie measurements and improving their spatio-temporal resolution. Therefore, space ties and carefully chosen (ground-based) local ties could thus be utilized for an improved derivation of TRF, and/or mitigation of systematic errors that are present in the space-geodetic techniques. The combined solutions can potentially result in an enhanced quality of target parameters such as station positions, EOP or spacecraft orbits. At the co-location ground stations, single troposphere and clock models can be applied to two observation types and thus improve the stability of the solutions (Krügel et al. 2007).

So far only few dedicated experiments have been performed with the purpose to track low Earth orbit (LEO) or medium Earth orbit (MEO) satellites with VLBI (Haas et al. 2014; Tornatore et al. 2014; Plank et al. 2017; Hellerschmied et al. 2018). However, these observations were neither performed with networks of globally distributed VLBI stations nor did they address determination of satellite orbits. A variety of simulation studies have also been carried out with the aim of understanding how one could benefit from tracking satellites in the geodetic VLBI mode (Plank 2013; Plank et al. 2016) and whether this technique could contribute to the concept of co-location in space (Männel 2016; Anderson et al. 2018). Although over the past years several interesting aspects have been discussed, studies whether geodetic VLBI has the potential to access geodetic parameters other than those currently obtained have not been performed so far. The latter aspect and the concept of co-location in space imply also precise determination of spacecraft orbits. Accurate orbit parameters are of high importance for Earth science missions when solving for global parameters of geophysical interest (Bertiger et al. 1994; Kang et al. 2006).

In this study, we investigate the feasibility of geodetic VLBI for precise orbit determination of MEO satellites with the use of extensive Monte Carlo simulations. The following sections explain the concept of satellite observations in the geodetic VLBI mode, describe the simulation environment and summarize the results obtained from our extensive Monte Carlo simulations. The latter involve quasars and observations of LAser GEOdynamics Satellite (LAGEOS-1 and LAGEOS-2) and a set of Galileo satellites in three consecutive 24-h geodetic VLBI sessions, which were used to derive 3-day solutions. In Sect. 2, the concept of observations of satellites with geodetic VLBI is described. Extensive information on the input data, simulation setup and parameterization applied in this study is given in Sect. 3. Results based on schedules representing the performance of both the legacy and the next-generation VLBI systems are presented in Sect. 4. The discussion concerning the obtained results and the impact of satellite observations on classical geodetic parameters is given in Sect. 5. The final section consists of a summary and outlook.

Geodetic VLBI observations of Earth-orbiting satellites

Recent experiments related to tracking of artificial radio sources with geodetic VLBI include observations of signals characterized by different strength and structure. Differential One-way Ranging (DOR) tones used for spacecraft tracking (range and range-rate measurements) constitute the first example. When applied to geodetic VLBI (Haas et al. 2017; Hellerschmied et al. 2018), the obtained group-delay observables are characterized by a theoretical precision on the sub-nanosecond level (Zheng et al. 2014; Klopotek et al. 2019). VLBI stations with L-band capability can observe GNSS satellites. This results in single-band delay uncertainties on a similar level (Plank et al. 2017). Besides these theoretical values, one needs also to consider additional factors that can degrade the quality of satellite observations. One example are ionosphere delays in the case of single-frequency observations. This effect can be reduced by using externally derived ionosphere delays, e.g., delays computed based on GNSS data (Männel and Rothacher 2016). In this case, however, non-negligible delay contributions would still be present (Sekido et al. 2003). In addition, effects due to troposphere and station clock variations need to be modeled at the data analysis stage and can be also estimated with the use of quasar observations (Plank et al. 2017; Klopotek et al. 2019). The different nature of quasar and satellite observations requires also changes of the usual observation and analysis approaches. The conventional VLBI delay model (Petit and Luzum 2010) is not applicable in the case of the Earth-orbiting satellites and so-called near-field VLBI delay models (Fukushima 1994; Sekido and Fukushima 2006; Duev et al. 2012) have to be used. This applies to both the correlation and data analysis stage (Klopotek et al. 2017; Hellerschmied et al. 2018). In addition, depending on the satellite orbital height, one additional challenge is that the mutual visibility to a satellite is much smaller than to a quasar.

Typical natural radio sources for geodetic VLBI are characterized by observed flux densities on the order of $10^{-26}$ W m$^{-2}\,{\text {Hz}}^{-1}$. GNSS L-band signals, as received on the surface of the Earth, are several orders of magnitude stronger (Steigenberger et al. 2018) than radiation from quasars. This implies that VLBI delay observables, based on observations of artificial radio sources, are in theory rather precise even for short measurements of only few seconds. Therefore, instead of observing natural radio sources for tens of seconds, several satellite scans¹ with even different satellites can be carried out during the same time, given that the antennas’ slew speeds are sufficiently high. The current VLBI telescopes are already capable of tracking objects at various orbital heights, including LEO satellites (Sun et al. 2018; Hellerschmied et al. 2018). This also should not be an issue for the next-generation VLBI telescopes due to their improved tracking capabilities (Petrachenko et al. 2009; Fukuzaki et al. 2015). However, a compromise needs to be found when utilizing such sources as very strong signals might be problematic for the dynamic range of the VLBI systems. If not potentially damage VLBI front-ends at the first place, they would pose the problem of varying attenuation levels for the VLBI back-ends, which is in general not preferable and may cause some problems at the data analysis stage (Plank et al. 2017). Furthermore, strong satellite signals do not allow to use the existing VLBI phase-calibration (PCAL) systems designed to reduce instrumental effects. Therefore, for a prospective VLBI-like transmitter placed on a GNSS satellite, signal strength on the order of tens of mW over a MHz bandwidth² would be suitable for observations in the geodetic VLBI mode (see Sect. 3.2).

Although it is possible to make use of DOR tones in the geodetic VLBI analysis (Hellerschmied et al. 2018; Klopotek et al. 2019), processing of such data at the post-correlation analysis stage, when the group delays are obtained, is not always a straightforward task and some alterations at this stage are necessary. Alternatively, a VLBI-like transmitter on a satellite could transmit signals reminiscing quasars, i.e., random signals with equal intensity over wide frequency bands. Such a solution would open the possibility of using standard tools from traditional geodetic VLBI. In that case, multiple few-MHz-wide channels spanning few hundred MHz would be favorable for observations in the geodetic VLBI mode. Realization of the proposed concept would thus not require any signal modulation while still providing relative delays on each baseline.

Good knowledge of technique-specific offsets/phase centers of the employed instruments is a prerequisite for deriving high-quality geodetic products of various kinds (Schmid et al. 2007). This applies to both the receiver antenna and the position of the satellite antenna phase center. VLBI telescopes are high-gain directive antennas and therefore suffer neither from multipath effects nor from phase-center variations. However, in the case of prospective VLBI observations of satellites equipped with dedicated transmitters, satellite phase-center offsets (PCOs) and phase-center variations (PCVs) have to be considered. The physical location of the antenna reference point and the average electronic phase-center location can be precisely measured prior to the satellite launch. However, this needs to be augmented with an in-flight calibration (based on post-fit observation data residuals) as the effective phase-center positions can vary significantly depending on the error sources additionally present in the actual spacecraft environment. Similarly to the analysis of GNSS observations in a global solution (Schmid and Rothacher 2003; Haines et al. 2004; Schmid et al. 2007; Montenbruck et al. 2008; Jäggi et al. 2009), corrections to the VLBI transmitter antenna characteristics, obtained from the ground calibration, could be determined from the VLBI data, together with other geodetic parameters of interest and represented as a function of nadir angle and azimuth in the satellite antenna frame. In the case of prospective observations including both satellites and quasars, the terrestrial scale is derived from quasar observations, which, along with SLR data, are used to realize the ITRF scale (Altamimi et al. 2016). Nevertheless, long time series and varying observation geometries are essential in order to obtain the most reliable phase-center corrections and properly decouple all solve-for parameters (Schmid and Rothacher 2003; Schmid et al. 2007).

Simulation setup and parameter estimation

Simulation studies are useful tools for assessing the performance of new concepts or technology in case no real observations are available. In Monte Carlo simulations, a large number of simulation runs provide the basis for deriving information on the investigated parameters, given the mathematical model and a set of input parameters with known stochastic behavior (probability distribution). In this study, Monte Carlo simulations were carried out with the c5++ analysis software (Hobiger et al. 2010), which was developed with the aim of processing VLBI, GNSS and SLR separately or in a multi-technique approach by combining them on the observation level (Hobiger and Otsubo 2014; Hobiger et al. 2014; Hobiger and Otsubo 2017). This is beneficial for the data analysis as processing several observation types with the same software provides high consistency w.r.t. the applied a priori models and parameterization.

The simulated geodetic VLBI observables consist of the geometric delays and a number of additional contributions. In the case of quasar observations, the so-called Consensus Model (Petit and Luzum 2010) is used to calculate the geometric delay. As stated in Sect. 2, this is not applicable to satellite observations and the conventional VLBI delay model needs to be replaced by a near-field model. The Monte Carlo approach is realized by changing atmospheric, station clock and measurement-noise contributions for each simulation run, providing in this way the basis for predicting the performance of the investigated ideas. The c5++ analysis software has already been used to conduct similar simulation studies. Extensive information concerning geodetic VLBI simulations in c5++ is given by Kareinen et al. (2017) and Klopotek et al. (2018).

Input data

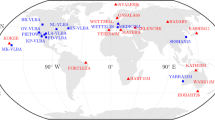
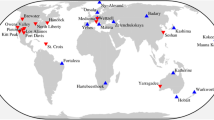
The International VLBI Service for Geodesy and Astrometry (IVS, Nothnagel et al. 2017) is an international collaboration of institutions, which operate and support the components of geodetic and astrometric VLBI. During the last two decades, every third year the performance of the VLBI systems was investigated by organizing a continuous VLBI campaign (CONT). In this study, the Legacy-1 observation network of CONT17 (Behrend et al. 2017) was chosen as a representative set of stations for the current (S/X) VLBI system. In order to combine satellite and quasar observations, the corresponding schedule files for the first three days of CONT17 were used, i.e., between 2017/11/28 00:00:00 UTC and 2017/12/01 00:00:00 UTC. Our study included also schedules related to the next-generation (broadband) VLBI system referred to as the VLBI Global Observing System (VGOS, Petrachenko et al. 2009; Niell et al. 2018). We created a VGOS-type schedule with a station network used during the conceptual phase of VGOS. It covered the same 3-day period as the CONT17 schedules. The distribution and quantity of VGOS stations used in this study thus does not exactly represent the currently realized VGOS network. Nevertheless, throughout our simulations, it is possible to investigate the dependence of the enhanced observation density, higher precision of quasar observations and a homogeneous network configuration on the determined satellite-based parameters. One can address therefore the question of the benefit of satellite observations carried out in the VGOS era, compared to using the current VLBI system. The distribution of the participating telescopes for both employed networks (CONT17 and VGOS) is illustrated in Fig. 1.

Fig. 1

VLBI stations of the 14-station CONT17 Legacy-1 network (red) and stations of a hypothetical 16-station VGOS network (yellow). The name labels refer to the CONT17 stations. Since the VGOS network employed here was used in the design phase of VGOS, no station names are given. The map created using ETOPO1 Global Relief Model (Amante and Eakins 2009)

Satellite observations were added into the geodetic VLBI schedules by modifying VLBI experiment (VEX) files (Whitney et al. 2002), managed by the IVS and publicly available through its server³. In the case of the VGOS-type observations, we used three VEX files converted from a single SKD file (Gipson 2010). A priori information based on real orbits (see below for more details) was used to compute the position of a satellite at any given time and then either every fourth or eighth quasar scan was replaced with few 10-s satellite scans (or a single satellite scan in the case of the VGOS schedule) for all stations that could see the satellite. In case a certain station could not see the satellite, it was placed back to observe the originally scheduled radio source. In order to decorrelate parameters requiring good observing geometries (troposphere model, station positions), quasar observations dominate our solutions in terms of sky coverage and quantity. Rather than observing a handful of satellites very frequently, VLBI telescopes have to spend a significant amount of time pointing at many different directions in the sky. A similar approach of modifying VEX files was applied by Klopotek et al. (2018) for combining quasar and lunar observations. This approach provides a simple method to utilize both data types while providing a sufficiently large number of non-quasar observations.

Two satellite constellations were examined in this study, assuming that they are observable with VLBI. GNSS was represented by a set of Galileo (GAL) satellites (E01, E02, E04, E07, E12 and E26), i.e., two satellites per orbital plane. The three equally-spaced GAL orbital planes, with a 56$^{\circ }$ inclination, are characterized by an orbital altitude of 23,222 km. Our simulations included also the LAGEOS-1 and LAGEOS-2 satellites, hereafter referred to as LAG satellites. LAGEOS-1 is located at an altitude of 5860 km and moves on an orbit inclined by $109.90^\circ$. In the case of LAGEOS-2, the orbital height and orbital inclination equal 5620 km and $52.67^\circ$, respectively. The LAG case can be seen as a pure theoretical study which only concerns the common visibility aspect and the sensitivity of geodetic VLBI to geocenter and Earth rotation parameters (ERP), see Sect. 4. However, the LAG-type schedules correspond also to some extent to scenarios related to co-location in space (Nerem et al. 2011). Satellites at LAG-like altitudes still allow to obtain a sufficiently large number of interferometric measurements at long baselines, compared to satellites at GNSS-like altitudes. On the contrary, a global network of VLBI stations and LEO satellites would result in too few observations and many baselines that could not observe satellites. As a consequence, this would lead to rather poor observing geometries for orbit determination and parameter estimation (Männel 2016).

Final orbit products⁴ (Dach et al. 2016) in the form of SP3 files from the Center for Orbit Determination in Europe (CODE) were used in the GAL-related simulations. For the LAG case, the a priori orbit information was based upon SP3 files, calculated at European Space Agency (ESA) and publicly available via a dedicated ftp server⁵ of the International Laser Ranging Service (ILRS, Pearlman et al. 2019). Such external orbit information for both employed constellations served as the basis for deriving initial state vectors necessary in the orbit determination process, see Sect. 3.4.1.

The overall number of observations in the modified schedules exceeded significantly the amount of observations present in the original schedules. As mentioned in Sect. 2, artificial radio sources can be observed for shorter periods of time due to their signal strength. Therefore, several satellite scans can be obtained from replacing a single quasar scan, and, e.g., a 10-s satellite scan duration is more than sufficient to reach typical targets for the baseline-based Signal-To-Noise Ratio (SNR), a criterion used at the scheduling stage. More details on the original and modified schedules are given in Table 1.

Table 1 Seven different schedules used in this study

Precision of the simulated observations

The simulations included contributions originating from three major error sources, i.e., tropospheric turbulence, behavior of hydrogen masers at observing sites, and baseline-based measurement noise (Petrachenko et al. 2009; Nilsson and Haas 2010). The precision of the simulated satellite observations was controlled in our case by modifying only the baseline-based (Gaussian) noise. Its level should in principle reflect the current (realistic) precision of such observations. However, it is also possible to investigate via this parameter how the quality of the derived target parameters depends on the precision of satellite observations. Therefore, eight different baseline noise levels for satellite observations were used. They covered the levels between 1.4 mm and 300.0 mm in logarithmic steps. For quasar observations, 14.1 mm (47 ps) and 1.4 mm (4.7 ps) were used to reflect the performance of the current (S/X) VLBI and VGOS systems, respectively. In each simulation run (60 runs per noise level), the a priori satellite position states were perturbed randomly with a standard deviation of 30 m, before being used in the second stage of the analysis (see Sect. 3.4). Hence, it could be verified whether the orbit solutions converged toward the a priori orbit used to generate the satellite observations.

A millimeter-level satellite observation precision, also examined in our study, is theoretically possible. Assuming VGOS-compliant observations providing a root-mean-square (RMS) spanned bandwidth⁶$\text {B}_{RMS}$ of about 0.34 GHz per band, group-delay VLBI observables with an uncertainty of approximately 1.4 mm (4.7 ps) could be then obtained while reaching baseline-based SNR targets on the order of 100 for 1-s scan lengths and 2-bit quantization (Takahashi et al. 2000). For GNSS-type orbits and a VLBI-like transmitter with a 3 dBi antenna gain, this would imply, for instance, transmission of radio signals with power levels below one Watt and over a spanned frequency range of approximately 0.85 GHz, assuming utilization of multiple few-MHz-wide channels per band and polarization (Niell et al. 2018). Accordingly, smaller SNR targets would imply larger $\text {B}_{RMS}$ in order to still operate within a millimeter observation precision regime.

The presented simulation setup provides a close-to-reality assessment of the feasibility of geodetic VLBI for an accurate orbit determination of Earth satellites. However, since it was assumed in this study that all the force models are perfectly known and no acceleration noise is present, the same models were applied both in the simulation and in the analysis (recovery) step.

Orbit quality assessment

Various methods can be used to assess the quality of the obtained orbit solutions. This often includes n-day orbit overlaps, day-boundary discontinuities or inter-technique comparison of the derived orbits (Hackel et al. 2015). In our case, the orbit quality was assessed by investigating the scatter among the individual 3-day orbit solutions w.r.t. the mean 3-day orbit. This indicates a precision of the orbit solutions. When the individual solutions are compared to the a priori orbit information, accuracy of the obtained orbits can be assessed. Such computations were performed with 5-min intervals for the radial, cross-track and along-track components as well as for the three-dimensional positions. This approach is illustrated in Fig. 2. An average value calculated based on such quantities represents therefore an overall mean orbit quality.

Fig. 2

Performance metrics (precision and accuracy) calculated based upon the Monte Carlo simulations and using external orbits. The same routine applies also to LAG satellites

Analysis setup

The target parameters were derived with various analysis options, but always employing a two-stage approach. The second-order clock polynomials were derived in stage-1. The estimation of one 3-day continuous piece-wise linear function for the station clocks was thus possible and was carried out in stage-2 along with estimation of the parameters of interest and for different analysis options.

Estimation of additional parameters, i.e., zenith wet delays (ZWD), tropospheric gradients, station clocks, as well as estimation of station positions with No-Net-Translation/No-Net-Rotation (NNT/NNR) conditions (using nine out of fourteen stations for the CONT17 network, i.e., excluding FORTLEZA, HOBART26, KOKEE, WARK12M, KASHIM11, and utilizing all stations for the VGOS network, see Sect. 5) was carried out in all of the employed analysis options. The parameters estimated in our analysis are listed in Table 2 for all of the employed analysis options. For each satellite-quasar schedule used in this study (Table 1), a corresponding reference solution containing only quasar (Q) observations is available. In the presence of an identical quasar observation geometry, the impact of satellite observations on the solve-for parameters can be easily studied and understood. Therefore, seven reference solutions in which station positions and additional parameters were estimated are referred throughout the text to as Q-S. In the second analysis option, additionally ERP (polar motion and UT1-UTC) were estimated with a daily resolution. This analysis option is abbreviated as Q-SE. The QS-S and QS-SE analysis options correspond to Q-S and Q-SE in terms of the parameterization, but include satellite (S) observations with satellite orbits fixed to their a priori values. The next analysis option, related to the modified schedules and abbreviated as QS-OS, included determination of satellite orbits (O), estimation of station positions and additional parameters and had ERP fixed to their a priori values. A similar analysis option, but with estimation of the geocenter offsets (G), is abbreviated as QS-OSG. The QS-OSE option is similar to QS-OS, but included estimation of ERP. In the analysis option referred to as QS-OSEG, additionally one set of geocenter offsets was estimated per solution.

The consideration of the geocenter (offset) in our study is motivated by the fact that observations of geodetic satellites allow for determination of geocenter motion (Dong et al. 1997; Chen et al. 1999; Wu et al. 2012) in the terrestrial reference frame (TRF). Solutions including estimation of station positions reflect a case of an instantaneous observation network with its center in the instantaneous center of the network (CN). The latter most often only approximates the center of figure (CF) of the outer surface due to an insufficient and inhomogeneous coverage of the Earth by geodetic stations and results in the so-called network effects (Collilieux et al. 2009), which tend to bias the global geodetic parameters. Nevertheless, an analysis of satellite data, covering longer time spans (months, years), allows to investigate diurnal or inter-seasonal geocenter motion w.r.t. the mean center of mass (CM) of the Earth or the origin of the International Terrestrial Reference Frame (ITRF, Altamimi et al. 2016) as the geocenter offset expresses the spatial relation between CF and CM. Due to the orbit characteristics and the low impact of non-gravitational perturbing forces, the ITRF origin is derived solely based on SLR measurements of geodetic satellites at low altitudes (Petit and Luzum 2010; Sośnica et al. 2014) as they are more sensitive to gravity than, for instance, GNSS satellites. The cannonball shape of the satellites, used for the frame origin derivation, facilitates also the orbit modeling and results in lower correlation of geocenter parameters with empirical orbit model parameters (Meindl et al. 2013). In our simulation environment, however, one can investigate the sensitivity of the technique and the used observing network for the geocenter offset estimation. The presence of biases or large parameter uncertainties can therefore indicate a lack of sensitivity, bad performance of the chosen network or satellite constellation as well as deficiencies in the orbit modeling. In reality, the geocenter motion is not expected to be zero as it is mainly driven by mass redistribution not considered in the estimation process. In addition, the derived time series of that parameter contain signals originating from the orbit modeling deficiencies and network effects (Riddell et al. 2017; Couhert et al. 2018).

For the CONT17 network, VLBI station positions were expressed in ITRF2014 (Altamimi et al. 2016). For both CONT17 and VGOS schedules, the S/X source catalog of the third realization of the International Celestial Reference Frame (ICRF3)⁷ was used to obtain the positions of quasars. The quasar coordinates were not estimated in this study and were fixed to their catalogue values. We used EOP information available as the IERS-14-C04 series (Bizouard and Gambis 2018). In addition, in each simulation that included satellite observations, station clock biases (w.r.t. a reference station) were determined once per solution as constant parameters. Unfortunately, such clock biases cannot be avoided, and when estimated, they degrade the determination of satellite-based parameters, see Sect. 5.

Table 2 Parameterization of the estimated parameters for different analysis options

The created simulation data set was analyzed in an iterative least-squares (LSQ) fashion. Satellite and quasar observations were combined on the observation level to simultaneously determine common target parameters and to perform precise orbit determination (POD) of satellites of interest. Since the problem is nonlinear, an iterative LSQ method was carried out until the weighted RMS post-fit residuals from two consecutive iteration steps differed less than a predefined convergence threshold. It has to be emphasized at this point that the common parameters such as ZWD, troposphere gradients, station positions, ERP or short-term variations of VLBI station clocks were derived using both observation types, proportionally to the applied weighting. In this case, each observation was weighted with a value corresponding to the noise level used for generating the baseline noise as well as the wet mapping functions (Lagler et al. 2013). The weighted iterative least-squares adjustment in c5++ was supported in stage-2 with the variance-component-estimation algorithm (Hobiger and Otsubo 2017) as a simple tool for relative weighting between two observation types.

Orbit modeling

POD of Earth-orbiting satellites with geodetic VLBI has been recently implemented in c5++. Since POD in this software is carried out mainly with SLR data (Otsubo et al. 2016), it was already equipped with numerous satellite force models, a numerical integrator (Otsubo et al. 1996), and a batch estimator using state transition matrices. In this study, a conventional dynamic POD approach was performed using publicly available satellite information for the force modeling.⁸ The parametrization of the orbit parameters is given in Table 2.

The satellite state vector (geocentric position and velocity) fully defines a set of initial conditions for an equation of motion of artificial satellites. The estimation of empirical accelerations in the simulation environment, as stated in Table 2, is motivated by the fact that POD of geodetic satellites with SLR or GNSS always includes additional parameters (pseudo-stochastic orbit parameters, once-per-revolution empirical accelerations), which (only partly) absorb deficiencies in the modeling of gravitational and non-gravitational forces perturbing satellite orbits (Colombo 1989; Springer et al. 1999; Beutler et al. 2006). Empirical accelerations are often substantially correlated with some of the geodetic parameters as they do not take into account the physical processes causing those accelerations and a large number of such parameters tends to weaken the solution (Sośnica et al. 2014; Montenbruck et al. 2015).

The LAG-related orbit modeling considered a spherically symmetric cannonball satellite and included solar radiation pressure (SRP) and Earth radiation pressure coefficients set to 1.13 and 1.0, respectively. For the GAL satellites, we applied a hybrid model, namely a simple (GPS-applicable) box-wing model (Milani et al. 1988) and the five-parameter Empirical CODE Orbit Model (ECOM, Beutler et al. 1994), referred throughout the text to as ECOM-1. The same set of empirical accelerations was used in the LAG case. In view of the prospective co-location missions at LAG-like altitudes, where satellites are equipped with multiple space-geodetic instruments and attitude control systems, the usage of empirical accelerations expressed in a Sun-oriented frame, as ECOM-1 or its updated version (ECOM-2, Arnold et al. 2015), are preferable. Such a frame is, in general, suitable for proper treatment of perturbations induced by direct solar radiation pressure and acting upon box-wing-type satellites (Meindl et al. 2013; Montenbruck et al. 2015)

We considered only 3-day arcs in order to investigate the feasibility and assess the performance of the proposed concept. There is definitely no standard solution length to be applied, and its selection depends upon many factors such as the type and quantity of parameters to estimate or the satellite orbital height. Solutions with longer observation periods (5-day solutions, 7-day solutions) would result in an increased number of satellite observations, satellite revolutions and an improved observation geometry, helping to decorrelate parameters of different nature (Haines et al. 2015). In some cases, however, the extended observation arcs could degrade the orbit parameters due to the insufficient modeling of some external forces, which may change throughout the considered periods.

Results

The conduced simulations allow to calculate repeatabilities in the form of Weighted Root-Mean-Square errors (WRMS) for each of the parameters of interest. The obtained estimates can be studied concerning both their uncertainty, i.e., precision, and their correctness, namely accuracy. Similarly to the satellite orbits (see Sect. 3.3), the scatter of values around the mean from all Monte Carlo runs can be interpreted as an empirically determined precision of the investigated parameters, whereas the scatter around an a priori value, treated in the simulation environment as truth, can be interpreted as the parameter accuracy. One expects that both statistical measures should depend on the observing geometry, the number of estimated parameters and the precision of the simulated observations.

Orbit quality

Among other target parameters, each simulation run resulted in a state vector (position and velocity) per satellite. That information was used subsequently to evaluate the position of satellites with a 5-min resolution for the 3-day observation period (see Sect. 3.3) and the corresponding location-dependent position scatter (location-dependent WRMS values) was then used to calculate the mean position scatter for each satellite observation precision level. For a 3D orbit quality, such quantity is referred throughout the text to as $\text {WRMS}_{O3D}$. A general relation between the quantity of satellite observations, the number of satellites, the analysis option and the quality of the derived orbits can be inferred from Table 3 for a case where the satellite observation precision is set to 14.1 mm (47 ps). An example of the dependence of the satellite observation precision on the quality of the derived orbits from QS-OS is shown in Fig. 3 for LAG and GAL satellites.

Table 3 Legacy VLBI results: quality of orbit solutions in terms of the mean three-dimensional position scatter ($\text {WRMS}_{O3D}$) for each of the analysis options and the precision of satellite observations set to 14.1 mm (47 ps)

Fig. 3

Legacy VLBI results: Precision (P) and accuracy (A) of the determined orbits as a function of the satellite observation precision. The WRMS values were calculated for the along-track, cross-track and radial components and also expressed as a 3D orbit scatter ($\text {WRMS}_{O3D}$). The results are shown for the QS-OS analysis option including schedules with (a–d) LAG and (e–h) GAL satellites (only E02 and E12). For both satellite constellations, the accuracy curves are in close vicinity to the precision curves, making them barely distinguishable in the plots

For GAL satellites, a clear dependence is visible between the orbit quality and both the number of the observed satellites and the number of satellite observations. The orbit precision in this case ranges between 3.9 and 9.6 cm, with an average value of 6.3 cm. In terms of the accuracy, 6.3 cm characterizes an average quality of the derived GAL orbits. The number of observations and the observation density do not affect significantly POD of LAG satellites in most of the cases, as illustrated with the use of the LAG-S2-R4 and LAG-S2-R8 schedules. The latter observing geometry has more than a factor of two less satellite observations, but this does not correspond directly to the lower orbit quality for both satellites. The value of 2.0 cm characterizes a general orbit precision for the CONT17 network and LAG satellites. The same applies to the general orbit accuracy.

An increased observation density and an enhanced satellite observation precision generally lead to the improved orbit solutions (precision and accuracy), as shown in Fig. 3. In the case of low-quality satellite data, a clear relation between the baseline noise and the WRMS values is present. The same does not hold for observations with the precision better than 20 mm as WRMS values do not decrease for lower satellite observation noise levels. This is related to the major error sources dominating the noise budget in that case (see Sect. 5).

Since the WRMS statistics were calculated, at the first place, for satellite positions evaluated every 5 min, it is also possible to investigate the obtained orbit scatter with regard to the location of the used satellites. The relation between $\text {WRMS}_{O3D}$ and the satellite location is illustrated in Fig. 4 for LAGEOS-1 and a set of GAL satellites. Based upon the results shown in Fig. 4, one can indicate few factors impacting the quality of the derived orbits. The $\text {WRMS}_{O3D}$ values are smaller for satellite-track segments containing more observations. This is related to the replacement strategy used in this study, but also to the distribution of the participating stations on the globe. Therefore, areas with the absence of VLBI stations, or characterized by a lack of mutual visibility to satellites, impact negatively the average orbit quality, represented as $\text {WRMS}_{O3D}$ values in Table 3. This is clearly visible in the southern hemisphere where the orbit solutions are worse by at least a factor of two for both satellite types, compared to the northern hemisphere.

Fig. 4

Legacy VLBI results: location-dependent $\text {WRMS}_{O3D}$ (precision) of the orbit solutions for a LAGEOS-1 from LAG-S2-R4 and b GAL (E02, E04, E12) satellites from GAL-S3-R4. The locations of satellites at observation epochs are represented by small dots. The large red dots represent the stations of the CONT17 network. The results are shown for the QS-OS analysis option and the satellite observation precision set to 14.1 mm (47 ps)

Station positions

Combination of quasar and satellite observations allows to investigate the impact of the latter on the estimation of station positions. WRMS values were evaluated for both the reference and LAG/GAL schedules from all analysis options in which the satellite observation precision was set to 14.1 mm. This allows to assess the impact of satellite geometry on the estimated coordinates as the quality of satellite and quasar observations is similar in this case. The corresponding accuracy measure for individual stations, and expressed in the form of $\text {WRMS}_{3D}$, is shown in Fig. 5 for each of the employed analysis options.

Observations of satellites should in principle help in separating troposphere delays from station heights, since such targets cross the local skies relatively fast. For the considered precision of satellite observations and the applied replacement strategy, however, the satellite geometry improves the station position estimates only marginally, regardless of the applied analysis option. A general tendency is visible for stations located in Europe and South Africa, where satellite observations and the orbit determination process itself do not degrade largely the quality of the estimated station positions. In absolute terms, the maximum improvement for this group of stations, and both satellite constellations, reaches approximately 0.5 mm. For other stations, located in the southern hemisphere, one can notice in most cases a degradation of the station position estimates in the presence of satellite observations, with a similar effect of analysis options including orbit determination or when the orbits are fixed to their a priori values.

Similarly to the derived orbits, the relation between the varying quality of satellite observations and the determined station positions can be investigated. This is illustrated in Fig. 6 by means of the 3D position accuracy ($\text {WRMS}_{3D}$) and with the use of the reference solutions. The inclusion of satellite observations with a precision of not better than 20 mm does not seem to have a negative impact on the determined station positions, compared to the reference solutions. For very precise satellite observations and the standard quality of quasar observations (14.1 mm), however, an overall degradation, w.r.t. the reference solutions, of the station position estimates, can be noticed for schedules including either LAG or GAL satellites, on average reaching almost a factor of two for an observation precision of 1.4 mm. In this case, satellite observations dominate the solution and thus degrade in a significant manner parameters relying on a good observing geometry (see Sect. 5).

Fig. 5

Legacy VLBI results: $\text {WRMS}_{3D}$ (accuracy) of the station positions derived from a, b LAG and c–f GAL schedules. The results are shown for quasar and satellite observation precision set to 14.1 mm (47 ps)

Fig. 6

Legacy VLBI results: $\text {WRMS}_{3D}$ (accuracy) of the station positions derived from a–d LAG and e–l GAL schedules. The results shown are based upon all stations (mean values) and the minimum and maximum values of $\text {WRMS}_{3D}$ (per station) found for each noise level. All schedules are simulated with the same observation precision for quasars (14.1 mm)

Earth rotation parameters

Earth rotation parameters are products provided by geodetic VLBI on a daily basis (Nothnagel et al. 2017), and it is rather important to examine how the performed combination of quasar and satellite observations impacts ERP. This is illustrated in Fig. 7, where WRMS values (accuracy) of the derived polar motion (${x}_\mathrm{p}$, ${y}_\mathrm{p}$) and $\text {UT1-UTC}$ from schedules including LAG and GAL satellites are shown in dependence on the satellite observation precision and along with the corresponding ERP estimates from the reference solutions ($\textit{Q-SE}$) containing only quasar observations.

Fig. 7

Legacy VLBI results: WRMS (accuracy) of polar motion (${x}_\mathrm{p}$, ${y}_\mathrm{p}$) and $\text {UT1-UTC}$ from a, b LAG-type and c–f GAL-type schedules. For each schedule type, the color-coded (blue, green, orange) values correspond to ERP derived from the related reference (Q-SE) solution (the same geometry, but without satellite observations). All schedules were processed with the quasar observation precision set to 14.1 mm

As in the case of the estimated station positions, a similar pattern in the results is present, where more precise satellite observations degrade the quality of the derived ERP. This effect is more pronounced for GAL satellites and when more satellite observations are used in the combination, as visible in the case of the GAL-S3-R4 and GAL-S6-R4 schedules. Regardless of the satellite type, for the cases where satellite observation precision is worse than 20 mm, the identified decrease in accuracy of the ERP estimates is rather small, w.r.t. the values from the reference solutions, as the satellite observations do not dominate the solution anymore. Apart from the sky-coverage issue, the mutual visibility constraints emerging from observations of LAG or GAL satellites as well as the applied replacement strategy also contribute to less optimal observing geometries in terms of the ERP estimation. This is noticeable especially in the case of very precise satellite observations and when their number increases, such as for the R4-type schedules. Although the schedules with satellites contain in total more observations, they were modified in a non-optimal fashion, i.e., with no consideration on the orientation of the baselines nor their lengths and thus may not improve the ERP estimates (see Sect. 5).

Geocenter

Geocenter offsets ($\text {X}_{GC}$,$\text {Y}_{GC}$, $\text {Z}_{GC}$) were estimated both in the QS-OSG and QS-OSEG analysis options. The WRMS (precision and accuracy) of the derived geocenter offsets for simulations including LAG and GAL satellites are shown in Fig. 8 on the basis of the CONT17 network and in dependence on the satellite observation precision.

Fig. 8

Legacy VLBI results: WRMS (precision (P) and accuracy (A)) of the geocenter offsets from the schedules including a, b LAG and c–f GAL satellites. The results are shown for different satellite observation precision levels. The quasar observation precision was set to 14.1 mm for all of the analysed schedules

As one would expect, more precise satellite observations provide better geocenter offsets, regardless of the satellite type. On the other hand, the increased number of satellite observations does not improve the precision/accuracy of these parameters. The GAL-type schedules and CONT17 network leads to the precision of the geocenter offsets on the order of 2–4 cm, for almost noise-free satellite observations. In the case of LAG satellites and the satellite precision better than 20 mm, an improvement w.r.t. the Galileo-derived geocenter can be noticed, and the precision for all three components settles at approximately 9 mm. Similarly to satellite orbits, a linear dependence of the observation precision on the obtained WRMS values cannot be noticed, and this result has to be interpreted in relation to the residual effects originating from three major error sources, as further explained in Sect. 5. In terms of the accuracy of the LAG-derived and Galileo-derived geocenter offsets, an identical pattern, coinciding with the results for the precision of those parameters, for all geocenter components can be noticed and no major biases can be identified.

VGOS network

The simulations concerning VGOS-type schedules can be studied accordingly. In this case, however, we consider only GAL satellites (using $\textit{GAL-S6-R8}$) and utilize three satellite observation precision levels, namely 1.4 mm, 14.1 mm and 138.6 mm. The corresponding results are summarized in Table 4 in the form of $\text {WRMS}_{O3D}$ concerning the orbit solutions and by means of $\text {WRMS}$ calculated for each geocenter components (offsets). The relation between the $\text {WRMS}_{O3D}$ and the satellite location is shown in Fig. 9 for a set of three Galileo satellites and the satellite observation precision of 14.1 mm.

Table 4 VGOS results: $\text {WRMS}_{O3D}$ of the orbit solutions and $\text {WRMS}$ of the geocenter offsets for the GAL-S6-R8-VGOS schedule

Fig. 9

VGOS results: location-dependent $\text {WRMS}_{O3D}$ (precision) of the orbit solutions for GAL (E02, E04 and E12) satellites from the GAL-S6-R8-VGOS schedule and the QS-OS analysis option. The locations of satellites at observation epochs are represented by small dots. The large yellow dots represent VGOS stations used in this study. The results are shown for the satellite observation precision set to 14.1 mm

Observations based upon the GAL-S6-R8-VGOS schedule lead to the improved orbit solutions w.r.t. the corresponding results derived from the GAL-S6-R8 schedule and when comparing the results for the satellite observation precision of 14.1 mm. With regard to the QS-OS analysis option, the improvement reaches on average 80% in terms of the orbit precision and accuracy. The homogeneous network provides in this case proper observation conditions for POD. The $\text {WRMS}_{O3D}$ are in most parts of the globe similar with exception that, for satellite-track segments with no observations, this quantity tends to be higher than the average $\text {WRMS}_{O3D}$, as visible for one of the tracks located between South America and Australia. However, this issue is related now only to the replacement strategy applied in our study and its deficiencies are expected to be overcome when sophisticated scheduling strategies are considered. The derived geocenter offsets also benefit from the observations in the VGOS era as the parameter precision and accuracy are improved by at least 70% for all of its components, compared to the results based upon GAL-S6-R8 and satellite observation precision of 14.1 mm. In addition, no visible biases are present for these parameters. However, the $\text {Z}_{GC}$ precision/accuracy is still visibly worse than for the other two components as the same GAL orbit parameterization was used for the VGOS-type schedule. This issue is discussed in more detail in Sect. 5.

Similarly to the CONT17 network, the impact of additional satellite observations on the estimated station positions and ERP can be investigated in this case. The corresponding results for VGOS-type observations and GAL-S6-R8-VGOS are summarized in Fig. 10. In the case of the employed schedule, the obtained results indicate that the satellite observations do not negatively impact the determination of station positions and ERP, also in the case of the most precise satellite observations (1.4 mm). The lack of the negative impact can be associated with the ratio of satellite to quasar observations as well as the similar measurement precision set for both observation types. This is further discussed in Sect. 5.

Discussion

The results of our extensive Monte Carlo simulations indicate that POD of GAL or LAG-like satellites would be possible even for severe mutual-visibility constraints resulting from the differential nature of VLBI and orbital heights of the considered satellites. If geodetic VLBI observations of GAL satellites could reach a few-centimeter-level precision with today’s legacy systems, one could compute dynamic orbit solutions which are characterized on average by a 3D orbit precision of up to 10 cm. This is approximately the same level of quality as present in GNSS-only or SLR-only solutions, with the 3D orbit precision for GAL between 14 cm and 36 cm (Hackel et al. 2015; Montenbruck et al. 2017; Bury et al. 2019). Concerning the GNSS technique, a good quality of orbit products is achieved in the case of the Global Positioning System (GPS), where the 3D orbit precision is well below 10 cm (Montenbruck et al. 2017). This is possible due to a rather simple satellite shape and greater mass, compared to GAL satellites (Montenbruck et al. 2015), both factors facilitating handling of non-gravitational perturbing forces acting upon GPS satellites. In terms of the prospective VLBI-derived GAL orbits, the most encouraging are therefore results for VGOS-type observations, where GAL orbit solutions are improved and might reach few-centimeter-level precision. For schedules including LAG satellites, the obtained orbit precision is on the few-centimeter-level, which is also comparable to the orbits determined with SLR (Appleby et al. 2016; Pearlman et al. 2019). However, the direct comparison does not hold in the LAG case as different assumptions were made in our study concerning the orbit parameterization.

Fig. 10

VGOS results: the quality of ERP and station positions based upon the GAL-S6-R8-VGOS schedule: a, b$\text {WRMS}_{3D}$ (accuracy) of station positions; c WRMS (accuracy) of polar motion (${x}_\mathrm{p}$, ${y}_\mathrm{p}$) and $\text {UT1-UTC}$. The color-coded values correspond to WRMS derived from the reference (Q-S and Q-SE) solutions. As shown, different analysis options provide very similar results in terms of the ERP and station positions, making them indistinguishable in the plots

For satellite observations with a precision better than about 20 mm and a CONT17-type network, one can identify a settling of the WRMS values of the orbit solutions (and geocenter offsets) for schedules including LAG or GAL satellites. This implies that the observation precision is not the only limiting factor. In the presence of almost perfect satellite observations, the target parameter estimation is driven by a much lower quality of quasar observations (14.1 mm) and the residual contributions of the turbulent troposphere and station clocks, both still present in the solution (Klopotek et al. 2018). Reducing contributions from the station clocks and diminishing troposphere effects could enhance the solution. This is confirmed with the simulations for the VGOS era, where the orbit quality is significantly, but not exclusively, improved due to better handling of major error sources and a magnitude lower (1.44 mm) quasar observation noise. The major factor in this case is also the homogeneous observing network resulting in satellite observations that are better distributed over the entire orbital arcs. In the case of the CONT17 station geometry, mainly the northern-hemisphere parts of the orbits are observed resulting in unevenly distributed observations over the arc. This in turn could lead to orbit deformation or shifting. As a consequence, these orbit-related effects impact negatively the station coordinates for analysis options including POD.

The quality of the geocenter estimates should be considered as a combined effect of the sensitivity of geodetic VLBI to geocenter motion, network geometry, satellite orbit type, orbit modeling accuracy, residual troposphere and station clock effects, and finally the precision of satellite observations. As shown in this study, legacy geodetic VLBI applied to geocenter estimation from observations of LAGEOS-1/-2 satellites would perform not as well as SLR (Sośnica et al. 2014), with the precision of geocenter offsets on the order of up to a single centimeter, for the considered satellite observation precision of better than 20 mm. Accordingly, the precision of those components is at least a factor of two worse for Galileo-derived offsets. For GAL satellites, $\text {Z}_{GC}$ is always recovered with less precision/accuracy than the remaining ($\text {X}_{GC}$, $\text {Y}_{GC}$) components. This stems from the orbit characteristics (and modeling) of those satellites and can be connected to the orbit inclination, i.e., a lack of satellites on polar orbits (Sośnica et al. 2014).

Fig. 11

Correlations between satellite state vectors (denoted as X, Y, Z and VX, VY, VZ), estimated empirical accelerations (denoted as D0, Y0, B0, Bc and Bs) and geocenter offsets (denoted as XGC, YGC, ZGC) from 3-day GAL-S3-R4-type (lower triangle) and LAG-S2-R4-type (upper triangle) schedules (for the QS-OSEG analysis option) for CONT17 (legacy VLBI)

The question that still remains is whether the obtained quality of geocenter estimates would be sufficient to detect geocenter motion. The situation definitely improves in the case of observations in the VGOS era, where geocenter components (not biased here by the inhomogenous station distribution) can be retrieved, for the most precise satellite observations, with the accuracy on the level of approximately 4 and 7 mm for equatorial ($\text {X}_{GC}$, $\text {Y}_{GC}$) and $\text {Z}_{GC}$ components, respectively. Although the geocenter signal considered on an annual basis is smaller (Collilieux et al. 2009; Wu et al. 2012; Sośnica et al. 2014), the VGOS-derived geocenter estimates are close to detection of that phenomenon and further improvements may be expected, e.g., with more sophisticated scheduling schemes, utilization of satellites at lower altitudes and more optimal orbital inclinations for that purpose. Incorporation of an independent data set, as VGOS-derived time series from observations of LEO or MEO satellites, would create an opportunity to enhance the geocenter motion estimates and contribute to the ITRF origin realization while separating various technique-specific issues from geophysical signals (Collilieux et al. 2009; Wu et al. 2012; Meindl et al. 2013; Riddell et al. 2017; Couhert et al. 2018).

The Galileo-derived geocenter motion for all space-geodetic techniques is rather problematic due to the characteristics of the GNSS orbits and the applied orbit parameterization (Meindl et al. 2013; Thaller et al. 2014; Meindl et al. 2015). The reduced sensitivity due to the higher orbits and less revolutions, compared to LEO or LAG satellites, further degrades the retrieval of that parameter. For GAL satellites, the estimated constant accelerations in the direction toward Sun ($D_0$) and Bc, Bs parameters are highly correlated with $\text {Z}_{GC}$. Such problem does not exist for LAG satellites due to the different orbit characteristics of those targets and much smaller (direct and indirect) SRP effects (Meindl et al. 2013). However, SRP-induced effects are still (theoretically) absorbed in our case by the constant and once-per-revolution sine and cosine terms. Therefore, $\text {Z}_{GC}$ from observations of LAG satellites is much more accurate than the corresponding Galileo-derived quantity. An example of correlations between the satellite-based parameters and geocenter offsets is shown in Fig. 11 for two of our schedules and the applied orbit parameterization. Concluding, observations of LAG-like satellites benefit geocenter solutions, an improved SRP modeling becomes essential for GNSS-like orbits (and satellite shapes) observed by all space-geodetic techniques, and consideration of polar orbits could be useful for an improved $\text {Z}_{GC}$ estimation.

The combination of satellite and quasar observations seems to be a reasonable solution when estimating positions of VLBI telescopes, especially for poor satellite geometries. The latter should be understood in this context as a low number of satellite passes and non-varying satellite tracks over local skies of the participating stations. This kind of geometry prevents from reliable estimation (reducing correlations) of troposphere parameters, station clocks and positions of VLBI antennas (Herring 1986; Rothacher 2002). In terms of the sky coverage, quasar observations outperformed observations of both chosen satellite constellations and allowed to sample the sky more uniformly. An example of the distribution of satellite and quasar observations at local skies obtained in our case is shown in Fig. 12 for both GAL-type and LAG-type schedules.

Fig. 12

Distribution of satellite and quasar observations on local skies shown for four stations and based on 3-day a LAG-S2-R4 and bGAL-S6-R4 schedules for CONT17 (legacy VLBI)

A full multi-GNSS satellite constellation without quasars could in principle provide proper observations for resolving troposphere parameters and estimating station positions. However, even a 3-day quasar-only solution and a considerable VLBI network, as shown in this study (Fig. 6), may outperform sophisticated satellite-only scheduling approaches characterized by homogeneous networks and longer observation periods (Plank 2013; Plank et al. 2016). It is also unclear whether satellite-only schedules would be suitable for handling technique-specific effects (and satellite-dependent errors) or simultaneous POD and ERP estimation (Plank et al. 2016) as the quality of ERP is also related to the separation between two stations forming a baseline (Nothnagel and Schnell 2008; Nothnagel et al. 2017). In our case, the satellite scans, that replaced the quasar scans, may contain shorter baselines. This negatively impacts ERP estimation as the solution becomes less sensitive to those parameters, compared to the reference schedules with very long (north–south, east–west) baselines. Although not shown here, the same in principle can occur in the case of EOP estimation. The following aspects are rather important and therefore should be taken into account when scheduling both quasar and satellite observations for the estimation of global geodetic parameters. The accuracy of the derived polar motion depends also upon the stations (geometry) used in the NNT/NNR constraints. Therefore, an alteration of the later can result in an improved/decreased estimation of polar motion. Care has to be taken in this matter as an inclusion of poorly determined stations in the NNT/NNR constraints leads to the distribution of the related station-position uncertainties into the whole network. In our case, this corresponds to CONT17-related solutions in the presence of almost noise-free satellite observations and stations that are characterized by a low number of satellite observations (see, e.g., Männel 2016). In addition, the analysis options QS-S, QS-SE, QS-OS, QS-OSE were obtained also with the use of the NNT constraint, leading to over-constrained solutions that may be suboptimal. Over-constraining results in a distortion of the network and allows less freedom to the solution. This fact should be also considered when interpreting the results concerning the estimated station positions.

For very precise satellite observations (with an observation precision better than 20 mm), a degradation in the quality of station positions and ERP is noticeable, including to some extent also the estimated orbits. The aforementioned effect of the poor satellite geometry (and the station definition for the datum constraints) is amplified in this case as the solutions are dominated by the satellite observations due to large weights imposed on them (up to a factor of one hundred between the two observation types) in the adjustment process. This negatively impacts the estimation of parameters such as station clocks, ZWD and troposphere gradients. In consequence, the station positions and ERP estimates are also degraded. The same does not hold for observations in the VGOS era where the noise level of 1.4 mm was used to reflect the quality of quasar observations as well as the number of quasar observations in the investigated schedule is more than 20 times larger than the number of satellite observations.

In this study, station-dependent clock biases were estimated once per 3-day arcs. Consideration of this parameter is inevitable in reality as some timing problems, or instrumental (station-based and satellite-based) issues may occur, or only single-frequency data are used (Himwich et al. 2017; Hellerschmied et al. 2018; Anderson et al. 2018; Klopotek et al. 2019). In conventional geodetic VLBI, the size and variation of the absolute (reference-formatter) time offsets directly impact the UT1 estimates (Hobiger et al. 2009) and are significant for 24-h VLBI experiments where long baselines are employed (Himwich et al. 2017). If valid also for satellite observations, the prospective time offset at VLBI stations could also introduce position offsets in the along-track direction (Anderson et al. 2018). Nevertheless, this problem should be addressed with the use of empirical accelerations and station clock biases estimated in our case, which should account for an unknown time offset between the VLBI frame and the frame defined by the observed spacecrafts (and their clocks). As this unknown offset affects both quasar and satellite observations, a proper strategy for handling the reference-formatter time offsets needs to be considered anyway to obtain utmost accurate estimates of the Earth’s rotation angle (Hobiger et al. 2009; Himwich et al. 2017). An attractive option would be to encode information on the spacecraft-clock time in the signal, which could be received by a VLBI station for time-of-flight measurements (Anderson et al. 2018). The latter could be of benefit for obtaining the missing information on formatter-clock offsets and improving UT1 products. This is, however, associated with significantly higher costs related to the transmitter, compared to random noise present in standard geodetic VLBI.

Similarly to SLR stations, VLBI telescopes can observe only one target at a time. The 3-day solutions were sufficient in our study to determine reliable orbits of the considered satellites. In the case of SLR, the same arc lengths may be insufficient and longer observation periods are preferred when tracking multiple satellites (Bury et al. 2019). Although most SLR stations can operate in both day and night time (Sośnica et al. 2015; Pearlman et al. 2019), this space-geodetic technique is highly weather dependent. On the contrary, VLBI observations can be performed under any (to a reasonable degree) weather conditions and regardless of the time of the day. Hence, much more satellite observations per station can be in principle obtained within 24-h sessions, compared to SLR (Bury et al. 2019; Pearlman et al. 2019; Sośnica et al. 2019). This could be advantageous to geodetic VLBI considering also the proposed approach in which VLBI stations could track satellites and quasars within the same 24-h experiments and with almost no additional organizational effort. However, SLR observations are affected by less errors, compared to geodetic VLBI or GNSS. Laser measurements are free from ionosphere effects and significant contribution of the wet part of the tropospheric delay (almost negligible) as well as not affected by other signal characteristics (phase ambiguities, satellite clocks, satellite antenna phase-center variations). The remaining effects can be corrected rather well (range biases). Therefore, SLR will continuously serve as an independent and important validation tool concerning orbits derived from space-geodetic techniques operating with microwave-based measurements.

Summary and conclusions

The possibility of employing geodetic VLBI for precise orbit determination of Earth-orbiting satellites was investigated with the use of extensive Monte Carlo simulations in which quasar observations and observations of either LAGEOS-1/-2 or a set of Galileo satellites were combined on the observation level in 3-day solutions. The performed simulations reflected close-to-reality scenarios and, apart from the simulated measurement noise, they included realistic stochastic models related to troposphere and station clocks as well as considered different satellite observation precision levels. The derived orbit solutions were investigated both in terms of their precision and accuracy. Moreover, we examined the impact of this novel concept on classical geodetic parameters such as VLBI station positions and Earth rotation parameters. We also studied the potential of geodetic VLBI for determining geocenter offsets from either of the used satellite constellations.

In the case of LAGEOS-1/-2 satellites, the obtained orbits are characterized by the precision of approximately 2.0 cm for CONT17-type schedules. The same quantity for Galileo orbits reached on average 6.3 cm for the group of satellites used in this study (either one or two satellites per orbital plane within the same schedule). A major factor affecting the orbit solutions is the characteristics of an observing network, where stations in the most optimal case are distributed homogeneously on the globe. This benefits precise determination of satellite orbits, geocenter offset estimates as well as the standard geodetic VLBI observations. The effect of a non-optimal station distribution is clearly visible in our study, on the basis of the CONT17 network, for both LAGEOS-1/-2 and Galileo satellites, where the precision of the orbit solutions is diminished by almost a factor of two for the areas where no stations are present and thus no observations are available. With simulated legacy VLBI observations to LAGEOS-like and a set of chosen Galileo satellites, the obtained precision of geocenter offsets was only on the order of a single centimeter and a few centimeters, respectively. Unfortunately, this is insufficient for detection of geocenter motion as this phenomenon has an annual signal that is on the order of few millimeters (Wu et al. 2017). In addition, the Z geocenter offset cannot be derived reliably in this case due to deficiencies in the modeling related to solar radiation pressure. However, it was also shown that satellite observations in the VGOS era provide a noticeable improvement of both the orbit solutions and the geocenter components (nearly reaching the detection limit of geocenter motion) due to the enhanced observation density, homogeneous station distribution and a factor of ten more precise quasar observations. This results in a good observation geometry for POD and significantly better handling of major error sources affecting geodetic VLBI observations at large.

A simplified scheduling strategy was applied in our study in order to include satellite observations into the employed schedules. In the proposed concept, scheduling of satellite observations was restricted only by the common-visibility criterion. This is a non-optimal approach and few additional factors need to be considered such as the baseline length or its orientation. Nevertheless, it was shown that the combination of quasar and satellite observations could allow theoretically for simultaneous estimation of ERP (polar motion and UT1-UTC) along with geocenter offsets, VLBI station positions and satellite orbits. Compared to the reference solution including only quasar observations, ERP and station positions, derived based on the CONT17 network, were degraded only slightly for satellite observation precision levels not better than the precision level of the quasar observations. No negative impact was noticeable, however, in the case of satellite observations and the VGOS-type network. As VLBI telescopes can track only one target at a time, the inclusion of satellite observations is a trade-off between the number of the tracked satellite passes and the maximum number of the tracked satellites on one side and the baseline lengths and their orientation on the other. Combination of satellite and quasar observations could be an optimal solution for estimation of target parameters as the quality of the latter is susceptible to poor satellite geometries. Therefore, the presented results highlight the importance of optimized scheduling of prospective sessions comprising both observation types. This aspect was, however, not investigated in this study and needs to be addressed in the future.

Geodetic VLBI is the only technique that provides the full set of EOP (polar motion, UT1, celestial pole offsets), contributes to the ITRF scale, and uniquely realizes the International Celestial Reference System, as opposed to the satellite-based techniques, i.e., SLR, GNSS and DORIS. The results presented in this study address several important questions concerning the usefulness of geodetic VLBI for POD of Earth-orbiting satellites. As shown throughout the text, observations of satellites with geodetic VLBI could extent the field of its research with novel and important applications. The discussed concept poses a very attractive way of directly relating the celestial reference frame, TRF, EOP and satellite orbits in a single framework for a consistent set of global geodetic products, besides the aspect of the combination of space-geodetic techniques in space. In addition, antenna-related effects, which are of major importance in GNSS (multi-path, antenna phase center offsets and the related variations), are not of concern at VLBI stations due to the use of highly directive parabolic antennas. This makes this space-geodetic technique also an attractive tool for an inter-technique orbit validation. However, a number of technical hurdles need to be addressed prior one could consider testing such a novel concept on global scales. Any related efforts should be also discussed with the GNSS, VLBI and GGOS communities in order to make the most out of the concept of VLBI and satellite observations. Dedicated transmitters sending VGOS-compliant broadband signals and located on boards of LEO, GNSS or co-location satellites are in favor as a network of small, fast-slewing VGOS antennas is more suitable for satellite observations than the current VLBI system. If successful, geodetic VLBI could be another space-geodetic technique with the capability of providing independent orbit solutions with high accuracy and also with the potential of contributing (to a certain extent) to the ITRF origin. Observations of quasars and carefully chosen satellites within the same sessions would undeniably bring new challenges, but could also provide the geodetic community with a great opportunity of redefining the role of VLBI in space geodesy.