Coupled topology and shape optimization using an embedding domain discretization method

Abstract

Density-based topology optimization and node-based shape optimization are often used sequentially to generate production-ready designs. In this work, we address the challenge to couple density-based topology optimization and node-based shape optimization into a single optimization problem by using an embedding domain discretization technique. In our approach, a variable shape is explicitly represented by the boundary of an embedded body. Furthermore, the embedding domain in form of a structured mesh allows us to introduce a variable, pseudo-density field. In this way, we attempt to bring the advantages of both topology and shape optimization methods together and to provide an efficient way to design fine-tuned structures without predefined topological features.

1 Introduction

Combining shape and topology optimization is favourable due to their dissimilar but complementary nature. The inherent limitations of the first method are overcome by the second method and vice versa. On the one hand, density-based topology optimization is capable of producing complex structures, but fails to represent the component boundary exactly. On the other hand, shape optimization represents the component boundary exactly, but it does not support topological changes and it is not well suited for large design changes. A coupling of topology and shape optimization is possible when an embedding domain discretization is employed. The embedding domain discretization method allows us to incorporate both the density and nodal design variables. The structured mesh that serves as a computational (embedding) domain is assigned with pseudo-densities, whereas the vertices of the discretized boundary of the embedded body serve as nodal design variables.

Shape optimization in its original form treats the finite element nodes directly as design variables (Zienkiewicz 1973). Another approach is to use a parametrized boundary description to improve the smoothness of the final design. Some of the approaches involve using cubic spline functions (Luchi et al. 1980) or B-spline polynomials (Braibant and Fleury 1984) which are used for CAD parametrization. To improve the smoothness of the optimized geometries and the convergence of the optimization algorithms, regularization techniques are employed. Some of these techniques include sensitivity filtering (Bletzinger 2014), sensitivity weighting (normalization) (Kiendl et al. 2014; Wang et al. 2017) or the traction method (Azegami and Wu 1996; Azegami and Takeuchi 2006). The latter treats the sensitivity vector as an external force in a fictitious boundary value problem (BVP). The solution of such BVP yields a smooth, mesh-independent update vector which also handles the update of internal nodes. The traction method is exceptionally attractive due to its flexibility, i.e. the formulation of the fictitious BVP can be modified to obtain any desired smoothing behaviour. Therefore, it is adapted for the shape optimization used in this work. Thanks to these developments, node-based shape optimization is capable of generating smooth, mesh-independent designs. Therefore, it lends itself as a good choice for optimization problems requiring an exact boundary representation. Despite all the improved methodology in shape optimization, its application is still usually limited to problems involving small design changes, the so-called fine tuning steps.

As opposed to node-based shape optimization, topology optimization offers almost unlimited flexibility in designing geometrically complex structures. Without doubt, the most extensive research was devoted to the density method introduced by Bendsøe (1989). For the past three decades, density-based topology optimization has been continuously improved and it successfully found its way into a number of commercial software applications. For a detailed description of the method, we refer to the book by Bendsoe and Sigmund (2013) and the review article by Sigmund and Maute (2013), which also studies the similarities to other approaches in topology optimization. The density-based topology optimization is offered as an easy to implement, powerful tool, see for instance the work by Sigmund (2001a) and by Andreassen et al. (2011), in which compact topology optimization codes are outlined. An inherent challenge of density-based topology optimization is the placement of a crisp boundary based on the grey transition regions. There are a number of methods that treat this matter, including various projection and filtering techniques, see for instance the work by Wang et al. (2011). Additionally, regarding the accuracy of stress computation, De Troya and Tortorelli (2018) incorporated an adaptive mesh refinement scheme in topology optimization to increase the accuracy of stress computation. da Silva et al. (2019) achieved very good accuracy in stress computation using the robust approach, in which smoothed heaviside projection is employed to obtain three black and white density fields to consider manufacturing uncertainties.

In the context of this article, another approach worth discussing is the levet set method (LSM) (Allaire et al. 2002; Wang et al. 2003). Conceptually, LSM can be positioned between density-based topology optimization and node-based shape optimization as it offers a possibility to perform topological changes, namely it allows topological holes to be merged (however, it inherently does not support hole nucleation), and it provides an exact boundary representation. Nevertheless, as pointed out by Sigmund and Maute (2013), most approaches to the LSM, which use an ersatz material for the geometry mapping, do suffer from blurred (grey) boundary regions in the mechanical model, similar to the density-based topology optimization. In the approaches involving an ersatz material for the geometry mapping, the challenge of hole nucleation has been addressed e.g. in the works by Burger et al. (2004) and Allaire et al. (2005), in which topological derivatives (Sokolowski and Zochowski 1999) are incorporated and holes are systematically introduced. While these methods fully support topological changes, their boundary representation is not mechanically crisp due to the fact that mechanical models are based on a density distribution. An alternative formulation utilizing the LSM has been proposed by Yamada et al. (2010), which incorporates a fictitious interface energy. In this method, full topological flexibility is allowed, at the same time guaranteeing a mechanically crisp mechanical model by using a Heaviside function in the equilibrium equation.

One way to ensure a mechanically crisp boundary representation in LSM is to employ a conforming discretization (Ha and Cho 2008). However, this approach shares the drawbacks of node-based shape optimization due to the necessary mesh deformation during design updates. Therefore, to overcome the difficulties that arise with mesh deformation, more preferable approach is to incorporate immersed boundary techniques (IBTs). One of such technique is the extended finite element method (XFEM). The core concept in XFEM is the introduction of additional shape functions to handle discontinuities of the solution fields and their spatial gradients within the elements. XFEM in combination with LSM (LSM-XFEM) has been successfully applied in the works by Belytschko et al. (2003) for simple 2D elasticity, by Kreissl and Maute (2012) for fluid flow, by Villanueva and Maute (2014) for 3D elasticity and by Jenkins and Maute (2015) for fluid-structure interaction. Villanueva and Maute (2017) incorporate CutFEM for fluid flow problems, which is a combination of LSM, XFEM and face-oriented ghost penalty method. Moreover, stress-based topology optimization using LSM-XFEM has been introduced by Sharma and Maute (2018), in which an improved stress computation is carried out using an XFEM informed stabilization scheme. The LSM-XFEM for structural optimization proves to be a successful approach thanks to the mechanically exact representation of the boundary and the ability of hole elimination. Nevertheless, in the context of topological flexibility, LSM for structural optimization involving IBTs still exhibits the abrupt nature of hole nucleation schemes.

Due to the fact that each of the previously introduced methods exhibits a certain set of advantages and drawbacks, it is generally not simple to indicate a single method that is definitely superior over the others. Hence, there is recently a growing number of publications that treat ways to combine different approaches in structural optimization. Eschenauer et al. (1994) introduced a bubble method, in which shape optimization is followed by an introduction of a topological change in form of a spherical hole (bubble). The sequence is then repeated until a certain number of holes were introduced. This allows one to select an optimal topology out of a series of solutions with varying number of holes. Hassani et al. (2013) proposed a method, in which a shell structure is designed at the same time by density variables and, in the out of plane direction, by shape optimization. Christiansen et al. (2014) and Lian et al. (2017) presented a topology optimization using the Deformable Simplicial Complex (DSC) method which utilizes an unstructured mesh able to represent the boundary exactly. The optimization problem is driven by shape sensitivity information and the topological changes are performed using the topological derivatives. Riehl and Steinmann (2015) proposed a staggered approach in which optimization is driven concurrently by an element removal scheme and shape refinement steps. Andreasen et al. (2020) incorporated a cut element discretization used in LSM into a density-based optimization problem. The methodologies adopted in aforementioned contributions incorporate hole insertion schemes, which generally provide good results, and the boundary is represented exactly before and after the topological change. However, the hole insertion schemes often utilize simple spherical or mesh-dependent geometrical forms (single element removal or element patch removal) and exhibit a sudden solid-to-void transition. For further discussion about the hole insertion schemes and their comparison to the shape generation scheme used in this work, please consult Sect.  3.3.4. Alternatively, Nguyen et al. (2020) combined implicit and explicit discretizations to optimize the topology and generate a structure with crisp interfaces with adaptive mesh coarsening using the DSC method, respectively. In other words, this approach provides an automated transition step from topology to shape optimization.

In the following work, we exploit the shape optimization method using an embedding domain technique, introduced by Riehl and Steinmann (2017), and couple it with a density-based topology optimization. The optimization problem now operates on design variables adopted from both methods, namely the pseudo-densities of the inner elements and the degrees of freedom of the vertices of the embedded boundary. The key feature of the coupling is that both sets of design variables operate on the same mechanical model. This provides full flexibility to perform topological changes using the variable density in the embedding domain and at the same time, define a mechanically crisp interface by means of embedded boundary.

In this coupling method, there is no need to include a hole nucleation scheme, because the holes emerge naturally as a consequence of the pseudo-density updates. Instead, we provide a functionality that recognizes topological holes and introduces a variable shape. This approach is characterized by a significantly less discontinuous nature as compared to the standard hole nucleation schemes. Furthermore, by employing the embedding domain discretization, the shape updates only require the deformation of the embedded boundary as opposed to classical shape optimization using an explicit mesh, in which mesh movement strategies are necessary for the update of dependent nodes. Therefore, larger shape design changes are easy to handle and, consequently, the regularization is simpler. At the end of the optimization run, the design is in general free from grey regions and is defined by an exact boundary.

Thus, this article’s contribution to the field of structural optimization can be understood twofold. (1) It extends the shape optimization approach of Riehl and Steinmann (2017) by introducing density design variables into the embedding domain. This allows to perform topological changes in a flexible manner, characteristic to density-based topology optimization. (2) It enhances the density-based topology optimization with a d-1 dimensional (where d corresponds to the number of dimensions of the computational space) boundary mesh which serves as a variable, mechanically crisp boundary that clearly defines the shape of the optimized structure. Our method brings a number of advantages as compared to other methods of combining topology and shape optimization and, naturally, at the same time introduces a set of challenges, which are thoroughly studied in the scope of this article.

At this point we would like to remark that the purpose of this article is not to strive for an approach that is ultimately superior over the other, well-established methods, but rather to show that (1) an actual coupling of density-based topology optimization and node-based shape optimization is indeed possible and (2) it offers a certain set of advantages that makes this approach a reasonable choice for a number of engineering problems. Nonetheless, the scope of this article is limited to a number of simple, benchmark problems of linear elasticity.

2 Embedding Domain method

We consider a body ${\mathcal {B}}$, embedded into a d-dimensional domain $\Omega \subset {\mathbb {R}}^{d}$ such that ${\mathcal {B}}\subset \Omega$ (see Fig. 1). The boundary of ${\mathcal {B}}$ is defined by the Dirichlet portion $\Gamma ^D$ and the Neumann portion $\Gamma ^N$, such that $\Gamma ^D \cup \Gamma ^N = \Gamma$ and $\Gamma ^D \cap \Gamma ^N = \emptyset$.

Fig. 1

Embedded body

2.1 Physical problem

For the verification of the proposed coupling method by means of classical benchmark examples, we employ the BVP formulation based on linear isotropic elasticity, which is given by the following system of equations:

$$\begin{aligned} \begin{aligned} \text {div}\,\varvec{\sigma } + \varvec{b}&= 0 \\ \varvec{\sigma } \cdot \varvec{n}&= \bar{\varvec{t}} \ \ \ \text {on} \, \, \Gamma ^N \\ \varvec{u}&= \bar{\varvec{u}} \ \ \text {on} \, \, \Gamma ^D \\ \varvec{\sigma }&= {\mathbb {C}} : \varvec{\epsilon } \\ \varvec{\epsilon }&= \frac{1}{2} \left[ \nabla \varvec{u} + \nabla \varvec{u}^T \right] \end{aligned} \end{aligned},$$

(1)

where $\varvec{\sigma }$ is the Cauchy stress tensor, $\varvec{b}$ body forces, $\varvec{n}$ outward pointing normal to $\Gamma ^N$, $\bar{\varvec{t}}$ prescribed traction forces, $\varvec{u}$ the sought-after displacement vector, $\bar{\varvec{u}}$ imposed displacement and ${\mathbb {C}}$ the fourth-order elasticity tensor.

The weak form of equilibrium, adapted for the embedding domain method, is given by

$$\begin{aligned}&\int _{\Omega }\ \chi \left[ \varvec{\sigma } : \delta \varvec{\epsilon } \right] \text {\,dV}- \int _{\Omega }\ \chi \left[ \varvec{b} \cdot \delta \varvec{u} \right] \text {\,dV}\nonumber \\&\quad - \int _{\Gamma ^N}\ \bar{\varvec{t}} \cdot \delta \varvec{u} \text {\,dA}= 0 \end{aligned},$$

(2)

where $\chi$ is a characteristic function defined as

$$\begin{aligned} \chi = \chi \left( \varvec{x} \right) = {\left\{ \begin{array}{ll} 1,&{} \text {if } \varvec{x} \in {\mathcal {B}}\\ 0,&{} \text {if } \varvec{x} \in \Omega \setminus {\mathcal {B}}. \end{array}\right. } \end{aligned}$$

(3)

Equation (2) represents the principle of virtual work, given by

$$\begin{aligned} \delta W_{\chi } \left( \varvec{u}, \delta \varvec{u} \right) = a_{\chi } \left( \varvec{u}, \delta \varvec{u} \right) - l_{\chi } \left( \delta \varvec{u} \right) = 0 \end{aligned},$$

(4)

where $a_{\chi } \left( \varvec{u}, \delta \varvec{u} \right)$ is the bilinear form representing the variation of stored energy

$$\begin{aligned} a_{\chi } \left( \varvec{u}, \delta \varvec{u} \right) = \int _{\Omega }\ \chi \left[ \varvec{\sigma } : \delta \varvec{\epsilon } \right] \text {\,dV}\end{aligned},$$

(5)

and $l_{\chi } \left( \delta \varvec{u} \right)$ is the linear form representing the variation of external energy

$$\begin{aligned} l_{\chi } \left( \delta \varvec{u} \right) = \int _{\Omega }\ \chi \left[ \varvec{b} \cdot \delta \varvec{u} \right] \text {\,dV}+ \int _{\Gamma ^N}\ \bar{\varvec{t}} \cdot \delta \varvec{u} \text {\,dA}. \end{aligned}$$

(6)

The treatment of the Dirichlet boundary conditions cannot be realized directly due to the misalignment of the finite element nodes of $\Omega ^h$ with the boundary $\Gamma ^D$. Thus, we introduce a penalty functional to Eq. (4), so that the total (penalized) variation of the virtual work is given by

$$\begin{aligned} \delta W^p_{\chi } \left( \varvec{u}, \delta \varvec{u} \right) = \delta W_{\chi } \left( \varvec{u}, \delta \varvec{u} \right) + \beta \int _{\Gamma ^D}\ \left[ \varvec{u} - \bar{\varvec{u}} \right] \cdot \delta \varvec{u} \text {\,dA}\end{aligned},$$

(7)

where the penalty factor is in the range $\beta \in \left[ 10^{6}, 10^{9}\right] \times \Vert {\mathbb {C}} \Vert$.

Fig. 2

Embedding domain discretization

2.2 Discretization

In order to solve the equilibrium equation given by Eq. (2), we introduce an approximation of the embedding domain $\Omega$ by d dimensional finite elements

$$\begin{aligned} \Omega \approx \Omega ^h = \bigcup _{e = 1}^{n_e} \Omega _e. \end{aligned}$$

(8)

Consequently, we introduce a piecewise linear representation of the boundary $\Gamma \approx \Gamma ^h$ consisting of $d-1$ dimensional element-like segments $\Gamma ^s$, i.e. (1) line segments for $d=2$, (2) polygons for $d=3$

$$\begin{aligned} \Gamma \approx \Gamma ^h = \bigcup _{s = 1}^{n_s} \Gamma _s \end{aligned},$$

(9)

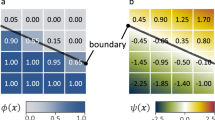
where $n_s$ corresponds to the number of segments that belong to $\Gamma ^h$. As depicted in Fig. 2a, the embedded boundary $\Gamma ^h$ assigns the finite elements $\Omega ^e$ of the embedding domain $\Omega ^h$ into three sets: inner elements $\Omega ^e_{\mathrm{in}}$ that are completely enclosed within the embedded body, boundary elements $\Omega ^e_{\mathrm{bnd}}$ collecting all the elements intersected by the embedded boundary, and outer elements $\Omega ^e_{\mathrm{out}}$ that lie outside of the embedded body.

Following the isoparametric concept, the geometry and the solution field are both interpolated using the same (vector-valued) shape functions

$$\begin{aligned} \varvec{X}^e\left( \varvec{\xi } \right)= & {} \sum _{n = 1}^{n_{\mathrm{dof}}} \varvec{N}^{(i)} \left( \varvec{\xi } \right) X^{(i)}, \end{aligned}$$

(10)

$$\begin{aligned} \varvec{u}^e\left( \varvec{\xi } \right)= & {} \sum _{n = 1}^{n_{\mathrm{dof}}} \varvec{N}^{(i)} \left( \varvec{\xi } \right) u^{(i)}. \end{aligned}$$

(11)

The system of equations resulting from discretization of Eq. (2) is then given by

$$\begin{aligned} \mathbf{K} \mathbf{u} ^h = \mathbf{f} , \end{aligned}$$

(12)

where the IJ-th contribution (capital letters I,J indicate global numbering of the DoFs) of the stiffness matrix $\mathbf{K}$ reads

(13)

and the force vector is given by

(14)

2.3 Integration schemes

Evaluation of the domain integrals in the inner elements $\Omega _{\mathrm{in}}$ incorporates the usual Gaussian quadrature rule as in the standard finite element discretization (see Fig. 2b). The elements that lie entirely outside of the embedded domain $\Omega _{\mathrm{out}}$ are excluded from the assembly routine and, thus, the size of the mechanical problem is greatly reduced. Boundary elements $\Omega _{\mathrm{bnd}}$ are only partially enclosed within the embedded body and, hence, they require a special treatment during numerical integration. There are several different approaches for the integration of cut elements advocated in the literature, which, for instance, involve the area weighting method (Dunning et al. 2011; García-Ruíz and Steven 1999), subtriangulation of the boundary elements (Nadal et al. 2013) or introduction of additional, discontinuous shape functions (XFEM) (Chessa et al. 2002). The first approach does not capture the actual location of the boundary resulting in a low accuracy, whereas the second method loosens the concept of a structured mesh. On the other side, XFEM formulation does not suffer from these drawbacks. In our work, we employ a simple method of integration points oversampling (Riehl 2019) in which a larger amount of integration points, which are usually in the range $n_{ip} = (5 . \, . 10)^d$, is considered. As depicted in Fig. 2b, for each integration point, we individually decide whether it contributes to the integral, based on the value of the characteristic function $\chi$

$$\begin{aligned} \int _{\Omega ^e}\ {\bar{\chi }} \left( \varvec{x} \left( \varvec{\xi } \right) \right) f \left( \varvec{\xi } \right) \text {\,dV}\approx \sum _{m = 1}^{n_{ip}} {\bar{\chi }} f \left( \varvec{\xi }_m \right) J \left( \varvec{\xi }_m \right) w_m. \end{aligned}$$

(15)

To avoid numerical instabilities due to sharp material discontinuity at the boundary of the embedded body, we slightly regularize the definition of the characteristic function

$$\begin{aligned} {\bar{\chi }} = {\bar{\chi }} \left( \varvec{x}^e \left( \varvec{\xi }_m \right) \right) = {\left\{ \begin{array}{ll} 1, &{}\text {if} \ \ \varvec{x} \in {\mathcal {B}}\\ 10^{-3}, &{}\text {if} \ \ \varvec{x} \in \Omega ^h \setminus {\mathcal {B}}\ \text {and} \ e \in \Omega _{\mathrm{bnd}} \\ 0, &{}\text {if} \ \ e \in \Omega _{\mathrm{out}}. \end{array}\right. } \end{aligned}$$

(16)

in which $\varvec{x} \in {\mathcal {B}}$ indicates that $\varvec{x}$ belongs to the inside elements $\Omega _{\mathrm{in}}$ and inside portion of the boundary elements $\Omega _{\mathrm{bnd}}$. The treatment of the boundary integrals is more straightforward as compared to the domain integrals. As shown in Fig. 2c, one needs to further split each segment $\Gamma ^s$ at their intersections with the element boundaries $\partial \Omega ^e$ (coloured white in Fig. 2c) and integrate each of the subsegments using the standard Gauss quadrature rule. Contributions from these subsegments (see for instance the subsegments $s^1_i$ and $s^2_i$ in Fig. 2c) are then assembled at the respective nodes of the boundary elements $\Omega ^e$ (coloured red in Fig. 2c).

Contribution of the k-th node in the element e from the tractions is then given by

$$\begin{aligned} \int _{\Gamma ^N \cap \, \Omega ^e}\ \bar{\varvec{t}} \cdot \varvec{N}^k \text {\,dA}= \sum _{i = 1}^{n_{s}} \int _{s^i} \bar{\varvec{t}} \cdot \varvec{N}^k \text {\,dA}. \end{aligned}$$

(17)

3 Optimization method

In the following work, we employ the augmented Lagrangian formulation for a constrained optimization problem and solve it using the Multiplier Method (Hestenes 1969; Rockafellar 1973). Since the purpose of this article is to primarily demonstrate a method to unify topology and shape optimization, we restrict ourselves to a standard compliance minimization problem with a volume constraint.

3.1 Tackling shape

The boundary of the embedded body $\Gamma$ explicitly represents the variable shape. Discretization of $\Gamma$ into segments $\Gamma _s$ introduces vertices, which are naturally adopted as a vector of discrete design variables $\mathbf{v}$ for shape optimization. At this point we would to like remark that working directly with the vertices $\mathbf{v}$ is essentially equivalent to working with the finite element nodes of an explicit mesh in a standard shape optimization procedure. The difference is that in case of an embedded body we deal with a $d-1$ dimensional mesh, which can be imagined as a hollow body. This fact means that no morphing of the so-called dependent nodes of the interior of a shape is necessary to maintain mesh regularity. Thus, by using the embedding domain discretization, we overcome one of the main difficulties associated with the classical shape optimization method. Furthermore, easier manipulation of the shape means that much larger design changes can be handled without sacrificing the mesh quality.

The shape sensitivity information is obtained on the continuum level and transformed into boundary integral form (Choi and Kim 2004). For a detailed account on this matter, see the Appendix in Sect. 1.

Fig. 3

Shape optimization of the cantilever using embedding domain discretization

No need for expensive remeshing/morphing schemes for the dependent, inner nodes does not mean that we can directly treat the sensitivity information as the design update. Jagged boundaries and mesh dependency is an integral part of any shape optimization routine and need to be addressed in any event. To handle this issue, we have adapted the traction method by Azegami and Takeuchi (2006) for the embedded body. For details, please consult Sect. 1.

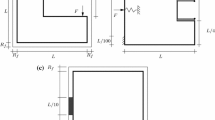
In Fig. 3, a benchmark compliance minimization problem was solved with a volume fraction constraint of 0.5. Fig. 3a depicts the problem setup and Fig. 3b, c show the optimized shape together with the embedding mesh. The material parameters used are $E = 70 \ {\text{GPa}}; \ \upsilon = 0.3$; the bending load equals $F = 0.1 \ N$ for an assumed thickness of $t = 1 \ {\text{mm}}$. One can immediately notice the large shape change to reach the optimal state. In particular, the left hand side region was updated towards the inside of the cantilever by more than half of the cantilever length. Instead, if a standard approach with an unstructured mesh were used, the optimization would lead to severe mesh distortion and, thus, the usability of the solution would be questionable.

3.2 Tackling topology

The mechanical model in density methods for topology optimization is based on a perfectly structured mesh, which also is the case with an embedding domain discretization. Upon further inspection, one can come to the conclusion that the characteristic function $\chi$ (see Eq. (2)) and the pseudo-density field $\rho$ used in density methods are in a certain sense equivalent. Both of the functions indicate how much material is stored (or whether there is material or not) in each finite element. Hence, one can understand the characteristic function $\chi$ as a pseudo-density that is 1 only within the embedded body ${\mathcal {B}}$. The difference is that the original pseudo-density can take intermediate values within the range $\rho \in \left[ 0, 1\right]$ and it cannot assign two distinct values within a single element. The similarity between $\chi$ and $\rho$ can be used to our advance. In the following, we introduce the pseudo-density field to the inner domain by defining a hybrid function $\zeta$

$$\begin{aligned} \zeta = \zeta \left( \varvec{x}, \rho \left( \varvec{x} \right) \right) = {\left\{ \begin{array}{ll} \rho \left( \varvec{x} \right) , &{}\text {if} \ \ \varvec{x} \in {\mathcal {B}}\\ 0, &{}\text {if} \ \ \varvec{x} \in \Omega \setminus {\mathcal {B}}\end{array}\right. } \end{aligned}$$

(18)

which is a slight enhancement of the characteristic function $\chi$ in which all the points $\varvec{x}$ within the body ${\mathcal {B}}$ are assigned a pseudo-density $\rho$. The weak form of equilibrium is then given by

$$\begin{aligned} \int _{\Omega }\ \zeta ^p \left[ \varvec{\sigma } : \delta \varvec{\epsilon } \right] \text {\,dV}- \int _{\Omega }\ \zeta \left[ \varvec{b} \cdot \delta \varvec{u} \right] \text {\,dV}- \int _{\Gamma ^N}\ \bar{\varvec{t}} \cdot \delta \varvec{u} \text {\,dA}= 0, \end{aligned}$$

(19)

where a penalization parameter is chosen as $p = 3$. Based on our experiments, the discretized version of the hybrid function $\zeta$ performs best when adapted in the following manner

$$\begin{aligned} {\bar{\zeta }} \left( \varvec{x}^e , \rho \left( \varvec{x}^e \right) \right) = {\left\{ \begin{array}{ll} \rho \left( \varvec{x}^e \right) , &{}\text {if} \ \ e \in \Omega _{\mathrm{in}} \\ 1, &{}\text {if} \ \ e \in \Omega _{\mathrm{bnd}} \ \text {and} \ \varvec{x}^e \in {\mathcal {B}}\\ 10^{-3}, &{}\text {if} \ \ e \in \Omega _{\mathrm{bnd}} \ \text {and} \ \varvec{x}^e \in \Omega ^h \setminus {\mathcal {B}}\\ 0, &{}\text {if} \ \ e \in \Omega _{\mathrm{out}}. \end{array}\right. } \end{aligned}$$

(20)

Fig. 4

Pseudo-density field in the discretized embedding domain

in which the only difference with respect to the characteristic function ${\bar{\chi }}$ (see Eq. 16) is that the inner elements $\Omega _{\mathrm{in}}$ are assigned the pseudo-density field $\rho$ (see Fig. 4a for a graphical intepretation of the regions defined in Eq. (20)). The elements that belong to the boundary set $\Omega _{\mathrm{bnd}}$ are excluded from the pseudo-density field and, thus, treated in an unchanged manner. The motivation behind this exclusion comes from the fact that the shape sensitivities would otherwise show dependence on the value of the pseudo-density. This dependency occurs when coupling of shape and topology optimization is considered and can be avoided by assigning full density to the boundary elements. That is, as already mentioned in Sect. 3.1, due to the fact that the shape sensitivities are expressed exclusively in terms of boundary integrals.

The authors are aware that assigning full density to boundary elements is not conforming with the continuous formulation of the problem and it is, indeed, a discretization related simplification. However, we observe that the finer the embedding domain mesh, the narrower the band of full density along the boundary. The thickness of this band is on average half of the element size. Hence, we discuss that for a fine enough discretization, the "full density" band is small enough to be considered negligible. See Fig. 4b for an exemplary distribution of pseudo-density.

3.3 Coupled optimization

In Sects. 3.1 and 3.2 we have introduced the design variables of shape and topology into a model defined using the embedding domain discretization technique. In the following, we setup an optimization problem that involves both sets of design variables simultaneously. In a continuum sense, we consider the shape of the embedded body and the pseudo-density of its interior as design variables. In the discretized model, the vector of design variables is given by concatenation of the vector of vertices of the embedded boundary $\mathbf{v}$ and the vector of pseudo densities $\varvec{\rho }$ of the inner elements $\Omega _{\mathrm{in}}$ of the embedding domain

$$\begin{aligned} \bar{\mathbf{v }} = \begin{bmatrix} \mathbf{v} \\ \varvec{\rho } \end{bmatrix}. \end{aligned}$$

(21)

3.3.1 Optimization workflow

The coupling of topology and shape optimization manifests itself in two ways: (1) there is a single mechanical model that contains both shape and density variables; (2) each iteration of the augmented Lagrange (AL) subproblem involves both shape and density sensitivity analysis, regularization and update. However, we cannot state that this is a fully coupled approach, since the update of shape and density is realized in separate line search steps (although in the same iteration). That means, the density and shape variables are treated in a different manner and they could not be randomly intermixed. In Algorithm 1, we show the workflow for the coupled optimization.

The workflow is modified to account for the coupling between topology and shape optimization. Tracking of density variables is a consequence of changing the number of discrete density variables. Shape projection deals with open void regions, that is, zero or close to zero density regions adjacent to the shape. Shape generation introduces shape elements in place of closed void regions (topological holes). Furthermore, adaptive shape refinement is implemented to refine those shape elements, that elongate or create sharp corners as a consequence of design update.

In the following sections, we address these steps and the aspects related to coupling of shape and topology optimization and discuss both the profits and the limitations related to them.

3.3.2 Tracking of density variables

Update of the shape might result in truncated (shape contraction) or newly introduced (shape expansion) discrete density variables. Most of the time, due to the volume fraction constraint, the variable shape is contracted and, as a consequence, density design variables are eliminated. While this occurrence is trivial to handle, a special treatment has to be introduced when the shape expands and introduces new inner elements.

At this point, we would like to stress that the varying number of density design variables is related purely to the discretization. In a continuum formulation, understanding of what happens with the pseudo-density field as the shape expands (or contracts) is given more freedom. On the one hand, we might say that the pseudo-density field is being stretched since the amount of matter within the embedded body remains the same. On the other hand, the matter might be added or substracted but no stretching of pseudo-density field takes place. To the specifics of the embedding domain discretization, in particular, the use of a structured mesh, only the second interpretation is suitable.

In order not to over-complicate the method, we introduce a simple approach based on the filtering schemes of Bruns and Tortorelli (2001). In our approach, an initial density of a newly introduced design region $\bar{\varvec{x}}$ is computed by

$$\begin{aligned} \rho \left( \bar{\varvec{x}} \right) = \int _{{\mathcal {N}}_R ( \bar{\varvec{x}} ) \cap {\mathcal {B}}} f \left( \bar{\varvec{x}} - \varvec{x} \right) \rho \left( \varvec{x} \right) \text {\,dV}\end{aligned},$$

(22)

where ${\mathcal {N}}_R \left( \bar{\varvec{x}} \right)$ is a neighbourhood region of $\bar{\varvec{x}}$ within a radius R. In a discrete variant, for a new, jth finite element, its density is computed by

$$\begin{aligned} {\tilde{\rho }}^{e_j} = \frac{\displaystyle {\sum\nolimits _{e \in {\mathcal {S}}_i} \rho ^e w \left( \varvec{x}^e \right) v^e}}{\displaystyle {\sum \nolimits _{e \in {\mathcal {S}}_i} w \left( \varvec{x}^e \right) v^e}} \end{aligned},$$

(23)

Fig. 5

Tracking of the density design variables. Initial density of the newly introduced density design variable is computed based on the density values of the neighbouring elements within radius R

where ${\mathcal {S}}_j$ is a set of support elements of the jth element, i.e. ${\mathcal {S}}_j = \{ e \ | \ e \in {\mathcal {N}}\left( e_j \right) \ \text {and} \ e \ne e_j \ \text {and} \ e \notin \Omega _{\mathrm{out}} \}$, see Fig. 5. The boundary elements are purposely included in ${\mathcal {S}}_j$ and we use $\rho ^e = 1$ for them. In this manner, we avoid a special case scenario when ${\mathcal {S}}_j \cap \Omega _{\mathrm{in}} = \emptyset$ and the jth element is surrounded only by the boundary elements instead. By making sure that ${\mathcal {S}}_j \cap \Omega _{\mathrm{bnd}} \ne \emptyset$, the starting density of the jth will be non-zero and, moreover, it would ensure a smooth density distribution in the proximity of the boundary. To maintain simplicity, the initial sensitivities of the new elements are computed in a similar fashion, i.e. utilizing the filtering scheme without density weighting

$$\begin{aligned} \tilde{\frac{\partial {\mathcal {F}}}{\partial \rho }^{e_j}} = \frac{\displaystyle {\sum \nolimits _{e \in {\mathcal {S}}_i} \frac{\partial {\mathcal {F}}}{\partial \rho }^{e_i} w \left( \varvec{x}^e \right) }}{\displaystyle {\sum \nolimits _{e \in {\mathcal {S}}_i} w \left( \varvec{x}^e \right) }} \end{aligned},$$

(24)

as proposed by Sigmund (2001b).

3.3.3 Shape projection

The shape update is preferably limited to small step sizes in order to avoid unwanted distortions. On the contrary, the topology undergoes large design changes, especially at the early stage, as it evolves from an evenly distributed pseudo-density to a recognizable skeleton of topological members. We observed that in a coupled optimization this phenomenon leads to creation of, what we call, open topological voids. That is, when the topology of a structure becomes clearly defined, regions of zero pseudo-density emerge, that are directly adjacent to the shape. Practice shows that these open topological voids eventually disappear as the shape approaches the closest topological feature. However, this might require a large number of iterations. Hence, in order to improve the robustness of our method, we introduce a shape projection step which aims to speed up the elimination of open topological voids.

In Fig. 6a, a raw projection vector is depicted that serves as a basis for the shape projection step. The raw projection vector defines the displacement of shape vertices along the normal to the shape direction, which is needed in order to eliminate the open topological void in one step. Our experience shows that the use of a raw projection vector is not robust enough to deal with certain, difficult scenarios. For example, it happens that the normal directions of neighbouring shape vertices differ to a level, that during projection the shape vertices interchange their positions. We resolved this issue by utilizing the regularization scheme that is primarily used for shape sensitivity (see the Appendix in Sect. 1). As a result, we obtain a smooth projection vector that fixes the issue of interchanging vertices. Furthermore, we introduce a relaxation factor $\theta$ to scale down the magnitude of the projection vector in order to limit its effect onto the property of the descent direction and to prevent the shape from an eventual penetration of the topological features.

Fig. 6

Shape projection

The regularized and relaxed projection vector is given by

$$\begin{aligned} \tilde{\mathbf{p }} = \theta \left[ \alpha \left[ \mathbf{K} ^{-1} \mathbf{p} \right] + \left[ 1 - \alpha \right] \mathbf{v} _N \right] \end{aligned},$$

(25)

where $\alpha$ is a weighting parameter, $\mathbf{v} _N$ is a nodal averaging vector, $\mathbf{p}$ is the raw projection vector, $\mathbf{K} ^{-1} \mathbf{p}$ is a solution of the traction method BVP (for more details on these quantities, see Sect. 1). In Fig. 6b, a regularized and relaxed (with $\theta = 0.2$) projection vector is shown. Simulations show, that the relaxation vector works best within the range $\theta \in \left[ 0.2, 0.5 \right]$.

We remark that this regularization procedure is not introduced specially for the shape projection, rather we directly make use of the already available regularization for the shape sensitivities. From the implementation point of view, the only additional work related to a shape projection step is the computation of the raw projection vector.

The shape projection step is purely heuristic, therefore, the property of descent direction of the total shape update is not guaranteed anymore. Practice shows, however, that the addition of the regularized and relaxed projection step negligibly affects the final design.

3.3.4 Shape generation

As the topology optimization converges, recognizable hole-like features of topological members evolve. We call these regions closed topological voids, as opposed to open topological voids defined in Sect. 3.3.3. The key difference between these two types of topological voids is that closed ones are not adjacent to the shape boundary. To obtain crisp boundaries in place of the closed topological voids, we add a framework to introduce an additional, variable shape enclosing these regions. These newly introduced shape design variables will further undergo shape optimization to generate a smooth geometry.

Fig. 7

Three steps in shape generation scheme. Note that the boundary elements $\Omega _{\mathrm{bnd}}$ are depicted with full black colour due to limitations of the visualization tool used

The first step of shape generation is to identify the clusters of void cells. To determine these clusters, we do a neighbourhood search for each cell that is classified as a member of a closed topological void. For this classification, we choose all cells which pseudo-density is less than half solid, that is $\rho < 0.5$. This way, the newly introduced shape can ideally be positioned in the middle of the grey transition zone from solid feature to void hole. All the connected cells with $\rho < 0.5$ represent a cluster. In Fig. 7a these clusters are represented in different colours.

The second step is to establish a convex hull that encloses these clusters. To achieve this, we use a generic convex hull generation algorithm to develop a polygon that encloses a cluster. Our implementation is based on the algorithm presented in Cormen et al. (2009). Once the enclosing polygons are determined, we append them to the existing boundary of the embedded body. The updated shape is shown in Fig. 7b.

To prevent the generation of shape in place of closed topological voids too early, we introduce a control parameter that delays the shape generation until a desired "crispness" of the topological design is obtained. We measure the "crispness" by the percentage of grey cells remaining in the structure. We define a cell to be grey if its pseudo-density is in the range $\rho \in \left[ 0.01, 0.99\right]$. When the participation of the grey cells in all of the inside cells $\Omega _{\mathrm{in}}$ of the current iteration falls below a user-defined threshold

$$\begin{aligned} \frac{n_{\mathrm{grey}}}{|\Omega _{\mathrm{in}} |} < \theta _{\mathrm{grey}} \end{aligned},$$

(26)

which we choose from the range $\theta _{\mathrm{grey}} \in \left[ 0.01, 0.25 \right]$, the shape generation function is allowed to be invoked in any iteration.

Intersecting holes The selection of the grey cell threshold for the shape generation step is based on experience. The general rule is the lower the value for the grey cell threshold the better, because the topological features are then easier to recognize. User might, however, prefer to invoke the shape generation step as early as possible and, therefore, a greater value of the grey cell threshold will be selected. In such case, the shapes might be generated in place of the topological voids that are not fully formed. This sometimes leads to a scenario in which two newly introduced shapes attempt to combine into one, leading to an intersection of shapes, as depicted in Fig. 8a. In this scenario, the convex hull algorithm is reinvoked to regenerate a single shape, see Fig. 8b.

Fig. 8

Merging of two intersecting holes using the convex hull algorithm. An example taken from the cantilever optimization

Continuity of the optimization routine Any design change not based on a response gradient information with respect to the design variables introduces a certain amount of discontinuity to the optimization routine. That is particularly pronounced in the hole insertion schemes, in which a solid, spherical region is replaced with a void region or a patch of finite elements is removed with no allowance for intermediate states. On the contrary, the aim of the shape generation step is not to introduce a new hole but rather to modify the discretization in a region that is already void, in order to allow for shape sensitivity to control the design. The main requirement for the shape generation step is to alter the design state in a minimal amount. In other words, it is a quasi-void-to-void transition rather than solid-to-void transition. Moreover, shape generation does not suffer from the heuristics behind the choice of initial geometry in the hole nucleation schemes, which often assume a spherical form with a certain radius. Hence, we assess that the shape generation scheme exhibits a less abrupt nature as compared to hole insertion schemes. Although we believe that the discontinuity introduced by the shape generation is negligible, a mathematical treatment on this aspect is necessary for a further discussion.

3.3.5 Adaptive shape refinement

Use of a $d-1$ dimensional mesh makes large shape updates possible. Although we do not have to incorporate morphing algorithms to handle mesh deformation (at least in 2D optimization), we still need to put some effort to maintain regularity of the shape discretization. On the one hand, we utilize the traction method and dual descent smoothing to ensure a smooth, mesh-independent design update. On the other hand, we still need to make sure that the discretization is able to represent the shape accurately. In particular, we tackle two aspects of discretization: elongation of the segments and creation of sharp corners. We introduce two simple criteria, based on which a single shape segment can be refined. The length criterion is given by

$$\begin{aligned} l(\Gamma _{s_i}) < l_{\mathrm{avg}} c_l \end{aligned},$$

(27)

where $l_{\mathrm{avg}}$ is the average shape segment size from iteration 0 and $c_l$ is a user-defined criterion for the allowable elongation. Most often, we choose $c_l = 1.5$. The curvature criterion is

Fig. 9

Adaptive shape refinement in a shape optimization example of a cantilever. Large shape update of the left hand side wall caused the shape segments to elongate significantly and form a U-shaped feature with just three shape segments. When the shape adaptive refinement is utilized, the issues with elongated elements and sharp corners are overcome

Fig. 10

Stages of cantilever optimization. The variable shape is depicted as red line. (Color figure online)

$$\begin{aligned} \varvec{N}_{s_i} \cdot \varvec{N}_{s_j} > c_a \end{aligned},$$

(28)

where $\varvec{N}_{s_i}$ is a unit normal vector of the ith shape segment and $c_a$ is the angular criterion for the allowable angle between the normals of two adjacent shape segments. By default, we choose $c_a = 0.9$. See Fig. 9 for a comparison between shape optimization of the cantilever from Fig. 3a without and with shape adaptive refinement.

4 Results

We verify our method with two most commonly used benchmark examples: the cantilever and the Messerschmitt-Bolkow-Blohm (MBB) beam. Both examples are optimized with varying values of the filter radius for density sensitivities (please refer to the filtering scheme of Bruns and Tortorelli (2001). We also investigate the influence of the choice of the grey cell threshold for the delay of the shape generation. In particular, we are interested in how does the premature shape generation affects the final design. For the regularization of the shape sensitivities, we established a set of parameters that remains the same for all of the presented examples. We employ a standard setting for the optimization problem, that is minimization of the total compliance with an upper limit constraint on the volume fraction.

Cantilever In Fig. 10 we show a course of cantilever optimization using our method. For this, we choose an embedding domain discretization with element size of $h = 0.007$ and a filter radius for density-based sensitivities of $r = 0.02$. The cantilever is constrained with a volume fraction of $V_{\mathrm{frac}} = 0.5$. The BVP setup is the same as in 3a.

In the initial configuration (Fig. 10a) the variable shape is only present on the outside of a filled body (no initial holes). The initial pseudo-density of the inner cells is chosen to be 0.5 so that the volume fraction constraint is only slightly violated¹. In the initial iterations the topology undergoes large changes and open topological voids occur, as depicted in Fig. 10b. At this stage, the shape update is supported by the shape projection scheme. Within the next ten iterations the open topological voids are almost eliminated (Fig. 10c) and the topological features become recognizable. At this stage, the grey cell participation decreases rapidly until it reaches the threshold value of $\theta _{\mathrm{grey}} = 0.1$ in the 23rd iteration (Fig. 10d). From this point, the shape generation function is allowed to introduce variable shapes in the place of the topological voids. Naturally, with a participation of grey cells below 10% the closed topological voids are recognized, therefore, variable shapes are introduced before the 24th iteration, see Fig. 10e. After invoking the shape generation step for the first time, the shape updates become dominating as compared to the density updates. Nevertheless, the density updates of the coupled optimization are still active and, as shown in Fig. 10f), the topology is further fine-tuned and two more pairs of topological holes are formed. Consequently, the shape generation step is activated in the 30th and the 31st iterations to complement these holes with variable shapes (Fig. 10g, h). It is worth a notice, that at this point the open topological voids are fully eliminated. Hence, the shape updates are driven exclusively by the optimizer. In the 44th and the 51st iterations, a shape intersection occurred as the optimizer tried to eliminate two topological members (see Fig. 10i, j). To account for this, the shapes were merged to form a single hole. Although the design appears fully black and white, the density variables are still active and are free to react to the shape changes. As a consequence another topological void formed and a new shape was generated in the 63rd iteration, see Fig. 10k. The remainder of the optimization run fine-tunes the shape and converges in the 132nd iteration (Fig. 10l).

As the next step we examine the complexity of the design by choosing varying filter radii for the density sensitivities and the robustness of the method against a choice of varying grey cells thresholds. In Fig. 11a–i filter radii of $r = \{0.04, 0.03, 0.02\}$ (sorted row-wise) and grey cells thresholds of $\theta _{\mathrm{grey}} = \{20\%, 10\%, 2\%\}$ (sorted column-wise) were chosen. The element size for the embedding domain discretization is $h = 0.007$.

The optimized structures show a mechanically crisp, smooth boundary thanks to the variable shape. The method produces similar outputs for different settings of the grey cell threshold ranging from $\theta _{\mathrm{grey}} = 20\%$ to $\theta _{\mathrm{grey}} = 2\%$ for all the filter choices. This proves that the user has enough flexibility in the choice of the grey cell threshold. As the filter radius for density-based sensitivities decreases, the complexity of the topological design increases. This complexity can be further increased by choosing smaller filter radii and, consequently, with finer embedding domain mesh. However, we believe that the advantage of our method is that we can achieve finely optimized geometries with relatively coarse discretization of the embedding domain, since the actual geometry is represented only by the boundary of the embedded body. In other words, by using a relatively coarse embedding domain discretization, thin geometrical features can still be represented smoothly as opposed to pure topology optimization, in which a visible staircase-like pattern appears. Moreover, truncation of the outside elements $\Omega _{\mathrm{out}}$ means a smaller mechanical domain. On the top of that, the size of the problem decreases with the decreasing volume of the design. This is particularly pronounced after the shape generation step, during which the elements within the topological voids are excluded from the BVP. For instance, the initial configuration in the examples from Fig. 11 contains 13944 inner $e \in \Omega ^h_{\mathrm{in}}$ and boundary elements $e \in \Omega ^h_{\mathrm{bnd}}$ together. The BVPs of the final designs for all the setups with $\theta _{\mathrm{grey}} = 10\%$ (see Fig. 11b, e, h) involve 7494, 7568 and 7657 inner and boundary elements together, respectively.

Fig. 11

Optimized designs of the cantilever for varying filter radii and grey cell thresholds

In Fig. 12, the distribution of the shape vertices for the final designs from Fig. 11b, e, h are shown. The usage of the adaptive shape refinement scheme (see Sect. 3.3.5) for the length and curvature control allowed for a precise representation of the shape at the intersections of the topological features.

In Fig. 13, the participation of the grey cells in the first 50 iterations is shown for the examples from Fig. 11. One can immediately see that for all the cases the grey cells (almost) fully disappear between the 30th and 40th iteration. This indicates that the topology forms and the problem transforms into a shape-driven optimization. Moreover, since in the final designs only two phases remain in the model: solid material and void, we deduce that the obtained structures are physically meaningful.

To gain an insight into the performance difference between the designs from Fig. 11, the final values of the compliance are shown in Table 1.

Table 1 Final compliance and grey cell participation for the cantilever

The differences in compliance values are exiguous, what suggests that the performance of the design is insensitive to the choice of grey cells threshold.

Fig. 12

Optimized designs of the cantilever for varying filter radii. Distribution of the shape vertices

Fig. 13

Participation of grey cells as a function of iteration count for the first 50 iterations

In the next step, the volume fraction constraint is set to $V_{\mathrm{frac}} = 0.3$. Additionally, we use a relatively coarse mesh with element size of $h = 0.015$ and we test two cases of the grey cell thresold $\theta _{\mathrm{grey}} = 30\%$ and $\theta _{\mathrm{grey}} = 5\%$. The filter radius is set to $r = 0.04$ for both cases. The shape generation steps and the final results are shown in Fig. 14. Moreover, the final results are depicted with shape vertices (Fig. 14c, f). As shown in Fig. 14a, b, d, e, although significantly varying grey cell thresholds were used, the generated shapes in 14b, e are very similar. The final shapes in Fig. 14c, f are almost identical, what confirms that the method deals well with varying setting of the grey cell threshold. On the top of that, the usage of the adaptive shape refinement resulted in a finely rendered geometry.

MBB Beam We continue benchmarking of our method with the MBB beam. In Fig. 15 we show the BVP setup for half of the beam with symmetry constraint on the left hand edge. The material parameters used are $E = 70 \ GPa; \ \upsilon = 0.3$; the bending load equals $F = 0.1 \ N$ for an assumed thickness of $t = 1 \ mm$

Fig. 14

Optimized cantilever with volume constraint of $V_{\mathrm{frac}} = 0.3$, element size of $h = 0.015$ and filter radius of $r = 0.04$

.

Fig. 15

BVP setup of the MBB beam

Fig. 16

Stages of MBB optimization. The variable shape is depicted as red line. (Color figure online)

Fig. 17

Optimized designs of the MBB beam for varying filter radii

Fig. 18

Optimized designs of the MBB beam for varying filter radii. Distribution of the shape vertices

The selected element size is $h = 0.005$ for all the presented designs. As demonstrated with the cantilever example, the coupled optimization method is robust enough to produce similar results for different choices of grey cell levels. Hence, this time we restrict the setup of the optimization problems to $\theta _{\mathrm{grey}} = 10\%$ only.

In Fig. 16, the design evolution of the MBB beam with filter radius of $r = 0.01$ is shown. In a similar manner to the cantilever design, in the early iterations (Fig. 16b) the topology undergoes large design changes, whereas the shape update is supported by the projection scheme. With the partial elimination of open topological voids the inner skeleton of topological features appear, see Fig. 16c. In 23rd iteration (Fig. 16d), the grey cell participation drops below the threshold value of $\theta _{\mathrm{grey}} = 10\%$ and the shape generation step is invoked (Fig. 16e). Further development of the topology design yields a particular scenario in which an open topological void appears adjacent to a shape hole, see Fig. 16f. Subsequent iterations successfully deal with the elimination of the open topological voids and two additional shapes are introduced (see Fig. 16g, h). The remaining iterations are naturally dominated by the shape update until the convergence is reached (Fig. 16i).

In Fig. 17, final designs of the MBB beam for varying filter radii are depicted. All three configurations shared the same initial step size for the shape update $\tau _{x}^{\mathrm{init}} = 0.015$ and density update $\tau _{\rho }^{\mathrm{init}} = 0.2$. The only varying quantity is the filter radius for density sensitivities. The obtained topologies naturally become more complex with decreasing filter radius. In the cases from Fig. 17a,b the end results are not fully black and white. This is caused by the Lagrange updates which caused a sudden volume drop in the design. The Lagrange updates affected those regions, which for smaller values of the volume constraint would most probably become void.

Figure 18 depicts the distribution of the vertices for the designs from Fig. 17. As in the case of the cantilever, highly curved regions are rendered with finely discretized shape to avoid sharp corners.

The final value of compliance and grey cells participation are listed in Table 2.

Table 2 Final compliance and grey cell participation for the MBB beam

One can see that with the decreasing filter radius the compliance of the final design also slightly decreases. The grey cells participation values are non-zero for the cases with $r = 0.03$ and $r = 0.02$. Nevertheless, we consider the amount of the remaining grey cells as negligible. Therefore, we can safely state that the optimized structures are physically realistic.

The evolution of the participation of grey cells is shown in Fig. 19. In all of cases the percentage drops to values close to zero between the 30th and 35th iterations. At this stage, the coupled optimization becomes dominated by the shape updates.

Fig. 19

Participation of grey cells as a function of iteration count for the first 50 iterations

5 Conclusions

In this contribution, we propose a method that is an alternative to the traditional, sequential approach to topology and shape optimization. By exploiting the specifics of the embedding domain discretization, we couple density-based topology optimization and node-based shape optimization. An embedding domain, which is discretized with a structured finite element mesh, is assigned a pseudo-density field, whereas the boundary of the embedded body serves as a variable shape. In this manner, we setup a single optimization problem that operates on a hybrid design space that is comprised of two sets of design variables.

Our goal was to demonstrate that coupled topology and shape optimization might offer practical advantages. Considering the current state of our work, we discuss the characteristics of the method as compared to sequential and other combinations of topology and shape optimization.

First and foremost, the usage of the same computational domain for shape and topology optimization is the key feature. We skip any transition steps that are necessary in transforming the topological results into a shape mesh, which is general practice in sequential topology and shape optimization.

Moreover, shape variation is given a larger flexibility as compared to the standard, node-based shape optimization due to the usage of embedded boundary. As a consequence, the shape sensitivity analysis is numerically less expensive and the regularization is much easier. Moreover, adaptive shape refinement becomes a relatively simple task as, for 2D problems, it just requires vertex insertion in the segment centre. Besides that, the mechanical model relies upon the structured mesh that is made of quadrilateral elements (in case od 2D), whereas in shape optimization usually triangular elements are used, which offer a lower accuracy.

A common practice in a combined shape and topology optimization routines is to employ a hole insertion scheme. This approach shows a few inherent drawbacks, i.e. its abrupt and discontinuous nature and a limited flexibility in performing topological changes. In our work, we mitigate these issues by enabling a full topological flexibility by introducing a pseudo-density field and the shape generation scheme, which inserts a variable shape in place of already present topological holes.

Furthermore, the fact that the embedding domain must be larger than the design space means one can easily get rid of the bounding box constraints and allow for a geometrically unrestricted setup. Furthermore, since the design is ultimately defined by the boundary of the embedded body, one can use a coarser discretization of the embedding domain and still achieve geometrically refined designs.

A typical phenomenon in our method is the constant interaction of the topology and evolving shape. Although in early iterations the topology changes are dominant and the shape changes are of low influence, in later stages the shape changes take over to position, form and smoothen the features. We are aware that this interaction might in fact be more of an issue than advantage. Practice shows, however, that the interaction is robust enough in a sense that the topological features manage to emerge in an early stage of optimization despite the shape changes. On the other hand, creation of the open topological voids takes place as a result of shape updates being more delicate than the topology changes. Although it is an unwanted phenomenon, the open topological voids are eventually eliminated within the course of optimization. Moreover, we enhance this elimination as described in Sect. 3.3.3.

The key drawback of our method is its inherent complexity and, consequently, less freedom in the selection of an optimization algorithm. Besides the augmented Lagrange formulation, which is utilized in this work, no other approach was tested.

Appendices

A Continuum approach to shape sensitivity

We perform shape sensitivity analysis using the continuum approach, as described in Choi and Kim (2004). We utilize the material derivative concept, which we do not introduce here, but refer interested readers to Arora (1993); Choi and Kim (2004). In the following, we define the compliance functional as

$$\begin{aligned} {\mathcal {F}}^{\mathrm{com}} = \int _{{\mathcal {B}}}\ \varvec{b} \cdot \varvec{u} \text {\,dV}+ \int _{\Gamma ^N}\ \bar{\varvec{t}} \cdot \varvec{u} \text {\,dA}. \end{aligned}$$

(A.29)

We exploit the adjoint method and augment the compliance functional by a weak form of equilibrium equation, in which the variations of the state fields have been replaced by the adjoint variables:

$$\begin{aligned} {\mathcal {L}}= & {} {\mathcal {F}}^{\mathrm{com}} + {\mathcal {W}}^{\mathrm{a}} = \int _{{\mathcal {B}}}\ {\bar{G}} \text {\,dV}+ \int _{\Gamma ^D}\ {\bar{g}} \text {\,dA}+ \int _{\Gamma ^N}\ {\bar{h}} \text {\,dA}, \end{aligned}$$

(A.30)

$$\begin{aligned} {\mathcal {W}}^{\mathrm{a}}= & {} -\int _{{\mathcal {B}}}\ \varvec{\sigma } : \varvec{\epsilon }^{\mathrm{a}} \text {\,dV}+ \int _{{\mathcal {B}}}\ \varvec{b} \cdot \varvec{u}^{\mathrm{a}} \text {\,dV}\nonumber \\&\quad + \int _{\Gamma ^N}\ \bar{\varvec{t}} \cdot \varvec{u}^{\mathrm{a}} \text {\,dA}+ \int _{\Gamma ^D}\ \varvec{t} \cdot \bar{\varvec{u}}^{\mathrm{a}} = \varvec{0}. \end{aligned}$$

(A.31)

By means of variational calculus it was proven that $\delta {\mathcal {W}}^{\mathrm{a}} = 0$ (Arora and Cardoso 1992). Thus, we obtain

$$\begin{aligned} {\dot{{\mathcal {F}}}}^{\mathrm{com}} = {\dot{{\mathcal {L}}}} - \dot{{\mathcal {W}}^{\mathrm{a}}} = {\dot{{\mathcal {L}}}}. \end{aligned}$$

(A.32)

Next, the boundary integral method (Arora 1993) is employed to express the material derivative of the augmented functional in the following form

$$\begin{aligned} \begin{aligned} {\dot{{\mathcal {F}}}}^{\mathrm{com}} =&\int _{{\mathcal {B}}}\ {\bar{G}}' \text {\,dV}+ \int _{\Gamma }\ {\bar{G}} \left[ \varvec{\theta } \cdot \varvec{n} \right] \text {\,dV}\\&+ \int _{\Gamma ^D}\ {\bar{g}}' \text {\,dA}+ \int _{\Gamma ^D}\ \left[ \nabla {\bar{g}} \cdot \varvec{n} + {\bar{g}} H \right] \left[ \varvec{\theta } \cdot \varvec{n} \right] \text {\,dA}\\&+ \int _{\Gamma ^N}\ {\bar{h}}' \text {\,dA}+ \int _{\Gamma ^N}\ \left[ \nabla {\bar{h}} \cdot \varvec{n} + {\bar{h}} H \right] \left[ \varvec{\theta } \cdot \varvec{n} \right] \text {\,dA}. \end{aligned} \end{aligned}$$

(A.33)

We calculate the partial derivatives of the integrands ${\bar{G}}$, ${\bar{g}}$ and ${\bar{h}}$ as follows:

$$\begin{aligned} \begin{aligned} {\bar{G}}'&= \partial _{\varvec{u}}G \cdot \varvec{u}' - \varvec{\sigma }' : \varvec{\epsilon }^{\mathrm{a}} - \varvec{\sigma } : \left[ \varvec{\epsilon }^{a}\right] ' + \varvec{b}' \cdot \varvec{u}^{\mathrm{a}} + \varvec{b} \cdot \left[ \varvec{u}^{\mathrm{a}}\right] ',\\ {\bar{g}}'&= \varvec{t}' \cdot \bar{\varvec{u}}^{\mathrm{a}} + \varvec{t} \cdot \left[ \bar{\varvec{u}}^{\mathrm{a}}\right] ',\\ {\bar{h}}'&= \partial _{\varvec{t}}h \cdot \bar{\varvec{t}}' + \partial _{\varvec{u}}h \cdot \varvec{u}' + \bar{\varvec{t}}' \cdot \varvec{u}^{\mathrm{a}} + \bar{\varvec{t}} \cdot \left[ \varvec{u}^{\mathrm{a}}\right] '. \end{aligned} \end{aligned}$$

(A.34)

Finally, we introduce A.29 and A.34 into A.33 to arrive at a full expression for the material derivative of the augmented compliance functional.

$$\begin{aligned} \begin{aligned} {\dot{{\mathcal {F}}}}^{\mathrm{com}} =&\int _{{\mathcal {B}}}\ \varvec{b}' \cdot \varvec{u}^{\mathrm{a}} \text {\,dV}\\&+ \int _{\Gamma }\ \left[ \varvec{b} \cdot \varvec{u} - \varvec{\sigma } : \varvec{\epsilon }^{\mathrm{a}} + \varvec{b} \cdot \varvec{u}^{\mathrm{a}} \right] \left[ \varvec{\theta }\cdot \varvec{n} \right] \text {\,dA}\\&+ \int _{\Gamma ^D}\ \varvec{t}' \cdot \bar{\varvec{u}}^{\mathrm{a}} \text {\,dA}\\&+ \int _{\Gamma ^D}\ \left[ \nabla \left[ \varvec{t} \cdot \bar{\varvec{u}}^{\mathrm{a}} \right] \cdot \varvec{n} + \left[ \varvec{t} \cdot \bar{\varvec{u}}^{\mathrm{a}} \right] H \right] \left[ \varvec{\theta }\cdot \varvec{n} \right] \text {\,dA}\\&+ \int _{\Gamma ^N}\ \partial _{\varvec{t}} h \cdot \bar{\varvec{t}}' + \bar{\varvec{t}}' \cdot \varvec{u}^{\mathrm{a}} \text {\,dA}\\&+ \int _{\Gamma ^N}\ \left[ \nabla \left[ \bar{\varvec{t}} \cdot \varvec{u} + \bar{\varvec{t}} \cdot \varvec{u}^{\mathrm{a}} \right] \cdot \varvec{n} \right. \\&+ \left. \left[ \bar{\varvec{t}} \cdot \varvec{u} + \bar{\varvec{t}} \cdot \varvec{u}^{\mathrm{a}} \right] H \right] \left[ \varvec{\theta }\cdot \varvec{n} \right] \text {\,dA}\\&+ \left\{ -\int _{{\mathcal {B}}}\ \varvec{\sigma } : \left[ \varvec{\epsilon }^{\mathrm{a}}\right] ' \text {\,dV}+ \int _{{\mathcal {B}}}\ \varvec{b} \cdot \left[ \varvec{u}^{\mathrm{a}}\right] ' \text {\,dV}\right. \\&+ \left. \int _{\Gamma ^N}\ \bar{\varvec{t}} \cdot \left[ \varvec{u}^{\mathrm{a}}\right] ' \text {\,dA}+ \int _{\Gamma ^D}\ \varvec{t} \cdot \left[ \bar{\varvec{u}}^{\mathrm{a}}\right] ' \text {\,dA}\right\} \\&+ \left\{ \int _{{\mathcal {B}}}\ \partial _{\varvec{u}}G \cdot \varvec{u}' - \varvec{\sigma }' : \varvec{\epsilon }^{\mathrm{a}} \text {\,dA}+ \int _{\Gamma ^N}\ \partial _{\varvec{u}}h \cdot \varvec{u}' \text {\,dA}\right\} \end{aligned} \end{aligned}$$

(A.35)

By exploiting the variational principle for design sensitivity analysis, it is required that the variation of the augmented functional w.r.t. the primary and adjoint state fields vanishes. Hence, the sum of the two expressions within curly braces vanishes. Moreover, the first expression within curly braces represents the weak form of equilibrium for the primary structure, in which the explicit derivative of the adjoint state field $\left[ \varvec{u}^{\mathrm{a}}\right] '$ serves as a kinematically admissible test function and $\left[ \varvec{\epsilon }^{\mathrm{a}}\right] '$ is a compatible strain tensor. We may express the first expression in the curly braces as

$$\begin{aligned} {\mathcal {W}}\left( \varvec{u}, \left[ \varvec{u}^{\mathrm{a}} \right] '\right) = 0 \end{aligned},$$

(A.36)

and, consequently, we obtain

$$\begin{aligned} \int _{{\mathcal {B}}}\ \partial _{\varvec{u}}G \cdot \varvec{u}' - \varvec{\sigma }' : \varvec{\epsilon }^{\mathrm{a}} \text {\,dA}+ \int _{\Gamma ^N}\ \partial _{\varvec{u}}h \cdot \varvec{u}' \text {\,dA}= 0. \end{aligned}$$

(A.37)

Now, we utilize the symmetry of the Cauchy stress tensor and major symmetry of the tangent tensor

$$\begin{aligned} \varvec{\sigma }' : \varvec{\epsilon }^{\mathrm{a}} = \varvec{\epsilon }' : {\mathbb {E}} : \varvec{\epsilon }^{\mathrm{a}} = \varvec{\epsilon }' : \varvec{\sigma }^{\mathrm{a}} = \varvec{\sigma }^{\mathrm{a}} : \varvec{\epsilon }' \end{aligned},$$

(A.38)

to obtain the weak form of equilibrium for the adjoint structure

$$\begin{aligned} \begin{aligned} {\mathcal {W}}\left( \varvec{u}^{\mathrm{a}}, \varvec{u}' \right) =&\int _{{\mathcal {B}}}\ \partial _{\varvec{u}}G \cdot \varvec{u}' - \varvec{\sigma }^{\mathrm{a}} : \varvec{\epsilon }' \text {\,dA}\\&+ \int _{\Gamma ^N}\ \partial _{\varvec{u}}h \cdot \varvec{u}' \text {\,dA}= 0 \end{aligned} \end{aligned},$$

(A.39)

in which $\varvec{u}'$ is a kinematically admissible test function and $\varvec{\epsilon }'$ a compatible strain tensor. By evaluating the boundary conditions:

$$\begin{aligned} \begin{aligned} \varvec{b}^{\mathrm{a}}&= \partial _{\varvec{u}}G = {\varvec{b}} \, {\text {in}} \> {\mathcal {B}},\\ \bar{\varvec{t}}^{\mathrm{a}}&= \partial _{\varvec{u}}h = {\varvec{t}}\, {\text{on}} \, \Gamma ^{N},\\ \bar{\varvec{u}}^{\mathrm{a}}&= \partial _{\varvec{u}}g = {\varvec{0}}\, {\text{on}} \, \Gamma ^{D}, \end{aligned} \end{aligned}$$

(A.40)

we realize that the loading of the adjoint structure is the same as of the primary structure. Thus, the problem is self-adjoint and $\varvec{u} = \varvec{u}^{\mathrm{a}}$. Under the assumption that the explicit derivatives of the external loads are zero, i.e. $\varvec{b}' = \varvec{0}$, $\bar{\varvec{t}}' = \varvec{0}$ and by using the fact that $\bar{\varvec{u}}^{\mathrm{a}} = \varvec{0}$ we obtain the final expression for the continuum shape sensitivity of the compliance functional

$$\begin{aligned} \begin{aligned} {\dot{{\mathcal {F}}}}^{\mathrm{com}} =&\int _{\Gamma }\ \left[ 2 \left[ \varvec{b} \cdot \varvec{u} \right] - \varvec{\sigma } : \varvec{\epsilon } \right] \left[ \varvec{\theta }\cdot \varvec{n} \right] \text {\,dA}\\&+ \int _{\Gamma ^N}\ \left[ 2 \nabla \left[ \bar{\varvec{t}} \cdot \varvec{u} \right] \cdot \varvec{n} + 2 \left[ \bar{\varvec{t}} \cdot \varvec{u} \right] H \right] \left[ \varvec{\theta }\cdot \varvec{n} \right] \text {\,dA}. \end{aligned} \end{aligned}$$

(A.41)

If the body force $\varvec{b}$ is zero and the region with traction force is not a part of the design space, then the sensitivity expression reduces to a very simple formula

$$\begin{aligned} {\dot{{\mathcal {F}}}}^{\mathrm{com}} = - \int _{\Gamma }\ \varvec{\sigma } : \varvec{\epsilon } \left[ \varvec{\theta }\cdot \varvec{n} \right] \text {\,dA}. \end{aligned}$$

(A.42)

The sensitivity of the volume functional, given by

$$\begin{aligned} {\mathcal {F}}^{\mathrm{vol}} = \int _{{\mathcal {B}}}\ 1 \text {\,dV}, \end{aligned}$$

(A.43)

is obtained by direct differentiation. Thus, it reads

$$\begin{aligned} {\dot{{\mathcal {F}}}}^{\mathrm{vol}} = \int _{\Gamma }\ 1 \left[ \varvec{\theta }\cdot \varvec{n} \right] \text {\,dA}. \end{aligned}$$

(A.44)

The derived expressions for the continuum sensitivity are then discretized to obtain the nodal contributions in the form

$$\begin{aligned} {\dot{{\mathcal {F}}}}^I = \varvec{g}_n^I \cdot \varvec{\theta }^I \end{aligned},$$

(A.45)

where $\varvec{g}_n^I$ is the sought-after nodal shape sensitivity.

B Shape design update

2.1 B.1 Modified traction method

For the specifics of the embedding domain discretization we adapt the traction method, which was originally introduced in Azegami and Wu (1996); Azegami and Takeuchi (2006). Briefly explained, the traction method is based upon solving an auxiliary BVP, in which the raw shape sensitivity is employed in form of external, nodal traction forces. The solution of such BVP yields a smooth, mesh-independent design update vector. The original traction method (using Robin conditions) relies upon an elasticity energy in form of a body integral. Our adaptation concerns (1) the integration domain, that is, all the energies are defined by means of boundary integrals and (2) the substitution of the elastic energy with a simple spring and Laplacian smoothing energies. In this way, the auxiliary BVP can be directly defined over the embedded boundary in which we treat the shape segments as d-1 dimensional finite elements.

The energy form of our version of the traction method is given by

$$\begin{aligned} \Pi _t = \Pi _{\mathrm{int}} + \beta \left[ \Pi _{\mathrm{ext}} \ + {\mathcal {P}}\right] \ \rightarrow \ \text {Min} \end{aligned}$$

(B.46)

where $\Pi _{\mathrm{ext}}$ is the energy of the external forces in form of the raw sensitivities, ${\mathcal {P}}$ is the penalty functional, which is responsible for the bounding box constraints and $\beta$ is the scaling factor which ensures that the solution of the traction method BVP yields an exact design update vector.

The internal energy in our adapted formulation is defined as a sum of smeared spring and Laplacian smoothing energies as follows

$$\begin{aligned} \begin{aligned} \Pi _{\mathrm{int}} =&\Pi _{\mathrm{sp}} + \Pi _{\mathrm{sm}}\\ =&\int _{\Gamma }\ \frac{c_{sp,N}}{2} \left[ \varvec{u}_N \right] ^2 \text {\,dA}\\&+ \int _{\Gamma }\ \frac{c_{sp,T}}{2} \left[ \varvec{u}_T \right] ^2 \text {\,dA}\\&+ \int _{\Gamma }\ \frac{c_{\mathrm{sm}}}{2} \nabla {\varvec{u}} : \nabla {\varvec{u}} \text {\,dA}. \end{aligned} \end{aligned}$$

(B.47)

At this point, we remark that the chosen smoothing procedure is based on the following boundary value problem:

$$\begin{aligned} \begin{aligned} \Delta \varvec{u}&= \varvec{u} \ \ \ \text {on} \ \Gamma ,\\ \varvec{u}&= \varvec{0} \ \ \ \text {on} \ \partial \Gamma \end{aligned} \end{aligned},$$

(B.48)

where, as opposed to Poisson’s equation, the BVP solves for a vector field instead of a scalar field. The motivation behind using a vector field is that, besides the normal to shape smoothing, we additionally introduce the tangent to shape smoothing to control the node distribution of the variable shape. The vector Laplacian, in the particular case when a cartesian coordinate system is utilized, is given by

$$\begin{aligned} \Delta \varvec{u} = \frac{\partial ^2{\varvec{u}}}{\partial {x}^2} + \frac{\partial ^2{\varvec{u}}}{\partial {y}^2} + \frac{\partial ^2{\varvec{u}}}{\partial {z}^2} = \text {div}\,\left[ \nabla \varvec{u} \right] . \end{aligned}$$

(B.49)

Moreover, note that the spring energy is split into the normal to shape and tangent to shape contributions. This division is specifically introduced for the discrete variant of the sensitivity. This is because with help of the normal spring we eliminate the mesh dependency of sensitivities, whereas with the tangent spring, in conjuction with the Laplacian smoothing, we introduce and control the in-plane regularization.

2.2 B.2 Geometrical smoothing

While the traction method deals with sensitivity regularization, it does not address the irregularities of the geometry itself, for instance, the ear formation problem. To account for that, we additionally introduce a geometric smoothing strategy, in which the final design update is given as a weighted sum of the regularized design update and a nodal averaging vector in the following form

$$\begin{aligned} \bar{\varvec{u}}_{\mathrm{upd}} = \alpha \varvec{u}_{\mathrm{upd}} + \left[ 1 - \alpha \right] \varvec{u}_{\mathrm{avg}} \end{aligned}$$

(B.50)

where $\alpha \in \left[ 0, 1 \right]$ is a weighting parameter, $\bar{\varvec{u}}_{\mathrm{upd}}$ is the final design update vector, $\varvec{u}_{\mathrm{upd}}$ is the regularized design update vector and $\varvec{u}_{\mathrm{avg}}$ is the nodal averaging vector, for the Ith node defined as

$$\begin{aligned} \varvec{u}_{\mathrm{avg}}^I = \frac{1}{| {\mathcal {N}}\left( \varvec{v}^I \right) |} \sum _{\varvec{v}^J \in {\mathcal {N}}\left( \varvec{v}^I \right) } \left[ \varvec{v}^J - \varvec{v}^I\right] . \end{aligned}$$

(B.51)

The weighting parameter $\alpha \in \left[ 0, 1 \right]$ is automatically determined such that the following conditions are met

$$\begin{aligned} \cos \left( \bar{\varvec{u}}_{\mathrm{upd}}, -\nabla _{\varvec{x}} {\mathcal {L}}\right) \ge 0, \end{aligned}$$

(B.52)

$$\begin{aligned} \cos \left( \bar{\varvec{u}}_{\mathrm{upd}}, -\nabla _{\varvec{x}} {\mathcal {L}}\right) \ge \eta \cos \left( \varvec{u}_{\mathrm{upd}}, -\nabla _{\varvec{x}} {\mathcal {L}}\right) \end{aligned},$$

(B.53)

where $\nabla _{\varvec{x}} {\mathcal {L}}$ is the raw augmented Lagrange sensitivity (steepest descent direction) and $\eta$ is the user-defined sufficient decrease parameter, usually in the range $\eta \in \left[ 0.85, 0.95 \right]$.