Multiscale optimisation of resonant frequencies for lattice-based additive manufactured structures

Abstract

This paper introduces a novel methodology for the optimisation of resonant frequencies in three-dimensional lattice structures. The method uses a multiscale approach in which the homogenised material properties of the lattice unit cell are defined by the spatially varying lattice parameters. Material properties derived from precomputed simulations of the small scale lattice are projected onto response surfaces, thereby describing the large-scale metamaterial properties as polynomial functions of the small-scale parameters. Resonant frequencies and mode shapes are obtained through the eigenvalue analysis of the large-scale finite element model which provides the basis for deriving the frequency sensitivities. Frequency tailoring is achieved by imposing constraints on the resonant frequency for a compliance minimisation optimisation. A sorting method based on the Modal Assurance Criterion allows for specific mode shapes to be optimised whilst simultaneously reducing the impact of localised modes on the optimisation. Three cases of frequency constraints are investigated and compared with an unconstrained optimisation to demonstrate the algorithms applicability. The results show that the optimisation is capable of handling strict frequency constraints and with the use of the modal tracking can even alter the original ordering of the resonant mode shapes. Frequency tailoring allows for improved functionality of compliance-minimised aerospace components by avoiding resonant frequencies and hence dynamic stresses.

1 Introduction

Lightweight structures that are able to mitigate or avoid dynamic loading are a key area of development within the aerospace industry. Failure caused by resonance is of particular interest in areas such as engine design and other applications involving vibration or shock loading. The design of lightweight structures capable of avoiding resonance is the primary focus of this work and is achieved using a novel, multiscale lattice-based method of structural optimisation.

Previous research into the optimisation of resonant frequencies has resulted in several methods being adopted within the industry, such as topology optimisation based on the Solid Isotropic Material with Penalisation (SIMP) (Bendsøe 1989) and Bi-directional Evolutionary Structural Optimisation (BESO) methodologies (Huang et al. 2009; Sivapuram and Picelli 2018). Resonant frequencies have also been optimised for using a level set shape and topology optimisation method (Xia et al. 2011; Xu et al. 2019).

A common issue associated with the SIMP approach when resonance is considered is the occurrence of localised modes corresponding to artificially low natural frequencies. These localised modes occur in regions of low-density material where the ratio between the penalised stiffness and the unpenalised mass is very small. The SIMP method has previously been adapted for solution of dynamic problems by adapting the formulations of both the stiffness and mass at these low densities (Pedersen 2000; Huang et al. 2009). However, the resulting designs may not be representative of a manufacturable structure and often still require heuristic post-processing, causing the resulting structures to be sub-optimal (Xu et al. 2019).

An alternative approach to topology optimisation which bypasses these issues is through the use of multi-scaled metamaterials. A metamaterial is one which exhibits different properties from its constituent base material. It achieves this through micro-architectures which allow for radically different properties to the bulk material. Vicente et al. (2016) implemented a multiscale BESO method in conjunction with metamaterials to optimise for dynamic properties using a uniform micro-scale architecture, potentially limiting the range of structures attainable by the macro-optimisation.

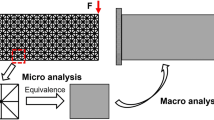
The objective of the work described in this paper is to produce varying lattice structures with functionally graded material properties capable of attaining specific natural frequencies. This is achieved using a two-scale approach where the microscale metamaterial properties of a parameterised and periodic lattice cell are computed and arranged to generate a continuous response surface of material properties. These material properties are then used as the basis for a structural optimisation algorithm implementing the small-scale lattice parameters as the large-scale design variables. The scales are coupled by the homogenised material properties of the lattice cell which are explicit functions of the small-scale parameters. This method avoids the issue of localised modes due to the lack of penalisation which causes the imbalance between the mass and stiffness of an element.

The small-scale formulation was introduced by Imediegwu et al. (2019) and features a parameterised, periodic lattice structure with 7 design variables representing the thickness of cylindrical members. These parameters are utilised in the macroscale optimisation as the control variables, providing a direct link between the macro- and microscales. This parameterisation allows the lattices to exhibit a wide range of metamaterial properties whilst maintaining an easily defined structure for manufacturing. Murphy et al. (2019) expanded this work by introducing a concurrent coupling of scales. This approach is capable of computing new microscale lattice permutations and their homogeneous properties as and when they are needed by the large-scale optimisation. This negates the need for a computationally expensive material database to be fully populated.

Recent works by Schumacher et al. (2015), Zhu et al. (2017), and Xia and Breitkopf (2018) all feature a similar approach of relating the required structural properties to corresponding micro-architectures. The advantage of the current work is provided by the use of a parameterised micro-architecture having parameters which are the control variables in the macro-optimisation, as opposed to optimising for material properties and later assigning corresponding metamaterials to the structure.

The additional features built upon from the work of Imediegwu et al. (2019) are the investigation into the dynamic properties of the resulting structures and incorporating them into the constraints of the optimisation process. This is achieved by specifying a required range within which the natural frequency must reside. Frequency tracking is incorporated into the algorithm to improve control over the desired frequencies as well as to ensure localised modes do not interfere with the optimisation. Several examples are provided to illustrate the effectiveness of the algorithm.

2 Method

The multiscale approach relies on the separation of the problem into the two distinct scales. The microscale involves relating the micro-architecture of the lattice unit cell into homogenised metamaterial properties whilst the macroscale utilises these material properties in the structural and dynamic finite element simulations used to solve the optimisation problem.

2.1 Microscale model

The small lattice is based on the parameterization used by Imediegwu et al. (2019), shown in Fig. 1. It is characterised by seven cylindrical members orientated in a face-centred cubic arrangement. Members labelled 1 to 4 in Fig. 1 run diagonally through the structure whilst members 5 to 7 are orientated in the orthogonal coordinate directions. This micro-architecture has been selected due to its periodic and parameterisable structure. Each of the 7 radii constitute a spatially varying design variable in the large-scale optimisation with each lattice unit cell being represented by an element in the global mesh. Each element has a homogenised anisotropic stiffness matrix and a homogenised unit cell lattice density which is defined by its 7 design variables and are determined from micro-scale simulations.

Fig. 1

Microscale lattice and parameterisation showing the orientation of each of the seven cylindrical members

These micro-scale simulations are performed on a 60 × 60 × 60 cube mesh of hexahedral elements. Material properties are assigned to the elements as either void or solid to create a representation of the particular micro-architecture being simulated. Periodic boundary conditions are imposed to simulate the micro-architecture as a unit cell within a larger lattice. Strain deformation analysis, consisting of three direct strains and three shear strains, is used to determine the homogenised stiffness tensor of the micro-architecture. The homogenised unit cell lattice density is determined from volume averaging of the element densities of the mesh.

The radius of each member is discretised into 7 levels with a micro-scale simulation run for each possible lattice permutation, hence requiring 7⁷ (823,543) permutations. However, due to the symmetry of the unit cell, only 40,817 simulations are required. Response surfaces can be generated to describe the properties as functions of the 7 member radii by fitting multi-variable polynomials of the design variables to the pre-computed material property database.

These homogenised stiffness matrices and densities are utilised as the spatially varying material properties for the large-scale optimisation and provide the crucial link between the micro- and macroscales. Further details on the extraction of the metamaterial properties and their application within the macroscale optimisation are described in Imediegwu et al. (2019).

2.2 Macroscale optimisation

The constraints of the large-scale optimisation are handled using a primal dual-interior point algorithm, the implementation of which is provided by the open-sourced optimisation software, IPOPT (Wachter and Biegler 2006). The large-scale finite element (FE) solutions were obtained using the open-source FE solver, FEniCS (Alnæs et al. 2015), and its subsidiary python library, DOLFIN (Logg and Wells 2010). The structural optimisation problem can be defined as

Minimise:

$${J}(u(\mathbf{r_{\eta \gamma}}),\mathbf{r_{\eta \gamma}}) $$

(1)

Subject to:

$${F}(u(\mathbf{r_{\eta \gamma}}),\mathbf{r_{\eta \gamma}}) ={K} u -{f} = 0 $$

(2)

$$ [{K} - \lambda_{n}{M}]{\phi_{n}} = 0 $$

(3)

$$ V(\mathbf{r_{\eta \gamma}}) \leq V_{D} $$

(4)

$$ {f}_{lower} \leq {f}_{n} \leq {f}_{upper} $$

(5)

$$ r_{min} \leq \mathbf{r_{\eta \gamma}} \leq r_{max} $$

(6)

where J represents the objective function and r_ηγ represents the vector of design variables corresponding to a lattice member η within an element γ. The constraint F = Ku − f = 0 dictates that the global stiffness matrix, K, the vector displacement field, u, and the global force vector f, satisfy the static linear elastic partial differential equation which governs the physics of the problem. The eigenvalue equation, [K − λ_nM]ϕ_n = 0, describes the dynamic properties of the structure where K and M are the global stiffness and mass matrices respectively, ϕ_n is the n th mass-normalised eigenmode, and λ_n is the corresponding eigenvalue. The eigenvalues and eigenmodes of the system are extracted using the iterative Krylov-Schur algorithm due to its robustness in handling large, sparse matrices (Hernȧndez and Romȧn 2007). The eigenmode corresponds to the resonant mode shape of the structure whilst the n th natural frequency (Hz) of the problem is found from

$$ {f}_{n} = \frac{\sqrt{\lambda_{n}}}{2 \pi} $$

(7)

The volume constraint V ≤ V_D imposes an upper limit on the available material for the optimal design where the volume fraction, V, is a measure of the average unit cell lattice density and is calculated from

$$ {V = \frac{\int \rho_{\gamma}d{\varOmega}}{Vol}} $$

(8)

where ρ_γ is the homogenised unit cell lattice density and V ol is the volume of the design space.

The frequency constraints, f_lower ≤ f_n ≤ f_upper, dictate the range of resonant frequencies that the optimal design must occupy. The constraint r_min ≤r_ηγ ≤ r_max also enforces bounds on the local design variables. The member radii are all non-dimensionalised and represent a fraction of the side length of their respective element. The bound r_min corresponds to the manufacturing constraint for the smallest possible radii whilst also preventing the formation of artificial localised modes in the optimisation by removing the possibility of empty space. The maximum radius, r_max, is represented as the highest perturbation of the microscale parameters which corresponds to a fully dense block of material where all radii are equal to 38% of the unit cell side length.

For the case of compliance minimisation with frequency and volume constraints the objective function is defined as

$$ J = u^{T} \mathit{K} u $$

(9)

in which u is the displacement vector subject to loading. The sensitivity of the objective function to the design variables was determined using adjoint equations due to the fact that both the stiffness matrix, K, and the displacement, u, are both functions of the design variable. These gradients are obtained using the built-in adjoint capabilities in the DOLFIN package (Logg and Wells 2010).

The Jacobian of the constraints is also required by the optimiser. The gradients of the frequency constraint are determined from differentiation of (7) with respect to r_ηγ, yielding

$$ \frac{\partial {f}_{n}}{\partial \mathbf{r_{\eta \gamma}}} = \frac{1}{4 \pi \sqrt{\lambda_{n}}} \frac{\partial \lambda_{n}}{\partial \mathbf{r_{\eta \gamma}}} = \frac{1}{8 \pi^{2} {f}_{n}} \frac{\partial \lambda_{n}}{\partial \mathbf{r_{\eta \gamma}}} . $$

(10)

The sensitivity of the eigenvalue, $\frac {\partial \lambda }{\partial \mathbf {r_{\eta \gamma }}}$ can be derived from [K − λ_nM]ϕ_n = 0 by differentiation with respect to r_ηγ to produce

$$ \frac{\partial[\boldsymbol{K} - \lambda_{n} \boldsymbol{M}]}{\partial \mathbf{r_{\eta \gamma}}}\phi_{n} + [\boldsymbol{K} - \lambda_{n} \boldsymbol{M}] \frac{\partial \phi_{n}}{\partial \mathbf{r}_{\eta \gamma}}) = 0. $$

(11)

Premultiplication by ${\phi _{n}^{T}}$ then results in

$$ {\phi_{n}^{T}} \frac{\partial[\boldsymbol{K} - \lambda_{n} \boldsymbol{M}]}{\partial \mathbf{r_{\eta \gamma}}}\phi_{n} + {\phi_{n}^{T}} [\boldsymbol{K} - \lambda_{n} \boldsymbol{M}] \frac{ \partial \phi_{n}}{\partial \mathbf{r}_{\eta \gamma}}) = 0. $$

(12)

Due to the symmetric nature of [K − λ_nM], the premultiplication is commutative; hence, substitution of (3) results in the second term of (12) being null,

$$ {\phi_{n}^{T}} [\boldsymbol{K} - \lambda_{n} \boldsymbol{M}] = [\boldsymbol{K} - \lambda_{n} \boldsymbol{M}]\phi_{n} = 0, $$

(13)

which after expansion of the first term in (12) results in

$$ {\phi^{T}_{n}} \left[\mathbf{\frac{\partial \boldsymbol {K}}{\partial \mathbf{r_{\eta \gamma}}}} - \lambda \mathbf{\frac{\partial \boldsymbol {M}}{\partial \mathbf{r_{\eta \gamma}}}}\right]{\phi_{n}} - {\phi^{T}_{n}} \mathbf{M} \phi_{n} \frac{\partial \lambda}{\partial \mathbf{r_{\eta \gamma}}} = 0 . $$

(14)

The mode shape ϕ_n represents a mass-normalised eigenvector, defined as

$$ {\phi_{n}^{T}} \boldsymbol{M} \phi_{n} = 1 . $$

(15)

Substituting this definition into (14) results in

$$ \frac{\partial \lambda}{\partial \mathbf{r_{\eta \gamma}}} = \phi^{T} \left[\mathbf{\frac{\partial \boldsymbol{K}}{\partial r_{\eta \gamma}}} - \lambda \mathbf{\frac{\partial \boldsymbol{M}}{\partial r_{\eta \gamma}}}\right]{\phi} $$

(16)

where the matrices $\frac {\partial \mathbf {K}}{\partial \mathbf {r}_{\eta \gamma }}$ and $\frac {\partial \mathbf {M}}{\partial \mathbf {r}_{\eta \gamma }}$ are the globally assembled sensitivity matrices,

$$ \frac{\partial \boldsymbol{K}}{\partial\mathbf{r_{\eta \gamma}}} = \sum\limits_{\gamma=1}^{NE} {\int}_{{\varOmega}_{\gamma}} \mathbf{B}^{T} \frac{\partial \mathbf{C}_{\gamma}}{\partial \mathbf{r_{\eta \gamma}}} \mathbf{B} d{\varOmega} $$

(17)

$$ \frac{\partial \boldsymbol{M}}{\partial \mathbf{r_{\eta \gamma}}} = \sum\limits_{\gamma=1}^{NE} \frac{\partial \rho_{\gamma}}{\partial \mathbf{r_{\eta \gamma}}} {\int}_{{\varOmega}_{\gamma}} \mathbf{N}^{T} \mathbf{N} d{\varOmega} $$

(18)

in which C_γ is the homogenised stiffness matrix of the element and ρ_γ is the homogenised density of the element. The terms B and N are the strain-displacement matrix and the vector of finite element shape functions, respectively, both of which are independent of the small-scale lattice parameters. An element’s stiffness and mass sensitivities are therefore direct functions of its local lattice parameters. The volume fraction sensitivities are found by pure differentiation of the governing microscale equations for density. These sensitivities of constraints were verified by comparing with a finite differencing scheme to ensure that the formulation provided the expected outputs.

2.3 Filtering of design variables

All evaluations of the objectives, constraints and gradients are performed using filtered design variables as this promotes the gradual variation in the lattice geometry and eliminates the presence of numerical checkerboarding in the solution. Filtering is achieved using a Helmholtz filter (Lazarov and Sigmund 2011) which is described as the solution to

$$ -\alpha^{2} \nabla^{2} \hat{\mathbf{r}}_{\eta \gamma} + \hat{\mathbf{r}}_{\eta \gamma} = \mathbf{r}_{\eta \gamma} $$

(19)

where $\hat {\mathbf {r}}_{\eta \gamma }$ is the vector of filtered design variables and α is the filter radius defining the extent of the filtering.

This filtering results in all gradients being calculated with respect to the filtered design variables. To obtain the gradient with respect to unfiltered design variables, the gradients are multiplied by the sensitivity of the filtered design variables with respect to unfiltered design variables as dictated by the chain rule

$$ \frac{\partial J}{\partial \mathbf{r_{\eta \gamma}}} = \frac{\partial J}{\partial \hat{\mathbf{r}}_{\eta \gamma}} \frac{\partial \hat{\mathbf{r}}_{\eta \gamma}}{\partial \mathbf{r_{\eta \gamma}}}. $$

(20)

Due to the objectives and constraints being calculated with respect to the filtered design variables, the original unfiltered variables no longer hold physical meaning, as discussed in Sigmund (2006). The final solution must therefore be presented as the filtered design variables.

2.4 Localised modes and frequency tracking

A localised mode is one which does not accurately represent the true vibrational response of a structure and results from regions in the finite element model having non-physical material properties. Figure 2 shows an example of a localised mode that appears during a conventional topology optimisation. In this solution, the pseudo-density in the lower tip corners has been reduced to almost zero. This results in their stiffness being greatly penalised with respect to the mass as described by the penalisation formulation used in SIMP,

$$ E_{e} = E_{0}{\rho_{e}^{p}} $$

(21)

where E_e and ρ_e (0 < ρ_min ≤ ρ_e ≤ 1) are Young’s modulus and relative material density of the element respectively, E₀ is Young’s modulus of the solid material and the penalisation factor, p, is equal to 3. At ρ_e = ρ_min, the extremely penalised stiffness coupled with the unpenalised mass results in artificially large displacements in localised areas relative to the rest of the structure. They would not realistically exist due to there being effectively zero material in those regions. Without a method of frequency tracking, these localised modes would interfere with the optimisation if they exhibit a lower natural frequency than the expected global resonant mode.

Fig. 2

Example of a localised mode forming during a topology optimisation due to low-density regions of the solution

Localised modes during the optimisation process can greatly impede convergence to a realistic result. They are a significant problem in topology optimisation requiring reformulation of the SIMP problem (Pedersen 2000; Du and Olhoff 2007). Localised modes could also potentially pose an issue if the minimum lattice member radii are not constrained. If the member radius is allowed to reach zero, then localised modes can form during the course of the lattice optimisation and begin to dominate the lowest natural frequencies, much like what occurs during topology optimisation. This would mean the algorithm would be optimising these unwanted localised modes instead of the global bending and torsional modes that are the usual focus of a typical engineering optimisation.

In order to ensure that the desired modes are being considered, a frequency tracking methodology has been implemented. This relies on comparing the mode shapes of the optimised structure to the original mode shapes of the unoptimised structure before any localised modes develop. The coherence between two mode shapes is defined as the Modal Assurance Criterion (MAC) given by

$$ MAC(\phi_{a},\phi_{b}) = \frac{|{\phi_{a}^{T}} \phi_{b}|^{2}}{({\phi_{a}^{T}} \phi_{a})({\phi_{b}^{T}} \phi_{b})} $$

(22)

where ϕ_a and ϕ_b represent the two mode shapes being compared. In the case of frequency tailoring, they would be the mode shapes of the current topology iteration compared with the original mode shapes.

A MAC number of 1 represents identical mode shapes. Within each iteration of the macroscale optimisation, after natural frequencies and mode shapes are calculated, the MAC number between every mode (lowest n frequencies) and every initial mode is calculated. The frequencies are then rearranged to the original order that initial mode shapes were found based on which of the current mode shapes best match the initial equivalent. This also allows the resonant modes to swap positions in the eigenvalue analysis without impeding the optimisation algorithm from satisfying the resonant frequency constraints, an example of which is detailed in Section 3.4. It also allows for any localised modes that appear to be disregarded by the optimiser. The process of ensuring that the correct modes are captured using an improved MAC tracking is the subject of future work.

3 Results and discussion

Four different test cases were considered for this work. The objective remained constant across all cases as the minimisation of the compliance of a cantilevered beam subject to a volume constraint, V ≤ 0.3. The base material used in the microscale simulations has Young’s modulus of E = 209 GPa, a Poisson’s ratio of ν = 0.3, and a density of ρ = 7800 kg m^− 3.

The structure to be optimised is shown in Fig. 3. A Dirichlet boundary condition was imposed on the root of the cantilever to constrain the displacement to 0 in all three directions and a uniformly distributed load, and F = 1000 was imposed on the top surface in the negative y direction. The member radii were also bounded to between r_min = 0.068h and r_max = 0.38h, where h represents the length of the side of the lattice unit. These values represent the minimum diameter that the scale abstraction is able to accurately represent and the diameter corresponding to a fully dense unit cell when all members are at this value.

Fig. 3

Test case geometry

A rectangular cross section was selected as it allowed for two bending modes whose frequencies were not initially equal to each other, hence avoiding repeated resonant frequencies. The expected mode shapes of the cantilever, shown in Fig. 4, will be the first two cantilever bending modes in the y and z directions followed by the torsional mode. Figure 4 also details the starting frequencies of these mode shapes for the initial conditions of a uniform lattice with a volume fraction V = 0.3. The dimensions of the cantilever were chosen to ensure that the first bending mode would be parallel to the direction of loading as well as the direction that compliance is being minimised for. The four test cases to be demonstrated are:

• 1. No frequency constraint applied, simple compliance minimisation.

• 2. Compliance minimisation with the first bending mode constrained to below 700 Hz and the second bending mode constrained to above 900 Hz.

  $$ {f}_{1} \leq 700 \text{Hz} $$
  $${f}_{2} \geq 900 \text{Hz} $$

• 3. Compliance minimisation with the second bending mode constrained to below 400 Hz.

  $$ {f}_{2} \leq 400 \text{Hz} $$

• 4. Compliance minimisation with the torsional mode constrained to below 600 Hz.

  $$ {f}_{3} \leq 600 \text{Hz} $$

Fig. 4

First three modes of the rectangular cantilever and their respective resonant frequencies for a uniform lattice with a volume fraction V = 0.3

A further investigation was conducted by minimising compliance whilst also varying the constraint on the second bending mode to investigate the relationship between the constraint boundaries and the objective function achieved.

3.1 Mesh convergence

The finite element method relies heavily on the concept of scale abstraction and will obtain more accurate results from a more refined mesh and better resolution (Hughes 2000). A mesh convergence study was conducted on the large-scale structure to determine the minimum number of cells required for a suitable mesh convergence.

The compliance and the first three natural frequencies of increasingly fine meshes were obtained as well as the processor time taken for both the compliance calculation and the eigenvalue extraction algorithm to run; the results of which are shown in Fig. 5. A mesh density of 27,000 nodes was selected as this results in an error below 0.25% for both the natural frequencies and compliance whilst also avoiding significantly computationally intensive mesh densities.

Fig. 5

Mesh convergence of the first two natural frequencies and compliance

3.2 Case 1: no frequency constraint applied

In order to understand the effects of the frequency constraint, the optimisation is first performed for the case with no frequency constraint to identify the expected compliance values as well as the structure to which the other designs can be compared against. The material distribution of the optimised case, which is a representation of the homogenised density of each lattice unit cell, is shown in Fig. 6. This representation has been clipped to only show regions with a lattice density greater than the domain average of 0.3.

Fig. 6

Material distribution within the bounding volume. All cells with a density less than 0.3 have been removed to highlight the structurally significant portions of the cantilever

Figure 7 shows the progression of the optimisation in terms of the compliance, volume fraction, and the values of the first three resonant frequencies. The compliance of all optimisations is normalised with respect to the compliance of a fully dense structure (V = 1.0). This removes the arbitrary comparison of compliance between two differently dimensioned structures as well as demonstrates the effectiveness of the optimisation against the most stiff structure achievable in a defined volume.

Fig. 7

Convergence plots of the relevant properties over the course of the optimisation

It can be noted from Fig. 7 that the optimisation has a relatively slow convergence at the start. This is due to a feature of the IPOPT algorithm in which it can adaptively change the step size between iterations. The first few iterations are therefore used to determine the relative scales between different constraints and objective functions using initially small steps. IPOPT is then able to select the most applicable step size, after which rapid convergence is observed. The convergence criterion used in all simulations was an acceptable tolerance of less than 0.1% change in objective function between successive iterations. However, all simulations were allowed to run on to the same iteration number to standardise the plots and to make for a fairer comparison of the structures after a set number of iterations.

I-beams are known for having a relatively high second moment of area and hence stiffness for a given mass; it can be seen that the optimised structure shown in Fig. 6 resembles a pair of diverging I-beams orientated to maximise the loading capability in the y direction. This anisotropic strengthening is highlighted in the resonant frequencies of the solution. All the frequencies have been increased during the optimisation and the first bending mode, which acts in the y direction, has been raised significantly to a final value of 749 Hz. This is an increase of 230% from its initial value as opposed to the less significant increase of 100% seen in the bending mode in the z direction. Table 1 compares both the normalised compliance and the resonant frequency of the the first bending mode amongst various material distributions. It can be seen that the frequency of the optimised beam is more than three times that of a uniformly distributed beam with the same mass and is even greater than that of a fully dense cantilever. This is due to the frequency being a function of both the stiffness and the mass distributions, and so simply adding more material does not necessarily result in a higher resonant frequency. The compliance obtained by the optimisation reaches a minimum of 2.53 times that of a fully dense beam but due to its mass constraint it will never be able to be as stiff as the fully dense case. Comparisons made by Imediegwu and Murphy have shown that in compliance minimisation the lattice-based method outperforms the traditional SIMP topology optimisation when using a penalisation factor of 3 but does not outperform the theoretical but non-physical best case of an unpenalised topology optimisation (Imediegwu et al. 2019; Murphy et al. 2019).

Table 1 Normalised compliance, resonant frequencies of the first bending mode, and normalised stiffness to weight ratio of various material distributions

A useful comparison is the normalised stiffness to weight ratio of the cantilever, α, which is calculated using

$$ \alpha = \frac{1}{V_{D} C_{min}} $$

(23)

where V_D is the volume fraction constraint used and C_min is the minimum normalised compliance achieved by the optimisation. A fully dense cantilever would therefore have a normalised stiffness to weight ratio of 1. Table 1 shows that the the optimised structure has a 32% improvement in the stiffness to weight ratio compared with the fully dense structure, whilst the unoptimised structure of the same allowable volume has an 80% lower stiffness to weight ratio.

Figure 8 provides a more detailed view of the contributions that each of the seven members provide to the structure. Members 1–4 are aligned diagonally across the cell and are concentrated at the root of the cantilever where the highest stresses are anticipated as well as the x − z midplane of the beam where maximum shear stress is located. The regions where these members are dominant run diagonally across x − y midplane with members 1 and 4 being mirror images of each other, as are members 2 and 3. This is due to the diagonal members in the macroscale being dominant along their respective directions in the microscale. This arrangement ensures connectivity between the thickest members along the load path in which they are most needed. Member 5 is aligned along the length of the cantilever, and hence is the most dominant member in terms of supporting the bending moments. It is therefore the most present member in the design and forms the bulk of the cantilever shape. It is most dominant on the upper and lower surfaces where the tensile and compressive stresses in the x direction are at their maximum. Member 6 is aligned in the y direction parallel to the loading which explains its significant contribution to the I-beam structure as well as its presence on the top surface where the force is acting. Member 7 does not act in the direction of either the loading or the stresses and so has less of an impact on compliance minimisation; hence, why it does not feature heavily in the structure. It should be noted that member 7 is still present in all regions of the structure, but does not have many radii greater than the clip threshold of 0.15 and therefore does not appear significantly in Fig. 8. This unconstrained case provides a useful comparison with the upcoming cases where the frequency constraint has been applied.

Fig. 8

Distribution of individual lattice members after compliance minimisation with no frequency constraints applied. All members are present throughout the domain but a visual threshold is used to hide members below radius of 0.15

3.3 Case 2: avoiding excitation frequency band

To demonstrate the effects of the frequency constraint, a case has been selected which requires both a reduction in the first bending mode and an increase in the second bending mode whilst maintaining the same objective of compliance minimisation in the y direction. From Fig. 7, it was shown that when no frequency constraint is applied both the first and second bending modes have a final value close to 800 Hz. If the structure in a practical application had an excitation frequency close to this value, then undesired resonance of the cantilever would occur. It may therefore be required to shift these resonant frequencies away from this frequency. The constraints imposed are a difference of 100 Hz above and below 800 Hz. The first bending mode therefore has a maximum allowable frequency of 700 Hz, whilst the second bending mode has a minimum allowable frequency of 900 Hz. These constraints were selected to demonstrate the effect of the optimisation algorithm by simultaneously increasing and decreasing resonant frequencies. The resulting structure from this optimisation is shown in Fig. 9 and the resulting frequencies and compliance are plotted in Fig. 10. It reveals the final normalised compliance to be 2.68 which results in a normalised stiffness to weight ratio of 1.24. The structure still has a 24% increase in stiffness to weight ratio compared with a fully dense beam despite the frequency constraints.

Fig. 9

Material distribution within the bounding volume. All cells with a density less than 0.3 have been removed to highlight the structurally significant portions of the cantilever

Fig. 10

Convergence plots of the relevant properties over the course of the optimisation

One means of maintaining the first resonant frequency below 700 Hz would be to reduce the effective stiffness of the cantilever in the y direction; however, this would be in opposition to the compliance minimisation stated as the objective function. An alternative would be to increase the effective mass of the cantilever which is the mass that can be used to represent the structure in an equivalent mass-spring system. Increasing the effective mass decreases the resulting natural frequency described by

$$ {f}_{n} = \sqrt{\frac{K_{eff}}{M_{eff}}} $$

(24)

where K_eff is the effective stiffness and M_eff is the effective mass. To increase the effective mass requires a portion of the allocated volume to be assigned as far from the cantilever root as possible as mass located further from the root has the greatest effect on decreasing the natural frequency. Mass located at the end of the cantilever is detrimental to the compliance minimisation because it reduces the material available to stiffen the cantilever root.

From Fig. 9, it can be seen that a combination of both methods has been used to satisfy the constraints with the mass distributed to the tip resulting in a smaller central I-beam than observed in the unconstrained structure. This increase in effective mass will also cause the second resonant frequency to decrease which might violate the constraint for the second bending mode to be above 900 Hz. To meet this constraint, the cantilever has been greatly stiffened in the z direction by assigning material to the left and right edges of the cantilever. This increases the second moment of area in the z direction and hence increases the second bending frequency. Any remaining material after the constraints have been met is focused on the central I-beam to minimise compliance.

A more detailed view of each of the 7 members contributing to the structure can be found in Fig. 11. The diagonal members, 1–4, exhibit significant concentrations at the root corners, primarily in the corner that aligns with their respective directions. Member 5 remains the most dominant as it serves to stiffen the beam in both bending modes as well as the direction of dominant principal stress. It should also be noted that member 7 now has a greater contribution on the top and bottom surfaces and the root of the cantilever. This is because it allows for anisotropic stiffening in the z direction, whilst having less impact on the stiffness in the y direction. This therefore makes it an important member for increasing the frequency of the second bending mode whilst not affecting the first bending mode. Material has also been assigned to all members at the tip of the cantilever to produce the effective mass required to lower the first bending mode.

Fig. 11

Distribution of individual lattice members after compliance minimisation whilst avoiding an excitation frequency band. All members are thresholded to eliminate members below radius of 0.15

3.4 Case 3: swapping the order of the first two bending modes

The third test case was performed to demonstrate the effectiveness of the modal tracking. A constraint was imposed to maintain the second bending mode at its starting value of 400 Hz, which corresponds to a uniform lattice where all unit cells have a lattice density equal to 0.3. This constraint must also be applied to the bending mode in the z direction regardless of the order of the resonant frequencies in the eigenvalue analysis. This value is well below the expected resonant frequency of the y bending mode of 749 Hz seen in the unconstrained case. The optimiser is therefore required to successfully distinguish between the two bending mode shapes and sort them to allow for the correct resonant frequency constraints to be met.

The resulting structure can be seen in Fig. 12, which resembles a much more narrow single I-beam compared with the unconstrained structure in Fig. 6. This slender beam shape is needed to reduce the second moment of area, and hence stiffness, in the z direction. Material has also been assigned to the tip, specifically on the left and right sides, as this increases the effective mass of the second bending mode whilst minimally affecting the other resonant modes.

Fig. 12

Material distribution within the bounding volume. All cells with a density less than 0.3 have been removed to highlight the structurally significant portions of the cantilever

Figure 13 shows that the frequencies are successfully able to swap their order, with the first bending mode reaching a final value of 591 Hz, 191 Hz greater than the second bending mode. The minimum compliance reached is 3.06 with a normalised stiffness to weight ratio of 1.09. This further proves that the optimiser is capable of producing structures with both better strength to weight ratios and well-defined resonant frequency constraints.

Fig. 13

Convergence plots of the relevant properties over the course of the optimisation

Inspection of the individual lattice contributions in Fig. 14 reveals that the most dominant member is now member 6. This is due to the anisotropic stiffening which increases stiffness greatly in the y direction to minimise compliance but does not stiffen the structure in the z direction. Member 7 does not feature significantly for a similar reason in that it does not act in the direction to minimise compliance and so is unfavourable for the optimiser to assign mass to. Member 5 is also prevalent as seen in previous cases to resist the tension and compression in the x direction. The diagonal members are all very similarly distributed at the root to resist the shear stresses and also at the tip to generate an effective mass.

Fig. 14

Distribution of individual lattice members after compliance minimisation with the second bending mode constrained below 400 Hz. All members are thresholded to eliminate members below radius of 0.15

3.5 Case 4: constraint on torsional mode

The final test case that was investigated was to enforce a significant reduction in the torsional natural frequency in an attempt to test the limits of the optimiser. An upper limit of 600 Hz was imposed on the third resonant frequency, which represents a reduction of 48% from the unconstrained value of 1158 Hz reached in Section 3.2 when no frequency constraints are applied.

To achieve this significant change in frequency, a large amount of material has been distributed to the tip of the cantilever as seen in Fig. 15. The lattice is particularly dense at the corners of the tip. This is done in order to increase the moment of inertia which in turn reduces the resonant frequency as described by

$$ {f}_{n} = \sqrt{\frac{K_{\theta eff}}{J_{eff}}} $$

(25)

where K_𝜃eff is the effective torsional stiffness and J_eff is the moment of inertia about the centre of rotation. Figure 16 shows the final resonant frequency for the first bending mode reaches 517 Hz which is the same resonant frequency as the fully dense cantilever. It is also noted that the compliance initially increases in order to satisfy the frequency constraint before decreasing to a final value of 3.56, which represents a normalised stiffness to weight ratio of 0.94. This test case reveals that the optimiser is robust towards many types of resonant mode and requires a significantly restrictive constraint on the frequency before resulting in a structure with a normalised stiffness to weight ratio of less than 1.

Fig. 15

Material distribution within the bounding volume. All cells with a density less than 0.3 have been removed to highlight the structurally significant portions of the cantilever

Fig. 16

Convergence plots of the relevant properties over the course of the optimisation

Figure 17 provides a detailed view of the contributions from each lattice member. It should be noted that all members feature heavily at the cantilever tip as they are all required in order to maximise the lattice density of the unit cells. This creates the significant effective mass which is required to reduce the resonant frequency. The diagonal members do not appear at the root of the cantilever. This is because the diagonal members would help increase the torsional stiffness of the beam which would undesirably increase the torsional resonant frequency as described by (25). Members 6 and 7 do not appear on the sides of the root of the cantilever as they would also increase the torsional stiffness, whereas member 5 acts in the x and therefore does not significantly contribute to torsional stiffness. It can therefore be found at the sides of the root without increasing the torsional resonant frequency.

Fig. 17

Distribution of individual lattice members after compliance minimisation with the torsional mode constrained below 600 Hz. All members are thresholded to eliminate members below radius of 0.15

Figure 18 shows the resulting lattice structure when reconstructed. The dense regions at the corners of the cantilever tip can be clearly seen and are highlighted in the zoomed in section A. Section B is a region of lower density when all lattice members are at their minimum value. The large amount of material located at the tip will also affect the two bending modes which both have frequencies considerably lower than the unconstrained compliance minimisation.

Fig. 18

Reconstruction of the lattice structure with highlighted areas of interest

3.6 Effect of frequency constraint on compliance

A further study was conducted to investigate the effect that the frequency constraints has on the objective function. A series of simulations were run with a range of frequency constraints imposed on the second bending mode. This mode acts in the z direction and therefore does not act in the same direction as the compliance minimisation.

Section 3.2 describes the unconstrained second resonant frequency as 826 Hz which will be the frequency at which the lowest compliance is achieved. Figure 19 shows the relationship between the minimum compliance reached in each optimisation and the final value for the second resonant frequency. It is revealed that the optimiser is able to achieve a relatively consistent compliance for a wide range of frequency constraints on the second bending mode. The second resonant frequency is able to be within the range of 650 to 1050 Hz before a change in compliance greater than 2% is observed. This 400 Hz band of possible frequencies is key to practical usage as it permits a wide range of design options to avoid any operating frequencies that the structure might be subjected to without compromising on compliance.

Fig. 19

Minimum compliance attained subject to varying constraints on the second natural frequency

The optimiser reaches its upper limit at 1125 Hz which is an increase of approximately 300 Hz with the trade-off being a lower stiffness to weight ratio of 1.25. This remains considerably greater than the fully dense cantilever. The upper limit occurs due to there being a finite stiffness that can be reached with an allowable volume. However, the lower limit is not reached as the relocation of material to the tip of the cantilever greatly affects the compliance of the structure. The stiffness to weight ratio falls below 1 at approximately 330 Hz. This allows the second resonant frequency to be reduced by 495 Hz, or 60%, before it is no longer as effective as the fully dense cantilever.

An evolution of the structures can also be seen in Fig. 19. A shift of material from the tip towards the root is clearly visible before the 826 Hz minimum and a further migration of material from the central I-beam towards the outer edges is seen for frequencies greater than the minimum. This highlights the range of possible structures that can be achieved by the multiscale lattice method.

4 Conclusions

This paper has illustrated the use of a metamaterial lattice approach to produce frequency tailored light weight structures. A seven-dimensional lattice microstructure uses a database of precomputed simulations to predict homogenised material properties for use in the large-scale optimisation.

Resonant frequency tailoring has been achieved by implying constraints on a traditional compliance minimisation problem, with frequency tracking implemented to allow for frequency ordering. The effectiveness of the optimisation technique has been demonstrated in four separate examples with comparisons made to both the unconstrained and fully dense solutions. The results show that the frequency constraints have a wide range of values that do not significantly impede the minimum compliance obtained by the optimiser. Introducing more strict frequency constraints beyond this range results in an increase in the minimum compliance. The increase in compliance not only appears proportional to the amount of mass redistributed in order to satisfy the frequency constraint, but is also affected by the direction that the frequency is being pulled and the mode shape that is being optimised for.

Frequency tailoring of lattice structures can offer improvements and cost savings for a wide range of applications within the aerospace industry and other engineering disciplines. The work presented allows for the rapid development of optimised structures that are capable of avoiding resonance whilst also offering improved strength to weight ratios.