Abstract
In this article, we are concerned with the existence of mild solutions and approximate controllability of Hilfer fractional evolution equations with almost sectorial operators and nonlocal conditions. The existence results are obtained by first defining Green’s function and approximate controllability by specifying a suitable control function. These results are established with the help of Schauder’s fixed point theorem and theory of almost sectorial operators in a Banach space. An example is also presented for the demonstration of obtained results.
Similar content being viewed by others
1 Introduction
In current times, the rising interest of researchers in fractional calculus reflects the popularity of this branch [1–3, 5–13, 15, 19, 30–32]. Differential equations of fractional order are widely applicable in the areas of physics, chemistry, electromagnetics, and mechanics. Fractional differential equations (FDEs) have been used widely in the identification of different physical systems, in control theory, in simulating viscoelastic materials, and in the modeling of different complex phenomena [22–29, 39, 42]. The concept of exact controllability and approximate controllability of FDEs is an active field of investigation because of its major applications in physical sciences. Under some admissible control inputs, exact controllability steers the system to arbitrary final state, while approximate controllability steers the system to the small neighborhood of arbitrary final state. In the published works, there are numerous articles focussing on the exact or approximate controllability of systems represented by FDEs, neutral FDEs, FDEs with impulsive inclusions, and FDEs with delay functions [4, 18, 40, 44].
In particular, approximate controllability of Hilfer FDEs under different conditions has been discussed widely. Mahmudov et al. [36] investigated the exact controllability of Hilfer FDEs in a Hilbert space under the assumption that a linear system of the given equation is approximate controllable. In 2017, Yang et al. [41] discussed the approximate controllability of Hilfer FDEs with nonlocal conditions in a Banach space with the help of semigroup theory, fixed point techniques, and multivalued analysis. Later on, Debbouche et al. [14] and Du et al. [17] studied the approximate controllability of Hilfer FDEs and semilinear Hilfer FDEs with impulsive control inclusions in Banach spaces, respectively. In 2018, Lv and Yang [34] investigated the approximate controllability of neutral Hilfer FDEs by applying the techniques of stochastic analysis theory and semigroup operator theory in a Hilbert space. In recent works, Lv and Yang [35], with the help of Banach contraction principle, discussed the approximate controllability for a class of Hilfer FDEs of order \(1< \alpha < 2\) and type \(0\le \beta \le 1\). It is noted that, in almost all the problems discussed above, a linear operator generates the strongly continuous semigroup of bounded linear operators.
In [37] Periago and Straub formulated theory to analyze almost sectorial operators. Here authors also mentioned the suitable assumptions required to establish the existence of mild solutions and classical solutions of FDEs with almost sectorial operator. There are numerous works focussing on the existence of mild solutions and analytical solutions of fractional evolution equations with almost sectorial operators [16, 33, 43]. Recently, Jaiswal et al. [21] proved the existence of mild solutions of Hilfer FDEs with almost sectorial operators. We found that in the available literature, approximate controllability of Hilfer FDEs with almost sectorial operators has not been discussed yet. Thus, motivated by the above-discussed works, we consider here the following system of Hilfer FDEs for investigating proposed results:

where \({}^{H}{\mathcal{D}}^{\nu , \mu }_{0^{+}}\) is the Hilfer fractional derivative of order \(0<\nu <1\) and type \(0\le \mu \le 1\). \({\mathcal{A}}:D({\mathcal{A}})\subset {\mathcal{V}}\longrightarrow { \mathcal{V}}\) is an almost sectorial operator in Banach space \({\mathcal{V}}\) and  ,
,  . The control function
. The control function  takes value in \(\mathcal{L}^{2}(\mathfrak{J}, \mathcal{W})\). \(\mathcal{L}^{2}(\mathfrak{J}, \mathcal{W} )\) denotes the space of admissible control functions for Banach space \(\mathcal{W}\). ϒ is a bounded linear operator from \(\mathcal{W}\) into \(\mathcal{V}\). \(\varPsi :\mathfrak{J}\times \mathcal{V} \times \mathcal{V} \longrightarrow \mathcal{V} \) is a continuous linear mapping,
takes value in \(\mathcal{L}^{2}(\mathfrak{J}, \mathcal{W})\). \(\mathcal{L}^{2}(\mathfrak{J}, \mathcal{W} )\) denotes the space of admissible control functions for Banach space \(\mathcal{W}\). ϒ is a bounded linear operator from \(\mathcal{W}\) into \(\mathcal{V}\). \(\varPsi :\mathfrak{J}\times \mathcal{V} \times \mathcal{V} \longrightarrow \mathcal{V} \) is a continuous linear mapping,  , \(\mathfrak{m}\in \mathbb{N}\), and
, \(\mathfrak{m}\in \mathbb{N}\), and  are real numbers such that
are real numbers such that  . The characteristics functions \(\mathfrak{q}(\mathfrak{t},\mathfrak{s}) : \varDelta \longrightarrow \mathbb{R}\) and \(\varphi : \varDelta \times \mathcal{V} \longrightarrow \mathcal{V}\),
. The characteristics functions \(\mathfrak{q}(\mathfrak{t},\mathfrak{s}) : \varDelta \longrightarrow \mathbb{R}\) and \(\varphi : \varDelta \times \mathcal{V} \longrightarrow \mathcal{V}\),  are specified in the next section.
are specified in the next section.
2 Preliminaries
Let us consider \(\mathcal{V}\) and \(\mathcal{W} \) as real Banach spaces with respective norms \(\lVert \cdot \rVert _{\mathcal{V}}\) and \(\lVert \cdot \rVert _{\mathcal{W}}\). \(\mathcal{C}(\mathfrak{J}, \mathcal{V})\) denotes the Banach space formed by all continuous functions from \(\mathfrak{J}\) into \(\mathcal{V}\) with corresponding norm function  . \(\mathcal{L}^{2}(\mathfrak{J}, \mathcal{W} )\) denotes the Banach space of all \(\mathcal{W}\)-valued Bochner square integrable functions defined on \(\mathfrak{J}\) w.r.t. norm function
. \(\mathcal{L}^{2}(\mathfrak{J}, \mathcal{W} )\) denotes the Banach space of all \(\mathcal{W}\)-valued Bochner square integrable functions defined on \(\mathfrak{J}\) w.r.t. norm function

Definition 2.1
([20])
Hilfer fractional derivative of a continuously differentiable function f of order \(0 < \nu <1\) and \(0\le \mu \le 1\) is defined as
where \({\mathcal{I}}^{\nu (1-\mu )}_{0^{+}}\) is a Riemann–Liouville fractional integral and \({\mathcal{D}}^{\nu +\mu -\nu \mu }_{0^{+}}\) is a Riemann–Liouville fractional derivative.
Definition 2.2
([38])
For \(\alpha >0\), the Riemann–Liouville fractional integral of a continuously differentiable f of order α is defined as follows:
Almost sectorial operator
Let \(0< \beta < \pi \) and \(-1<\gamma <0\). We define \(S^{o}_{\beta } = \lbrace \omega \in \mathbb{C}\setminus \lbrace 0 \rbrace \colon \lvert \operatorname{arg} \omega \rvert < \beta \rbrace\) and \(S_{\beta } =\bar{S^{o}_{\beta }}= \lbrace \omega \in \mathbb{C} \setminus \lbrace 0 \rbrace \colon \lvert \operatorname{arg} \omega \rvert \le \beta \rbrace \cup \lbrace 0 \rbrace \). A closed linear operator \({\mathcal{A}}:D({\mathcal{A}})\subset {\mathcal{V}}\longrightarrow { \mathcal{V}}\) is called an almost sectorial operator if the following hold:
-
1.
\(\sigma (\mathcal{A})\) is contained in \(S_{\omega }\).
-
2.
\(\forall \beta \in (\omega , \pi )\) there exists a constant \(\mathcal{M}_{\beta }>0\) such that \(\lVert \mathcal{R}(\mathfrak{z}, \mathcal{A} ) \rVert _{L( \mathcal{V})}\le {\mathcal{M}}_{\beta } |\mathfrak{z}|^{\gamma }\),
where \(\mathcal{R}(\mathfrak{z}, \mathcal{A})= (\mathfrak{z} I- \mathcal{A} )^{-1}\) is the resolvent operator of \(\mathcal{A} \) for \(\mathfrak{z} \in \rho (\mathcal{A}) \).
Let us define \(\Theta ^{\gamma }_{\omega }\) as a family of almost sectorial operators.
Proposition 2.1
([21])
Let  be the compact semigroup defined in [37] and \(\mathcal{A} \in \Theta ^{\gamma }_{\omega }\) for \(-1<\gamma <0\) and \(0<\omega <\frac{\pi }{2}\). Then following holds for
be the compact semigroup defined in [37] and \(\mathcal{A} \in \Theta ^{\gamma }_{\omega }\) for \(-1<\gamma <0\) and \(0<\omega <\frac{\pi }{2}\). Then following holds for  :
:
(i)  is analytic and
is analytic and  , \(\mathfrak{t} \in S^{o}_{ \frac{\pi }{2}-\omega } \). (ii)
, \(\mathfrak{t} \in S^{o}_{ \frac{\pi }{2}-\omega } \). (ii)  \(\forall \mathfrak{t}\), \(\mathfrak{s}\in S^{o}_{ \frac{\pi }{2}-\omega } \). (iii)
\(\forall \mathfrak{t}\), \(\mathfrak{s}\in S^{o}_{ \frac{\pi }{2}-\omega } \). (iii)  , \(\mathfrak{t}>0\); where \(c_{0}>0 \) is a constant. (iv) Let
, \(\mathfrak{t}>0\); where \(c_{0}>0 \) is a constant. (iv) Let  , then
, then  if \(\theta > 1+\gamma \).
if \(\theta > 1+\gamma \).
Let us define the operator families  and
and  as follows:
as follows:

where \(\mathcal{M}_{\nu }(\theta )\) is a Wright-type function defined as follows:
Proposition 2.2
([21])
(i) For each fixed \(\mathfrak{t} \in S^{o}_{\frac{\pi }{2}-\omega }\),  and
and  are bounded linear operators in \(\mathcal{V}\). Also
are bounded linear operators in \(\mathcal{V}\). Also

where  and
and  are constants depending only on ν and γ. (ii)
are constants depending only on ν and γ. (ii)  and
and  are continuous in the uniform operator topology for \(\mathfrak{t}>0 \).
are continuous in the uniform operator topology for \(\mathfrak{t}>0 \).
Lemma 2.1
The mild solution for the system of equations Eq. (1.1) is defined as follows:

where  and
and  .
.
Proposition 2.3
([21])
(i) For every fixed \(\mathfrak{t}\in S^{o}_{\frac{\pi }{2}-\omega }\),  and
and  are bounded linear operators on \(\mathcal{V}\). For \(\mathfrak{t}>0\),
are bounded linear operators on \(\mathcal{V}\). For \(\mathfrak{t}>0\),

(ii)  and
and  are strongly continuous operators.
are strongly continuous operators.
Let  ,
,  . Assume that
. Assume that  .
.
We have

By the operator spectrum theorem,  exists bounded and \(D( \mathcal{O})= \mathcal{V}\).
exists bounded and \(D( \mathcal{O})= \mathcal{V}\).
By the Neumann series expression, \(\mathcal{O}\) can be expressed as  .
.
Therefore

By Lemma 2.1 mild solutions of Eq. (1.1) are given by

At  ,
,

Thus the mild solutions of Eq. (1.1) are defined as follows:

Now we introduce the Green’s function \(\mathcal{G}(\mathfrak{t}, \mathfrak{s})\) as follows:

where

The mild solutions of Eq. (1.1) in terms of the Green’s function are expressed as

In addition to the above-mentioned propositions and lemma, we assume here the following assumptions to establish the proposed results:
-
(A1)
For each \(\mathfrak{t} \in \mathfrak{J}^{\prime }\), \(\varPsi :\mathfrak{J}^{\prime } \times \mathcal{V} \times \mathcal{V} \longrightarrow \mathcal{V}\) is a Caratheodory function.
-
(A2)
There exist \(\psi _{1}\in L^{1}(\mathfrak{J}, \mathbb{R}^{+})\) and a continuous function \(\psi _{2}\) such that, for
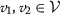 and \(\mathfrak{t} \in \mathfrak{J}\),
and \(\mathfrak{t} \in \mathfrak{J}\), 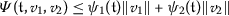 .
. -
(A3)
\(\varphi (\mathfrak{t},\mathfrak{s}, \cdot): \mathcal{V} \longrightarrow \mathcal{V}\) is a Caratheodory function and there exists
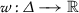 with
with
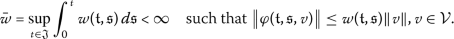
-
(A4)
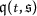 is bounded on
is bounded on 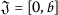 with
with 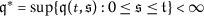 .
. -
(A5)
There exists \(\kappa \in L^{1}(\mathfrak{J}, \mathbb{R}^{+})\) such that
 , \(\forall \mathfrak{t} \in \mathfrak{J}\) and
, \(\forall \mathfrak{t} \in \mathfrak{J}\) and 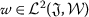 .
.
3 Existence result
For  and
and  , we introduce
, we introduce

with the norm defined as  .
.
Let  . Then
. Then  iff
iff  and
and  .
.
We define

Define an operator \(\mathcal{P} : \mathcal{B}_{\delta }(\mathfrak{J}) \longrightarrow \mathcal{B}_{\delta }(\mathfrak{J}) \) such that

where  is defined as
is defined as

Let us denote  ,
,  , \(\hat{\mathfrak{m}}= \sup_{\mathfrak{t}\in \mathfrak{J}^{\prime } } \lbrace \kappa (\mathfrak{t}) \rbrace \), and
, \(\hat{\mathfrak{m}}= \sup_{\mathfrak{t}\in \mathfrak{J}^{\prime } } \lbrace \kappa (\mathfrak{t}) \rbrace \), and  .
.
Lemma 3.1
Let \(\mathcal{A} \in \Theta ^{\gamma }_{\omega }\) for \(-1<\gamma <0\) and \(0<\omega <\frac{\pi }{2}\). Assume that assumptions (A1)–(A5) and Proposition 2.3hold. Then the operator  is bounded and continuous if
is bounded and continuous if  .
.
Proof
For  , we have
, we have

If possible, suppose  .
.
This implies

Applying \(\lim_{\delta \longrightarrow \infty }\) on both sides, we have

which is a contradiction.
So our supposition is wrong. Therefore  . This implies the boundedness of operator \(\mathcal{P}\).
. This implies the boundedness of operator \(\mathcal{P}\).
Now, to show that \(\mathcal{P}: \mathcal{B}_{\delta }(\mathfrak{J}) \longrightarrow \mathcal{B}_{\delta }(\mathfrak{J})\) is a continuous operator, let  and
and  with
with  , \(n \in \mathbb{N}\).
, \(n \in \mathbb{N}\).
By the continuity of function Ψ w.r.t. to the second and third variable

For \(\mathfrak{t} \in \mathfrak{J}\),

Since

by the Lebesgue dominated convergence theorem and the continuity of function Ψ,

This completes the proof of Lemma 3.1. □
Lemma 3.2
Let \(\mathcal{A} \in \Theta ^{\gamma }_{\omega }\) for \(-1<\gamma <0\) and \(0<\omega <\frac{\pi }{2}\). If assumptions (A1)–(A5) and Proposition 2.3are satisfied, the operator  is equicontinuous for \(\mathfrak{t} \in \mathfrak{J}\).
is equicontinuous for \(\mathfrak{t} \in \mathfrak{J}\).
Proof
For  and
and  ,
,

Here,

The strong continuity of operator  yields
yields  as \(\mathfrak{t}_{1}\longrightarrow \mathfrak{t}_{2}\).
as \(\mathfrak{t}_{1}\longrightarrow \mathfrak{t}_{2}\).

Following Lemma 3.1 and assumptions (A1)–(A5), it is easy to see that

exists and is bounded. Thus  as \(\mathfrak{t}_{2} \longrightarrow \mathfrak{t}_{1}\).
as \(\mathfrak{t}_{2} \longrightarrow \mathfrak{t}_{1}\).

After following the given assumptions and performing some steps of calculation, we have

Clearly,  as \(\mathfrak{t}_{2} \longrightarrow \mathfrak{t}_{1} \).
as \(\mathfrak{t}_{2} \longrightarrow \mathfrak{t}_{1} \).
So, we have

This proves the equicontinuity of operator  . □
. □
Theorem 3.1
Let \(-1<\gamma <0\), \(0<\omega <\frac{\pi }{2}\), and  . The system of equations Eq. (1.1) has at least one mild solution in
. The system of equations Eq. (1.1) has at least one mild solution in  if assumptions (A1)–(A5) hold along with Lemma 3.1and Lemma 3.2.
if assumptions (A1)–(A5) hold along with Lemma 3.1and Lemma 3.2.
Proof
The mild solution of Eq. (1.1) is equivalent to the fixed point of operator \(\mathcal{P} : \mathcal{B}_{\delta }(\mathfrak{J}) \longrightarrow \mathcal{B}_{\delta }(\mathfrak{J}) \). Here we prove that the operator \(\mathcal{P}\) has at least one fixed point.
In the following, we show that the operator \(\mathcal{P}\) is relatively compact in \(\mathcal{V}\) for every \(\mathfrak{t} \in \mathfrak{J}\).
We prove this by showing that there is a relatively compact set  arbitrarily close to the set
arbitrarily close to the set  in \(\mathcal{V}\) for
in \(\mathcal{V}\) for  .
.
Define the operator  by
by

Since  and
and  are compact for \(\mathfrak{t}>0\), the set
are compact for \(\mathfrak{t}>0\), the set  is compact for \(\mathfrak{t} \in \mathfrak{J}^{\prime }\). In the following
is compact for \(\mathfrak{t} \in \mathfrak{J}^{\prime }\). In the following

Clearly,

We have shown that the set  is arbitrarily close to the relatively compact set
is arbitrarily close to the relatively compact set  . This implies
. This implies  is relatively compact in \(\mathcal{V}\). Also, by Lemma 3.1 and Lemma 3.2, the operator \(\mathcal{P} : \mathcal{B}_{\delta }(\mathfrak{J}^{\prime }) \longrightarrow \mathcal{B}_{\delta }(\mathfrak{J}^{\prime }) \) is bounded, continuous, and equicontinuous in \(\mathcal{V}\). So by the Arzela–Ascoli theorem,
is relatively compact in \(\mathcal{V}\). Also, by Lemma 3.1 and Lemma 3.2, the operator \(\mathcal{P} : \mathcal{B}_{\delta }(\mathfrak{J}^{\prime }) \longrightarrow \mathcal{B}_{\delta }(\mathfrak{J}^{\prime }) \) is bounded, continuous, and equicontinuous in \(\mathcal{V}\). So by the Arzela–Ascoli theorem,  is a compact operator. Hence, by Schauder’s fixed point theorem, \(\mathcal{P}\) has at least one fixed point
is a compact operator. Hence, by Schauder’s fixed point theorem, \(\mathcal{P}\) has at least one fixed point  .
.
Let  . Then
. Then  is a mild solution of Eq. (1.1). This completes the proof. □
is a mild solution of Eq. (1.1). This completes the proof. □
4 Approximate controllability
In this section, we discuss the approximate controllability of Eq. (1.1).
The system of equations Eq. (1.1) is said to be approximate controllable on  if, for every desired final state
if, for every desired final state  and \(\epsilon >0\), there exists a control function
and \(\epsilon >0\), there exists a control function  such that the mild solution
such that the mild solution  of Eq. (1.1) satisfies
of Eq. (1.1) satisfies

Following this, we first introduce the following two operators:

where \(\varUpsilon ^{*}\), \(\mathcal{O}^{*}\),  , and
, and  characterize the adjoint operators of ϒ, \(\mathcal{O}\),
characterize the adjoint operators of ϒ, \(\mathcal{O}\),  , and
, and  respectively,
respectively,

Theorem 4.1
Let \(\mathcal{A} \in \Theta ^{\gamma }_{\omega }\) for \(-1<\gamma <0\) and \(0<\omega <\frac{\pi }{2}\). Assume that assumptions (A1)–(A5) and Proposition 2.3hold. The system of equations Eq. (1.1) is approximate controllable on \(\mathfrak{J}\) if  as \(\lambda \longrightarrow 0^{+}\) in the strong operator topology.
as \(\lambda \longrightarrow 0^{+}\) in the strong operator topology.
Proof
By Theorem 3.1, the system of equations Eq. (1.1) has at least one mild solution  given by
given by

where we define the control function  as
as

with

At  ,
,

which implies that the sequence  is bounded in the Hilbert space
is bounded in the Hilbert space  . Therefore, there exists a subsequence of the sequence
. Therefore, there exists a subsequence of the sequence  converging weakly to some point
converging weakly to some point  .
.
Let us write

Hence, by Eqs. (4.4) and (4.6), we have

By the compactness of operators  and
and  for \(\mathfrak{t}>0\), one gets the compactness of Green’s function \(\mathcal{G}(\mathfrak{t}, \mathfrak{s})\) for \(\mathfrak{t}, \mathfrak{s}>0\), which implies that
for \(\mathfrak{t}>0\), one gets the compactness of Green’s function \(\mathcal{G}(\mathfrak{t}, \mathfrak{s})\) for \(\mathfrak{t}, \mathfrak{s}>0\), which implies that

Thus from Eq. (4.7) and Eq. (4.8) we get

Equation (4.5) implies that

Hence the approximate controllability of Eq. (1.1). □
5 Applications
Here we investigate the proposed results for the following Cauchy problem:

in the Banach space  , \(0<\eta <1\), where \(\nu = \frac{1}{4}\), \(\mu = \frac{1}{2}\), \(\wp >0\) and
, \(0<\eta <1\), where \(\nu = \frac{1}{4}\), \(\mu = \frac{1}{2}\), \(\wp >0\) and  ,
,  , are such that
, are such that  . On substituting
. On substituting  , Eq. (5.1) reduces to Eq. (1.1) with
, Eq. (5.1) reduces to Eq. (1.1) with  and
and  . It follows from article [37] that there exist constants \(\rho , \epsilon >0\) such that \(\mathcal{A}+ \rho \in \Theta ^{\frac{\eta }{2}-1}_{\frac{\pi }{2}- \epsilon }(\mathcal{V})\). The compactness of semigroup \(\lbrace \mathfrak{T}(\mathfrak{t}) \rbrace \) follows from (Lemma 4.66) [42]. Since
. It follows from article [37] that there exist constants \(\rho , \epsilon >0\) such that \(\mathcal{A}+ \rho \in \Theta ^{\frac{\eta }{2}-1}_{\frac{\pi }{2}- \epsilon }(\mathcal{V})\). The compactness of semigroup \(\lbrace \mathfrak{T}(\mathfrak{t}) \rbrace \) follows from (Lemma 4.66) [42]. Since  and
and  is embedded in
is embedded in  , the compactness of resolvent operators follows for every \(\eta >0\).
, the compactness of resolvent operators follows for every \(\eta >0\).

The bounded linear operator \(\varUpsilon :\mathcal{W}= \mathcal{V}\longrightarrow \mathcal{V}\) is defined as  .
.
Following this discussion and the definition of function Ψ and bounded operator ϒ, it is easy to verify that assumptions (A1)–(A5) hold with

Hence the existence and approximate controllability of Eq. (5.1) follow from Theorem 3.1 and Theorem 4.1 respectively.
6 Conclusion
In this paper, we discussed the approximate controllability of Hilfer fractional differential equations with almost sectorial operators. We first prove the existence of mild solutions for similar equations by applying fixed point theory. We will try to investigate the exact controllability and stability of a similar problem in our future research work.
Availability of data and materials
Not applicable.
References
Alkhazzan, A., Jiang, P., Baleanu, D., Khan, H., Khan, A.: Stability and existence results for a class of nonlinear fractional differential equations with singularity. Math. Methods Appl. Sci. 41(18), 9321–9334 (2018). https://doi.org/10.1002/mma.5263
Bedi, P., Kumar, A., Abdeljawad, T., Khan, A.: Existence of mild solutions for impulsive neutral Hilfer fractional evolution equations. Adv. Differ. Equ. 2020, 155 (2020). https://doi.org/10.1186/s13662-020-02615-y
Bedi, P., Kumar, A., Abdeljawad, T., Khan, A.: S-asymptotically ω-periodic mild solutions and stability analysis of Hilfer fractional evolution equations. Evol. Equ. Control Theory (2020). https://doi.org/10.3934/eect.2020089
Chang, Y.K., Pereira, A., Ponce, R.: Approximate controllability for fractional differential equations of Sobolev type via properties on resolvent operators. Fract. Calc. Appl. Anal. 20(4), 963–987 (2017)
Chen, P., Zhang, X.: Approximate controllability of nonlocal problem for non-autonomous stochastic evolution equations. Evol. Equ. Control Theory (2019). https://doi.org/10.3934/eect.2020076
Chen, P., Zhang, X., Li, Y.: Approximation technique for fractional evolution equations with nonlocal integral conditions. Mediterr. J. Math. 14(6), 226 (2017). https://doi.org/10.1007/s00009-017-1029-0
Chen, P., Zhang, X., Li, Y.: A blowup alternative result for fractional nonautonomous evolution equation of Volterra type. Commun. Pure Appl. Anal. 17(5), 1975–1992 (2018)
Chen, P., Zhang, X., Li, Y.: Non-autonomous parabolic evolution equations with non-instantaneous impulses governed by noncompact evolution families. J. Fixed Point Theory Appl. 21(3), 84 (2019). https://doi.org/10.1007/s11784-019-0719-6
Chen, P., Zhang, X., Li, Y.: Non-autonomous evolution equations of parabolic type with non-instantaneous impulses. Mediterr. J. Math. 16(5), 118 (2019). https://doi.org/10.1007/s00009-019-1384-0
Chen, P., Zhang, X., Li, Y.: Fractional non-autonomous evolution equation with nonlocal conditions. J. Pseudo-Differ. Oper. Appl. 10(4), 955–973 (2019). https://doi.org/10.1007/s11868-018-0257-9
Chen, P., Zhang, X., Li, Y.: Existence and approximate controllability of fractional evolution equations with nonlocal conditions via resolvent operators. Fract. Calc. Appl. Anal. 23(1), 268–291 (2020). https://doi.org/10.1515/fca-2020-0011
Chen, P., Zhang, X., Li, Y.: Approximate controllability of non-autonomous evolution system with nonlocal conditions. J. Dyn. Control Syst. 26(1), 1–16 (2020). https://doi.org/10.1007/s10883-018-9423-x
Chen, P., Zhang, X., Li, Y.: Cauchy problem for fractional non-autonomous evolution equations. Banach J. Math. Anal. 14(2), 559–584 (2020). https://doi.org/10.1007/s43037-019-00008-2
Debbouche, A., Antonov, V.: Approximate controllability of semilinear Hilfer fractional differential inclusions with impulsive control inclusion conditions in Banach spaces. Chaos Solitons Fractals 102, 140–148 (2017). https://doi.org/10.1016/j.chaos.2017.03.023
Devi, A., Kumar, A., Abdeljawad, T., Khan, A.: Existence and stability analysis of solutions for fractional Langevin equation with nonlocal integral and anti-periodic type boundary conditions. Fractals (2020). https://doi.org/10.1142/S0218348X2040006X
Ding, X.L., Ahmad, B.: Analytical solutions to fractional evolution equations with almost sectorial operators. Adv. Differ. Equ. 2016(1), 203 (2016). https://doi.org/10.1186/s13662-016-0927-y
Du, J., Jiang, W., Niazi, A.U.K.: Approximate controllability of impulsive Hilfer fractional differential inclusions. J. Nonlinear Sci. Appl. 10(2), 595–611 (2017)
Fu, X.: Approximate controllability of semilinear non-autonomous evolution systems with state-dependent delay. Evol. Equ. Control Theory 6(4), 517–534 (2017). https://doi.org/10.3934/eect.2017026
Gomez-Aguilar, J.F., Cordova-Fraga, T., Abdeljawad, T., Khan, A., Khan, H.: Analysis of fractal-fractional malaria transmission model. Fractals (2020). https://doi.org/10.1142/S0218348X20400411
Gu, H., Trujillo, J.J.: Existence of mild solution for evolution equation with Hilfer fractional derivative. Appl. Math. Comput. 257, 344–354 (2015). https://doi.org/10.1016/j.amc.2014.10.083
Jaiswal, A., Bahuguna, D.: Hilfer fractional differential equations with almost sectorial operators. Differ. Equ. Dyn. Syst. (2020). https://doi.org/10.1007/s12591-020-00514-y
Khan, A., Khan, T.S., Syam, M.I., Khan, H.: Analytical solutions of time-fractional wave equation by double Laplace transform method. Eur. Phys. J. Plus 134(4), 163 (2019). https://doi.org/10.1140/epjp/i2019-12499-y
Khan, A., Shah, K., Li, Y., Khan, T.S.: Ulam type stability for a coupled system of boundary value problems of nonlinear fractional differential equations. J. Funct. Spaces (2017). https://doi.org/10.1155/2017/3046013
Khan, A., Syam, M.I., Zada, A., Khan, H.: Stability analysis of nonlinear fractional differential equations with Caputo and Riemann–Liouville derivatives. Eur. Phys. J. Plus 133(7), 264 (2018). https://doi.org/10.1140/epjp/i2018-12119-6
Khan, H., Alipour, M., Khan, R.A., Tajadodi, H., Khan, A.: On approximate solution of fractional order logistic equations by operational matrices of Bernstein polynomials. J. Math. Comput. Sci. 14, 222–232 (2015)
Khan, H., Chen, W., Khan, A., Khan, T.S., Al-Madlal, Q.M.: Hyers–Ulam stability and existence criteria for coupled fractional differential equations involving p-Laplacian operator. Adv. Differ. Equ. 2018(1), 455 (2018). https://doi.org/10.1186/s13662-018-1899-x
Khan, H., Gomez Aguilar, J.F., Abdeljawad, T., Khan, A.: Existence results and stability criteria for ABC-fuzzy-Volterra integro-differential equation. Fractals (2020). https://doi.org/10.1142/S0218348X20400484
Khan, H., Gómez-Aguilar, J.F., Alkhazzan, A., Khan, A.: A fractional order HIV-TB coinfection model with nonsingular Mittag-Leffler law. Math. Methods Appl. Sci. 43(6), 3786–3806 (2020). https://doi.org/10.1002/mma.6155
Khan, H., Tunç, C., Alkhazan, A., Ameen, B., Khan, A.: A generalization of Minkowski’s inequality by Hahn integral operator. J. Taibah Univ. Sci. 12(5), 506–513 (2018). https://doi.org/10.1080/16583655.2018.1493859
Khan, Z.A.: Integral inequality of Gronwall type with an application. J. Math. Comput. Sci. 5(1), 34–41 (2015)
Khan, Z.A.: Solvability for a class of integral inequalities with maxima on the theory of time scales and their applications. Bound. Value Probl. 2019, 146 (2019). https://doi.org/10.1186/s13661-019-1259-0
Khan, Z.A.: Analysis on some powered integral inequalities with retarded argument and application. J. Taibah Univ. Sci. 14(1), 488–495 (2020). https://doi.org/10.1080/16583655.2020.1747218
Li, F.: Mild solutions for abstract fractional differential equations with almost sectorial operators and infinite delay. Adv. Differ. Equ. 2013(1), 327 (2013). https://doi.org/10.1186/1687-1847-2013-327
Lv, J., Yang, X.: Approximate controllability of Hilfer fractional neutral stochastic differential equations. Dyn. Syst. Appl. 27(4), 691–713 (2018). https://doi.org/10.12732/dsa.v27i4.1
Lv, J., Yang, X.: Approximate controllability of Hilfer fractional differential equations. Math. Methods Appl. Sci. 43(1), 242–254 (2020). https://doi.org/10.1002/mma.5862
Mahmudov, N.I., McKibben, M.A.: On the approximate controllability of fractional evolution equations with generalized Riemann–Liouville fractional derivative. J. Funct. Spaces 2015, Article ID 263823 (2015). https://doi.org/10.1155/2015/263823
Periago, F., Straub, B.: A functional calculus for almost sectorial operators and applications to abstract evolution equations. J. Evol. Equ. 2(1), 41–68 (2002). https://doi.org/10.1007/s00028-002-8079-9
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Ullah, M., Sarwar, M., Khan, H., Abdeljawad, T., Khan, A.: Near-coincidence point results in metric interval space and hyperspace via simulation functions. Adv. Differ. Equ. 2020(1), 291 (2020). https://doi.org/10.1186/s13662-020-02734-6
Wang, J., Fečkan, M., Zhou, Y.: Approximate controllability of Sobolev type fractional evolution systems with nonlocal conditions. Evol. Equ. Control Theory 6(3), 471 (2017)
Yang, M., Wang, Q.R.: Approximate controllability of Hilfer fractional differential inclusions with nonlocal conditions. Math. Methods Appl. Sci. 40(4), 1126–1138 (2017). https://doi.org/10.1002/mma.4040
Yong, Z., Jinrong, W., Lu, Z.: Basic Theory of Fractional Differential Equations. World Scientific, Singapore (2016)
Zhang, L., Zhou, Y.: Fractional Cauchy problems with almost sectorial operators. Appl. Math. Comput. 257, 145–157 (2015). https://doi.org/10.1016/j.amc.2014.07.024
Zhou, Y., Vijayakumar, V., Ravichandran, C., Murugesu, R.: Controllability results for fractional order neutral functional differential inclusions with infinite delay. Fixed Point Theory 18(2), 773–798 (2017). https://doi.org/10.24193/fpt-ro.2017.2.62
Acknowledgements
The first author (Pallavi Bedi) acknowledges the support of Council of Scientific and Industrial Research (CSIR)-New Delhi, India, and the third author (Thabet Abdeljawad) acknowledges the support of Prince Sultan University for funding this work through research group in Applied Mathematics (NAMAM) group number RG-DES-201701-17.
Funding
Prince Sultan University for funding this work through research group in Applied Mathematics (NAMAM) group number RG-DES-201701-17.
Author information
Authors and Affiliations
Contributions
All the authors have made equal contributions in this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bedi, P., Kumar, A., Abdeljawad, T. et al. Existence and approximate controllability of Hilfer fractional evolution equations with almost sectorial operators. Adv Differ Equ 2020, 615 (2020). https://doi.org/10.1186/s13662-020-03074-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-03074-1



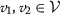 and
and 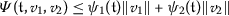 .
.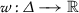 with
with
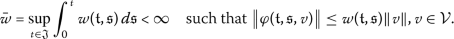
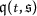 is bounded on
is bounded on 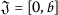 with
with 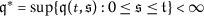 .
. ,
, 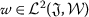 .
.