1 Introduction

Competitive neural networks (CNNs), firstly proposed by Meyer-Bäse et al. in [1], involve two types of memory: long-term and short-term memories. Viewed mathematically, there are two classes of state variables in such a network model described by ODEs, one is short-term memory, which depicts fast neuronal activity, another one is long-term memory, which depicts the slow unsupervised synaptic modifications. Such a network model possesses a two-layer structure and then extensive fundamental results have been reported to address the dynamic behaviors of such a network model. For example, Lu and He in [2] gave some sufficient conditions for the global exponential stability of delayed competitive neural networks with different time scales. Nie and Cao [3], Duan and Huang [4] studied the dynamics of equilibrium for two different kinds of competitive neural networks with time-varying delay and discontinuous activations, respectively. Nie et al. [5, 6], and Xu et al. [7], respectively, investigated the multistability issue of CNNs by using the fixed point theorem and the contraction mapping theorem. Pratap [8] and Yang [9] investigated the finite time synchronization and adaptive lag synchronization problem of delayed CNNs. For other interesting theoretical results of CNNs, one may refer to [10–16] and the references therein.

On the other hand, for evident engineering and biological reasons, it is often useful to bring an inertial term into a neural system. For instance, comparing to electronic neural networks of the standard resistor–capacitor variety, Babcocka and Westervelt showed that the dynamics could be complex when the neuron couplings were of an inertial nature [17]. Another evident biological reason for introducing an inertial term into the standard neural system is the implementation of the membrane of a hair cell by equivalent circuits containing an inductance in semicircular canals of some animals, such as pigeon [18]. Therefore, various dynamical behaviors for types of neural networks with inertial terms have been studied by many authors, such as in [19–26] and the references therein. However, the method employed in the aforementioned works are all through a reduced-order approach, that is, by changing the second-order inertial neural networks into the first-order system, the reduced-order method clearly expanding the dimension of the system, which increases the difficulty of the theoretical analysis for the NNs.

In this paper, abandoning the traditional reduced-order method and being inspired by recent work [27, 28], we further study the issue of exponential stability of a delayed inertial CNNs. The main contribution of this paper lies in the following aspects.

  1. (1)

    By introducing the non-reduced-order approach, a novel Lyapunov–Krasovskii functional proposed and new criteria are established for the exponential stability of the considered model.

  2. (2)

    Different from existing works on the stability analysis of delayed CNNs in which the reduced-order approach is employed, the presented non-reduced-order approach significantly reduces the computational complexity and improves some recently reported ones.

This paper is outlined as follows. In Sect. 2, a model description and preliminaries are presented. In Sect. 3, exponential stability of the considered model is studied. In Sect. 4, a numerical example is provided. Finally, a conclusion is drawn in Sect. 5.

2 Model description and preliminaries

In this paper, we consider the following delayed inertial CNN model:

$$\begin{aligned} \textstyle\begin{cases} {\mathrm{STM}}: {x}''_{i}(t)=-a_{i}{x'_{i}}(t)-{b_{i}}{x_{i}(t)}+ {\sum_{j=1}^{n}}D_{ij}f_{j}(x_{j}(t)) +{\sum_{j=1}^{n}}D _{ij}^{\tau }g_{j}(x_{j}(t-\tau (t))) \\ \hphantom{{\mathrm{STM}}: {x}''_{i}(t)=}{}+c_{i}\sum_{l=1}^{q}m_{il}(t)p_{l}+I_{i}, \\ \mathrm{LTM}: {m}''_{il}(t)=-m'_{il}(t)-m_{il}(t)+p_{l}f_{i}(x_{i}(t)),\quad i=1,\ldots,n, l=1,\ldots,q, \end{cases}\displaystyle \end{aligned}$$
(2.1)

where \(x_{i}(t) \) is the neuron current activity level, \(f_{j}(t) \) and \(g_{j}(t-\tau (t))\) are the activation functions, \(m_{il}(t)\) is the synaptic efficiency, \(p_{l}\) is the constant external stimulus, \(D _{ij}\) represents the connection weight between the ith neuron and the jth neuron, \(c_{i}\) is the strength of the external stimulus, \(D _{ij}^{\tau }\) represents the synaptic weight of delayed feedback and \(I_{i}\) is the constant input. In system (2.1), the second derivatives are called inertial terms, and the time-varying delay \(\tau (t)\) is a differentiable function satisfying

$$ 0\leq \tau (t)\leq \tau ,\qquad \tau '(t)\leq \mu < 1. $$
(2.2)

Firstly, we shall rewrite system (2.1) as follows:

Setting

$$ s_{i}(t)=\sum_{l=1}^{q}m_{il}(t)p_{l}= \mathbf{p}^{T}{\mathbf{m_{i}(t)}}, $$

where \(\mathbf{p}=(p_{1},p_{2},\ldots ,p_{q})^{T}\), \(\mathbf{m_{i}(t)}=(m _{i1}(t),m_{i2}(t),\ldots ,m_{iq}(t))^{T}\), and summing up the LTM over l, the neural networks (2.1) can be rewritten as the state-space form

$$\begin{aligned} \textstyle\begin{cases} {\mathrm{STM}}: {x}''_{i}(t)=-a_{i}{x'_{i}}(t)-{b_{i}}{x_{i}(t)}+ {\sum_{j=1}^{n}}D_{ij}f_{j}(x_{j}(t)) +{\sum_{j=1}^{n}}D _{ij}^{\tau }g_{j}(x_{j}(t-\tau (t))) \\ \hphantom{{\mathrm{STM}}: {x}''_{i}(t)=}{}+c_{i}s_{i}+I_{i}, \\ \mathrm{LTM}: {s}''_{i}(t)=-s'_{i}(t)-s_{i}(t)+ \Vert \mathbf{p} \Vert ^{2}f _{i}(x_{i}(t)), \end{cases}\displaystyle \end{aligned}$$

where \(\|\mathbf{p}\|^{2}=p^{2}_{1}+\cdots +p^{2}_{q}\) is a constant. Without loss of generality, the input stimulus p is assumed to be normalized with unit magnitude \(\|\mathbf{p}\|^{2}=1\), then the above networks are simplified as

$$\begin{aligned} \textstyle\begin{cases} {\mathrm{STM}}: {x}''_{i}(t)=-a_{i}{x'_{i}}(t)-{b_{i}}{x_{i}(t)}+ {\sum_{j=1}^{n}}D_{ij}f_{j}(x_{j}(t)) +{\sum_{j=1}^{n}}D _{ij}^{\tau }g_{j}(x_{j}(t-\tau (t))) \\ \hphantom{{\mathrm{STM}}: {x}''_{i}(t)=}{}+c_{i}s_{i}+I_{i}, \\ \mathrm{LTM}: {s}''_{i}(t)=-s'_{i}(t)-s_{i}(t)+f_{i}(x_{i}(t)), \end{cases}\displaystyle \end{aligned}$$
(2.3)

the initial conditions associated with (2.1) or (2.3) are to be of the form

$$\begin{aligned} \textstyle\begin{cases} x_{i}(\theta )=\phi _{i}(\theta ),\qquad x'_{i}(\theta )=\tilde{\phi } _{i}(\theta ), \quad \theta \in [-\tau ,0], \\ s_{i}(\theta )=\psi _{i}(\theta ),\qquad s'_{i}(\theta )=\tilde{\psi } _{i}(\theta ), \quad \theta \in [-\tau ,0], \end{cases}\displaystyle \quad i=1,2,\ldots,n. \end{aligned}$$
(2.4)

Throughout this paper, the activation functions are assumed to satisfy the following assumption.

(H1):

For any \(i=1,2,\ldots ,n\), the activation functions \(f_{i}\) and \(g_{i}\) satisfy Lipschitz condition, that is, there exist constants \(L_{i}^{F}\) and \(L_{i}^{G}\) such that for all u,v∈R

$$ \bigl\vert f_{i}(u)-f_{i}(v) \bigr\vert \leq L_{i}^{F} \vert u-v \vert ,\qquad \bigl\vert g_{i}(u)-g_{i}(v) \bigr\vert \leq L_{i}^{G} \vert u-v \vert . $$

Definition 2.1

Suppose \((\mathbf{x}(t),\mathbf{s}(t))^{T}\) and \((\mathbf{x}^{*}(t),\mathbf{s}^{*}(t))^{T}\) are two solutions of the system satisfying the initial condition, the system is said to be globally exponentially stable if there are two positive constants ε and M depending on the initial values, such that

$$ \bigl\vert x_{i}(t)-x^{*}_{i}(t) \bigr\vert \leq Me^{-\varepsilon t},\qquad \bigl\vert s_{i}(t)-s^{*}_{i}(t) \bigr\vert \leq Me^{-\varepsilon t}, \quad i=1,2,\ldots ,n. $$

3 Main result

In this section, we will derive some sufficient conditions which ensure the global exponential stability for system (2.3).

Theorem 3.1

Suppose that Assumption (H1) holds. The inertial CNNs (2.3) with initial values (2.4) are globally exponentially stable if the algebra conditions hold:

$$ \mathscr{A}_{i}< 0, \qquad \mathcal{A}_{i}< 0, $$
(3.1)

and

$$ 4\mathscr{A}_{i}\mathscr{B}_{i}>(\mathscr{C}_{i})^{2}, \qquad 4 \mathcal{A}_{i}\mathcal{B}_{i}>( \mathcal{C}_{i})^{2}, $$
(3.2)

where

$$\begin{aligned} \textstyle\begin{cases} \mathscr{A}_{i}=\xi _{1i}\eta _{1i}+\frac{1}{2}{\sum_{j=1}^{n}} \xi ^{2}_{1i}( \vert D_{ij} \vert L_{j}^{F}+ \vert D_{ij}^{\tau } \vert L_{j}^{G})-a_{i}\xi ^{2}_{1i}, \\ \mathscr{B}_{i}=\frac{1}{2} {\sum_{j=1}^{n}}\xi _{1i}\eta _{1i}( \vert D _{ij} \vert L_{j}^{F}+ \vert D_{ij}^{\tau } \vert L_{j}^{G})+ \frac{1}{2}\sum_{j=1}^{n}(\xi ^{2}_{1j}+\xi _{1j}\eta _{1j}) \vert D_{ji} \vert L_{i}^{F} \\ \hphantom{\mathscr{B}_{i}=}{}+ \frac{1}{2(1-\mu )}{\sum_{j=1}^{n}}(\xi ^{2}_{1j} +\xi _{1j} \eta _{1j}) \vert D^{\tau }_{ji} \vert +\frac{1}{2}(\xi _{2i}+\xi _{2i}\eta _{2i})L _{i}^{F}-b_{i}\xi _{1i}\eta _{1i}, \\ \mathscr{C}_{i}=\lambda _{1i}+\eta ^{2}_{1i}-a_{i}\xi _{1i}\eta _{1i}-b _{i}\xi ^{2}_{1i}, \end{cases}\displaystyle \end{aligned}$$

and

$$\begin{aligned} \textstyle\begin{cases} \mathcal{A}_{i}=\xi _{2i}\eta _{2i}+\frac{1}{2}\xi _{2i}L_{i}^{F}-\xi ^{2}_{2i}, \\ \mathcal{B}_{i}=\frac{1}{2}\xi _{2i}\eta _{2i}L_{i}^{F}-\xi _{2i}\eta _{2i}, \\ \mathcal{C}_{i}=\lambda _{2i}+\eta ^{2}_{2i}-\xi _{2i}\eta _{2i}-\xi ^{2}_{2i}. \end{cases}\displaystyle \end{aligned}$$

Proof

Let \((\mathbf{x(t), s(t)})^{T}=(x_{1}(t),x_{2}(t),\ldots ,x_{n}(t),s_{1}(t),s_{2}(t), \ldots ,s_{n}(t))^{T} \) and \((\mathbf{x^{*}(t),s^{*}(t)})^{T}=(x^{*} _{1}(t),x^{*}_{2}(t),\ldots ,x^{*}_{n}(t),s^{*}_{1}(t),s^{*}_{2}(t), \ldots ,s^{*}_{n}(t))^{T} \) be two solutions of inertial CNNs (2.1).

Define \(y_{i}(t)=x_{i}(t)-x^{*}_{i}(t)\), \(z_{i}(t)=s_{i}(t)-s^{*}_{i}(t)\), then system (2.3) can be rewritten as

$$\begin{aligned} \textstyle\begin{cases} {y}''_{i}(t)=-a_{i}{y'_{i}}(t)-{b_{i}}{y_{i}(t)}+{\sum_{j=1} ^{n}}D_{ij}F_{j}(y_{j}(t)) +{\sum_{j=1}^{n}}D_{ij}^{\tau }G _{j}(y_{j}(t-\tau (t))), \\ {z}''_{i}(t)=-z'_{i}(t)-z_{i}(t)+F_{i}(y_{i}(t)), \end{cases}\displaystyle \end{aligned}$$
(3.3)

where

$$ F_{i}\bigl(y_{i}(\cdot )\bigr)=f_{i} \bigl(x_{i}(\cdot )\bigr)-f_{i}\bigl(x^{*}_{i}( \cdot )\bigr), \qquad G_{i}\bigl(y_{i}(\cdot ) \bigr)=g_{i}\bigl(x_{i}(\cdot )\bigr)-g_{i} \bigl(x^{*}_{i}( \cdot )\bigr),\quad i=1,2,\ldots,n. $$

In view of (3.1), (3.2) and combining with the continuity theory, there exists a sufficiently small \(\varepsilon >0\) such that

$$ \mathscr{A}_{i}^{\varepsilon }< 0,\qquad \mathcal{A}_{i}^{\varepsilon }< 0, $$
(3.4)

and

$$ 4\mathscr{A}_{i}^{\varepsilon }\mathscr{B}_{i}^{\varepsilon }> \bigl( \mathscr{C}_{i}^{\varepsilon }\bigr)^{2},\qquad 4 \mathcal{A}_{i}^{\varepsilon } \mathcal{B}_{i}^{\varepsilon }> \bigl(\mathcal{C}_{i}^{\varepsilon }\bigr)^{2}, $$
(3.5)

where

$$\begin{aligned} \textstyle\begin{cases} \mathscr{A}_{i}^{\varepsilon }=\xi ^{2}_{1i}+\xi _{1i}\eta _{1i}+ \frac{1}{2}{\sum_{j=1}^{n}}\xi ^{2}_{1i}( \vert D_{ij} \vert L_{j}^{F}+ \vert D _{ij}^{\tau } \vert L_{j}^{G})-a_{i}\xi ^{2}_{1i}, \\ \mathscr{B}_{i}^{\varepsilon }=\lambda _{1i}\varepsilon +\eta ^{2} _{1i}\varepsilon +\frac{1}{2} {\sum_{j=1}^{n}}\xi _{1i}\eta _{1i}( \vert D _{ij} \vert L_{j}^{F}+ \vert D_{ij}^{\tau } \vert L_{j}^{G})+ \frac{1}{2}\sum_{j=1}^{n}(\xi ^{2}_{1j}+\xi _{1j}\eta _{1j}) \vert D_{ji} \vert L_{i}^{F} \\ \hphantom{\mathscr{B}_{i}^{\varepsilon }=}{}+ \frac{1}{2(1-\mu )}{\sum_{j=1}^{n}}(\xi ^{2}_{1j} \xi _{1j} \eta _{1j}) \vert D^{\tau }_{ji} \vert e^{2\varepsilon \tau } +\frac{1}{2}(\xi _{2i}+ \xi _{2i}\eta _{2i})L_{i}^{F}-b_{i}\xi _{1i}\eta _{1i}, \\ \mathscr{C}_{i}^{\varepsilon }=\lambda _{1i}+\eta ^{2}_{1i}+2\varepsilon \xi _{1i}\eta _{1i}-a_{i}\xi _{1i}\eta _{1i}-b_{i}\xi ^{2}_{1i}, \end{cases}\displaystyle \end{aligned}$$

and

$$\begin{aligned} \textstyle\begin{cases} \mathcal{A}_{i}^{\varepsilon }=\xi ^{2}_{2i}\varepsilon +\xi _{2i}\eta _{2i}+\frac{1}{2}\xi _{2i}L_{i}^{F}-\xi ^{2}_{2i}, \\ \mathcal{B}_{i}^{\varepsilon }=\lambda _{2i}\varepsilon +\eta ^{2} _{2i}\varepsilon +\frac{1}{2}\xi _{2i}\eta _{2i}L_{i}^{F}-\xi _{2i}\eta _{2i}, \\ \mathcal{C}_{i}^{\varepsilon }=\lambda _{2i}+\eta ^{2}_{2i}+2\varepsilon \xi _{2i}\eta _{2i}-\xi _{2i}\eta _{2i}-\xi ^{2}_{2i}. \end{cases}\displaystyle \end{aligned}$$

Consider a Lyapunov–Krasovskii functional given by

$$\begin{aligned} V(t)&=\underbrace{\frac{1}{2}{\sum_{i=1}^{n}} \lambda _{1i}y^{2} _{i}(t)e^{2\varepsilon t}+ \frac{1}{2}{\sum_{i=1}^{n}}\bigl(\xi _{1i}y'_{i}(t)+ \eta _{1i}y_{i}(t) \bigr)^{2}e^{2\varepsilon t}}_{V_{1}} \\ &\quad{}+\underbrace{\frac{1}{2}{\sum_{i=1}^{n}} \lambda _{2i}z^{2} _{i}(t)e^{2\varepsilon t}+ \frac{1}{2}{\sum_{i=1}^{n}}\bigl(\xi _{2i}z'_{i}(t)+ \eta _{2i}z_{i}(t) \bigr)^{2}e^{2\varepsilon t}}_{V_{2}} \\ &\quad{}+\underbrace{\frac{1}{2(1-\mu )} {\sum_{i=1}^{n}} {\sum_{j=1}^{n}}\bigl(\xi ^{2}_{1i}+\xi _{1i}\eta _{1i}\bigr) \bigl\vert D_{ij}^{\tau } \bigr\vert \int _{t-\tau (t)}^{t}y^{2}_{j}(s)e^{2\varepsilon (s+\tau (t))}}_{V _{3}}\,ds. \end{aligned}$$
(3.6)

First, let us compute the derivative of \(V_{1}(t)\), we have

$$\begin{aligned} \frac{dV_{1}(t)}{dt}&=\sum_{i=1}^{n}\lambda _{1i}y_{i}(t)y'_{i}(t)e ^{2\varepsilon t}+\varepsilon \sum_{i=1}^{n} \lambda _{1i}y^{2} _{i}(t)e^{2\varepsilon t} \\ &\quad{}+\sum_{i=1}^{n}\bigl(\xi _{1i}y'_{i}(t)+\eta _{1i}y_{i}(t) \bigr) \bigl(\xi _{1i}y''_{i}(t)+ \eta _{1i}y'_{i}(t)\bigr) e^{2\varepsilon t}+ \varepsilon \sum_{i=1} ^{n}\bigl(\xi _{1i}y'_{i}(t)+\eta _{1i}y_{i}(t) \bigr)^{2} e^{2\varepsilon t} \\ &=e^{2\varepsilon t} \Biggl\{ \sum_{i=1}^{n} \lambda _{1i}y_{i}(t)y'_{i}(t)+ \varepsilon {\sum_{i=1}^{n}}\lambda _{1i}y^{2}_{i}(t) +\varepsilon {\sum _{i=1}^{n}}\xi ^{2}_{1i} \bigl(y'_{i}(t) \bigr)^{2} \\ &\quad {}+\varepsilon {\sum _{i=1}^{n}}\eta ^{2}_{1i}y^{2}_{i}(t) +2\varepsilon \xi _{1i}\eta _{1i}y_{i}(t)y'_{i}(t) +\sum_{i=1}^{n} \Biggl\{ -a_{i}\xi ^{2}_{1i} \bigl(y'_{i}(t) \bigr)^{2}- {b_{i}}\xi ^{2}_{1i}{y_{i}(t)} {y'_{i}(t)} \\ &\quad {}+\xi ^{2}_{1i}{y'_{i}(t)} \Biggl[\sum_{j=1}^{n}D_{ij}F_{j} \bigl(y_{j}(t)\bigr) +\sum_{j=1} ^{n}D_{ij}^{\tau }G_{j}\bigl(y_{j} \bigl(t-\tau (t)\bigr)\bigr) \Biggr] \Biggr\} \\ &\quad{}+\sum_{i=1}^{n}\xi _{1i} \eta _{1i} \bigl(y'_{i}(t) \bigr)^{2}+ \sum_{i=1}^{n} \Biggl\{ -a_{i}\xi _{1i}\eta _{1i}y_{i}(t)y'_{i}(t)- {b_{i}}\xi _{1i}\eta _{1i}{y^{2}_{i}(t)} \\ &\quad{}+ \xi _{1i} \eta _{1i}{y_{i}(t)} \Biggl[\sum _{i=1}^{n}D_{ij}F_{j} \bigl(y_{j}(t)\bigr)+{\sum_{i=1}^{n}}D_{ij}^{\tau }G_{j} \bigl(y_{j}\bigl(t-\tau (t)\bigr)\bigr) \Biggr] \Biggr\} +\eta ^{2}_{1i}y_{i}(t)y'_{i}(t) \Biggr\} \\ &=e^{2\varepsilon t} \Biggl\{ {\sum_{i=1}^{n}} \bigl(\lambda _{1i}+\eta ^{2}_{1i}+2\varepsilon \xi _{1i}\eta _{1i}-a_{i}\xi _{1i}\eta _{1i}-b_{i} \xi ^{2}_{1i} \bigr)y_{i}(t)y'_{i}(t) \\ &\quad {} +{\sum _{i=1}^{n}}\bigl(\xi ^{2}_{1i} \varepsilon +\xi _{1i}\eta _{1i}-a_{i}\xi ^{2}_{1i}\bigr) \bigl(y'_{i}(t) \bigr)^{2} \\ &\quad{}+{\sum_{i=1}^{n}}\bigl(\lambda _{1i}\varepsilon +\eta ^{2}_{1i} \varepsilon -b_{i}\xi _{1i}\eta _{1i}\bigr)y^{2}_{i}(t) +{\sum_{i=1} ^{n}} {\sum _{j=1}^{n}}\bigl(\xi ^{2}_{1i}y'_{i}(t)+ \xi _{1i}\eta _{1i}y _{i}(t)\bigr)D_{ij}F_{j} \bigl(y_{j}(t)\bigr) \\ &\quad{}+{\sum_{i=1}^{n}} {\sum _{j=1}^{n}}\bigl(\xi ^{2}_{1i}y'_{i}(t)+ \xi _{1i}\eta _{1i}y_{i}(t)\bigr)D^{\tau }_{ij}G_{j} \bigl(y_{j}\bigl(t-\tau (t)\bigr)\bigr) \Biggr\} . \end{aligned}$$
(3.7)

It follows from (H1) and the fundamental inequality \(uv\leq \frac{1}{2}(u^{2}+v^{2})\) (u,v∈R) that

$$\begin{aligned} &\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\xi ^{2}_{1i}y'_{i}(t)+ \xi _{1i}\eta _{1i}y_{i}(t)\bigr)D_{ij}F_{j} \bigl(y_{j}(t)\bigr) \\ &\quad \leq \frac{1}{2}{\sum_{i=1}^{n}} { \sum_{j=1}^{n}}\xi ^{2}_{1i} \vert D_{ij} \vert L_{j}^{F} \bigl( \bigl(y'_{i}(t)\bigr)^{2}+y^{2}_{j}(t) \bigr)+ \frac{1}{2}{\sum_{i=1}^{n}} { \sum_{j=1}^{n}}\xi _{1i}\eta _{1i} \vert D_{ij} \vert L_{j}^{F} \bigl(y^{2}_{i}(t)+y^{2}_{j}(t) \bigr) \\ &\quad =\frac{1}{2}{\sum_{i=1}^{n}} {\sum _{j=1}^{n}}\xi ^{2} _{1i} \vert D_{ij} \vert L_{j}^{F} \bigl(y'_{i}(t)\bigr)^{2}+ \frac{1}{2} \sum_{i=1} ^{n}\sum _{j=1}^{n} \bigl(\xi _{1i}\eta _{1i} \vert D_{ij} \vert L_{j}^{F} \\ &\qquad {}+ \xi ^{2}_{1j} \vert D_{ji} \vert L_{i}^{F}+\xi _{1j}\eta _{1j} \vert D_{ji} \vert L_{i}^{F} \bigr)y ^{2}_{i}(t) \end{aligned}$$
(3.8)

and

$$\begin{aligned} &{\sum_{i=1}^{n}} {\sum _{j=1}^{n}}\bigl(\xi ^{2}_{1i}y'_{i}(t)+ \xi _{1i}\eta _{1i}y_{i}(t)\bigr)D^{\tau }_{ij}G_{j} \bigl(y_{j}\bigl(t-\tau (t)\bigr)\bigr) \\ &\quad \leq \frac{1}{2}{\sum_{i=1}^{n}} { \sum_{j=1}^{n}}\xi ^{2}_{1i} \bigl\vert D^{\tau }_{ij} \bigr\vert L_{j}^{G} \bigl(\bigl(y'_{i}(t)\bigr)^{2}+y^{2}_{j} \bigl(t- \tau (t)\bigr) \bigr) \\ &\qquad {}+\frac{1}{2}{\sum _{i=1}^{n}} {\sum_{j=1} ^{n}} \xi _{1i}\eta _{1i} \bigl\vert D^{\tau }_{ij} \bigr\vert L_{j}^{G} \bigl(y^{2}_{i}(t)+y ^{2}_{j}\bigl(t- \tau (t)\bigr) \bigr) \\ &\quad =\frac{1}{2}{\sum_{i=1}^{n}} {\sum _{j=1}^{n}}\xi ^{2} _{1i} \bigl\vert D^{\tau }_{ij} \bigr\vert L_{j}^{G} \bigl[y'_{i}(t)\bigr]^{2} +\frac{1}{2}{ \sum_{i=1}^{n}} {\sum _{j=1}^{n}}\xi _{1i}\eta _{1i} \bigl\vert D^{\tau } _{ij} \bigr\vert L_{j}^{G}y^{2}_{i}(t) \\ &\qquad{}+\frac{1}{2}{\sum_{i=1}^{n}} {\sum_{j=1}^{n}} \bigl(\xi ^{2} _{1i}+\xi _{1i}\eta _{1i}\bigr) \bigl\vert D^{\tau }_{ij} \bigr\vert L_{j}^{G}y^{2}_{j} \bigl(t-\tau (t)\bigr). \end{aligned}$$
(3.9)

Substituting (3.8), (3.9) into (3.7) leads to

$$\begin{aligned} \frac{dV_{1}(t)}{dt}&\leq e^{2\varepsilon t} \Biggl\{ {\sum _{i=1} ^{n}}\bigl(\lambda _{1i}+\eta ^{2}_{1i}+2\varepsilon \xi _{1i}\eta _{1i}-a_{i} \xi _{1i}\eta _{1i}-b_{i} \xi ^{2}_{1i}\bigr)y_{i}(t)y'_{i}(t) \\ &\quad{}+{\sum_{i=1}^{n}} \Biggl(\xi ^{2}_{1i}\varepsilon +\xi _{1i}\eta _{1i}+\frac{1}{2}{\sum_{j=1}^{n}} \xi ^{2}_{1i}\bigl( \vert D_{ij} \vert L_{j} ^{F}+ \bigl\vert D^{\tau }_{ij} \bigr\vert L_{j}^{G}\bigr)-a_{i}\xi ^{2}_{1i} \Biggr) \bigl(y'_{i}(t) \bigr)^{2} \\ &\quad{}+ \sum_{i=1}^{n} \Biggl(\lambda _{1i}\varepsilon +\eta ^{2}_{1i} \varepsilon + \frac{1}{2}{\sum_{j=1}^{n}} \xi _{1i}\eta _{1i}\bigl( \vert D _{ij} \vert L_{j}^{F}+ \bigl\vert D^{\tau }_{ij} \bigr\vert L_{j}^{G}\bigr) \\ &\quad {} +\frac{1}{2}{\sum _{j=1}^{n}}\bigl(\xi _{1j}^{2}+\xi _{1j}\eta _{1j}\bigr) \vert D_{ji} \vert L_{i}^{F}-b_{i}\xi _{1i}\eta _{1i} \Biggr) y^{2}_{i}(t) \\ &\quad{}+\frac{1}{2}{\sum _{i=1}^{n}} {\sum_{j=1}^{n}} \bigl(\xi ^{2}_{1i}+ \xi _{1i}\eta _{1i} \bigr) \bigl\vert D^{\tau }_{ij} \bigr\vert L_{j}^{G}y^{2}_{j}\bigl(t-\tau (t) \bigr) \Biggr\} . \end{aligned}$$
(3.10)

Secondly, calculating the derivative of \(V_{2}(t)\), we obtain

$$\begin{aligned} \frac{dV_{2}(t)}{dt}&={\sum_{i=1}^{n}}\lambda _{2i}z_{i}(t)z'_{i}(t)e ^{2\varepsilon t}+\varepsilon {\sum_{i=1}^{n}} \lambda _{2i}z ^{2}_{i}(t)e^{2\varepsilon t} \\ &\quad{}+{\sum_{i=1}^{n}}\bigl(\xi _{2i}z'_{i}(t)+\eta _{2i}z_{i}(t) \bigr) \bigl(\xi _{2i}z''_{i}(t)+ \eta _{2i}z'_{i}(t)\bigr) e^{2\varepsilon t} \\ &\quad {}+ \varepsilon {\sum_{i=1}^{n}}\bigl(\xi _{2i}z'_{i}(t)+\eta _{2i}z_{i}(t) \bigr)^{2} e ^{2\varepsilon t} \\ &=e^{2\varepsilon t} \Biggl\{ {\sum_{i=1}^{n}} \lambda _{2i}z_{i}(t)z'_{i}(t)+ \varepsilon {\sum_{i=1}^{n}}\lambda _{2i}z^{2}_{i}(t) +\varepsilon {\sum _{i=1}^{n}}\xi ^{2}_{2i} \bigl(z'_{i}(t)\bigr)^{2} \\ &\quad {}+\varepsilon {\sum _{i=1}^{n}}\eta ^{2}_{2i}z^{2}_{i}(t) +2\varepsilon \xi _{2i} \eta _{2i}z_{i}(t)z'_{i}(t) \\ &\quad{}+{\sum_{i=1}^{n}}\xi ^{2}_{2i}z'_{i}(t) \bigl(-z'_{i}(t)-z_{i}(t)+F _{i} \bigl(y_{i}(t)\bigr) \bigr)+\xi _{2i}\eta _{2i}z_{i}(t) \bigl(-z'_{i}(t)-z_{i}(t)+F _{i}\bigl(y_{i}(t)\bigr) \bigr) \\ &\quad{}+\xi _{2i}\eta _{2i}\bigl(z'_{i}(t) \bigr)^{2}+\eta ^{2}_{2i}z_{i}(t)z'_{i}(t) \Biggr\} \\ &=e^{2\varepsilon t} \Biggl\{ {\sum_{i=1}^{n}} \bigl(\lambda _{2i}+\eta ^{2}_{2i}+2\varepsilon \xi _{2i}\eta _{2i}-\xi _{2i}\eta _{2i}-\xi ^{2} _{2i}\bigr)z_{i}(t)z'_{i}(t) \\ &\quad {}+{\sum_{i=1}^{n}}\bigl(\xi ^{2}_{2i}\varepsilon +\xi _{2i}\eta _{2i}-\xi ^{2}_{2i}\bigr) \bigl(z'_{i}(t) \bigr)^{2} \\ &\quad{}+{\sum_{i=1}^{n}}\bigl(\lambda _{2i}\varepsilon +\eta ^{2}_{2i} \varepsilon -\xi _{2i}\eta _{2i}\bigr)z^{2}_{i}(t) +{\sum _{i=1}^{n}}\bigl( \xi ^{2}_{2i}z'_{i}(t)+ \xi _{2i}\eta _{2i}z_{i}(t)\bigr)F_{i} \bigl(y_{i}(t)\bigr) \Biggr\} . \end{aligned}$$
(3.11)

One can easily deduce that

$$\begin{aligned} &{\sum_{i=1}^{n}}\bigl(\xi ^{2}_{2i}z'_{i}(t)+\xi _{2i}\eta _{2i}z_{i}(t)\bigr)F _{i} \bigl(y_{i}(t)\bigr) \\ &\quad \leq \frac{1}{2}{\sum_{i=1}^{n}}\xi ^{2}_{2i}L_{i}^{F} \bigl( \bigl(z'_{i}(t)\bigr)^{2}+y ^{2}_{i}(t) \bigr)+\frac{1}{2}{\sum_{i=1}^{n}}\xi _{2i}\eta _{2i}L _{i}^{F} \bigl(z^{2}_{i}(t)+y^{2}_{i}(t) \bigr) \\ &\quad =\frac{1}{2}{\sum_{i=1}^{n}}\xi ^{2}_{2i}L_{i}^{F}\bigl(z'_{i}(t) \bigr)^{2}+ \frac{1}{2}{\sum_{i=1}^{n}} \xi _{2i}\eta _{2i}L_{i}^{F}z^{2}_{i}(t) +\frac{1}{2}{\sum_{i=1}^{n}}\bigl(\xi ^{2}_{2i}+\xi _{2i}\eta _{2i}\bigr)L _{i}^{F}y^{2}_{i}(t) \end{aligned}$$

and thus

$$\begin{aligned} \frac{dV_{2}(t)}{dt}&\leq e^{2\varepsilon t} \{{\sum_{i=1} ^{n}}\bigl(\lambda _{2i}+\eta ^{2}_{2i}+2 \varepsilon \xi _{2i}\eta _{2i}-\xi _{2i}\eta _{2i}-\xi ^{2}_{2i}\bigr)z_{i}(t)z'_{i}(t) \\ &\quad{}+{\sum_{i=1}^{n}}\biggl(\xi ^{2}_{2i}\varepsilon +\xi _{2i}\eta _{2i}+ \frac{1}{2} \xi ^{2}_{2i}L_{i}^{F}- \xi ^{2}_{2i}\biggr) \bigl(z'_{i}(t) \bigr)^{2} \\ &\quad{}+{\sum_{i=1}^{n}}\biggl(\lambda _{2i}\varepsilon +\eta ^{2}_{2i} \varepsilon + \frac{1}{2} \xi _{2i}\eta _{2i}L_{i}^{F}- \xi _{2i}\eta _{2i}\biggr)z ^{2}_{i}(t) \\ &\quad{}+\frac{1}{2}{\sum_{i=1}^{n}} \bigl(\xi ^{2}_{2i}+\xi _{2i}\eta _{2i} \bigr)L _{i}^{F}y^{2}_{i}(t). \end{aligned}$$
(3.12)

By virtue of (2.3) and a straightforward computation

$$\begin{aligned} \frac{dV_{3}(t)}{dt}&=\frac{1}{2(1-\mu )}{\sum_{i=1}^{n}} {\sum_{j=1}^{n}}\bigl(\xi ^{2}_{1i} \bigl\vert D^{\tau }_{ij} \bigr\vert +\xi _{1i}\eta _{1i} \bigl\vert D ^{\tau }_{ij} \bigr\vert \bigr)y^{2}_{j}(t)e^{2\varepsilon (t+\tau (t))} \\ &\quad{}-\frac{1}{2(1-\mu )}{\sum_{i=1}^{n}} {\sum_{j=1}^{n}}\bigl( \xi ^{2}_{1i} \bigl\vert D^{\tau }_{ij} \bigr\vert +\xi _{1i}\eta _{1i} \bigl\vert D^{\tau }_{ij} \bigr\vert \bigr)y^{2} _{j}\bigl(t-\tau (t) \bigr)e^{2\varepsilon t}\bigl(1-\dot{\tau }(t)\bigr) \\ &\leq \frac{1}{2(1-\mu )}{\sum_{i=1}^{n}} { \sum_{j=1} ^{n}}\bigl(\xi ^{2}_{1j} \bigl\vert D^{\tau }_{ji} \bigr\vert +\xi _{1j}\eta _{1j} \bigl\vert D^{\tau }_{ji} \bigr\vert \bigr)y ^{2}_{i}(t)e^{2\varepsilon (t+\tau )} \\ &\quad {}- \frac{1}{2}{\sum_{i=1}^{n}} {\sum _{j=1}^{n}}\bigl(\xi ^{2} _{1i} \bigl\vert D^{\tau }_{ij} \bigr\vert +\xi _{1i}\eta _{1i} \bigl\vert D^{\tau }_{ij} \bigr\vert \bigr)y^{2}_{j}\bigl(t- \tau (t) \bigr)e^{2\varepsilon t}, \end{aligned}$$

which, together with (3.10), and (3.11), gives

$$\begin{aligned} \frac{dV(t)}{dt}&\leq e^{2\varepsilon t} \{{\sum_{i=1}^{n}} \bigl(\lambda _{1i}+\eta ^{2}_{1i}+2\varepsilon \xi _{1i}\eta _{1i}-a_{i}\xi _{1i} \eta _{1i}-b_{i}\xi ^{2}_{1i} \bigr)y_{i}(t)y'_{i}(t) \\ &\quad{}+{\sum_{i=1}^{n}}\Biggl(\xi ^{2}_{1i}+\xi _{1i}\eta _{1i}+ \frac{1}{2} {\sum_{j=1}^{n}}\xi ^{2}_{1i} \bigl( \vert D_{ij} \vert L_{j}^{F}+ \bigl\vert D_{ij}^{ \tau } \bigr\vert L_{j}^{G}\bigr)-a_{i}\xi ^{2}_{1i}\Biggr)\bigl[y'_{i}(t) \bigr]^{2} \\ &\quad{}+{\sum_{i=1}^{n}}\Biggl\{ \lambda _{1i}\varepsilon +\eta ^{2}_{1i} \varepsilon + \frac{1}{2} {\sum_{j=1}^{n}}\xi _{1i}\eta _{1i}\bigl( \vert D _{ij} \vert L_{j}^{F}+ \bigl\vert D_{ij}^{\tau } \bigr\vert L_{j}^{G}\bigr) \\ &\quad {}+ \frac{1}{2}\sum _{j=1}^{n}\bigl(\xi ^{2}_{1j}+\xi _{1j}\eta _{1j}\bigr) \vert D_{ji} \vert L_{i}^{F} \\ &\quad{}+ \frac{1}{2(1-\mu )}{\sum_{j=1}^{n}} \bigl(\xi ^{2}_{1j} +\xi _{1j} \eta _{1j} \bigr) \vert D^{\tau }_{ji}|e^{2\varepsilon \tau } + \frac{1}{2}(\xi _{2i}+ \xi _{2i}\eta _{2i})L_{i}^{F}-b_{i}\xi _{1i}\eta _{1i}\Biggr\} y^{2}_{i}(t) \\ &\quad{}+{\sum_{i=1}^{n}}\bigl(\lambda _{2i}+\eta ^{2}_{2i}+2\varepsilon \xi _{2i}\eta _{2i}-\xi _{2i}\eta _{2i} -\xi ^{2}_{2i}\bigr)z_{i}(t)z'_{i}(t) \\ &\quad {}+ {\sum_{i=1}^{n}}\biggl(\xi ^{2}_{2i}\varepsilon +\xi _{2i}\eta _{2i}+ \frac{1}{2}\xi ^{2}_{2i}L_{i}^{F}- \xi ^{2}_{2i}\biggr)\bigl[z'_{i}(t) \bigr]^{2} \\ &\quad{}+{\sum_{i=1}^{n}}\biggl(\lambda _{2i}\varepsilon +\eta ^{2}_{2i} \varepsilon + \frac{1}{2}\xi _{2i} \eta _{2i}L_{i}^{F}- \xi _{2i}\eta _{2i}\biggr)z ^{2}_{i}(t) \\ &=e^{2\varepsilon t} \Biggl\{ {\sum_{i=1}^{n}} \bigl(\mathscr{A} _{i}^{\varepsilon }\bigl(y'_{i}(t) \bigr)^{2}+\mathscr{B}_{i}^{\varepsilon }\bigl(y ^{2}_{i}(t)\bigr)^{2}+\mathscr{C}_{i}^{\varepsilon }y_{i}(t)y'_{i}(t) \bigr) \\ &\quad {}+ \bigl(\mathcal{A}_{i}^{\varepsilon }\bigl(z'_{i}(t) \bigr)^{2}+\mathcal{B} _{i}^{\varepsilon } \bigl(z^{2}_{i}(t)\bigr)^{2} +\mathcal{C}_{i}^{\varepsilon }z _{i}(t)z'_{i}(t) \bigr) \Biggr\} \\ &=e^{2\varepsilon t} \Biggl\{ {\sum_{i=1}^{n}} \mathscr{A}_{i} ^{\varepsilon } \biggl(y'_{i}(t)+ \frac{\mathscr{C}_{i}^{\varepsilon }}{2 \mathscr{A}_{i}^{\varepsilon }}y_{i}(t) \biggr)^{2}+{\sum _{i=1} ^{n}} \biggl(\mathscr{B}_{i}^{\varepsilon }- \frac{(\mathscr{C}_{i}^{ \varepsilon })^{2}}{4\mathscr{A}_{i}^{\varepsilon }} \biggr) \bigl(y_{i}(t)\bigr)^{2} \\ &\quad{}+{\sum_{i=1}^{n}} \mathcal{A}_{i}^{\varepsilon } \biggl(z'_{i}(t)+ \frac{ \mathcal{B}_{i}^{\varepsilon }}{2\mathscr{A}_{i}^{\varepsilon }}y_{i}(t) \biggr)^{2}+{\sum _{i=1}^{n}} \biggl(\mathscr{B} _{i}^{\varepsilon }- \frac{( \mathcal{C}_{i}^{\varepsilon })^{2}}{4\mathcal{A}_{i}^{\varepsilon }} \biggr) \bigl(z_{i}(t)\bigr) ^{2} \Biggr\} \\ &\leq 0, \quad \text{for all } t\in [0,+\infty ). \end{aligned}$$

Hence,

$$ V(t)\leq V(0), \quad \text{for all } t\in [0,+\infty ), $$

which implies that

$$ \bigl\vert y_{i}(t) \bigr\vert =\mathcal{O}\bigl(e^{-\varepsilon t} \bigr),\qquad \bigl\vert z_{i}(t) \bigr\vert =\mathcal{O}\bigl(e ^{-\varepsilon t}\bigr), $$

where \(\mathcal{O}(e^{-\varepsilon t})\) means that \(|y_{i}(t)|\), \(|z_{i}(t)|\) exponentially converge to 0 with the same order as \(e^{-\varepsilon t}\). This completes the proof of Theorem 3.1. □

4 Numerical simulations

In this section, a numerical example is presented to justify the effectiveness of the proposed exponential stability results. The simulation is performed using Matlab software.

Example 4.1

Let us consider the following inertial CNNs:

$$\begin{aligned} \textstyle\begin{cases} x''_{i}(t)=-a_{i}{x'_{i}}(t)-{b_{i}}{x_{i}(t)}+{\sum_{j=1} ^{2}}D_{ij}f_{j}(x_{j}(t)) +{\sum_{j=1}^{2}}D_{ij}^{\tau }g _{j}(x_{j}(t-\tau (t))) \\ \hphantom{x''_{i}(t)=}{}+c_{i}s_{i}+I_{i}, \\ s''_{i}(t)=-s'_{ij}(t)-s_{ij}(t)+f_{i}(x_{i}(t)), \end{cases}\displaystyle \end{aligned}$$
(4.1)

where \(f_{i}(u)=g_{i}(u)=\frac{1}{2}(|u+1|-|u-1|)\), \(i=1,2\). The parameters in (4.1) are assumed to be \(a_{1}=2\), \(a_{2}=3\), \(b_{1}=5\), \(b_{2}=3\), \(I _{1}=3\), \(I_{2}=2.5\), \(c_{1}=c_{2}=0.6\), and

$$ D= \begin{bmatrix} -0.5 &0.5 \\ 0.4 & -0.9 \end{bmatrix} ,\qquad D^{\tau }= \begin{bmatrix} -0.3 &0.3 \\ 0.4 & -0.4 \end{bmatrix} . $$

It is not difficult to check that \(L_{i}^{F}=L_{i}^{G}=1\), \(i=1,2\). Let us chose \(\xi _{11}=\xi _{12}=\eta _{11}=\eta _{12}=1\), \(\eta _{21}=0.5\), \(\eta _{22}=0.1\), \(\xi _{21}=1.3\), \(\xi _{22}=1.7\), \(\lambda _{11}=6.67\), \(\lambda _{12}=5.89\), \(\lambda _{21}=2.79\), \(\lambda _{22}=3.33\), \(\mathscr{B}_{1}=-0.575\), \(\mathscr{B}_{2}=-0.215\), \(\mathcal{B}_{1}=-0.325\), \(\mathcal{B}_{2}=-0.085\). Through simple manipulation, we have

$$\begin{aligned}& \mathscr{A}_{1}=-0.2< 0,\qquad 4\mathscr{A}_{1} \mathscr{B}_{1}\approx 0.46>0.4489= \mathscr{C}_{1}^{2}=0.67^{2}, \\& \mathscr{A}_{2}=-0.95< 0,\qquad 4\mathscr{A}_{2} \mathscr{B}_{2}\approx 0.817>0.792= \mathscr{C}_{2}^{2}=0.89^{2}, \end{aligned}$$

and

$$\begin{aligned}& \mathcal{A}_{1}=-0.39< 0,\qquad 4\mathcal{A}_{1} \mathcal{B}_{1}\approx 0.507>0.49= \mathcal{C}_{1}^{2}=0.7^{2}, \\& \mathcal{A}_{2}=-0.24< 0,\qquad 4\mathcal{A}_{2} \mathcal{B}_{2}\approx 0.0816>0.0784= \mathcal{C}_{2}^{2}=0.28^{2}. \end{aligned}$$

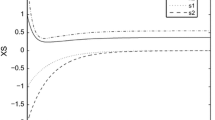
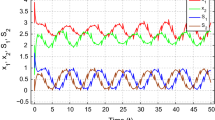
Then, all the conditions of Theorem 3.1 are satisfied and thus the inertial CNN (4.1) is exponentially stable. This fact is revealed in Fig. 1.

Figure 1
figure 1

The state trajectories of state variables \(x_{i}(t)\), \(s _{i}(t)\) with different values, \(i=1,2\)

Full size image

Remark 4.1

In recent years, many excellent theoretical results on competitive neural networks have been published (see [10, 11, 29–32] and the references therein), however, these references do not consider the effect of inertia terms. On the other hand, to the best of our knowledge, fewer dynamic results on delayed inertial CNNs have been reported. Therefore, our results are new and complement some existing ones.

Remark 4.2

For technical reasons, we impose some conditions on the derivatives of the time-varying delay (see (2.2)), that is, we demand that the delay increase not too fast. As for the case of \(\mu >1\) or the stability criteria are independent of time delay, which are our objectives for future research.

5 Conclusion

In this paper, different from the existing methods which usually apply the variable substitution to transform the second-order inertial system into the first-order differential equations, we investigated the exponential stability for a class of delayed inertial CNNs. A new Lyapunov functional is constructed and the well-known Barbalat lemma is used to obtain the stability criteria. Secondly, the asymptotic and adaptive synchronization of the addressed inertial networks is studied by designing two new control strategies. Finally, two examples with numerical simulations are provided to show the effectiveness of the derived theoretical results.