Abstract
In the present paper, the potential Kadomtsev–Petviashvili equation and (\(3+1\))-dimensional potential-YTSF equation are investigated, which can be used to describe many mathematical and physical backgrounds, e.g., fluid dynamics and communications. Based on Hirota bilinear method, the bilinear equation for the (\(3+1\))-dimensional potential-YTSF equation is obtained by applying an appropriate dependent variable transformation. Then N-soliton solutions of nonlinear evolution equation are derived by the perturbation technique, and the periodic wave solutions for potential Kadomtsev–Petviashvili equation and (\(3+1\))-dimensional potential-YTSF equation are constructed by employing the Riemann theta function. Furthermore, the asymptotic properties of periodic wave solutions show that soliton solutions can be derived from periodic wave solutions.
Similar content being viewed by others
1 Introduction
The construction of analytic solutions for nonlinear evolution equations (NLEEs) is a key topic in the study of nonlinear phenomena [1,2,3,4,5,6,7]. Analytic solutions can help one to well understand the mechanism of physical phenomena modeled by a nonlinear evolution equation. With the development of soliton theory and computer algebraic system like Maple, much attention has been paid to finding analytic solutions of nonlinear evolution equations, including soliton solutions, periodic wave solutions, shock wave solutions, and so on. Up to now, many powerful methods of searching for exact solutions to NLEEs have been proposed and developed. For example, Biswas and Bhrawy [8] employed the extended Jacobi elliptic function expansion method to study the Zakharov equation and the Davey–Stewartson equation and obtained cnoidal and snoidal wavesolutions. Ma and Lee et al. [9] investigated a \(3+1\) dimensional Jimbo–Miwa equation via a transformed rational function method and obtained exact solutions. Other methods, such as Bäcklund transformation [10, 11], Darboux transformation [12, 13], Hirota bilinear method [14], the inverse scattering transform, the variable separation method [15], the sine–cosine method, the tanh-function method [16], the auxiliary equation method [17], the trial function method [18], etc., were also employed. Based on these methods, a variety of nonlinear equations have been investigated and solved.
Among them, the Hirota method is one of the most effective methods of constructing multiple soliton solutions of NLEEs. It can transform the given nonlinear evolution equations to the corresponding bilinear forms through the dependent variable transformation. Then employing the perturbation expansion method, multi-soliton solutions with exponential function are derived. Also through the bilinear Bäcklund transformation, Lax pairs are obtained. In recent years, the Hirota method has been developed to construct the Wronskian solutions, Pfaffian solutions, and periodic wave solutions by use of the Riemann theta functions [19,20,21,22,23,24]. By means of this method, Tian et al. have investigated the HS equation for shallow water waves and BLMP equation [19]. And Ma, Zhang et al. have constructed periodic wave solutions of (\(2+1\))-dimensional Hirota bilinear equations and Ito equation [20, 21]. The advantage of this method lies in the fact that we obtain the periodic wave solutions in a direct method without algebraic-geometric theory. Furthermore, the soliton solutions can be derived from the periodic wave solutions via asymptotic analysis.
With a motivation to further expand the area of applications of this method, in the present paper, we study the potential Kadomtsev–Petviashvili equation and (\(3+1\))-dimensional potential-YTSF equation to illustrate the efficiency of using the combination of the Hirota method and the Riemann theta function. To the best of our knowledge, these results are up to date and have not been reported.
The rest of the paper is organized as follows. In Sect. 2, the bilinear form of (\(3+1\))-dimensional potential-YTSF equation is given by applying the Hirota bilinear method. In Sect. 3, N-soliton solutions are presented by using the perturbation approach. In Sect. 4, by virtue of the Riemann theta function, periodic wave solutions are derived successfully, and the asymptotic properties of periodic wave solutions show that periodic wave solution degenerate to soliton solution. Finally, the concluding remarks are presented in Sect. 5.
2 Bilinear form for (\(3+1\))-dimensional potential-YTSF equation
In this section, we will give the bilinear form for the (\(3+1\))-dimensional potential-YTSF equation by applying the Hirota direct method and the dependent variable transformation.
A new (\(3+1\))-dimensional nonlinear evolution equation, called the potential YTSF equation, was first introduced by Yu, Toda, Sasa and Fukuyama (YTSF) [25]. The (\(3+1\))-dimensional potential-YTSF equation can be written as
Setting \(u = \frac{3}{4}w_{x}\), substituting it into Eq. (2.1) and integrating with respect to x yields
which is transformed into the bilinear representation
under the dependent variable transformation \(w = 2\ln F\), where \(\lambda = \lambda (y,z,t)\) is an integration constant; \(D_{x}\), \(D_{y}\) and \(D_{t}\) are the well-known Hirota operators defined by [21]
The D-operators have the following nice property when acting on exponential functions:
where \(\xi_{i} = P_{i}x + Q_{i}y + \varOmega_{i}t + \xi_{i}^{0}\) (\(i = 1,2\)).
More generally, we get
Remark 1
D operates on a product of two functions like the Leibniz rule, except for a crucial sign difference. For example,
3 N-soliton solutions for (\(3+1\))-dimensional potential-YTSF equation
In the following, we will give N-soliton solutions for the (\(3+1\))-dimensional potential-YTSF equation by virtue of the Hirota method and the perturbation expansion and truncation technique, as well as property (2.5).
Expanding F into the power series with respect to a small parameter ε gives
Substituting (3.1) into bilinear equation (2.3) and setting the coefficients of the same power of ε to zero, we obtain the recursion relations for \(f_{i}\).
Single-soliton solution
For \(n = 1\), Eq. (3.1) becomes
where \(k_{1}\), \(l_{1}\), \(m_{1}\), \(\omega_{1}\) are arbitrary constants, and \(- 4k_{1}\omega_{1} + k_{1}^{3}m_{1} + 3l_{1}^{2} = 0\) is the dispersion relation.
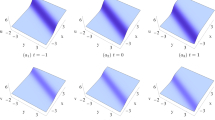
Substituting (3.2) into bilinear equation (2.3), a single-soliton solution of Eq. (2.1) is given by
Two-soliton solution
A two-soliton solution is given by
where \(- 4k_{i}\omega_{i} + k_{i}^{3}m_{i} + 3l_{i}^{2} = 0\) (\(i = 1,2\)) are the dispersion relations and the phase shift term is
N-soliton solution
Now we derive N-soliton solutions as
where the phase shift term is
Here \(\sum_{\mu = 0,1}\) means a summation over all possible combinations of \(\mu_{j} = 0,1\) (\(j = 1,2, \ldots,N\)) and \(\sum_{i < j}^{N}\) is a summation over all possible pairs \((i,j)\) (\(i = 1, \ldots,N\), \(j = 1, \ldots,N\)) with the condition that \(i < j\).
4 Periodic wave solutions of two equations
In this section, we will construct periodic wave solutions for the potential Kadomtsev–Petviashvili equation and the (\(3+1\))-dimensional potential-YTSF equation by employing the Hirota method and the Riemann theta function, as well as property (2.5).
4.1 Potential Kadomtsev–Petviashvili equation
The following (\(2+1\))-dimensional potential Kadomtsev–Petviashvili equation [26] is considered:
which is transformed into the bilinear form
under the dependent variable transformation \(u = 2(\ln F)_{x}\).
We introduce the Riemann theta function solution of Eq. (4.1) as
where \(n \in \mathcal {Z}\), \(\tau \in \mathcal {C}\), \(\operatorname{Im}\tau > 0\) and \(\zeta = kx + ly + \omega t\).
Substituting (4.3) into (4.2), we get
where \(n + m = p\). Noting that
which indicates that if \(\bar{G}(0) = \bar{G}(1) = 0\), then
Therefore, we may let
Denote
Then Eqs. (4.5) and (4.6) can be written as
By solving this system, we get
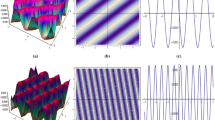
Thus the periodic wave solution is given by
where ω and F are determined by Eqs. (4.7) and (4.3), respectively.
Next, we will demonstrate that the soliton solution can be obtained as a limit of a periodic wave solution. From Eq. (4.3), we rewrite F as
where \(\alpha = e^{\pi i\tau} \).
Setting
we get
Thus, the periodic wave solution (4.8) turns to the soliton solution
if we can prove that
In fact, it is easy to known that
which lead to
According to (4.7), we get
which is equivalent to
4.2 (\(3+1\))-dimensional potential-YTSF equation
By a similar analysis process as in Sect. 4.1, we have
Denote
Then Eqs. (4.15) and (4.16) can be written as
By solving the system, we get
Thus, the periodic wave solution is given by
where ω and F are determined by Eqs. (4.17) and (4.3), respectively.
From Eq. (4.3), we rewrite F as
where \(\delta = e^{\pi i\tau} \).
Setting
yields
Thus, if we can prove that
the periodic wave solution (4.18) turns to the soliton solution
In fact, it is easy to known that
which lead to
According to (4.17), we get
which is equivalent to
5 Discussion and conclusion
In the present paper, we investigate the (\(2+1\))-dimensional potential KP equation and (\(3+1\))-dimensional potential-YTSF equation based on the Hirota method and the Riemann theta function. As a result, we obtain the bilinear form and N-soliton solutions of the (\(3+1\))-dimensional potential-YTSF equation under constraint conditions. By virtue of the Hirota method and the Riemann theta function, periodic wave solutions have been presented. And via asymptotic analysis, classical soliton solutions have been derived from their periodic wave solutions. Finally, it is worthwhile to note that the Hirota direct method can be applied to other variable coefficient NLEEs in mathematical physics.
References
Lv, X., Ma, W.X., Khalique, C.M.: A direct bilinear Bäcklund transformation of a (\(2+1\))-dimensional Korteweg–de Vries-like model. Appl. Math. Lett. 50, 37–42 (2015)
Lu, X., Chen, S.T., Ma, W.X.: Constructing lump solutions to a generalized Kadomtsev–Petviashvili–Boussinesq equation. Nonlinear Dyn. 86, 523–534 (2016)
Lin, F.H., Wang, J.P., Zhou, X.W., Ma, W.X., et al.: Observation of interaction phenomena for two dimensionally reduced nonlinear models. Nonlinear Dyn. 94, 2643–2654 (2018)
Yin, Y.H., Ma, W.X., Liu, J.G., Lv, X.: Diversity of exact solutions to a (\(3+1\))-dimensional nonlinear evolution equation and its reduction. Comput. Math. Appl. 76, 1275–1283 (2018)
Gao, X.Y.: Mathematical view with observational/experimental consideration on certain (\(2+1\))-dimensional waves in the cosmic/laboratory dusty plasmas. Appl. Math. Lett. 91, 165–172 (2019)
Yuan, Y.Q., Tian, B., Liu, L., et al.: Solitons for the (\(2+1\))-dimensional Konopelchenko–Dubrovsky equations. J. Math. Anal. Appl. 460, 476–486 (2018)
Liu, M.S., Li, X.Y., Zhao, Q.L.: Exact solutions to Euler equation and Navier–Stokes equation. Z. Angew. Math. Phys. 70(2), 1–13 (2019)
Bhrawy, A.H., Abdelkawy, M.A., Biswas, A.: Cnoidal and snoidal wave solutions to coupled nonlinear wave equations by the extended Jacobi’s elliptic function method. Nonlinear Sci. Numer. Simul. 18, 915–925 (2013)
Ma, W.X., Lee, J.H.: A transformed rational function method and exact solutions to the \(3+1\) dimensional Jimbo–Miwa equation. Chaos Solitons Fractals 42, 1356–1363 (2009)
Gao, L.N., Zi, Y.Y., Yin, Y.H., Ma, W.X., et al.: Bäcklund transformation, multiple wave solutions and lump solutions to a (\(3 + 1\))-dimensional nonlinear evolution equation. Nonlinear Dyn. 89, 2233–2240 (2017)
Weiss, J.: The Painleve property for partial differential equations. Bäcklund transformation, Lax pairs, and the Schwarzian derivative. J. Math. Phys. 24, 1405–1413 (1983)
Liu, L., Tian, B., Yuan, Y.Q., Du, Z.: Dark-bright solitons and semirational rogue waves for the coupled Sasa–Satsuma equations. Phys. Rev. E 97, 052217 (2018)
Ha, J.T., Zhang, H.Q., Zhao, Q.L.: Exact solutions for a Dirac-type equation with N-fold Darboux transformation. J. Appl. Anal. Comput. 9(1), 200–210 (2019)
Hirota, R.: The Direct Methods in Soliton Theory. Cambridge University, Cambridge (2004)
Ying, J.P., Lou, S.Y.: Multilinear variable separation approach in (\(3+1\))-dimensions: the Burgers equation. Chin. Phys. Lett. 20, 1448–1451 (2003)
Wazwaz, A.M.: The Camassa–Holm–KP equations with compact and noncompact travelling wave solutions. Appl. Math. Comput. 170, 347–360 (2005)
Zhang, X.L., Zhang, H.Q.: A new generalized Riccati equation rational expansion method to a class of nonlinear evolution equation with nonlinear terms of any order. Appl. Math. Comput. 186, 705–714 (2007)
Cao, R., Zhang, J.: Trial function method and exact solutions to the generalized nonlinear Schrödinger equation with time-dependent coefficient. Chin. Phys. B 22, 100507 (2013)
Cai, K.J., Tian, B., Zhang, H., Meng, X.H.: Direct approach to construct the periodic wave solutions for two nonlinear evolution equations. Commun. Theor. Phys. 52, 473–478 (2009)
Ma, W.X., Zhou, R.G.: Exact one-periodic and two-periodic wave solutions to Hirota bilinear equations in (\(2+1\)) dimensions. Mod. Phys. Lett. A 24(21), 1677–1688 (2009)
Tian, S.F., Zhang, H.Q.: Riemann theta functions periodic wave solutions and rational characteristics for the (\(1+1\))-dimensional and (\(2+1\))-dimensional ito equation. Chaos Solitons Fractals 47, 27–41 (2013)
Wang, X.B., Tian, S.F., Xu, M.J., et al.: On integrability and quasi-periodic wave solutions to a (\(3+1\))-dimensional generalized KdV-like model equation. Comput. Math. Appl. 283, 216–233 (2016)
Chen, Y.R., Liu, Z.R.: Riemann theta solutions and their asymptotic property for a (\(3+1\))-dimensional water wave equation. Nonlinear Dyn. 87(2), 1069–1080 (2017)
Demiray, S., Tascan, F.: Quasi-periodic solutions of (\(3+1\)) generalized BKP equation by using Riemann theta functions. Appl. Math. Comput. 273, 131–141 (2016)
Yu, S.J., Toda, K., Sasa, N., Fukuyama, T.: N-soliton solutions to the Bogoyavlenskii–Schiff equation and a quest for the soliton solution in (\(3+1\)) dimensions. Physica A 31, 3337–3347 (1998)
Ja’afar, A., Jawad, M., Petkovic, M.D.: Soliton solutions for nonlinear Calaogero–Degasperis and potential Kadomtsev–Petviashvili equations. Comput. Math. Appl. 62, 2621–2628 (2011)
Acknowledgements
The authors are very grateful to the editor and the referees for their insightful and constructive comments and suggestions, which have led to an improved version of this paper.
Funding
This work is supported in part by the NNSF of China (No. 11701334, 11347102), the Natural Science Foundation of Shandong Province (ZR2014AM032), the project of Shandong Province Higher Educational Science and Technology Program (J16LI15) and the Fund Project of Heze University (XY16BS12, XY18KJ09).
Author information
Authors and Affiliations
Contributions
The authors carried out the calculation and conceived of the study. The authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that there is no conflict of interest regarding the publication of this paper.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Cao, R., Zhao, Q. & Gao, L. Bilinear approach to soliton and periodic wave solutions of two nonlinear evolution equations of Mathematical Physics. Adv Differ Equ 2019, 156 (2019). https://doi.org/10.1186/s13662-019-2051-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2051-2