Skip to main content
SpringerLink
Log in

Constructing lump solutions to a generalized Kadomtsev–Petviashvili–Boussinesq equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

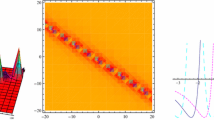
Associated with the prime number \(p=3\), a combined model of generalized bilinear Kadomtsev–Petviashvili and Boussinesq equation (gbKPB for short) in terms of the function f is proposed, which involves four arbitrary coefficients. To guarantee the existence of lump solutions, a constraint among these four coefficients is presented firstly, and then, the lump solutions are constructed and classified via searching for positive quadratic function solutions to the gbKPB equation. Different conditions posed on lump parameters are investigated to keep the analyticity and rational localization of the resulting solutions. Finally, 3-dimensional plots, density plots and 2-dimensional curves with particular choices of the involved parameters are given to show the profile characteristics of the presented lump solutions for the potential function \(u=2(\mathrm{{ln}}f)_x\).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. The transformation employed here is motivated by the Bell polynomial theories (see, e.g., [22–24, 35–37]), and actually, we have \(\left[ \frac{\ \mathrm {bKPB}\ }{f^{2}}\right] _{x}=\mathrm {cKPB}\).

References

  1. Biswas, A.: Solitary wave solution for KdV equation with power-law nonlinearity and time-dependent coefficients. Nonlinear Dyn. 58, 345 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  2. Mani Rajan, M.S., Mahalingam, A.: Nonautonomous solitons in modified inhomogeneous Hirota equation: soliton control and soliton interaction. Nonlinear Dyn. 79, 2469 (2015)

    Article  MathSciNet  Google Scholar 

  3. Ablowitz, M.J., Clarkson, P.A.: Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge (1991)

    Book  MATH  Google Scholar 

  4. Krishnan, E.V., Triki, H., Labidi, M., Biswas, A.: A study of shallow water waves with Gardner’s equation. Nonlinear Dyn. 66, 497 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  5. Morris, R.M., Kara, A.H., Biswas, A.: An analysis of the Zhiber–Shabat equation including Lie point symmetries and conservation laws. Collect. Math. 67, 55 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  6. Lü, X., Ma, W.X., Yu, J., Khalique, C.M.: Solitary waves with the Madelung fluid description: a generalized derivative nonlinear Schrödinger equation. Commun. Nonlinear Sci. Numer. Simul. 31, 40 (2016)

    Article  MathSciNet  Google Scholar 

  7. Lü, X., Ma, W.X., Chen, S.T., Khalique, C.M.: A note on rational solutions to a Hirota-Satsuma-like equation. Appl. Math. Lett. 58, 13 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  8. Razborova, P., Kara, A.H., Biswas, A.: Additional conservation laws for Rosenau-KdV-RLW equation with power law nonlinearity by Lie symmetry. Nonlinear Dyn. 79, 743 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  9. Razborova, P., Kara, A.H., Biswas, A.: Optical solitons in nonlinear directional couplers by sine-cosine function method and Bernoulli’s equation approach. Nonlinear Dyn. 81, 1933 (2015)

    Article  MathSciNet  Google Scholar 

  10. Lü, X., Ma, W.X., Zhou, Y., Khalique, C.M.: Rational solutions to an extended Kadomtsev–Petviashvili-like equation with symbolic computation. Comput. Math. Appl. 71, 1560 (2016)

    Article  MathSciNet  Google Scholar 

  11. Lü, X., Lin, F.: Soliton excitations and shape-changing collisions in alpha helical proteins with interspine coupling at higher order. Commun. Nonlinear Sci. Numer. Simu. 32, 241 (2016)

    Article  MathSciNet  Google Scholar 

  12. Wang, D.S., Wei, X.: Integrability and exact solutions of a two-component Korteweg-de Vries system. Appl. Math. Lett. 51, 60 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  13. Dai, C.Q., Wang, Y.Y., Zhang, X.F.: Spatiotemporal localizations in (3+1)-dimensional PT-symmetric and strongly nonlocal nonlinear media. Nonlinear Dyn. 83, 2453 (2016)

    Article  MathSciNet  Google Scholar 

  14. Satsuma, J., Ablowitz, M.J.: Two-dimensional lumps in nonlinear dispersive systems. J. Math. Phys. 20, 1496 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  15. Gilson, C.R., Nimmo, J.J.C.: Lump solutions of the BKP equation. Phys. Lett. A 147, 472 (1990)

    Article  MathSciNet  Google Scholar 

  16. Kaup, D.J.: The lump solutions and the Bäklund transformation for the three-dimensional three-wave resonant interaction. J. Math. Phys. 22, 1176 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  17. Imai, K.: Dromion and lump solutions of the Ishimori-I equation. Prog. Theor. Phys. 98, 1013 (1997)

    Article  Google Scholar 

  18. Ma, W.X.: Lump solutions to the Kadomtsev–Petviashvili equation. Phys. Lett. A 379, 1975 (2015)

    Article  MathSciNet  Google Scholar 

  19. Ma, W.X., Qin, Z.Y., Lü, X.: Lump solutions to dimensionally reduced p-gKP and p-gBKP equations. Nonlinear Dyn. 84, 923 (2016)

    Article  MathSciNet  Google Scholar 

  20. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  21. Ma, W.X., Li, C.X., He, J.S.: Nonlinear Anal. 70, 4245 (2009)

  22. Ma, W.X.: Generalized bilinear differential equations. Stud. Nonlinear Sci. 2, 140 (2011)

    Google Scholar 

  23. Ma, W.X.: Bilinear equations, Bell polynomials and linear superposition principle. J. Phys. Conf. Ser. 411, 012021 (2013)

    Article  Google Scholar 

  24. Ma, W.X.: Bilinear equations and resonant solutions characterized by Bell polynomials. Rep. Math. Phys. 72, 41 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  25. Ma, W.X., Fan, E.G.: Linear superposition principle applying to Hirota bilinear equations. Comput. Math. Appl. 61, 950 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  26. Ma, W.X., Zhang, Y., Tang, Y.N., Tu, J.Y.: Hirota bilinear equations with linear subspaces of solutions. Appl. Math. Comput. 218, 7174 (2012)

    MathSciNet  MATH  Google Scholar 

  27. Lü, X., Li, J.: Integrability with symbolic computation on the Bogoyavlensky Konoplechenko model: Bell-polynomial manipulation, bilinear representation, and Wronskian solution. Nonlinear Dyn. 77, 135 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  28. Lü, X.: New bilinear Bäcklund transformation with multisoliton solutions for the (2+1)-dimensional Sawada-Kotera mode. Nonlinear Dyn. 76, 161 (2014)

    Article  MATH  Google Scholar 

  29. Shi, C.G., Zhao, B.Z., Ma, W.X.: Exact rational solutions to a Boussinesq-like equation in (1+1)-dimensions. Appl. Math. Lett. 48, 170 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  30. Zhang, Y., Ma, W.X.: Rational solutions to a KdV-like equation. Appl. Math. Comput. 256, 252 (2015)

  31. Zhang, Y.F., Ma, W.X.: A study on rational solutions to a KP-like equation. Z. Naturforsch 70a, 263 (2015)

    Google Scholar 

  32. Li, D.S., Zhang, H.Q.: Appl. Math. Comput. 145, 351 (2003)

  33. Li, D.S., Zhang, H.Q.: Appl. Math. Comput. 146, 381 (2003)

  34. El-Wakil, S.A., Abulwafa, E.M., Elhanbaly, A., El-Shewy, E.K.: Astrophys Space Sci. 353, 501 (2014)

  35. Bell, E.T.: Exponential polynomials. Ann. Math. 35, 258 (1934)

    Article  MathSciNet  MATH  Google Scholar 

  36. Lü, X., Tian, B., Sun, K., Wang, P.: Bell-polynomial manipulations on the Bäcklund transformations and Lax pairs for some soliton equations with one Tau-function. J. Math. Phys. 51, 113506 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  37. Lü, X., Tian, B., Qi, F.H.: Bell-polynomial construction of Bäcklund transformations with auxiliary independent variable for some soliton equations with one Tau-function. Nonlinear Anal. Real World Appl 13, 1130 (2012)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This work is supported by the 111 Project of China (B16002), the National Natural Science Foundation of China under Grant No. 61308018, by China Postdoctoral Science Foundation under Grant No. 2014T70031, by the Fundamental Research Funds for the Central Universities of China (2015JBM111). Dr. Ma is supported in part by the National Natural Science Foundation of China under Grant Nos. 11371326 and 11271008, Natural Science Foundation of Shanghai under Grant No. 11ZR1414100, Zhejiang Innovation Project of China under Grant No. T200905, the First-class Discipline of Universities in Shanghai and the Shanghai University Leading Academic Discipline Project (No. A13-0101-12-004) and the Distinguished Professorship at Shanghai University of Electric Power. Dr. Chen is supported by the National Natural Science Foundation of China under Grant Nos. 11301454 and 11271168, the Natural Science Foundation for Colleges and Universities in Jiangsu Province (13KJD110009), the Jiangsu Qing Lan Project (2014) and XZIT (XKY 2013202).

Author information

Authors and Affiliations

  1. Department of Mathematics, Beijing Jiao Tong University, Beijing, 100044, China

    Xing Lü

  2. School of Mathematics and Physical Science, Xuzhou Institute of Technology, Jiangsu, 221111, China

    Shou-Ting Chen

  3. Department of Mathematics and Statistics, University of South Florida, Tampa, FL, 33620, USA

    Wen-Xiu Ma

  4. Department of Mathematical Sciences, International Institute for Symmetry Analysis and Mathematical Modelling, North-West University, Mafikeng Campus, Private Bag X 2046, Mmabatho, 2735, South Africa

    Wen-Xiu Ma

Authors
  1. Xing Lü
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shou-Ting Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wen-Xiu Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xing Lü.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lü, X., Chen, ST. & Ma, WX. Constructing lump solutions to a generalized Kadomtsev–Petviashvili–Boussinesq equation. Nonlinear Dyn 86, 523–534 (2016). https://doi.org/10.1007/s11071-016-2905-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-2905-z

Keywords

Mathematics Subject Classification

Search

Navigation