Observation of interaction phenomena for two dimensionally reduced nonlinear models

Abstract

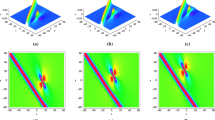
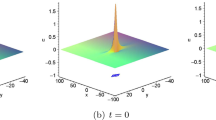
To study the lump–soliton interaction phenomenon for the (3 + 1)-dimensional nonlinear model with dimensional reduction, interaction solutions have been formulated by combining positive quadratic functions with hyperbolic function in bilinear equations. The collision between lump and soliton has been analyzed and simulated. When the lump is induced by a bounded twin soliton, the rogue wave turns up, which can only be visible at an instant time. Based on the solutions, it is easy to find the amplitude, the place and the arrival time of the rogue waves. The mechanism investigated in this paper may shed some light on the study of rogue waves in oceanography, fluid dynamics and nonlinear optics.

Appendices

Appendix A

Corresponding to Eqs. (8), we choose the parameters

$$\begin{aligned}&\Bigg \{a_{1}=1,\ a_{2}=0,\ a_{3}=0,\ a_{4}=0,\ a_{5}=0, \nonumber \\&\quad a_{6}=-\,6,\ a_{7}=1,\ a_{8}=0,\ a_{9}=\frac{\sqrt{3}}{6},\ \varepsilon =1, \nonumber \\&\quad k=1,\ k_{1}=3^{-\frac{1}{4}},\ k_{2}=-2\cdot 3^{\frac{1}{4}},\ k_{3}=(\sqrt{2}-1)3^{\frac{1}{4}} \Bigg \}, \end{aligned}$$

(28)

to get the interaction solutions $u_1$ with $w_1$ as

$$\begin{aligned}&u_1\nonumber \\&\quad =\frac{4x+2\cdot 3^{-\frac{1}{4}}{\mathrm {sinh}}\left( 3^{-\frac{1}{4}}x-2 \cdot 3^{\frac{1}{4}}y +3^{\frac{1}{4}}\left( \sqrt{2}-1\right) t\right) }{x^2+\left( -\,6y+t\right) ^2+{\mathrm {cosh}}\left( 3^{-\frac{1}{4}}x{-}2\cdot 3^{\frac{1}{4}}y {+}3^{\frac{1}{4}}\left( \sqrt{2}-1\right) t\right) {+}\frac{\sqrt{3}}{6}}, \end{aligned}$$

(29)

and

$$\begin{aligned} w_1&=\frac{2\left[ 2+3^{-\frac{1}{2}}{\mathrm {cosh}}\left( 3^{-\frac{1}{4}}x-2\cdot 3^{\frac{1}{4}}y +3^{\frac{1}{4}}\left( \sqrt{2}-1\right) t\right) \right] }{x^2+\left( -6y+t\right) ^2+{\mathrm {cosh}}\left( 3^{ -\frac{1}{4}}x-2\cdot 3^{\frac{1}{4}}y +3^{\frac{1}{4}}\left( \sqrt{2}-1\right) t\right) +\frac{\sqrt{3}}{6}}\nonumber \\&\quad -\frac{2\left[ 2x+3^{-\frac{1}{4}}{\mathrm {sinh}}\left( 3^{-\frac{1}{4}}x-2\cdot 3^{\frac{1}{4}}y +3^{\frac{1}{4}}\left( \sqrt{2}-1\right) t\right) \right] ^2}{\left[ x^2+\left( -6y+t\right) ^2+{\mathrm {cosh}}\left( 3^{-\frac{1}{4}} x-2\cdot 3^{\frac{1}{4}}y +3^{\frac{1}{4}}\left( \sqrt{2}-1\right) t\right) +\frac{\sqrt{3}}{6}\right] ^2}. \end{aligned}$$

(30)

Corresponding to Eqs. (9), we choose the parameters

$$\begin{aligned}&\Bigg \{a_{1}=2,\ a_{2}=0,\ a_{3}=0,\ a_{4}=0,\ a_{5}=0, \nonumber \\&\quad a_{6}=-15,\ a_{7}=1,\ a_{8}=0,\ a_{9}=\frac{1}{8},\ \varepsilon =1, \nonumber \\&k=1,\ k_{1}=1,\ k_{2}=-2,\ k_{3}=\frac{13}{9} \Bigg \}, \end{aligned}$$

(31)

to get the interaction solutions $u_2$ with $w_2$ as

$$\begin{aligned}&u_2=\frac{16x+2{\mathrm {sinh}}(x-2y +\frac{13}{9}t)}{4x^2+(-15y+t)^2+{\mathrm {cosh}}(x-2y +\frac{13}{9}t)+\frac{1}{8}}, \end{aligned}$$

(32)

and

$$\begin{aligned} w_2&=\frac{2\left[ 8+{\mathrm {cosh}}\left( x-2y +\frac{13}{9}t\right) \right] }{4x^2+(-15y+t)^2+{\mathrm {cosh}}\left( x-2y +\frac{13}{9}t\right) +\frac{1}{8}}\nonumber \\&\quad -\frac{2\left[ 8x+{\mathrm {sinh}}\left( x-2y +\frac{13}{9}t\right) \right] ^2}{\left[ 4x^2+(-15y+t)^2+{\mathrm {cosh}}\left( x-2y +\frac{13}{9}t\right) +\frac{1}{8}\right] ^2}. \end{aligned}$$

(33)

Appendix B

Corresponding to the parameters given in Eqs. (14) and (15), we choose the following two special sets of the parameters:

$$\begin{aligned}&\Bigg \{a_{1}=-1,\ a_{2}=2,\ a_{3}=0,\ a_{4}=0,\ a_{5}=1, \nonumber \\&\quad a_{6}=2,\ a_{7}=0,\ a_{8}=0,\ a_{9}=2, \nonumber \\&\quad k=10,\ k_{1}=-\frac{1}{2},\ k_{2}=0,\ k_{3}=-\frac{1}{8} \Bigg \}, \end{aligned}$$

(34)

and

$$\begin{aligned}&\Bigg \{a_{1}=1,\ a_{2}=0,\ a_{3}=0,\ a_{4}=0,\ a_{5}=0, \nonumber \\&\quad a_{6}=2,\ a_{7}=0,\ a_{8}=0,\ a_{9}=1, \nonumber \\&\quad k=3,\ k_{1}=-\frac{1}{2},\ k_{2}=0,\ k_{3}=-\frac{1}{8} \Bigg \}, \end{aligned}$$

(35)

which generate two interaction solutions to the dimensionally reduced Eq. (12), respectively, as

$$\begin{aligned}&u_3=\frac{8x-10\,{\mathrm {sinh}}\left( -\frac{1}{2}x -\frac{1}{8}t\right) }{(-x+2y)^2+(x+2y)^2+10\,{\mathrm {cosh}}\left( -\frac{1}{2}x -\frac{1}{8}t\right) +2}, \end{aligned}$$

(36)

and

$$\begin{aligned}&u_4=\frac{4x-3\,{\mathrm {sinh}}\left( -\frac{1}{2}x -\frac{1}{8}t\right) }{x^2+4y^2+3\,{\mathrm {cosh}}\left( -\frac{1}{2}x -\frac{1}{8}t\right) +1}, \end{aligned}$$

(37)

Associated with Eqs. (36) and (37), the derivative form of the interaction solutions can be obtained with $w=u_x$, respectively, as

$$\begin{aligned} w_3&=\frac{8+5\,{\mathrm {cosh}}\left( -\frac{1}{2}x -\frac{1}{8}t\right) }{\left( -x+2y\right) ^2+\left( x+2y\right) ^2+10\,{\mathrm {cosh}}\left( -\frac{1}{2}x -\frac{1}{8}t\right) +2}\nonumber \\&\quad -\frac{2\left[ 4x-5\,{\mathrm {sinh}}\left( -\frac{1}{2}x -\frac{1}{8}t\right) \right] ^2}{\left[ \left( -x+2y\right) ^2+\left( x+2y\right) ^2+10\, {\mathrm {cosh}}\left( -\frac{1}{2}x -\frac{1}{8}t\right) +2\right] ^2}, \end{aligned}$$

(38)

and

$$\begin{aligned} w_4&=\frac{4+\frac{3}{2}\,{\mathrm {cosh}}\left( -\frac{1}{2}x -\frac{1}{8}t\right) }{x^2+4y^2+3\,{\mathrm {cosh}}\left( -\frac{1}{2}x -\frac{1}{8}t\right) +1}\nonumber \\&\quad -\frac{2\left[ 2x-\frac{3}{2}\,{\mathrm {sinh}}\left( -\frac{1}{2}x -\frac{1}{8}t\right) \right] ^2}{\left[ x^2+4y^2+3\,{\mathrm {cosh}}\left( -\frac{1}{2}x -\frac{1}{8}t\right) +1\right] ^2}. \end{aligned}$$

(39)

Appendix C

Corresponding to the parameters given in Eqs. (18),  (19) and (20), we choose the following three special sets of the parameters:

$$\begin{aligned}&\Bigg \{a_{1}=0,\ a_{2}=2,\ a_{3}=0,\ a_{4}=0,\ a_{5}=1, \nonumber \\&\quad a_{6}=0,\ a_{7}=0,\ a_{8}=0,\ a_{9}=1, \nonumber \\&\quad k=2,\ k_{1}=0,\ k_{2}=\frac{1}{2},\ k_{3}=0 \Bigg \}, \end{aligned}$$

(40)

$$\begin{aligned}&\Bigg \{a_{1}=1,\ a_{2}=0,\ a_{3}=2,\ a_{4}=2,\ a_{5}=1,\nonumber \\&\quad a_{6}=0,\ a_{7}=-1,\ a_{8}=2,\ a_{9}=1, \nonumber \\&\quad k=2,\ k_{1}=-\frac{1}{2},\ k_{2}=0,\ k_{3}=\frac{1}{2} \Bigg \}, \end{aligned}$$

(41)

and

$$\begin{aligned}&\Bigg \{a_{1}=1,\ a_{2}=-2,\ a_{3}=0,\ a_{4}=0,\ a_{5}=1, \nonumber \\&\quad a_{6}=2,\ a_{7}=0,\ a_{8}=0,\ a_{9}=1, \nonumber \\&\quad k=2,\ k_{1}=0,\ k_{2}=\frac{1}{2},\ k_{3}=0 \Bigg \}, \end{aligned}$$

(42)

to derive the exact solutions in the form of u and w, respectively, as

$$\begin{aligned} u_5&=\frac{4x}{4y^2+x^2+2\,{\mathrm {cosh}}\left( \frac{1}{2}y\right) +1}, \end{aligned}$$

(43)

$$\begin{aligned} w_5&=\frac{4}{4y^2+x^2+2\,{\mathrm {cosh}}\left( \frac{1}{2}y\right) +1}\nonumber \\&\quad -\frac{8\,x^2}{[4y^2+x^2+2\, {\mathrm {cosh}}\left( \frac{1}{2}y\right) +1]^2}, \end{aligned}$$

(44)

$$\begin{aligned} u_6&=\frac{8x+4t-2\,{\mathrm {sinh}}\left( -\frac{1}{2}x +\frac{1}{2}t\right) +16}{\left( x+2t+2\right) ^2+\left( x-t+2\right) ^2+2\,{\mathrm {cosh}}\left( -\frac{1}{2}x +\frac{1}{2}t\right) +1}, \end{aligned}$$

(45)

$$\begin{aligned} w_6&=\frac{8+{\mathrm {cosh}}\left( -\frac{1}{2}x +\frac{1}{2}t\right) }{\left( x+2t+2\right) ^2+\left( x-t+2\right) ^2+2\,{\mathrm {cosh}}\left( -\frac{1}{2}x +\frac{1}{2}t\right) +1}\nonumber \\&\quad -\frac{2\left[ 4x+2t-{\mathrm {sinh}}\left( -\frac{1}{2}x +\frac{1}{2}t\right) +8\right] ^2}{\left[ \left( x+2t+2\right) ^2+\left( x-t+2\right) ^2+2\,{\mathrm {cosh}}\left( -\frac{1}{2}x +\frac{1}{2}t\right) +1\right] ^2}, \end{aligned}$$

(46)

and

$$\begin{aligned} u_7&=\frac{8x}{\left( x-2y\right) ^2+\left( x+2y\right) ^2+2\,{\mathrm {cosh}}\left( \frac{1}{2}y\right) +1}, \end{aligned}$$

(47)

$$\begin{aligned} w_7&=\frac{8}{\left( x-2y\right) ^2+\left( x+2y\right) ^2+2\,{\mathrm {cosh}}\left( \frac{1}{2}y\right) +1}\nonumber \\&\quad -\frac{32x^2}{\left[ \left( x-2y\right) ^2+\left( x+2y\right) ^2+2\,{\mathrm {cosh}}\left( \frac{1}{2}y\right) +1\right] ^2}. \end{aligned}$$

(48)