Abstract
In this paper, the dynamic behaviors of a competition model in the turbidostat with discrete delay are investigated. The stability of the positive equilibrium and the existence of a Hopf bifurcation are discussed by choosing the delay of digestion as a bifurcation parameter. Furthermore, we determine the direction and stability of the bifurcating periodic solutions by the normal form and the center manifold theorem. Moreover, some examples are given to illustrate our main results.
Similar content being viewed by others
1 Introduction
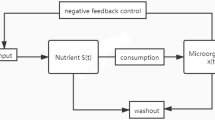
Chemostat models have been fruitful as a source of mathematical problems (see [1–11]). Generally, chemostat models lead to competitive exclusion results, which means that only one organism can survive in the competition at last. The phenomenon of coexistence of the organisms is a common thing in reality [3, 4, 12–14]. In a sense, coexistence reflects the ecological balance. The turbidostat as well as the chemostat is an important laboratory set for continuous cultivation of microorganisms, and also a very important medium between principle and application. Turbidostat model is one of the most important models in mathematical biology. Figure 1 [15] is the schematic diagram of the competition in the turbidostat. However, little work has been done in the study of mathematical models on the turbidostat, and the existing main studies can be listed as follows. Flegr [16] showed the coexistence of two organisms in the turbidostat by numerical analysis, De Leenheer and Smith [17] also verified Flegr’s results by theoretical analysis. Li [18] and Cammarota and Miccio [19], respectively, established a mathematical model of competition in a turbidostat for an inhibitory nutrient, and one obtained sufficient conditions for coexistence solutions. Recently, to ensure the coexistence of the species, some scholars have considered turbidostat models by controlling the dilution rate of the turbidostat (see [20–22]).
De Leenheer and Smith [17] have considered the following system:
Here \(S(t)\) is the nutrient concentration and \(x_{i}(t)\) (\(i=1, 2\)) is the density of the ith organism at time t, respectively. \(S^{0}>0\) represents the input concentration of the nutrient. \(\gamma_{i}>0\) (\(i=1,2\)) stands for the yield constant. \(f_{i}(S(t))= \frac{m_{i}S(t)}{a_{i}+S(t)}\) (\(m_{i}>0\), \(a_{i}>0\), \(i=1,2\)) are uptakes functions. \(D(x(t))=d+k_{1}x_{1}(t)+k_{2}x_{2}(t)\) (\(d>0\), \(k_{i}>0\), \(i=1,2\)) is the dilution of the turbidostat. \(k_{i}\) is the gain of the ith organism. System (1.1) is called ‘turbidostat’ by Li [18].
It was shown in [17] that a turbidostat with two organisms can be made coexistent if the dilution rate depends on the concentrations of two competing organisms. The authors showed that system (1.1) possessed a unique coexistence equilibrium under the specific conditions, and it is globally asymptotically stable. Yet people have recognized that time delay have a complex impact on the dynamics of a system in reality (see [23–25] and [26]). Yuan et al. [27] considered the effect of delay on the dilution rate \(D(x(t))\) of system (1.1). The authors have investigated the stability of the positive equilibrium, the existence, and the stability of Hopf bifurcation. Further we note that the chemostat models with discrete delay due to the possibility that the organism digests (stores) the nutrient are natural and reasonable (see Bush and Cook [28], Freedman et al. [14] and Zhao [29]). Generally, different microorganisms have the different delays of digestion, but a single time delay is common in reality (see Lin et al. [30], Bender et al. [31] and Kharitonov [32]), so we assume that the two competitive microorganisms are homogeneous species and they have the same delay of digestion. Based on motivation from the work of Bush and Cook [28], Freedman et al. [14] and Zhao [29], in this study we focus on the dynamics of a turbidostat model with time delay of digestion which follows:
Here \(S(t)\), \(x_{1}(t)\), \(x_{2}(t)\), \(D(x(t))\), \(f_{i}(S(t-\tau))\) (\(i=1,2\)) and the parameters play similar roles to system (1.1), \(\tau>0\) is the time delay of digestion.
The organization of this paper is as follows. We investigate the local stability and Hopf bifurcation of the positive equilibrium of system (1.2) in the next section. In Section 3, by using the normal form method and the center manifold theory introduced by Hassard et al. [33], we analyze the direction of Hopf bifurcation and the stability of bifurcating periodic solutions. In Section 4, some examples are given to illustrate our results.
2 Local stability and Hopf bifurcation
In the section, we focus on investigating the local stability of the positive equilibrium and the existence of local Hopf bifurcations for system (1.2).
For the sake of simplicity, we let
The bars dropped, system (1.2) becomes
As in [17], we introduce the same hypothesis:
-
(H)
The graphs of the functions \(f_{1}\) and \(f_{2}\) intersect once at \(S^{*}\):
$$f_{1}\bigl(S^{*}\bigr)=f_{2}\bigl(S^{*}\bigr)=D^{*}, $$where \(S^{*}\in(0, 1)\) and \(f_{1}'(S^{*})\neq f_{2}'(S^{*})\).
Assume that \(d\in(0, D^{*})\) and
then system (2.1) has a unique positive equilibrium \(E^{*}=(S^{*} ,x_{1}^{*}, x_{2}^{*})\), where
In the following, we will investigate the local stability of \(E^{*}\) and the existence of Hopf bifurcations induced by the time delay.
Set \(y_{1}(t) =S(t)-S^{*}\), \(y_{2}(t) =x_{1}(t)-x_{1}^{*}\), \(y_{3}(t) =x_{2}(t)-x_{2}^{*}\). Then system (2.1) can be written as
Here
So the linearized system of (2.1) at \(E^{*}\) is
We obtain the characteristic equation from (2.3)
where
In order to study the distribution of the roots of (2.4), we consider the following two cases: \(\tau=0\) and \(\tau>0\).
For \(\tau=0\), (2.4) becomes
It is obvious that \(p>0\). According to the Routh-Hurwitz criterion, we immediately have the following lemma.
Lemma 2.1
If (H2) \(k>0\), \(p(q+r)>k\), then all roots of (2.5) have negative real parts.
For \(\tau>0\), Beretta and Kuang [34] have studied the general characteristic equation with delay dependent parameters:
where \(P_{n}\) and \(Q_{m}\) are, respectively, n-degree and m-degree polynomials in λ, with \(n>m\) and with delay dependent polynomial coefficients. In (2.4), the parameters are delay independent, so the stability switch of the (2.4) can be obtained as a particular case of the results in [34].
We set
We assume that \(P_{n}(\lambda; \tau)\) and \(Q_{m}(\lambda; \tau)\) cannot have imaginary roots. That is, for any real number w,
We have
Hence, \(F(w)=0\) implies
Set \(v=w^{2}\), then (2.8) becomes
Denote
Since \(f(0)=-k^{2}<0\), \({\lim_{v\rightarrow +\infty}}f(v)=+\infty\), it is obvious that (2.9) has at least one positive root. By (2.10), we get
Denote \(\Delta=4(p^{2}-2q)^{2}-12(q^{2}-r^{2})\). If \(\Delta\leq0\), then the function \(f(v)\) is monotone increasing in \(v\in[0, \infty)\). Thus, (2.9) has only a positive real root; on the other hand, when \(\Delta>0\), the equation \(3v^{2}+2(p^{2}-2q)v+q^{2}-r^{2}=0\) has two real roots \(v_{1}= \frac{-2(p^{2}-2q)+\sqrt{\Delta}}{6} \) and \(v_{2}= \frac{-2(p^{2}-2q)-\sqrt{\Delta}}{6}\). Since \(p^{2}-2q>0\), one can get \(v_{2}<0\). We immediately know that \(f(v)\) has only a positive real root too, and \(f(v)\) is monotone increasing in \(v\in(v_{1}, \infty)\). Thus, (2.9) has only a positive root denoted by \(v_{0}\). Furthermore, we have the fact that \(v_{0}>v_{1}\) is true when \(\Delta>0\). Then (2.8) has unique positive root \(w_{0}=\sqrt{v_{0}}\).
Furthermore, \(P_{R}(iw_{0}, \tau)=-pw_{0}^{2}\), \(P_{I}(iw_{0}, \tau)=-w_{0}^{3}+qw_{0}\), \(Q_{R}(iw_{0}, \tau)=k\), \(Q_{I}(iw_{0}, \tau)=rw_{0}\). Hence, we have
We denote the corresponding critical value of time delay that is satisfied \(\tau^{*}\),
Thus,
From (2.7), we have
Differentiating (2.4) with respect to τ, we have
Hence, a direct calculation shows that
Also we have
Hence,
We conclude that the sign of \(( \frac{d(\operatorname{Re}\lambda)}{d\tau} )_{\lambda=iw_{0}}\) is determined by that of \(f'(w_{0}^{2})\).
According to the above discussion, we know \(f'(v_{0})>0\). Thus, \(\delta(\tau^{*})>0\).
From Theorem 2.2 in [34], we have the following result.
Lemma 2.2
The characteristic equation (2.4) has a pair of simple and conjugate pure imaginary roots \(\lambda=\pm iw_{0}\) at \(\tau ^{*}\) if \(S_{n}(\tau^{*})=\tau^{*}-\tau_{n}(\tau^{*})=0\) for some \(n\in N_{0}\). Since \(\delta(\tau^{*})>0\), this pair of simple conjugate pure imaginary roots crosses the imaginary axis from left to right.
From Lemmas 2.1 and 2.2, we have the following lemma.
Lemma 2.3
If (H2) holds, then (2.4) has a pair of simple imaginary roots \(\pm iw_{0}\) when \(\tau=\tau_{n}\), \(n\in N_{0}\). Furthermore, when \(\tau\in[0, \tau_{0})\), all roots of (2.4) have negative real parts; when \(\tau=\tau_{0}\), all roots of (2.4) except \(\pm iw_{0}\) have negative real parts; when \(\tau\in(\tau_{n}, \tau_{n+1}]\), (2.4) has \(2(n+1)\) roots with positive real parts.
Thus, from Lemmas 2.1-2.3 and Theorem 6.1 in [25], we have the following theorem.
Theorem 2.1
For system (2.1), assume that (H1) and (H2) hold, there exists a positive number \(\tau_{0}\) such that the positive equilibrium \(E^{*}\) is asymptotically stable when \(\tau\in[0, \tau_{0})\) and unstable when \(\tau>\tau_{0}\). Furthermore, system (2.1) undergoes a Hopf bifurcation at \(E^{*}\) when \(\tau=\tau_{0}\).
3 Direction and stability of the bifurcating periodic solutions
In Section 2, we have obtained the conditions under which system (2.1) undergoes Hopf bifurcation when \(\tau=\tau_{0}\). In this section, by using the normal form and the center manifold theory that introduced by Hassard et al. [33], we will consider the direction of the Hopf bifurcation and the stability of bifurcating periodic solutions of system (2.1).
Set \(\bar{y}_{i}(t)=y_{i}(\tau t)\), \(\tau=\tau_{0}+\mu\), where \(\tau_{0}\) is defined by (2.11), and drop the bars for convenience, then system (2.1) can be written as a FDE in \(C=C([-1, 0], R^{3})\),
where \(y(t)=(y_{1}(t), y_{2}(t), y_{3}(t))^{T} \in R^{3}\), and \(L_{\mu}: C\rightarrow R^{3}\), \(h : R\times C\rightarrow R^{3}\) are, respectively, given by
and
Here
and \(\varphi=(\varphi_{1}, \varphi_{2}, \varphi_{3})^{T}\in C\).
By the Riesz representation theorem, there exists a function \(\eta(\theta, \mu)\) of bounded variation for \(\theta\in[-1, 0]\) such that
In fact, we can choose
where δ is the Dirac delta function.
For \(\varphi\in C^{1} ([-1, 0], R^{3})\), we define the operators A and R as
and
Then system (3.1) becomes
where \(y_{t}(\theta)=y(t+\theta)\) for \(\theta\in[-1, 0]\).
As in [35], the bifurcating periodic solutions \(y(t, \mu)\) of system (3.1) are indexed by a small parameter ε. The solution \(y(t, \mu(\varepsilon))\) has an amplitude \(O(\varepsilon)\), a nonzero Floquet exponent \(\beta(\varepsilon)\) with \(\beta(0)=0\) and a period \(T(\varepsilon)\). Under the assumptions, μ, T, and β have expansions
Here \(\mu_{2}\) determines the directions of the bifurcation: if \(\mu_{2}<0\) (>0), then the Hopf bifurcation is subcritical (supercritical); \(\beta_{2}\) determines the stability of the bifurcating periodic solutions: the bifurcating periodic solutions are stable (unstable) if \(\beta_{2}<0\) (>0); and the period of the bifurcating periodic solutions is determined by \(T_{2}\): if \(T_{2}>0\) (<0), the period increases (decreases).
Next, we only need to compute the coefficients \(\mu_{2}\), \(T_{2}\), \(\beta_{2}\) in the above expansions.
For \(\psi\in C^{1}([0, 1], (R^{3})^{*})\), we define the adjoint operator \(A^{*}\) of A as
Meanwhile, we define a bilinear inner product as follows:
where \(\eta(\theta)=\eta(\theta, 0)\).
From the discussion in Section 2, we know that \(\pm iw_{0}\tau_{0}\) are eigenvalues of \(A(0)\). Thus, they are also eigenvalues of \(A^{*}\), we first need to calculate the eigenvectors of \(A(0)\) and \(A^{*}\) corresponding to \(iw_{0}\tau_{0}\) and \(-iw_{0}\tau_{0}\), respectively.
Assume that \(q(\theta)=(1, \alpha_{1}, \beta_{1})^{T} e^{iw_{0}\tau_{0} \theta}\) is the eigenvector of \(A(0)\) corresponding to \(iw_{0}\tau_{0}\), then \(A(0)q(\theta)=iw_{0}\tau_{0}q(\theta)\). By the definition of \(A(0)\) and (3.2), (3.4), and (3.5), we obtain
which yields
Similarly, set \(q^{*}(s)= D(1, \alpha_{2}, \beta_{2}) e^{iw_{0}\tau_{0} s}\) is the eigenvector of \(A^{*}\) corresponding to \(-iw_{0}\tau_{0}\). It follows from the definition of \(A^{*}\) and (3.2), (3.4), and (3.5) that
we can easily obtain
From (3.11), we have
Since \(\langle q^{*}(s), q(\theta)\rangle=1\), we have
In the following, we follow the ideas in Hassard et al. and use the same notations to compute the coordinates describing the center manifold \(C_{0}\) at \(\mu=0\). Set \(y_{t}\) be the solution of (3.1) when \(\mu=0\). Define
On the center manifold \(C_{0}\), we have
where z and z̄ are local coordinates for center manifold \(C_{0}\) in the direction of \(q^{*}\) and \(\bar{q}^{*}\). Note that W is real if \(y_{t}\) is real. We consider only real solutions. For the solution \(y_{t}\in C_{0}\) of (3.8), since \(\mu=0\), we have
We rewrite the equation as
where
The expressions of \(\mu_{2}\), \(T_{2}\), and \(\beta_{2}\) include the coefficients \(g_{20}\), \(g_{11}\), \(g_{02}\), and \(g_{21}\). Next, we need to compute \(g_{20}\), \(g_{11}\), \(g_{02}\), and \(g_{21}\).
By (3.15), we have \(y_{t}(\theta)=(y_{1t}(\theta), y_{2t}(\theta), y_{3t}(\theta))^{T} =W(t, \theta)+zq(\theta)+\overline{z q(\theta)}\), and then
From (3.19), we obtain
By substituting (3.20) into (3.21) and comparing the coefficients with (3.19), we obtain
In order to determine \(g_{21}\), we still need to compute \(W_{20}(\theta)\) and \(W_{11}(\theta)\). From (3.8) and (3.17), we get
where
By comparing the coefficients (3.23), we get
From (3.23), we know that, for \(\theta\in[-1, 0)\),
By comparing the coefficients with (3.24), we have
It follows from (3.25), (3.27), and the definition of A that
Notice \(q(\theta)=(1, \alpha_{1}, \beta_{1})^{T} e^{iw_{0}\tau_{0} \theta}\), then
where \(E_{1}=(E_{11}, E_{12}, E_{13})^{T}\in R^{3} \) is a constant vector.
Similarly, from (3.25) and (3.27), it follows that
where \(E_{2}=(E_{21}, E_{22}, E_{23})^{T}\in R^{3} \) is also a constant vector.
Next, we will search \(E_{1}\) and \(E_{2}\). From (3.25) and the definition of A, we can obtain
where \(\eta(\theta)=\eta(\theta, 0)\).
Noting that \(q(\theta)\) is the eigenvector of \(A(0)\) and from (3.28) and the definition of \(A(0)\), we have
and
Hence, the first equation of (3.30) becomes
Similarly, from (3.29), it follows that
Thus, the second equation of (3.30) becomes
From (3.23), it follows that
where
Also
where
From (3.33) and (3.36), we have
which leads to
Thus, we have
Similarly, from (3.35) and (3.37), we have
Then we have
Hence, we can determine \(W_{20}(\theta)\) and \(W_{11}(\theta)\) from (3.28) and (3.29). Furthermore, \(g_{21}\) can be expressed explicitly. Next, we can compute the following values:
It follows that \(\operatorname{Re}(\lambda'(\tau_{0}))>0\) from Lemma 2.3. Thus, \(\operatorname{Re}(c_{1}(0))\) determines the signs of \(\mu_{2}\) and \(\beta_{2}\). We have the following theorem.
Theorem 3.1
If \(\operatorname{Re}(c_{1}(0))<0\) (>0), then the direction of the Hopf bifurcation of the system (2.1) at the positive equilibrium \(E^{*}(S^{*}, x^{*})\) when \(\tau=\tau_{0}\) is supercritical (subcritical) and the bifurcating periodic solutions are stable (unstable).
4 Numerical simulation and discussion
It was shown in [17] that the coexistence of two organisms was achieved in the turbidostat. While it was also shown in [27] that the coexistence was achieved if we consider system (1.1) with the delay on the dilution rate. In this paper, system (1.1) with the time delay of digestion was investigated. By choosing the time delay as the bifurcation parameter and analyzing the characteristic equation, we obtained sufficient conditions for the local stability of the positive equilibrium and the existence of a Hopf bifurcation. The direction, stability, and the other properties of the bifurcating periodic solutions were determined by the normal form theory and the center manifold theorem. These results show that it is possible to make the two organisms in the turbidostat coexist.
We next take an example to illustrate our main results. Setting \(a_{1}=0.25\), \(a_{2}=0.8\), \(m_{1}=3\), \(m_{2}=5\), \(k_{1}=2.2\), \(k_{2}=1.05\), and \(d=1.4\), we consider the following example of system (2.1):
It is easy to verify that the conditions (H1) and (H2) hold, and then we can obtain the positive equilibrium \(E^{*}=(S^{*}, x_{1}^{*}, x_{2}^{*})=(0.5750, 0.2127, 0.2123)\). By a simple calculation, we have \(w_{0}\doteq0.0670\), \(\tau_{0}\doteq29.85\), and \(( \frac{d(\operatorname{Re}\lambda)}{d\tau})_{\tau=\tau_{0}}=9.8772\times10^{-4}>0 \). By Theorem 2.1, the positive equilibrium \(E^{*}\) is asymptotically stable when \(\tau=29.3\) (or 29.6) \(<\tau_{0}\) (see Figure 2 and Figure 3). The positive equilibrium \(E^{*}\) is unstable and a Hopf bifurcation occurs, i.e., a bifurcating periodic solution occurs from \(E^{*}\) when \(\tau=29.9\) (or 31) \(>\tau_{0}\) (see Figure 4 and Figure 5).
The positive equilibrium \(\pmb{E^{*}=(0.5750, 0.2127, 0.2123)}\) of ( 4.1 ) is asymptotically stable when \(\pmb{\tau=29.3 <\tau_{0}\doteq29.85}\) . Here \((S(0), x_{1}(0), x_{2}(0))=(0.5, 0.2, 0.3)\).
The positive equilibrium \(\pmb{E^{*}=(0.5750, 0.2127, 0.2123)}\) of ( 4.1 ) is also asymptotically stable when \(\pmb{\tau=29.6 <\tau_{0}\doteq29.85}\) . Here \((S(0), x_{1}(0), x_{2}(0))=(0.4, 0.3, 0.3)\).
The positive equilibrium \(\pmb{E^{*}=(0.5750, 0.2127, 0.2123)}\) of ( 4.1 ) is unstable and a bifurcating periodic solution occurs from \(\pmb{E^{*}}\) when \(\pmb{\tau=29.9 >\tau_{0}\doteq29.85}\) . Here \((S(0), x_{1}(0), x_{2}(0))=(0.4, 0.3, 0.2)\).
The positive equilibrium \(\pmb{E^{*}=(0.5750, 0.2127, 0.2123)}\) of ( 4.1 ) is unstable and a bifurcating periodic solution occurs from \(\pmb{E^{*}}\) when \(\pmb{\tau=31 >\tau_{0}\doteq29.85}\) . Here \((S(0), x_{1}(0), x_{2}(0))=(0.4, 0.3, 0.3)\).
According to (3.22), we can compute
Hence, from (3.40), we can obtain
Therefore, when \(\tau=29.9\) (or 31) \(\in(\tau_{0}, \tau_{1})\), \(\mu_{2}>0\), and \(\beta_{2}<0\), then the Hopf bifurcation for system (4.1) is supercritical, and the stable bifurcating periodic solutions can occur from the positive equilibrium \(E^{*}(0.5750, 0.2127, 0.2123)\). From Figure 3 and Figure 4, we can find that the dynamics of system (4.1) changes when τ is located near \(\tau_{0}\). Comparing Figure 2 and Figure 3, we can see that the size of τ affects the dynamical behaviors of the turbidostat model. These are also shown by Figure 6. By Figures 7 and 8, we see that the bifurcating periodic solutions increase.
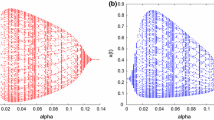
τ - \(\pmb{S(t)}\) , τ - \(\pmb{x_{1}(t)}\) , and τ - \(\pmb{x_{2}(t)}\) are simulated by numerical investigation of system ( 4.1 ). Here \((S(0), x_{1}(0), x_{2}(0))=(0.5, 0.2, 0.3)\).
Matlab simulations of system ( 4.1 ) when \(\pmb{\tau=130 \in(\tau_{1},\tau_{2})}\) . Here \((S(0), x_{1}(0), x_{2}(0))=(0.5, 0.2, 0.3)\).
Matlab simulations of system ( 4.1 ) when \(\pmb{\tau=300 \in(\tau_{2},\tau_{3})}\) . Here \((S(0), x_{1}(0), x_{2}(0))=(0.5, 0.2, 0.3)\).
References
Smith, HL: The Theory of the Chemostat: Dynamics of Microbial Competition. Cambridge University Press, Cambridge (1995)
Ajbar, A, Alhumaizi, K: Dynamics of the Chemostat: A Bifurcation Theory Approach. CRC Press, Boca Raton (2012)
Nie, H, Liu, N, Wu, JH: Coexistence solutions and their stability of an unstirred chemostat model with toxins. Nonlinear Anal., Real World Appl. 20, 36-51 (2014)
Grognard, F, Masci, P, Benoît, E, Bernard, O: Competition between phytoplankton and bacteria: exclusion and coexistence. J. Math. Biol. 70, 959-1006 (2015)
Zhao, Z, Zhang, XQ, Chen, LS: Nonlinear modelling of chemostat model with time delay and impulsive effect. Nonlinear Dyn. 63, 95-104 (2011)
Wang, Y, Wang, HB, Jiang, WH: Stability switches and global Hopf bifurcation in a nutrient-plankton model. Nonlinear Dyn. 78, 981-994 (2014)
Fekih-Salem, R, Harmand, J, Lobry, C, Rapaport, A, Sari, T: Extensions of the chemostat model with flocculation. J. Math. Anal. Appl. 397, 292-306 (2013)
Li, ZX, Chen, LS, Liu, ZJ: Periodic solution of a chemostat model with variable yield and impulsive state feedback control. Appl. Math. Model. 36, 1255-1266 (2012)
Zhou, Y, Song, XY, Shi, XY: Analysis of competitive chemostat models with the Beddington-DeAngelis functional response and impulsive effect. Appl. Math. Model. 31, 2299-2312 (2007)
Patnaik, PR: Dynamic sensitivity of a chemostat for a microbial reaction with substrate and product inhibition. Appl. Math. Model. 18, 620-627 (1994)
Jia, JW, Lv, TT: Study of two-nutrient and two-micro-organism chemostat model with pulsed input in a polluted environment. Int. J. Biomath. 8, 1550042 (2015)
Zhou, H, Lin, ZG: Coexistence in a strongly coupled system describing a two-species cooperative model. Appl. Math. Lett. 20, 1126-1130 (2007)
Butler, GJ, Hsu, SB, Waltman, P: Coexistence of competing predators in a chemostat. J. Math. Biol. 17, 133-151 (1983)
Freedman, HI, Joseph, WH, Waltman, P: Coexistence in a model of competition in the chemostat incorporating discrete delays. SIAM J. Appl. Math. 49, 859-870 (1989)
Li, ZX, Wang, TY, Chen, LS: Periodic solution of a chemostat model with Beddington-DeAngelis uptake function and impulsive state feedback control. J. Theor. Biol. 261, 23-32 (2009)
Flegr, J: Two distinct types of natural selection in turbidostat-like and chemostat-like ecosystems. J. Theor. Biol. 188, 121-126 (1997)
De Leenheer, P, Smith, H: Feedback control for the chemostat. J. Math. Biol. 46, 48-70 (2003)
Li, BT: Competition in a turbidostat for an inhibitory nutrient. J. Biol. Dyn. 2, 208-220 (2008)
Cammarota, A, Miccio, M: Competition of two microbial species in a turbidostat. Comput.-Aided Chem. Eng. 28, 331-336 (2010)
Li, ZX, Chen, LS: Periodic solution of a turbidostat model with impulsive state feedback control. Nonlinear Dyn. 58, 525-538 (2009)
Zhao, Z, Wang, TY, Chen, LS: Dynamic analysis of a turbidostat model with the feedback control. Commun. Nonlinear Sci. Numer. Simul. 15, 1028-1035 (2010)
Yao, Y, Li, ZX, Liu, ZJ: Hopf bifurcation analysis of a turbidostat model with discrete delay. Appl. Math. Comput. 262, 267-281 (2015)
Wang, L, Wolkowicz, GSK: A delayed chemostat model with general nonmonotone response functions and differential removal rates. J. Math. Anal. Appl. 321, 452-468 (2006)
Kuang, Y: Delay Differential Equations with Applications in Population Dynamics. Academic Press, San Diego (1993)
Smith, HL: An Introduction to Delay Differential Equations with Applications to the Life Sciences. Springer, Berlin (2011)
Erneux, T: Applied Delay Differential Equations. Springer, Berlin (2009)
Yuan, SL, Li, P, Song, YL: Delay induced oscillations in a turbidostat with feedback control. J. Math. Chem. 49, 1646-1666 (2011)
Bush, AW, Cook, AE: The effect of time delay and growth rate inhibition in the bacterial treatment of wastewater. J. Theor. Biol. 63, 385-396 (1975)
Zhao, T: Global periodic solutions for a differential delay system modeling a microbial population in the chemostat. J. Math. Anal. Appl. 193, 329-352 (1995)
Lin, Q, Wu, XF, Chen, Y: Frequency-domain criterion for the chaos synchronization of time-delay power systems under linear feedback control. Pramana J. Phys. 85, 1131-1142 (2015)
Bender, M, Büttner, S, Krumke, SO: Online delay management on a singe train line: beyond competitive analysis. Public Transp. 5, 243-266 (2013)
Kharitonov, VL: Time-Delay Systems: Lyapunov Functionals and Matrices. Springer, Berlin (2013)
Hassard, BD, Kazarinoff, ND, Wan, YH: Theory and Applications of Hopf Bifurcation. Cambridge University Press, Cambridge (1981)
Beretta, E, Kuang, Y: Geometric stability switch criteria in delay differential systems with delay dependent parameters. SIAM J. Math. Anal. 35, 1144-1165 (2002)
Mircea, G, Neamtu, M, Opris, D: Dynamical Systems from Economy, Mechanic and Biology Described by Differential Equations with Time Delay. Editura Mirton, Timişoara (2003)
Acknowledgements
The authors thank the anonymous referees and the editor for their careful reading of the original manuscript and their kind comments and valuable suggestions. This work is supported by the National Nature Science Foundation of China (Grant No. 11561022 and Grant No. 11261017), the China Postdoctoral Science Foundation (Grant No. 2014M562008).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors read and approved the manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Li, Z., Yao, Y., Wang, H. et al. Dynamical analysis of a competition model in the turbidostat with discrete delay. Adv Differ Equ 2016, 249 (2016). https://doi.org/10.1186/s13662-016-0955-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-016-0955-7