1 Introduction

Motivated by work on Lifshitz scaling in condensed matter physics, it is possible to take different Lifshitz scalings for space and time, and the resultant theory is called Horava–Lifshitz gravity [1, 2]. In the IR limit this gravity reduces to general relativity, and so it can be considered as a UV completion of general relativity. Motivated by this work on Horava–Lifshitz gravity, different Lifshitz scalings for space and time have been considered for type IIA string theory [3], type IIB string theory [4], the AdS/CFT correspondence [5–8], dilatonic black branes [9, 10], and dilatonic black holes [11, 12]. Another UV completion theory of general relativity which reduces to general relativity in the IR limit is called gravity’s rainbow [13]. In fact, it has been demonstrated that gravity’s rainbow is related to Horava–Lifshitz gravity [14]. This is because both of these theories are based on modifying the usual energy-momentum dispersion relation in the UV limit such that it reduces to the usual energy-momentum dispersion relation in the IR limit. It may be noted that such a modification of the usual energy-momentum has also been obtained in discrete spacetime [15], spacetime foam [16], the spin-network in loop quantum gravity (LQG) [17], ghost condensation [18], and non-commutative geometry [19, 20]. The non-commutative geometry occurs due to background fluxes in string theory [21, 22], and it is used to derive one of the most important rainbow functions in gravity’s rainbow [23, 24].

It may be noted that the UV modification of the usual energy-momentum dispersion relation implies the breaking of the Lorentz symmetry in the UV limit of the theory. The spontaneous breaking of the Lorentz symmetry can occur in string theory because of the existence of an unstable perturbative string vacuum [25]. It is possible for a tachyon field to have the wrong sign for its mass squared in string field theory, and this causes the perturbative string vacuum to become unstable. The theory becomes ill defined if the vacuum expectation value of the tachyon field is infinite. It is also possible for the vacuum expectation value of the tachyon field to be finite and negative. In this case, the coefficient of the quadratic term for the massless vector field is non-zero and negative, and this breaks the Lorentz symmetry. The spontaneous breaking of the Lorentz symmetry in string theory has also been investigated using the gravitational version of the Higgs mechanism [26]. This has been done for the low-energy effective action obtained from string theory. Lorentz symmetry breaking has also been studied using the black brane in type IIB string theory [27]. In this analysis, moduli stabilization was studied using a KKLT-type moduli potential in the context of type IIB warped flux compactification. It was demonstrated that a Higgs phase for gravity will exist if all moduli are stabilized. Another study regarding the breaking of Lorentz symmetry was done by using compactification in string field theory [28]. It may be noted that various other approaches to quantum gravity also indicate that the Lorentz symmetry might only be an effective symmetry which occurs in the IR limit of some fundamental theories of quantum gravity [29–33].

Hence, there is a good motivation to study the UV deformation of geometries that occur in string theory. In fact, motivated by Lifshitz deformation of such geometries, and the relation between Horava–Lifshitz gravity and gravity’s rainbow [14], recently rainbow deformation of geometries that occur in string theory has been performed. Thus, the modifications of the thermodynamics of black rings has been analyzed using gravity’s rainbow [34]. It has been observed that a remnant exists for black rings in gravity’s rainbow. It has also been argued that a remnant might exist for all black objects in gravity’s rainbow [35]. This has been explicitly demonstrated for Kerr black holes, Kerr–Newman black holes in de Sitter space, charged AdS black holes, higher-dimensional Kerr–AdS black holes, and black saturn [35]. This was done by generalizing the work done on the thermodynamics of black holes in gravity’s rainbow [36]. The usual uncertainty principle still holds in gravity’s rainbow [37, 38], and it is possible to obtain a lower bound on the energy \(E\ge 1/\Delta x\), using the usual uncertainty principle. This energy can be related to the energy of a particle emitted in Hawking radiation. Furthermore, the value of the uncertainty in position can be equated to the radius of the event horizon, \(E\ge 1/{\Delta x}\approx 1/{ r_{+}}.\) This energy can be related to the energy at which spacetime is probed, and hence it describes the energy E in gravity’s rainbow. This is because effectively this particle emitted with energy E can be viewed as a probe of the geometry of the black hole. This consideration modifies the temperature of the black hole [36]. The entropy and the heat capacity of black hole in gravity’s rainbow can be calculated using this modified temperature. An interesting consequence of this modified solution is that it predicts the existence of remnants for the black hole. Thus, the temperature of the black hole reduces to zero when the black hole has a small but finite size. At this size, the black hole does not emit any Hawking radiation. The existence of black hole remnants can be used as a solution for the information paradox [39, 40]. Furthermore, it also solves a problem related to the existence of a naked singularity at the last stage of the evaporation of a black hole. In this picture, a black hole does not evaporate completely producing a naked singularity, but rather a remnant is produced at the last stage of the evaporation of the black hole. The existence of a remnant also has phenomenological consequences. This is because it is not possible to produce black holes smaller than these remnants. This increases the energy at which mini black holes can be produced at the LHC [41]. Recently, a lot of interest has been generated in gravity’s rainbow [42–47]. It may be noted that the rainbow functions have been constrained from experimental data [47]. Black hole solutions in gravity’s rainbow with nonlinear sources have been investigated in [48]. In addition, the hydrostatic equilibrium equation for this gravity was obtained in Ref. [49]. As there is a strong motivation to study rainbow deformation of geometries that occur in string theory, we analyze the rainbow deformation of charged dilatonic black holes in this paper. It may be noted that dilaton gravity arises as a low-energy effective field theory of string theory [50, 51]. The dilaton field is also a candidate for dark matter [52]. In fact, in order to have a better picture of nature of the dark energy, a new scalar field is added to the field content of the original theory [53, 54]. Black objects in the presence of dilaton gravity have also been investigated [55–57]. Recently, the dilaton field has been used for analyzing compact objects and hydrostatic equilibrium of stars [58, 59]. The evaporation of quantum black holes has also been investigated using two-dimensional dilaton gravity [60, 61]. Motivated by these applications, we analyze the dilaton field using the formalism of gravity’s rainbow. Thermodynamical aspects of black holes have been of great interest ever since of pioneering work of Hawking and Bekenstein [62, 63]. The idea that geometrical aspects of black holes could be interpreted as thermodynamical quantities provides a deep insight into the connection between gravity and quantum mechanics. On the other hand, the introduction of and developments in gauge/gravity duality highlighted the importance of black hole thermodynamics [64–78]. In addition, Hawking and Page showed the existence of a phase transition for asymptotically anti de-Sitter black holes [79]. This phase transition was reconsidered through the use of the AdS/CFT correspondence by Witten [80]. This work motivated a great deal of research to be conducted in context of black holes thermodynamics, stability, and their phase transitions [81–90].

Recently, it has been demonstrated that it is possible to treat the cosmological constant as the thermodynamic pressure in extended phase space. There are several reasons for such a consideration; e.g. one can point out the existence of a second order phase transition for black holes, Van der Waals like liquid/gas behavior in phase diagrams, and the formation of the triple point [91–109]. The consideration of the cosmological constant as a thermodynamical variable could be supported by studies that are conducted in the context of AdS/CFT [120–123]. In addition, it was shown that a case of ensemble dependency exists for charged three-dimensional black holes which could be removed by considering the cosmological constant as a thermodynamical variable [124]. The thermodynamical critical behavior of black holes in the presence of different matter fields and gravities has been investigated in the literature [91–109].

Another interesting method of studying the thermodynamical structure of black holes is through the use of geometry. It is proposed that one can build a phase space of the black holes by employing one of the thermodynamical quantities of the black holes as thermodynamical potential and its corresponding extensive parameters as components of the phase space. The information regarding phase transitions of the black holes is within the singularities of the Ricci scalar of the constructed phase space. In other words, the divergencies of the Ricci scalar of a thermodynamical metric represent bound and phase transition points. The thermodynamical potential for this method could be the mass, which is used in Weinhold [110, 111], Quevedo [112–114] and HPEM [115–117] metrics or entropy, which is employed in Ruppeiner [118, 119] metric. It was pointed out that the Ruppeiner and Weinhold methods are related to each other with temperature as the conformal factor [112–114]. It was shown that for specific cases of black holes, the Weinhold, Ruppeiner, and Quevedo metrics may fail to provide consistent results regarding phase transitions, while the HPEM metric is proven to be a successful one [115–117]. In the following, we use all of these methods to study phase transitions of the black holes.

This paper is organized as follows. We obtain the charged black hole solutions in dilaton gravity’s rainbow and analyze their properties. This will be done by making the metric of charged black hole solutions in dilaton gravity depends on the energy. We also examine the first law of thermodynamics for this solution. Next, we study the stability of such solutions in gravity’s rainbow and phase transition of these black holes through the heat capacity, geometrical thermodynamics, and the analogy between the cosmological constant and the thermodynamical pressure. Finally, we obtain the critical pressure and the radius of the horizon through another method. The last section is devoted to our conclusion.

2 Charged dilatonic black hole solutions in gravity’s rainbow

In this section, we obtain charged black hole solutions in dilaton gravity’s rainbow and investigate their properties. This will be done by writing an energy dependent version of the metric for dilaton-Maxwell gravity. It may be noted that gravity’s rainbow is based on the generalization of doubly special relativity [125], so it is not possible for a particle to attain an energy greater than the Planck energy in gravity’s rainbow. This is because gravity affects particles of different energies differently, and so the spacetime is represented by a family of energy dependent metrics in gravity’s rainbow [13]. The gravity’s rainbow can be constructed by considering the following deformation of the standard energy-momentum relation:

$$\begin{aligned} E^2f^{2}(\varepsilon )-p^2g^{2}(\varepsilon )=m^2, \end{aligned}$$
(1)

where the energy ratio is \(\varepsilon =E/E_{P}\), in which E and \(E_P\) are, respectively, the energy of the test particle and the Planck energy. The functions \(f(\varepsilon )\) and \(g(\varepsilon )\) are required to be constrained in such a way that the standard energy-momentum relation is obtained in the infrared limit. Thus, we require

$$\begin{aligned} \lim \limits _{\varepsilon \rightarrow 0} f(\varepsilon )=1,\qquad \lim \limits _{\varepsilon \rightarrow 0} g(\varepsilon )=1. \end{aligned}$$
(2)

It may be noted that the spacetime is probed at the energy E, and by definition this cannot be greater than the Planck energy. \( f^{2}(\varepsilon ) \) and \(g^{2}(\varepsilon )\) are called the rainbow functions and their functional forms are phenomenologically motivated. Now it is possible to define an energy dependent deformation of the metric \(\hat{g}(\varepsilon )\) [126]:

$$\begin{aligned} \hat{g}(\varepsilon )=\eta ^{ab}e_a(\varepsilon )\otimes e_b(\varepsilon ), \end{aligned}$$
(3)

where

$$\begin{aligned} e_0(\varepsilon )=\frac{1}{f(\varepsilon )}\tilde{e}_0, \qquad e_i(\varepsilon )=\frac{1}{g(\varepsilon )}\tilde{e}_i; \end{aligned}$$
(4)

here \(\tilde{e}_0\) and \(\tilde{ e}_i\) refer to the energy independent frame fields.

The four-dimensional action of charged dilaton gravity is [127]

$$\begin{aligned} \mathcal {I}=\frac{1}{16\pi }\int \mathrm{d}^{4}x\sqrt{-g}\left[ \mathcal {R}-2\left( \nabla \Phi \right) ^{2}-V\left( \Phi \right) -\mathrm{e}^{-2\alpha \Phi }F_{\mu \nu }F^{\mu \nu }\right] , \end{aligned}$$
(5)

where \(\mathcal {R}\) is the Ricci scalar curvature, \(\Phi \) is the dilaton field, and \(V\left( \Phi \right) \) is a potential for \(\Phi \). The electromagnetic field is \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\) in which \(A_{\mu }\) is the electromagnetic potential. In addition, it should be pointed out that \(\alpha \) is a constant which determines the strength of the coupling of the scalar and electromagnetic field. Due to the fact that we are looking for the black hole with a radial electric field (\(F_{tr}(r)=-F_{rt}(r) \ne 0\)), the electromagnetic potential will be in the following form:

$$\begin{aligned} A_{\mu }=\delta _{\mu }^{0}h\left( r\right) . \end{aligned}$$
(6)

Using the variational principle and varying Eq. (5) with respect to the gravitational field \(g_{\mu \nu }\), the dilaton field \(\Phi \), and the gauge field \(A_{\mu }\), we can obtain the following field equations:

$$\begin{aligned} R_{\mu \nu }= & {} 2\left( \partial _{\mu }\Phi \partial _{\nu }\Phi +\frac{1}{4} g_{\mu \nu }V(\Phi )\right) \nonumber \\&+\,2\mathrm{e}^{-2\alpha \Phi }\left( F_{\mu \eta }F_{\nu }^{\eta }-\frac{1}{4}g_{\mu \nu }F_{\lambda \eta }F^{\lambda \eta }\right) , \end{aligned}$$
(7)
$$\begin{aligned} \nabla ^{2}\Phi =\frac{1}{4}\frac{\partial V}{\partial \Phi }-\frac{\alpha }{ 2}\mathrm{e}^{-2\alpha \Phi }F_{\lambda \eta }F^{\lambda \eta }, \end{aligned}$$
(8)
$$\begin{aligned} \nabla _{\mu }\left( \mathrm{e}^{-2\alpha \Phi }F^{\mu \nu }\right) =0. \end{aligned}$$
(9)

In this paper we attempt to obtain dilaton-Maxwell rainbow solutions. To do so, one can employ the following static metric ansatz:

$$\begin{aligned} \mathrm{d}s^{2}=-\frac{\Psi (r)}{f^{2}(\varepsilon )}\mathrm{d}t^{2}+\frac{1}{g^{2}(\varepsilon ) }\left[ \frac{\mathrm{d}r^{2}}{\Psi (r)}+r^{2}R^{2}(r)\mathrm{d}\Omega _{k}^{2}\right] , \end{aligned}$$
(10)

where \(\Psi (r)\) and R(r) are radially dependent functions which should be determined, and \(\mathrm{d}\Omega _{k}^{2}\) represents the line element of a two-dimensional hypersurface with the constant curvature 2k and volume \(\varpi _{2}\). We should note that the constant k indicates that the boundary of \(t=\) constant and \(r=\) constant can be a positive (elliptic), zero (flat) or negative (hyperbolic) constant curvature hypersurface with the following explicit forms:

$$\begin{aligned} \mathrm{d}\Omega _{k}^{2}=\left\{ \begin{array}{l@{\quad }l} \mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\varphi ^{2}, &{} k=1, \\ \mathrm{d}\theta ^{2}+\sinh ^{2}\theta \mathrm{d}\varphi ^{2}, &{} k=-1, \\ \mathrm{d}\theta ^{2}+\mathrm{d}\varphi ^{2}, &{} k=0. \end{array} \right. \end{aligned}$$
(11)

Using Eq. (9), one can obtain the electromagnetic tensor as

$$\begin{aligned} F_{tr}=\frac{q\mathrm{e}^{2\alpha \Phi }}{ r^{2}R(r)^{2} }, \end{aligned}$$
(12)

where q is an integration constant which is related to the electric charge of the black hole.

Here, in order to find consistent metric functions, we use a modified version of a Liouville-type dilation potential with the following form:

$$\begin{aligned} V(\Phi )=\frac{2k\alpha ^{2}}{b^{2}\mathcal {K}_{-1,1}}g^{2}(\varepsilon )\mathrm{e}^{ \frac{2\Phi }{\alpha }}+2\Lambda \mathrm{e}^{2\alpha \Phi }, \end{aligned}$$
(13)

where b is a non-zero positive constant, \(\mathcal {K}_{i,j}=i+j\alpha ^{2}\), and \(\Lambda \) is a free parameter which plays the role of the cosmological constant. It is worthwhile to mention that for the case of \(g(\varepsilon )=f(\varepsilon )=1\), one obtains

$$\begin{aligned} \lim _{g(\varepsilon )=f(\varepsilon )\rightarrow 1}V(\Phi )=\frac{2k\alpha ^{2} }{b^{2}\mathcal {K}_{-1,1}}\mathrm{e}^{\frac{2\Phi }{\alpha }}+2\Lambda \mathrm{e}^{2\alpha \Phi }, \end{aligned}$$
(14)

which is the usual Liouville-type dilation potential that is used in the context of Friedman–Robertson–Walker scalar field cosmologies [128] and Einstein–Maxwell-dilaton black holes [127, 129, 130].

Next, we employ an ansatz, \(R(r)=\mathrm{e}^{\alpha \Phi (r)}\), in the field equations. The motivation for considering such an ansatz is due to black string solutions of Einstein–Maxwell-dilaton gravity which were first introduced in Ref. [131]. Now, we are in a position to obtain the metric functions. It is a matter of calculation to show that, by using Eq. (12), the metric (10) and the mentioned ansatz for R(r), we have the following solutions for the field equations (Eqs. (7) and (8)):

$$\begin{aligned} \Psi (r)= & {} -\frac{\mathcal {K}_{1,1}}{\mathcal {K}_{-1,1}}\left( \frac{b}{r} \right) ^{-2\gamma }k-\frac{m}{r^{\frac{\mathcal {K}_{1,-1}}{\mathcal {K}_{1,1} }}}+\frac{\mathcal {K}_{1,1}^{2}\Lambda r^{2}}{g^{2}(\varepsilon )\mathcal {K} _{-3,1}}\left( \frac{b}{r}\!\right) ^{2\gamma }\nonumber \\&+\,\frac{q^{2}\mathcal {K}_{1,1}f^{2}(\varepsilon )}{r^{2}}\left( \frac{b}{r} \right) ^{-2\gamma }, \end{aligned}$$
(15)
$$\begin{aligned} \Phi (r)=\frac{\alpha }{\mathcal {K}_{1,1}}\ln \left( \frac{b}{r}\right) , \end{aligned}$$
(16)

where \(\gamma =\alpha ^{2}/\mathcal {K} _{1,1} \). In the above expression, m is an integration constant which is related to the total mass of the black hole. It is notable that, in the absence of a non-trivial dilaton (\(\alpha =\gamma =0\)), the solution (15) reduces to

$$\begin{aligned} \Psi (r)=k-\frac{m}{r}-\frac{\Lambda }{3}\frac{r^{2}}{g^{2}(\varepsilon )}+ \frac{f^{2}(\varepsilon )q^{2}}{r^{2}}, \end{aligned}$$
(17)

which describes a four-dimensional asymptotically AdS topological charged black hole in gravity’s rainbow with a positive, zero or negative constant curvature hypersurface.

In order to confirm the black hole interpretation of the solutions, we look for the curvature singularity. To do so, we calculate the Kretschmann scalar. Calculations show that for finite values of radial coordinate, the Kretschmann scalar is finite. On the other hand, for very small and very large values of r, we obtain

$$\begin{aligned} \lim _{r\rightarrow 0}R_{\alpha \beta \mu \nu }R^{\alpha \beta \mu \nu }\propto & {} r^{-\frac{4\mathcal {K}_{2,1}}{\mathcal {K}_{1,1}}}, \end{aligned}$$
(18)
$$\begin{aligned} \lim _{r\rightarrow \infty }R_{\alpha \beta \mu \nu }R^{\alpha \beta \mu \nu }= & {} \frac{12\Lambda (\alpha ^{4}-2\alpha ^{2}+2)}{\mathcal {K}_{3,-1}^{2}} \left( \frac{b}{r}\right) ^{4\gamma }. \end{aligned}$$
(19)

Equation (18) confirms that there is an essential singularity located at \(r=0\), while Eq. (19) shows that for non-zero \(\alpha \), the asymptotical behavior of the solutions is not AdS. It is easy to show that the metric function may contain real positive roots (see Fig. 1), and therefore the curvature singularity can be covered with an event horizon and interpreted as a black hole. It is also notable that for non-zero positive b and \(r_{+}\), the scalar field, \(\Phi (r)\), is finite on the event horizon.

Fig. 1
figure 1

\(\Psi (r)\) versus r for \(k=1\), \(m=5\), \(\Lambda =-0.5\), \(b=1.2\) and \( q=0.68\). Left panel for \(\alpha =0.9\), \(f^{2}(\varepsilon )=1\), \(g^{2}( \varepsilon )=0.85\) (dashed line), \(g^{2}(\varepsilon )=0.96\) (bold line), and \(g^{2}(\varepsilon )=1.20\) (continuous line). Middle panel for \(\alpha =0.9\), \(g^{2}(\varepsilon )=1\), \( f^{2}(\varepsilon )=0.80\) (dashed line), \(f^{2}(\varepsilon )=1.05\) (bold line) and \(f^{2}(\varepsilon )=1.20\) (continuous line). Right panel for \(g^{2}(\varepsilon )=1.3\), \(f^{2}(\varepsilon )=1.3\), \(\alpha =0.85\) (dashed line), \(\alpha =0.87\) (bold line), and \(\alpha =0.9\) (continuous line)

Full size image

3 Thermodynamical quantities

Now, we are in a position to calculate thermodynamic and conserved quantities of the solutions obtained and examine the validity of the first law of thermodynamics.

In order to obtain the temperature, we use the concept of surface gravity to show that the temperature of these solutions has the following form:

$$\begin{aligned} T= & {} -\frac{g(\varepsilon )\mathcal {K}_{1,1}\left( \frac{b}{r_{+}}\right) ^{-2\gamma }}{4\pi }\nonumber \\&\times \left[ \frac{q^{2}f(\varepsilon )}{r_{+}^{3}}+\frac{ r_{+}\Lambda }{g^{2}(\varepsilon )f(\varepsilon )}\left( \frac{b}{r_{+}} \right) ^{4\gamma }+\frac{k}{f(\varepsilon )r_{+}\mathcal {K}_{-1,1}}\right] .\nonumber \\ \end{aligned}$$
(20)

On the other hand, one can use the area law for extracting a modified version of the entropy related to the Einsteinian class of black objects with the following structure:

$$\begin{aligned} S=\frac{\varpi _{2}r_{+}^{2}}{4g^{2}(\varepsilon )}\left( \frac{b}{r_{+}} \right) ^{2\gamma }, \end{aligned}$$
(21)

in which by setting \(\alpha =0\) and \( g(\varepsilon )=1 \), the entropy of Einstein–Maxwell-dilation black holes is recovered. In order to find the total electric charge of the solutions, one can use the Gauss law. Calculating the flux of electric field helps us to find the total electric charge with the following form:

$$\begin{aligned} Q=\frac{\varpi _{2}qf(\varepsilon )}{4\pi g(\varepsilon )}. \end{aligned}$$
(22)

Next, we are interested in obtaining the electric potential. Using the following standard relation, one can obtain the electric potential at the event horizon with respect to the infinity as a reference:

$$\begin{aligned} U\left( r\right) =\left. A_{\mu }\chi ^{\mu }\right| _{r\longrightarrow \infty }-\left. A_{\mu }\chi ^{\mu }\right| _{r\longrightarrow r_{+}}=- \frac{2q}{r_{+}^{3}}. \end{aligned}$$
(23)

Finally, according to the definition of the mass due to Abbott and Deser [132–134], the total mass of the solution is

$$\begin{aligned} M=\frac{\varpi _{2}b^{2\gamma }}{8\pi \mathcal {K}_{1,1}g(\varepsilon )f( \varepsilon )}m. \end{aligned}$$
(24)

It is worthwhile to mention that for the limit case of \(g(\varepsilon )=f( \varepsilon )=1\) and \(\alpha =0\), Eq. (24) reduces to the mass of the Einstein–Maxwell black holes [130]. In addition, in the conserved and thermodynamical quantities obtained, only the electric potential remains unaffected by considering gravity’s rainbow.

Now, we are in a position to check the validity of the first law of thermodynamics. To do so, first, we calculate the geometrical mass, m, by using \(f\left( r=r_{+}\right) =0\). Then, by employing obtained relation for geometrical mass and Eq. (24) for total mass of the black holes, we find

$$\begin{aligned} M(r_{+},q)=\frac{\varpi _{2}Ab^{2\gamma }}{8\pi \mathcal {K} _{1,-1}g(\varepsilon )f(\varepsilon )}, \end{aligned}$$
(25)

where

$$\begin{aligned} A= & {} \left( \frac{b}{r_{+}}\right) ^{2\gamma }\left[ kr_{+}^{\frac{\mathcal {K} _{1,-1}}{\mathcal {K}_{1,1}}}-q^{2}f^{2}(\varepsilon )\mathcal {K} _{-1,1}r_{+}^{\frac{-\mathcal {K}_{1,3}}{\mathcal {K}_{1,1}}}p\right. \nonumber \\&\left. +\frac{\Lambda \mathcal {K}_{1,1}\mathcal {K}_{1,-1}}{g^{2}(\varepsilon )\mathcal {K}_{-3,1}} r_{+}^{\frac{\mathcal {K}_{3,1}}{\mathcal {K}_{1,1}}}\left( \frac{b}{r_{+}} \right) ^{4\gamma }\right] . \end{aligned}$$

It is a matter of calculation to show that

$$ \begin{aligned} \left( \frac{\partial M}{\partial S}\right) _{Q}=T \quad \& \quad \left( \frac{\partial M}{\partial Q}\right) _{S}=U. \end{aligned}$$
(26)

Therefore, we proved that the first law is valid as

$$\begin{aligned} \mathrm{d}M=\left( \frac{\partial M}{\partial S}\right) _{Q}\mathrm{d}S+\left( \frac{\partial M }{\partial Q}\right) _{S}\mathrm{d}Q. \end{aligned}$$
(27)

4 Thermal stability

In this section, we study the thermal stability of the solutions in context of the canonical ensemble. The stability conditions in the context of canonical ensemble are determined by the sign of the heat capacity. In other words, the positivity/negativity of the heat capacity for the black object determines system being in a stable/unstable state. Therefore, in order to study the stability of the charged black holes in dilatonic gravity’s rainbow, we study the changes in the sign of the corresponding heat capacity. It is worthwhile to mention that investigating the behavior of the heat capacity enables one to obtain the phase transitions of the solutions at the same time. The root and divergence point of the heat capacity are called the bounded point (\(r_{+0}\)) and second order phase transition point (\(r_{+c}\)), respectively. The bounded point is related to the root of temperature and the sign of T changes at \(r_{+0}\), while we expect to obtain a positive temperature at \(r_{+c}\).

The system in the canonical ensemble is considered to have a fixed charge. Therefore, we have

$$\begin{aligned} C_{Q}=\left( \frac{\partial M}{\partial S}\right) _{Q}\left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}^{-1}. \end{aligned}$$
(28)

Considering the mentioned bounded and phase transition points, one can obtain

$$\begin{aligned} \left\{ \begin{array}{ll} T=\left( \frac{\partial M}{\partial S}\right) _{Q}=0 &{}\quad \text { bounded }\,\, \text {point}, \\ &{} \\ \left( \frac{\partial T}{\partial S}\right) _{Q}=\left( \frac{\partial ^{2}M }{\partial S^{2}}\right) _{Q}=0 &{}\quad \text {phase}\,\, \text {transition}\,\, \text { point}. \end{array} \right. . \end{aligned}$$
(29)

There are three valuable known cases for the rainbow functions, which are characteristics of the rainbow solutions. These three cases arise from different phenomenological origins with an upper limit for considering the energy of the test particle E,

$$\begin{aligned} \varepsilon =\frac{E}{E_{P}}\le 1. \end{aligned}$$

The first case originates from loop quantum gravity and non-commutative geometry. In this case, we have the following relations for the rainbow functions of the metric [23, 24]:

$$\begin{aligned} f(\varepsilon )=1,g(\varepsilon ) =\sqrt{1-\eta \varepsilon ^{n}}. \end{aligned}$$
(30)

The other case is constructed by considering the hard spectra from gamma-ray bursts, which leads to [16]

$$\begin{aligned} f(\varepsilon )=\frac{\mathrm{e}^{\beta \varepsilon }-1}{\beta \varepsilon }, g(\varepsilon ) =1. \end{aligned}$$
(31)

Interestingly, opposite to the previous case, in this one the effect of \( g(\varepsilon ) \), which is coupled to the spatial coordinates of the metric, vanishes, whereas in the former case, related to loop quantum gravity, the effect of the coupling term for time component of the metric vanishes.

Finally, in the third case, the choices of the rainbow functions are due to constancy of the velocity of the light [135],

$$\begin{aligned} f( \varepsilon ) =g(\varepsilon ) =\frac{1}{1-\lambda \varepsilon }. \end{aligned}$$
(32)

Using first law of thermodynamics, one can rewrite the relation for heat capacity into

$$\begin{aligned} C_{Q}=T\left( \frac{\partial S}{\partial r_{+}}\right) _{Q}\left( \frac{ \partial T}{\partial r_{+}}\right) _{Q}^{-1}. \end{aligned}$$
(33)

Now, by employing Eqs. (20) and (21) with (33), one can show that the heat capacity is

$$\begin{aligned} C_{Q}=\frac{r_{+}^{2}\left( \frac{b}{r_{+}}\right) ^{2\gamma }\left( q^{2} \mathcal {K}_{-1,1}g^{2}(\varepsilon )f^{2}(\varepsilon )+r_{+}^{2}kg^{2}(\varepsilon )+r_{+}^{4}\Lambda \mathcal {K}_{-1,1}\left( \frac{b}{r_{+}}\right) ^{4\gamma }\right) }{2g^{2}(\varepsilon )\mathcal {K} _{-1,1}\left( r_{+}^{2}kg^{2}(\varepsilon )-q^{2}\mathcal {K} _{3,1}g^{2}(\varepsilon )f^{2}(\varepsilon )-r_{+}^{4}\Lambda \mathcal {K} _{-1,1}\left( \frac{b}{r_{+}}\right) ^{4\gamma }\right) }\!. \end{aligned}$$
(34)

Considering obtained relation for the heat capacity (Eq. (34)) and the three cases mentioned for the rainbow functions of the metric (Eqs. (30)–(32)), we study the stability of the solutions. In the flat case of a horizon (\(k=0\)), one can find that the root(s) of the heat capacity and divergence point(s) are given by the following relations:

$$\begin{aligned} r_{+0}=b\left( -\frac{b^{4}\Lambda }{g^{2}(\varepsilon )f^{2}(\varepsilon )q^{2}}\right) ^{-\frac{\mathcal {K}_{1,1}}{4}}, \end{aligned}$$
(35)
$$\begin{aligned} r_{+c}=b\left( -\frac{b^{4}\Lambda \mathcal {K}_{-1,1}}{g^{2}(\varepsilon )f^{2}(\varepsilon )q^{2}\mathcal {K}_{3,1}}\right) ^{-\frac{\mathcal {K}_{1,1} }{4}}. \end{aligned}$$
(36)
Fig. 2
figure 2

\(C_{Q}\) (continuous line), T (dotted line), and \(\mathcal {R}\) (dashed line) versus \(r_{+}\) for \(k=1\), \(\Lambda =-1\), \(b=5\), \(E=1\), \(E_{p}=5\), and \(q=1\). \(\alpha =0.9\) (left panel) and \(\alpha =1.09\) (right panel) “different scales”

Full size image
Fig. 3
figure 3

\(C_{Q}\) (continuous line), T (dotted line), and \(\mathcal {R}\) (dashed line) versus \(r_{+}\) for \(k=1\), \(\Lambda =-1\), \(b=5\), \(E=1\), \(E_{p}=5\), and \(q=1\). \(\alpha =1.1\) (left panel) and \(\alpha =1.3\) (middle and right panels) “different scales”

Full size image

Interestingly, for a flat horizon, the root of the heat capacity, hence the bound point is independent of the dilaton parameter, \(\alpha \), while the divergency of the heat capacity is a function of this parameter. On the other hand, in order to have a positive real valued divergency in AdS spacetime, we have the restriction \( \alpha >1\) for the dilaton parameter. This condition for dS spacetime is opposite. In other words, the real valued divergency is obtained if \(0\le \alpha <1\) (see Eq. (36) for more details). In order for charged black holes in dilatonic gravity’s rainbow with flat horizon to be stable, the following conditions must hold:

$$\begin{aligned} \left\{ \begin{array}{l} -\Lambda r_{+}^{4}\left( \frac{b}{r_{+}}\right) ^{6\gamma }\le q^{2}g(\varepsilon )^{2}f(\varepsilon )^{2}\left( \frac{b}{r_{+}}\right) ^{2\gamma } \\ -\Lambda r_{+}^{4}\mathcal {K}_{-1,1}\left( \frac{b}{r_{+}} \right) ^{2\gamma }\ge q^{2}g(\varepsilon )^{2}f(\varepsilon )^{2}\mathcal {K }_{3,1}\left( \frac{b}{r_{+}}\right) ^{-2\gamma }. \end{array} \right. \end{aligned}$$

As for the cases of \(k=\pm 1\), it was not possible to obtain the analytical relations for the root and divergence point of the heat capacity. Therefore, we employ numerical methods for studying the properties of the heat capacity for the spherical and hyperbolic horizons. As for the stability conditions, there are different orders of the radius of the horizon for each term. These terms will have dominant effects in specific regions of the radius of the horizon and other parameters. Considering the effectiveness of these terms, the stability conditions will vary from one case to another. Also, these effective behaviors may present different regions of stability and instability. Taking a closer look at different terms, one can see that the most effective parameter in stability conditions which modifies the exponent of horizon radius highly and changes the positivity and negativity of each term is the dilaton parameter, \(\alpha \). In other words, considering different values of \(\alpha \), stable/unstable regions will be modified highly. This highlights the effect of the dilaton field on the thermodynamical behavior of the solutions.

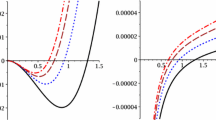
In order to have a better insight regarding the thermodynamical behavior of these black holes, we study the behavior of the temperature. The reason is the fact that negativity of the temperature represents non-physical systems, which are not of our interest. Therefore, we study the conditions for positivity/negativity of the temperature. Considering Eq. (20), there are three terms which are related to the electric charge, the cosmological constant, and the topological structure of the metric. The effectiveness of each term is a function of their factors. Therefore, considering different values for these factors may lead to one of the following scenarios: one root and the temperature is an increasing function of the radius of the horizon (left panel of Fig. 2), no root and the temperature is negative with one maximum (right panel of Fig. 2), two roots with one region of positivity and two regions of negativity (Fig. 3), one root and the temperature is a decreasing function of the radius of the horizon (Fig. 4).

Fig. 4
figure 4

\(C_{Q}\) (continuous line), T (dotted line), and \(\mathcal {R}\) (dashed line) versus \(r_{+}\) for \(k=1\), \(\Lambda =-1\), \(b=5\), \(E=1\), \(E_{p}=5\), and \(q=1\). \(\alpha =10\) (left panel) and \(\alpha =15\) (right panel) “different scales”

Full size image

In general, the charge term is always negative in Eq. (20). If one considers AdS solutions, the second term will be positive. As for the last term, if a spherical solution is chosen, then in order for the topological term to be positive, the dilaton parameter must be \(\alpha <1\). In the case of a hyperbolic horizon the condition will be modified into \(\alpha >1\). On the other hand, if dS solutions are considered, the second term will be negative. Therefore, the possibility of having a positive temperature depends on the topological term with the mentioned conditions for the spherical and hyperbolic cases. It is worthwhile to mention that a flat horizon of dS solutions has negative temperature. Therefore, it is not physical. Considering the mentioned changes in the different terms of the temperature, depending on the dominant regions of the different terms, the temperature will have a positive/negative value with different behavior (which are pointed out in the plotted diagrams).

Fig. 5
figure 5

\(C_{Q}\) (continuous line), T (dotted line), and \(\mathcal {R}\) (dashed line) versus \(r_{+}\) for \(k=1\), \(\Lambda =-1\), \(b=5\), \(E=1\), \(E_{p}=5\), \(q=1\), and \(\alpha =1.1\). Weinhold (left panel), Ruppeiner (middle panel), and Quevedo (middle panel) “different scales”

Full size image

In order to elaborate the effects of the dilation field on the thermal stability and mentioned behaviors for the temperature, we plot various diagrams using the first model of rainbow functions of gravity’s rainbow.

It is evident that in the case of temperature being an increasing function of the radius of the horizon, for positive temperature, we have stable black holes and the heat capacity is an increasing function of \(r_{+}\) (Fig. 2 left panel). Increasing the dilaton parameter will lead to the formation of two stable and unstable states where both of these states have negative temperature (Fig. 2 right panel). On the other hand, by increasing the dilaton parameter, the temperature will have two regions of negativity and one positivity. In the positive region, a phase transition takes place between an unstable larger state to a smaller stable state. This phase transition point is represented by a divergency of the heat capacity. Increasing dilaton parameter leads to decreasing the place of the divergency of the heat capacity and increasing the region in which we have unstable physical solutions (Fig. 3). The larger root of the temperature is highly sensitive to variation of \(\alpha \) (see Fig. 3). For sufficiently large values of the dilaton parameter, the temperature is a decreasing function of the radius of the horizon with one root. The heat capacity in the region of the positive temperature is negative, therefore in this case rainbow solutions are unstable (Fig. 4). It is worthwhile to mention that the root in this case is an increasing function of the dilaton parameter (compare the two diagrams of Fig. 4).

5 Geometrical thermodynamics

In this section, we will conduct a study regarding the phase transition points of the obtained black holes through the use of the concept of geometrical thermodynamics. In this concept, one can construct the thermodynamical structure of the black hole through the use of thermodynamical variables. In other words, by using one of the thermodynamical variable as potential and its corresponding extensive parameters, it is possible to build the phase space. The singularities of the Ricci scalar of this phase space marks two different properties of the solutions: one is a bound point which is related to the root of the temperature and marks the physical and non-physical solutions. The other one is related to singularities of the heat capacity which mark the points at which system undergoes a phase transition.

Considering such a property for the constructed phase space, a valid approach of the geometrical thermodynamics produces a Ricci scalar which has singularities that cover both of the mentioned points. Depending on the thermodynamical potential, the extensive parameters would be different for each phase space. One of these potentials could be the entropy which could be used to construct the Ruppeiner phase space. Another potential could be the mass, which is employed to build the Weinhold, Quevedo, and HPEM phase spaces. The mentioned phase spaces have the following forms [115–117]:

$$\begin{aligned} \mathrm{d}s^{2}=\left\{ \begin{array}{ll} Mg_{ab}^{W}\mathrm{d}X^{a}\mathrm{d}X^{b} &{} \mathrm{Weinhold}, \\ \\ -MT^{-1} g_{ab}^{W}\mathrm{d}X^{a}\mathrm{d}X^{b} &{} \mathrm{Ruppeiner} ,\\ \\ \left( SM_{S}+QM_{Q}\right) \left( -M_{SS}\mathrm{d}S^{2}+M_{QQ}\mathrm{d}Q^{2}\right) &{} \mathrm{Quevedo}, \\ \\ S\frac{M_{S}}{M_{QQ}^{3}}\left( -M_{SS}\mathrm{d}S^{2}+M_{QQ}\mathrm{d}Q^{2}\right) &{} \mathrm{HPEM}, \end{array} \right. \end{aligned}$$
(37)

where their corresponding denominators of the Ricci scalars are

$$\begin{aligned} \mathrm{denom}(\mathcal {R})=\left\{ \begin{array}{ll} \left( M_{SS}M_{QQ}-M_{SQ}^{2}\right) ^{2}M^{2}\left( S,Q\right) &{} \mathrm{Weinhold}, \\ \\ \left( M_{SS}M_{QQ}-M_{SQ}^{2}\right) ^{2}T(S,Q)M^{2}\left( S,Q\right) &{} \mathrm{Ruppeiner}, \\ \\ \left( SM_{S}+QM_{Q}\right) ^{3}M_{SS}^{2}M_{QQ}^{2} &{} \mathrm{Quevedo} ,\\ \\ S^{3}M_{S}^{3}M_{SS}^{2} &{} \mathrm{HPEM}, \end{array} \right. \end{aligned}$$
(38)

in which \(M_{QQ}=( \frac{\partial ^{2}M}{\partial Q^{2}}) _{S}\), \( M_{SQ}=\frac{\partial ^{2}M}{\partial S\partial Q}\), \(M_{SS}=( \frac{ \partial ^{2}M}{\partial S^{2}}) _{Q}\), and \(M_{S}=( \frac{ \partial M}{\partial S}) _{Q}\).

Now, by using Eqs. (21), (22), (25), and (37 ), one can construct the mentioned phase spaces and calculate the corresponding curvature scalars for these black holes. Due to economical reasons, we will not present obtained relations for the Ricci scalars but demonstrate results in the plotted diagrams (see Figs. 2, 3, 4 for the HPEM metric and Fig. 5 for the other metrics). Figure 5 shows that for specific values one can find cases in which the Weinhold (left panel of Fig. 5), the Ruppeiner (middle panel of Fig. 5), and the Quevedo (right panel Fig. 5) cases will not produce suitable divergencies in the Ricci scalar to cover the mentioned points. In other words, the divergencies of their Ricci scalar may not coincide with the root and divergencies of the heat capacity. On the other hand, it is seen that all the divergencies of the curvature scalar of the HPEM metric match with the bound and phase transition points of the heat capacity. The nature of the behavior of the Ricci scalar around each of these divergencies enables one to recognize whether it is a bound point or a divergence point in the heat capacity [115–117].

6 Phase transitions in extended phase space

In this section, we investigate the existence of a second order phase transition through the analogy between a negative cosmological constant and the thermodynamical pressure. The usual relation for pressure and cosmological constant is given by [99–101, 136]

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }. \end{aligned}$$
(39)

It has been shown that the gravitational theory under consideration may affect this relation and modifies it [137, 138]. In calculations of the conserved and thermodynamical quantities, we found that these quantities were modified due to the existence of gravity’s rainbow and the dilaton field. It is natural to ask the question whether the usual relation between cosmological constant and thermodynamical pressure could be modified in the presence of the dilaton field as well as rainbow functions. To investigate such a modification, we use Eq. (7). It is a matter of calculation to show that (after removing the parts related to the electromagnetic field)

$$\begin{aligned} T_{r}^{r}\propto \Lambda \left( \frac{b}{r_{+}}\right) ^{2\gamma }. \end{aligned}$$
(40)

The relation obtained indicates that, although both dilaton field and rainbow functions modified the thermodynamical quantities, only the dilatonic part has a direct effect on the relation between the cosmological constant and pressure. Therefore, we use the following analogy for studying the critical behavior of the system:

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }\left( \frac{b}{r_{+}}\right) ^{2\gamma }. \end{aligned}$$
(41)

The conjugating quantity related to the pressure is obtained through the use of the enthalpy

$$\begin{aligned} V=\left( \frac{\partial H}{\partial P}\right) _{T}. \end{aligned}$$
(42)

Since a consideration of the cosmological constant extends our thermodynamical phase space, the mass term plays the role of enthalpy. Therefore, by using Eqs. (24), (41), and (42), one can find the modified volume of these dilatonic black holes:

$$\begin{aligned} V=\frac{\mathcal {K}_{1,1}}{\mathcal {K}_{3,-1}g^{3}(\varepsilon )f(\varepsilon )}r_{+}^{\frac{\mathcal {K}_{5,3}}{\mathcal {K}_{1,1}} }b^{2\gamma }. \end{aligned}$$
(43)

Clearly, the volume of these black holes is a function of both rainbow functions and dilaton parameter. In other words, contrary to some specific modified gravities, in this version of gravity, the volume of the black hole is affected by the presence of rainbow and dilaton gravities. Here, in order to have a positive and non-zero volume, we find the restriction \(-\sqrt{3}<\alpha <\sqrt{3}\). Since we are not interested in negative values of \(\alpha \), we restrict ourselves to \(0<\alpha <\sqrt{3}\).

It should be pointed out that due to the relation between the volume of the black hole and the radius of the horizon, one is able to introduce a specific volume for these black holes which enables us to use the radius of the horizon instead of the volume in the following calculations. Regarding the first law of thermodynamics in the extended phase space, one can obtain temperature via pressure. Accordingly, the pressure is given by

$$\begin{aligned} P= & {} \frac{\mathcal {K}_{3,-1}g(\varepsilon )f(\varepsilon )\left( {\frac{b}{ r_{+}}}\right) ^{2\gamma }r_{+}^{\frac{\mathcal {K}_{-1,1}}{\mathcal {K}_{1,1}}}b^{-2\gamma }}{2\mathcal {K}_{1,1}\mathcal {K}_{3,1}}\,{T}\nonumber \\&+\frac{\mathcal {K} _{3,-1}g^{2}(\varepsilon )\left[ f^{2}(\varepsilon )\mathcal {K}_{-1,1}{q} ^{2}+{r}_{+}^{2}\right] }{8{r}_{+}^{4}{\pi }\mathcal {K}_{-1,1}\mathcal {K} _{3,1}}\left( {\frac{b}{r_{+}}}\right) ^{-2\gamma }. \end{aligned}$$
(44)

In order to find a relation for calculating the critical volume, hence the critical radius of the horizon, we use the concept of inflection point. In this method, one uses

$$\begin{aligned} \left( \frac{\partial P}{\partial r_{+}}\right) _{T}=\left( \frac{\partial ^{2}P}{\partial r_{+}^{2}}\right) _{T}=0 \end{aligned}$$

to find the critical radius of the horizon which in the case of this thermodynamical system is

$$\begin{aligned} r_{c}=qf(\varepsilon )\sqrt{\mathcal {K}_{3,1}\mathcal {K}_{2,1}}, \end{aligned}$$
(45)

which will lead to the following critical temperature and pressure:

$$\begin{aligned} T_{c}= & {} \frac{\mathcal {K}_{1,1}g(\varepsilon )r_{c}^{\frac{\mathcal {K} _{1,-1}}{\mathcal {K}_{1,1}}}b^{2\gamma }}{f^{3}(\varepsilon ){q}^{2}{\pi } \mathcal {K}_{1,-1}\mathcal {K}_{2,1}\mathcal {K}_{3,1}^{2}}\left( \frac{b}{ r_{c}}\right) ^{^{-4\gamma }},\end{aligned}$$
(46)
$$\begin{aligned} P_{c}= & {} \,\frac{g^{2}(\varepsilon )\mathcal {K}_{3,-1}\left( {\frac{b}{r_{c}} }\right) ^{-2\gamma }}{8\pi f^{2}(\varepsilon ){q}^{2}\mathcal {K}_{3,1}^{2} \mathcal {K}_{2,1}^{2}}. \end{aligned}$$
(47)

It is worthwhile to mention that the restriction that was observed originated only from the dilatonic part of the solutions. In other words, we have no restriction on the values that charge and rainbow functions can acquire and our system is only thermodynamically restricted by the dilaton parameter.

Fig. 6
figure 6

P–\(r_{+}\) (left), T–\(r_{+}\) (middle), and G–T (right) diagrams for \(q=0.1\), \(b=1\), \(\alpha =0.7\), \(g(\varepsilon )=f(\varepsilon )=0.9\) (continuous line), \(g(\varepsilon )=f(\varepsilon )=1\) (dotted line), and \(g(\varepsilon )=f(\varepsilon )=1.1\) (dashed line). P–\(r_{+}\) diagram for \(T=T_{c}\), T–\(r_{+}\) diagram for \(P=P_{c}\), and G–T diagram for \(P=0.5P_{c}\)

Full size image
Fig. 7
figure 7

P–\(r_{+}\) (left), T–\(r_{+}\) (middle) and G–T (right) diagrams for \(q=0.1\), \(b=1\), \(g(\varepsilon )=f(\varepsilon )=0.9\), \( \alpha =0.75\) (continuous line), \(\alpha =0.76\) (dotted line), and \(\alpha =0.77\) (dashed line). P–\(r_{+}\) diagram for \(T=T_{c}\), T–\(r_{+}\) diagram for \(P=P_{c}\), and G–T diagram for \(P=0.4P_{c}\)

Full size image
Fig. 8
figure 8

P–\(r_{+}\) (left), T–\(r_{+}\) (middle), and G–T (right) diagrams for \(q=1\), \(b=20\), \(g(\varepsilon )=f(\varepsilon )=2.5\), \( \alpha =0.75\) (continuous line), \(\alpha =0.76\) (dotted line), and \(\alpha =0.77\) (dashed line). P–\(r_{+}\) diagram for \(T=T_{c}\), T–\(r_{+}\) diagram for \(P=P_{c},\) and G–T diagram for \(P=0.5P_{c}\)

Full size image

Using the obtained critical values, one can find the following critical ratio:

$$\begin{aligned} \frac{P_{c}r_{c}}{T_{c}}\!=\!\frac{qg(\varepsilon )f^{2}(\varepsilon )\mathcal {K} _{-1,1}\mathcal {K}_{-3,1}\mathcal {K}_{3,1}^{1/2}}{8\mathcal {K}_{1,1}\mathcal {K}_{2,1}^{1/2}} \left( {\frac{b}{r_{c}}}\right) ^{2\gamma }r_{c}^{\frac{\mathcal {K}_{1,-1}}{ \mathcal {-K}_{1,1}}}b^{-2\gamma }, \end{aligned}$$
(48)

which shows that this critical ratio was modified due to the presence of the dilaton field as well as the rainbow functions. It is worthwhile to mention that the critical radius of the horizon depends only on one of the rainbow functions, whereas the other critical values and also the ratio \(\frac{P_{c}r_{c}}{T_{c}}\) are functions of both of them. In addition, it is notable that in the absence of a dilaton field (\(\alpha =0\)) and in the low-energy limit (\(f(\varepsilon )=g(\varepsilon )=1\)), Eq. (48) reduces to the usual universal ratio in four-dimensional Einstein gravity [95, 99].

Next, using the renewed role of the total mass of the black holes, we have the Gibbs free energy

$$\begin{aligned} G=H-TS=M-TS, \end{aligned}$$
(49)

which by using Eqs. (20), (21), (24), and (41) will be

$$\begin{aligned} G\!= & {} \!\frac{\mathcal {K}_{1,1}^{2}\,{b}^{2\gamma }{r}_{+}^{{\frac{{K}_{3,1} }{\mathcal {K}_{1,1}}}}}{2\mathcal {K}_{-3,1}f(\varepsilon )g^{3}(\varepsilon ) }P\!+\!\frac{\mathcal {K}_{3,1}f(\varepsilon )\left( {\frac{b}{r_{+}}}\right) ^{-2\gamma }r_{+}^{-\frac{\mathcal {K}_{1,3}}{\mathcal {K}_{1,1}}}b^{2\gamma } }{16\pi g(\varepsilon )}{q}^{2}\nonumber \\&+\,\frac{\left( {\frac{b}{r_{+}}}\right) ^{-2\gamma }r_{+}^{\frac{\mathcal {K}_{1,-1}}{\mathcal {K}_{1,1}}}b^{2\gamma } }{16\pi f(\varepsilon )g(\varepsilon )}. \end{aligned}$$
(50)

In order to see whether the obtained critical values represent a second order phase transition, we study the phase diagrams (P–\(r_{+}\), T–\(r_{+}\), and G–T diagrams) in Figs. 6, 7, and 8.

Fig. 9
figure 9

P versus \(r_{+}\) diagrams for \(q=0.1\), \(b=1\) and \(k=1\). Left panel \(g(\varepsilon )=f(\varepsilon )=0.9\) and \(\alpha =0.75\) (bold continuous line), \(P=0.0455693\) (continuous line), \(\alpha =0.76\) (bold dotted line), \(P=0.0438404\) (dotted line), \(\alpha =0.77\) (bold dashed line), \(P=0.0421757\) (dashed line). Middle panel \(g(\varepsilon )=f(\varepsilon )=0.9\) and \( \alpha =1.65\) (bold continuous line), \(P=0.0000080\) (continuous line), \( \alpha =1.66\) (bold dotted line), \(P=0.0000069\) (dotted line), \( \alpha =1.67\) (bold dashed line), \(P=0.0000059\) (dashed line), right panel \(\alpha =0.7\) and \(g(\varepsilon )=f(\varepsilon )=0.9\) (bold continuous line), \(P=0.0552557\) (continuous line), \(g( \varepsilon )=f(\varepsilon )=1\) (bold dotted line), \( P=0.0592206\) (dotted line), \(g(\varepsilon )=f(\varepsilon )=1.1\) (bold dashed line), \(P=0.0630518\) (dashed line)

Full size image

It is evident that for specific values of the different parameters, a second order phase transition is observed for the obtained critical values (see Figs. 6, 7). The critical pressure (left panels of Figs. , 7), temperature and subcritical isobars (middle panels of Figs. 6, 7), the energy of different phases and the size of the swallow-tails (right panels of Figs. 6, 7) are functions of gravity’s rainbow and the dilaton parameter. The effects of rainbow functions and the dilaton parameter on the critical values are different from each other (compare Figs. 6 with 7).

Interestingly, for a set of values, it is possible to obtain a positive critical pressure and radius of the horizon, whereas the temperature is negative. The plotted diagrams for these cases show a normal critical behavior in the \( P-r_{+}\) diagram (left panel of Fig. 8) whereas in the G–T diagram an abnormal behavior is observed (right panel of Fig. 8). In the case of the T–\(r_{+}\) diagram, also the normal critical behavior is observed except that this behavior is located at negative temperature.

7 Phase transition points through heat capacity

In this section, we will obtain the critical points through a method which was developed in Ref. [104]. In this method, the denominator of the heat capacity is employed to obtain an explicit relation for the thermodynamical pressure. The obtained relation may yield a maximum(s) for pressure which is (are) critical pressure(s) in which a second order phase transition takes place. This critical pressure is exactly the same as that obtained through the use of phase diagrams.

Considering the heat capacity which is calculated through the first and second derivatives of mass with respect to entropy in the extended phase space, and solving its denominator via the thermodynamical pressure will lead to the following explicit relation for the pressure:

$$\begin{aligned} P=\frac{\mathcal {K}_{-3,1}\left[ q^{2}f^{2}(\varepsilon )\mathcal {K} _{3,1}-r_{+}^{2}\right] g^{2}(\varepsilon )}{8\pi r_{+}^{4}\mathcal {K}_{3,1} \mathcal {K}_{1,1}}\left( \frac{b}{r_{+}}\right) ^{-2\gamma }. \end{aligned}$$
(51)

It is evident that this relation is different from the previously obtained relation for pressure (Eq. (44)). Now, by using values that are employed for plotting phase diagrams (Figs. 6, 7, 8), we plot the following diagrams (Fig. 9). A simple comparison shows that the maximums of the plotted diagrams are exactly where the corresponding critical pressure and radius of the horizon are located in the phase diagrams. This shows that these two approaches yield a consistent picture regarding the critical behavior of these black holes. On the other hand, the plotted diagram which corresponds to abnormal behavior (middle panel of Fig. 9) also represents the characteristic behavior of the phase transition point. Therefore, in the case of these black holes, a phase transition occurs in the mentioned critical point.

As a final comment, we make some remarks regarding scalar hair. The scalar hairs on a dilatonic black hole have been studied, and it has been demonstrated that such black holes satisfy the scalar no-hair theorems [139]. The no-hair theorem also holds for the most general static, spherically symmetric solutions of heterotic string compactified on a six-torus [140]. It has been shown that the no-hair theorem is valid for all the charged spherically symmetric black hole in four dimension in general relativity as well as in all scalar tensor theories [141]. The late-time evolution of a self-interacting scalar field for a dilatonic black hole has also been analyzed [142]. It may be noted that the scalar hair for charged Gauss–Bonnet black holes have been studied [143]. It has been demonstrated that the solitons with scalar hair exist for a particular range of the charge and the gauge coupling. Furthermore, there is a forbidden band for the intermediate values of the gauge coupling of charges for the hairy solitons. Conformal scalar hairs have also been studied for the AdS solutions [144]. The shadows of Kerr black holes with scalar hair have been investigated by using backwards ray tracing [145]. It may be noted that the divergence of the scalar field at the horizon has also been discussed [146, 147]. It has been demonstrated that due to gravity’s rainbow the singular behavior at the horizon can be removed [39]. This is because the gravity’s rainbow can be used to impose a cut-off at the Planck energy for all physical processes. In fact, it can be argued that all divergences can be removed in gravity’s rainbow for a suitable choice of rainbow functions [42, 148–150]. So, we expect that the scalar fields will not diverge at the horizon in gravity’s rainbow. Hence, we do not expect the scalar field to diverge at the horizon. However, as the gravity’s rainbow reduces to general relativity in the IR limit, we expect that the no-hair theorem for the black holes not to be affected at least in the IR limit. Furthermore, the gravity’s rainbow does change the dynamics of the evolution of the black hole, when the black hole is really small. However, the change in the dynamics of the evolution of large black holes in gravity’s rainbow is approximately like its evolution in general relativity, and so we expect that the behavior of scalar hairs does not get effected by gravity’s rainbow, for very large black holes. However, it would be interesting to demonstrate this explicitly and analyze the effect of gravity’s rainbow on scalar hairs for a black hole.

8 Conclusion

In this paper, we studied four-dimensional charged dilatonic black holes in gravity’s rainbow and their thermal stability conditions. We obtained thermodynamical quantities such as temperature, electric charge, entropy, and the total mass of the black holes. These quantities were modified in gravity’s rainbow and became energy dependent.

Next, we conducted a study regarding physical/non-physical black holes (positivity/negativity of temperature) and thermal stability of the solutions. It was pointed out that the dominant factor in studying these properties is the dilaton parameter. In other words, these properties were highly sensitive to variation of \(\alpha \). Due to the different factors of the dilaton parameter, different types of behavior were observed for the temperature which put restrictions on the solutions being physical. The observed behaviors for the temperature were: (a) two roots with maximum, (b) an increasing (a decreasing) function of the radius of the horizon with one root, (c) a negative definite function with one maximum.

The analyzed behaviors were: an increasing function of the radius of the horizon with one root, increasing and decreasing functions of the radius of the horizon with two roots, a decreasing function of \(r_{+}\) with one root located and being negative with one maximum located at negative temperature.

As for the stability and phase transition, we found, depending on the behavior of the temperature, that the heat capacity could have a phase transition and a stable state for larger values of the radius of the horizon. In the case of two roots for temperature, interestingly, a phase transition of larger/smaller black holes was observed. Finally, as for temperature being a decreasing function of \( r_{+} \), for physical solutions (positive temperature), unstable solutions were observed. In other words, in this case, physical solutions are unstable.

Next, a geometrical approach was employed to study the bound and phase transition points of these black holes. It was demonstrated that the Ricci scalars of the phase spaces of the Weinhold, Ruppeiner, and Quevedo metrics have divergencies which do not match with the mentioned points, while the singular points of the curvature scalar of the HPEM coincide with the roots and divergence points of the heat capacity.

We also studied the critical behavior of these black holes in extended phase space. It was shown that the usual relation between the cosmological constant and thermodynamical pressure was modified due to the existence of dilaton gravity whereas such a modification was not seen for gravity’s rainbow. On the contrary, it was shown that the volume of the black holes depends on both of these modifications.

Then we showed that the critical values are related to the rainbow functions as well as the dilaton parameter. In order to have a positive critical temperature, we found restrictions which were purely dilaton dependent. Therefore, one is not free to choose any value for the dilaton parameter.

In studying the phase diagrams, two different behaviors were observed for the different diagrams, especially in the G–T diagrams. Interestingly, although we observed an anomaly in these diagrams, other corresponding phase diagrams presented usual thermodynamical behavior around critical points. In other words, the observed abnormal behaviors in the phase diagrams present the existence of a second order phase transition for these black holes.

Next, we used a new method, which was introduced in Ref. [104], for studying the critical behavior of the system. This method is based on obtaining an explicit form for the thermodynamical pressure from the denominator of the heat capacity. It was seen that the maximum of this relation is located at the critical pressure and radius of the horizon in which the second order phase transition takes place. It was shown that in this method, for the irregular behavior which was observed in the phase diagrams, also a second order phase transition occurs. This indicates that these points are phase transition points despite their abnormal behavior.

Finally, it is worthwhile to think about the physical interpretation of the abnormal behavior which was seen in this paper. It is notable that one can generalize the obtained linear solutions in this paper to the nonlinear case of electrodynamics and investigate the effects of this nonlinearity [151]. In addition, one may investigate the extended phase space and thermodynamic criticality in higher order Lovelock–Maxwell gravity’s rainbow as well as Lovelock-nonlinear electrodynamics [152, 153]. These subjects are under examination.