1 Introduction

Albeit there extremely successful consequences of Einstein’s theory of gravity, there are various issues which signal that this theory should be modified, at least at high energy regime. Regarding the physical processes at energies of order of the Planck scale, one is expected to modify Einstein gravity to a quantum theory of gravity which is related to quantum field theory and could be the correct framework to describe processes at ultraviolet (UV) energies. Considering the UV-completion regime of black holes, the gravitational interaction at energies exceeding the Planck mass implies that the UV-completion must be achieved by new quantum degrees of freedom of wavelength much shorter than the Planck length. However, it is expected that one might recover the semi-classical (thermodynamical) behavior of black holes in the mean-field approximation [1, 2]. Horava–Lifshitz gravity [3] is one of the interesting UV modifications of general relativity (GR), in which reduces to GR at infrared (IR) limit. Based on Lifshitz scaling for space and time, different attractive subjects have been considered such as string theory of types IIA and IIB [4, 5], AdS/CFT correspondence [6,7,8], dilatonic black holes/branes [9,10,11,12,13] and phase transitions/geometrical thermodynamics of black holes [14,15,16].

On the other hand, another point of view regarding the UV-completion of GR is related to gravity’s rainbow [17, 18]. In order to introduce the gravity’s rainbow, we can start from its historical origin; doubly special relativity. It is well known that the special theory of relativity is based on two postulates [19]; (1) the laws of physics are invariant in all inertial frames, and (2) the constant invariant speed of light in the vacuum for all observers, regardless of the relative motion of the light source. This results in the fact that the speed of a massive particle cannot be equal to or larger than the speed of light. Based on high energy point of view, if one consider an upper bound for the energy of a test particle and add this assumption as a postulate to the others mentioned above, the doubly special relativity will be constructed [20,21,22]. So, in this manner, the energy of test particle cannot be greater than the Planck energy. Following the gravity supplementing special relativity which leads to GR, one can generalize doubly special relativity in the presence of gravity to obtain the so-called doubly general relativity or gravity’s rainbow [18].

Another way for constructing such theories is considering a modification of the standard energy-momentum relation. The modification of usual energy-momentum relation in gravity’s rainbow is given as

$$\begin{aligned} E^{2}f^{2}( \varepsilon ) -p^{2}g^{2}( \varepsilon ) =m^{2}, \end{aligned}$$

where E and \(E_{p}\) are the energy of a test particle and the Planck energy, respectively, and they are related; we have \(\varepsilon =E/E_{p} \) in which \(\varepsilon \le 1\), because the energy of a test particle E cannot be greater than \(E_{p}\) [23]. The functions \(f\left( \varepsilon \right) \) and \(g\left( \varepsilon \right) \) are called rainbow functions. They are phenomenologically motivated and could be extracted by experimental data [24]; see Refs. [17, 25, 26] for more details. It is worthwhile to mention that the rainbow functions are required to satisfy \(\underset{\varepsilon \rightarrow 0}{\lim }f\left( \varepsilon \right) =1\) and \(\underset{ \varepsilon \rightarrow 0}{\lim }g\left( \varepsilon \right) =1\), where these conditions ensure that the modified energy-momentum relation reduces to its usual form in the IR limit. It is worth mentioning that such a justification is based on the standard model of particle physics. Since quantum theories of gravity are different from classical one in high energy regime, a full quantum theory has to be valid in UV regime. It is notable that both the Horava–Lifshitz gravity and gravity’s rainbow are valid in the UV regime. On the other hand, considering suitable choice of the energy functions, the Horava–Lifshitz gravity can be related to the gravity’s rainbow [27]. For the reasons mentioned, we consider the gravity’s rainbow in this paper.

Recently, there has been a growing interest in gravity’s rainbow because of its interesting achievements in the context of theoretical physics, such as providing possible solutions for information paradox [28, 29], admitting the usual uncertainty principle [30, 31], the existence of remnants for black holes after evaporation [32, 33], and absence of black hole production at LHC [34]. In addition, from cosmological point of view, it is possible to remove the big bang singularity by using gravity’s rainbow [35,36,37,38]. Black hole thermodynamics in the presence of gravity’s rainbow coupled to (non)linear electrodynamics has been discussed in the literature [39,40,41]. Moreover, the effects of rainbow functions on the thermodynamics properties and phase transition of black holes have been studied in Gauss–Bonnet gravity [42], Kaluza–Klein theory [43], massive gravity [44], and F(R) theories of gravity [45, 46]. In the view point of astrophysics, the structure of neutron stars have been investigated and it is found that by increasing the rainbow function more than one, the maximum mass of neutron stars increases [47, 48].

Regarding various aspects of black holes in the context of gravity’s rainbow, it will be interesting to look for possible coupling of rainbow functions with scalar field and its self interacting potential. Astronomical observations indicated that our Universe has an accelerated expansion [49, 50]. Einstein gravity cannot explain such acceleration. In this regards, various modifications of Einstein gravity are proposed in the literature. Among them, scalar tensor gravity and string theory are most acceptable ones with interesting properties. It is worth mentioning that the low-energy limit of effective string theory could lead to appearance of a dilaton scalar field [51, 52] which motivates one to investigate GR coupled with such a scalar field. In addition, dilaton field coupled with other gauge fields has significant effects on the solutions [53,54,55,56]. In Ref. [57], it was shown that dilaton field can be an appropriate candidate for dark matter. In addition, in order to have deep picture regarding the nature of dark energy, a new scalar field can be added to the field content of original theory [58, 59]. Also, GR coupled with a dilaton field can explain the accelerated expansion of our Universe, properly. Moreover, it was shown that in the presence of dilaton scalar field, the asymptotic behavior of black hole spacetimes is neither flat nor (a)dS [60,61,62,63,64]. This is due to the fact that in the limit \(r\rightarrow \infty \), the effects of dilaton field is still present. Besides, it was shown that the dilatonic black hole solutions can be constructed in the (a)dS spacetime background [65]. Black objects in the presence of dilaton gravity and their thermodynamics have been studied in Refs. [66,67,68,69,70,71,72,73,74,75]. Recently, considering the dilaton field, the hydrostatic equilibrium equation of compact objects has been obtained and the properties of neutron stars have been analyzed in Refs. [76, 77]. The evaporation of quantum black holes has also been investigated using two dimensional dilaton gravity [78, 79]. In addition, there is a strong motivation to study rainbow deformation of geometries that occur in the string theory.

Nonlinear field theory is one of the most interesting branches in physical sciences because most physical systems presented in the nature are nonlinear. On the other hand, the existence of some limitations in the linear Maxwell theory motivates one to consider nonlinear electrodynamics (NED) [80,81,82,83]. One of the main advantages of considering NED theories comes from the fact that these theories are richer than the linear Maxwell theory and in some special cases they reduce to the Maxwell field. Besides, it was shown that NED can remove the black hole and big bang singularities [84,85,86]. In addition, the effects of NED become quite important in superstrongly magnetized compact objects [87, 88]. Studying general relativity coupled to NED is an attractive subject because of its specific properties in gauge/gravity duality. One of the most important NED theories is so-called Born–Infeld NED (BI NED) which has been introduced by Born and Infeld in 1934 [89]. This interesting type of NED removes the divergence of electric field of a point-like charge and such a property was the main motivation for introducing this kind of NED. Other strong motivation for considering BI NED comes from the fact that it naturally arises in the low-energy limit of open string theory [90,91,92,93]. We have the following incomplete list showing the investigation of: gravitational fields coupled to BI NED for static black holes [94,95,96,97,98,99,100,101], wormholes [102, 103], rotating black objects [104, 105], and superconductors [106].

Motivated by these applications, in this paper, we analyze dilaton field using the formalism of gravity’s rainbow in the presence of BI NED. So in the present paper, we are going to study the dilatonic black hole solutions in Einstein gravity’s rainbow coupled to BI NED with considering the effects of thermal fluctuations.

2 Black hole solutions of dilaton gravity’s rainbow in the presence of BI NED

Here, we are interested in dilatonic charged black holes in the context of gravity’s rainbow with BI source. Since we are interested in minimal coupling, the action can be written as [61]

$$\begin{aligned} I=\frac{1}{16\pi }\int \mathrm{d}^{4}x\sqrt{-g}\left[ R-2\left( \nabla \Phi \right) ^{2}-V\left( \Phi \right) -L\left( F,\Phi \right) \right] , \end{aligned}$$
(1)

where R is the Ricci scalar, and \(\Phi \) and \(V(\Phi )\) are, respectively, dilaton field and its corresponding potential. \(L( F,\Phi )\) is the Lagrangian of the BI electromagnetic field under consideration with the following explicit form:

$$\begin{aligned} L\left( F,\Phi \right) =4\beta ^{2}e^{2\alpha \Phi }\left( 1-\sqrt{1+\frac{ e^{-4\alpha \Phi }F}{2\beta ^{2}}}\right) , \end{aligned}$$
(2)

where the Maxwell invariant is denoted by \(F=F_{\mu \nu }F^{\mu \nu }\) (\( F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\) in which \( A_{\mu }\) is the gauge potential). Also, \(\beta \) is the nonlinearity parameter and dilatonic constant is identified by \(\alpha \), which is a parameter for determining the strength of coupling between the scalar field and electrodynamics.

For the sake of simplification in calculation, we use the following redefinition:

$$\begin{aligned} L\left( F,\Phi \right) =4\beta ^{2}e^{2\alpha \Phi }L\left( Y\right) , \end{aligned}$$
(3)

where \(L(Y)=1-\sqrt{1+Y}\) and \(Y=\frac{e^{-4\alpha \Phi }F}{2\beta ^{2}}\).

Variation of the action (1) leads to the following field equations:

$$\begin{aligned} R_{\mu \nu }= & {} 2\left( \partial _{\mu }\Phi \partial _{\nu }\Phi +\frac{g_{\mu \nu }}{4} V(\Phi )\right) \nonumber \\&-\,4e^{-2\alpha \Phi }\partial _{Y}L\left( Y\right) F_{\mu \eta }F_{\nu }^{\eta } \nonumber \\&+\, 2\beta ^{2}e^{2\alpha \Phi }\left[ 2Y\partial _{Y}L\left( Y\right) -L\left( Y\right) \right] g_{\mu \nu }, \end{aligned}$$
(4)
$$\begin{aligned} \nabla ^{2}\Phi =\frac{1}{4}\frac{\partial V}{\partial \Phi }+2\alpha \beta ^{2}e^{2\alpha \Phi }\left[ 2Y\partial _{Y}L\left( Y\right) -L\left( Y\right) \right] , \end{aligned}$$
(5)
$$\begin{aligned} \nabla _{\mu }\left( e^{-2\alpha \Phi }\partial _{Y}L\left( Y\right) F^{\mu \nu }\right) =0. \end{aligned}$$
(6)

Here, we consider the following energy dependent line element:

$$\begin{aligned} \mathrm{d}s^{2}= & {} -\frac{\Psi (r)}{f^{2}(\varepsilon )}\mathrm{d}t^{2}+\frac{1}{g^{2}(\varepsilon )}\nonumber \\&\times \,\left[ \frac{\mathrm{d}r^{2}}{\Psi (r)}+r^{2}R^{2}(r)\mathrm{d}\Omega _{k}^{2}\right] , \end{aligned}$$
(7)

in which R(r) and \(\Psi (r)\) are metric functions which should be determined. We recall that these two functions \(g(\varepsilon )\) and \(f(\varepsilon )\) are energy (or rainbow) functions that are chosen phenomenologically. In addition, \(d\Omega _{k}^{2}\) is the metric of two dimensional subspace which depends on topology of the boundary of spacetime and could have positive (elliptic \(k=1\)), zero (flat \(k=0\)) or negative (hyperbolic \(k=-1\)) curvature such as

$$\begin{aligned} \mathrm{d}\Omega _{k}^{2}=\left\{ \begin{array}{ll} \mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\varphi ^{2}, &{} k=1 \\ \mathrm{d}\theta ^{2}+\sinh ^{2}\theta \mathrm{d}\varphi ^{2}, &{} k=-1 \\ \mathrm{d}\theta ^{2}+\mathrm{d}\varphi ^{2}, &{} k=0 \end{array} \right. . \end{aligned}$$
(8)

Since we are interested in black holes with radial electric field, the suitable choice of gauge potential is

$$\begin{aligned} A_{\mu }=\delta _{\mu }^{t}h\left( r\right) , \end{aligned}$$
(9)

which by using Eq. (6), we can obtain the following field equation:

$$\begin{aligned}&\beta ^{2}e^{4\alpha \Phi }\left[ R(r)\left( r\alpha F_{tr}\Phi ^{\prime }- \frac{r}{2}F_{tr}^{\prime }-F_{tr}\right) -rF_{tr}R^{\prime }(r)\right] \nonumber \\&\quad +\, f^{2}(\varepsilon )g^{2}(\varepsilon )F_{tr}^{3}\left[ R(r)+rR^{\prime }(r) \right] =0, \end{aligned}$$
(10)

where \(F_{tr}=A_{t}^{\prime }\) is the tr-component of the electromagnetic tensor field and prime denotes \(\mathrm{d}/\mathrm{d}r\). Solving Eq. (10), we obtain

$$\begin{aligned} F_{tr}=\frac{qe^{2\alpha \Phi }}{r^{2}R^{2}(r)\sqrt{1+\frac{ q^{2}f^{2}(\varepsilon )g^{2}(\varepsilon )}{\beta ^{2}r^{4}R^{4}(r)}}}, \end{aligned}$$
(11)

where q is an integration constant which is related to the total electric charge of the solutions. In order to find the metric functions, we consider the following modified version of the Liouville-type dilaton potential:

$$\begin{aligned} V(\Phi )=\frac{2k\alpha ^{2}}{b^{2}\Theta _{-1,1}}g^{2}(\varepsilon )e^{ \frac{2\Phi }{\alpha }}+2\Lambda e^{2\alpha \Phi }, \end{aligned}$$
(12)

where \(\Lambda \) is a free parameter which plays the role of cosmological constant. It is worthwhile to mention that in IR limit (\(g(\varepsilon )=f(\varepsilon )=1\)), Eq. (12) reduces to the known Liouville-type dilaton potential that is employed for finding Friedman–Robertson–Walker scalar field cosmologies [107] and Einstein–Maxwell–Dilaton black holes [61, 108].

Here, we consider \(R(r)=e^{\alpha \Phi (r)}\) as an ansatz for finding the metric function. This ansatz is supported by studies conducted in Einstein–Maxwell–Dilaton gravity [109].

Now, by using Eqs. (4), (5) and the metric (7) with obtained electromagnetic field tensor, one can find the following differential equation for calculating the metric function, analytically:

$$\begin{aligned}&\frac{kr^{2}\alpha ^{2}}{b^2\Theta _{-1,1}}\left( \frac{b}{r}\right) ^{ \frac{\gamma }{\alpha ^{2}}}+\frac{ r\Theta _{1,1}\Psi ^{\prime }(r)-\Theta _{-1,1}\Psi (r)}{\Theta _{1,1}^{2}}-k\left( \frac{b}{r}\right) ^{\gamma } \nonumber \\&\quad +\,\frac{2r^{2}}{g^{2}(\varepsilon )}\left( \frac{b}{r}\right) ^{3\gamma }\left[ \beta ^{2}\left( 1+ \sqrt{1+\eta }\right) +\frac{\Lambda }{2}\right] =0 \end{aligned}$$
(13)

where \(\Theta _{i,j}=i+j\alpha ^{2}\), \(\eta =\frac{q^{2}f^{2}(\varepsilon )g^{2}(\varepsilon )}{\beta ^{2}r^{4}}\left( \frac{r}{b}\right) ^{2\gamma }\) and \(\gamma =2\alpha ^{2}/\Theta _{1,1}\). Using obtained field equations, one can find both the metric function and the dilatonic field in the following forms:

$$\begin{aligned} \Psi (r)= & {} -\frac{\Theta _{1,1}}{\Theta _{-1,1}}k\left( \frac{b}{r}\right) ^{-\gamma }-\frac{m}{r^{1-\gamma }}+\frac{\Lambda \Theta _{1,1}^{2}b^{\gamma }}{g^{2}(\varepsilon )\Theta _{-3,1}}r^{(2-\gamma )} \nonumber \\&-\,\frac{2\beta ^{2}\Theta _{1,1}^{2}b^{\gamma }r^{(2-\gamma )}}{ g^{2}(\varepsilon )\Theta _{-3,1}}\left[ 1-H_{1}\right] , \end{aligned}$$
(14)
$$\begin{aligned} \Phi (r)= & {} \frac{\alpha }{\Theta _{1,1}}\ln \left( \frac{b}{r}\right) , \end{aligned}$$
(15)

where \(H_{1}= {}_{2}F_{1}([ -\frac{1}{2},\frac{\Theta _{-3,1}}{4}] ,[ \frac{\Theta _{1,1}}{4}] ,-\eta )\) is the hypergeometric function. Also, b is an arbitrary constant related to the scalar field and m is an integration constant which is related to total mass of the solutions. It is worthwhile to mention that, for the limiting case of \(\beta \longrightarrow \infty \), obtained metric function will lead to

$$\begin{aligned} \Psi (r)= & {} -\frac{k\Theta _{1,1}}{\Theta _{-1,1}}\left( \frac{r}{b}\right) ^{\gamma }-\frac{m}{r^{1-\gamma }}\nonumber \\&+\,\frac{\Lambda \Theta _{1,1}^{2}b^{\gamma } r^{(2-\gamma )}}{g^{2}(\varepsilon )\Theta _{-3,1}}+\frac{q^2f(\varepsilon )^2\Theta _{1,1}}{r^{2}}\left( \frac{r}{b}\right) ^{\gamma }, \end{aligned}$$
(16)

which is charged black hole in gravity’s rainbow [110]. On the other hand, for limiting case of \(\alpha =\gamma =0\) and \(\beta \longrightarrow \infty \), our solutions reduce to

$$\begin{aligned} \Psi (r)=k-\frac{m}{r}-\frac{\Lambda }{3}\frac{r^{2}}{g^{2}(\varepsilon )}+\frac{ q^{2}f^{2}(\varepsilon )}{r^{2}}, \end{aligned}$$
(17)

which is the metric function of 4-dimensional asymptotically AdS topological charged black hole in gravity’s rainbow [46].

In order to study the effects of matter fields as well as dilatonic gravity, we will investigate the behavior of the Kretschmann scalar for small and large values of radial coordinate. The existence of divergence for this scalar means that our solution contains a curvature singularity. If this singularity is covered with a horizon, obtained solution is interpreted as black hole. It is a matter of calculation to show that, for this black hole, we have

$$\begin{aligned} \lim _{r\rightarrow 0}R_{\alpha \beta \mu \nu }R^{\alpha \beta \mu \nu }\propto & {} r^{-\frac{4\Theta _{2,1}}{\Theta _{1,1}}}, \end{aligned}$$
(18)
$$\begin{aligned} \lim _{r\rightarrow \infty }R_{\alpha \beta \mu \nu }R^{\alpha \beta \mu \nu }= & {} \frac{12\Lambda ^2 (\alpha ^{4}-2\alpha ^{2}+2)}{\Theta _{3,-1}^{2}}\left( \frac{b}{r}\right) ^{4\gamma }. \end{aligned}$$
(19)

It is evident from Eq. (18) that there is an essential singularity located at the origin for this solution. Therefore, the first condition for having black hole is satisfied. On the other hand, the asymptotical behavior of system is modified due to dilatonic gravity and it is not (A)dS. It is notable that the existence of horizon for the solution is investigated through following diagrams (Fig. 1).

Fig. 1
figure 1

\(\Psi (r)\) versus r for \(k=1\), \(m=5\), \(\Lambda =-1\), \(b=1.2\) and \( q=1\). \(\alpha =0.9\), \(f(\varepsilon )=g(\varepsilon )=0.9\), \(\beta =0.1\) (continues line), \(\beta =0.3\) (dotted line), \( \beta =0.534\) (dashed line) and \(\beta =0.7\) (dashed-dotted line)

Full size image

Plotted diagram shows that depending on the choices of different parameters, obtained solutions may present black holes with two horizons, extremal black holes and naked singularity. For exampe, in the case of BI theory, for small values of the nonlinearity parameter observed behavior is Schwarzschild like (continues line of Fig. 1). Increasing nonlinearity parameter will change the behavior of the metric function into Rissner–Nordstrom like which may yield two horizons (dotted line of Fig. 1), extremal black holes (dashed line of Fig. 1) or naked singularity (dashed-dotted line of Fig. 1). Here, we saw that generalization to nonlinear electrodynamics as well as gravity’s rainbow, provided a richer phenomenologies for black holes. We see that geometrical structure of the black holes have been modified due to these generalizations. Depending on the choices of different parameters, the type of singularity, the general behavior of metric function and number and type of horizons have been modified. These modifications highlight the contributions of this matter field and gravities. We will continue to study the effects of these generalizations on conserved and thermodynamical quantities in the next section.

3 Thermodynamics

3.1 Usual thermodynamics (non-correction)

This section is devoted to the calculation of conserved quantities without thermal fluctuations. Here, we investigate the effects of gravity’s rainbow, dilaton scalar field and nonlinear BI electrodynamics on the thermodynamical quantities and check the validity of the first law of black hole thermodynamics. Using the concept of surface gravity, one can show that the Hawking temperature for obtained solutions will be

$$\begin{aligned} T=\frac{\Theta _{1,1}\left( \frac{b}{r_{+}}\right) ^{\gamma }\left[ \Theta _{1,-1}r_{+}^{2}\left( \beta ^{2}-\frac{\Lambda }{2}\right) -\frac{ kg^{2}(\varepsilon )}{2}\left( \frac{b}{r_{+}}\right) ^{-2\gamma }-\Theta _{1,-1}\beta ^{2}r_{+}^{2}\sqrt{1+\eta _{+}}\right] }{2\pi \Theta _{1,-1}r_{+}f(\varepsilon )g(\varepsilon )}, \end{aligned}$$
(20)

where \(\eta _{+}=\eta _{\left| _{r=r_{+}}\right. }\). Since we are working in an Einstein framework, the entropy of these black holes could be obtained by the area law

$$\begin{aligned} S=\frac{A}{4}=\frac{r_{+}^{2}\left( \frac{b}{r_{+}}\right) ^{\gamma }}{ 4g^{2}(\varepsilon )}, \end{aligned}$$
(21)

in which by setting \(\alpha =0\) and \(g(\varepsilon )=1\), the entropy of black holes in Einstein gravity is recovered. In order to find the total electric charge of these black holes, one can use the Gauss’ law, which leads to following result:

$$\begin{aligned} Q=\frac{qf(\varepsilon )}{4\pi g(\varepsilon )}. \end{aligned}$$
(22)

The electric potential of the black holes at the horizon radius with respect to spatial infinity as a reference could be calculated with the following relation:

$$\begin{aligned} U\left( r\right) =\left. A_{\mu }\chi ^{\mu }\right| _{r\longrightarrow \infty }-\left. A_{\mu }\chi ^{\mu }\right| _{r\longrightarrow r_{+}}, \end{aligned}$$
(23)

where for nonlinear BI theory we obtain

$$\begin{aligned} U=\frac{q}{r} \;{}_{2}F _{1}\left( \left[ -\frac{1}{2},\frac{\Theta _{1,1} }{4}\right] ,\left[ \frac{\Theta _{5,1}}{4}\right] ,-\eta _{+}\right) . \end{aligned}$$
(24)

In order to obtain the total mass of black holes, one can use the definition of Abbott and Deser [111,112,113], which leads to

$$\begin{aligned} M=\frac{b^{\gamma }}{8\pi \Theta _{1,1}f(\varepsilon )g(\varepsilon )}m. \end{aligned}$$
(25)

It is worthwhile to mention that, for the IR limit (\(g(\varepsilon )=f(\varepsilon )=1\)) and by setting \(\alpha =0\), Eq. (25) reduces to the mass of Einstein–Maxwell black holes.

Now, we are in a position to examine the validity of the first law of thermodynamics. To do so, first, we should obtain geometrical mass of the solutions, m, as a function of other parameters, by using \(\Psi \left( r=r_{+}\right) =0\). Then, by replacing it in Eq. (25), we obtain a relation for the total mass of the black holes versus entropy and electric charge. In this case, the extensive parameters will be the entropy and total electric charge and their corresponding conjugating quantities are the temperature and the electric potential, respectively. Therefore, the validation of the first law of black holes thermodynamics is done by

$$ \begin{aligned} \left( \frac{\partial M}{\partial S}\right) _{Q}=T \& \left( \frac{\partial M}{\partial Q}\right) _{S}=U. \end{aligned}$$
(26)

It is a matter of the calculation to show that obtained quantities in Eq. ( 26) are exactly the same as those obtained in Eqs. (20) and (24). Therefore, we find that the first law is valid as

$$\begin{aligned} \mathrm{d}M=\left( \frac{\partial M}{\partial S}\right) _{Q}\mathrm{d}S+\left( \frac{\partial M }{\partial Q}\right) _{S}\mathrm{d}Q. \end{aligned}$$
(27)

Our final subject of the interest in this section is heat capacity. The information that are provided by this quantity could be used to render the thermodynamical structure of black holes in the context of their thermal stability/instability. In addition, the existence of discontinuity for this quantity signals the presence of thermal phase transition. It is worthwhile to mention that the discontinuities in the heat capacity usually are observed in the form of divergences. For black holes in canonical ensemble, the heat capacity is calculated by the following relation:

$$\begin{aligned} C=T\left( \frac{\partial S}{\partial T}\right) _{Q}, \end{aligned}$$
(28)

in which, by using the obtained temperature (20) and entropy (21), one can find it for these specific thermodynamical quantities:

$$\begin{aligned} C=\frac{r_{+}^{4}\left( \frac{b}{r_{+}}\right) ^{\gamma }\left[ \frac{ kg^{2}(\varepsilon )}{2\Theta _{-1,1}}\left( \frac{b}{r_{+}}\right) ^{-2\gamma }+\beta ^{2}r_{+}^{2}\eta _{+}-r_{+}^{2}\left( \beta ^{2}-\frac{ \Lambda }{2}\right) \right] \eta _{+}}{\Theta _{-1,1}g^{2}(\varepsilon ) \left[ r_{+}^{2}\left( \frac{kg^{2}(\varepsilon )}{\Theta _{-1,1}\left( \frac{b}{r_{+}}\right) ^{2\gamma }}+2r_{+}^{2}\left( \beta ^{2}-\frac{ \Lambda }{2}\right) \right) \eta _{+}-2\beta ^{2}r_{+}^{4}-\frac{2\Theta _{1,1}q^{2}f^{2}(\varepsilon )g^{2}(\varepsilon )}{\Theta _{-1,1}\left( \frac{b}{r_{+}}\right) ^{2\gamma }}\right] }. \end{aligned}$$
(29)

The thermodynamical stability and possible phase transition of the black holes in this case will be discussed in the following sections. In the next section, we will obtain the thermodynamical quantities for the case where entropy is corrected so as to include a logarithmic correction.

3.2 Thermal fluctuations: correction

Here, we want to investigate the effects of thermal fluctuations on obtained solutions. Consideration of thermal fluctuations results into modifications of different thermodynamical quantities, though some of the quantities remain fixed. To the leading order, the entropy gets logarithmic correction and given by

$$\begin{aligned} S=S_{0}-\frac{\zeta }{2}\log \left( S_{0}T^{2}\right) , \end{aligned}$$
(30)

in which \(S_{0}\) is the uncorrected entropy which is given in Eq. (21). Also, \(\zeta \) is the thermal fluctuation parameter which we will call it correction parameter through the paper. Using Eqs. (20) and (21), we can obtain the corrected entropy as

$$\begin{aligned} S=\frac{r_{+}^{2}\left( \frac{b}{r_{+}}\right) ^{\gamma }}{4g^{2}(\varepsilon )}-\frac{ \zeta }{2}\log \left( \frac{r_{+}^{2}\left( \frac{b}{r_{+}}\right) ^{\gamma } }{4g^{2}(\varepsilon )}T^{2}\right) . \end{aligned}$$
(31)

Our investigation regarding surface gravity confirms that the temperature is one of the thermodynamical quantities which is not affected by the presence of a first order correction. In other words, for this case, the obtained temperature will be same as that was previously obtained (20). Using the corrected entropy (31) and the temperature (20), we are able to compute the Helmholtz free energy as

$$\begin{aligned} F=-\int S\mathrm{d}T=\frac{1}{16\pi f(\varepsilon )g^{3}(\varepsilon )}\int \frac{\Pi _{1}\Pi _{2}\mathrm{d}r_{+}}{r_{+}^{2}\sqrt{1+\eta _{+}}}, \end{aligned}$$
(32)

where

$$\begin{aligned} \Pi _{1}= & {} 1-\frac{2g^{2}(\varepsilon )\zeta }{r_{+}^{2}\bigg ( \frac{b}{r_{+}} \bigg ) ^{\gamma }}\ln \Biggl ( \Biggl [ \frac{\bigg ( \frac{b}{r_{+}}\bigg ) ^{ \frac{3\gamma }{2}}\Theta _{1,1}}{4\pi f(\varepsilon )g^{2}(\varepsilon )} \Biggl ( \beta ^{2}r_{+}^{2}\sqrt{1+\eta _{+}}\\&+\,\frac{kg^{2}(\varepsilon )}{ 2\Theta _{-1,1}}\bigg ( \frac{b}{r_{+}}\bigg ) ^{-2\gamma }-\frac{r_{+}^{2}}{2 }( 2\beta ^{2}-\Lambda ) \Biggr ) \Biggr ] ^{2}\Biggr ), \end{aligned}$$
$$\begin{aligned} \Pi _{2}= & {} r_{+}^{2}\sqrt{1+\eta _{+}}\Biggl [ kg^{2}(\varepsilon )+r_{+}^{2}\\&\times \,\bigg ( \frac{b}{r_{+}}\bigg ) ^{2\gamma }\Theta _{-1,1}( 2\beta ^{2}-\Lambda ) \Biggr ]\\&-\,2\left[ \Theta _{1,1}f^{2}(\varepsilon )g^{2}(\varepsilon )q^{2}+\Theta _{-1,1}\beta ^{2}r_{+}^{4}\left( \frac{b}{ r_{+}}\right) ^{2\gamma }\right] . \end{aligned}$$

Now, by using the obtained Helmholtz free energy and employing its relation with mass, \(M=F+TS\), one can calculate the corrected mass in the following form:

$$\begin{aligned} M= & {} F-\frac{r_{+}\Pi _{1}\Theta _{1,1}}{16\pi f(\varepsilon )g^{3}(\varepsilon )\Theta _{-1,1}}\nonumber \\&\times \,\left[ kg^{2}(\varepsilon )+2\beta ^{2}r_{+}^{2}\Theta _{-1,1}\left( \frac{b}{r_{+}}\right) ^{2\gamma }\right. \nonumber \\&\left. \times \,\sqrt{1+\eta _{+}} -r_{+}^{2}\Theta _{-1,1}\left( \frac{b}{r_{+}}\right) ^{2\gamma }\left( 2\beta ^{2}-\Lambda \right) \right] . \end{aligned}$$
(33)

We obtain the electric charge (Q) and the electric (chemical) potential (U), which are similar to Eqs. (22) and (24), respectively. Therefore, by using the obtained thermodynamic quantities, the first law of black hole thermodynamics satisfy as

$$\begin{aligned} \mathrm{d}M=T\mathrm{d}S+U\mathrm{d}Q. \end{aligned}$$
(34)

Finally, the heat capacity of this case is of interest. It is a matter of calculation to obtain this quantity by using Eqs. (20) and (31) with (28) as

$$\begin{aligned} C= & {} T\left( \frac{\mathrm{d}S}{\mathrm{d}T}\right) _{Q} =\frac{r_{+}^{4}\left( \frac{b}{r_{+}} \right) ^{\gamma }\left[ \frac{kg^{2}(\varepsilon )}{2\Theta _{-1,1}}\left( \frac{b}{r_{+}}\right) ^{-2\gamma }+\beta ^{2}r_{+}^{2}\eta _{+}-r_{+}^{2}\left( \beta ^{2}-\frac{\Lambda }{2}\right) \right] \eta _{+}}{ \Theta _{-1,1}g^{2}(\varepsilon )\left[ r_{+}^{2}\left( \frac{ kg^{2}(\varepsilon )}{\Theta _{-1,1}\left( \frac{b}{r_{+}}\right) ^{2\gamma } }+2r_{+}^{2}\left( \beta ^{2}-\frac{\Lambda }{2}\right) \right) \eta _{+}-2\beta ^{2}r_{+}^{4}-\frac{2\Theta _{1,1}q^{2}f^{2}(\varepsilon )g^{2}(\varepsilon )}{\Theta _{-1,1}\left( \frac{b}{r_{+}}\right) ^{2\gamma } }\right] } \nonumber \\&-\frac{\zeta \left[ r_{+}^{2}\left( \frac{k\alpha ^{2}g^{2}(\varepsilon )\left( \frac{b}{r_{+}}\right) ^{-2\gamma }}{\Theta _{-1,1}}+2\Theta _{-2,1}r_{+}^{2}\left( \beta ^{2}-\frac{\Lambda }{2}\right) \right) \eta _{+}-2\left( \Theta _{-2,1}\beta ^{2}r_{+}^{4}+\frac{\alpha ^{2}q^{2}f^{2}(\varepsilon )g^{2}(\varepsilon )}{\left( \frac{b}{r_{+}} \right) ^{2\gamma }}\right) \right] }{\Theta _{-1,1}g^{2}(\varepsilon )\left[ r_{+}^{2}\left( \frac{kg^{2}(\varepsilon )}{\Theta _{-1,1}\left( \frac{b}{ r_{+}}\right) ^{2\gamma }}+2r_{+}^{2}\left( \beta ^{2}-\frac{\Lambda }{2} \right) \right) \eta _{+}-2\beta ^{2}r_{+}^{4}-\frac{2\Theta _{1,1}q^{2}f^{2}(\varepsilon )g^{2}(\varepsilon )}{\Theta _{-1,1}\left( \frac{b}{r_{+}}\right) ^{2\gamma }}\right] }. \end{aligned}$$
(35)

Let us highlight some important properties of the obtained heat capacity in the presence of a first order correction. First of all, the effects of a first order correction are observed only in the numerator of the heat capacity which indicates that divergences of the heat capacity, hence phase transition points are independent of first order correction. On the other hand, since the first order correction is present in numerator, it is expected that roots of the heat capacity and stability conditions are first order correction dependent. The contributions of a first order correction and differences between correction and non-correction cases will be discussed in detail in the next section.

3.3 Thermal structure: comparison between correction and non-correction

In this section, the main goal is to understand the possible scenarios regarding thermal structure of the black hole solutions. Since we have obtained thermodynamical properties in the context of both first order correction and non-corrected solutions, we will give details in the context of both of them. Furthermore, we also investigate the details of contribution of the first order correction.

The obtained temperatures for the correction and non-correction cases are the same. On the other hand, from the first law of thermodynamics, we can see that the temperature is calculated as a function of fluctuation in internal energy with changes of the entropy. This shows that change in entropy due to variation of the correction parameter results in modifications in internal energy on a level that the temperature of this system remains fixed. In other words, modifications of the entropy is realized by internal energy in a manner that the temperature remains fixed. This provides us with a tool to increase/decrease the entropy and internal energy without any concern regarding the possible changes in the temperature. This is in a manner, isothermal like behavior, although further tests are required to establish the isothermal nature of this property.

Returning to the obtained temperature, one can recognizes specific properties for it: (1) obtained temperature provides us with imposing a limit on the values that dilatonic parameter could acquire (\( \alpha \ne 1\)). Such limitation prevents temperature to have divergent value, (2) using this limit, one can see that essentially two branches exist for the dilatonic parameter, hence for the temperature: \(\alpha >1\) and \(\alpha <1\). This is due to fact that the signature of different terms in the temperature would be opposite for these two cases. Only exceptions are the cosmological constant and purely nonlinear terms. Later, we will show how these two branches give different pictures regarding the thermodynamics of these black holes, (3) dilatonic parameter is coupled with all presented terms in the temperature. This shows that dilatonic gravity has profound effects on the behavior of the temperature, hence thermodynamical structure of the black holes.

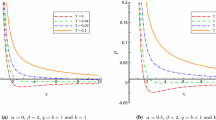
Now, in order to investigate the behavior of the temperature, we have plotted various diagrams for variation of dilatonic parameter, \(\alpha \). As was pointed out, we have divided the effects of dilatonic parameter into two branches of \(\alpha <1\) (left panel of Fig. 2) and \(\alpha >1\) (left panel of Fig. 3).

First, we investigate \(\alpha <1\) case. Evidently, depending on the choices of dilatonic parameter, the temperature could have different properties such as: (1) the existence of one root and being increasing function of the horizon radius (continuous and dotted lines in left panel of Fig. 2). (2) the existence of one root and one extremum (dashed line in left panel of Fig. 2). (3) existence of one root and two extrema (dashed-dotted line in left panel of Fig. 2). Evidently, for small values of the dilatonic parameter, the contribution of scalar field is not significant and general behavior of the temperature is similar to the absence of this parameter. Increasing the dilatonic parameter leads to formation of an extremum. Further increment leads to existence of two extrema: a maximum and then a minimum in which maximum is formed in smaller horizon radius comparing to minimum. The extrema in temperature are matched with divergences in the heat capacity. Therefore, one can conclude that in the case of \(\alpha <1\), increasing the dilatonic parameter leads to introduction of critical behavior in thermodynamical structure of the black holes. Later in studying the heat capacity, we will give more details regarding the types of critical behavior that could exist for these black holes.

Fig. 2
figure 2

For \(k=1\), \(m=5\), \(\Lambda =-1\), \(b=1\), \(q=1\), \(\beta =1\), \( f(\varepsilon )=g(\varepsilon )=0.9\), \(\alpha =0\) (continuous line), \(\alpha =0.5\) (dotted line), \(\alpha =0.79983\) (dashed line) and \(\alpha =0.81\) (dashed-dotted line). T (left panel) and C (middle panel) versus \(r_{+}\); S versus T (right panel)

Full size image
Fig. 3
figure 3

For \(k=1\), \(m=5\), \(\Lambda =-1\), \(b=1\), \(q=1\), \(\beta =1\), \(f( \varepsilon )=g(\varepsilon )=0.9\), \(\alpha =1.2\) (continuous line), \(\alpha =1.6941\) (dotted line), \(\alpha =2\) (dashed line) and \(\alpha =2.4\) (dashed-dotted line). T (left panel) and C (middle panel) versus \(r_{+}\); S versus T (right panel)

Full size image

Let us now turn our attention to the case of \(\alpha >1\). Interestingly, for small values of the dilatonic parameter, the temperature is negative valued everywhere (continuous line in left panel of Fig. 3). This indicates that our solutions are thermodynamically non-physical. It is worthwhile to mention that, for this case, the temperature enjoys a maximum in its structure. The maximum value of the temperature is an increasing function of dilatonic parameter. For specific value of dilatonic parameter, one can find a root for the temperature (dotted line in left panel of Fig. 3). The root is an extreme point, but then again, we should point out that except for the root, the temperature is negative everywhere. Increasing dilatonic parameter more than this specific value leads to formation of two roots for the temperature (dashed and dashed-dotted lines in left panel of Fig. 3). The maximum is located between these roots, which shows that the physical black holes could only be observed for medium black holes. Whereas, for small and large black holes, the temperature is negative valued and solutions are thermally non-physical.

The behavior that we observed in plotted diagrams for \(\alpha <1\) case actually shows the existence of subcritical isobars. Presence of subcritical isobar, so far has been reported only for AdS black holes. On the other hand, the behavior that we observed for temperature in \(\alpha >1\) case was similar to the one that previously was reported for dS black holes. These two specific properties confirms a very important result regarding the dilatonic parameter: for \(\alpha <1\) case, thermodynamical behavior or temperature of black holes is AdS like while for \(\alpha >1\) case, this behavior is dS like. This indicates that in general, for \(\alpha <1\), the black holes have AdS like behavior while for the \(\alpha >1\) the behavior is dS like. If one is interested to study the AdS/CFT duality in the context of these black holes, the valid branch is where \(\alpha <1\).

Now, we turn our attention to the heat capacity which contains information regarding thermal stability and possible phase transition points. Unlike temperature, the heat capacity could be correction dependent. In other words, considering the first order correction to the entropy, the heat capacity would be modified. Interestingly, the effects of correction could be observed in the numerator of the heat capacity while its denominator is independent of it. This confirms two important things regarding the effects of first order correction: (1) The phase transition points that are realized through divergences in the heat capacity are not affected by the first order correction. In other words, the first order correction has no effect on phase transition points. (2) In the usual black holes without the first order correction, the heat capacity and the temperature have the same roots. But since the numerator of the heat capacity in the presence of a first order correction is modified, temperature and the heat capacity no longer share the same roots. This modifies the conditions regarding thermal stability of the solutions.

Fig. 4
figure 4

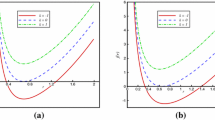
C versus \(r_{+}\) (up panels) and S versus T (lower panels) for \(k=1\), \(m=5\), \(\Lambda =-1\), \(b=1\), \(q=1\), \(\beta =1\), \(f(\varepsilon )=g(\varepsilon )=0.9\), \(\zeta =0\) (continuous line), \(\zeta =1\) (dotted line), \(\zeta =3\) (dashed line), \( \zeta =5\) (dashed-dotted line), \(\zeta =7\) (bold continuous line) and \(\zeta =8\) (bold dotted line). Left panel: \(\alpha =0.5\); middle panel: \(\alpha =0.79883\); right panel: \(\alpha =0.81\)

Full size image

We recall that in the case of \(\alpha <1\), the behavior is AdS like. For this case, there exists a critical value for dilatonic parameter, say \(\alpha _{c}\) (c stands for “critical”) which could be used to divide possible scenarios available for the heat capacity. For \(0<\alpha <\alpha _{c}\), the effects of dilatonic gravity is significant on the place of the root of the heat capacity. Before the root, the heat capacity is negative and solutions are thermally unstable while after it, the opposite is seen and solutions are thermally stable (see continuous and dotted lines in the middle panel of Fig. 2). This shows that, for small values of the dilatonic parameter, region of stability is modified. At the critical value (\(\alpha =\alpha _{c}\)), the heat capacity acquires a divergence which is interpreted as critical behavior (dashed line in the middle panel of Fig. 2). The sign of the heat capacity around this divergence point is positive which indicates that the critical characteristic takes place between two stable phases, as expected. In this case, the heat capacity enjoys a root as well, and it is located before the divergence. Finally, for \(\alpha _{c}<\alpha <1\), the heat capacity has two divergences in its structure (dashed-dotted line in the middle panel of Fig. 2). Between the divergences, the sign of the heat capacity is negative which shows that solutions are thermally unstable. This indicates that there is a phase transition taking place between two divergences. Therefore, the only stable phases provided for the black holes in this case are small and large black holes while the medium black holes suffers thermal instability. It is worthwhile to mention that before the smaller divergence, there also exists a root for the heat capacity. Before this root, the temperature is negative, therefore solutions are non-physical. The behavior that we observed for the heat capacity here completely matches to the one that was observed for the heat capacity of AdS black holes (see the appendix for more details). This confirms that thermal stability structure of these black holes in the case of \(\alpha <1\) is the same as for AdS black holes. This provides us with further proof to recognize the branch \(\alpha <1\) as AdS spacetime.

Fig. 5
figure 5

C versus \(r_{+}\) (up panels) and S versus T (lower panels) for \(k=1\), \(m=5\), \(\Lambda =-1\), \(b=1\), \(q=1\), \(\beta =1\), \(f(\varepsilon )=g(\varepsilon )=0.9\), \(\alpha =2\), \(\zeta =0\) (continuous line), \(\zeta =1\) (dotted line), \(\zeta =3\) (dashed line), \(\zeta =5\) (dashed-dotted line), \(\zeta =7\) (bold continuous line) and \(\zeta =8\) (bold dotted line)

Full size image

In case of \(\alpha >1\), the general behavior in the temperature was dS like. Here, it is possible to divide the general behavior of the heat capacity into three groups by a specific value of \(\alpha \), say \(\alpha _{er}\) (er stands for extreme root). For \(1<\alpha <\alpha _{er}\), the heat capacity has only one divergence in which the heat capacity switches from negative to positive (continuous line in middle panel of Fig. 3). This case has negative temperature everywhere. Therefore, although the heat capacity signals the existence of stable state, the negative temperature shows that no physical solution exists in this case. This highlights the importance of studying the temperature alongside of the heat capacity to separate physical solutions from non-physical ones. For \(\alpha =\alpha _{er}\), interestingly no divergence is observed for the heat capacity, although the temperature gives us the detail of its existence by having a maximum (dotted line in left and middle panels of Fig. 3). In this case, the temperature is negative valued everywhere except at its root which is an extreme one. But the heat capacity in this case shows the existence of only one root which after it, the heat capacity is positive valued. The absence of divergence in heat capacity is due to the fact that extremum and root of the temperature are identical. Considering the relation for the heat capacity (28), it is obvious that no divergence could be observed for the heat capacity in this case. Finally, for \(\alpha _{er}<\alpha \), the heat capacity enjoys two roots with a divergence located between them (dashed and dashed-dotted lines in the middle panel of Fig. 3). Between smaller root and divergence, and after the larger root, the heat capacity is positive. Whereas, before smaller root, and between divergence and larger root, the heat capacity is negative and solutions are thermally unstable. But we should remind the reader that the only physical region for this case is between two roots (positive T). Therefore, there is one physical stable phase and a physical unstable one around divergence and small black holes are stable. The behaviors that we have observed for the heat capacity in this case (\(\alpha >1\)) is exactly the same as the one that was observed for dS case (see the appendix for more details). Therefore, this confirms the analogy of consideration of \(\alpha >1\) as dS case.

Now, we give more details regarding the effects of first order correction on the thermodynamical behavior of the solutions. To do so, we have considered different behaviors that were reported for the heat capacity before and study the effects of variation of the first order parameter, \(\zeta \).

In brief, we should note that, for \(\alpha <1\), we had three cases for the heat capacity: (1) the existence of only one root (\(0<\alpha <\alpha _{c}\)); for this case, the variation of correction parameter leads to modification in place of the root which is an increasing function of \(\zeta \) (upper-left panel of Fig. 4), (2) the existence of one root and one divergence (\(\alpha =\alpha _{c}\)); for small values of the first order correction parameter, \(\zeta \), the place of the root is modified to larger values, but the sign of the heat capacity around divergence point remains positive. Interestingly, for sufficiently large values of the correction parameter, the place of the root will be shifted to after the divergence and the sign of the heat capacity before it and also around divergence point will be negative (up-middle panel of Fig. 4). Therefore, the only thermally stable phase is after the root and around the divergence point, phase transition is between two unstable black holes, (3) the xistence of one root and two divergences (\(\alpha _{c}<\alpha \)); in this case, for small values of the correction parameter, the place of root is modified to larger values of the horizon radius but before the divergences. The stability conditions remain unchanged. But for medium values of the correction parameter, the root will be located between the divergences (upper-right panel of Fig. 4). Interestingly, before smaller divergence, and between the root and larger divergence, the heat capacity is negative. Whereas, between the root and smaller divergence, and also after the larger divergence, the heat capacity is positive (dashed and dashed-dotted lines in the upper-right panel of Fig. 4). Increasing the value of correction parameter leads to root being place after the larger divergence. In this case, the only stable phases (positive heat capacity) are between the divergences and after the root (bold continuous and bold dotted lines in the upper-right panel of Fig. 4).

For \(\alpha >1\), we only consider the physical case in which the temperature has two roots and between them, the temperature has positive values. Evidently, the contribution of the first order correction results in a modification of the place of the root for the heat capacity to higher values of the horizon radius. The root will be located after divergence (up panels of Fig. 5). Before root (around the divergence point as well) the heat capacity is negative. The positive heat capacity could be observed after its root. But the root of the heat capacity is located after the larger root of the temperature, therefore, even though the heat capacity changes its sign to positive after its root, but it is within non-physical region. This results in the conclusion that the existence of the first order correction for this case leads to instability of the black holes within the physical region. We see that contribution of the first order correction destabilizes the solutions.

Our next study here is measuring the modifications in entropy by studying the fluctuation in the temperature. To do so, we have plotted diagrams for both cases of \(\alpha <1\) and \(\alpha >1\) corresponding to those plotted for the temperature and the heat capacity. In addition, we have plotted other diagrams to understand the effects of first order correction on the thermodynamical behavior of the entropy as a function of the temperature.

For \(\alpha <1\), which is interpreted as the AdS case, evidently, three distinctive behaviors could be observed for the entropy. These behaviors could be divided and addressed by \(\alpha _{c}\), which was introduced before in the context of the heat capacity. For \(0<\alpha <\alpha _{c}\), the general behavior of the entropy is not modified on a significant level. Here, entropy is an increasing function of temperature (continuous and dotted lines in right panel of Fig. 2). By setting \(\alpha =\alpha _{c}\), an extremum is formed for entropy versus temperature diagrams (dashed line in right panel of Fig. 2). This case corresponds to the cases where the temperature and the heat capacity enjoy an extremum and divergence, respectively, in their structures. Therefore, one can conclude that the entropy of extremum point is the critical entropy where the system has a thermal phase transition. Increasing the dilatonic parameter to reach the region of \(\alpha _{c}<\alpha \) results in the formation of two extrema which could be recognized by \(T_{1}\) and \(T_{2}\) (dashed-dotted line in right panel of Fig. 2). Between these two indications, the temperature is a decreasing function of the entropy and for every temperature, there exist three different entropies. For \(T=T_{1},T_{2}\) every temperature has two specific entropies. This case corresponds to the existence of two divergences in the heat capacity. The thermodynamical principle informs us that system is in favor of increasing its entropy. This indicates that, for the case where three (two) entropies are available for temperature, the system moves to the case which has the highest entropy. This is indeed the characteristic behavior of the phase transition. Therefore, we see that measurement of the entropy as a function of the fluctuation of the temperature provides us specific characteristic that enables us to recognize critical behavior.

For \(\alpha >1\), which is interpreted as the dS case, we see that, for the non-physical case where the system has the negative temperature, the entropy is positive valued (continuous line in right panel of Fig. 3). Increasing dilatonic parameter leads to temperature acquires an extreme root where, interestingly, entropy has a positive and non-zero value (dotted line in right panel of Fig. 3). Increasing the dilatonic parameter furthermore leads to formation of a region of positive temperature with a maximum provided for temperature (dashed and dashed-dotted lines in right panel of Fig. 3). In this case, except for the maximum, every temperature has two different entropies. The maximum of the temperature is where the system acquires divergence in its heat capacity. Now remembering that for the system one desires higher values of the entropy, we can see that characteristic phase transition behavior is observed by system jumping from smaller entropy to larger one at the same temperature. Interestingly, even for vanishing temperature, there are two values provided for the entropy of system.

Now, let us focus on the effects of a first order correction. As was pointed out, the case \(\alpha <1\) (AdS case) enjoys larger number of the possibilities in its structure depending on the value of dilatonic parameter. For more conclusive discussion regarding the results of a first order correction, we study the effects of variation of the correction parameter for different cases provided \(\alpha <1\) and for the physical case observed in \(\alpha >1\) separately.

(1) For \(0<\alpha <\alpha _{c}\) in the case of \(\alpha <1\), we see that adding first order correction results in the formation of a minimum for entropy, \(S_\mathrm{min}\) (lower-left panel of Fig. 4). In addition, for vanishing temperature, entropy is positive and non-zero valued, \(S_{0}\). In the region \(S_\mathrm{min}<S<S_{0}\), for every entropy, there exist two different temperatures. The minimum and \(S_{0}\) are increasing functions of the correction parameter.

(2) For \(\alpha =\alpha _{c}\) in the case of \(\alpha <1\), where an extremum was observed in the absence of a correction term, adding the correction results in the formation of a minimum for the entropy alongside the extremum that was observed before (lower-middle panel of Fig. 4). But interestingly, the entropies of minimum and extremum points are increasing functions of the correction parameter. Here too, similar to the previous case, for a specific region of the entropy, every entropy has two different temperatures. Now, remembering that the extremum point is where the system has a phase transition, one can conclude that the entropy of the critical point depends on the value of the correction parameter. This shows that the critical behavior in the presence of a first order correction is reached for higher values of the disorder in the system, hence for the entropy.

Fig. 6
figure 6

T (left panels) and C (right panels) versus \(r_{+}\) for \(k=1\), \( m=5\), \(\Lambda =-1\), \(b=1\), \(q=1\), \(f(\varepsilon )=g(\varepsilon )=0.9\), \(\beta =0\) (continuous line), \(\beta =0.15\) (dotted line), \(\beta =0.1898\) (dashed line) and \(\beta =2\). Upper panels: \(\alpha =0.5\); lower panel: \(\alpha =1.5\)

Full size image
Fig. 7
figure 7

T (left panels) and C (right panels) versus \(r_{+}\) for \(k=1\), \( m=5\), \(\Lambda =-1\), \(b=1\), \(q=1\), \(\beta =1\), \(g(\varepsilon )=1.1\), \(f(\varepsilon )=0.2\) (continuous line), \(f(\varepsilon )=0.3\) (dotted line), \(f(\varepsilon )=0.3567\) (dashed line) and \(f(\varepsilon )=0.4\). Upper panels: \(\alpha =0.5\); lower panel: \(\alpha =1.5\)

Full size image

(3) For \(\alpha _{c}<\alpha \) in the case of \(\alpha <1\), as was pointed out, two distinctive temperatures where available, \(T_{1}\) and \(T_{2}\), for which, between them, every temperature has three different entropies. In addition, the entropy related to \(T_{1}\) is larger than the entropy corresponding to \(T_{2}\) (continuous line in the lower-right panel of Fig. 4). Now, the effects of a first order correction in this case could be divided into four groups, which are characterized by \(\zeta _{1}\), \(\zeta _{2}\) and \(\zeta _{3}\), in which \(\zeta _{1}<\zeta _{2}<\zeta _{3}\). For \(0<\zeta <\zeta _{1}\), the general behavior of the entropy versus temperature is the same as that observed for vanishing T with the one difference that entropies corresponding to \(T_{1}\) and \(T_{2}\) are higher than for vanishing temperature (dotted line in the lower-right panel of Fig. 4). Increasing the correction parameter to reach the region of \(\zeta _{1}<\zeta <\zeta _{2}\), interestingly, results in the formation of cycle for entropy versus temperature (dashed line in the lower-right panel of Fig. 4). This means that between \(T_{1}\) and \(T_{2}\), there is yet another temperature, \(T^{\prime }\), which has two different entropies corresponding to it. In this case, the entropy of \(T_{1}\) is still bigger than entropy of \(T_{2}\). If we choose the correction parameter from the region of \(\zeta _{2}<\zeta <\zeta _{3}\), the cyclic behavior could be observed, but interestingly, the entropy corresponding to \(T_{2} \) is larger than the one related to \(T_{1}\) (dashed-dotted line in the lower-right panel of Fig. 4). This means that although the entropies related to these two temperatures are increasing functions of the correction parameter, but the entropy related to \(T_{2}\) grows faster comparing to the one corresponding to \(T_{1}\). Finally, for the region of \(\zeta _{3}<\zeta \), the cyclic behavior vanishes, but since the entropy of \(T_{2}\) is now bigger than the one related to \(T_{1}\), the diagrams have opposite curves compared to small values of the correction parameter (bold continuous and dotted lines in the lower-right panel of Fig. 4).

(4) Finally, for the physical case observed in \(\alpha >1\), in the absence of correction, we observed a maximum for the temperature. Interestingly, the existence of a first order correction results in a cyclic (closed) diagram for the entropy versus temperature (lower panels of Fig. 5). In addition, there is a minimum obtained for the entropy which has maximum temperature as its correspondence. In this case, for every temperature (entropy) there exist two entropies (temperatures). The minimum of the entropy is an increasing function of the correction parameter.

In order to complete our study, we finally investigate the effects of the nonlinearity parameter and energy functions on the thermodynamical behavior of these black holes for the two branches of \(\alpha <1\) (AdS case) and \(\alpha >1\) (dS case).

First, we turn our attention to the nonlinear nature of solutions. For case of \(\alpha <1\), evidently, the effects of nonlinear electrodynamics could be divided into three categories with a critical value for nonlinearity parameter, \(\beta _{c}\) (in which c stands for critical). In the absence of the nonlinearity parameter, temperature has a minimum and it is positive valued everywhere (continuous line in the upper-left panel of Fig. 6). In the presence of the nonlinearity parameter and for the region of \(\beta <\beta _{c} \), the temperature enjoys a root, a maximum and a minimum in its structure (dotted line in the upper-left panel of Fig. 6). As for \(\beta =\beta _{c}\), the number of extrema is reduced to one which is located after the temperature (dashed line in the upper-left panel of Fig. 6). Increasing the nonlinearity parameter beyond \(\beta _{c}<\beta \) results in vanishing of the extremum in the temperature, and the temperature will be an increasing function of the horizon radius with a root (dashed-dotted line in the upper-left panel of Fig. 6). The corresponding heat capacity diagram shows that the temperature and the heat capacity have the same roots and the extrema of the temperature are matched with divergences in the heat capacity (compare upper-left and upper-right panels of Fig. 6). Considering this fact, one can conclude two important points for the \(\alpha <1\) branch: (1) for small values of the nonlinearity parameter, thermodynamical structure of the black holes enjoys the existence of phase transition, (2) increasing the nonlinearity parameter results in the absence of the phase transition for these black holes. It is worthwhile to mention that, for vanishing nonlinearity parameter, since temperature has a minimum, heat capacity has a divergence, which signals for possible critical behavior. The sign of the heat capacity changes from negative to positive around divergence which indicates a phase transition between small unstable black holes to large stable ones. For case of \( \alpha >1\), in the absence of the nonlinearity parameter, temperature is a decreasing function of the horizon radius with a root (continuous line in the lower-left panel of Fig. 6). In the presence of the nonlinearity parameter, the temperature acquires a maximum with two roots. The maximum and number of the roots are decreasing functions of the nonlinearity parameter. This indicates that, for sufficiently large values of the nonlinearity parameter, the maximum will be relocated to negative values and roots will be vanished (dashed-dotted line in the lower-left panel of Fig. 6). Therefore, one can conclude that, for the \(\alpha >1\) branch, the effects of increasing nonlinearity parameter result in the elimination of physical solutions. As for the stability, interestingly, in the absence of the nonlinearity parameter and in the region where the temperature is positive, the heat capacity is negative, hence solutions are thermally unstable. After the root, although the heat capacity is positive, the temperature is negative valued. Therefore, for this case, only unstable solutions exist. In the presence of nonlinearity parameter, if the maximum of the temperature is located at positive values (leading to the presence of two roots for the temperature), the heat capacity enjoys a phase transition between large unstable and small stable black holes (dotted and dashed lines in the lower-right panel of Fig. 6).

The situation for the effects of the energy functions is investigated in Fig. 7. Here, we have investigated the effects of gravity’s rainbow for both branches of \(\alpha <1\) (up panels of Fig. 7) and \( \alpha >1\) (lower panels of Fig. 7). Evidently, for small values of the rainbow functions, temperature enjoys a root and a maximum and a minimum in its structure which correspondingly, heat capacity would have the same and two divergences matching extrema points in the temperature (continuous line in up panel of Fig. 7). This shows that these black holes, for small values of the energy functions, enjoy a phase transition over a region which is located between two divergences of the heat capacity. The number of extrema in temperature, hence divergence in heat capacity is a decreasing function of the energy function. For a certain value of the energy function, the temperature will have an extremum and the heat capacity enjoys a divergence (dashed lines in up panel of Fig. 7). In this case, a phase transition between two stable black holes takes place. Increasing the energy function beyond this value results in the absence of an extremum in the temperature, hence the divergence in the heat capacity. Therefore, the existence of the critical behavior depends on values of the energy functions for the \(\alpha <1\) branch. As for \(\alpha >1\), it is evident that a maximum exists for the temperature which corresponds to a divergence in the heat capacity (lower panels of Fig. 7). For small values of the energy function, this maximum is within the positive valued region and the temperature also enjoys existence of two roots. The maximum is a decreasing function of \(f(\varepsilon )\) and for sufficiently large values of this energy function, it will be relocated into negative region indicating negative temperature without root, hence absence of physical solutions. Therefore, one can conclude that the existence of physical solutions for \(\alpha >1\) depends on the values that energy functions can acquire.

4 Conclusion

Regarding the fact that we should consider high energy (UV) regime near the black holes motivates us to consider an energy dependent spacetime with a minimal coupling between gravity, dilaton scalar field and a nonlinear U(1) gauge field. In this paper, we have studied the black hole solutions in dilaton gravity’s rainbow in the presence of BI source. It was shown that the nonlinearity parameter, energy functions and dilatonic parameter modify the type of the singularity, the places and number of horizon radii and their type as well. These modifications highlighted the importance of matter fields and gravities.

Next, we obtained conserved and thermodynamical quantities and we proved that despite the mortifications of the gravity’s rainbow, dilatonic gravity and BI field, the first law of the black holes thermodynamics is valid.

Our study in the context of the temperature and the heat capacity provided us with interesting properties for dilatonic parameter. First of all, we were able to impose a specific limit on the dilatonic parameter in order to avoid a divergent temperature. In addition, it was shown that, for \(\alpha <1\), the characteristic behaviors of the temperature and the heat capacity are exactly the same as those that were observed for black holes in AdS spacetime. However, for \(\alpha >1\), the properties extracted for the temperature and the heat capacity match those observed for black holes in the dS case. These two specifications provide us with the possibility of conducting studies that are specified for the branch AdS/dS such as AdS/CFT correspondence.

We have investigated the effects of thermal fluctuations on thermodynamical quantities. Although the entropy and mass were affected by thermal fluctuation, the first law remained valid in this case as well. In studying the effects of first order correction, it was shown that although the phase transition points are independent of a first order correction, the stability conditions, which determine thermal structure of the black holes, are highly sensitive to variation of the first order correction parameter. Here, we observed that depending on the choice for correction parameter, the stability regions for black holes are modified on high level depending on the possible scenarios provided for \(\alpha <1\). On the other hand, the contribution of a first order correction resulted in a destabilization of the solutions for the \(\alpha >1\) case. Remembering that \(\alpha <1\) could be interpreted as an AdS spacetime and \(\alpha >1\) as a dS case, one can conclude that, for the AdS case, the stability conditions depend on the correction parameter, while, for dS case, a first order correction makes the solutions unstable within the physical region. Furthermore, one can observe that generalization to include the first order correction results in larger families of the thermal structures provided for these black holes in the AdS case.

The measurement of the entropy as a function of the fluctuation in temperature revealed a profound deviation from the non-correction case. In the case \(\alpha <1\), it was shown that depending on the choices of the correction parameter, it was possible to introduce phenomena such as cyclic behavior and transition from one specific curve for diagrams to an opposite curve. As for \(\alpha >1\), the existence of a first order correction resulted in cyclic behavior as well for entropy versus temperature diagrams and a minimum for the entropy which correspondingly has a maximum of temperature. Generally speaking, the possibilities of such behaviors were provided due to the fact that entropy is correction dependent while the temperature is independent of it. In addition to the mentioned important effects of the first order correction, there is another effect that is of importance; the temperatures of the critical point through entropy versus temperature diagrams remained fixed but the critical entropies were shifted to higher values. This confirms that, generically, the black holes with first order correction included have a phase transition in a higher level of disorder in their system.

To complete our thermodynamical investigation, we studied the effects of the nonlinearity parameter and energy functions on temperature and heat capacity. In the \(\alpha <1\) case, interestingly, it was observed that, for small values of the energy function and nonlinearity parameter, the system enjoys a phase transition over a region. Increasing these quantities leads to formation of an extremum for the temperature, hence a divergence for heat capacity. In this case, the phase transition was taking place over a single point. As for \(\alpha >1\), the maximum for the temperature was a decreasing function of the energy functions and nonlinearity parameter, and for sufficiency large values of these quantities, the maximum will be in the negative region of the temperature, which is interpreted as absence of physical solutions. It is worthwhile to mention that, for vanishing nonlinearity parameter, the general behavior of the temperature and type of divergences were completely different, indicating the high contribution of the nonlinear electromagnetic field generalization.

Our study in this paper confirmed that consideration of the first order correction result into larger classes of thermodynamical structure provided for black holes. But there are two questions that should be answered: (1) are we free to choose any value for the correction parameter? (2) Are all possibilities that are provided for the thermal structure of the black holes, physical ones? One method to regard these questions is through the extended phase space. The concept of extended phase space provides the possibility of studying specific properties for black holes such as compressibility coefficient and speed of sound. These properties along with the concept that speed of sound must not exceed the speed of light, provide us with the possibility of finding upper/lower limit on the values that the correction parameter can acquire and distinguish physical thermodynamical structures from non-physical ones that were obtained in this paper. The only shortcoming of this method is the fact that extended phase space could only be introduced for the AdS case. In any case, this issue is now under investigation and we hope to address these questions in another paper.