1 Introduction

Although the concept of fractional derivative is as old as that of the classical one, its advancement is not so old. Though relatively new, its use is increasing day by day due to its advantages in modeling and widespread applications to real-world problems, and thus it has generated much interest among researchers. There are many physical phenomena and processes, such as anomalous diffusion processes in physics, chemistry, and biology, complex diffusion process, diffusion in heterogeneous medium, diffusion processes in porous medium, viscoelasticity, viscoelastic deformation, viscous fluid, groundwater investigations [1–3], and so on, which can be analyzed more accurately through fractional differential equations than through integer-order differential equations. Fractional differential and integral operators have eliminated the drawback of classical integer-order difficulties considering their nonlocal characteristics [4–11]. There are different definitions of fractional derivatives and integrals, such as variable-order fractional derivative, Riemann–Liouville fractional derivative, Jumarie fractional derivative, Caputo fractional derivative, Weyl fractional derivative, and so on. To describe anomalous diffusion phenomena, constant-order fractional diffusion equations are introduced and have had great success. On the contrary, to characterize some complex diffusion processes, for instance, diffusion processes in heterogeneous medium [12] and diffusion processes in porous medium, if the medium structure or external field changes with time, then the variable-order fractional diffusion equations properly model the incidents [13]. The Riemann–Liouville and Jumarie derivatives are recognized as a powerful modeling approach in the fields of viscoelasticity, viscoelastic deformation, viscous fluid [14–16], anomalous diffusion [17], and so on. The problem in groundwater investigation can be better analyzed by the Weyl fractional-order derivative [18]. The Caputo-type fractional derivative [19] is useful in investigating numerical solutions of a model equation. Therefore, in the recent years, fractional calculus has become an emerging and interesting branch of applied mathematics and analysis.

Referring to mathematical models of the problems, the estimation of traveling wave solutions of fractional nonlinear differential equations (FNDEs) helps us to better understand these phenomena. Therefore various mathematical approaches have been proposed over the past few decades to extract soliton solutions to FNDEs, such as the auxiliary equation method [20], the exp-function method [21, 22], the simplest equation method [23], the sine–cosine method [24], the first integral method [25, 26], the \(( {G'} / {G)}\)-expansion method [27–29], the \({(G'} / {G}, {1} / {G} )\)-expansion method [30–32], the Kudryashov method [33–35], the subequation method [36], the Jacobi elliptic equation method [37], the Ricatti–Bernoulli sub-ODE method [38–40], and so on.

The exact traveling solutions to the coupled BB equation have been established in [41]. By using the Lie symmetry analysis Mhlanga and Khalique [42] described the traveling wave solutions to the generalized coupled BB equation. The envelope soliton and periodic wave solutions have been studied by Ebadi et al. [43]. The coupled WBK equations are examined by other researchers using different analytical and numerical methods, such as the exp-function method [44], the Adomian decomposition method [45], the \(( {G '} / {G}^{2} )\)-expansion method [46], the hyperbolic function method [47], the Lie symmetry analysis [48], the differential transformation method [49], the homotopy analysis method [50], and so on. Recently, Amjad et al. [51] used the result of a standard order coupled fractional-order Whitham—Broer–Kaup equation by the Laplace decomposition method. To the best of our knowledge, the coupled Boussinesq–Burger and Whitham–Broer–Kaup nonlinear fractional differential equations have not been examined through the \(( {G'} / {G)}\)-expansion method [52] and the \({(G'} / {G}, {1} / {G} )\)-expansion method [53]. Therefore, motivated by the studies mentioned, the objective of our study is to extract general solutions, some classical wave solutions, and some compatible soliton solutions entangled with parameters to the equations mentioned. When we set definite values of the parameters, bell-shape soliton, kink, periodic, and other solitary wave solutions are originated from the broad-ranging general solution.

The rest of the paper is arranged as follows: In Sect. 2, we present the properties of the conformable derivative. In Sect. 3, we present the basic idea of the \(( {G'} / {G)}\)-expansion method. In Sect. 4, we give the algorithm of the \({(G'} / {G}, {1} / {G} )\)-expansion method. In Sect. 5, we implement the methods to extract soliton solutions to the coupled BB and coupled WBK systems of time-fractional order. In Sect. 6, we provide a physical explanation and graphs of the solutions. In Sect. 7, we present conclusions.

2 The conformable derivative and some its properties

The conformable derivative of a function g of order α is defined as [54–57]

$$ T_{\alpha } (g) (t)= \lim_{x\rightarrow 0} \frac{g(t+x t^{1-\alpha } )-g(t)}{x},\quad t> 0, \alpha \in ( 0, 1), $$
(2.1)

where \(g: [ 0, \infty ) \rightarrow R\), \(t>0\), and \(\alpha \in ( 0, 1 )\).

Let \(\alpha \in ( 0, 1 )\), and let g, f be α-differentiable at the point t. Then \(T_{\alpha }\) satisfies the following important properties:

$$\begin{aligned}& T_{\alpha } ( a g+b f ) =a T_{\alpha } ( g ) +b T_{\alpha } ( f ),\quad a, b\in R; \end{aligned}$$
(2.2)
$$\begin{aligned}& T_{\alpha } \bigl( t^{\mu } \bigr) =\mu t^{\mu -\alpha },\quad \mu \in R; \end{aligned}$$
(2.3)
$$\begin{aligned}& T_{\alpha } ( gof ) ( t ) = t^{1-\alpha } f ' ( t ) g ' \bigl( f ( t ) \bigr); \end{aligned}$$
(2.4)
$$\begin{aligned}& T_{\alpha } ( g f ) ( t ) =g T_{\alpha } ( f ) +f T_{\alpha } ( g ); \end{aligned}$$
(2.5)
$$\begin{aligned}& T_{\alpha } \biggl( \frac{g}{f} \biggr) ( t ) = \frac{f T_{\alpha } ( g ) - gT_{\alpha } ( f )}{f^{2}}. \end{aligned}$$
(2.6)

If g is a differentiable function, then \(T_{\alpha } ( g ) ( t ) = t^{1 - \alpha } \frac{dg}{dt} ( t )\).

3 The algorithm of the \(( {G'} / {G)}\)-expansion method for FNDEs

Consider an FNDE of the form

$$ F \bigl( v, D_{t}^{\alpha } v, D_{t}^{\alpha } D_{t}^{\alpha } v,\ldots \bigr) = 0,\quad 0 < \alpha < 1, $$
(3.1)

where F is a polynomial of v and fractional partial derivatives of s, and \(v=v(x, t)\) is an unidentified function to be computed.

By using the wave transformation

$$ v ( x, t ) = V ( \zeta ),\qquad \zeta = k x - w\frac{t^{\alpha }}{\alpha }, $$
(3.2)

where w is the wave velocity, and k is the wave number, both nonzero constants, the FNDE (3.1) can be rewritten as the following ordinary differential equation (ODE):

$$ P \biggl( V, \frac{dV}{d\zeta }, \frac{d^{2}V}{d\zeta ^{2}}, \ldots \biggr) = 0. $$
(3.3)

Assume that Eq. (3.3) has the formal solution

$$ V ( \zeta ) = \sum_{i = 0}^{N} \alpha _{i} \biggl( \frac{G' ( \zeta )}{G ( \zeta )} \biggr)^{i},\quad \alpha _{N} \ne 0, $$
(3.4)

where \(\alpha _{i} \) (\(i= 0, 1, \ldots, N\)) are constants, and the function \(G ( \zeta )\) satisfies the auxiliary equation

$$ G'' ( \zeta ) + \lambda G' ( \zeta ) + \mu G ( \zeta ) = 0. $$
(3.5)

The constant N in Eq. (3.4) can be determined by balancing the highest-order derivatives and nonlinear terms turn up in Eq. (3.3). Substituting solution (3.4) into (3.3), using (3.5), summing up all terms of the same order of (\({G '} / {G} \)), and setting the coefficients to zero yield a system of algebraic equations for \(\alpha _{i} \) (\(i=0, 1, \dots , N\)), k, w, λ, and μ. We obtain the values of constants \(\alpha _{i} \) (\(i=0, 1, \dots , N\)), k, w, λ, and μ by unraveling this system, and substituting these constants and the general solutions of (3.5) into solution (3.4), we attain adequate travelling wave solutions to the FNDE (3.1).

4 Description of the \(( {G'} / {G, {1} / {G)}}\)-expansion method for FNDEs

In this section, we interpret the \(( {G'} / {G, {1} / {G)}}\)-expansion method as follows [53]. For the auxiliary differential equation

$$ G'' ( \zeta ) + \lambda G ( \zeta ) = \mu , $$
(4.1)

we set

$$ \phi = \frac{G'}{G},\qquad \psi = \frac{1}{G}, $$
(4.2)

Thus from (4.1) and (4.2) we can derive

$$ \phi ' = - \phi ^{2} + \mu \psi - \lambda ,\qquad \psi ' = - \phi \psi . $$
(4.3)

The solutions of Eq. (4.1) are subject to the following three cases.

Case 1: If \(\lambda < 0\), then the formal solution of Eq. (4.1) is

$$ G ( \zeta ) = A_{1}\sinh ( \sqrt{ - \lambda } \zeta ) + A_{2}\cosh ( \sqrt{ - \lambda } \zeta ) + \mu / \lambda , $$
(4.4)

and the corresponding relation is

$$ \psi ^{2} = - \lambda \biggl( \frac{\phi ^{2} - 2\mu \psi + \lambda }{\lambda ^{2}\sigma + \mu ^{2}} \biggr), $$
(4.5)

where \(\sigma = A_{1}^{2} - A_{2}^{2}\).

Case 2: If \(\lambda > 0\), then the standard solution of Eq. (4.1) is

$$ G ( \zeta ) = A_{1} \sin ( \sqrt{\lambda } \zeta ) + A_{2} \cos ( \sqrt{\lambda } \zeta ) + {\mu } / {\lambda }. $$
(4.6)

Thus the relation between ϕ and ψ is

$$ \psi ^{2} = \lambda \biggl( \frac{\phi ^{2} - 2\mu \psi + \lambda }{\lambda ^{2}\sigma - \mu ^{2}} \biggr), $$
(4.7)

where \(\sigma = A_{1}^{2} + A_{2}^{2}\).

Case 3: If \(\lambda = 0\), then the typical solution of Eq. (4.1) is

$$ G ( \zeta ) = \frac{\mu }{2}\zeta ^{2} + A_{1}\zeta + A_{2}, $$
(4.8)

and the relations between ϕ and ψ is

$$ \psi ^{2} = \frac{\phi ^{2} -2\mu \psi }{A_{1}^{2} -2\mu A_{2}}, $$
(4.9)

where \(A_{1}\), \(A_{2}\) are integral constants.

The major steps of the \(( {G'} / {G, {1} / {G)}}\)-expansion method are described as follows.

Step 1: We assume that Eq. (3.3) has the general solution

$$ V ( \zeta ) = \sum_{i = 0}^{S} \alpha _{i}\phi ^{i} + \sum_{i = 1}^{S} \beta _{i}\phi ^{i - 1}\psi , $$
(4.10)

where G is the solution of the auxiliary Eq. (4.1), \(\alpha _{i}\) (\(i= 0, 1, \ldots, S \)), \(\beta _{i}\) (\(i= 1, 2, \ldots, S\)), μ, and λ are constants, and S in solution (4.10) can be determined by the balancing theory from Eq. (3.3).

Step 2: Substituting (4.10) into (3.3) with (4.3) and (4.5), we obtain a polynomial in ψ and ϕ, where the degree of ψ is not greater than one. Setting all coefficients of the polynomial to zero yields a set of algebraic equations, which can be solved with the help of Maple software package, and substituting the values of k, w, μ, λ, \(\alpha _{i}\), \(\beta _{i}\) into (4.10), we get analytical exact solutions to Eq. (3.3) expressed by the hyperbolic function.

Step 3: Substituting (4.10) into (3.3) with (4.3) and (4.7) (or (4.3) and (4.9)), we get exact solutions to Eq. (3.1) expressed by trigonometric or rational functions, respectively.

5 Extraction of soliton solutions

In this section, we extract the traveling wave, including periodic, kink, bell-shape soliton, and so on wave solutions to the following fractional systems utilizing the methods described in Sects. 3 and 4.

First, we consider the model based on the nonlinear time fractional coupled BB equations [58, 59]:

$$ \begin{gathered} D_{t}^{\alpha } u- \frac{1}{2} v_{x} +2u u_{x} =0, \\ t> 0, \qquad 0< \alpha < 1, \\ D_{t}^{\alpha } v- \frac{1}{2} u_{xxx} +2 ( u v )_{x} =0, \end{gathered} $$
(5.1)

where \(u ( x, t )\) represents the horizontal velocity field, and \(v ( x, t )\) indicates the water surface height above a horizontal level from the bottom.

Second, we consider a model based on the nonlinear time fractional coupled WBK equations [49]:

$$ \begin{gathered} D_{t}^{\alpha } u+u u_{x} + v_{x} +c u_{xx} =0, \\ t> 0, \qquad 0< \alpha < 1, \\ D_{t}^{\alpha } v+ (uv)_{x} +b u_{xxx} -c v_{xx} =0, \end{gathered} $$
(5.2)

where the constants b and c represent the coefficients of diffusion and dissipation, respectively, \(u ( x, t )\) represents the horizontal field of horizontal velocity, and \(v ( x, t )\) indicates the height of deviation from the liquid equilibrium position.

5.1 The time-fractional coupled BB equations

For the time-fractional coupled BB equations, we put the wave transformation

$$ \begin{gathered} u ( x, t ) = U ( \zeta ),\qquad v ( x, t ) = V ( \zeta ), \\ \zeta = x - w \frac{t^{\alpha }}{\alpha }. \end{gathered} $$
(5.3)

We will take the advantage of fractional wave transformation to turn system (5.1) into the ODEs:

$$ \begin{gathered} wU' + \frac{1}{2}V' - 2UU' = 0, \\ wV' + \frac{1}{2}U''' - 2 ( UV )^{\prime } = 0, \end{gathered} $$
(5.4)

By integrating we obtain

$$ \begin{gathered} w U+ \frac{1}{2} V- U^{2} + c_{1} =0, \\ w V+ \frac{1}{2} U^{\prime \prime } -2 U V+ c_{2} =0, \end{gathered} $$
(5.5)

where \(c_{1}\) and \(c_{2}\) are integrating constants.

Balancing between V and \(U^{2}\), \(U''\), and UV in (5.5), we find \(N_{1} =1\) and \(N_{2} =2\).

Therefore the formal solutions of (5.5) can be presented by a polynomial in \(( G' / G )\):

$$ \begin{gathered} U ( \zeta ) = \alpha _{0} + \alpha _{1} \bigl( G' / G \bigr), \quad \alpha _{1} \ne 0, \\ V ( \zeta ) = \beta _{0} + \beta _{1} \bigl( G' / G \bigr) + \beta _{2} \bigl( G' / G \bigr)^{2},\quad \beta _{2} \ne 0. \end{gathered} $$
(5.6)

Embedding (5.6) into (5.5) and applying the procedure stated in Sect. 3, we get the following result:

$$ \begin{gathered} \alpha _{0} =\mp {\lambda } / {4} + {w} / {2},\qquad \alpha _{1} = \mp {1} / {2},\qquad \beta _{0} = {\mu } / {2}, \qquad \beta _{1} = {\lambda } / {2},\qquad \beta _{2} = {1} / {2},\\ c_{1} = {\lambda ^{2}} / {16} - {w^{2}} / {4} - {\mu } / {4},\qquad c_{2} =0, \end{gathered} $$
(5.7)

where w is an arbitrary constant.

By means of the values assembled in (5.7) and the general solutions of (3.5), from solution (5.6) we accomplish three types of solitary wave solutions to the coupled BB Eq. (5.1) as follows.

Type I: When \(( \lambda ^{2} - 4\mu ) > 0\), we attain the hyperbolic function solutions of (5.1):

$$ \begin{gathered} u_{1} ( x, t ) = \frac{w}{2} \mp \frac{\sqrt{\lambda ^{2} - 4\mu }}{4} \times \biggl( \frac{B_{1}\cosh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} + B_{2}\sinh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2}}{B_{1}\sinh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} + B_{2}\cosh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2}} \biggr), \\ v_{1} ( x, t ) = \frac{ ( \lambda ^{2} - 4\mu )}{8} \times \biggl[ \biggl( \frac{B_{1}\cosh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} + B_{2}\sinh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2}}{B_{1}\sinh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} + B_{2}\cosh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2}} \biggr)^{2} - 1 \biggr], \end{gathered} $$
(5.8)

where \(\zeta = x - w \frac{t^{\alpha }}{\alpha } \). Solution (5.8) is the general hyperbolic type of the coupled BB equation, from which different compact-form solutions can be extracted for definite values of the integral constants.

For \(B_{1} = 0\), \(B_{2} \ne 0\), we get the squeezed bell-shape and kink-type solitary wave solutions to the coupled BB Eqs. (5.1):

$$ \begin{gathered} u_{1_{1}} (x, t)= \frac{w}{2} \mp \frac{\sqrt{\lambda ^{2} -4\mu }}{4} \tanh \biggl( \sqrt{\lambda ^{2} -4\mu } \frac{\zeta }{2} \biggr), \\ v_{1_{1}} ( x, t ) =- \frac{ ( \lambda ^{2} -4\mu )}{8} \operatorname{sech}^{2} \biggl( \sqrt{\lambda ^{2} -4\mu } \frac{\zeta }{2} \biggr). \end{gathered} $$
(5.9)

On the other hand, if we put \(B_{2} = 0\), \(B_{1} \ne 0\), we gain singular solitary wave solutions of (5.1):

$$ \begin{gathered} u_{1_{2}} (x, t)= \frac{w}{2} \mp \frac{\sqrt{\lambda ^{2} -4\mu }}{4} \coth \biggl( \sqrt{\lambda ^{2} -4\mu } \frac{\zeta }{2} \biggr), \\ v_{1_{2}} ( x, t ) = \frac{ ( \lambda ^{2} -4\mu )}{8} \operatorname{csch}^{2} \biggl( \sqrt{\lambda ^{2} -4\mu } \frac{\zeta }{2} \biggr). \end{gathered} $$
(5.10)

Again, if we set \(B_{2} \ne 0\), \(B_{2}^{2} > B_{1}^{2}\), we accomplish the solitary wave solutions of (5.1):

$$ \begin{gathered} u_{1_{3}} ( x, t ) = \frac{w}{2} \mp \frac{\sqrt{\lambda ^{2} - 4\mu }}{4}\tanh \biggl( \zeta _{0} + \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} \biggr), \\ v_{1_{3}} ( x, t ) = - \frac{ ( \lambda ^{2} - 4\mu )}{8}\operatorname{sech}^{2} \biggl( \zeta _{0} + \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} \biggr), \end{gathered} $$
(5.11)

where \(\zeta _{0} = \tanh ^{ - 1}\frac{B_{1}}{B_{2}}\).

However, if we set \(B_{1} \ne 0\), \(B_{1}^{2} > B_{2}^{2}\), we attain the singular solitary wave solutions of (5.1):

$$ \begin{gathered} u_{1_{4}} ( x, t ) = \frac{w}{2} \mp \frac{\sqrt{\lambda ^{2} - 4\mu }}{4}\coth \biggl( \zeta _{0} + \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} \biggr), \\ v_{1_{4}} ( x, t ) = \frac{ ( \lambda ^{2} - 4\mu )}{8}\operatorname{csch}^{2} \biggl( \zeta _{0} + \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} \biggr), \end{gathered} $$
(5.12)

where \(\zeta _{0} = \tanh ^{ - 1}\frac{B_{2}}{B_{1}}\).

Type II: When \(( \lambda ^{2} - 4\mu ) < 0\), we derive the trigonometric function solutions of (5.1):

$$ \begin{gathered} u_{2} ( x, t ) = \frac{w}{2} \mp \frac{\sqrt{4\mu - \lambda ^{2}}}{4} \biggl( \frac{ - B_{1}\sin \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} + B_{2}\cos \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2}}{B_{1}\cos \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} + B_{2}\sin \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2}} \biggr), \\ v_{2} ( x, t ) = \frac{ ( 4\mu - \lambda ^{2} )}{8} \times \biggl[ 1 + \biggl( \frac{ - B_{1}\sin \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} + B_{2}\cos \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2}}{B_{1}\cos \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} + B_{2}\sin \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2}} \biggr)^{2} \biggr]. \end{gathered} $$
(5.13)

Since \(B_{1}\) and \(B_{2}\) are integral constants; someone is able to accept their values spontaneously. Therefore, if we accept \(B_{1} = 0\), \(B_{2} \ne 0\), we attain the subsequent singular periodic wave solutions to the nonlinear coupled Boussinesq–Burger equations:

$$ \begin{gathered} u_{2_{1}} (x, t)= \frac{w}{2} \mp \frac{\sqrt{4\mu - \lambda ^{2}}}{4} \cot \biggl( \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr), \\ v_{2_{1}} ( x, t ) = \frac{ ( 4\mu - \lambda ^{2} )}{8} \operatorname{csc}^{2} \biggl( \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr). \end{gathered} $$
(5.14)

Furthermore, if we accept \(B_{2} = 0\), \(B_{1} \ne 0\), then we determine the following singular periodic wave solutions to the nonlinear coupled BB equations:

$$ \begin{gathered} u_{2_{2}} (x, t)= \frac{w}{2} \pm \frac{\sqrt{4\mu - \lambda ^{2}}}{4} \tan \biggl( \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr), \\ v_{2_{2}} ( x, t ) = \frac{ ( 4\mu - \lambda ^{2} )}{8} \operatorname{sec}^{2} \biggl( \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr). \end{gathered} $$
(5.15)

However, if \(B_{2} \ne 0\), \(B_{2}^{2} > B_{1}^{2}\), then we obtain the singular periodic wave solutions of (5.1) as follows:

$$ \begin{gathered} u_{2_{3}} ( x, t ) = \frac{w}{2} \mp \frac{\sqrt{4\mu - \lambda ^{2}}}{4}\cot \biggl( \zeta _{0} + \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr), \\ v_{2_{3}} ( x, t ) = \frac{ ( 4\mu - \lambda ^{2} )}{8}\csc ^{2} \biggl( \zeta _{0} + \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr), \end{gathered} $$
(5.16)

where \(\zeta _{0} = \tan ^{ - 1}\frac{B_{1}}{B_{2}}\).

On the other hand, if \(B_{1} \ne 0\), \(B_{1}^{2} > B_{2}^{2}\), then we attain the periodic wave solutions of (5.1) as follows:

$$ \begin{gathered} u_{2_{4}} ( x, t ) = \frac{w}{2} \pm \frac{\sqrt{4\mu - \lambda ^{2}}}{4}\tan \biggl( \zeta _{0} - \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr), \\ v_{2_{4}} ( x, t ) = \frac{ ( 4\mu - \lambda ^{2} )}{8}\sec ^{2} \biggl( \zeta _{0} - \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr), \end{gathered} $$
(5.17)

where \(\zeta _{0} = \tan ^{ - 1}\frac{B_{2}}{B_{1}}\).

Type III: When \(( \lambda ^{2} - 4\mu ) = 0\), we ensure the subsequent rational function solutions of (5.1):

$$ \begin{gathered} u_{3} (x, t)= \frac{w}{2} \mp \frac{1}{2} \frac{B_{2}}{B_{1} + B_{2} \zeta }, \\ v_{3} ( x, t ) = \frac{1}{2} \biggl( \frac{ B_{2}}{B_{1} + B_{2} \zeta } \biggr)^{2}, \end{gathered} $$
(5.18)

wherein \(B_{1}\) could be zero, but \(B_{2}\) cannot be zero; otherwise, solution (5.18) would turn into steady solution, which has no physical significance.

Now we use the two-variable \(( G' / G, 1 / G )\)-expansion method to analyze the wave solutions to the coupled BB equation. Accordingly, we look for the solutions in the form

$$ \begin{gathered} U ( \zeta ) = a_{0} + a_{1} \phi + b_{1} \psi , \\ V ( \zeta ) = \alpha _{0} + \alpha _{1} \phi + \alpha _{2} \phi ^{2} + \beta _{1} \psi + \beta _{2} \phi \psi , \end{gathered} $$
(5.19)

where \(a_{0}\), \(a_{1}\), \(b_{1}\), \(\alpha _{0}\), \(\alpha _{1}\), \(\alpha _{2}\), \(\beta _{1}\), and \(\beta _{2}\) are constants to be determined. As we mentioned in Sect. 4, we have three cases.

Case 1: When \(\lambda < 0\), inserting (5.19) into (5.5), by (4.3), (4.4), and (4.5) system (5.5) turns into a polynomial in ψ and ϕ. The coefficients of this equation yield a system of algebraic equations in \(a_{0}\), \(a_{1}\), \(b_{1}\), \(\alpha _{0}\), \(\alpha _{1}\), \(\alpha _{2}\), \(\beta _{1}\), \(\beta _{2}\), w, λ, μ, σ, \(\zeta _{1}\), and \(\zeta _{2}\). Solving the algebraic equations via Maple software package, we obtain three different sets of results.

Result 1

$$ \begin{gathered} a_{0} = \pm \frac{1}{2}\sqrt{ - 4 \zeta _{1} + \frac{2\lambda ^{3}\sigma - \lambda \mu ^{2}}{4\lambda ^{2}\sigma + 4\mu ^{2}}} \pm \frac{\mu }{4}\sqrt{ - \frac{\lambda }{\lambda ^{2}\sigma + \mu ^{2}}},\\ a_{1} = 0,\qquad b_{1} = \pm \sqrt{ - \frac{\lambda ^{2}\sigma + \mu ^{2}}{4\lambda }}, \\ \alpha _{0} = \frac{1}{4}\frac{\lambda ^{3}\sigma + 2\lambda \mu ^{2}}{\lambda ^{2}\sigma + \mu ^{2}},\qquad \alpha _{1} = 0,\qquad \alpha _{2} = \frac{1}{2},\qquad \beta _{1} = - \frac{1}{2}\mu ,\qquad \beta _{2} = 0, \\ w = \pm \sqrt{ - 4\zeta _{1} + \frac{2\lambda ^{3}\sigma - \lambda \mu ^{2}}{4\lambda ^{2}\sigma + 4\mu ^{2}}},\qquad \zeta _{1} = \zeta _{1}, \qquad \zeta _{2} = \mp \frac{\sigma \lambda ^{3}\mu \sqrt{ - \lambda }}{8 ( \lambda ^{2}\sigma + \mu ^{2} )\sqrt{\lambda ^{2}\sigma + \mu ^{2}}}. \end{gathered} $$
(5.20)

From (4.4), (5.19), and (5.20) with (5.3) we derive the following hyperbolic function solutions of (5.1):

$$ \begin{gathered} u_{1} ( x, t ) = \pm \frac{1}{2} \sqrt{ - 4\zeta _{1} + \frac{2\lambda ^{3}\sigma - \lambda \mu ^{2}}{4\lambda ^{2}\sigma + 4\mu ^{2}}} \pm \frac{1}{4} \frac{\mu \sqrt{ - \lambda }}{\sqrt{\lambda ^{2}\sigma + \mu ^{2}}} \\ \hphantom{ u_{1} ( x, t ) =}{}\pm \frac{1}{2\sqrt{ - \lambda }} \frac{\sqrt{\lambda ^{2}\sigma + \mu ^{2}}}{A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda }, \\ v_{1} ( x, t ) = \frac{\lambda ^{3}\sigma + 2\lambda \mu ^{2}}{4\lambda ^{2}\sigma + 4\mu ^{2}} - \frac{\lambda }{2} \biggl( \frac{A_{1}\cosh \sqrt{ - \lambda } \zeta + A_{2}\sinh \sqrt{ - \lambda } \zeta }{A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda } \biggr)^{2} \\ \hphantom{v_{1} ( x, t ) =}{}- \frac{1}{2}\frac{\mu }{A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda }, \end{gathered} $$
(5.21)

where \(\zeta = x \mp \sqrt{ - 4\zeta _{1} + \frac{2\lambda ^{3}\sigma - \lambda \mu ^{2}}{4\lambda ^{2}\sigma + 4\mu ^{2}}} \frac{t^{\alpha }}{\alpha } \) and \(\sigma = A_{1}^{2} - A_{2}^{2}\).

Inasmuch as \(A_{1}\), \(A_{2}\), and μ are free parameters, choosing \(A_{1} = 0\), \(\mu = 0\), and \(A_{2} > 0\), from (5.21) we attain the following solitary wave solutions:

$$ \begin{gathered} u_{1_{1}} (x, t)=\pm \frac{1}{2} \biggl( \sqrt{-4 \zeta _{1} + \frac{\lambda }{2}} +i \sqrt{-\lambda } \operatorname{sech} \sqrt{-\lambda } \zeta \biggr), \\ v_{1_{1}} ( x, t ) = \frac{\lambda }{4} - \frac{\lambda }{2} \tanh ^{2} \sqrt{-\lambda } \zeta . \end{gathered} $$
(5.22)

Alternatively, choosing \(A_{2} = 0\), \(\mu = 0\), and \(A_{1} > 0\), we attain the solitary wave solutions

$$ \begin{gathered} u_{1_{2}} ( x, t ) = \pm \frac{1}{2} \biggl( \sqrt{ - 4\zeta _{1} + \frac{\lambda }{2}} + \sqrt{ - \lambda } \operatorname{csch} \sqrt{ - \lambda } \zeta \biggr), \\ v_{1_{2}} ( x, t ) = \frac{\lambda }{4} - \frac{\lambda }{2}\coth ^{2}\sqrt{ - \lambda } \zeta . \end{gathered} $$
(5.23)

Result 2

$$ \begin{gathered} a_{0} = \pm \frac{1}{4}\sqrt{ - \lambda - 16\zeta _{1}},\qquad a_{1} = \frac{1}{4},\qquad b_{1} = \pm \frac{1}{4}\sqrt{ - \frac{\lambda ^{2}\sigma + \mu ^{2}}{\lambda }}, \\ \alpha _{0} = \frac{1}{4}\lambda ,\qquad \alpha _{1} = 0,\qquad \alpha _{2} = \frac{1}{4},\qquad \beta _{1} = - \frac{1}{4}\mu ,\qquad \beta _{2} = \pm \frac{1}{4}\sqrt{ - \frac{\lambda ^{2}\sigma + \mu ^{2}}{\lambda }}, \\ w = \pm \frac{1}{2}\sqrt{ - \lambda - 16\zeta _{1}},\qquad \zeta _{1} = \zeta _{1},\qquad \zeta _{2} = 0. \end{gathered} $$
(5.24)

From (4.4), (5.19), and (5.24) with (5.3) we find the following hyperbolic function solutions of (5.1):

$$ \begin{gathered} u_{2} ( x, t ) = \pm \frac{1}{4} \sqrt{ - \lambda - 16\zeta _{1}} \\ \hphantom{u_{2} ( x, t ) =}{}+ \frac{\sqrt{ - \lambda }}{4}\frac{A_{1}\cosh \sqrt{ - \lambda } \zeta + A_{2}\sinh \sqrt{ - \lambda } \zeta }{A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda } \\ \hphantom{u_{2} ( x, t ) =}{}\pm \frac{1}{4\sqrt{ - \lambda }} \frac{\sqrt{\lambda ^{2}\sigma + \mu ^{2}}}{A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda }, \\ v_{2} ( x, t ) = \frac{\lambda }{4} - \frac{1}{4} \frac{\mu }{A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda } \\ \hphantom{v_{2} ( x, t ) =}{}- \frac{1}{4}\frac{A_{1}\cosh \sqrt{ - \lambda } \zeta + A_{2}\sinh \sqrt{ - \lambda } \zeta }{ ( A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda )^{2}} \\ \hphantom{v_{2} ( x, t ) =}{}\times \bigl[ A_{1}\lambda \cosh \sqrt{ - \lambda } \zeta + A_{2}\lambda \sinh \sqrt{ - \lambda } \zeta \mp \sqrt{\lambda ^{2}\sigma + \mu ^{2}} \bigr], \end{gathered} $$
(5.25)

where \(\zeta = x \mp \frac{1}{2}\sqrt{ - \lambda - 16\zeta _{1}} \frac{t^{\alpha }}{\alpha } \).

In particular, if we set \(A_{1} = 0\), \(\mu = 0\), and \(A_{2} > 0\) into (5.25), we attain the following solitary wave solutions:

$$ \begin{gathered} u_{2_{1}} ( x, t ) = \pm \frac{1}{4} \sqrt{ - \lambda - 16\zeta _{1}} + \frac{\sqrt{ - \lambda }}{4} [ \tanh \sqrt{ - \lambda } \zeta \pm i\operatorname{sech} \sqrt{ - \lambda } \zeta ], \\ v_{2_{1}} ( x, t ) = \frac{\lambda }{4} - \frac{\lambda }{4}\tanh \sqrt{ - \lambda } \zeta [ \tanh \sqrt{ - \lambda } \zeta \pm i\operatorname{sech} \sqrt{ - \lambda } \zeta ]. \end{gathered} $$
(5.26)

On the contrary, if we set \(A_{2} = 0\), \(\mu = 0\), and \(A_{1} > 0\), we attain the solitary wave solutions

$$ \begin{gathered} u_{2_{2}} ( x, t ) = \pm \frac{1}{4} \sqrt{ - \lambda - 16\zeta _{1}} + \frac{\sqrt{ - \lambda }}{4} [ \coth \sqrt{ - \lambda } \zeta \pm \operatorname{csch} \sqrt{ - \lambda } \zeta ], \\ v_{2_{2}} ( x, t ) = \frac{\lambda }{4} - \frac{\lambda }{4}\coth \sqrt{ - \lambda } \zeta [ \coth \sqrt{ - \lambda } \zeta \mp \operatorname{csch} \sqrt{ - \lambda } \zeta ]. \end{gathered} $$
(5.27)

Result 3

$$ \begin{gathered} a_{0} = \pm \frac{1}{4}\sqrt{ - \lambda - 16\zeta _{1}},\qquad a_{1} = - \frac{1}{4},\qquad b_{1} = \pm \frac{1}{4}\sqrt{ - \frac{\lambda ^{2}\sigma + \mu ^{2}}{\lambda }}, \\ \alpha _{0} = \frac{1}{4}\lambda ,\qquad \alpha _{1} = 0,\qquad \alpha _{2} = \frac{1}{4},\\ \beta _{1} = - \frac{1}{4}\mu ,\qquad \beta _{2} = \mp \frac{1}{4}\sqrt{ - \frac{\lambda ^{2}\sigma + \mu ^{2}}{\lambda }}, \\ w = \pm \frac{1}{2}\sqrt{ - \lambda - 16\zeta _{1}},\qquad \zeta _{1} = \zeta _{1},\qquad \zeta _{2} = 0. \end{gathered} $$
(5.28)

From result 3 we gain other hyperbolic function solutions of (5.1):

$$ \begin{gathered} u_{3} ( x, t ) = \pm \frac{1}{4} \sqrt{ - \lambda - 16\zeta _{1}} - \frac{\sqrt{ - \lambda }}{4}\frac{A_{1}\cosh \sqrt{ - \lambda } \zeta + A_{2}\sinh \sqrt{ - \lambda } \zeta }{A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda } \\ \hphantom{u_{3} ( x, t ) =}{}\pm \frac{1}{4\sqrt{ - \lambda }} \frac{\sqrt{\lambda ^{2}\sigma + \mu ^{2}}}{A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda }, \\ v_{3} ( x, t ) = \frac{\lambda }{4} - \frac{1}{4} \frac{\mu }{A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda }\\ \hphantom{v_{3} ( x, t ) =}{} - \frac{1}{4}\frac{A_{1}\cosh \sqrt{ - \lambda } \zeta + A_{2}\sinh \sqrt{ - \lambda } \zeta }{ ( A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda )^{2}} \\ \hphantom{v_{3} ( x, t ) =}{}\times \bigl[ A_{1}\lambda \cosh \sqrt{ - \lambda } \zeta + A_{2}\lambda \sinh \sqrt{ - \lambda } \zeta \pm \sqrt{\lambda ^{2}\sigma + \mu ^{2}} \bigr], \end{gathered} $$
(5.29)

where \(\zeta = x \mp \frac{1}{2}\sqrt{ - \lambda - 16\zeta _{1}} \frac{t^{\alpha }}{\alpha } \).

Similarly, if the parameters take distinct values, then we deduce many other solitary wave solutions, but for conciseness, here we do not document the other solutions.

Case 2 When \(\lambda > 0\), substituting (5.19) into (5.5) and using (4.3), (4.6), and (4.7), system (5.5) can be expressed as a polynomial in ψ and ϕ. Vanishing all coefficients from this polynomial, we obtain a system of algebraic equations, which can be solved by utilizing Maple software package to get different results.

Result 1

$$ \begin{gathered} a_{0} = \pm \frac{1}{2}\sqrt{ - 4 \zeta _{1} + \frac{2\lambda ^{3}\sigma + \lambda \mu ^{2}}{4\lambda ^{2}\sigma - 4\mu ^{2}}} \pm \frac{\mu }{4}\sqrt{ \frac{\lambda }{\lambda ^{2}\sigma - \mu ^{2}}},\\ a_{1} = 0,\qquad b_{1} = \pm \frac{1}{2}\sqrt{\frac{\lambda ^{2}\sigma - \mu ^{2}}{\lambda }}, \\ \alpha _{0} = \frac{1}{4}\frac{\lambda ^{3}\sigma - 2\lambda \mu ^{2}}{\lambda ^{2}\sigma - \mu ^{2}},\qquad \alpha _{1} = 0,\qquad \alpha _{2} = \frac{1}{2},\qquad \beta _{1} = - \frac{1}{2}\mu ,\qquad \beta _{2} = 0, \\ w = \pm \sqrt{ - 4\zeta _{1} + \frac{2\lambda ^{3}\sigma + \lambda \mu ^{2}}{4\lambda ^{2}\sigma - 4\mu ^{2}}},\qquad \zeta _{1} = \zeta _{1},\qquad \zeta _{2} = \mp \frac{\sigma \lambda ^{3}\mu \sqrt{\lambda }}{8 ( \lambda ^{2}\sigma - \mu ^{2} )\sqrt{\lambda ^{2}\sigma - \mu ^{2}}}. \end{gathered} $$
(5.30)

From (4.6), (5.19), and (5.30) with (5.3), we deduce the following trigonometric function solutions of (5.1):

$$ \begin{gathered} u_{1} ( x, t ) = \pm \frac{1}{2} \sqrt{ - 4\zeta _{1} + \frac{2\lambda ^{3}\sigma + \lambda \mu ^{2}}{4\lambda ^{2}\sigma - 4\mu ^{2}}} \pm \frac{\mu }{4} \frac{\sqrt{\lambda }}{\sqrt{\lambda ^{2}\sigma - \mu ^{2}}} \\ \hphantom{u_{1} ( x, t ) =}{}\pm \frac{1}{2 \sqrt{\lambda }} \frac{\sqrt{\lambda ^{2}\sigma - \mu ^{2}}}{A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda }, \\ v_{1} ( x, t ) = \frac{\lambda ^{3}\sigma - 2\lambda \mu ^{2}}{4\lambda ^{2}\sigma - 4\mu ^{2}} + \frac{\lambda }{2} \biggl( \frac{A_{1}\cos \sqrt{\lambda } \zeta - A_{2}\sin \sqrt{\lambda } \zeta }{A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda } \biggr)^{2} \\ \hphantom{v_{1} ( x, t ) =}{}- \frac{1}{2}\frac{\mu }{A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda }, \end{gathered} $$
(5.31)

where \(\zeta = x \mp \sqrt{ - 4\zeta _{1} + \frac{2\lambda ^{3}\sigma + \lambda \mu ^{2}}{4\lambda ^{2}\sigma - 4\mu ^{2}}} \frac{t^{\alpha }}{\alpha } \) and \(\sigma = A_{1}^{2} + A_{2}^{2}\).

In particular, by taking \(A_{1} = 0\), \(\mu = 0\), and \(A_{2} > 0\) in (5.31), we achieve the following periodic wave solutions:

$$ \begin{gathered} u_{1_{1}} ( x, t ) = \pm \frac{1}{2} \sqrt{ - 4\zeta _{1} + \frac{\lambda }{2}} \pm \frac{\sqrt{\lambda }}{2}\sec \sqrt{\lambda } \zeta , \\ v_{1_{1}} ( x, t ) = \frac{\lambda }{4} + \frac{\lambda }{2}\tan ^{2}\sqrt{\lambda } \zeta , \end{gathered} $$
(5.32)

whereas for \(A_{2} = 0\), \(\mu = 0\), and \(A_{1} > 0\), we deduce the periodic wave solutions

$$ \begin{gathered} u_{1_{2}} ( x, t ) = \pm \frac{1}{2} \sqrt{ - 4\zeta _{1} + \frac{\lambda }{2}} \pm \frac{\sqrt{\lambda }}{2}\csc \sqrt{\lambda } \zeta , \\ v_{1_{2}} ( x, t ) = \frac{\lambda }{4} + \frac{\lambda }{2}\cot ^{2}\sqrt{\lambda } \zeta . \end{gathered} $$
(5.33)

Result 2

$$ \begin{gathered} a_{0} = \pm \frac{1}{4}\sqrt{ - \lambda - 16\zeta _{1}},\qquad a_{1} = \frac{1}{4},\qquad b_{1} = \pm \frac{1}{4}\sqrt{\frac{\lambda ^{2}\sigma - \mu ^{2}}{\lambda }}, \\ \alpha _{0} = \frac{1}{4}\lambda ,\qquad \alpha _{1} = 0,\qquad \alpha _{2} = \frac{1}{4},\qquad \beta _{1} = - \frac{1}{4}\mu ,\qquad \beta _{2} = \pm \frac{1}{4}\sqrt{ \frac{\lambda ^{2}\sigma - \mu ^{2}}{\lambda }}, \\ w = \pm \frac{1}{2}\sqrt{ - \lambda - 16\zeta _{1}},\qquad \zeta _{1} = \zeta _{1},\qquad \zeta _{2} = 0. \end{gathered} $$
(5.34)

From (4.6), (5.19), and (5.34) with (5.3), we get the following trigonometric function solutions of (5.1):

$$ \begin{gathered} u_{2} ( x, t ) = \pm \frac{1}{4} \sqrt{ - \lambda - 16\zeta _{1}} + \frac{\sqrt{\lambda }}{4}\frac{A_{1}\cos \sqrt{\lambda } \zeta - A_{2}\sin \sqrt{\lambda } \zeta }{A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda } \\ \hphantom{u_{2} ( x, t ) =}{}\pm \frac{1}{4 \sqrt{\lambda }} \frac{\sqrt{\lambda ^{2}\sigma - \mu ^{2}}}{A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda }, \\ v_{2} ( x, t ) = \frac{\lambda }{4} - \frac{1}{4} \frac{\mu }{A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda } \\ \hphantom{v_{2} ( x, t ) =}{}+ \frac{1}{4}\frac{A_{1}\cos \sqrt{\lambda } \zeta - A_{2}\sin \sqrt{\lambda } \zeta }{ ( A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda )^{2}} \\ \hphantom{v_{2} ( x, t ) =}{}\times \bigl[ A_{1}\lambda \cos \sqrt{\lambda } \zeta - A_{2}\lambda \sin \sqrt{\lambda } \zeta \pm \sqrt{\lambda ^{2}\sigma - \mu ^{2}} \bigr], \end{gathered} $$
(5.35)

where \(\zeta = x \mp \frac{1}{2}\sqrt{ - \lambda - 16\zeta _{1}} \frac{t^{\alpha }}{\alpha } \).

In particular, if we set \(A_{1} = 0\), \(\mu = 0\), and \(A_{2} > 0\) into (5.35), then we get the following periodic wave solutions:

$$ \begin{gathered} u_{2_{1}} ( x, t ) = \pm \frac{1}{4} \sqrt{ - \lambda - 16\zeta _{1}} - \frac{\sqrt{\lambda }}{4} [ \tan \sqrt{ \lambda } \zeta \mp \sec \sqrt{\lambda } \zeta ], \\ v_{2_{1}} ( x, t ) = \frac{\lambda }{4} + \frac{\lambda }{4}\tan \sqrt{ \lambda } \zeta [ \tan \sqrt{\lambda } \zeta \mp \sec \sqrt{\lambda } \zeta ]. \end{gathered} $$
(5.36)

Moreover, if we set \(A_{2} = 0\), \(\mu = 0\), and \(A_{1} > 0\), then we find the periodic wave solutions

$$ \begin{gathered} u_{2_{2}} ( x, t ) = \pm \frac{1}{4} \sqrt{ - \lambda - 16\zeta _{1}} + \frac{\sqrt{\lambda }}{4} [ \cot \sqrt{ \lambda } \zeta \pm \csc \sqrt{\lambda } \zeta ], \\ v_{2_{2}} ( x, t ) = \frac{\lambda }{4} + \frac{\lambda }{4}\cot \sqrt{ \lambda } \zeta [ \cot \sqrt{\lambda } \zeta \pm \csc \sqrt{\lambda } \zeta ]. \end{gathered} $$
(5.37)

Result 3

$$ \begin{gathered} a_{0} = \pm \frac{1}{4}\sqrt{ - \lambda - 16\zeta _{1}},\qquad a_{1} = - \frac{1}{4},\qquad b_{1} = \pm \frac{1}{4}\sqrt{\frac{\lambda ^{2}\sigma - \mu ^{2}}{\lambda }}, \\ \alpha _{0} = \frac{1}{4}\lambda ,\qquad \alpha _{1} = 0,\qquad \alpha _{2} = \frac{1}{4},\qquad \beta _{1} = - \frac{1}{4}\mu , \qquad \beta _{2} = \mp \frac{1}{4}\sqrt{ \frac{\lambda ^{2}\sigma - \mu ^{2}}{\lambda }}, \\ w = \pm \frac{1}{2}\sqrt{ - \lambda - 16\zeta _{1}},\qquad \zeta _{1} = \zeta _{1},\qquad \zeta _{2} = 0. \end{gathered} $$
(5.38)

From result, we have other trigonometric function solutions of (5.1):

$$ \begin{gathered} u_{3} ( x, t ) = \pm \frac{1}{4} \sqrt{ - \lambda - 16\zeta _{1}} - \frac{\sqrt{\lambda }}{4}\frac{A_{1}\cos \sqrt{\lambda } \zeta - A_{2}\sin \sqrt{\lambda } \zeta }{A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda } \\ \hphantom{u_{3} ( x, t ) =}{}\pm \frac{1}{4 \sqrt{\lambda }} \frac{\sqrt{\lambda ^{2}\sigma - \mu ^{2}}}{A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda }, \\ v_{3} ( x, t ) = \frac{\lambda }{4} - \frac{1}{4} \frac{\mu }{A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda }\\ \hphantom{v_{3} ( x, t ) =}{} + \frac{1}{4}\frac{A_{1}\cos \sqrt{\lambda } \zeta - A_{2}\sin \sqrt{\lambda } \zeta }{ ( A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda )^{2}} \\ \hphantom{v_{3} ( x, t ) =}{}\times \bigl[ A_{1}\lambda \cos \sqrt{\lambda } \zeta - A_{2}\lambda \sin \sqrt{\lambda } \zeta \mp \sqrt{\lambda ^{2}\sigma - \mu ^{2}} \bigr], \end{gathered} $$
(5.39)

where \(\zeta = x \mp \frac{1}{2}\sqrt{ - \lambda - 16\zeta _{1}} \frac{t^{\alpha }}{\alpha } \).

Similarly, By taking special values of the parameters we deduce many other periodic wave solutions.

Case 3 When \(\lambda = 0\), substituting (5.19) into (5.5), by (4.3), (4.8), and (4.9) system (5.5) can be exposed as a polynomial in ψ and ϕ. Equating each coefficient of this polynomial to zero, we obtain a system of algebraic equations, which is analyzed by applying Maple software package, and get the following results:

$$\begin{aligned}& \left \{ \textstyle\begin{array}{l} a_{0} = a_{0},\qquad a_{1} = 0,\qquad b_{1} = \pm \frac{1}{2}\sqrt{A_{1}^{2} - 2A_{2}\mu },\qquad w = 2a_{0} \mp \frac{\mu }{2\sqrt{A_{1}^{2} - 2A_{2}\mu }}, \\ \alpha _{0} = - \frac{1}{4}\frac{\mu ^{2}}{A_{1}^{2} - 2A_{2}\mu },\qquad \alpha _{1} = 0,\qquad \alpha _{2} = \frac{1}{2},\qquad \beta _{1} = - \frac{1}{2}\mu ,\qquad \beta _{2} = 0, \\ \zeta _{1} = - a_{0}^{2} + \frac{\mu ^{2} \pm 4a_{0} \mu \sqrt{A_{1}^{2} - 2A_{2}\mu }}{8 ( A_{1}^{2} - 2A_{2}\mu )},\qquad \zeta _{2} = \mp \frac{\mu ^{3}}{8 ( A_{1}^{2} - 2A_{2}\mu )\sqrt{A_{1}^{2} - 2A_{2}\mu }} \end{array}\displaystyle \right \} , \end{aligned}$$
(5.40)
$$\begin{aligned}& \left \{ \textstyle\begin{array}{l} a_{0} = a_{0},\qquad a_{1} = \frac{1}{4},\qquad b_{1} = \pm \frac{1}{4}\sqrt{A_{1}^{2} - 2A_{2}\mu }, \\ \alpha _{0} = 0,\qquad \alpha _{1} = 0,\qquad \alpha _{2} = \frac{1}{4},\qquad \beta _{1} = - \frac{1}{4}\mu ,\qquad \beta _{2} = \pm \frac{1}{4}\sqrt{A_{1}^{2} - 2A_{2}\mu }, \\ w = 2a_{0},\qquad \zeta _{1} = - a_{0}^{2},\qquad \zeta _{2} = 0 \end{array}\displaystyle \right \} , \end{aligned}$$
(5.41)
$$\begin{aligned}& \left \{ \textstyle\begin{array}{l} a_{0} = a_{0},\qquad a_{1} = - \frac{1}{4},\qquad b_{1} = \pm \frac{1}{4}\sqrt{A_{1}^{2} - 2A_{2}\mu }, \\ \alpha _{0} = 0,\qquad \alpha _{1} = 0,\qquad \alpha _{2} = \frac{1}{4},\qquad \beta _{1} = - \frac{1}{4}\mu ,\qquad \beta _{2} = \mp \frac{1}{4}\sqrt{A_{1}^{2} - 2A_{2}\mu }, \\ w = 2a_{0},\qquad \zeta _{1} = - a_{0}^{2},\qquad \zeta _{2} = 0 \end{array}\displaystyle \right \} . \end{aligned}$$
(5.42)

In this case the rational function solutions to the coupled BB (5.1) are:

$$ \begin{gathered} u_{1} ( x, t ) = a_{0} \pm \frac{\sqrt{A_{1}^{2} - 2A_{2}\mu }}{\mu \zeta ^{2} + 2A_{1}\zeta + 2A_{2}}, \\ v_{1} ( x, t ) = - \frac{1}{4}\frac{\mu ^{2}}{A_{1}^{2} - 2A_{2}\mu } + \frac{1}{2} \biggl( \frac{\mu \zeta + A_{1}}{\frac{\mu }{2}\zeta ^{2} + A_{1}\zeta + A_{2}} \biggr)^{2} - \frac{\mu }{\mu \zeta ^{2} + 2A_{1}\zeta + 2A_{2}}, \end{gathered} $$
(5.43)

where \(\zeta =x- ( 2 a_{0} \mp \frac{\mu }{2 \sqrt{A_{1}^{2} -2 A_{2} \mu }} ) \frac{t^{\alpha }}{\alpha }\);

$$ \begin{gathered} u_{2} ( x, t ) = a_{0} + \frac{\mu \zeta + A_{1}}{2\mu \zeta ^{2} + 4A_{1}\zeta + 4A_{2}} \pm \frac{\sqrt{A_{1}^{2} - 2A_{2}\mu }}{2\mu \zeta ^{2} + 4A_{1}\zeta + 4A_{2}}, \\ v_{2} ( x, t ) = - \frac{\mu }{2\mu \zeta ^{2} + 4A_{1}\zeta + 4A_{2}} \\ \hphantom{v_{2} ( x, t ) = }{}+ \frac{1}{4} \frac{\mu \zeta + A_{1}}{ ( \frac{\mu }{2}\zeta ^{2} + A_{1}\zeta + A_{2} )^{2}} \times \Bigl[ \mu \zeta + A_{1} \pm \sqrt {A_{1}^{2} - 2A_{2}\mu } \Bigr], \end{gathered} $$
(5.44)

where \(\zeta =x-2 a_{0} \frac{t^{\alpha }}{\alpha }\); and

$$ \begin{gathered} u_{3} ( x, t ) = a_{0} - \frac{\mu \zeta + A_{1}}{2\mu \zeta ^{2} + 4A_{1}\zeta + 4A_{2}} \pm \frac{\sqrt{A_{1}^{2} - 2A_{2}\mu }}{2\mu \zeta ^{2} + 4A_{1}\zeta + 4A_{2}}, \\ v_{3} ( x, t ) = - \frac{\mu }{2\mu \zeta ^{2} + 4A_{1}\zeta + 4A_{2}}\\ \hphantom{v_{3} ( x, t ) =}{} + \frac{1}{4} \frac{\mu \zeta + A_{1}}{ ( \frac{\mu }{2}\zeta ^{2} + A_{1}\zeta + A_{2} )^{2}} \times \Bigl[ \mu \zeta + A_{1} \mp \sqrt {A_{1}^{2} - 2A_{2}\mu } \Bigr], \end{gathered} $$
(5.45)

where \(\zeta = x - 2a_{0}\frac{t^{\alpha }}{\alpha } \).

These solutions are generalized further and also contain extra free parameters. The definite values of these parameters yield some solutions available in the literature as particular cases. This modification validates the achieved results.

5.2 The nonlinear time-fractional coupled WBK equations

In this section, we use transformation (5.3) to reduce system (5.2) into the following ODEs:

$$ \begin{gathered} w U ' -U U ' - V ' -c U^{\prime \prime } = 0, \\ w V ' - ( UV ) ' -b U^{\prime \prime \prime } +c V^{\prime \prime } = 0. \end{gathered} $$
(5.46)

Integrating Eq. (5.46), we get

$$ \begin{gathered} wU- \frac{1}{2} U^{2} -V-c U ' + \zeta _{1} = 0, \\ wV-UV-b U^{\prime \prime } +c V ' + \zeta _{2} = 0. \end{gathered} $$
(5.47)

By balancing theory, from V and \(U^{2}\) and from \(U''\) and UV appearing in (5.47) we get \(N = 1\) and \(S = 2\). Therefore the formal solutions to Eq. (5.47) are of the following form:

$$ \begin{gathered} U ( \zeta ) = \alpha _{0} + \alpha _{1} \bigl( G' / G \bigr),\quad \alpha _{1} \ne 0, \\ V ( \zeta ) = \beta _{0} + \beta _{1} \bigl( G' / G \bigr) + \beta _{2} \bigl( G' / G \bigr)^{2},\quad \beta _{2} \ne 0. \end{gathered} $$
(5.48)

Substituting (5.48) into (5.47) and applying the same procedure discussed in Sect. 3, we get the following results:

$$ \begin{gathered} \alpha _{0} = \mp \lambda \sqrt{c^{2} + b} + w,\qquad \alpha _{1} = \mp 2 \sqrt{c^{2} + b},\\ \beta _{0} = 2\mu \bigl( \mp c \sqrt{c^{2} + b} - c^{2} - b \bigr),\qquad \beta _{1} = 2 \lambda \bigl( \mp c\sqrt{c^{2} + b} - c^{2} - b \bigr), \\ \beta _{2} = 2 \bigl( \mp c\sqrt{c^{2} + b} - c^{2} - b \bigr),\qquad w = w, \\ \xi _{1} = \frac{1}{2} \bigl( \lambda ^{2} - 4\mu \bigr) \bigl( c^{2} + b \bigr) - \frac{1}{2}w^{2},\qquad \xi _{2} = 0. \end{gathered} $$
(5.49)

By substituting (5.49) and general solutions of Eq. (3.5) into (5.48) with (5.3) we deduce three types of solitary wave solutions of the coupled WBK Eq. (5.2).

Type I: When \(( \lambda ^{2} - 4\mu ) > 0\), we acquire the hyperbolic function solutions of (5.2):

$$ \begin{gathered} u_{1} ( x, t ) = w \mp \sqrt{ \bigl( \lambda ^{2} - 4\mu \bigr) \bigl( c^{2} + b \bigr)} \biggl( \frac{B_{1}\cosh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} + B_{2}\sinh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2}}{B_{1}\sinh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} + B_{2}\cosh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2}} \biggr), \\ v_{1} ( x, t ) = \frac{\lambda ^{2} - 4\mu }{2} \bigl( \mp c\sqrt{c^{2} + b} - c^{2} - b \bigr) \\ \hphantom{v_{1} ( x, t ) =}{}\times \biggl[ \biggl( \frac{B_{1}\cosh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} + B_{2}\sinh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2}}{B_{1}\sinh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} + B_{2}\cosh \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2}} \biggr)^{2} - 1 \biggr], \end{gathered} $$
(5.50)

where \(\zeta = x - w \frac{t^{\alpha }}{\alpha } \).

Here \(B_{1}\) and \(B_{2}\) are integral constants. Therefore we can randomly select their values. Thus, if we select \(B_{1} = 0\), \(B_{2} \ne 0\), then we accomplish the kink and bell-shape solitary wave solutions of (5.2) of the form

$$ \begin{gathered} u_{1_{1}} (x, t)=w\mp \sqrt{\bigl( \lambda ^{2} -4\mu \bigr) \bigl( c^{2} +b\bigr)} \tanh \biggl( \sqrt{ \lambda ^{2} -4\mu } \frac{\zeta }{2} \biggr), \\ v_{1_{1}} ( x, t ) = \frac{\lambda ^{2} -4\mu }{2} \bigl( \pm c \sqrt{c^{2} +b} + c^{2} +b \bigr) \operatorname{sech}^{2} \biggl( \sqrt{\lambda ^{2} -4\mu } \frac{\zeta }{2} \biggr). \end{gathered} $$
(5.51)

Moreover, if we select \(B_{2} = 0\), \(B_{1} \ne 0\), then we obtain the singular solitary wave solutions of (5.2):

$$ \begin{gathered} u_{1_{2}} ( x, t ) = w \mp \sqrt{ \bigl( \lambda ^{2} - 4\mu \bigr) \bigl( c^{2} + b \bigr)} \coth \biggl( \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} \biggr), \\ v_{1_{2}} ( x, t ) = \frac{\lambda ^{2} - 4\mu }{2} \bigl( \mp c\sqrt{c^{2} + b} - c^{2} - b \bigr)\operatorname{csch}^{2} \biggl( \sqrt{ \lambda ^{2} - 4\mu } \frac{\zeta }{2} \biggr). \end{gathered} $$
(5.52)

In addition, if we select \(B_{2} \ne 0\), \(B_{2}^{2} > B_{1}^{2}\), then we get the solitary wave solutions of (5.2):

$$ \begin{gathered} u_{1_{3}} ( x, t ) = w \mp \sqrt{ \bigl( \lambda ^{2} - 4\mu \bigr) \bigl( c^{2} + b \bigr)} \tanh \biggl( \zeta _{0} + \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} \biggr), \\ v_{1_{3}} ( x, t ) = \frac{\lambda ^{2} - 4\mu }{2} \bigl( \pm c\sqrt{c^{2} + b} + c^{2} + b \bigr)\operatorname{sech}^{2} \biggl( \zeta _{0} + \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} \biggr), \end{gathered} $$
(5.53)

where \(\zeta _{0} = \tanh ^{ - 1}\frac{B_{1}}{B_{2}}\).

However, if we select \(B_{1} \ne 0\), \(B_{1}^{2} > B_{2}^{2}\), then we carry out the solitary wave solutions of (5.2):

$$ \begin{gathered} u_{1_{4}} ( x, t ) = w \mp \sqrt{ \bigl( \lambda ^{2} - 4\mu \bigr) \bigl( c^{2} + b \bigr)} \coth \biggl( \zeta _{0} + \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} \biggr), \\ v_{1_{4}} ( x, t ) = \frac{\lambda ^{2} - 4\mu }{2} \bigl( \mp c\sqrt{c^{2} + b} - c^{2} - b \bigr)\operatorname{csch}^{2} \biggl( \zeta _{0} + \sqrt{\lambda ^{2} - 4\mu } \frac{\zeta }{2} \biggr), \end{gathered} $$
(5.54)

where \(\zeta _{0} = \tanh ^{ - 1}\frac{B_{2}}{B_{1}}\).

Type II. When \(( \lambda ^{2} - 4\mu ) < 0\), we get trigonometric function solutions of (5.2) of the form

$$ \begin{gathered} u_{2} ( x, t ) = w \mp \sqrt{ \bigl( 4\mu - \lambda ^{2} \bigr) \bigl( c^{2} + b \bigr)} \biggl( \frac{ - B_{1}\sin \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} + B_{2}\cos \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2}}{B_{1}\cos \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} + B_{2}\sin \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2}} \biggr), \\ v_{2} ( x, t ) = \frac{4\mu - \lambda ^{2}}{2} \bigl( \mp c\sqrt{c^{2} + b} - c^{2} - b \bigr)\\ \hphantom{v_{2} ( x, t ) =}{}\times \biggl[ \biggl( \frac{ - B_{1}\sin \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} + B_{2}\cos \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2}}{B_{1}\cos \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} + B_{2}\sin \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2}} \biggr)^{2} + 1 \biggr]. \end{gathered} $$
(5.55)

We might accept \(B_{1} = 0\), \(B_{2} \ne 0\), Since \(B_{1}\) and \(B_{2}\) are integral constants, we find the following periodic wave solutions of (5.2):

$$ \begin{gathered} u_{2_{1}} (x, t)=w\mp \sqrt{\bigl(4\mu - \lambda ^{2} \bigr) \bigl( c^{2} +b\bigr)} \cot \biggl( \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr), \\ v_{2_{1}} ( x, t ) = \frac{4\mu - \lambda ^{2}}{2} \bigl( \mp c \sqrt{c^{2} +b} - c^{2} -b \bigr) \operatorname{csc}^{2} \biggl( \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr). \end{gathered} $$
(5.56)

In addition, if we put \(B_{2} = 0\), \(B_{1} \ne 0\), then we find the following the periodic wave solutions of (5.2):

$$ \begin{gathered} u_{2_{2}} (x, t)=w\pm \sqrt{\bigl(4\mu - \lambda ^{2} \bigr) \bigl( c^{2} +b\bigr)} \tan \biggl( \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr), \\ v_{2_{2}} ( x, t ) = \frac{4\mu - \lambda ^{2}}{2} \bigl( \mp c \sqrt{c^{2} +b} - c^{2} -b \bigr) \operatorname{sec}^{2} \biggl( \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr). \end{gathered} $$
(5.57)

Besides, if we set \(B_{2} \ne 0\), \(B_{2}^{2} > B_{1}^{2}\), then we achieve the following periodic wave solutions of (5.2):

$$ \begin{gathered} u_{2_{3}} ( x, t ) = w \mp \sqrt{ \bigl( 4\mu - \lambda ^{2} \bigr) \bigl( c^{2} + b \bigr)} \cot \biggl( \zeta _{0} + \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr), \\ v_{2_{3}} ( x, t ) = \frac{4\mu - \lambda ^{2}}{2} \bigl( \mp c\sqrt{c^{2} + b} - c^{2} - b \bigr)\csc ^{2} \biggl( \zeta _{0} + \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr), \end{gathered} $$
(5.58)

where \(\zeta _{0} = \tan ^{ - 1}\frac{B_{1}}{B_{2}}\).

Additionally, if we set \(B_{1} \ne 0\), \(B_{1}^{2} > B_{2}^{2}\), then we achieve the periodic wave solutions of (5.2):

$$ \begin{gathered} u_{2_{4}} ( x, t ) = w \mp \sqrt{ \bigl( 4\mu - \lambda ^{2} \bigr) \bigl( c^{2} + b \bigr)} \tan \biggl( \zeta _{0} - \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr), \\ v_{2_{4}} ( x, t ) = \frac{4\mu - \lambda ^{2}}{2} \bigl( \mp c\sqrt{c^{2} + b} - c^{2} - b \bigr)\sec ^{2} \biggl( \zeta _{0} - \sqrt{4\mu - \lambda ^{2}} \frac{\zeta }{2} \biggr), \end{gathered} $$
(5.59)

where \(\zeta _{0} = \tan ^{ - 1}\frac{B_{2}}{B_{1}}\).

Type III: When \(( \lambda ^{2} - 4\mu ) = 0\), we find the following rational function solutions of (5.2):

$$ \begin{gathered} u_{3} ( x, t ) = w \mp \frac{2B_{2}\sqrt{c^{2} + b}}{B_{1} + B_{2}\zeta }, \\ v_{3} ( x, t ) = 2 \bigl( \mp c\sqrt{c^{2} + b} - c^{2} - b \bigr) \biggl( \frac{ B_{2}}{B_{1} + B_{2}\zeta } \biggr)^{2}. \end{gathered} $$
(5.60)

Now we examine the coupled WBK equations by means of the \(( G' / G, 1 / G )\)-expansion method. For the balance number attained in the earlier section for this equation, the shape of the solution is of the form

$$ \begin{gathered} U ( \zeta ) = a_{0} + a_{1} \phi + b_{1} \psi , \\ V ( \zeta ) = \alpha _{0} + \alpha _{1} \phi + \alpha _{2} \phi ^{2} + \beta _{1} \psi + \beta _{2} \phi \psi , \end{gathered} $$
(5.61)

where \(a_{0}\), \(a_{1}\), \(b_{1}\), \(\alpha _{0}\), \(\alpha _{1}\), \(\alpha _{2}\), \(\beta _{1}\), and \(\beta _{2}\) are constants to be determined. Now we take into account the following three cases.

Case 1: When \(\lambda < 0\), inserting (5.61) into (5.47), by (4.3)–(4.5) system (5.47) will be transfigured to a polynomial in ψ and ϕ. A system of algebraic equations can be obtained by equalizing the coefficients of this polynomial for the unknown \(a_{0}\), \(a_{1}\), \(b_{1}\), \(\alpha _{0}\), \(\alpha _{1}\), \(\alpha _{2}\), \(\beta _{1}\), \(\beta _{2}\), w, λ, μ, σ, \(\zeta _{1}\), and \(\zeta _{2}\). Solving the algebraic equations via Maple software package, we get three different sets of solution.

Result 1

$$ \begin{gathered} a_{0} = w,\qquad a_{1} = 0,\qquad b_{1} = b_{1},\qquad \alpha _{0} = \frac{b_{1}^{2}}{4\sigma },\qquad \alpha _{1} = 0, \\ \alpha _{2} = \frac{b_{1}^{2}}{2\lambda \sigma },\qquad \beta _{1} = 0,\qquad \beta _{2} = b_{1}c,\qquad b = - \frac{4c^{2}\lambda \sigma + b_{1}^{2}}{4\lambda \sigma }, \\ w = w,\qquad \mu = 0,\qquad \zeta _{1} = - \frac{2\sigma w^{2} + b_{1}^{2}}{4\sigma },\qquad \zeta _{2} = 0. \end{gathered} $$
(5.62)

From (4.4), (5.61), and (5.62), with the help of (5.3), we deduce the following hyperbolic function solutions of (5.2):

$$ \begin{gathered} u_{1} ( x, t ) = w + \frac{b_{1}}{A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta }, \\ v_{1} ( x, t ) = \frac{b_{1}^{2}}{4\sigma } - \frac{A_{1}b_{1}\cosh \sqrt{ - \lambda } \zeta + A_{2}b_{1}\sinh \sqrt{ - \lambda } \zeta }{ ( A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta )^{2}} \\ \hphantom{v_{1} ( x, t ) =}{}\times \biggl[ \frac{b_{1}}{2\sigma } ( A_{1}\cosh \sqrt{ - \lambda } \zeta + A_{2}\sinh \sqrt{ - \lambda } \zeta ) - c\sqrt{ - \lambda } \biggr], \end{gathered} $$
(5.63)

where \(\zeta = x - w\frac{t^{\alpha }}{\alpha } \) and \(\sigma = A_{1}^{2} - A_{2}^{2}\).

In particular, by taking \(A_{1} = 0\) and \(A_{2} \ne 0\) in (5.63), we attain the following solitary wave solution:

$$ \begin{gathered} u_{1_{1}} (x, t)=w+ \frac{b_{1}}{A_{2}} \operatorname{sech} \sqrt{-\lambda } \zeta , \\ v_{1_{1}} ( x, t ) =- \frac{b_{1}^{2}}{4 A_{2}^{2}} + \frac{b_{1}}{A_{2}} \tanh \sqrt{-\lambda } \zeta \biggl[ \frac{b_{1}}{2 A_{2}} \tanh \sqrt{-\lambda } \zeta +c \sqrt{-\lambda } \operatorname{sech} \sqrt{-\lambda } \zeta \biggr]. \end{gathered} $$
(5.64)

When \(A_{2} = 0\) and \(A_{1} \ne 0\), we obtain the previously mentioned wave solutions

$$ \begin{gathered} u_{1_{2}} ( x, t ) = w + \frac{b_{1}}{A_{1}} \operatorname{csch} \sqrt{ - \lambda } \zeta , \\ v_{1_{2}} ( x, t ) = \frac{b_{1}^{2}}{4A_{1}^{2}} - \frac{b_{1}}{A_{1}}\coth \sqrt{ - \lambda } \zeta \biggl[ \frac{b_{1}}{2A_{1}}\coth \sqrt{ - \lambda } \zeta - c\sqrt{ - \lambda } \operatorname{csch} \sqrt{ - \lambda } \zeta \biggr]. \end{gathered} $$
(5.65)

Result 2

$$ \begin{gathered} a_{0} = w,\qquad a_{1} = a_{1},\qquad b_{1} = \pm a_{1}\sqrt{ - \frac{\lambda ^{2}\sigma + \mu ^{2}}{\lambda }},\\ \alpha _{0} = - a_{1}\lambda ( a_{1} - c ),\qquad \alpha _{1} = 0,\qquad\alpha _{2} = - a_{1} ( a_{1} - c ), \\ \beta _{1} = a_{1}\mu ( a_{1} - c ),\qquad \beta _{2} = \mp a_{1} ( a_{1} - c )\sqrt{ - \frac{\lambda ^{2}\sigma + \mu ^{2}}{\lambda }}, \\ b = a_{1}^{2} - c^{2},\qquad w = w,\qquad \zeta _{1} = - \frac{1}{2} \bigl( w^{2} + \lambda a_{1}^{2} \bigr),\qquad \zeta _{2} = 0. \end{gathered} $$
(5.66)

From (4.4), (5.61), and (5.66) with (5.3) we find the following hyperbolic function solutions of (5.2):

$$ \begin{gathered} u_{2} ( x, t ) = w + \frac{a_{1}}{A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda } \\ \hphantom{u_{2} ( x, t ) = }{}\times \biggl[ A_{1}\sqrt{ - \lambda } \cosh \sqrt{ - \lambda } \zeta + A_{2}\sqrt{ - \lambda } \sinh \sqrt{ - \lambda } \zeta \pm \frac{\sqrt{\lambda ^{2}\sigma + \mu ^{2}}}{\sqrt{ - \lambda }} \biggr], \\ v_{2} ( x, t ) = - a_{1}\lambda ( a_{1} - c ) + \frac{a_{1}\mu ( a_{1} - c )}{A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda } \\ \hphantom{v_{2} ( x, t ) =}{}+ \frac{a_{1} ( a_{1} - c ) ( A_{1}\cosh \sqrt{ - \lambda } \zeta + A_{2}\sinh \sqrt{ - \lambda } \zeta )}{ ( A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda )^{2}} \\ \hphantom{v_{2} ( x, t ) =}{}\times \bigl[ A_{1}\lambda \cosh \sqrt{ - \lambda } \zeta + A_{2}\lambda \sinh \sqrt{ - \lambda } \zeta \mp \sqrt{\lambda ^{2}\sigma + \mu ^{2}} \bigr], \end{gathered} $$
(5.67)

where \(\zeta = x - w\frac{t^{\alpha }}{\alpha } \).

In particular, if we substitute \(A_{1} = 0\), \(\mu = 0\), and \(A_{2} > 0\) into (5.67), we get the following wave solutions:

$$ \begin{gathered} u_{2_{1}} (x, t)=w+ a_{1} \sqrt{- \lambda } [ \tanh \sqrt{-\lambda } \zeta \pm i \operatorname{sech} \sqrt{-\lambda } \zeta ], \\ v_{2_{1}} ( x, t ) =- a_{1} \lambda ( a_{1} -c ) + a_{1} \lambda ( a_{1} -c ) \tanh \sqrt{-\lambda } \zeta [ \tanh \sqrt{-\lambda } \zeta \pm i \operatorname{sech} \sqrt{-\lambda } \zeta ]. \end{gathered} $$
(5.68)

On the other hand, if we introduce \(A_{2} = 0\), \(\mu = 0\), and \(A_{1} > 0\), then we get the following wave solutions:

$$ \begin{gathered} u_{2_{2}} ( x, t ) = w + a_{1} \sqrt{ - \lambda } ( \coth \sqrt{ - \lambda } \zeta \pm \operatorname{csch} \sqrt{ - \lambda } \zeta ), \\ v_{2_{2}} ( x, t ) = - a_{1}\lambda ( a_{1} - c ) + a_{1}\lambda ( a_{1} - c )\coth \sqrt{ - \lambda } \zeta ( \coth \sqrt{ - \lambda } \zeta \pm \operatorname{csch} \sqrt{ - \lambda } \zeta ). \end{gathered} $$
(5.69)

Result 3

$$ \begin{gathered} a_{0} = a_{0},\qquad a_{1} = 0,\qquad b_{1} = - \frac{2 ( a_{0} - w ) ( \lambda ^{2}\sigma + \mu ^{2} )}{\lambda \mu },\\ \alpha _{0} = \frac{ ( a_{0} - w )^{2} ( \lambda ^{2}\sigma + 2\mu ^{2} )}{\mu ^{2}},\qquad\alpha _{1} = 0, \\ \alpha _{2} = \frac{2 ( a_{0} - w )^{2} ( \lambda ^{2}\sigma + \mu ^{2} )}{\lambda \mu ^{2}},\qquad \beta _{1} = - \frac{2 ( a_{0} - w )^{2} ( \lambda ^{2}\sigma + \mu ^{2} )}{\lambda \mu }, \\ \beta _{2} = - \frac{2c ( a_{0} - w ) ( \lambda ^{2}\sigma + \mu ^{2} )}{\lambda \mu },\qquad b = - \frac{ ( a_{0} - w )^{2} ( \lambda ^{2}\sigma + \mu ^{2} ) + c^{2}\lambda \mu ^{2}}{\lambda \mu ^{2}}, \\ w = w,\qquad \zeta _{1} = - \frac{a_{0} ( a_{0} - 2w ) ( 2\lambda ^{2}\sigma - \mu ^{2} ) + 2\lambda ^{2}\sigma w^{2}}{2\mu ^{2}},\qquad \zeta _{2} = - \frac{\lambda ^{2}\sigma ( a_{0} - w )^{3}}{\mu ^{2}}. \end{gathered} $$
(5.70)

For the values of the parameters organized in (5.70), we carry out other hyperbolic function solutions of (5.2) given in the underneath:

$$ \begin{gathered} u_{3} ( x, t ) = a_{0} - \frac{2 ( a_{0} - w ) ( \lambda ^{2}\sigma + \mu ^{2} )}{A_{1}\lambda \mu \sinh \sqrt{ - \lambda } \zeta + A_{2}\lambda \mu \cosh \sqrt{ - \lambda } \zeta + \mu ^{2}}, \\ v_{3} ( x, t ) = \frac{1}{\mu ^{2}} ( a_{0} - w )^{2} \bigl( \lambda ^{2}\sigma + 2\mu ^{2} \bigr) \\ \hphantom{v_{3} ( x, t ) =}{}- \frac{2 ( a_{0} - w )^{2} ( \lambda ^{2}\sigma + \mu ^{2} )}{A_{1}\lambda \mu \sinh \sqrt{ - \lambda } \zeta + A_{2}\lambda \mu \cosh \sqrt{ - \lambda } \zeta + \mu ^{2}} \\ \hphantom{v_{3} ( x, t ) =}{}- \frac{2}{\mu } \frac{ ( a_{0} - w ) ( \lambda ^{2}\sigma + \mu ^{2} ) ( A_{1}\cosh \sqrt{ - \lambda } \zeta + A_{2}\sinh \sqrt{ - \lambda } \zeta )}{ ( A_{1}\sinh \sqrt{ - \lambda } \zeta + A_{2}\cosh \sqrt{ - \lambda } \zeta + \mu / \lambda )^{2}} \\ \hphantom{v_{3} ( x, t ) =}{}\times \biggl[ \frac{1}{\mu } ( a_{0} - w ) ( A_{1} \cosh \sqrt{ - \lambda } \zeta + A_{2}\sinh \sqrt{ - \lambda } \zeta ) - \frac{c}{\sqrt{ - \lambda }} \biggr], \end{gathered} $$
(5.71)

where \(\zeta = x - w\frac{t^{\alpha }}{\alpha } \).

Similarly, by taking special values of the parameters we might attain many other solitary wave solutions, but for simplicity, the solutions are not designated here.

Case 2: When \(\lambda > 0\), in this case, solving the system of algebraic equations with Maple software package, we obtain three different sets of results.

Result 1

$$ \begin{gathered} a_{0} = w,\qquad a_{1} = 0,\qquad b_{1} = b_{1},\qquad \alpha _{0} = - \frac{b_{1}^{2}}{4\sigma },\qquad \alpha _{1} = 0, \\ \alpha _{2} = - \frac{b_{1}^{2}}{2\lambda \sigma },\qquad \beta _{1} = 0,\qquad \beta _{2} = b_{1}c,\qquad b = \frac{ - 4c^{2}\lambda \sigma + b_{1}^{2}}{4\lambda \sigma }, \\ w = w,\qquad \mu = 0,\qquad \zeta _{1} = \frac{ - 2\sigma w^{2} + b_{1}^{2}}{4\sigma },\qquad \zeta _{2} = 0. \end{gathered} $$
(5.72)

For these values, the trigonometric function solutions of (5.2) are:

$$ \begin{gathered} u_{1} ( x, t ) = w + \frac{b_{1}}{A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta }, \\ v_{1} ( x, t ) = - \frac{b_{1}^{2}}{4\sigma } - \frac{A_{1}b_{1}\cos \sqrt{\lambda } \zeta - A_{2}b_{1}\sin \sqrt{\lambda } \zeta }{ ( A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta )^{2}} \\ \hphantom{v_{1} ( x, t ) =}{}\times \biggl[ \frac{b_{1}}{2\sigma } ( A_{1}\cos \sqrt{\lambda } \zeta - A_{2}\sin \sqrt{\lambda } \zeta ) - c\sqrt{\lambda } \biggr], \end{gathered} $$
(5.73)

where \(\zeta = x - w\frac{t^{\alpha }}{\alpha } \) and \(\sigma = A_{1}^{2} + A_{2}^{2}\).

In particular, by taking \(A_{1} = 0\) and \(A_{2} \ne 0\) in (5.73), we determine the following periodic wave solutions:

$$ \begin{gathered} u_{1_{1}} ( x, t ) = w + \frac{b_{1}}{A_{2}} \sec \sqrt{\lambda } \zeta , \\ v_{1_{1}} ( x, t ) = - \frac{b_{1}^{2}}{4A_{2}^{2}} - \frac{b_{1}}{A_{2}}\tan \sqrt{\lambda } \zeta \biggl[ \frac{b_{1}}{2A_{2}}\tan \sqrt{\lambda } \zeta + c \sqrt{\lambda } \sec \sqrt{\lambda } \zeta \biggr], \end{gathered} $$
(5.74)

Alternatively, taking \(A_{2} = 0\) and \(A_{1} \ne 0\), we determine the following periodic wave solutions:

$$ \begin{gathered} u_{1_{2}} ( x, t ) = w + \frac{b_{1}}{A_{1}} \csc \sqrt{\lambda } \zeta , \\ v_{1_{2}} ( x, t ) = - \frac{b_{1}^{2}}{4A_{1}^{2}} - \frac{b_{1}}{A_{1}}\cot \sqrt{\lambda } \zeta \biggl[ \frac{b_{1}}{2A_{1}}\cot \sqrt{\lambda } \zeta - c \sqrt{\lambda } \csc \sqrt{\lambda } \zeta \biggr]. \end{gathered} $$
(5.75)

Result 2

$$ \begin{gathered} a_{0} = w,\qquad a_{1} = a_{1},\qquad b_{1} = \pm a_{1}\sqrt{ \frac{\lambda ^{2}\sigma - \mu ^{2}}{\lambda }},\\ \alpha _{0} = - a_{1}\lambda ( a_{1} - c ),\qquad \alpha _{1} = 0,\qquad\alpha _{2} = - a_{1} ( a_{1} - c ), \\ \beta _{1} = a_{1}\mu ( a_{1} - c ),\qquad \beta _{2} = \mp a_{1} ( a_{1} - c )\sqrt{ \frac{\lambda ^{2}\sigma - \mu ^{2}}{\lambda }}, \\ b = a_{1}^{2} - c^{2},\qquad w = w,\qquad \zeta _{1} = - \frac{1}{2} \bigl( w^{2} + \lambda a_{1}^{2} \bigr),\qquad \zeta _{2} = 0. \end{gathered} $$
(5.76)

In this case, the trigonometric function solutions of (5.2) are:

$$ \begin{gathered} u_{2} ( x, t ) = w + \frac{a_{1}}{A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda } \\ \hphantom{u_{2} ( x, t ) =}{}\times \biggl[ A_{1}\sqrt{\lambda } \cos \sqrt{\lambda } \zeta - A_{2}\sqrt{\lambda } \sin \sqrt{\lambda } \zeta \pm \frac{\sqrt{\lambda ^{2}\sigma - \mu ^{2}}}{\sqrt{\lambda }} \biggr], \\ v_{2} ( x, t ) = - a_{1}\lambda ( a_{1} - c ) + \frac{a_{1}\mu ( a_{1} - c )}{A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda }\\ \hphantom{v_{2} ( x, t ) =}{} - \frac{a_{1} ( a_{1} - c ) ( A_{1}\cos \sqrt{\lambda } \zeta - A_{2}\sin \sqrt{\lambda } \zeta )}{ ( A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda )^{2}} \\ \hphantom{v_{2} ( x, t ) =}{}\times \bigl[ A_{1}\lambda \cos \sqrt{\lambda } \zeta - A_{2}\lambda \sin \sqrt{\lambda } \zeta \pm \sqrt{\lambda ^{2}\sigma - \mu ^{2}} \bigr], \end{gathered} $$
(5.77)

where \(\zeta = x - w\frac{t^{\alpha }}{\alpha } \).

For the values \(A_{1} = 0\), \(\mu = 0\), and \(A_{2} > 0\), of the parameters, we get the following periodic wave solutions:

$$ \begin{gathered} u_{2_{1}} (x, t)=w- a_{1} \sqrt{ \lambda } [ \tan \sqrt{\lambda } \zeta \mp \operatorname{sec} \sqrt{\lambda } \zeta ], \\ v_{2_{1}} ( x, t ) =- a_{1} \lambda ( a_{1} -c ) - a_{1} \lambda ( a_{1} -c ) \tan \sqrt{\lambda } \zeta [ \tan \sqrt{\lambda } \zeta \mp \operatorname{sec} \sqrt{\lambda } \zeta ]. \end{gathered} $$
(5.78)

Moreover, for the values \(A_{2} = 0\), \(\mu = 0\), and \(A_{1} > 0\), we get the following periodic wave solutions:

$$ \begin{gathered} u_{2_{2}} ( x, t ) = w + a_{1} \sqrt{\lambda } [ \cot \sqrt{\lambda } \zeta \pm \csc \sqrt{\lambda } \zeta ], \\ v_{2_{2}} ( x, t ) = - a_{1}\lambda ( a_{1} - c ) - a_{1}\lambda ( a_{1} - c )\cot \sqrt{\lambda } \zeta [ \cot \sqrt{\lambda } \zeta \pm \csc \sqrt{\lambda } \zeta ]. \end{gathered} $$
(5.79)

Result 3

$$ \begin{gathered} a_{0} = a_{0},\qquad a_{1} = 0,\qquad b_{1} = \frac{2 ( a_{0} - w ) ( \lambda ^{2}\sigma - \mu ^{2} )}{\lambda \mu },\\ \alpha _{0} = - \frac{ ( a_{0} - w )^{2} ( \lambda ^{2}\sigma - 2\mu ^{2} )}{\mu ^{2}},\qquad \alpha _{1} = 0, \\ \alpha _{2} = - \frac{2 ( a_{0} - w )^{2} ( \lambda ^{2}\sigma - \mu ^{2} )}{\lambda \mu ^{2}},\qquad \beta _{1} = \frac{2 ( a_{0} - w )^{2} ( \lambda ^{2}\sigma - \mu ^{2} )}{\lambda \mu }, \\ \beta _{2} = \frac{2c ( a_{0} - w ) ( \lambda ^{2}\sigma - \mu ^{2} )}{\lambda \mu },\qquad b = \frac{ ( a_{0} - w )^{2} ( \lambda ^{2}\sigma - \mu ^{2} ) - c^{2}\lambda \mu ^{2}}{\lambda \mu ^{2}},\qquad w = w, \\ \zeta _{1} = \frac{a_{0} ( a_{0} - 2w ) ( 2\lambda ^{2}\sigma + \mu ^{2} ) + 2\lambda ^{2}\sigma w^{2}}{2\mu ^{2}},\qquad \zeta _{2} = \frac{\lambda ^{2}\sigma ( a_{0} - w )^{3}}{\mu ^{2}}. \end{gathered} $$
(5.80)

For the values in (5.80), we establish other trigonometric function solutions of (5.2):

$$ \begin{gathered} u_{3} ( x, t ) = a_{0} + \frac{2 ( a_{0} - w ) ( \lambda ^{2}\sigma - \mu ^{2} )}{A_{1}\lambda \mu \sin \sqrt{\lambda } \zeta + A_{2}\lambda \mu \cos \sqrt{\lambda } \zeta + \mu ^{2}}, \\ v_{3} ( x, t ) = - \frac{1}{\mu ^{2}} ( a_{0} - w )^{2} \bigl( \lambda ^{2}\sigma - 2\mu ^{2} \bigr) + \frac{2 ( a_{0} - w )^{2} ( \lambda ^{2}\sigma - \mu ^{2} )}{A_{1}\lambda \mu \sin \sqrt{\lambda } \zeta + A_{2}\lambda \mu \cos \sqrt{\lambda } \zeta + \mu ^{2}} \\ \hphantom{v_{3} ( x, t ) =}{}- \frac{2}{\mu } \frac{ ( a_{0} - w ) ( \lambda ^{2}\sigma - \mu ^{2} ) ( A_{1}\cos \sqrt{\lambda } \zeta - A_{2}\sin \sqrt{\lambda } \zeta )}{ ( A_{1}\sin \sqrt{\lambda } \zeta + A_{2}\cos \sqrt{\lambda } \zeta + \mu / \lambda )^{2}} \\ \hphantom{v_{3} ( x, t ) =}{}\times \biggl[ \frac{1}{\mu } ( a_{0} - w ) ( A_{1} \cos \sqrt{\lambda } \zeta - A_{2}\sin \sqrt{\lambda } \zeta ) - \frac{c}{\sqrt{\lambda }} \biggr], \end{gathered} $$
(5.81)

where \(\zeta = x - w\frac{t^{\alpha }}{\alpha } \).

If the parameters receive diverse definite values, then we might accomplish many other periodic wave solutions, but for succinctness, these solutions are not displayed her.

Case 3 When \(\lambda = 0\), in this case, solving the system of algebraic equations with Maple software package, we get the following results:

$$\begin{aligned}& \left \{ \textstyle\begin{array}{l} a_{0} = w,\qquad a_{1} = \pm \frac{b_{1}}{\sqrt{A_{1}^{2} - 2A_{2}\mu }},\qquad b_{1} = b_{1},\qquad \alpha _{0} = 0,\qquad \alpha _{1} = 0, \\ \alpha _{2} = \pm \frac{b_{1}c}{\sqrt{A_{1}^{2} - 2A_{2}\mu }} - \frac{b_{1}^{2}}{A_{1}^{2} - 2A_{2}\mu },\qquad \beta _{1} = \mp \frac{b_{1}\mu c}{\sqrt{A_{1}^{2} - 2A_{2}\mu }} + \frac{b_{1}^{2}\mu }{A_{1}^{2} - 2A_{2}\mu }, \\ \beta _{2} = \mp \frac{b_{1}^{2}}{\sqrt{A_{1}^{2} - 2A_{2}\mu }} + b_{1}c,\qquad b = \frac{b_{1}^{2}}{A_{1}^{2} - 2A_{2}\mu } - c^{2},\\ w = w,\qquad \zeta _{1} = - \frac{1}{2}w^{2},\qquad \zeta _{2} = 0. \end{array}\displaystyle \right \} , \end{aligned}$$
(5.82)
$$\begin{aligned}& \left \{ \textstyle\begin{array}{l} a_{0} = a_{0},\qquad a_{1} = 0,\qquad b_{1} = \frac{2}{\mu } ( a_{0} - w ) ( A_{1}^{2} - 2A_{2}\mu ), \\ \alpha _{0} = ( a_{0} - w )^{2},\qquad \alpha _{1} = 0, \qquad \alpha _{2} = - \frac{2}{\mu ^{2}} ( a_{0} - w )^{2} ( A_{1}^{2} - 2A_{2}\mu ), \\ \beta _{1} = \frac{2}{\mu } ( a_{0} - w )^{2} ( A_{1}^{2} - 2A_{2}\mu ),\qquad \beta _{2} = \frac{2c}{\mu } ( a_{0} - w ) ( A_{1}^{2} - 2A_{2}\mu ), \\ b = \frac{1}{\mu ^{2}} ( a_{0} - w )^{2} ( A_{1}^{2} - 2A_{2}\mu ) - c^{2},\qquad w = w,\\ \zeta _{1} = \frac{3}{2}a_{0}^{2} - 3a_{0}w + w^{2},\qquad \zeta _{2} = ( a_{0} - w )^{3}. \end{array}\displaystyle \right \} , \end{aligned}$$
(5.83)

In this case, the rational function solutions of (5.2) are

$$ \begin{gathered} u_{1} ( x, t ) = w + \frac{b_{1}}{\frac{\mu }{2}\zeta ^{2} + A_{1}\zeta + A_{2}} \times \biggl[ 1 \pm \frac{\mu \zeta + A_{1}}{\sqrt{A_{1}^{2} - 2A_{2}\mu }} \biggr], \\ v_{1} ( x, t ) = \frac{b_{1}\mu }{\frac{\mu }{2}\zeta ^{2} + A_{1}\zeta + A_{2}} \times \biggl[ \frac{b_{1}}{A_{1}^{2} - 2A_{2}\mu } \mp \frac{c}{\sqrt{A_{1}^{2} - 2A_{2}\mu }} \biggr] \\ \hphantom{v_{1} ( x, t ) = }{}+ \frac{b_{1} ( \mu \zeta + A_{1} )}{ ( \frac{\mu }{2}\zeta ^{2} + A_{1}\zeta + A_{2} )^{2}} \times \biggl[ c \mp \frac{b_{1} - c\mu \zeta - A_{1}c}{\sqrt{A_{1}^{2} - 2A_{2}\mu }} - \frac{b_{1} ( \mu \zeta + A_{1} )}{A_{1}^{2} - 2A_{2}\mu } \biggr], \end{gathered} $$
(5.84)

where \(\zeta =x-w \frac{t^{\alpha }}{\alpha }\); and

$$ \begin{gathered} u_{2} ( x, t ) = a_{0} + \frac{2}{\mu } \frac{ ( a_{0} - w ) ( A_{1}^{2} - 2A_{2}\mu )}{\frac{\mu }{2}\zeta ^{2} + A_{1}\zeta + A_{2}}, \\ v_{2} ( x, t ) = ( a_{0} - w )^{2} + \frac{2}{\mu } \frac{ ( a_{0} - w )^{2} ( A_{1}^{2} - 2A_{2}\mu )}{\frac{\mu }{2}\zeta ^{2} + A_{1}\zeta + A_{2}} \\ \hphantom{v_{2} ( x, t ) =}{}- \frac{2}{\mu } \frac{ ( a_{0} - w ) ( A_{1}^{2} - 2A_{2}\mu ) ( \mu \zeta + A_{1} )}{ ( \frac{\mu }{2}\zeta ^{2} + A_{1}\zeta + A_{2} )^{2}} \times \biggl[ \frac{1}{\mu } ( a_{0} - w ) ( \mu \zeta + A_{1} ) - c \biggr], \end{gathered} $$
(5.85)

where \(\zeta = x - w\frac{t^{\alpha }}{\alpha } \).

The solutions obtained are more general and useful to analyze the shallow water wave profile.

Note: It is worth mentioning that all the solutions derived in this study were confirmed using the Maple software package by returning them to the original equation and found correct.

6 Physical explanation and graphical representations

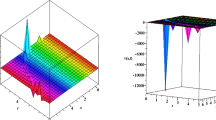
In this section, we present some 3-D and 2-D figures of some of the obtained solutions. The figures are carried out by taking suitable values of the parameters to objectify the inward contrivance of the incidents, which are analyzed through the time-fractional coupled BB equations and the coupled WBK equations and are displayed in Figs. 1–6. For example, Fig. 1 shows the kink-shaped soliton depicted from the solution (5.9) when \(\lambda =7\), \(\mu =12\), \(w=0.5\), \(\xi =x- t^{0.5}\), wherein the fractional order is \(\alpha =0.5\) within the intervals \(-15\leq x\leq 15\) and \(0.1\leq t\leq 15\). Solution (5.15) presents the singular periodic wave for \(\lambda =4\), \(\mu =4.25\), \(w= {1} / {3}\), \(\xi =x- {(20} / {51)} t^{0.85}\) with fractional order \(\alpha =0.85\) and is sketched in Fig. 2 within the limits \(-10\leq x\leq 10\) and \(0.1\leq t\leq 0.2\). The modulus of solution (5.26) signifies the cuspon for \(\lambda =-1\), \(\xi _{1} =0\), \(w= {1} / {2}\), \(\xi =x- {(10} / {19)} t^{0.95}\) with fractional order \(\alpha =0.95\) and is shown in Fig. 3 within the range \(-50\leq x\leq 50\) and \(0.01\leq t\leq 0.5\). Solution (5.51) indicates the kink-shape soliton for \(\lambda =3\), \(\mu =2\), \(c=1\), \(b=1\), \(w=0.5\), \(\xi =x-2 t^{0.5}\) with fractional order \(\alpha =0.5\) and is depicted in Fig. 4 within the intervals \(-90\leq x\leq 90\) and \(0.1\leq t\leq 90\). Solution (5.52) characterizes the singular kink wave for \(\lambda =3\), \(\mu =2\), \(c=1\), \(b=1\), \(w=1\), \(\xi =x-2 t^{0.5}\) with fractional order \(\alpha =0.5\) and is plotted in Fig. 5 within the limits \(-100\leq x\leq 100\) and \(0.1\leq t\leq 1\). Solution (5.64) represents the bell-shape soliton for \(\lambda =-1\), \(b_{1} =1\), \(A_{2} =1\), \(w=1\), \(\xi =x- \frac{20}{19} t^{0.95}\) with fractional order \(\alpha =0.95\) and outlined in Fig. 6 within the range \(-5\leq x\leq 5\) and \(0.1\leq t\leq 0.5\).

Figure 1
figure 1

Modulus plot of solution (5.9) which is a kink-shape soliton

Full size image
Figure 2
figure 2

Modulus plot of solution (5.15), which is a singular periodic wave

Full size image
Figure 3
figure 3

Modulus plot of solution (5.26) which is a cuspon

Full size image
Figure 4
figure 4

Modulus plot of solution (5.51) which is a kink-shape soliton

Full size image
Figure 5
figure 5

Modulus plot of solution (5.52) which is a singular kink-shape soliton

Full size image
Figure 6
figure 6

Modulus plot of solution (5.64) which is a bell-shape soliton

Full size image

7 Conclusion

By means of the basic \({(G'} / {G} )\)-expansion method and the two-variable \({(G'} / {G}, {1} / {G} )\)-expansion method, in this study, we have ascertained further general solitary wave solutions to the time-fractional coupled Boussinesq–Burger equations and the coupled Whitham—Broer–Kaup system as a linear combination of the exponential, rational, and hyperbolic functions or separately including several free parameters. For definite values of the associated parameters, some well-known solutions are extracted from the broad-ranging solutions, which are available in the literature, and some fresh solutions are derived, which confirm the correctness and validity of the general solutions and the method. We have exposed the graphical representations and discussed the physical significance of the obtained solutions. Every nonlinear equation is distinct and atypical; therefore not all equations can be examined through a single method. The greater the scope of application of a method, the greater the acceptability of that method. Since this study shows that the introduced methods are straightforward, compatible, and powerful mathematical tools for obtaining abundant traveling wave solutions, to test the range of applicability and consistency, the method can be implemented to other types of nonlinear fractional differential systems to analyze closed-form soliton solutions, and this is the concern of further research. Numerical solutions to these equations can also be explored in the future by following the effective schemes discussed in [60, 61].