1 Introduction

Fractional differential equations (FDEs) can be viewed as the generalized type of the ordinary differential equations (ODEs). The FDEs have attracted the researchers’ attention over the past two decades because the effects in ODEs are neglected. Oldham and Spanier [1] are the first researchers who have taken the FDEs into consideration. The search for the exact solutions of FDEs plays an important role in understanding the qualitative and quantitative features of many physical phenomena, which are described by these equations. For instance, the nonlinear oscillation of an earthquake can be modeled by derivatives of fractional order. Actually, the physical phenomena may not depend only on the time moment but also on the former time history, which can be successfully modeled utilizing the theory of fractional integrals and derivatives [2–4]. Fractional evolution equations play a significant role in various fields like engineering, biology, physics, signal processing, rheology, fluid flow, finance, electrochemistry, and so on [5–9]. Several efficient methods have recently been developed to get analytical solutions for FDEs. For example, the generalized tanh-coth method [10], the auxiliary equation method [11], the \(( \frac{G'}{G} ) \)-expansion method [12–23], the improved F-expansion method [24], the exponential rational function method [25–27], the simplest equation method [28], the modified simple equation method [29–32], the first integral method [33–37], the Kudryashov method [38–43], the modified extended tanh expansion method [44], the \(( \frac{G'}{G},\frac{1}{G} ) \)-expansion method [45–51], etc. [52–56]. The basic idea of the \(( \frac{G'}{G} ) \)-expansion method is that the traveling wave solutions of nonlinear FDEs can be presented via a polynomial in one variable \(( \frac{G'}{G} ) \), where G satisfies the equation \(G'' + \lambda G' + \mu G = 0\). In this study, the \(( \frac{G'}{G},\frac{1}{G} ) \)-expansion method is employed. It can be an extension of the \(( \frac{G'}{G} ) \)-expansion method. The main idea of the \(( \frac{G'}{G},\frac{1}{G} ) \)-expansion method is that the traveling wave solutions for NTFDEs can be presented via a polynomial in the \(( \frac{1}{G} ) \) and \(( \frac{G'}{G} ) \), where G satisfies the equation \(G'' + \lambda G = \mu \). Li et al. [45] are the first researchers, who proposed the \(( \frac{G'}{G}, \frac{1}{G} ) \)-expansion method to solve the Zakharov equations. Sar et al. [46], Guner et al. [47] and Topsakal et al. [48] have used this method to extract the exact solutions for some space-time NFDEs.

This research paper aims to implement the \(( \frac{G'}{G}, \frac{1}{G} ) \)-expansion method to obtain new exact solutions for some NTFDEs in biology and mathematical physics. The first considered model is a nonlinear \((2+1)\)-dimensional BP model with time-fractional derivative [13, 41]:

$$ D_{t}^{\beta } u = \bigl( u^{2} \bigr) _{xx} + \bigl( u^{2} \bigr) _{yy} + h \bigl( u^{2} - r \bigr) ,\quad t > 0, 0 < \beta < 1, x,y \in R, $$
(1.1)

in which u denotes the density of population, \(h ( u^{2} - r ) \) shows the population supply because of deaths and births and h, r are constants. When \(\beta \to 1\), the BP model assists us to understand the dynamical proceeding of population changes and provides valuable predictions. Recently, Zhang and Zhang [57], Lu [58], Bekir et al. [59], Bekir and \(\mathrm{G}\ddot{\mathrm{u}}\mathrm{ner}\) [13] and Manafian and Lakestani [10] have found the exact solutions of Eq. (1.1) using the fractional sub-equation method, the Bäcklund transformation of fractional Riccati equation, the exp-function method, the \(( \frac{G'}{G} ) \)-expansion method, and the generalized tanh-coth method, respectively. The comparison of the obtained results with the results obtained in [13, 57–59] will be discussed in the following sections of the paper.

The second studied model is nonlinear \((3+1)\)-dimensional KdV–ZK equation with time-fractional derivative [60]:

$$ D_{t}^{\beta } u + a uu_{x} + u_{xxx} + c (u_{yyx} + u_{zzx} ) = 0,\quad t > 0, a, c = \mathrm{const.}, 0< \beta < 1. $$
(1.2)

When \(\beta \to 1\), the KdV–ZK equation is derived for plasma comprised of hot and cool electrons and fluid ions species. Recently, Sahoo et al. [60] have found the exact solutions of Eq. (1.2) utilizing the improved fractional sub-equation method, whereas Kaplan et al. [61] have obtained the exact solutions of Eq. (1.2) using the exp\(( - \phi ( \xi ) ) \) method. The study is organized as follows: In Sect. 2, the description of the conformable fractional derivative and its important properties are presented. In Sect. 3, the main ideas of the \(( \frac{G'}{G},\frac{1}{G} ) \)-expansion method are discussed. In Sect. 4, the new exact solutions for the conformable BP model and KdV–ZK equation with time-fractional derivative by the \(( \frac{G'}{G},\frac{1}{G} ) \)-expansion method are constructed. Finally, conclusions are presented in Sect. 5 of this paper.

2 Conformable fractional derivative and its important properties

The conformable fractional derivative of g of order β is defined as follows [62–64]:

$$ \mathrm{T}_{\beta } ( g ) ( t ) = \lim_{x \to 0}\frac{g ( t + x t^{1 - \beta } ) - g ( t ) }{x}, $$

which \(g:[ 0,\infty ) \to R\), \(t > 0\) and \(\beta \in ( 0, 1 ) \). Some important properties of the above definition are given by

$$\begin{aligned}& \mathrm{T}_{\beta } ( a g + b f ) = a\mathrm{T}_{\beta } ( g ) + b \mathrm{T}_{\beta } ( f ) , \quad \forall a, b \in R. \\& \mathrm{T}_{\beta } \bigl( t^{\mu } \bigr) = \mu t^{\mu - \beta }, \quad \forall \mu \in R. \\& \mathrm{T}_{\beta } ( g\circ f ) ( t ) = t^{1 -\beta }f' ( t ) g' \bigl( f ( t ) \bigr) . \end{aligned}$$

3 Key ideas of the \(( \frac{G'}{G},\frac{1}{G} ) \)-expansion method to the NTFDEs

Li et al. [45] suggested the \(( \frac{G'}{G},\frac{1}{G} ) \)-expansion method as follows:

For the auxiliary equation

$$ G'' + \lambda G = \mu , $$
(3.1)

we set

$$ \phi = \frac{G' ( \xi ) }{G ( \xi ) }, \qquad \psi = \frac{1}{G ( \xi ) }. $$
(3.2)

From Eqs. (3.1) and (3.2), we get

$$ \phi ' = - \phi^{2} + \mu \psi - \lambda , \qquad \psi ' = - \phi \psi . $$
(3.3)

The general solution of the ODE (3.1), in the following three distinct subcases:

Case 1 If \(\lambda < 0\), the general solution of the ODE (3.1) is

$$ G = A_{1}\sinh \sqrt{ - \lambda } \xi + A_{2}\cosh \sqrt{ - \lambda } \xi + \frac{\mu }{\lambda }, $$
(3.4)

and thus

$$ \psi^{2} = - \frac{\lambda }{\lambda^{2}\sigma + \mu^{2}} \bigl[ \phi ^{2} - 2\mu \psi + \lambda \bigr] , $$
(3.5)

where \(A_{1}\), \(A_{2}\) are two arbitrary constants and \(\sigma = A_{1} ^{2} - A_{2}^{2}\).

Case 2 If \(\lambda > 0\), the general solution of the ODE (3.1) is given by

$$ G = A_{1}\sin \sqrt{\lambda } \xi + A_{2}\cos \sqrt{\lambda } \xi + \frac{\mu }{\lambda }, $$
(3.6)

therefore, we have

$$ \psi^{2} = \frac{\lambda }{\lambda^{2}\sigma - \mu^{2}} \bigl[ \phi ^{2} - 2\mu \psi + \lambda \bigr] , $$
(3.7)

where \(\sigma = A_{1}^{2} + A_{2}^{2}\).

Case 3 If \(\lambda = 0\), the general solution of the ODE (3.1) is

$$ G = \frac{1}{2} \mu \xi^{2} + A_{1} \xi + A_{2}, $$
(3.8)

and hence

$$ \psi^{2} = \frac{1}{A_{1}^{2} - 2 \mu A_{2}} \bigl[ \phi^{2} - 2\mu \psi \bigr] . $$
(3.9)

The main steps of the two variables \(( \frac{G'}{G},\frac{1}{G} ) \)-expansion method are described in the following steps.

Step 1 Assume that we have the following general NFDE

$$ F \biggl( u, \frac{\partial^{\beta } u}{\partial t^{\beta }}, \frac{ \partial u}{\partial x}, \frac{\partial u}{\partial y}, \frac{\partial u}{\partial z}, \frac{\partial^{2\beta } u}{\partial t^{2\beta }}, \frac{ \partial^{2} u}{\partial x^{2}},\ldots \biggr) = 0,\quad 0 < \beta < 1. $$
(3.10)

By introducing the transformation

$$ u ( x, y, z, t ) = f ( \xi ) , \quad \xi = a x + b y + c z - l \frac{ t^{\beta }}{\beta }, $$
(3.11)

where l, a, b and c are nonzero arbitrary constants. Equation (3.10) can be reduced into ODE in the following form:

$$ P \bigl( f, f', f'', f''', \ldots \bigr) = 0. $$
(3.12)

Step 2 Assume that the solution of ODE (3.12) can be expressed by a polynomial in ϕ, ψ as follows:

$$ f ( \xi ) = \sum_{i = 0}^{m} \alpha_{i} \phi^{i} + \sum_{i = 1}^{m} \beta_{i} \phi^{i - 1}\psi , $$
(3.13)

where \(\alpha_{i}\) (\(i = 0,\ldots, m\)) and \(\beta_{i}\) (\(i =1,\ldots, m\)) are constants, and m in (3.13) can be determined by utilizing the homogeneous balance between the nonlinear terms and the highest-order derivative in (3.12).

Step 3 Substituting (3.13) into Eq. (3.12) utilizing (3.3) and (3.5), we obtain a polynomial in ψ and ϕ, where the degree of ψ is not bigger than one. Setting the coefficients of \(\phi^{i}\) (\(i = 0, 1,\ldots\)) and \(\psi^{j}\) (\(j = 0, 1\)) to be zero, yields a set of algebraic equations, which can be solved with the help of Mathematica or Maple software package to obtain the values of \(\alpha_{i}\), \(\beta_{i}\), l, a, b and c in which \(( \lambda < 0 ) \).

Step 4 Substituting (3.13) into (3.12) with (3.3) and (3.7) or ((3.3) and (3.9)), we get the exact solutions of Eq. (3.12).

4 Applications of \(( \frac{G'}{G},\frac{1}{G} ) \)-expansion method to NTFDEs in mathematical physics

In this part, new exact solutions of the \((2+1)\)-dimensional BP model and \((3+1)\)-dimensional KdV–ZK equation with time-fractional derivative are extricated by utilizing the \(( \frac{G'}{G},\frac{1}{G} ) \)-expansion method.

4.1 \((2+1)\)-dimensional BP model with time-fractional derivative

Using the fractional traveling wave variable,

$$ u ( x, y, t ) = f ( \xi ) ,\quad \xi = x + y - l \frac{t ^{\beta }}{\beta }, $$
(4.1)

the nonlinear BP model can be reduced into ODE:

$$ l f' + 4f f'' + 4 \bigl( f' \bigr) ^{2} + h f^{2} - h r = 0. $$
(4.2)

To get the exact solution, we utilize the transformation

$$ f = V^{ - 1}, $$
(4.3)

in Eq. (4.2) to find a new equation,

$$ - lV^{2}V' - 4V V'' + 12 \bigl( V' \bigr) ^{2} + hV^{2} - hrV^{4} = 0. $$
(4.4)

By utilizing the homogeneous balance principle, we get \(m =1\). Therefore, Eq. (1.1) has the formal solution

$$ V ( \xi ) = \alpha_{0} + \alpha_{1}\phi + \beta_{1}\psi , $$
(4.5)

where \(\alpha_{0}\), \(\alpha_{1}\) and \(\beta_{1}\) are constants.

Case 1 When \(\lambda < 0\) (hyperbolic function solutions)

By substituting (4.5) into (4.4) and utilizing (3.3) and (3.5), we obtain a polynomial in ψ and ϕ. Equating the coefficients of the equation to zero, we get a system of algebraic equations for \(\alpha_{0}\), \(\alpha_{1}\), \(\beta_{1}\) and l as follows:

$$\begin{aligned}& \phi^{4}: - \frac{\beta_{1}^{4}h \lambda^{2}r}{ ( \lambda^{2} \sigma + \mu^{2} ) ^{2}} - \frac{4\beta_{1}^{2} \lambda }{\lambda ^{2}\sigma + \mu^{2}} - \frac{3\alpha_{1}\beta_{1}^{2}l\lambda }{ \lambda^{2}\sigma + \mu^{2}} + \frac{6\alpha_{1}^{2}\beta_{1}^{2}h \lambda r}{\lambda^{2}\sigma + \mu^{2}} - \alpha_{1}^{4}hr + \alpha _{1}^{3}l + 4\alpha_{1}^{2} = 0, \\& \phi^{3}\psi : \frac{4\alpha_{1}\beta_{1}^{3}h\lambda r}{\lambda^{2} \sigma + \mu^{2}} - \frac{\beta_{1}^{3}l\lambda }{\lambda^{2}\sigma + \mu^{2}} + 8 \alpha_{1}\beta_{1} + 3\alpha_{1}^{2} \beta_{1}l - 4\alpha _{1}^{3} \beta_{1}hr = 0, \\& \phi^{3}: - \frac{2\beta_{1}^{3}l\lambda^{2}\mu }{ ( \lambda^{2} \sigma + \mu^{2} ) ^{2}} + \frac{8\alpha_{1}\beta_{1}^{3}h\lambda ^{2}r\mu }{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} + \frac{12 \alpha_{0}\alpha_{1}\beta_{1}^{2}h\lambda r}{\lambda^{2}\sigma + \mu ^{2}} + \frac{8\alpha_{1}\beta_{1}\mu \lambda }{\lambda^{2}\sigma + \mu^{2}} \\& \hphantom{\phi^{3}:}{}+ \frac{2\alpha_{1}^{2}\beta_{1}l\mu \lambda }{\lambda^{2}\sigma + \mu ^{2}} - \frac{2\alpha_{0}\beta_{1}^{2}l\lambda }{\lambda^{2}\sigma + \mu^{2}} + 2\alpha_{0} \alpha_{1}^{2}l - 4\alpha_{0}\alpha_{1}^{3}hr - 8\alpha_{0}\alpha_{1} = 0, \\& \phi^{2}\psi : \frac{4\beta_{1}^{4}h\lambda^{2}r\mu }{ ( \lambda ^{2}\sigma + \mu^{2} ) ^{2}} + \frac{4\alpha_{0}\beta_{1}^{3}h \lambda r}{\lambda^{2}\sigma + \mu^{2}} - \frac{12\alpha_{1}^{2}\beta _{1}^{2}h\lambda r\mu }{\lambda^{2}\sigma + \mu^{2}} + \frac{4\beta _{1}^{2} \lambda \mu }{\lambda^{2}\sigma + \mu^{2}} \\& \hphantom{\phi^{2}\psi :}{}+ \frac{7\alpha_{1}\beta_{1}^{2}l\lambda \mu }{\lambda^{2}\sigma + \mu ^{2}} - \alpha_{1}^{3}l\mu - 8 \alpha_{0}\beta_{1} - 12\alpha_{1}^{2} \mu - 12\alpha_{0}\alpha_{1}^{2} \beta_{1}hr + 4\alpha_{0}\alpha_{1} \beta_{1}l = 0, \\& \phi^{2}: \frac{4\beta_{1}^{4}h\lambda^{3}r\mu^{2}}{ ( \lambda ^{2}\sigma + \mu^{2} ) ^{3}} + \frac{2\alpha_{1}\beta_{1}^{2}l \lambda^{2}\mu^{2}}{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} + \frac{8\alpha_{0}\beta_{1}^{3}h\lambda^{2}r\mu }{ ( \lambda^{2} \sigma + \mu^{2} ) ^{2}} - \frac{8\beta_{1}^{2}\lambda^{2}\mu ^{2}}{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} - \frac{2\beta _{1}^{4}h\lambda^{3}r}{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} \\& \hphantom{\phi^{2}:}{}+ \frac{2\alpha_{0}\alpha_{1}\beta_{1}l\mu \lambda }{\lambda^{2} \sigma + \mu^{2}} + \frac{6\alpha_{1}^{2}\beta_{1}^{2}h\lambda^{2}r}{ \lambda^{2}\sigma + \mu^{2}} - \frac{\beta_{1}^{2}h \lambda }{\lambda ^{2}\sigma + \mu^{2}} - \frac{4\alpha_{0}\beta_{1}\mu \lambda }{ \lambda^{2}\sigma + \mu^{2}} + \frac{6\alpha_{0}^{2}\beta_{1}^{2}h \lambda r}{\lambda^{2}\sigma + \mu^{2}} - \frac{12\alpha_{1}^{2}\mu ^{2}\lambda }{\lambda^{2}\sigma + \mu^{2}} \\& \hphantom{\phi^{2}:}{}- \frac{4\alpha_{1}\beta_{1}^{2}l\lambda^{2}}{\lambda^{2}\sigma + \mu ^{2}} - 6\alpha_{0}^{2}\alpha_{1}^{2}hr + \alpha_{1}^{3}l\lambda + \alpha_{1}^{2}h + \alpha_{0}^{2}\alpha_{1}l + 16 \alpha_{1}^{2}\lambda = 0, \\& \phi \psi : \frac{4\beta_{1}^{3}l\lambda^{2}\mu^{2}}{ ( \lambda ^{2}\sigma + \mu^{2} ) ^{2}} - \frac{16\alpha_{1}\beta_{1}^{3}h \lambda^{2}r\mu^{2}}{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} - \frac{4\alpha_{1}^{2}\beta_{1}l\mu^{2}\lambda }{\lambda^{2}\sigma + \mu^{2}} + \frac{4\alpha_{1}\beta_{1}^{3}h\lambda^{2}r}{\lambda^{2} \sigma + \mu^{2}} - \frac{16\alpha_{1}\beta_{1}\mu^{2}\lambda }{ \lambda^{2}\sigma + \mu^{2}} \\& \hphantom{\phi \psi :}{}+ \frac{4\alpha_{0}\beta_{1}^{2}l\lambda \mu }{\lambda^{2}\sigma + \mu ^{2}} - \frac{24\alpha_{0}\alpha_{1}\beta_{1}^{2}hr\mu \lambda }{ \lambda^{2}\sigma + \mu^{2}} - \frac{\beta_{1}^{3}l\lambda^{2}}{ \lambda^{2}\sigma + \mu^{2}} + 2 \alpha_{1}\beta_{1}h - 12\alpha_{0} ^{2}\alpha_{1}\beta_{1}hr \\& \hphantom{\phi \psi :}{}+ 2\alpha_{1}^{2}\beta_{1}l\lambda - 2 \alpha_{0}\alpha_{1}^{2}l\mu + \alpha_{0}^{2}\beta_{1}l + 12\alpha_{1} \beta_{1}\lambda + 12\alpha _{0}\alpha_{1}\mu = 0, \\& \phi : \frac{8\alpha_{1}\beta_{1}^{3}h\lambda^{3}r\mu }{ ( \lambda ^{2}\sigma + \mu^{2} ) ^{2}} - \frac{2\beta_{1}^{3}l\lambda^{3} \mu }{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} + \frac{12\alpha _{0}\alpha_{1}\beta_{1}^{2}h\lambda^{2}r}{\lambda^{2}\sigma + \mu^{2}} + \frac{2\alpha_{1}^{2}\beta_{1}l\mu \lambda^{2}}{\lambda^{2}\sigma + \mu^{2}} - \frac{2\alpha_{0}\beta_{1}^{2}l\lambda^{2}}{\lambda^{2} \sigma + \mu^{2}} \\& \hphantom{\phi :}{}+ \frac{8\alpha_{1}\beta_{1}\mu \lambda^{2}}{\lambda^{2}\sigma + \mu ^{2}} - 4\alpha_{1}\alpha_{0}^{3}hr - 8\alpha_{0}\alpha_{1}\lambda + 2 \alpha_{0} \alpha_{1}^{2}l\lambda + 2\alpha_{0} \alpha_{1}h = 0, \\& \psi : - \frac{8\beta_{1}^{4}h\lambda^{3}r\mu^{3}}{ ( \lambda^{2} \sigma + \mu^{2} ) ^{3}} - \frac{4\alpha_{1}\beta_{1}^{2}l\lambda ^{2}\mu^{3}}{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} - \frac{16 \alpha_{0}\beta_{1}^{3}h\lambda^{2}r\mu^{2}}{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} + \frac{16\beta_{1}^{2}\lambda^{2}\mu^{3}}{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} + \frac{4\beta_{1} ^{4}h\lambda^{3}r\mu }{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} \\& \hphantom{\psi :}{}+ \frac{3\alpha_{1}\beta_{1}^{2}l\lambda^{2}\mu }{\lambda^{2}\sigma + \mu^{2}} - \frac{4\alpha_{0}\alpha_{1}\beta_{1}l\mu^{2}\lambda }{ \lambda^{2}\sigma + \mu^{2}} + \frac{8\alpha_{0}\beta_{1}\mu^{2} \lambda }{\lambda^{2}\sigma + \mu^{2}} + \frac{4\alpha_{0}\beta_{1} ^{3}h\lambda^{2}r}{\lambda^{2}\sigma + \mu^{2}} + \frac{24\alpha_{1} ^{2}\mu^{3}\lambda }{\lambda^{2}\sigma + \mu^{2}} \\& \hphantom{\psi :}{}- \frac{12\alpha_{0}^{2}\beta_{1}^{2}h\lambda r\mu }{\lambda^{2} \sigma + \mu^{2}} - \frac{12\beta_{1}^{2}\lambda^{2}\mu }{\lambda^{2} \sigma + \mu^{2}} + \frac{2\beta_{1}^{2}h \lambda \mu }{\lambda^{2} \sigma + \mu^{2}} + 2 \alpha_{0}\beta_{1}h - 4\alpha_{0} \beta_{1} \lambda \\& \hphantom{\psi :}{}- 24\alpha_{1}^{2}\lambda \mu - \alpha_{0}^{2} \alpha_{1}l\mu - 4\alpha _{0}^{3} \beta_{1}hr + 2\alpha_{0}\alpha_{1} \beta_{1}l\lambda = 0, \\& \phi^{0}: \frac{4\beta_{1}^{4}h\lambda^{4}r\mu^{2}}{ ( \lambda ^{2}\sigma + \mu^{2} ) ^{3}} + \frac{8\alpha_{0}\beta_{1}^{3}h \lambda^{3}r\mu }{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} - \frac{ \beta_{1}^{4}h\lambda^{4}r}{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} - \frac{8\beta_{1}^{2}\lambda^{3}\mu^{2}}{ ( \lambda^{2} \sigma + \mu^{2} ) ^{2}} + \frac{2\alpha_{1}\beta_{1}^{2}l\lambda ^{3}\mu^{2}}{ ( \lambda^{2}\sigma + \mu^{2} ) ^{2}} \\& \hphantom{\phi^{0}:}{}+ \frac{2\alpha_{0}\alpha_{1}\beta_{1}l\mu \lambda^{2}}{\lambda^{2} \sigma + \mu^{2}} + \frac{4\beta_{1}^{2}\lambda^{3}}{\lambda^{2} \sigma + \mu^{2}} - \frac{\alpha_{1}\beta_{1}^{2}l\lambda^{3}}{\lambda ^{2}\sigma + \mu^{2}} - \frac{4\alpha_{0}\beta_{1}\mu \lambda^{2}}{ \lambda^{2}\sigma + \mu^{2}} + \frac{6\alpha_{0}^{2}\beta_{1}^{2}h \lambda^{2}r}{\lambda^{2}\sigma + \mu^{2}} \\& \hphantom{\phi^{0}:}{}- \frac{\beta_{1}^{2}h \lambda^{2}}{\lambda^{2}\sigma + \mu^{2}} - \frac{12 \alpha_{1}^{2}\lambda^{2}\mu^{2}}{\lambda^{2}\sigma + \mu^{2}} + 12 \alpha_{1}^{2} \lambda^{2} + \alpha_{0}^{2}h + \alpha_{0}^{2}\alpha _{1}l\lambda - \alpha_{0}^{4}hr = 0. \end{aligned}$$

By solving the algebraic equations mentioned above utilizing the Maple software package, the following results are obtained.

Result 1

$$ \begin{aligned} &\alpha_{0} = \mp \frac{1}{2\sqrt{r}}, \qquad \alpha_{1} = \mp \frac{2 \sqrt{2}}{\sqrt{ - hr}},\quad \quad \beta_{1} = 0, \\ & l = \pm \frac{6}{\sqrt{2}} \sqrt{ - h} \sqrt{r}, \qquad h = 32\lambda , \qquad \mu = 0. \end{aligned} $$
(4.6)

By substituting (4.6) into (4.5) with (4.3) and (4.1), utilizing (3.2) and (3.4), we get the exact solutions of Eq. (1.1) as follows:

$$ u_{1} ( x, y, t ) = \mp 2\sqrt{r} \biggl( 1 + \frac{A_{1} \cosh ( \sqrt{ - \lambda } \xi ) + A_{2}\sinh ( \sqrt{ - \lambda } \xi ) }{A_{1}\sinh ( \sqrt{ - \lambda } \xi ) + A_{2}\cosh ( \sqrt{ - \lambda } \xi ) } \biggr) ^{ - 1}. $$
(4.7)

In particular, if we put \(A_{1} = 0\) and \(A_{2} > 0\) in Eq. (4.7), we get the solitary solution

$$ u_{1_{1}} ( x, y, t ) = \mp \frac{2\sqrt{r}}{1 + \tanh ( \sqrt{ - \lambda } \xi ) }, $$
(4.8)

while if we set \(A_{2} = 0\) and \(A_{1} > 0\), then we get the solitary solution

$$ u_{1_{2}} ( x, y, t ) = \mp \frac{2\sqrt{r}}{1 + \coth ( \sqrt{ - \lambda } \xi ) }, $$
(4.9)

where \(\xi = x + y \pm 24\sqrt{ - \lambda r} \frac{t^{\beta }}{ \beta }\).

Result 2

$$ \begin{aligned} &\alpha_{0} = \mp \frac{1}{2\sqrt{r}}, \qquad \alpha_{1} = \mp \frac{ \sqrt{2}}{\sqrt{ - hr}}, \qquad \beta_{1} = \mp \sqrt{\frac{h^{2}\sigma + 64\mu^{2}}{4h^{2}r}}, \\ & l = \pm \frac{6}{\sqrt{2}} \sqrt{ - h} \sqrt{r},\qquad h = 8\lambda . \end{aligned} $$
(4.10)

Based on Result 2, an exact solution of Eq. (1.1) is obtained. We have

$$ u_{2} ( x, y, t ) = \biggl( \mp \frac{1}{2\sqrt{r}} \mp \frac{\frac{1}{2 \sqrt{r}} ( A_{1}\cosh ( \sqrt{ - \lambda } \xi ) + A_{2}\sinh ( \sqrt{ - \lambda } \xi ) ) + \sqrt{\frac{ \lambda^{2}\sigma + \mu^{2}}{4r\lambda^{2}}}}{A_{1}\sinh ( \sqrt{ - \lambda } \xi ) + A_{2}\cosh ( \sqrt{ - \lambda } \xi ) + \frac{\mu }{\lambda }} \biggr) ^{ - 1}. $$
(4.11)

In particular, if we put \(\mu = 0, A_{1} = 0\) and \(A_{2} > 0\) in Eq. (4.11), we get the solitary solution

$$ u_{2_{1}} ( x, y, t ) = \biggl( \mp \frac{1}{2\sqrt{r}} \mp \frac{1}{2\sqrt{r}} \tanh ( \sqrt{ - \lambda } \xi ) \mp \frac{1}{2\sqrt{ - r}} \operatorname{sech} ( \sqrt{ - \lambda } \xi ) \biggr) ^{ - 1}, $$
(4.12)

but if we set \(\mu = 0, A_{2} = 0\) and \(A_{1} > 0\), then we get the solitary solution

$$ u_{2_{2}} ( x, y, t ) = \mp \frac{2\sqrt{r}}{1 + \coth ( \sqrt{ - \lambda } \xi ) + \operatorname{csch} ( \sqrt{ - \lambda } \xi ) }, $$
(4.13)

where \(\xi = x + y \pm 12\sqrt{ - \lambda r} \frac{t^{\beta }}{ \beta }\).

Case 2 When \(\lambda > 0\) (trigonometric function solutions)

By substituting (4.5) into (4.4) and utilizing (3.3) and (3.7), we obtain a polynomial in ψand ϕ. Equating the coefficients of the equation to zero to obtain a set of algebraic equations for \(\alpha_{0}\), \(\alpha_{1}\), \(\beta_{1}\) and l as follows:

$$\begin{aligned}& \phi^{4}: - \frac{\beta_{1}^{4}h \lambda^{2}r}{ ( \lambda^{2} \sigma - \mu^{2} ) ^{2}} + \frac{4\beta_{1}^{2} \lambda }{\lambda ^{2}\sigma - \mu^{2}} + \frac{3\alpha_{1}\beta_{1}^{2}l\lambda }{ \lambda^{2}\sigma - \mu^{2}} - \frac{6\alpha_{1}^{2}\beta_{1}^{2}h \lambda r}{\lambda^{2}\sigma - \mu^{2}} - \alpha_{1}^{4}hr + \alpha _{1}^{3}l + 4\alpha_{1}^{2} = 0, \\& \phi^{3}\psi : - \frac{4\alpha_{1}\beta_{1}^{3}h\lambda r}{\lambda ^{2}\sigma - \mu^{2}} + \frac{\beta_{1}^{3}l\lambda }{\lambda^{2} \sigma - \mu^{2}} + 8 \alpha_{1}\beta_{1} + 3\alpha_{1}^{2} \beta_{1}l - 4\alpha_{1}^{3}\beta_{1}hr = 0, \\& \phi^{3}: - \frac{2\beta_{1}^{3}l\lambda^{2}\mu }{ ( \lambda^{2} \sigma - \mu^{2} ) ^{2}} + \frac{8\alpha_{1}\beta_{1}^{3}h\lambda ^{2}r\mu }{ ( \lambda^{2}\sigma - \mu^{2} ) ^{2}} - \frac{12 \alpha_{0}\alpha_{1}\beta_{1}^{2}h\lambda r}{\lambda^{2}\sigma - \mu ^{2}} - \frac{8\alpha_{1}\beta_{1}\mu \lambda }{\lambda^{2}\sigma - \mu^{2}} \\& \hphantom{\phi^{3}:}{}- \frac{2\alpha_{1}^{2}\beta_{1}l\mu \lambda }{\lambda^{2}\sigma - \mu ^{2}} + \frac{2\alpha_{0}\beta_{1}^{2}l\lambda }{\lambda^{2}\sigma - \mu^{2}} + 2 \alpha_{0}\alpha_{1}^{2}l - 4\alpha_{0} \alpha_{1}^{3}hr - 8\alpha_{0} \alpha_{1} = 0, \\& \phi^{2}\psi : \frac{4\beta_{1}^{4}h\lambda^{2}r\mu }{ ( \lambda ^{2}\sigma - \mu^{2} ) ^{2}} - \frac{4\alpha_{0}\beta_{1}^{3}h \lambda r}{\lambda^{2}\sigma - \mu^{2}} + \frac{12\alpha_{1}^{2}\beta _{1}^{2}h\lambda r\mu }{\lambda^{2}\sigma - \mu^{2}} - \frac{4\beta _{1}^{2} \lambda \mu }{\lambda^{2}\sigma - \mu^{2}} \\& \hphantom{\phi^{2}\phi:}{}- \frac{7\alpha_{1}\beta_{1}^{2}l\lambda \mu }{\lambda^{2}\sigma - \mu ^{2}} - \alpha_{1}^{3}l \mu - 8\alpha_{0}\beta_{1} - 12\alpha_{1}^{2} \mu - 12\alpha_{0}\alpha_{1}^{2} \beta_{1}hr + 4\alpha_{0}\alpha_{1} \beta_{1}l = 0, \\& \phi^{2}: - \frac{4\beta_{1}^{4}h\lambda^{3}r\mu^{2}}{ ( \lambda ^{2}\sigma - \mu^{2} ) ^{3}} + \frac{2\alpha_{1}\beta_{1}^{2}l \lambda^{2}\mu^{2}}{ ( \lambda^{2}\sigma - \mu^{2} ) ^{2}} + \frac{8\alpha_{0}\beta_{1}^{3}h\lambda^{2}r\mu }{ ( \lambda^{2} \sigma - \mu^{2} ) ^{2}} - \frac{8\beta_{1}^{2}\lambda^{2}\mu ^{2}}{ ( \lambda^{2}\sigma - \mu^{2} ) ^{2}} - \frac{2\beta _{1}^{4}h\lambda^{3}r}{ ( \lambda^{2}\sigma - \mu^{2} ) ^{2}} \\& \hphantom{\phi^{2}:}{}- \frac{2\alpha_{0}\alpha_{1}\beta_{1}l\mu \lambda }{\lambda^{2} \sigma - \mu^{2}} - \frac{6\alpha_{1}^{2}\beta_{1}^{2}h\lambda^{2}r}{ \lambda^{2}\sigma - \mu^{2}} + \frac{\beta_{1}^{2}h \lambda }{\lambda ^{2}\sigma - \mu^{2}} + \frac{4\alpha_{0}\beta_{1}\mu \lambda }{ \lambda^{2}\sigma - \mu^{2}} - \frac{6\alpha_{0}^{2}\beta_{1}^{2}h \lambda r}{\lambda^{2}\sigma 0 - \mu^{2}} + \frac{12\alpha_{1}^{2}\mu ^{2}\lambda }{\lambda^{2}\sigma - \mu^{2}} \\& \hphantom{\phi^{2}:}{}+ \frac{4\alpha_{1}\beta_{1}^{2}l\lambda^{2}}{\lambda^{2}\sigma - \mu ^{2}} - 6\alpha_{0}^{2} \alpha_{1}^{2}hr + \alpha_{1}^{3}l \lambda + \alpha_{1}^{2}h + \alpha_{0}^{2} \alpha_{1}l + 16\alpha_{1}^{2}\lambda = 0, \\& \phi \psi : \frac{4\beta_{1}^{3}l\lambda^{2}\mu^{2}}{ ( \lambda ^{2}\sigma - \mu^{2} ) ^{2}} - \frac{16\alpha_{1}\beta_{1}^{3}h \lambda^{2}r\mu^{2}}{ ( \lambda^{2}\sigma - \mu^{2} ) ^{2}} + \frac{4\alpha_{1}^{2}\beta_{1}l\mu^{2}\lambda }{\lambda^{2}\sigma - \mu^{2}} - \frac{4\alpha_{1}\beta_{1}^{3}h\lambda^{2}r}{\lambda^{2} \sigma - \mu^{2}} + \frac{16\alpha_{1}\beta_{1}\mu^{2}\lambda }{ \lambda^{2}\sigma - \mu^{2}} \\& \hphantom{\phi \psi:}{}- \frac{4\alpha_{0}\beta_{1}^{2}l\lambda \mu }{\lambda^{2}\sigma - \mu ^{2}} \hphantom{\phi:}{}+ \frac{24\alpha_{0}\alpha_{1}\beta_{1}^{2}hr\mu \lambda }{ \lambda^{2}\sigma - \mu^{2}} + \frac{\beta_{1}^{3}l\lambda^{2}}{ \lambda^{2}\sigma - \mu^{2}} + 2\alpha_{1}\beta_{1}h - 12 \alpha_{0} ^{2}\alpha_{1}\beta_{1}hr \\& \hphantom{\phi \psi:}{}+ 2\alpha_{1}^{2}\beta_{1}l \lambda - 2\alpha_{0}\alpha_{1}^{2}l\mu + \alpha_{0}^{2}\beta_{1}l + 12\alpha_{1} \beta_{1}\lambda + 12\alpha _{0}\alpha_{1}\mu = 0, \\& \phi : \frac{8\alpha_{1}\beta_{1}^{3}h\lambda^{3}r\mu }{ (\lambda^{2}\sigma - \mu^{2} ) ^{2}} - \frac{2\beta_{1}^{3}l\lambda^{3} \mu }{ ( \lambda^{2}\sigma - \mu^{2} ) ^{2}} - \frac{12\alpha_{0}\alpha_{1}\beta_{1}^{2}h\lambda^{2}r}{\lambda^{2}\sigma - \mu^{2}}- \frac{2\alpha_{1}^{2}\beta_{1}l\mu \lambda^{2}}{\lambda^{2}\sigma - \mu^{2}} + \frac{2\alpha_{0}\beta_{1}^{2}l\lambda^{2}}{\lambda^{2} \sigma - \mu^{2}} \\& \hphantom{\phi:}{}- \frac{8\alpha_{1}\beta_{1}\mu \lambda^{2}}{\lambda^{2}\sigma - \mu ^{2}} - 4\alpha_{1} \alpha_{0}^{3}hr - 8\alpha_{0} \alpha_{1}\lambda + 2 \alpha_{0}\alpha_{1}^{2}l \lambda + 2\alpha_{0}\alpha_{1}h = 0, \\& \psi : \frac{8\beta_{1}^{4}h\lambda^{3}r\mu^{3}}{ (\lambda^{2}\sigma - \mu^{2} ) ^{3}} - \frac{4\alpha_{1}\beta_{1}^{2}l\lambda ^{2}\mu^{3}}{ ( \lambda^{2}\sigma - \mu^{2} ) ^{2}} - \frac{16 \alpha_{0}\beta_{1}^{3}h\lambda^{2}r\mu^{2}}{ (\lambda^{2}\sigma - \mu^{2} ) ^{2}} + \frac{16\beta_{1}^{2}\lambda^{2}\mu^{3}}{ ( \lambda^{2}\sigma - \mu^{2} ) ^{2}} + \frac{4\beta_{1} ^{4}h\lambda^{3}r\mu }{ ( \lambda^{2}\sigma - \mu^{2} ) ^{2}} \\& \hphantom{\psi:}{}- \frac{3\alpha_{1}\beta_{1}^{2}l\lambda^{2}\mu }{\lambda^{2}\sigma - \mu^{2}} + \frac{4\alpha_{0}\alpha_{1}\beta_{1}l\mu^{2}\lambda }{ \lambda^{2}\sigma - \mu^{2}} - \frac{8\alpha_{0}\beta_{1}\mu^{2} \lambda }{\lambda^{2}\sigma - \mu^{2}} - \frac{4\alpha_{0}\beta_{1} ^{3}h\lambda^{2}r}{\lambda^{2}\sigma + \mu^{2}} - \frac{24\alpha_{1} ^{2}\mu^{3}\lambda }{\lambda^{2}\sigma - \mu^{2}} \\& \hphantom{\phi:}{}+ \frac{12\alpha_{0}^{2}\beta_{1}^{2}h\lambda r\mu }{\lambda^{2} \sigma - \mu^{2}} + \frac{12\beta_{1}^{2}\lambda^{2}\mu }{\lambda^{2} \sigma - \mu^{2}} - \frac{2\beta_{1}^{2}h \lambda \mu }{\lambda^{2} \sigma - \mu^{2}} + 2\alpha_{0}\beta_{1}h - 4 \alpha_{0}\beta_{1} \lambda \\& \hphantom{\phi:}{}- 24\alpha_{1}^{2}\lambda \mu - \alpha_{0}^{2}\alpha_{1}l\mu - 4\alpha _{0}^{3}\beta_{1}hr + 2\alpha_{0} \alpha_{1}\beta_{1}l\lambda = 0, \\& \phi^{0}: - \frac{4\beta_{1}^{4}h\lambda^{4}r\mu^{2}}{ ( \lambda ^{2}\sigma - \mu^{2} ) ^{3}} + \frac{8\alpha_{0}\beta_{1}^{3}h \lambda^{3}r\mu }{ ( \lambda^{2}\sigma - \mu^{2} ) ^{2}} - \frac{ \beta_{1}^{4}h\lambda^{4}r}{ ( \lambda^{2}\sigma - \mu^{2} ) ^{2}} - \frac{8\beta_{1}^{2}\lambda^{3}\mu^{2}}{ ( \lambda^{2} \sigma - \mu^{2} ) ^{2}} + \frac{2\alpha_{1}\beta_{1}^{2}l\lambda ^{3}\mu^{2}}{ ( \lambda^{2}\sigma - \mu^{2} ) ^{2}} \\& \hphantom{\phi^{0}:}{}- \frac{2\alpha_{0}\alpha_{1}\beta_{1}l\mu \lambda^{2}}{\lambda^{2} \sigma - \mu^{2}} - \frac{4\beta_{1}^{2}\lambda^{3}}{\lambda^{2} \sigma - \mu^{2}} + \frac{\alpha_{1}\beta_{1}^{2}l\lambda^{3}}{\lambda ^{2}\sigma - \mu^{2}} + \frac{4\alpha_{0}\beta_{1}\mu \lambda^{2}}{ \lambda^{2}\sigma - \mu^{2}} - \frac{6\alpha_{0}^{2}\beta_{1}^{2}h \lambda^{2}r}{\lambda^{2}\sigma - \mu^{2}} + \frac{\beta_{1}^{2}h \lambda^{2}}{\lambda^{2}\sigma - \mu^{2}} \\& \hphantom{\phi^{0}:}{}+ \frac{12\alpha_{1}^{2}\lambda^{2}\mu^{2}}{\lambda^{2}\sigma - \mu ^{2}} + 12\alpha_{1}^{2} \lambda^{2} + \alpha_{0}^{2}h + \alpha_{0} ^{2}\alpha_{1}l\lambda - \alpha_{0}^{4}hr = 0. \end{aligned}$$

By solving the algebraic equations mentioned above utilizing the Maple software package, the following results are obtained.

Result 1

$$ \begin{aligned} &\alpha_{0} = \mp \frac{1}{2\sqrt{r}}, \qquad \alpha_{1} = \mp \frac{2 \sqrt{2}}{\sqrt{ - hr}},\qquad \beta_{1} = 0, \\ & l = \pm \frac{6}{\sqrt{2}} \sqrt{h} \sqrt{ - r},\qquad h = 32\lambda ,\qquad \mu = 0. \end{aligned} $$
(4.14)

By substituting (4.14) into (4.5) with (4.3) and (4.1), utilizing (3.2) and (3.6), we get the exact solutions of Eq. (1.1) as follows:

$$ u_{1} ( x, y, t ) = \biggl( \mp \frac{1}{2\sqrt{r}} \mp \frac{1}{2\sqrt{ - r}} \biggl( \frac{A_{1}\cos ( \sqrt{ \lambda } \xi ) - A_{2}\sin ( \sqrt{\lambda } \xi ) }{A _{1}\sin ( \sqrt{\lambda } \xi ) + A_{2}\cos ( \sqrt{ \lambda } \xi ) } \biggr) \biggr) ^{ - 1}. $$
(4.15)

In particular, if we put \(A_{1} = 0\) and \(A_{2} > 0\) in Eq. (4.15), we get the periodic solution

$$ u_{1_{1}} ( x, y, t ) = \biggl( \mp \frac{1}{2\sqrt{r}} \pm \frac{1}{2\sqrt{ - r}} \tan ( \sqrt{\lambda } \xi ) \biggr) ^{ - 1}, $$
(4.16)

whereas if we set \(A_{2} = 0\) and \(A_{1} > 0\), then we get the periodic solution

$$ u_{1_{2}} ( x, y, t ) = \biggl( \mp \frac{1}{2\sqrt{r}} \mp \frac{1}{2\sqrt{ - r}} \cot ( \sqrt{\lambda } \xi ) \biggr) ^{ - 1}, $$
(4.17)

where \(\xi = x + y \pm 24\sqrt{ - \lambda r} \frac{t^{\beta }}{ \beta }\).

Result 2

$$ \begin{aligned} &\alpha_{0} = \mp \frac{1}{2\sqrt{r}}, \qquad \alpha_{1} = \mp \frac{ \sqrt{2}}{\sqrt{ - hr}}, \qquad \beta_{1} = \mp \sqrt{\frac{64\mu^{2} - h ^{2}\sigma }{4h^{2}r}}, \\ &l = \pm \frac{6}{\sqrt{2}} \sqrt{h} \sqrt{ - r}, \qquad h = 8\lambda . \end{aligned} $$
(4.18)

Based on Result 2, exact solutions of Eq. (1.1) are obtained. We have

$$ u_{2} ( x, y, t ) = \biggl( \mp \frac{1}{2\sqrt{r}} \mp \frac{\frac{1}{2\sqrt{ - r}} ( A_{1}\cos ( \sqrt{ \lambda } \xi ) - A_{2}\sin ( \sqrt{\lambda } \xi ) ) + \sqrt{\frac{\mu^{2} - \lambda^{2}\sigma }{4\lambda^{2}r}}}{A _{1}\sin ( \sqrt{\lambda } \xi ) + A_{2}\cos ( \sqrt{ \lambda } \xi ) + \frac{\mu }{\lambda }} \biggr) ^{ - 1}. $$
(4.19)

In particular, if we put \(\mu = 0, A_{1} = 0\) and \(A_{2} > 0\) in Eq. (4.19), we get the periodic solution

$$ u_{2_{1}} ( x, y, t ) = \biggl( \mp \frac{1}{2\sqrt{r}} \pm \frac{1}{2\sqrt{ - r}} \tan ( \sqrt{\lambda } \xi ) \mp \frac{1}{2\sqrt{ - r}} \sec ( \sqrt{\lambda } \xi ) \biggr) ^{ - 1}, $$
(4.20)

but if we set \(\mu = 0, A_{2} = 0\) and \(A_{1} > 0\), then we get the periodic solution

$$ u_{2_{2}} ( x, y, t ) = \biggl( \mp \frac{1}{2\sqrt{r}} \mp \frac{1}{2\sqrt{ - r}} \cot ( \sqrt{\lambda } \xi ) \mp \frac{1}{2\sqrt{ - r}} \csc ( \sqrt{\lambda } \xi ) \biggr) ^{ - 1}, $$
(4.21)

where \(\xi = x + y \pm 12\sqrt{ - \lambda r} \frac{t^{\beta }}{ \beta }\).

Remark 1

By comparing our results with the results obtained by Lu [58], Zhang and Zhang [57], Bekir et al. [59], Bekir and \(\mathrm{G} \ddot{\mathrm{u}}\mathrm{ner}\)[13] and Manafian and Lakestani [10], we conclude that all our solutions of Eq. (1.1) are new and satisfy the equation.

4.2 \((3+1)\)-dimensional KdV–ZK equation with time-fractional derivative

The fractional traveling wave variable

$$ u ( x, y, z, t ) = f ( \xi ) ,\quad \xi = x + y + z - l \frac{t^{\beta }}{\beta }, $$
(4.22)

reduces Eq. (1.2) to the following ODE:

$$ - l f + \frac{a}{2}f^{2} + ( 2c + 1 ) f'' + \xi_{0} = 0. $$
(4.23)

By balancing \(f''\) with \(f^{2}\) in Eq. (4.23), we get \(m = 2\). Thus, we get

$$ f ( \xi ) = \alpha_{0} + \alpha_{1}\phi + \alpha_{2}\phi ^{2} + \beta_{1}\psi + \beta_{2}\phi \psi , $$
(4.24)

in which \(\alpha_{0}\), \(\alpha_{1}\), \(\alpha_{2}\), \(\beta_{1}\) and \(\beta_{2}\) are constants.

Case 1 Hyperbolic function solution when \(\lambda < 0\).

If \(\lambda < 0\) substituting (4.24) into (4.23) and using (3.3) and (3.5), we obtain a polynomial in ψ and ϕ. Equating the coefficients of this equation to zero yields a set of algebraic equations in \(\alpha_{0}\), \(\alpha_{1}\), \(\alpha_{2}\), \(\beta_{1}\), \(\beta _{2}\), σ, λ and μ which can be solved by applying Maple to get the following values:

$$ \begin{aligned} &\alpha_{0} = - \frac{5\lambda ( 2c + 1 ) - l}{a}, \qquad \alpha _{1} = 0,\qquad \alpha_{2} = - \frac{6 ( 2c + 1 ) }{a}, \\ & \beta_{1} = \frac{6\mu ( 2c + 1 ) }{a},\qquad \beta_{2} = \mp \frac{6 ( 2c + 1 ) }{a}\sqrt{ - \frac{ \lambda^{2}\sigma + \mu^{2}}{\lambda }}, \\ & \xi_{0} = - \frac{\lambda ^{2} ( 2c + 1 ) ^{2} - l^{2}}{2a}. \end{aligned} $$
(4.25)

From (3.4), (4.24) and (4.25), we get the exact solution of Eq. (1.2) as follows:

$$\begin{aligned} u_{1} ( x, y, z, t ) & = \frac{l - 10c\lambda - 5\lambda }{a} + \frac{6\mu ( 2c + 1 ) }{a ( A_{1}\sinh \sqrt{ - \lambda } \xi + A_{2}\cosh \sqrt{ - \lambda } \xi + \frac{\mu }{ \lambda } ) } \\ &\quad {}+ \frac{ ( 12c + 6 ) ( A_{1}\cosh \sqrt{ - \lambda } \xi + A_{2}\sinh \sqrt{ - \lambda } \xi ) }{a ( A_{1} \sinh \sqrt{ - \lambda } \xi + A_{2}\cosh \sqrt{ - \lambda } \xi + \frac{\mu }{\lambda } ) ^{2}} \\ &\quad {}\times \bigl( A_{1}\lambda \cosh \sqrt{ - \lambda } \xi + A_{2} \lambda \sinh \sqrt{ - \lambda } \xi \mp \sqrt{ \lambda^{2}\sigma + \mu^{2}} \bigr) . \end{aligned}$$
(4.26)

In particular, if we put \(\mu = 0, A_{1} = 0\) and \(A_{2} > 0\) in Eq. (4.26), we get the solitary solution

$$\begin{aligned} &u_{1_{1}} ( x, y, z, t ) \\ &\quad = \frac{l - 10c\lambda - 5\lambda }{a} + \frac{6\lambda ( 2c + 1 ) }{a} ( \tanh \sqrt{ - \lambda } \xi ) ( \tanh \sqrt{ - \lambda } \xi \mp i \operatorname{sech} \sqrt{ - \lambda } \xi ) , \end{aligned}$$
(4.27)

while if we set \(\mu = 0\), \(A_{2} = 0\) and \(A_{1} > 0\), then we get the solitary solution

$$\begin{aligned} &u_{1_{2}} ( x, y, z, t ) \\ &\quad = \frac{l - 10c\lambda - 5\lambda }{a} + \frac{6\lambda ( 2c + 1 ) }{a} ( \coth \sqrt{ - \lambda } \xi ) ( \coth \sqrt{ - \lambda } \xi \mp \operatorname{csch} \sqrt{ - \lambda } \xi ) , \end{aligned}$$
(4.28)

in which \(\xi = x + y + z - l \frac{t^{\beta }}{\beta }\).

Case 2 Trigonometric function solution when \(\lambda > 0\).

If \(\lambda > 0\) substituting (4.24) into (4.23) and using (3.3) and (3.7), we obtain a polynomial in ψ and ϕ. Equating the coefficients of this equation to zero yields a set of algebraic equations, which can be solved by applying Maple to get the following values:

$$ \begin{aligned} &\alpha_{0} = - \frac{5\lambda ( 2c + 1 ) - l}{a}, \qquad \alpha _{1} = 0, \qquad \alpha_{2} = - \frac{6 ( 2c + 1 ) }{a}, \\ & \beta_{1} =\frac{6\mu ( 2c + 1 ) }{a},\qquad \beta_{2} = \mp \frac{6 ( 2c + 1 ) }{a}\sqrt{\frac{\lambda ^{2}\sigma - \mu^{2}}{\lambda }}, \\ & \xi_{0} = - \frac{\lambda^{2} ( 2c + 1 ) ^{2} - l^{2}}{2a}. \end{aligned} $$
(4.29)

From (3.6), (4.24) and (4.29), we get the exact solution of Eq. (1.2) as follows:

$$\begin{aligned} u_{1} ( x, y, z, t ) &= \frac{l - 10c\lambda - 5\lambda }{a} + \frac{6\mu ( 2c + 1 ) }{a ( A_{1}\sin \sqrt{\lambda } \xi + A_{2}\cos \sqrt{\lambda } \xi + \frac{\mu }{\lambda } ) } \\ &\quad {}- \frac{6 ( 2c + 1 ) ( A_{1}\cos \sqrt{\lambda } \xi - A_{2}\sin \sqrt{\lambda } \xi ) }{a ( A_{1}\sin \sqrt{ \lambda } \xi + A_{2}\cos \sqrt{\lambda } \xi + \frac{\mu }{\lambda } ) ^{2}} \\ &\quad {}\times \bigl( A_{1}\lambda \cos \sqrt{\lambda } \xi - A_{2}\lambda \sin \sqrt{\lambda } \xi \pm \sqrt{\lambda^{2} \sigma - \mu^{2}} \bigr) . \end{aligned}$$
(4.30)

Particularly, if we put \(\mu = 0, A_{1} = 0\) and \(A_{2} > 0\) in Eq. (4.30), we get the periodic solution

$$ u_{1_{1}} ( x, y, z, t ) = \frac{l - 10c\lambda - 5\lambda }{a} - \frac{6\lambda ( 2c + 1 ) }{a} ( \tan \sqrt{ \lambda } \xi ) ( \tan \sqrt{\lambda } \xi \mp \sec \sqrt{ \lambda } \xi ) , $$
(4.31)

but if we set \(\mu = 0, A_{2} = 0\) and \(A_{1} > 0\), then we get the periodic solution

$$ u_{1_{2}} ( x, y, z, t ) = \frac{l - 10c\lambda - 5\lambda }{a} - \frac{6\lambda ( 2c + 1 ) }{a} ( \cot \sqrt{ \lambda } \xi ) ( \cot \sqrt{\lambda } \xi \pm \csc \sqrt{ \lambda } \xi ) , $$
(4.32)

where \(\xi = x + y + z - l \frac{t^{\beta }}{\beta }\).

Case 3 Rational function solution when \(\lambda = 0\).

If \(\lambda = 0\) substituting (4.24) into (4.23) and using (3.3) and (3.9), we obtain a polynomial in ψ and ϕ. Equating the coefficients of this equation to zero yields a set of algebraic equations, which can be solved by applying Maple to get the following values:

$$ \begin{aligned} &\alpha_{0} = \alpha_{0}, \qquad \alpha_{1} = 0, \qquad \alpha_{2} = - \frac{6 ( 2c + 1 ) }{a}, \qquad \beta_{1} = \frac{6\mu ( 2c + 1 ) }{a}, \\ & l = a\alpha_{0}, \qquad \beta_{2} = \mp \frac{6 ( 2c + 1 ) }{a}\sqrt{A _{1}^{2} - 2A_{2}\mu }, \qquad \xi_{0} = \frac{1}{2}a\alpha_{0}^{2}. \end{aligned} $$
(4.33)

From (3.8), (4.24) and (4.33), we get the exact solution of Eq. (1.2) as follows:

$$\begin{aligned} u_{1} ( x, y, z, t ) &= \alpha_{0} + \frac{6\mu ( 2c + 1 ) }{a ( \mu / 2 \xi^{2} + A_{1} \xi + A_{2} ) } - \frac{6 ( 2c + 1 ) ( \mu \xi + A_{1} ) }{a ( \mu / 2 \xi^{2} + A_{1} \xi + A_{2} ) ^{2}} \\ &\quad {}\times \Bigl( \mu \xi + A_{1} \pm \sqrt{A_{1}^{2} - 2A_{2}\mu } \Bigr) , \end{aligned}$$
(4.34)

where \(\xi = x + y + z - a\alpha_{0} \frac{t^{\beta }}{\beta }\).

Remark 2

If we compare our results with the results obtained by [60, 61], we can see that our solutions of Eq. (1.2) are new and satisfy the equation.

4.2.1 Graphical presentation of some exact solutions

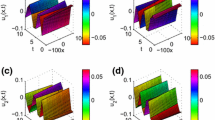
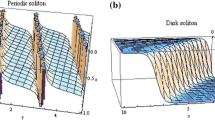
We presented some graphs to illustrate the behavior of exact solutions of Eqs. (1.1) and (1.2). Figures 1–5 show the solitary and periodic wave forms.

Figure 1
figure 1

Solitary wave solution of Eq. (4.8) with \(\beta = 0.5\) and \(\beta = 0.9\), respectively, when \(\lambda = - 1\)

Full size image
Figure 2
figure 2

Solitary wave solution of Eq. (4.9) with \(\beta = 0.25\) and \(\beta = 0.5\), respectively, when \(\lambda = - 1\)

Full size image
Figure 3
figure 3

Solitary wave solution of real part for Eq. (4.27) with \(\beta = 0.25\) and \(\beta = 0.9\), respectively, when \(\lambda = - 1\)

Full size image
Figure 4
figure 4

Periodic wave solution of Eq. (4.31) with \(\beta = 0.25\) and \(\beta = 0.9\), respectively, when \(\lambda = 1\)

Full size image
Figure 5
figure 5

Periodic wave solution of Eq. (4.32) with \(\beta = 0.25\) and \(\beta = 0.9\), respectively, when \(\lambda = 1\)

Full size image

5 Conclusion

The \(( \frac{G'}{G},\frac{1}{G} ) \)-expansion method is used to discuss the exact solutions to NFDEs. The \(( \frac{G'}{G}, \frac{1}{G} ) \) is successfully implemented to solve two NTFDEs. As applications, new exact solutions for \((2+1)\)-dimensional BP model and \((3+1)\)-dimensional KdV–ZK equation with time-fractional derivative are obtained. When the parameters μ, \(A_{1}\), and \(A_{2}\) are given special values, the solitary wave solutions (4.8), (4.9), (4.12), (4.13), (4.27) and (4.28) and the periodic solutions (4.16), (4.17), (4.20), (4.21), (4.31) and (4.32) are obtained. When \(\mu = 0\) and \(\beta_{i} = 0\) in Eq. (3.1) and Eq. (3.13), respectively, the \(( \frac{G'}{G},\frac{1}{G} ) \)-expansion method is reduced to the \(( \frac{G'}{G} ) \)-expansion method. Therefore, it can be concluded that the \(( \frac{G'}{G}, \frac{1}{G} ) \)-expansion method is more general and efficient than the \(( \frac{G'}{G} ) \)-expansion method. In comparison with other methods, the key feature of this method is that it possesses all three types of solutions. Some diagrams have been given in three dimensions for fractional order to illustrate the behavior of the solutions when the parameters take some special values.