Abstract
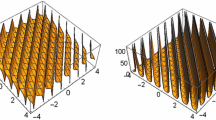
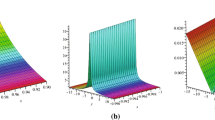
In this work, we present \(\left (G^{\prime }/G, 1/G\right )\)-expansion method for solving fractional differential equations based on a fractional complex transform. We apply this method for solving space–time fractional Cahn–Allen equation and space–time fractional Klein–Gordon equation. The fractional derivatives are described in the sense of modified Riemann–Lioville. As a result of some exact solution in the form of hyperbolic, trigonometric and rational solutions are deduced. The obtained solutions may be used for explaining of some physical problems. The \( \left (G^{\prime }/G, 1/G\right )\)-expansion method has a wider applicability for nonlinear equations. We have verified all the obtained solutions with the aid of Maple.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
K B Oldham and J Spanier, The fractional calculus (Academic Press, New York, USA, 1974)
K S Miller and B Ross, An introduction to the fractional calculus and fractional differential equations (Wiley, New York, 1993)
S Samko, A A Kilbas and O Marichev, Fractional integrals and derivatives: Theory and applications (Gordon and Breach Science, Yverdon, Switzerland, 1993)
R Sahadevan and T Bakkyaraj, J. Math. Anal. Appl. 393, 341 (2012)
Q Huang and R Zhdanov, Physica A 409, 110 (2014)
A Bekir, Ö Güner and A C Çevikel Ab. Appl. Anal. 2013, 426462 (2013)
E Babolian, A R Vahidi and A Shoja, Indian J. Pure Appl. Math. 45(6), 1017 (2014)
S S Ray and S Sahoo, Rep. Math. Phys. 75, 63 (2015)
A Bekir, Ö Güner and Ö Ünsal, J. Comput. Nonlinear Dyn. 10, 021020 (2015)
B Zheng, Commun. Theor. Phys. 58(5), 623 (2012)
G Jumarie, Comput. Math. Appl. 51, 1367 (2006)
Z B Li and J He, Comput. Appl. 15(5), 970 (2010)
Z B Li and J H He, Nonlinear Sci. Lett. A 2, 121 (2011)
X L Li, Q E Li and L M Wang, Appl. Math. J. Chin. Univ. 25, 454 (2010)
E M E Zayed and M A M Abdelaziz Math. Prob. Eng. 2012, 725061 (2012)
S M Allen and J W Cahn, Acta Metall. 27, 1085 (1979)
F Taşcan and A Bekir, Appl. Math. Comput. 207(1), 279 (2009)
H Jafari, H Tajadodi, N Kadkhoda and D Baleanu Ab. Appl. Anal. 2013, 587179 (2013)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
YAŞAR, E., GIRESUNLU, İ.B. The \(\boldsymbol {\left (G^{\prime }/G,1/G\right )}\)-expansion method for solving nonlinear space–time fractional differential equations. Pramana - J Phys 87, 17 (2016). https://doi.org/10.1007/s12043-016-1225-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12043-016-1225-7
Keywords
- Exact solution
- modified Riemann–Liouville fractional derivative
- space–time Cahn–Allen equation; space–time Klein–Gordon equation
- \(\left (G^{\prime }/G, \protect 1/G\right ) \)-expansion method