1 Introduction

It is well known that increased use of synthetic drugs such as crystal methamphetamine, ketamine, ecstasy and others, which are a new type of mental drugs based on chemical synthesis is an issue of concern in many parts of the world. Synthetic drugs are becoming increasingly popular in drug markets as they mainly appear in entertainment venues. Taking China for example, the number of reported synthetic drug abusers increased from 1.459 millon in the end of 2014 to 1.538 million in the end of 2017 by the report of China’s Drug Situations Report in the past five years (2014–2018) [1]. The number of methamphetamine abusers was up to 1.35 millon which accounted for 56.1% among the 2.404 million drug-users by the end of 2018 according to China’s Drug Situations Report (2018) [2]. What is more serious is that synthetic drugs are more addictive because they can directly affect the central nervous system and show the stronger psychological dependence compared with traditional drugs including heroin, morphine and marijuana, etc. In addition, any drug abuse and dependence constitute one of the most important modes of transmitting human immunodeficiency virus (HIV) and the Hepatitis C virus (HCV) [3–5]. Obviously, it is urgent to take effective measures to control the spread of synthetic drugs in order to eradicate the tremendous damages and panics brought by synthetic drugs abuse to social and public health system.

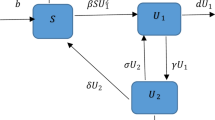
Since the heroin addiction was first defined as epidemic in 1981–1983 in Ireland, the heroin-using can be modeled in a similar way to the epidemic models [6] and mathematical modeling has been used extensively to address issues of public health importance. For example, Ma et al. developed different forms of heroin epidemic models [3, 6–10] to study the transmission of heroin epidemics. Sharomi et al. formulated different smoking models [11–17] for giving up smoking. There were also some drinking models [18–21] proposed by Mushayabasa et al. to analyze the influence of binge drinking to public health. Similarly, mathematical modeling can be also used to describe the spread of synthetic drugs. In [22, 23], Nyabadza et al. analyzed the methamphetamine transmission in South Africa by constructing a suitable mathematical model. In [24], Liu et al. formulated a synthetic drugs transmission model with treatment and studied global stability and backward bifurcation of the model. Considering the effect of synthetic drugs transmission caused by psychology, Ma et al. [25] proposed the following synthetic drugs transmission model with psychological addicts:

$$ \left \{ \textstyle\begin{array}{l} \frac{dS(t)}{dt}=A-dS(t)-\beta(N)S(t)(P(t)+H(t)), \\ \frac{dP(t)}{dt}=\beta(N)S(t)(P(t)+H(t))-\pi P(t)-(d+\gamma)P(t), \\ [3pt] \frac{dH(t)}{dt}=\pi P(t)+\theta T(t)-\sigma H(t)-d H(t), \\ \frac{dT(t)}{dt}=\gamma P(t)+\sigma H(t)-\theta T(t)-d T(t), \end{array}\displaystyle \right . $$
(1)

in which the total population (\(N(t)\)) is divided into four classes at time t such as the susceptible (\(S(t)\)), the psychological addicts (\(P(t)\)), the physiological addicts (\(H(t)\)) and the drug-users in treatment (\(T(t)\)). A is the recruitment rate of the susceptible; \(\beta(N)\) is the contact rate; d is the natural death rate of the populations; π, γ, θ and σ are state transition rates. Ma et al. [25] studied stability of system (1).

As stated in [25], a susceptible one is more likely to initiated drug abuse when he contacts with a physiological addict compared to a psychological addict. On the other hand, there should be a period for a drug user in treatment before he relapses into the physiological addicts due to the effect of treatment and his self-control. With an eye to such considerations and motivated by the work of some other dynamical systems with time delay [26–30], we investigate a more realistic synthetic drugs transmission model as follows:

$$ \left \{ \textstyle\begin{array}{l} \frac{dS(t)}{dt}=A-dS(t)-\beta_{1}S(t)P(t)-\beta_{2}S(t)H(t), \\ [3pt] \frac{dP(t)}{dt}=\beta_{1}S(t)P(t)+\beta_{2}S(t)H(t)-\pi P(t)-(d+\gamma)P(t), \\ [3pt] \frac{dH(t)}{dt}=\pi P(t)+\theta T(t-\tau)-\sigma H(t)-d H(t), \\ \frac{dT(t)}{dt}=\gamma P(t)+\sigma H(t)-\theta T(t-\tau)-d T(t), \end{array}\displaystyle \right . $$
(2)

where \(\beta_{1}\) and \(\beta_{2}\) are the contact rates of the psychological addicts and the physiological addicts, respectively. τ is the time delay due to the period that a drug user in treatment uses before he relapses into the physiological addicts.

We organize this paper as follows: in the following section, we analyze the local stability and appearance of Hopf bifurcation of system (2). Section 3 is concerned with the formulas determining the direction and stability of the Hopf bifurcation. Some numerical simulations are executed to illustrate the analytical results in Sect. 4. Finally, conclusions are presented in Sect. 5.

2 Local stability and existence of Hopf bifurcation

The stability and existence of unique positive equilibrium of system (2) is related to basic reproductive number \(\Re_{0}\) on free drug equilibrium point (FEP) \(D_{0}\), which is determined with the help of next generation matrix method [31]. The free drug equilibrium point is

$$D_{0}= \biggl(\frac{A}{d},0,0,0 \biggr). $$

Consider the following matrices for finding the basic reproductive number \(\Re_{0}\):

$$\begin{gathered} \mathbb{F}= \left ( \textstyle\begin{array}{c} \beta_{1}S(t)P(t)+\beta_{2}S(t)H(t) \\ 0 \end{array}\displaystyle \right ), \\ \mathbb{V}= \left ( \textstyle\begin{array}{c} \pi P(t)+(d+\gamma)P(t)\\ -\pi P(t)-\theta T(t)+\sigma H(t)+d H(t) \end{array}\displaystyle \right ).\end{gathered} $$

Now the Jacobians of \(\mathbb{F}\) and \(\mathbb{V}\) at \(D_{0}\) are

$$F= \left ( \textstyle\begin{array}{c@{\quad}c} \beta_{1}\frac{A}{d} & \beta_{2}\frac{A}{d} \\ 0 & 0 \end{array}\displaystyle \right ) $$

and

$$V= \left ( \textstyle\begin{array}{c@{\quad}c} b_{0} & 0 \\ -\pi& b_{1} \end{array}\displaystyle \right ). $$

Here \(b_{0}=\pi+d+\gamma\), \(b_{1}=\sigma+d\). The dominant eigenvalue of \(FV^{-1}\) represents \(\Re_{0}=\rho (FV^{-1})\), which is

$$\Re_{0}=\frac{A[\beta_{1}(\sigma+d)+\beta_{2}\pi]}{d(\sigma+d)(\pi +\gamma+d)}. $$

For \(\Re_{0}>1\), system (2) has a unique synthetic drug addiction equilibrium \(D_{*}(S_{*}, P_{*}, H_{*}, T_{*})\), where

$$\begin{aligned}& S_{*}=\frac{(\pi+d+\gamma)P_{*}}{\beta_{1}P_{*}+\beta_{2}H_{*}}, \qquad P_{*}=\frac {(\Re_{0}-1)+\tilde{L}_{1}}{[(\beta_{1}+\beta_{2}\tilde {L_{2}})/d]}, \\& H_{*}=\tilde{L}P_{*},\quad T_{*}= \biggl[\frac{\gamma}{\theta+d}+\frac{\pi \sigma}{(\theta+d)(\sigma+d)} \biggr]P_{*} \Big/ \biggl[\frac{d(\theta +\sigma+d)}{(\theta+d)(\sigma+d)} \biggr], \end{aligned}$$

and

$$\begin{aligned}& \tilde{L_{1}}=\frac{A\beta_{2}\theta}{\sigma+d} \biggl[\frac{\gamma }{\theta+d}+ \frac{\pi\sigma}{(\theta+d)(\sigma+d)} \biggr] \Big/ \biggl[\frac{d^{2}(\theta+\sigma+d)(\pi+d+\gamma)}{(\theta +d)(\sigma+d)} \biggr], \\& \tilde{L_{2}}=\frac{\pi}{\sigma+d}+\frac{\theta}{\sigma+d} \biggl[ \frac{\gamma}{\theta+d}+\frac{\pi\sigma}{(\theta+d)(\sigma +d)} \biggr] \Big/ \biggl[\frac{d(\theta+\sigma+d)}{(\theta +d)(\sigma+d)} \biggr]. \end{aligned}$$

At the unique synthetic drug addiction equilibrium \(D_{*}(S_{*}, P_{*}, H_{*}, T_{*})\), system (2) can be linearized as

$$ \left \{ \textstyle\begin{array}{l} \frac{dS(t)}{dt}=u_{11} S(t)+u_{12} P(t)+u_{13} H(t), \\ [3pt] \frac{dP(t)}{dt}=u_{21} S(t)+u_{22} P(t)+u_{23} H(t), \\ [3pt] \frac{dH(t)}{dt}=u_{32} P(t)+u_{33} H(t)+v_{34} T(t-\tau), \\ \frac{dT(t)}{dt}=u_{42} P(t)+u_{43} H(t)+u_{44} T(t)+v_{44} T(t-\tau), \end{array}\displaystyle \right . $$
(3)

whose characteristic equation is

$$ \lambda^{4}+U_{3}\lambda^{3}+U_{2} \lambda^{2}+U_{1}\lambda+U_{0}+\bigl(V_{3} \lambda ^{3}+V_{2}\lambda^{2}+V_{1} \lambda+V_{0}\bigr)e^{-\lambda\tau}=0, $$
(4)

with

$$\begin{aligned}& U_{0}=u_{33}u_{44}(u_{11}u_{22}-u_{12}u_{21})+u_{32}u_{44}(u_{13}u_{21}-u_{11}u_{23}), \\& U_{1}=(u_{12}u_{21}-u_{11}u_{22}) (u_{33}+u_{44})-u_{13}u_{21}u_{32}-u_{33}u_{44}(u_{11}+u_{22}) \\& \phantom{U_{1}=}{}+u_{23}u_{32}(u_{11}+u_{44}), \\& U_{2}=(u_{11}+u_{22}) (u_{33}+u_{44})-u_{12}u_{21}-u_{23}u_{32}+u_{11}u_{22}+u_{33}u_{44}, \\& U_{3}=-(u_{11}+u_{22}+u_{33}+u_{44}), \\& V_{0}=u_{11}u_{23}(u_{42}v_{34}-u_{32}v_{44})+u_{21}v_{34}(u_{12}u_{43}-u_{13}u_{42}) \\& \phantom{V_{0}=}{}+u_{21}v_{44}(u_{13}u_{32}-u_{12}u_{33})+u_{11}u_{22}(u_{33}v_{44}-u_{43}v_{34}), \\& V_{1}=u_{23}(u_{32}v_{44}-u_{42}v_{34})-v_{44}(u_{11}u_{22}+u_{11}u_{33}+u_{22}u_{33}) \\& \phantom{V_{1}=}{}+u_{12}u_{21}v_{44}+(u_{11}+u_{22})u_{43}v_{34}, \\& V_{2}=v_{44}(u_{11}+u_{22}+u_{33})-u_{43}v_{34},\qquad V_{3}=-v_{44}, \end{aligned}$$

and

$$\begin{aligned}& u_{11}=-(d+\beta_{1}P_{*}+\beta_{2}H_{*}),\qquad u_{12}=-\beta_{1}S_{*},\qquad u_{13}=-\beta_{2}S_{*}, \\& u_{21}=\beta_{1}P_{*}+\beta_{2}H_{*},\qquad u_{22}=\beta_{1}S_{*}-(\pi+d+\gamma),\qquad u_{23}= \beta_{2}S_{*}, \\& u_{32}=\pi,\qquad u_{33}=-(\sigma+d),\qquad u_{42}=\gamma, u_{43}=\sigma,\qquad u_{44}=-d,\\& v_{34}=\theta,\qquad v_{44}=-\theta. \end{aligned}$$

When \(\tau=0\), the characteristic equation becomes

$$ \lambda^{4}+U_{03}\lambda^{3}+U_{02} \lambda^{2}+U_{01}\lambda+U_{00}=0. $$
(5)

We denote

$$U_{00}=U_{0}+V_{0},\qquad U_{01}=U_{1}+V_{1},\qquad U_{02}=U_{2}+V_{2},\qquad U_{03}=U_{3}+V_{3}. $$

and suppose that

$$(C_{1}){:}\quad U_{00}>0,\qquad U_{03}>0,\qquad U_{02}U_{03}>U_{01},\qquad U_{01}U_{02}U_{03}>U_{00}U_{03}^{2}+U_{01}^{2}. $$

It follows from the Routh–Hurwitz theorem that if the condition \((C_{1})\) holds, all roots of Eq. (5) have negative real parts.

For \(\tau>0\), assume that \(\lambda=i\omega\) with \(\omega>0\) is the root of Eq. (4), then we obtain

$$ \left \{ \textstyle\begin{array}{l} (V_{1}\omega-V_{3}\omega^{3})\sin\tau\omega+(V_{0}-V_{2}\omega^{2})\cos\tau \omega=U_{2}\omega^{2}-\omega^{4}-U_{0}, \\ (V_{1}\omega-V_{3}\omega^{3})\cos\tau\omega-(V_{0}-V_{2}\omega^{2})\sin\tau \omega=U_{3}\omega^{3}-U_{1}\omega. \end{array}\displaystyle \right . $$
(6)

This leads to

$$ \omega^{8}+d_{3}\omega^{6}+d_{2} \omega^{4}+d_{1}\omega^{2}+d_{0}=0, $$
(7)

with

$$\begin{aligned}& d_{0}=U_{0}^{2}-V_{0}^{2},\qquad d_{1}=U_{1}^{2}-2U_{0}U_{2}-V_{0}^{2}+2V_{0}V_{2}, \\& d_{2}=U_{2}^{2}+2U_{0}-2U_{1}U_{3}-V_{2}^{2}+2V_{1}V_{3},\qquad d_{3}=U_{3}^{2}-2U_{2}-V_{3}^{2}. \end{aligned}$$

Letting \(\omega^{2}=\chi\), we can rewrite Eq. (7) as follows:

$$ \chi^{4}+d_{3}\chi^{3}+d_{2} \chi^{2}+d_{1}\chi+d_{0}=0. $$
(8)

Lemma 1

If\(d_{0}<0\)Eq. (8) has at least one positive root.

Suppose that \(d_{0}\geq0\). Based on a similar discussion of the distribution of the roots of Eq. (8) in [32], we define

$$ h(\chi)=\chi^{4}+d_{3}\chi^{3}+d_{2} \chi^{2}+d_{1}\chi+d_{0}=0. $$
(9)

Then

$$ h^{\prime}(\chi)=4\chi^{3}+3d_{3} \chi^{2}+2d_{2}\chi+d_{1}. $$
(10)

Let

$$ 4\chi^{3}+3d_{3}\chi^{2}+2d_{2} \chi+d_{1}=0, $$
(11)

and \(z=\chi+\frac{3d_{3}}{4}\). Then Eq. (11) becomes

$$ z^{3}+\alpha_{1}z+\beta_{1}=0, $$
(12)

with

$$\alpha_{1}=\frac{d_{2}}{2}-\frac{3}{16}d_{3}^{2},\qquad \beta_{1}=\frac {d_{3}^{3}}{32}-\frac{d_{3}d_{2}}{8}+d_{1}. $$

Denote

$$\begin{gathered} D= \biggl(\frac{\beta_{1}}{2} \biggr)+ \biggl(\frac{\alpha_{1}}{3} \biggr),\qquad \nu= \frac{-1+\sqrt{3}i}{2}, \\ z_{1}=\sqrt[3]{-\frac{\beta_{1}}{2}+\sqrt{D}}+\sqrt[3]{- \frac{\beta _{1}}{2}-\sqrt{D}}, \\ z_{2}=\sqrt[3]{-\frac{\beta_{1}}{2}+\sqrt{D}}\nu+\sqrt[3]{- \frac {\beta_{1}}{2}-\sqrt{D}}\nu^{2}, \\ z_{3}=\sqrt[3]{-\frac{\beta_{1}}{2}+\sqrt{D}}\nu^{2}+ \sqrt[3]{-\frac {\beta_{1}}{2}-\sqrt{D}}\nu, \\ \chi_{i}=z_{i}-\frac{3d_{3}}{4},\quad i=1, 2, 3.\end{gathered} $$
(13)

Lemma 2

If\(D\geq0\), then Eq. (8) has positive roots if and only if\(\chi_{1}>0\)and\(h(\chi_{1})<0\); if\(D<0\), then Eq. (8) has positive roots if and only if there exists at least one\(\chi^{*}\in\{\chi_{1}, \chi_{2}, \chi_{3}\}\), such that\(\chi^{*}>0\)and\(h(\chi^{*})\leq0\).

Thus, if the condition\((C_{2})\)holds: (i) \(d_{0}<0\)or (ii) \(d_{0}\geq0\), \(D\geq0\), \(\chi_{1}>0\)and\(h(z_{1})\leq0\)or (iii) \(d_{0}\geq0\), \(D<0\), and there exists a\(\chi^{*}\in\{\chi_{1}, \chi_{2}, \chi_{3}\}\), such that\(\chi^{*}>0\)and\(h(\chi^{*})\leq0\), then Eq. (8) has at least one positive root.

Without loss of generality, we assume that Eq. (8) has four positive roots, denoted by \(\chi_{1}\), \(\chi_{2}\), \(\chi_{3}\) and \(\chi_{4}\). Then Eq. (7) has a positive root \(\omega_{i}=\sqrt{\chi _{i}}\), \(i=1, 2, 3, 4\). From Eq. (6), we have

$$ \tau_{i}^{j}=\left \{ \textstyle\begin{array}{l@{\quad}l} \frac{1}{\omega_{i}}\times\arccos \{\frac{l_{7}\omega _{i}^{6}+l_{6}\omega_{i}^{4}+l_{5}\omega_{i}^{2}+l_{4}}{l_{3}\omega_{i}^{6}+l_{2}\omega _{i}^{4}+l_{1}\omega_{i}^{2}+l_{0}} \}+2j\pi,& \sin(\tau_{i}\omega_{i})\geq0, \\ [3pt] \frac{1}{\omega_{i}}\times [2\pi-\arccos \{\frac {l_{7}\omega_{i}^{6}+l_{6}\omega_{i}^{4}+l_{5}\omega_{i}^{2}+l_{4}}{l_{3}\omega _{i}^{6}+l_{2}\omega_{i}^{4}+l_{1}\omega_{i}^{2}+l_{0}} \} ]+2j\pi,& \sin (\tau_{i}\omega_{i})< 0. \end{array}\displaystyle \right . $$
(14)

with \(i=1, 2, 3, 4\), \(j=0, 1, 2, \dots \), and

$$\begin{aligned}& l_{0}=V_{0}^{2},\quad\quad l_{1}=V_{1}^{2}-2V_{0}V_{2},\qquad l_{2}=V_{2}^{2}-2V_{1}V_{3},\quad\quad l_{3}=V_{3}^{2},\qquad l_{4}=-U_{0}V_{0}, \\& l_{5}=U_{0}V_{2}+U_{2}V_{0}-U_{1}V_{1},\qquad l_{6}=U_{1}V_{3}+U_{3}V_{1}-U_{2}V_{2}-V_{0},\qquad l_{7}=V_{2}-U_{3}V_{3}. \end{aligned}$$

Define

$$ \tau_{0}=\text{min}\bigl\{ \tau_{i}^{0}|i=1, 2, 3, 4\bigr\} , $$
(15)

such that Eq. (4) has a pair of purely imaginary roots \(\omega_{0}\) when \(\tau=\tau_{0}\).

Next, we examine the transversality condition. Differentiating Eq. (4) with regard to τ, we obtain the derivative of τ as follows:

$$ \biggl[\frac{d\lambda}{d\tau} \biggr]^{-1}=- \frac{4\lambda ^{4}+3U_{3}\lambda^{2}+2U_{2}\lambda+U_{1}}{\lambda(\lambda^{4}+U_{3}\lambda ^{3}+U_{2}\lambda^{2}+U_{1}\lambda+U_{0})}+\frac{3V_{3}\lambda^{2}+2V_{2}\lambda +V_{1}}{\lambda(V_{3}\lambda^{3}+V_{2}\lambda^{2}+V_{1}\lambda+V_{0})}-\frac {\lambda}{\tau}. $$
(16)

Replacing λ by \(i\omega_{0}\), we obtain

$$ \biggl[\frac{d\lambda}{d\tau} \biggr]^{-1}_{\lambda=i\omega _{0}}= \frac{h^{\prime}(\chi_{0})}{l_{3}\omega_{0}^{6}+l_{2}\omega_{0}^{4}+l_{1}\omega _{0}^{2}+l_{0}}, $$
(17)

where \(h(\chi)=\chi^{4}+d_{3}\chi^{3}+d_{2}\chi^{2}+d_{1}\chi+d_{0}\) and \(\chi _{0}=\omega_{0}^{2}\).

Therefore, if the condition \((C_{3})\): \(h^{\prime}(\chi_{0})\neq0\) holds, then the transversality condition is satisfied. Based on the discussion above and the fundamental Hopf bifurcation theorem in [33], we are able to formulate the following theorem.

Theorem 1

For system (2), if the conditions\((C_{1})\)–\((C_{3})\)hold, then the synthetic drug addiction equilibrium\(D_{*}(S_{*}, P_{*}, H_{*}, T_{*})\)is locally asymptotically stable when\(\tau_{\in}[0, \tau_{0})\); system (2) undergoes a Hopf bifurcation at the synthetic drug addiction equilibrium\(D_{*}(S_{*}, P_{*}, H_{*}, T_{*})\)when\(\tau=\tau_{0}\)and a family of periodic solutions bifurcate from the synthetic drug addiction equilibrium\(D_{*}(S_{*}, P_{*}, H_{*}, T_{*})\).

3 Direction and stability of Hopf bifurcation

In this section, direction and stability of Hopf bifurcation will be studied by using center manifold theorem and normal form theory introduced by Hassard et al. [33]. Let \(\tau=\tau_{0}+\mu\), \(\mu\in R\), \(u_{1}(t)=S(\tau t)\), \(u_{2}(t)=P(\tau t)\), \(u_{3}(t)=H(\tau t)\) and \(u_{4}(t)=T(\tau t)\). System (2) can be written in a functional differential equation in \(C=C([-1, 0], R^{4})\) as follows:

$$ \dot{u}(t)=L_{\mu}(u_{t})+F(\mu, u_{t}), $$
(18)

where \(u(t+\theta)=u_{t}(\theta)\), \(L_{\mu}: C\rightarrow R^{4}\) and \(F: R\times C\rightarrow R^{4}\),

$$\begin{aligned}& L_{\mu}\phi=(\tau_{0}+\mu) \bigl(U\phi(0)+V \phi(-1) \bigr), \end{aligned}$$
(19)
$$\begin{aligned}& F(\mu,\phi)=\left ( \textstyle\begin{array}{c} -\beta_{1}\phi_{1}(0)\phi_{2}(0)-\beta_{2}\phi_{1}(0)\phi_{3}(0)\\ \beta_{1}\phi_{1}(0)\phi_{2}(0)+\beta_{2}\phi_{1}(0)\phi_{3}(0)\\ {0}\\ {0} \end{array}\displaystyle \right ), \\& U_{\text{trix}}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} u_{11} &u_{12} &u_{13} &{0}\\ u_{21} &u_{22} &u_{23} &{0}\\ {0} &u_{32} &u_{33} &{0}\\ {0} &u_{42} &u_{43} &u_{44} \end{array}\displaystyle \right ),\qquad V_{\text{trix}}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} {0} &{0} &{0} &{0}\\ {0} &{0} &{0} &{0}\\ {0} &{0} &{0} &v_{34}\\ {0} &{0} &{0} &v_{44} \end{array}\displaystyle \right ). \end{aligned}$$
(20)

By using the Riesz representation theorem, let \(\eta(\theta, \mu ):[-1, 0]\rightarrow R^{4\times4}\) be a function of bounded variation. For \(\phi\in C[-1, 0]\), let

$$ L_{\mu}\phi= \int_{-1}^{0}d\eta(\theta, \mu)\phi(\theta). $$
(21)

Moreover, we can choose

$$ \eta(\theta, \mu)=(\tau_{0}+\mu) \bigl(U_{\text{trix}} \delta (\theta)+V_{\text{trix}}\delta(\theta+1) \bigr), $$
(22)

where \(\delta(\theta)\) is the Dirac delta function.

Define

$$ A(\mu)\phi=\left \{ \textstyle\begin{array}{l@{\quad}l} \frac{d\phi(\theta)}{d\theta}, &-1\leq\theta< 0, \\ [2pt] \int_{-1}^{0}d\eta(\theta,\varrho)\phi(\theta), & \theta=0, \end{array}\displaystyle \right . $$
(23)

and

$$ R(\mu)\phi=\left \{ \textstyle\begin{array}{l@{\quad}l} 0, &-1\leq\theta< 0, \\ F(\mu,\phi),& \theta=0, \end{array}\displaystyle \right . $$
(24)

where \(\phi\in C([-1,0], R^{4})\). Then system (18) is equivalent to

$$ \dot{u}(t)=A(\mu)u_{t}+R(\mu)u_{t}. $$
(25)

For \(\varphi\in C^{1}([0, 1], (R^{4})^{*})\), define the adjoint operator of \(A(0)\) as follows:

$$ A^{*}(\varphi)=\left \{ \textstyle\begin{array}{l@{\quad}l} -\frac{d\varphi(s)}{ds}, &0< s\leq1, \\ [2pt] \int_{-1}^{0}d{\eta}^{T}(s,0)\varphi(-s),& s=0, \end{array}\displaystyle \right . $$
(26)

and the inner product form

$$ \bigl\langle \varphi(s),\phi(\theta)\bigr\rangle =\bar{\varphi}(0) \phi (0)- \int_{\theta=-1}^{0} \int_{\xi=0}^{\theta}\bar{\varphi}(\xi -\theta)\,d\eta(\theta) \phi(\xi)\,d\xi, $$
(27)

with \(\eta(\theta)=\eta(\theta, 0)\).

Let \(g(\theta)=(1, g_{2}, g_{3}, g_{4})^{T}e^{i\tau_{0}\omega_{0}\theta}\) denote a eigenvector of \(A(0)\) and \(+i\tau_{0}\omega_{0}\) is the associated eigenvalue; \(\tilde{g}^{*}(\theta)=\tilde{G}(1, g_{2}^{*}, g_{3}^{*}, g_{4}^{*})^{T}e^{i\tau_{0}\omega_{0}\theta}\) denotes a eigenvector of \(A^{*}\) and \(-i\tau_{0}\omega_{0}\) is the associated eigenvalue. Then we obtain

$$\begin{aligned}& g_{2}=\frac{u_{23}(i\omega _{0}-u_{11})+u_{13}u_{21}}{u_{12}u_{23}+u_{13}(i\omega _{0}-u_{22})}, \\& g_{3}=\frac{(i\omega_{0}-u_{22})g_{2}-u_{21}}{u_{23}}, \\& g_{4}=\frac{u_{42}g_{2}+u_{43}g_{3}}{i\omega_{0}-u_{44}-v_{44}e^{-i\tau _{0}\omega_{0}}}, \\& g_{2}^{*}=-\frac{i\omega_{0}+u_{11}}{u_{21}}, \\& g_{3}^{*}=\frac{[u_{43}(i\omega_{0}+u_{22})-u_{23}u_{42}]\tilde {g}_{2}^{*}+u_{12}u_{43}-u_{13}u_{42}}{u_{42}(i\omega _{0}+u_{33})-u_{32}u_{43}}, \\& g_{4}^{*}=-\frac{v_{34}e^{i\tau_{0}\omega_{0}}\tilde{g}_{3}^{*}}{i\omega _{0}+u_{44}+v_{44}e^{i\tau_{0}\omega_{0}}}. \end{aligned}$$

From Eq. (27), we can obtain

$$ \bigl\langle g^{*}, g\bigr\rangle =\bar{G}\bigl[1+g_{2} \bar{g}_{2}^{*}+g_{3}\bar {g}_{3}^{*}+g_{4} \bar{g}_{4}^{*}+\tau_{0}e^{-i\tau_{0}\omega _{0}}g_{4} \bigl(v_{34}g_{3}^{*}+v_{44}g_{4}\bigr) \bigr]. $$
(28)

Let \(\langle g^{*}, g\rangle=1\), then

$$ \bar{G}=\bigl[1+g_{2}\bar{g}_{2}^{*}+g_{3} \bar{g}_{3}^{*}+g_{4}\bar{g}_{4}^{*}+\tau _{0}e^{-i\tau_{0}\omega_{0}}g_{4}\bigl(v_{34}g_{3}^{*}+v_{44}g_{4} \bigr)\bigr]^{-1}. $$
(29)

In the following part of this section, we use the similar computation process as that in [34–38] and then obtain the expressions of \(g_{20}\), \(g_{11}\), \(g_{02}\) and \(g_{21}\):

$$\begin{aligned}& g_{20}=2\bar{G}\tau_{0}\bigl(\bar{g}_{2}^{*}-1 \bigr) (\beta_{1}g_{2}+\beta _{2}g_{3}), \\& g_{11}=\bar{G}\tau_{0}\bigl(\bar{g}_{2}^{*}-1 \bigr)\bigl[\beta_{1}(g_{2}+\bar{g}_{2})+\beta _{2}(g_{3}+\bar{g}_{3})\bigr], \\ & g_{02}=2\bar{G}\tau_{0}\bigl(\bar{g}_{2}^{*}-1 \bigr) (\beta_{1}\bar{g}_{2}+\beta _{2} \bar{g}_{3}), \\ & g_{21}=2\bar{G}\tau_{0}\bigl(\bar{g}_{2}^{*}-1 \bigr) \biggl[\beta_{1} \biggl(W_{11}^{(1)}(0)g_{2}+ \frac{1}{2}W_{20}^{(1)}(0)\bar {g}_{2}+W_{11}^{(2)}(0)+ \frac{1}{2}W_{20}^{(2)}(0) \biggr) \\ & \phantom{g_{21}=}{}+\beta_{2} \biggl(W_{11}^{(1)}(0)g_{3}+ \frac{1}{2}W_{20}^{(1)}(0)\bar {g}_{3}+W_{11}^{(3)}(0)+ \frac{1}{2}W_{20}^{(3)}(0) \biggr) \biggr], \end{aligned}$$

with

$$\begin{aligned}& W_{20}(\theta)=\frac{ig_{20}g(0)}{\tau_{0}\omega_{0}}e^{i\tau _{0}\omega_{0}\theta}+ \frac{i\bar{g}_{02}\bar{g}(0)}{3\tau_{0}\omega _{0}}e^{-i\tau_{0}\omega_{0}\theta}+E_{1}e^{2i\tau_{0}\omega_{0}\theta}, \end{aligned}$$
(30)
$$\begin{aligned}& W_{11}(\theta)=-\frac{ig_{11}g(0)}{\tau_{0}\omega_{0}}e^{i\tau _{0}\omega_{0}\theta}+ \frac{i\bar{g}_{11}\bar{g}(0)}{\tau_{0}\omega _{0}}e^{-i\tau_{0}\omega_{0}\theta}+E_{2}. \end{aligned}$$
(31)

\(E_{1}\) and \(E_{2}\) can be obtained by the following two equations:

$$\begin{aligned}& \begin{aligned}E_{1}&=2\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 2i\omega_{0}-u_{11} &-u_{12} &-u_{13} &{0}\\ -u_{21} &2i\omega_{0}-u_{22} &-u_{23} &{0}\\ [-1pt] {0} &-u_{32} &2i\omega_{0}-u_{33} &-v_{34}e^{-2i\tau_{0}\omega_{0}}\\ {0} &-u_{42} &-u_{43} &2i\omega_{0}-u_{44}-v_{44}e^{-2i\tau_{0}\omega_{0}} \end{array}\displaystyle \right )^{-1}\\ &\quad\times \left ( \textstyle\begin{array}{c} -\beta_{1}g_{2}-\beta_{2}g_{3}\\ [-1pt] \beta_{1}g_{2}+\beta_{2}g_{3}\\ [-1pt] {0}\\ [-1pt] {0} \end{array}\displaystyle \right ),\end{aligned} \\& E_{2}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} u_{11} &u_{12} &u_{13} &{0}\\ u_{21} &u_{22} &u_{23} &{0}\\ {0} &u_{32} &u_{33} &v_{34}\\ {0} &u_{42} &u_{43} &u_{44}+v_{44} \end{array}\displaystyle \right )^{-1}\times \left ( \textstyle\begin{array}{c} -\beta_{1}(g_{2}+\bar{g}_{2})-\beta_{2}(g_{3}+\bar{g}_{3})\\ \beta_{1}(g_{2}+\bar{g}_{2})+\beta_{2}(g_{3}+\bar{g}_{3})\\ {0}\\ {0} \end{array}\displaystyle \right ). \end{aligned}$$

Then we obtain

$$ \left . \begin{gathered} C_{1}(0)=\frac{i}{2\tau_{0}\omega_{0}} \biggl(g_{11}g_{20}-2 \vert g_{11} \vert ^{2}-\frac{ \vert g_{02} \vert ^{2}}{3} \biggr)+\frac {g_{21}}{2},\\ \mu_{2} =-\frac{\text{Re}\{C_{1}(0)\}}{\text{Re}\{\lambda^{\prime}(\tau _{0})\}}, \\ \beta_{2}=2{\text{Re}\bigl\{ C_{1}(0)\bigr\} }, \\ T_{2}=-\frac{\text{Im}\{C_{1}(0)\}+\mu_{2}\text{Im}\{\lambda^{\prime}(\tau_{0})\}}{\tau_{0}\omega_{0}}. \end{gathered} \right . $$
(32)

From the above formulas, we can conclude as follows.

Theorem 2

For system (2), the following results hold. If\(\mu_{2}>0\) (\(\mu_{2}<0\)), then the Hopf bifurcation is supercritical (subcritical); if\(\beta_{2}<0\) (\(\beta_{2}>0\)), then the bifurcating periodic solutions are stable (unstable); if\(T_{2}>0\) (\(T_{2}<0\)), then the period of the bifurcating periodic solutions increase (decrease).

4 Numerical simulations

In this section, we carry out computer simulations using the Matlab software package to illustrate the obtained theoretical results. Taking \(A=2\), \(d=0.02\), \(\beta_{1}=0.016\), \(\beta_{2}=0.028\), \(\pi =0.03\), \(\gamma=0.095\), \(\theta=0.5\) and \(\sigma=0.421\), we obtain the following specific case of system (2):

$$ \left \{ \textstyle\begin{array}{l} \frac{dS(t)}{dt}=2-0.02 S(t)-0.016 S(t)P(t)-0.028 S(t)H(t), \\ \frac{dP(t)}{dt}=0.016 S(t)P(t)+0.028 S(t)H(t)-0.145 P(t), \\ [3pt] \frac{dH(t)}{dt}=0.03 P(t)+0.5 T(t-\tau)-0.441 H(t), \\ \frac{dT(t)}{dt}=0.095 P(t)+0.421 H(t)-0.5 T(t-\tau)-0.02 T(t). \end{array}\displaystyle \right . $$
(33)

Then one can obtain \(\Re_{0}=12.3481>1\) and the unique synthetic drug addiction equilibrium \(D_{*}(1.3196, 13.6111, 45.6355, 39.4338)\) of system (33). Through some calculations, Eq. (8) becomes

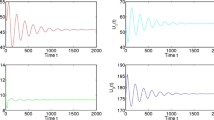
$$ \chi^{4}+0.0095\chi^{3}+1.0218 \chi^{2}-0.2006\chi-3.21=0. $$
(34)

Thus, it is easy to see that Eq. (34) has one positive root \(\chi_{0}=1.1885\). Then we obtain \(\omega_{0}=1.0902\) and \(\tau _{0}=9.7367\), \(h^{\prime}(\chi_{0})=7.7692>0\). According to Theorem 1, we can conclude that the synthetic drug addiction equilibrium \(D_{*}(1.3196, 13.6111, 45.6355, 39.4338)\) of system (33) is locally asymptotically stable when \(\tau\in[0, 9.7367)\), and a Hopf bifurcation appears when the value of τ passes through the critical value 9.7367, which can be indicated by bifurcation diagrams in Fig. 1. Furthermore, based on Eq. (32), \(\mu _{2}=1.5613>0\), \(\beta_{2}=-2.07<0\) and \(T_{2}=0.3611>0\) can be obtained. Accordingly, through Theorem 2, it can be concluded that the Hopf bifurcation at \(\tau_{0}\) is supercritical; the bifurcating periodic solutions are stable and increasing.

Figure 1
figure 1

The bifurcation diagram with respect to τ

Full size image

In addition, Fig. 2 manifests that the numbers of susceptibles and drug-users in treatment decrease, whereas the numbers of the psychological and physiological addicts increase as we increase θ from 0.5 to 0.6. Also, due to the increase in θ from 0.5 to 0.6, system (33) loses its stability and shows limit cycle behavior, which is illustrated in Fig. 3. It is interesting to note that Fig. 4 reveals the reverse effect of increasing σ in a particular range on the four populations in system (33). Figure 5 shows that system (33) changes its behavior from limit cycle to stable focus as we increase the value of σ.

Figure 2
figure 2

Time plots of S, P, H and T for different θ at \(\tau=5.835\). The remaining parameters are taken as given in the text

Full size image
Figure 3
figure 3

The phase plots of system (33) for different θ at \(\tau=5.7850\). The remaining parameters are taken as given in the text

Full size image
Figure 4
figure 4

Time plots of S, P, H and T for different σ at \(\tau=4.738\). The remaining parameters are taken as given in the text

Full size image
Figure 5
figure 5

The phase plots of system (33) for different σ at \(\tau=4.6805\). The remaining parameters are taken as given in the text

Full size image

5 Conclusions

The prevention and control of synthetic drugs have received great attention due to their increasingly serious consequences on population. Quite a few mathematical models describing synthetic drugs transmission have been put up by scholars at home and abroad in recent years. However, these models neglect the time delay during the process of synthetic drugs transmission. In the present article, synthetic drugs transmission model with time delay is established based on the work in [25]. A series of sufficient criteria guaranteeing the stability and appearance of Hopf bifurcation for the established model are derived by analyzing the corresponding characteristic equation. Moreover, the properties of the Hopf bifurcation are investigated by using the center manifold theorem and normal form theory.

The study shows that the time delay has an important impact on the stability and Hopf bifurcation of the model. When the value of the time delay is below the critical value \(\tau_{0}\), synthetic drugs transmission can be predicted and controlled. Contrarily, synthetic drugs transmission will be out of control once the value of the time delay passes through the critical value. Also, we observed that the change of the parameters of θ and σ in a particular range can affect the dynamics of the system based on numerical simulations. Since the numbers of the psychological and physiological addicts increase with the increase of θ but with the decrease of σ, it is strongly suggested that drug-users should have strong will once they decide to give up drugs. On the other hand, any person who has been contaminated with drugs should go to the regular detoxification center in time for treatment.