Abstract
This paper is concerned with a stage-structured predator-prey system with Holling-II functional response and two delays. Choosing a possible combination of the two delays as the bifurcation parameter, the existence of the Hopf bifurcation of the system is discussed. Furthermore, the properties of the Hopf bifurcation such as the direction and the stability are determined by using the normal form method and center manifold theorem. Finally, some numerical simulations are presented to justify the theoretical results.
Similar content being viewed by others
1 Introduction
It is well known that there are many species whose individual members have a life history that takes them through an immature stage and a mature stage. Based on this fact, stage-structured predator-prey systems have been investigated by many authors in recent years [1–8]. In [5], Xu considered the global stability and permanence of a predator-prey system with a stage structure for the predator:
where \(x(t)\) represents the density of the prey at time t. \(y_{1}(t)\) and \(y_{2}(t)\) represent the densities of the immature predator and the mature predator at time t, respectively. In [7], Li and Li investigated the Hopf bifurcation problem of a predator-prey system with stage structure for the prey:
where \(x_{1}(t)\) and \(x_{2}(t)\) represent the densities of the immature prey and the mature prey at time t, respectively. \(y(t)\) represents the density of the predator at time t.
Obviously, all the above researchers consider predator-prey systems with stage structure only for the predator or the prey. Since both predator and prey have a life history that takes them through an immature stage and a mature stage, it is reasonable to consider the predator-prey system with a stage structure for both the predator and the prey. Based on this consideration, Wang and Feng [9] proposed a predator-prey system with a stage structure for both the predator and the prey:
where \(x_{1}(t)\) and \(x_{2}(t)\) represent the densities of the immature prey and the mature prey at time t, respectively. \(y_{1}(t)\) and \(y_{2}(t)\) represent the densities of the immature predator and the mature predator at time t, respectively. a is the intra-specific competition rate among the mature prey; \(a_{1}\) is the predation rate of the mature predator; \(a_{2}\) is the conversion factor from the mature prey to the immature predator; \(d_{1}\), \(d_{2}\), \(d_{3}\), and \(d_{4}\) are the death rates of the immature prey, mature prey, immature predator, and mature predator, respectively. \(r_{1}\) (\(r_{2}\)) is the transformation rate from the immature prey (predator) to the mature prey (predator). r is the birth rate of the immature prey and m is the half saturation rate of the mature predator. Wang and Feng [9] studied the local and global stability of system (3).
As is well known, it is necessary to incorporate time delay into dynamical systems in order to reflect the dynamics of the systems depending on the past history of the systems. Dynamical systems with time delay have been investigated by many authors [10–13]. Ferrara et al. [10] investigated the properties of the Hopf bifurcation of a delayed continuous-time growth model with a special mound-shaped production function. Bianca et al. [12] studied the existence and properties of Hopf bifurcations in a delayed-energy-based model of capital accumulation. There are also some dynamical systems with two or multiple delays that have been studied by some scholars [14–21]. In [14], Bianca et al. studied the Hopf bifurcation of an economic growth model with two delays. In [16], Cui and Yan investigated a three-species Lotka-Volterra food chain system with two delays by taking the sum of the two delays as the bifurcation parameter and showed the effects of the two delays on the dynamical behaviors of the system. In [17], Meng et al. considered a two-competitor, one-prey system with two feedback delays and they investigated the Hopf bifurcation problem by choosing the possible combination of the two delays as the bifurcation parameter. They also discussed the direction of the Hopf bifurcation and stability of the bifurcating periodic solutions by using a center manifold theorem and the normal form method. To the best of our knowledge, there are few papers on the effect of time delays on system (3). Based on this and motivated by the work above, in the present paper, we incorporate the feedback delay of the mature prey and the time delay due to the gestation of the mature predator into system (3) and investigate the Hopf bifurcation of the following delayed system:
where \(\tau_{1}\) is the feedback delay of the mature prey and \(\tau_{2}\) is the time delay due to the gestation of the mature predator.
This paper is organized as follows. In Section 2, we discuss the local stability of the positive equilibrium and the existence of local Hopf bifurcation of system (4). In Section 3, the properties of the Hopf bifurcation such as the direction and stability are determined by using the normal form method and center manifold theorem. Some numerical simulations are performed to illustrate the theoretical results in Section 4. In Section 5, we derive some concluding remarks concerning the whole analysis.
2 Local stability of positive equilibrium and existence of Hopf bifurcation
It is easy to show that if \(a_{2}r_{2}>md_{4}(r_{2}+d_{3})\) and \(\frac{rr_{1}}{r_{1}+d_{1}}>d_{2}+\frac{ad_{4}(r_{2}+d_{3})}{a_{2}r_{2}-md_{4}(r_{2}+d_{3})}\), then system (4) has a unique positive equilibrium \(E^{*}(x_{1}^{*}, x_{2}^{*}, y_{1}^{*}, y_{2}^{*})\), where
Let \(\bar{x}_{1}(t)=x_{1}(t)-x_{1}^{*}\), \(\bar{x}_{2}(t)=x_{2}(t)-x_{2}^{*}\), \(\bar{y}_{1}(t)=y_{1}(t)-y_{1}^{*}\), \(\bar{y}_{2}(t)=y_{2}(t)-y_{2}^{*}\). Dropping the bars for convenience, system (4) gets the following form:
where
and
with
The linearized system of (5) is
The characteristic equation of system (6) at the positive equilibrium \(E^{*}\) is of the form
where
Case 1. \(\tau_{1}=\tau_{2}=0\). Equation (7) becomes
where
Obviously, \(\operatorname{det}_{1}=A_{13}=d_{1}+d_{2}+d_{3}+d_{4}+r_{1}+r_{2}+2ax_{2}^{*}+\frac {a_{1}y_{2}^{*}}{(1+mx_{2}^{*})^{2}}>0\). Thus, all roots of (8) have negative real parts if the condition (H1): (9) is satisfied. We have
Thus, the positive equilibrium of system (4) without delay is locally asymptotically stable under the condition (H1): (9) holds.
Case 2. \(\tau_{1}>0\), \(\tau_{2}=0\).
When \(\tau_{2}=0\), (7) becomes
where
Let \(\lambda=i\omega_{1}\) (\(\omega_{1}>0\)) be a root of (10). Then
from which it follows that
where
Let \(\omega_{1}^{2}=v_{1}\), then (11) becomes
Discussion of the roots of (12) is similar to that in [22]. Denote
Clearly, if \(e_{20}<0\), then (12) has at least one positive root. From (13), one can get
Set
Let \(y_{1}=v_{1}+\frac{3e_{23}}{4}\). Then (14) becomes
where
Define
Then we have the following results according to the Lemma 2.2 in [22].
Lemma 1
For (12),
-
(i)
if \(e_{20}\geq0\) and \(\alpha_{1}\geq0\), then (12) has positive roots if and only if \(v_{11}>0\) and \(f_{1}(v_{11})<0\);
-
(ii)
if \(e_{20}\geq0\) and \(\alpha_{1}<0\), then (12) has positive roots if and only if there exists at least one \(v_{1*}\in\{ v_{11}, v_{12}, v_{13}\}\), such that \(v_{1*}>0\) and \(f_{1}(v_{1*})\leq0\).
In what follows, we assume that we have (H21): the coefficients in \(f_{1}(v_{1})\) satisfy one of the following conditions in (α)-(γ): (α) \(e_{20}<0\); (β) \(e_{20}\geq0\), \(\alpha _{1}\geq0\), \(v_{11}>0\), and \(f_{1}(v_{11})<0\); (γ) \(e_{20}\geq0\), \(\alpha_{1}<0\), and there exists at least one \(v_{1*}\in\{v_{11}, v_{12}, v_{13}\}\), such that \(v_{1*}>0\) and \(f_{1}(v_{1*})\leq0\).
If the condition (H21) holds, (11) has at least one positive root \(\omega_{10}\) such that (10) has a pair of purely imaginary roots \(\pm i\omega_{10}\) and the corresponding critical value of the delay is
Differentiating the two sides of (10), we can get
Thus,
where \(v_{1}^{*}=\omega_{10}^{2}\). Obviously, if the condition (H22): \(f_{1}^{\prime}(v_{1}^{*})\neq0\) holds, then \(\operatorname{Re}[\frac{d\lambda}{d\tau_{1}}]^{-1}_{\tau_{1}=\tau_{10}}\neq 0\). In conclusion, we have the following results according to the Hopf bifurcation theorem in [23].
Theorem 1
Suppose that the conditions (H21)-(H22) hold. The positive equilibrium \(E^{*}(x_{1}^{*}, x_{2}^{*}, y_{1}^{*}, y_{2}^{*})\) of system (4) is asymptotically stable for \(\tau_{1}\in[0,\tau_{10})\) and system (4) undergoes a Hopf bifurcation at \(E^{*}(x_{1}^{*}, x_{2}^{*}, y_{1}^{*}, y_{2}^{*})\) when \(\tau_{1}=\tau_{10}\).
Case 3. \(\tau_{2}>0\), \(\tau_{1}=0\).
Substitute \(\tau_{1}=0\) into (7) and we have
where
Let \(\lambda=i\omega_{2}\) (\(\omega_{2}>0\)) be the root of (15). Then
from which it follows that
where
Let \(\omega_{2}^{2}=v_{2}\), then (16) becomes
Define
Then
Set
Let \(y_{2}=v_{2}+\frac{3e_{33}}{4}\). Then (18) becomes
where
Define
According to Lemma 1, we can conclude that if we may consider the condition (H31): the coefficients in \(f_{2}(v_{2})\) satisfy one of the following conditions in (\(\alpha^{\prime}\))-(\(\gamma^{\prime}\)): (\(\alpha^{\prime}\)) \(e_{30}<0\); (\(\beta^{\prime}\)) \(e_{30}\geq0\), \(\alpha _{2}\geq\), \(v_{21}>0\), and \(f_{2}(v_{21})<0\); (\(\gamma^{\prime}\)) \(e_{30}\geq 0\), \(\alpha_{2}<0\), and there exists at least one \(v_{2*}\in\{v_{21}, v_{22}, v_{23}\}\), such that \(v_{2*}>0\) and \(f_{2}(v_{2*})\leq0\).
If the condition (H31) holds, (16) has at least one positive root \(\omega_{20}\) such that (15) has a pair of purely imaginary roots \(\pm i\omega_{20}\) and the corresponding critical value of the delay is
Similar as in Case 2, if the condition (H32): \(f_{2}^{\prime}(v_{2}^{*})\neq0\) holds, where \(v_{2}^{*}=\omega_{20}^{2}\), then \(\operatorname{Re}[\frac {d\lambda}{d\tau_{2}}]^{-1}_{\tau_{2}=\tau_{20}}\neq0\). In conclusion, we have the following results according to the Hopf bifurcation theorem in [23].
Theorem 2
Suppose that the conditions (H31)-(H32) hold. The positive equilibrium \(E^{*}(x_{1}^{*}, x_{2}^{*}, y_{1}^{*}, y_{2}^{*})\) of system (4) is asymptotically stable for \(\tau_{2}\in[0,\tau_{20})\) and system (4) undergoes a Hopf bifurcation at \(E^{*}E^{*}(x_{1}^{*}, x_{2}^{*}, y_{1}^{*}, y_{2}^{*})\) when \(\tau_{2}=\tau_{20}\).
Case 4. \(\tau_{1}=\tau_{2}=\tau>0\).
Substitute \(\tau_{1}=\tau_{2}=\tau\) into (7); then (7) becomes
where
Multiplying (19) by \(e^{\lambda\tau}\), then (19) becomes
Let \(\lambda=i\omega\) (\(\omega>0\)) be the root of (20), then
from which it follows that
where
Then we can obtain
where
Let \(\omega^{2}=v\), then (21) becomes
If the coefficients of system (4) are given, the roots of (22) can be obtained by the Matlab software package. Therefore, we make the following assumption in order to get the main results in this paper.
Suppose that (H41): (22) has at least one positive root.
If the condition (H41) holds, without loss of generality, we assume that (22) has eight positive roots which are denoted by \(v_{1}, v_{2}, \ldots, v_{8}\), respectively. Then (21) has eight positive roots \(\omega_{k}=\sqrt{v_{k}}\), \(k =1, 2, \ldots, 8\). For every \(\omega_{k}\), the corresponding critical value of the time delay is
Let
Thus, when \(\tau=\tau_{0}\), (20) has a pair of purely imaginary roots \(\pm i\omega_{0}\).
Differentiating both sides of (20) with respect to τ, we get
Then we have
where
Obviously, if the condition (H42): \(P_{41}Q_{41}+P_{42}Q_{42}\neq 0\) holds, then \(\operatorname{Re}[\frac{d\lambda}{d\tau}]^{-1}_{\tau=\tau_{0}}\neq0\). Thus, according to the Hopf bifurcation theorem in [23], we have the following results.
Theorem 3
Suppose that the conditions (H41)-(H42) hold. The positive equilibrium \(E^{*}(x_{1}^{*}, x_{2}^{*}, y_{1}^{*}, y_{2}^{*})\) of system (4) is asymptotically stable for \(\tau_{1}\in[0,\tau_{0})\) and system (4) undergoes a Hopf bifurcation at \(E^{*}(x_{1}^{*}, x_{2}^{*}, y_{1}^{*}, y_{2}^{*})\) when \(\tau=\tau_{0}\).
Case 5. \(\tau_{2}>0\) and \(\tau_{1}\in(0, \tau_{10})\). We consider (7) with \(\tau_{1}\) in its stable interval and \(\tau_{2}\) is considered as a parameter.
Let \(\lambda=i\omega_{2}^{\prime}\) (\(\omega_{2}^{\prime}>0\)) be the root of (7). Then we get
where
It follows that
where
Suppose that we have (H51): (23) has at least finite positive roots. We denote the positive roots of (23) as \(\omega_{21}^{\prime}, \omega_{22}^{\prime}, \ldots, \omega_{2k}^{\prime}\). Then, for every fixed \(\omega_{2i}^{\prime}\) (\(i=1, 2, \ldots, k\)), the corresponding critical value of time delay is
with \(i=1, 2, \ldots, k\); \(j=0, 1, 2,\ldots\) .
Let \(\tau_{20}^{*}=\min\{\tau_{2i}^{(0)\prime}| i=1, 2, \ldots, k\} \). When \(\tau_{2}=\tau_{20}^{*}\), (7) has a pair of purely imaginary roots \(\pm i\omega_{2}^{*}\) for \(\tau_{1}\in(0, \tau_{10})\). Differentiating (7) with respect to \(\tau_{2}\), one can obtain
with
Hence,
where
Obviously, if the condition (H52): \(P_{51}Q_{51}\neq P_{52}Q_{52}\) holds, then \(\operatorname{Re}[\frac{d\lambda}{d\tau_{2}}]^{-1}_{\tau=\tau _{20}^{*}}\neq0\). Namely, if the condition (H52) holds, the transversality condition is satisfied. Thus, according to the Hopf bifurcation theorem in [23], we have the following results.
Theorem 4
If the conditions (H51)-(H52) hold and \(\tau_{1}\in(0, \tau_{10})\), then the positive equilibrium \(E^{*}(x_{1}^{*}, x_{2}^{*}, y_{1}^{*}, y_{2}^{*})\) of system (4) is asymptotically stable for \(\tau_{2}\in[0,\tau_{20}^{*})\) and system (4) undergoes a Hopf bifurcation at \(E^{*}(x_{1}^{*}, x_{2}^{*}, y_{1}^{*}, y_{2}^{*})\) when \(\tau_{2}=\tau_{20}^{*}\).
3 Stability of bifurcating periodic solutions
In this section, we shall derive the explicit formulas determining the direction and stability of the bifurcating periodic solutions with respect to \(\tau_{2}\) for \(\tau_{1}\in(0, \tau_{10})\). Throughout this section, we assume that \(\tau_{1*}<\tau_{20}^{*}\) where \(\tau_{1*}\in(0,\tau_{10})\).
Let \(\tau_{2}=\mu+\tau_{20}^{*}\), \(u_{1}(t)=x_{1}(t)-x_{1}^{*}\), \(u_{2}(t)=x_{2}(t)-x_{2}^{*}\), \(u_{3}(t)=y_{1}(t)-y_{1}^{*}\), \(u_{4}(t)=y_{2}(t)-y_{2}^{*}\), and rescale the time delay \(t\rightarrow(t/\tau_{2})\), then system (4) can be rewritten as
where
and
with
Therefore, according to the Riesz representation theorem, there exists a \(4\times4\) matrix function \(\eta(\theta,\mu):[-1,0]\rightarrow R^{4}\) whose elements are of bounded variation such that
In fact, we choose
For \(\phi\in C([-1,0], R^{4})\), we define
and
Then system (24) can be transformed into the following operator equation:
where \(u_{t}=u(t+\theta)=(u_{1}(t+\theta), u_{2}(t+\theta), u_{3}(t+\theta), u_{4}(t+\theta))\) for \(\theta\in[-1, 0]\).
For \(\varphi\in C^{1}([0,1], (R^{4})^{*})\), where \((R^{4})^{*}\) is the 4-dimensional space of row vectors, we define the adjoint operator \(A^{*}\) of A:
and a bilinear inner product:
where \(\eta(\theta)=\eta(\theta, 0)\).
Let \(q(\theta)=(1, q_{2}, q_{3}, q_{4})^{T} e^{i\omega_{2}^{*}\tau_{20}^{*}\theta }\) be the eigenvectors of \(A(0)\) corresponding to the eigenvalue \(+i\omega_{2}^{*}\tau_{20}^{*}\) and \(q^{*}(s)=D(1, q_{2}^{*}, q_{3}^{*}, q_{4}^{*})e^{i\omega_{2}^{*}\tau_{20}^{*}}s\) be the eigenvectors of \(A^{*}(0)\) corresponding to the eigenvalue \(-i\omega_{2}^{*}\tau_{20}^{*}\). It is not difficult to verify that
From (26), we choose
such that \(\langle q^{*}, q\rangle=1\), \(\langle q^{*}, \bar{q}\rangle=0\).
In the remainder of this section, we obtain the coefficients that can determine direction of the Hopf bifurcation and stability of the bifurcating periodic solutions by using the algorithms given in [23] and using the computation process which is similar to that in [14]:
with
where \(E_{1}\) and \(E_{2}\) can be computed as the following equations, respectively:
with
Therefore, we can calculate the following values:
Based on the discussion above, we can obtain the following results.
Theorem 5
For system (4), if \(\mu_{2}>0\) (\(\mu _{2}<0\)), then the Hopf bifurcation is supercritical (subcritical); if \(\beta_{2}<0\) (\(\beta_{2}>0\)), then the bifurcating periodic solutions are stable (unstable); if \(T_{2}>0\) (\(T_{2}<0\)), then the period of the bifurcating periodic solutions increases (decreases).
4 Numerical example
In this section, we give a numerical example to support the theoretical results in Section 2 and Section 3. We consider the following system:
which has a unique positive equilibrium \(E^{*}(0.15695067, 0.10463378, 0.20218508, 1.21311045)\).
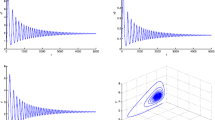
We have \(\tau_{1}>0\), \(\tau_{2}=0\). By some complex computations, we obtain \(\omega_{10}=2.5011\), \(\tau_{10}=1.3785\). Further, we have \(f_{1}^{\prime}(v_{1}^{*})=0.0914>0\). Thus, the conditions (H21) and (H22) hold. According to Theorem 1, the positive equilibrium \(E^{*}\) of system (28) is asymptotically stable when \(\tau_{1}<\tau_{10}\). This property can be illustrated by Figures 1 and 2. However, once \(\tau_{1}\) passes through the critical value \(\tau_{10}\), the positive equilibrium \(E^{*}\) of system (28) will lose its stability and a Hopf bifurcation occurs and a family of periodic solutions bifurcate from the positive equilibrium \(E^{*}\) of system (28), which can be shown as in Figures 3 and 4. This property can also be seen from the bifurcation diagram with respect to \(\tau_{1}\) in Figure 5. Similarly, we have \(\omega_{20}=0.7361\), \(\tau_{20}=8.7835\) for \(\tau_{1}=0\), \(\tau_{2}>0\). The corresponding waveforms, phase plots and bifurcation diagram are shown in Figures 6-10.
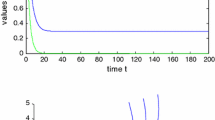
We have \(\tau_{1}=\tau_{2}=\tau>0\). We can obtain \(\omega_{0}=2.9285\) and then we get \(\tau_{0}=1.4126\). From Theorem 3, we can conclude that when τ increases from zero to \(\tau_{0}\) the positive equilibrium \(E^{*}\) of system (28) is asymptotically stable, then it will lose its stability and a Hopf bifurcation occurs once \(\tau>\tau_{0}\). As can be seen from Figures 11 and 12, when \(\tau=1.3820\in(0, 1.4126)\), the positive equilibrium \(E^{*}\) of system (28) is asymptotically stable. However, if we let \(\tau=1.4375>\tau_{0}=1.4126\), the positive equilibrium \(E^{*}\) of system (28) loses its stability and a Hopf bifurcation occurs, which can be shown as in Figures 13, 14 and 15.
We have \(\tau_{2}>0\) and \(\tau_{1}=1.05\in(0, \tau_{10})\). We can obtain \(\omega_{2}^{*}=0.3795\), \(\tau_{20}^{*}=10.3472\). By Theorem 4, the positive equilibrium \(E^{*}\) of system (28) is asymptotically stable when \(\tau_{2}\in[0, \tau_{20}^{*})\) and the positive equilibrium \(E^{*}\) of system (28) becomes unstable when \(\tau_{2}>\tau_{20}^{*}\) and a family of periodic solutions bifurcate from the positive equilibrium \(E^{*}\), which can be illustrated by Figures 16-20.
Finally, by complex computations, we obtain \(C_{1}(0)=-14.2305-23.6892i\), \(\lambda'(\tau_{20}^{*})=12.3301-19.7682i\). Further, we can obtain \(\mu _{2}=1.1541>0\), \(\beta_{2}=-28.4610<0\), \(T_{2}=11.8428>0\). According to Theorem 5, we know that the Hopf bifurcation of system (28) with respect to \(\tau_{2}\) with \(\tau_{1}=1.05\in(0, \tau_{10})\) is supercritical, the bifurcating periodic solutions are stable and increase.
5 Conclusion
In this paper, by incorporating the feedback delay of the mature prey and the time delay due to the gestation of the mature predator into the system considered in the literature [9], we get a delayed predator-prey system with stage structure for both the predator and the prey, which is an extension of the literature [9]. Compared with the literature [9], we mainly consider the effects of the two delays on the predator-prey system.
By regarding the possible combination of the two delays as the bifurcation parameter, and analyzing the characteristic equation of the linearized system at the positive equilibrium, the sufficient conditions for the local stability of the positive equilibrium and the existence of a Hopf bifurcation are established. It has been shown that when the value of the delay is below the corresponding critical value, the system is asymptotically stable. However, once the value of the delay is greater than the corresponding critical value, there will be a Hopf bifurcation at the positive equilibrium of the system and a family of periodic solutions occur. For the further investigation, formulas are derived to determine direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions by using the normal form theory and center manifold theorem. From the numerical simulations, one can conclude that the species in system (4) could coexist in an oscillatory mode with some available delays of the mature prey and the mature predator under some certain conditions. This is valuable from the point of view of ecology.
References
Xu, R, Chaplain, MAJ, Davidson, FA: Persistence and global stability of a ratio-dependent predator-prey mode with stage structure. Appl. Math. Comput. 158, 729-744 (2004)
Liu, SQ, Beretta, E: A stage-structured predator-prey model of Beddington-DeAngelis type. SIAM J. Appl. Math. 66, 1101-1129 (2006)
Kar, TK, Pahari, UK: Modelling and analysis of a prey-predator system with stage-structure and harvesting. Nonlinear Anal., Real World Appl. 8, 601-609 (2007)
Liu, SQ, Zhang, JH: Coexistence and stability of predator-prey model with Beddington-DeAngelis functional response and stage structure. J. Math. Anal. Appl. 342, 446-460 (2008)
Xu, R: Global stability and Hopf bifurcation of a predator-prey model with stage structure and delayed predator response. Nonlinear Dyn. 67, 1683-1693 (2012)
Chakraborty, K, Jana, S, Kar, TK: Global dynamics and bifurcation in a stage structured prey-predator fishery model with harvesting. Appl. Math. Comput. 218, 9271-9290 (2012)
Li, F, Li, HW: Hopf bifurcation of a predator-prey model with time delay and stage structure for the prey. Math. Comput. Model. 55, 672-679 (2012)
Liu, M, Wang, K: Global stability of stage-structured predator-prey models with Beddington-DeAngelis functional response. Commun. Nonlinear Sci. Numer. Simul. 16, 3792-3797 (2011)
Wang, LS, Feng, GH: Global dynamics of a predator-prey model with stage structure and Holling type-II functional response. Math. Appl. 26, 765-773 (2013)
Ferrara, M, Guerrini, L, Bisci, GM: Center manifold reduction and perturbation method in a delayed model with a mound-shaped Cobb-Douglas production function. Abstr. Appl. Anal. 2013, Article ID 738460 (2013)
Dong, T, Liao, XF, Li, HQ: Stability and Hopf bifurcation in a computer virus model with multistate antivirus. Abstr. Appl. Anal. 2012, Article ID 841987 (2012)
Bianca, C, Ferrara, M, Guerrini, L: Hopf bifurcations of a delayed-energy-based model of capital accumulation. Appl. Math. Inf. Sci. 7, 139-143 (2013)
Zhang, JF: Bifurcation analysis of a modified Holling-Tanner predator-prey model with time delay. Appl. Math. Model. 36, 1219-1231 (2012)
Bianca, C, Ferrara, M, Guerrini, L: The Cai model with time delay: existence of periodic solutions and asymptotic analysis. Appl. Math. Inf. Sci. 7, 21-27 (2013)
Meng, XY, Huo, HF, Xiang, H: Hopf bifurcation in a three-species system with delays. J. Appl. Math. Comput. 35, 635-661 (2011)
Cui, GH, Yan, XP: Stability and bifurcation analysis on a three-species food chain system with two delays. Commun. Nonlinear Sci. Numer. Simul. 16, 3704-3720 (2011)
Meng, XY, Huo, HF, Zhang, XB, Xiang, H: Stability and Hopf bifurcation in a three-species system with feedback delays. Nonlinear Dyn. 64, 349-364 (2011)
Xu, CJ, Tang, XH, Liao, MX: Stability and bifurcation analysis on a ring of five neurons with discrete delays. J. Dyn. Control Syst. 19, 237-275 (2013)
Xu, CJ, Tang, XH, Liao, MX: Stability and bifurcation analysis of a six-neuron BAM neural network model with discrete delays. Neurocomputing 74, 689-707 (2011)
Zhao, M: Hopf bifurcation analysis for a semiratio-dependent predator-prey system with two delays. Abstr. Appl. Anal. 2013, Article ID 495072 (2013)
Zhang, ZZ, Yang, HZ, Fu, M: Hopf bifurcation in a predator-prey system with Holling type III functional response and time delays. J. Appl. Math. Comput. 44, 337-356 (2014)
Li, XL, Wei, JJ: On the zeros of a fourth degree exponential polynomial with applications to a neural network model with delays. Chaos Solitons Fractals 26, 519-526 (2005)
Hassard, BD, Kazarinoff, ND, Wan, YH: Theory and Applications of Hopf Bifurcation. Cambridge University Press, Cambridge (1981)
Acknowledgements
The author would like to thank the editor and the anonymous referees for their work on the paper. This work was supported by Anhui Provincial Natural Science Foundation under Grant (No. 1508085QA13).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Author’s contributions
The author read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, J. Bifurcation analysis of a delayed predator-prey system with stage structure and Holling-II functional response. Adv Differ Equ 2015, 208 (2015). https://doi.org/10.1186/s13662-015-0535-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-015-0535-2