Introduction

Addiction to drugs is an extremely common phenomenon among drug abusers. According to the world drug report 2018, global heroin and opium production reached an all-time high and drug-related deaths increased by 60% between 2000 and 2015 (Djilali et al. 2017). Especially, in recent years, expanded utilization of heroin is an issue of concern in many parts of the world because that it can cross the blood–brain barrier within 15–20 s, which make the heroin users more prone to catch the human immunodeficiency virus (HIV) and the other blood-borne viruses diseases (Liu et al. 2019a, b; Yang et al. 2016b). The extended use of heroin habituation and addiction in population which is named as the heroin epidemic presents some phenomena of epidemics such as rapid diffusion and clear geographic boundaries (Wang et al. 2019). Therefore, mathematical modeling has been universally used to describe heroin addiction in the epidemic way since 1981–1983 in Ireland (Kelly et al. 2003).

The incidence rate is an important factor for epidemic mathematical modeling. There are some literature for heroin epidemic models with the bilinear incidence rate (Liu et al. 2019b; Fang et al. 2015; Huang and Liu 2013; Liu and Zhang 2011; Wang et al. 2011; Wangari and Stone 2017; Zhang and Wang 2019; Maji 2021). In 1979, an exponential model has been simplified from Kermack and McKendrick’s disease model by MacKintosh and Stewart (1979). Their model MacKintosh and Stewart (1979) describes the extent of heroin use over a large area in an epidemic fashion. An ODE has been formulated by White and Comiskey (2007) to study the dynamics of disease modeling to the drug-using career. For this, the population has been divided into three categories, namely: susceptible, heroin users, and heroin users undergoing treatment. Wang et al. (2011) proposed a heroin epidemic model with bilinear incidence rate and investigated the stability of drug-free equilibrium and the endemic equilibrium. Liu and Zhang (2011) and Huang and Liu (2013) investigated a heroin epidemic model with bilinear incidence rate and distributed delays, respectively. Liu and Zhang (2011) showed that the basic reproduction number characterizes the disease transmission dynamics. Huang and Liu (2013) investigated the global stability of the heroin epidemic model by using the constructing appropriate Lyapunov function which improved the obtained results by Liu et al. in the literature Liu and Zhang (2011). However, as stated in Fang et al. (2015), all the heroin epidemic models did not consider the influence of the treat-age for heroin users during the treatment. Based on this fact, Fang et al. (2015) formulated a heroin epidemic model bilinear incidence rate and treat-age and studied the global asymptotic properties of the proposed model. Wangari and Stone (2017) proposed a heroin epidemic model with bilinear incidence rate and saturated treatment function and derived a condition ensuring global stability of the model by making use of the geometric approach. Considering that it usually takes some time for a heroin user to be susceptible. Zhang and Wang (2019) developed a heroin model with time delay and saturated treatment function based on the model proposed by Wangari and Stone (2017). They have derived the sufficient conditions for local stability and existence of Hopf bifurcation of the model by taking the time delay due to the period used to cure heroin users as the bifurcation parameter and investigated the direction and stability of the Hopf bifurcation by using the normal form theory and the manifold center theorem.

The bilinear incidence rate is more appropriate for communicable diseases such as H3N2 and SARS. Based on the limitation of the heroin epidemic models above, there have some heroin epidemic models with nonlinear incidence rates been proposed in recent years. Yang et al. (2016a) proposed a heroin epidemic model with a nonlinear incidence rate and investigated the stability of the equilibria for the model. Considering the time needed to return to an untreated drug user, Liu and Wang (2016b) studied a delayed multi-group heroin epidemic model with relapse phenomenon and nonlinear incidence rate, and derived the sufficient conditions for the global stability of the equilibria with the help of suitable Lyapunov functionals. Djilali et al. (2017) presented the global dynamics of a heroin epidemic model with a very general nonlinear incidence rate. Recently, Ma et al. (2017) developed the following heroin model with nonlinear incidence rate as following:

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\mathrm{{d}}S(t)}{\mathrm{{d}}t} &{} = &{} b-\beta S(t)U_{1}^{2}(t)-\mathrm{{d}}S(t)+\delta U_{2}(t), \\ \frac{\mathrm{{d}}U_{1}(t)}{\mathrm{{d}}t} &{} = &{} \beta S(t)U_{1}^{2}(t)-\left( \gamma +d\right) U_{1}(t)+\sigma U_{2}(t), \\ \frac{\mathrm{{d}}U_{2}(t)}{\mathrm{{d}}t} &{} = &{} \gamma U_{1}(t)-(\sigma +d+\delta )U_{2}(t), \end{array} \right. \end{aligned}$$
(1)

where S(t), \(U_{1}(t)\) and \(U_{2}(t)\) denote numbers of the susceptible population, heroin users not in treatment and heroin users in treatment at time t, respectively. b is the recruitment rate of the susceptible population; \(\beta SU_{1}^{2}\) is the infection rate of the heroin users not in treatment, which means that a susceptible person will become a heroin-addict once he contacts with heroin users twice; d is the natural death rate of the population; treatment has been taken by the heroin users at a rate \(\gamma\); sometimes heroin users neglect the treatment and reuse heroin (\(\sigma\)); after the treatment the heroin users becomes the susceptible ones at the rate of \(\delta\) unit. Ma et al. (2017) showed that system (1) exhibits numerous kinds of bifurcation and the results obtained have certain effect to control the heroin spreading. The schematic diagram of our model (1) has been shown in Fig. 1.

Fig. 1
figure 1

The schematic diagram of the system (1)

Full size image

As stated in Ma et al. (2017), ’once someone addicts to the drug, it is difficult to abstain from it just depending on self-control because of the natural facts’. Therefore, there should be a period for heroin users in treatment before they become susceptible ones since they have certain self-control ability. In general, delay differential equations show more complex dynamics rather than ordinary differential equations, which have been shown in some work about traditional epidemic models (Liu and Wang 2016a; Sirijampa et al. 2018; Tipsri and Chinviriyasit 2015; Haldar et al. 2020; Chhetri et al. 2020) and computer virus propagation models (Keshri and Mishra 2014; Ren et al. 2012; Upadhyay and Kumari 2019; Zhao and Bi 2017). Motivated by the above, we consider the following heroin epidemic model with time delay:

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\mathrm{{d}}S(t)}{\mathrm{{d}}t} &{} = &{} b-\beta S(t)U_{1}^{2}(t)-\mathrm{{d}}S(t)+\delta U_{2}(t-\tau ), \\ \frac{\mathrm{{d}}U_{1}(t)}{\mathrm{{d}}t} &{} = &{} \beta S(t)U_{1}^{2}(t)-\left( \gamma +d\right) U_{1}(t)+\sigma U_{2}(t), \\ \frac{\mathrm{{d}}U_{2}(t)}{\mathrm{{d}}t} &{} = &{} \gamma U_{1}(t)-\left( \sigma +d\right) U_{2}(t)-\delta U_{2}(t-\tau ), \end{array} \right. \end{aligned}$$
(2)

where \(\tau\) is the immunity delay due to the self-control of the drug users in treatment. Our object of this work is to study the effect time delay on the dynamics of our assumed model. The model has extremely complicated kinetic features, which are mainly reflected in this article.

The paper is organized into several sections and subsections. In “Basic results”, it has been shown that solutions of system (2) are positive and bounded for a positive initial condition. The conditions for the existence of Hopf-bifurcation and local stability (“Local stability”) of the interior equilibrium point have been derived in “Hopf bifurcation”. Also, in this section, taking the delays as key parameters, different cases have been discussed for the occurrence of Hopf-bifurcation. Further, in “Properties of Hopf bifurcation”, the direction of Hopf-bifurcation and the stability of the periodic solution are examined. In “The reaction diffusion system”, we considered the reaction diffusion system associated to system (2), where in “Local existence and positivity of solutions”, we proved the local existence and positivity of solutions with Dirichlet boundary conditions and in “Global existence of solutions”, we proved the global existence, in time of the solutions. In “Turing instability (DDI)”, we studied the Turing instability of the reaction diffusion system but with homogeneous Neumann conditions. Some numerical simulations have been done for our expository results in “Numerical simulation”. The paper ends with a discussion of our work (“Conclusions”).

Basic results

Consider \({\mathbb {R}}_{+}^{3}=\{(S,U_{1},U_{2})|\quad S,U_{i}\ge 0,i=1,2\}\). The initial conditions for the model system (2) are:

$$\begin{aligned} S(\theta )=\phi _{1}(\theta ),U_{1}(\theta )=\phi _{2}(\theta ),U_{2}(\theta )=\phi _{3}(\theta ) \end{aligned}$$
(3)

with \(\phi _{i}(\theta )\geqslant 0,\phi _{i}(0)>0,i=1,2,3;\theta \in [-\tau ,0]\) and \((\phi _{1},\phi _{2},\phi _{3})\in C([-\tau ,0], {\mathbb {R}}_{+}^{3}),\) where \(C([-\tau ,0],{\mathbb {R}}_{+}^{3})\) be the space of functions which are continuous from \([-\tau ,0]\) to \({\mathbb {R}}_{+}^{3}\) with supremum norm, called Banach Space. By the elementary theory of functional differential equation, we can say that system (2) with initial conditions (3) admits a unique solution.Now, to show the system (2) has positive and bounded solutions, we state the following result:

Theorem 1

All solutions of system (2) with initial conditions (3) are positive and bounded for \(t\geqslant 0.\)

Proof

It can easily be shown that all the solutions of (2) with initial conditions (3) are defined on \({\mathbb {R}}{^3_+}\) and remain positive \(\forall\) \(t \ge 0.\) By adding the equations of system (2), we get \(\frac{\mathrm{{d}}}{\mathrm{{d}}t}N(t)=b-\mathrm{{d}} N(t)\) and \(N(t)=S(t)+U_1(t)+U_2(t).\) So, \(N(t)=\frac{b}{d}+\left( N(0)-\frac{b}{d}\right) e^{- \mathrm{{d}} t}.\) Hence \(N(0)<\frac{b}{d} \Rightarrow N(t)<\frac{b}{d}\) and \(\lim _{t\rightarrow \infty }N(t)=\frac{b}{d}.\) i.e. N(t) is bounded, namely \(|N(t)|<\frac{b}{d}.\) Hence \(S(t), U_1(t), U_2(t)\) are bounded. \(\square\)

Straightforward computation shows that for b sufficiently large, then system (2) has two positive equilibriums \(E_{*}(S_{*},U_{1*},U_{2*})\), where

$$\begin{aligned} S_{*}=\frac{b+\delta U_{2*}}{\beta U_{1*}^{2}+d},U_{1*}= \frac{\sigma +d+\delta }{\gamma }U_{2*}, \end{aligned}$$
(4)

and \(U_{2*}\) is the positive root of Eq. (5)

$$\begin{aligned} l_{2}U_{2}^{2}+l_{1}U_{2}+l_{0}=0, \end{aligned}$$
(5)

where,

$$\begin{aligned} l_{0}= & {} \frac{d\sigma \gamma ^{2}}{\beta (\sigma +d+\delta )^{2}}-\frac{ d \gamma (\gamma +d)}{\beta (\sigma +d+\delta )},\\ l_{1}= & {} b,\\ l_{2}= & {} \sigma +\delta -\frac{(\gamma +d)(\sigma +d+\delta )}{\gamma }, \end{aligned}$$

which can be written

$$\begin{aligned} l_{0}= & {} -d\gamma \frac{d\sigma +d\gamma +d\delta +\gamma \delta +d^{2}}{ \beta \left( d+\sigma +\delta \right) ^{2}}<0, \\ l_{1}= & {} b, \\ l_{2}= & {} -\frac{d(\sigma +d+\delta +\gamma )}{\gamma }<0. \end{aligned}$$

So the condition to get two positive critical points can be obtained for large values of b (from Eq. (5)):

$$\begin{aligned} b^{2}>4d^2\left[ \frac{\left( d\sigma +d\gamma +d\delta +\gamma \delta +d^{2}\right) \left( d+\sigma +\gamma +\delta \right) }{\beta \left( d+\sigma +\delta \right) ^{2}}\right] . \end{aligned}$$

Stability and bifurcation analysis of system (2)

The subject of bifurcation is a vast area to do research. In a system of differential equations Hopf-bifurcation happens when the complex conjugate set of eigenvalues of a linearised system become purely imaginary at a fixed point. So with these conditions, a system that contains at least two equations may have Hopf bifurcation. Hopf-bifurcation occurs at a point where a system changes state from stable to unstable, i.e. it is a local bifurcation in which a fixed point of a dynamical system loses stability. In this section by taking the delay \(\tau\) as bifurcation parameters the necessary conditions for the Hopf-bifurcation are derived.

Local stability

Local stability of an equilibrium point means that the equilibrium is stable to small perturbations, i.e., if we push the situation a bit out from the equilibrium point then the situation will return back on its own. Here we shall study the local stability with the help of Routh–Hurwitz criteria (Kundu et al. 2017).

The characteristic equation of the linear section of system (2) at \(E_{*}(S_{*},U_{1*},U_{2*})\) is

$$\begin{aligned} \lambda ^{3}+A_{2}\lambda ^{2}+A_{1}\lambda +A_{0}+(B_{2}\lambda ^{2}+B_{1}\lambda +B_{0})e^{-\lambda \tau }=0. \end{aligned}$$
(6)

with

$$\begin{aligned} A_{0}= & {} a_{33}(a_{12}a_{21}-a_{11}a_{22})+a_{11}a_{23}a_{32}, \\ A_{1}= & {} a_{11}a_{22}+a_{11}a_{33}+a_{22}a_{33}-a_{12}a_{21}-a_{23}a_{32}, \\ A_{2}= & {} -(a_{11}+a_{22}+a_{33}),\\ B_{0}= & {} b_{33}(a_{12}a_{21}-a_{11}a_{22})-a_{21}a_{32}b_{13},\\ B_{1}= & {} b_{33}(a_{11}+a_{22}),B_{2}=-b_{33}, \end{aligned}$$

and

$$\begin{aligned} a_{11}= & {} -(\beta U_{1*}^{2}+d),a_{12}=-2\beta S_{*}U_{1*}, \\ a_{21}= & {} \beta U_{1*}^{2},a_{22}=2\beta S_{*}U_{1*}-\gamma -d,a_{23}=\sigma , \\ a_{32}= & {} \gamma ,a_{33}=-(\sigma +d),b_{13}=\gamma ,b_{33}=-\delta . \end{aligned}$$

When \(\tau =0\), Eq. (6) becomes

$$\begin{aligned} \lambda ^{3}+(A_{2}+B_{2})\lambda ^{2}+(A_{1}+B_{1})\lambda +A_{0}+B_{0}=0, \end{aligned}$$
(7)

where

$$\begin{aligned} \left\{ \begin{array}{l} A_{2}+B_{2}=\beta U_{1*}^{2}-2\beta SU_{1*}+(\sigma +d+\delta +\gamma ), \\ A_{1}+B_{1}=(\sigma +2d+\delta +\gamma )\beta U_{1*}^{2}-2\beta (\sigma +d+\delta )SU_{1*}-\gamma (2\sigma +\delta )+d^{2}, \\ A_{0}+B_{0}=\beta \left[ -d(\sigma +d+\delta +\gamma )\right] U_{1*}^{2}+2\beta d\left[ (\sigma +d+\delta )\right] SU_{1*}+d\left[ \sigma \gamma -\left( \gamma +d\right) (\sigma +d+\delta )\right] . \end{array} \right. \end{aligned}$$

Now for \(\tau =0\), \(E_{*}(S_{*},U_{1*},U_{2*})\) is locally asymptotically stable if the condition (H): \(A_{0}+B_{0}>0\), \(A_{2}+B_{2}>0\), \((A_{1}+B_{1})(A_{2}+B_{2})>A_{0}+B_{0}>0\) is satisfied based on the the Routh–Hurwitz criteria, i.e., we have

$$\begin{aligned} \left\{ \begin{array}{l} U_{1*}^{2}-2SU_{1*}+\left( \frac{\sigma +d+\delta +\gamma }{\beta }\right)>0, \\ U_{1*}^{2}-2\left( \frac{\sigma +d+\delta }{\sigma +2d+\delta +\gamma } \right) SU_{1*}+\frac{-\gamma (2\sigma +\delta )+d^{2}}{\beta \left( \sigma +2d+\delta +\gamma \right) }>0, \\ U_{1*}^{2}-2\left( \frac{\sigma +d+\delta }{\sigma +d+\delta +\gamma } \right) SU_{1*}+\left[ \frac{-\sigma \gamma +\left( \gamma +d\right) (\sigma +d+\delta )}{\beta \left( \sigma +d+\delta +\gamma \right) }\right] <0, \\ (A_{1}+B_{1})(A_{2}+B_{2})>A_{0}+B_{0}, \end{array} \right. \end{aligned}$$

The stability condition for \(\tau \ne 0\) has been discussed in the next sub-section.

Hopf bifurcation

For \(\tau \ne 0\), we assume that \(\lambda =i\omega\) \((\omega >0)\) is a root of Eq. (6). Then separating real and imaginary part we have,

$$\begin{aligned} \left\{ \begin{array}{ll} B_{1}\omega \sin \tau \omega +(B_{0}-B_{2}\omega ^{2})\cos \tau \omega =A_{2}\omega ^{2}-A_{0}, &{} \\ B_{1}\omega \cos \tau \omega -(B_{0}-B_{2}\omega ^{2})\sin \tau \omega =\omega ^{3}-A_{1}\omega . &{} \end{array} \right. \end{aligned}$$

Thus we can obtain

$$\begin{aligned} \omega ^{6}+a_{2}\omega ^{4}+a_{1}\omega ^{2}+a_{0}=0, \end{aligned}$$
(8)

where

$$\begin{aligned} a_{0}= & {} A_{0}^{2}-B_{0}^{2}, \\ a_{1}= & {} A_{1}^{2}-2A_{0}A_{2}-B_{1}^{2}+2B_{0}B_{2}, \\ a_{2}= & {} A_{2}^{2}-2A_{1}-B_{2}^{2}. \end{aligned}$$

Let \(v=\omega ^{2}\), then Eq. (8) becomes

$$\begin{aligned} v^{3}+a_{2}v^{2}+a_{1}v+a_{0}=0. \end{aligned}$$
(9)

Suppose that \(a_{0}<0\), then Eq. (9) has at least one positive root say \(v_{0}\), i.e., Eq. (8) has a positive root \(\omega _{0}= \sqrt{v_{0}}\) and Eq. (7) has a pair of purely imaginary roots \(\pm i\omega _{0}\). For \(\omega _{0}\), we have

$$\begin{aligned} \tau _{0}=\frac{1}{\omega _{0}}\times \arccos \frac{B_{1}\omega _{0}\times (\omega _{0}^{3}-A_{1}\omega _{0})+(B_{0}-B_{2}\omega _{0})\times (A_{2}\omega _{0}^{2}-A_{0})}{B_{1}^{2}\omega _{0}^{2}+(B_{0}-B_{2}\omega _{0}^{2})^{2}}. \end{aligned}$$

Differentiating Eq. (7) with respect to \(\tau\), we get

$$\begin{aligned} \bigg [\frac{\mathrm{{d}}\lambda }{\mathrm{{d}}\tau }\bigg ]^{-1}=\frac{(3\lambda ^{2}+2A_{2}\lambda +A_{1})e^{\lambda \tau }}{\lambda (B_{2}\lambda ^{2}+B_{1}\lambda +B_{0})}- \frac{\tau }{\lambda }. \end{aligned}$$

Further,

$$\begin{aligned} \text {Re}\bigg [\frac{\mathrm{{d}}\lambda }{\mathrm{{d}}\tau }\bigg ]_{\tau =\tau _{0}}^{-1}=\frac{ f^{\prime }(v_{0})}{B_{1}^{2}\omega _{0}^{2}+(B_{0}-B_{2}\omega _{0}^{2})^{2} }, \end{aligned}$$

where \(f(v)=v^{3}+a_{2}v^{2}+a_{1}v+a_{0}\).

Obviously, if \(a_{1}>0\) and \(a_{2}>0\), then \(\text {Re}[\frac{\mathrm{{d}}\lambda }{ \mathrm{{d}}\tau }]_{\tau =\tau _{0}}^{-1}\ne 0\). Based on the discussion above and the Hopf bifurcation theorem in Upadhyay and Kumari (2019), we have the following results.

Theorem 2

For system (2), if the conditions (H) hold, then the positive equilibrium \(E_*(S_*, U_{1*}, U_{2*})\) is locally asymptotically stable when \(\tau \in [0, \tau _0)\); system (2) undergoes a Hopf bifurcation at \(E_*(S_*, U_{1*}, U_{2*})\) when \(\tau =\tau _{0}\) and a family of periodic solutions bifurcate from \(E_*(S_*, U_{1*}, U_{2*})\).

Properties of Hopf bifurcation

Introduce a new perturbation parameter \(\mu =\tau -\tau _0\) with \(\mu \in R\), then \(\mu =0\) is the Hopf bifurcation value of system (2). Let \(u_1(t)=S(t)-S_*\), \(u_2(t)=U_1(t)-U_{1*}\), \(u_3(t)=U_2(t)-U_{2*}\), and normalize \(\tau\) by \(t\rightarrow (t/\tau )\). Then, system (2) becomes the following equation in the phase space \(C=C([-1,0],R^3)\)

$$\begin{aligned} {\dot{u}}(t)=L_{\mu }(u_t)+F(\mu , u_t), \end{aligned}$$
(10)

where \(u(t)=(u_1, u_2, u_3)^\mathrm{{T}} \in R^3\), \(L_\mu\): \(C\rightarrow R^3\), F: \(R\times C\rightarrow R^3\), with

$$\begin{aligned} L_{\mu }\phi =(\tau _0+\mu )(A\phi (0)+B\phi (-1)). \end{aligned}$$

A and B are defined by the following form:

$$\begin{aligned} A= \begin{pmatrix} a_{11} &{} a_{12} &{} {0} \\ a_{21} &{} a_{22} &{} a_{23} \\ {0} &{} a_{32} &{} a_{33} \end{pmatrix} , B= \begin{pmatrix} {0} &{} {0} &{} b_{13} \\ {0} &{} {0} &{} {0} \\ {0} &{} {0} &{} b_{33} \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} F(\mu ,\phi )=(\tau _0+\mu ) \begin{pmatrix} a_{13}\phi _1(0)\phi _2(0)+a_{14}\phi _2^2(0) \\ a_{24}\phi _1(0)\phi _2(0)+a_{25}\phi _2^2(0) \\ {0} \end{pmatrix} \end{aligned}$$

where \(a_{13}=-2\beta U_{1*}\), \(a_{14}=-\beta S_*\), \(a_{24}=2\beta U_{1*}\), \(a_{25}=\beta S_*\) and the form of other elements in the matrix A and B are given before the Eq. (7).

From the Riesz representation theorem, there exists \(\eta (\theta ,\mu )\) of bounded variance such that

$$\begin{aligned} L_{\mu }\phi =\int _{-1}^0\mathrm{{d}}\eta (\theta , \mu )\phi (\theta ), \phi \in C. \end{aligned}$$
(11)

Choosing

$$\begin{aligned} \eta (\theta , \mu )=(\tau _0+\mu )(A\delta (\theta )+B\delta (\theta +1)), \end{aligned}$$

and \(\delta (\theta )\) is the Dirac delta function. For \(\phi \in C([-1,0], R^3)\), define the operator \(A(\mu )\)

$$\begin{aligned} A(\mu _0)\phi =\left\{ \begin{array}{ll} \frac{\mathrm{{d}}\phi (\theta )}{\mathrm{{d}}\theta }, -1\le \theta <0, &{} \\ \int _{-1}^0\mathrm{{d}}\eta (\theta , \mu _0)\phi (\theta ), \theta =0, &{} \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} R(\mu )\phi =\left\{ \begin{array}{ll} 0, -1\le \theta <0, &{} \\ F(\mu _0, \phi ), \theta =0. &{} \end{array} \right. \end{aligned}$$

Then, system (2) is equivalent to

$$\begin{aligned} {\dot{u}}(t)=A(\mu )u_t+R(\mu )u_t. \end{aligned}$$
(12)

For \(\varphi \in C^1([0, 1], (R^3)^*)\), define \(A^{*}\)

$$\begin{aligned} A^*(\varphi )=\left\{ \begin{array}{ll} -\frac{\mathrm{{d}}\varphi (s)}{\mathrm{{d}}s}, 0<s\le 1, &{} \\ \int _{-1}^0\mathrm{{d}}{\eta }^\mathrm{{T}}(s,0)\varphi (-s), s=0, &{} \end{array} \right. \end{aligned}$$

and a bilinear product

$$\begin{aligned}&\langle \varphi (s),\phi (\theta )\rangle ={\bar{\varphi }}(0)\phi (0)\nonumber \\&\quad -\int _{ \theta =-1}^0\int _{\xi =0}^{\theta }{\bar{\varphi }}(\xi -\theta )\mathrm{{d}}\eta (\theta )\phi ( \xi )\mathrm{{d}}\xi , \end{aligned}$$
(13)

with \(\eta (\theta )=\eta (\theta , 0)\).

Based on discussion above, we know that \(i\omega _{0}\) are eigenvalues of A(0) and \(A^{*}(0)\). Suppose that \(\rho (\theta )=(1,\rho _{2},\rho _{3})^\mathrm{{T}}e^{i\omega _{0}\theta }\) and \(\rho ^{*}(s)=V(1,\rho _{2}^{*},\rho _{3}^{*})e^{i\omega _{0}s}\) are the corresponding eigenfunctions. By direct calculation we obtain

$$\begin{aligned} q_{2}= & {} \frac{i\omega _{0}-a_{33}-b_{33}e^{-i\omega _{0}}}{a_{32}}q_{3}, \\ q_{3}= & {} \frac{a_{32}(i\omega _{0}-a_{11})}{a_{12}(i\omega _{0}-a_{33}-b_{33}e^{-i\omega _{0}})},\\ q_{2}^{*}= & {} -\frac{i\omega _{0}+a_{11}}{a_{21}},\\ q_{3}^{*}= & {} \frac{a_{32}(i\omega _{0}+a_{11})-a_{21}b_{13}e^{i\omega _{0}}}{a_{21}(i\omega _{0}+a_{33}+b_{33}e^{i\omega _{0}})}. \end{aligned}$$

From \(\langle \rho ^{*},\rho \rangle =1\), we have

$$\begin{aligned} {\bar{V}}=[1+\rho _{2}{\bar{\rho }}_{2}^{*}+\rho _{3}{\bar{\rho }}_{3}^{*}+\tau _{0}e^{-i\tau _{0}\omega _{0}}(b_{13}+b_{33}{\bar{\rho }}_{3}^{*})]^{-1}. \end{aligned}$$

Using the algorithm given in Hassard et al. (1981) and the similar computation process to that in Guo et al. (2019), Sirijampa et al. (2018) and Li (2017), we can obtain the expressions of \(g_{20}\), \(g_{11}\), \(g_{02}\) and \(g_{21}\) as follows:

$$\begin{aligned} g_{20}= & {} 2{\bar{V}}\tau _{0}[a_{13}\rho _{2}+a_{14}\rho _{2}^{2}+{\bar{\rho }} _{2}^{*}(a_{24}\rho _{2}+a_{25}\rho _{2}^{2})], \\ g_{11}= & {} {\bar{V}}\tau _{0}[a_{13}(\rho _{2}+{\bar{\rho }}_{2})+2a_{14}\rho _{2} {\bar{\rho }}_{2}+{\bar{\rho }}_{2}^{*}(a_{24}(\rho _{2}+{\bar{\rho }} _{2})+2a_{25}\rho _{2}{\bar{\rho }}_{2})], \\ g_{02}= & {} 2{\bar{V}}\tau _{0}[a_{13}{\bar{\rho }}_{2}+a_{14}{\bar{\rho }}_{2}^{2}+ {\bar{\rho }}_{2}^{*}(a_{24}{\bar{\rho }}_{2}+a_{25}{\bar{\rho }}_{2}^{2})], \\ g_{21}= & {} 2{\bar{V}}\tau _{0}\bigg [a_{13}\bigg (W_{11}^{(1)}(0)\rho _{2}+\frac{1 }{2}W_{20}^{(1)}(0){\bar{\rho }}_{2}+W_{11}^{(2)}(0)+\frac{1}{2}W_{20}^{(2)}(0) \bigg )\\&+a_{14}(2W_{11}^{(2)}(0)\rho _{2}+W_{20}^{(2)}(0){\bar{\rho }}_{2}) \\&+{\bar{\rho }}_{2}^{*}\bigg (a_{24}\bigg (W_{11}^{(1)}(0)\rho _{2}+\frac{1}{ 2}W_{20}^{(1)}(0){\bar{\rho }}_{2}+W_{11}^{(2)}(0)+\frac{1}{2}W_{20}^{(2)}(0) \bigg ) \\&+a_{25}(2W_{11}^{(2)}(0)\rho _{2}+W_{20}^{(2)}(0){\bar{\rho }}_{2})\bigg ) \bigg ], \end{aligned}$$

with

$$\begin{aligned} W_{20}(\theta )= & {} \frac{ig_{20}\rho (0)}{\tau _{0}\omega _{0}}e^{i\tau _{0}\omega _{0}\theta }+\frac{i{\bar{g}}_{02}{\bar{\rho }}(0)}{3\tau _{0}\omega _{0}}e^{-i\tau _{0}\omega _{0}\theta }+E_{1}e^{2i\tau _{0}\omega _{0}\theta },\\ W_{11}(\theta )= & {} -\frac{ig_{11}\rho (0)}{\tau _{0}\omega _{0}}e^{i\tau _{0}\omega _{0}\theta }+\frac{i{\bar{g}}_{11}{\bar{\rho }}(0)}{\tau _{0}\omega _{0}}e^{-i\tau _{0}\omega _{0}\theta }+E_{2}. \end{aligned}$$

\(E_{1}\) and \(E_{2}\) can be solved by

$$\begin{aligned} E_{1}= & {} 2\left( \begin{array}{ccc} 2i\omega _{0}-a_{11} &{} -a_{12} &{} -b_{13}e^{-2i\tau _{0}\omega _{0}} \\ -a_{21} &{} 2i\omega _{0}-a_{22} &{} -a_{23} \\ {0} &{} -a_{32} &{} 2i\omega _{0}-a_{33}-b_{33}e^{-2i\tau _{0}\omega _{0}} \end{array} \right) ^{-1}\times \left( \begin{array}{lll} a_{13}\rho _{2}+a_{14}\rho _{2}^{2} &{} &{} \\ a_{24}\rho _{2}+a_{25}\rho _{2}^{2} &{} &{} \\ {0} &{} &{} \end{array} \right) , \\ E_{2}= & {} 2\left( \begin{array}{ccc} a_{11} &{} a_{12} &{} b_{13} \\ a_{21} &{} a_{22} &{} a_{23} \\ {0} &{} a_{32} &{} a_{33}+b_{33} \end{array} \right) ^{-1}\times \left( \begin{array}{lll} a_{13}(\rho _{2}+{\bar{\rho }}_{2})+2a_{14}\rho _{2}{\bar{\rho }}_{2} &{} &{} \\ a_{24}(\rho _{2}+{\bar{\rho }}_{2})+2a_{25}\rho _{2}{\bar{\rho }}_{2} &{} &{} \\ {0} &{} &{} \end{array} \right) , \end{aligned}$$

Thus, we have

$$\begin{aligned} \left. \begin{array}{llll} C_{1}(0)=\frac{i}{2\tau _{0}\omega _{0}}\bigg (g_{11}g_{20}-2|g_{11}|^{2}- \frac{|g_{02}|^{2}}{3}\bigg )+\frac{g_{21}}{2} &{} &{} &{} \\ \mu _{2}=-\frac{\text {Re}\{C_{1}(0)\}}{\text {Re}\{\lambda ^{\prime }(\tau _{0})\}}, &{} &{} &{} \\ \beta _{2}=2{\text {Re}\{C_{1}(0)\}}, &{} &{} &{} \\ T_{2}=-\frac{\text {Im}\{C_{1}(0)\}+\mu _{2}\text {Im}\{\lambda ^{\prime }(\tau _{0})\}}{\tau _{0}\omega _{0}}, &{} &{} &{} \end{array} \right. \end{aligned}$$
(14)

where \(\mu _{2}\) determines the direction of the Hopf bifurcation; \(\beta _{2}\) determines the stability of the bifurcating periodic solutions and \(T_{2}\) determines the period of the bifurcating periodic solutions. In conclusion, we can obtain the following results based on the fundamental results about Hopf bifurcation in the literature Hassard et al. (1981).

Theorem 3

For system (2), if \(\mu _2>0\) (\(\mu _2<0\)), then the Hopf bifurcation is supercritical (subcritical); if \(\beta _2<0\) (\(\beta _2>0\)), then the bifurcating periodic solutions are stable (unstable); if \(T_2>0\) (\(T_2<0\)), then the period of the bifurcating periodic solutions increase (decrease).

The reaction diffusion system

We consider the following reaction diffusion system associated to the reaction system (1)

$$\begin{aligned} \left\{ \begin{array}{lll} \partial _{t}S-D_{1}\Delta S &{} = &{} b-\beta S(t)U_{1}^{2}(t)-\mathrm{{d}}S(t)+\delta U_{2}(t), \\ \partial _{t}U_{1}-D_{2}\Delta U_{1} &{} = &{} \beta S(t)U_{1}^{2}(t)-\left( \gamma +d\right) U_{1}(t)+\sigma U_{2}(t), \\ \partial _{t}U_{2}-D_{2}\Delta U_{2} &{} = &{} \gamma U_{1}(t)-\sigma U_{2}(t)-(d+\delta )U_{2}(t), \end{array} \right. \ \;\;\text {in }{\mathbb {R}}^{+}\times \Omega , \end{aligned}$$
(15)

with the Dirichlet boundary conditions

$$\begin{aligned} S=S_{*},U_{1}=U_{1*},\ U_{2}=U_{2*}\; \; \text {on}\;{\mathbb {R}} ^{+}\times \partial \Omega , \end{aligned}$$
(16)

where \(\Omega\) is an open bounded domain in \({\mathbb {R}}^{N}\) with smooth boundary \(\partial \Omega\). The positive constants \(D_{1},\ D_{2} \)and \(D_{3}\) are called the diffusion terms. The initial data

$$\begin{aligned} S(0,x)=S_{0}(x),\;U_{1}(0,x)=U_{10}(x),U_{2}(0,x)=U_{20}(x)\ \;\;\ \text {in }\Omega , \end{aligned}$$
(17)

are assumed to be nonnegative and uniformly bounded on \(\Omega\).

Local existence and positivity of solutions

Since the nonlinearities

$$\begin{aligned} \left\{ \begin{array}{l} f(S,U_{1},U_{2})=b-\beta S(t)U_{1}^{2}(t)-\mathrm{{d}}S(t)+\delta U_{2}(t), \\ \\ g(S,U_{1},U_{2})=\beta S(t)U_{1}^{2}(t)-\gamma U_{1}(t)+\sigma U_{2}(t)-\mathrm{{d}}U_{1}(t), \\ \\ h(S,U_{1},U_{2})=\gamma U_{1}(t)-\sigma U_{2}(t)-(d+\delta )U_{2}(t),, \end{array} \right. \end{aligned}$$
(18)

are continuously differentiable on \({\mathbb {R}}_{+}^{3}\), then for any initial data in \({\mathbb {L}}_{\infty }\left( {\overline{\Omega }}\right)\), it is easy to check directly their Lipschitz continuity on bounded subsets of the domain of a fractional power of the operator \(I_{3}\left( D_{1},D_{2},D_{3}\right) ^{t}\Delta\), where \(I_{3}\) the three dimensional identity matrix, \(\Delta\) is the Laplacian operator and \(\left( .\right) ^{t}\) denotes the transposition. Under these assumptions, the following local existence result is well known (see Smoller 2012; Henry 2006).

Proposition 1

The system (15)–(17) admits a unique, classical local solution \((S,U_{1},U_{2})\) on \([0,T_{\max }[\times \Omega\). If \(T_{\max }<\infty\) then

$$\begin{aligned} \underset{t\nearrow T_{\max }}{\lim }\left\{ \left\| S(t,.)\right\| _{\infty }+\left\| U_{1}(t,.)\right\| _{\infty }+\left\| U_{2}(t,.)\right\| _{\infty }\right\} =\infty . \end{aligned}$$

Since the reactions are quasi-positive, i.e.

$$\begin{aligned} f(0,U_{1},U_{2})\ge 0,\ g(S,0,U_{2})\ge 0,\ h\left( S,U_{1},0\right) \ge 0\ ,\ \ \text {for all }S,U_{1},U_{2}\ge 0, \end{aligned}$$
(19)

then the nonnegativity of the solutions is preserved by application of classical results on invariant regions.

Global existence of solutions

To prove global existence of system (15) with Dirichlet boundary conditions (16) and positive initial data (17), we apply an old general result of Morgan (1989) for m-components systems on the form (15) which we summarize in our case (i.e. \(m=3\)) as follows

Proposition 2

We suppose that the functions \(f,\ g\) and h are of polynomial growth and satisfy

$$\begin{aligned} \left\{ \begin{array}{l} \alpha _{11}f(S;U_{1};U_{2})\le c_{11}S+c_{12}U_{1}+c_{13}U_{2}+d_{1}; \\ (\alpha _{21}f+\alpha _{22}g)(S;U_{1};U_{2})\le c_{21}S+c_{22}U_{1}+c_{23}U_{2}+d_{2}; \\ (\alpha _{31}f+\alpha _{32}g+\alpha _{33}h)(S;U_{1};U_{2})\le c_{31}S+c_{32}U_{1}+c_{33}U_{2}+d_{3}; \end{array} \right. \end{aligned}$$
(20)

for all \(S;U_{1};U_{2}\ge 0\) where \(\alpha _{ij}\) ; \(c_{ij}\) and \(d_{i},1\le i;j\le 3\) are positive reels. Then all solutions of system (15) with positive Dirichlet boundary conditions and positive initial data are positive and global in time (i.e.\(T_{\max }=+\infty\)).

Since for our system all conditions of the above Proposition (2) are satisfied except (20) which can be verified, using the positivity of the solutions for all times, as follows

$$\begin{aligned} \left\{ \begin{array}{l} f(S;U_{1};U_{2})\le 0.S+0.U_{1}+\delta U_{2}+b; \\ (f+g)(S;U_{1};U_{2})\le 0.S+0.U_{1}+\left( \delta +\sigma \right) U_{2}+b; \\ (f+g+h)(S;U_{1};U_{2})\le 0.S+\gamma U_{1}+\left( \delta +\sigma \right) U_{2}+b. \end{array} \right. \end{aligned}$$

Then we have the following proposition

Proposition 3

All solutions of system (15) with Dirichlet boundary conditions (16) and positive initial data (17) are positive and global in time (i.e. \(T_\mathrm{{max}}=+\infty\)).

Turing instability (DDI)

We say that a system of the form

$$\begin{aligned} \frac{\partial u}{\partial t}=D\Delta u+F(u), \end{aligned}$$

exhibits Turing instability, or DDI, if the system without diffusion, i.e.

$$\begin{aligned} \frac{\partial u}{\partial t}=F(u), \end{aligned}$$

has locally stable equilibrium state which becomes unstable in the presence of diffusion. Here the function F (we assume it is regular) describes the reaction dynamics and D is a diagonal matrix of diffusion coefficients (see Elragig 2013). Diffusion-driven instability is considered one of the mechanisms implicated in the spatial organization in morphogenesis Turing (1992).

In studying pattern formation in RD systems the key first step is to determine the Turing space for a given model, i.e. the parameter set for the mode on which pattern formation can be triggered Murray (1982). This can then be followed by bifurcation analysis of specific pattern formations Hoyle and Hoyle (2006) . Turing instability, or diffusion driven instability (DDI), is a concept first proposed by Turing (1952).

We suppose that the boundary conditions are of Neumann and homogenous. Imposing such boundary conditions is due to their neutral nature as they do not pump the space with any additional material and this makes “self-organization” plausible. Taking other boundary conditions can influence the predictions where this can drive forming different patterns, (see Murray 2003).

To analyse DDI mathematically, we use linearized stability analysis and Fourier transform together to get an ordinary differential (reaction) system on the form

$$\begin{aligned} \frac{\mathrm{{d}}{\hat{u}}}{\mathrm{{d}}t}=\left( A-k^{2}D\right) {\hat{u}}, \end{aligned}$$

where A describes the Jacobian matrix of F (i.e. the linearized reaction matrix) and supposed to be stable (i.e. all its eigenvalues have negative real parts) and \({\hat{u}}\) is the Fourier transform of u in space.

Qian and Murray (2001), the authors presented a simple, practical, necessary and sufficient condition for diffusion-driven linear instability and parameter space determination in nonlinear reaction systems with three species is presented:

Proposition 4

A sufficient condition for diffusion-driven instability is that either

  1. (i)

    the largest diagonal elements of A is greater than zero with corresponding diffusion coefficient very small; or

  2. (ii)

    the smallest diagonal cofactors of A is less than zero with corresponding diffusion coefficient very large.

Let us apply Proposition (4), to system (15) with Neumann homogenous boundary conditions.The Jacobian of F at the critical point \(E_{*}(S_{*},U_{1*},U_{2*})\) is

$$\begin{aligned} A=\left( \begin{array}{lllllll} -(\beta U_{1*}^{2}+d) &{}&{}&{} -2\beta SU_{1*} &{}&{}&{} \delta \\ \beta U_{1*}^{2} &{}&{}&{} 2\beta SU_{1*}-\left( \gamma +d\right) &{}&{}&{} \sigma \\ 0 &{}&{}&{} \gamma &{}&{}&{} -(\sigma +d+\delta ) \end{array} \right) , \end{aligned}$$

where \(S_{*},U_{1*},U_{2*}\) are given by (4). The largest diagonal element of A is \(a_{22}=2\beta SU_{1*}-\left( \gamma +d\right)\) which is positive under the following condition

$$\begin{aligned} 2\beta S=:2\beta \frac{b+\delta U_{2*}}{\beta U_{1*}^{2}+d}=:2\beta \frac{b+\delta \frac{\gamma }{\sigma +d+\delta }U_{1*}}{\beta U_{1*}^{2}+d}>\left( \frac{\gamma +d}{U_{1*}}\right) , \end{aligned}$$

that is

$$\begin{aligned} \beta \frac{\left( \gamma +d\right) \left( \sigma +d+\delta \right) -2\delta \gamma }{\sigma +d+\delta }U_{1*}^{2}-2\beta \delta bU_{1*}+d\left( \gamma +d\right) <0. \end{aligned}$$
(21)

Theorem 4

A sufficient condition for diffusion-driven instability for the reaction diffusion system (15) is given by (21) for sufficiently small diffusion \(D_{2}\).

Example 1

For \(b=1\), \(\beta =0.003\), \(d=0.01\), \(\delta =0.2\), \(\gamma =0.005\), \(\sigma =0.001\), the above inequality is satisfied for

$$\begin{aligned} 0.125\,22<U_{1*}<72.\,321. \end{aligned}$$

For the Large diffusions, Straightforward computation shows that if the cofactors of the first and third diagonal elements of A are respectively less then zero under the following condition

$$\begin{aligned} M_{11}=-2\beta (\sigma +d+\delta )\left( \tfrac{bU_{1*}+\frac{\delta \gamma }{\sigma +d+\delta }U_{1*}^{2}}{\beta U_{1*}^{2}+d}\right) +\left( \gamma +d\right) (\sigma +d+\delta )-\gamma \sigma <0, \end{aligned}$$
(22)

and

$$\begin{aligned} M_{33}=\frac{\beta \left( \beta U_{1*}^{2}+d\right) \left( d+\gamma \right) U_{1*}^{2}-2d\beta \left( bU_{1*}+\frac{\delta \gamma }{ \sigma +d+\delta }U_{1*}^{2}\right) +\left( d^{2}+\gamma d\right) \left( \beta U_{1*}^{2}+d\right) }{\beta U_{1*}^{2}+d}<0. \end{aligned}$$
(23)

respectively. With some tedious but elementary algebra, we can show that the two above inequalities are analogous to (21) and are satisfied under analogous conditions. Applying Proposition 4, we have

Theorem 5

Each of the following conditions will lead to diffusion driven instability Condition-1: (22) and \(D_{1}\gg D_{2}\) and \(D_{1}\gg D_{3}\), or Condition-2: (23) and \(D_{3}\gg D_{1}\) and \(D_{3}\gg D_{2}.\)

Numerical simulation

In the previous sections, the conditions for stability and Hopf-bifurcation of the system (2) have been derived analytically. To illustrate our obtained analytical results in a better way, some numerical simulations have been performed. The parameters are chosen in such a way so that it satisfies the conditions for the existence of the Hopf-bifurcation. The set of parametric values are as follows: \(b=1\), \(\beta =0.003\), \(d=0.01\), \(\delta =0.2\), \(\gamma =0.005\), \(\sigma =0.001\). Then,

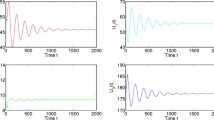
$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\mathrm{{d}}S(t)}{\mathrm{{d}}t} &{} = &{} 1-0.003S(t)U_1^2(t)-0.01S(t)+0.2U_2(t-\tau ), \\ \frac{\mathrm{{d}}U_1(t)}{\mathrm{{d}}t} &{} = &{} 0.003 S(t)U_1^2(t)-0.05 U_1(t)+0.001 U_2(t)-0.01U_1(t), \\ \frac{\mathrm{{d}}U_2(t)}{\mathrm{{d}}t} &{} = &{} 0.05 U_1(t)-0.011 U_2(t)-0.2 U_2(t-\tau ), \end{array} \right. \end{aligned}$$
(24)

from which we obtain the positive equilibrium \(E_*(0.0511, 97.6369, 2.3136)\). With this set of parameters, we can verify that the conditions (H) and \(\frac{ (\gamma +d)(\sigma +d+\delta )}{\gamma }>\sigma\) are satisfied by some complex computations and obtain \(\omega _0=0.6308\) and the critical value of delay \(\tau _0=7.375\). Based on Theorem (2), we conclude that \(E_*\) is seen to be stable for less value of the delay i.e., \(\tau \in [0, \tau _0)\) (Fig. 2). Now with the increased values of delays the oscillation of the individual also increases. Therefore, at the critical value of delay i.e., \(\tau =\tau _0\), we get a stable periodic solution where the Hopf-bifurcation occurs and there we get a stable limit cycle around the equilibrium point \(E_*\) (Fig. 3). For large value of delay (\(\tau >\tau _0\)) the system becomes unstable (Fig. 4). The one parameter bifurcation diagram for all the individuals with respect to the delay \(\tau\) has been plotted in Figs. 5, 6 and 7 respectively.

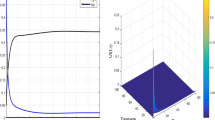
We have performed numerical solution for the spatially extended system of Eq. (24). We here have shown the existence of Hopf bifurcation in the reaction-diffusion system numerically with respect to delay parameter \(\tau\). The hopf bifurcation occurs at \(\tau _0 =7.375\). Stable dynamics has been observed after solving the above system. In Fig. 8, the reaction-diffusion system shows stable dynamics at \(\tau =5<\tau _0=7.375\). On the other hand for the increased value of time delay \(\tau =9>\tau _0=7.375\), the system admits oscillatory dynamics as shown in Fig. 9.

Fig. 2
figure 2

Time series solution of the system (2) for \(\tau <\tau _0\) when \(E_{1*}\) equilibrium point is stable. Parameters are written in the text

Full size image
Fig. 3
figure 3

Time series solution of the system (2) for \(\tau =\tau _0\) when \(E_{1*}\) equilibrium point is stable periodic. Parameters are written in the text

Full size image
Fig. 4
figure 4

Time series solution of the system (2) for \(\tau >\tau _0\) when \(E_{1*}\) equilibrium point has increasing oscillation. Parameters are written in the text

Full size image
Fig. 5
figure 5

One parameter bifurcation diagram for S with respect to \(\tau\)

Full size image
Fig. 6
figure 6

One parameter bifurcation diagram for \(U_1\) with respect to \(\tau\)

Full size image
Fig. 7
figure 7

One parameter bifurcation diagram for \(U_2\) with respect to \(\tau\)

Full size image
Fig. 8
figure 8

Hopf bifurcation in the reaction–diffusion system with delay, when \(\beta =0.003\), \(b=1\), \(d=0.01\), \(\delta =0.2\), \(\gamma =0.005\), \(\sigma =0.001\), \(D_1=D_2=D_3=1\) with time lag \(\tau =5<\tau _0=7.375\)

Full size image
Fig. 9
figure 9

Hopf bifurcation in the reaction–diffusion system with delay, when \(\beta =0.003\), \(b=1\), \(d=0.01\), \(\delta =0.2\), \(\gamma =0.005\), \(\sigma =0.001\), \(D_1=D_2=D_3=1\) with time lag \(\tau =9>\tau _0=7.375\)

Full size image

Conclusions

As we all know that in Europe and more specifically in Ireland heroin and other drugs are mostly used, the report has been mentioned in Kelly et al. (2003), Fang et al. (2015), Huang and Liu (2013), Liu and Zhang (2011), Wang et al. (2011), Wangari and Stone (2017), Zhang and Wang (2019), Maji (2021), White and Comiskey (2007), Yang et al. (2016a), Elragig (2013), Friedman (2008), Guo et al. (2019), Hassard et al. (1981), Henry (2006), Hoyle and Hoyle (2006), Keshri and Mishra (2014), Li (2017), Liu and Wang (2016a), Sirijampa et al. (2018), Tipsri and Chinviriyasit (2015), Haldar et al. (2020), Chhetri et al. (2020), Liu and Wang (2016b), Ma et al. (2017), Morgan (1989), Mulone and Straughan (2009), Murray (1982, 2003), Qian and Murray (2001), Ren et al. (2012), Upadhyay and Kumari (2019), Zhao and Bi (2017), Sekiguchi and Ishiwata (2010), Smoller (2012), Sporer (1999), Turing (1952, 1992), Wiessing and Hartnoll (1999). At that place, people are very much addicted to drugs and it causes many preventable deaths. In fat cells, heroin is well liquefiable, for that reason, it crosses the blood-brain barrier rapidly (‘within 15–20 s’) and “affects the brain and central nervous system, which causes both the ‘rush’ experience by users and the harmfulness” (Kelly et al. 2003). The death related to heroin is also related to the use of alcohol or other drugs (Sporer 1999). Nowadays heroin becomes as popular among the population that its treatment becomes typically a heavy one. The dynamics of infectious disease has been studied using the techniques used in mathematics and statistics; see, for example, Mulone and Straughan (2009), Sekiguchi and Ishiwata (2010), White and Comiskey (2007) and Zhang and Teng (2008); however, little has been done to apply this method to the heroin epidemics.

In this work, a heroin model with the incident rate in the form of \(\beta S U_1^2\) is discussed. In our model, we consider a susceptible person to turn into a heroin someone who is addicted when he/she is enticed twice. Also, a heroin-client without treatment can’t enter the susceptible population unexpectedly. This hypothesis may be more in line with the truth. Comparing with the works in Wang et al. (2019) and Ma et al. (2017), completely different dynamical properties are discovered in this paper according to discussions.

In the present study, we not only investigate the effect of the time delay parameter on the model system dynamics but also present the complete analysis of the model system including the positivity of solutions, boundedness, stability and the properties related to the Hopf bifurcation. In particular, we have ensured the existence and uniqueness of solutions of the proposed model using elementary theory of functional differential equations. Following the existence and uniqueness of solutions, the boundedness of solution has also been established using comparison theorem. Sufficient condition for the local stability of interior equilibrium point have been discussed by considering for different values of the delay parameter. Furthermore, the sufficient conditions for the local stability of the interior equilibrium point have been investigated for various range of delay parameter. Along with this, in each case, the occurrence of Hopf bifurcation has been obtained by considering the time delay as a bifurcation parameter and the critical value of the delay parameter has also been obtained. From the analysis, we conclude that if the values of time delay for system (2) is less that it’s corresponding critical value then the equilibrium for the system remains in a stable state while if the value of the delay is greater than its corresponding critical value, then the equilibrium for system (2) losses its stability. The properties of Hopf bifurcation , such as direction and stability have also been studied by means of the center manifold and normal form theory.

Our result, however, indicates that when the recruitment rate of the susceptible population (i.e. b) is large enough then the system has two steady-states which are stable and can also lose, each one, its stability (bifurcation in the case of the reaction system and Turing instability when the diffusion are added) due to diffusion in the following three cases:

  • For sufficiently small diffusion for \(U_{1}\) with respect to those of S and \(U_{2}\), or

  • For sufficiently large diffusion for S with respect to those of \(U_{1}\) and \(U_{2}\), or

  • For sufficiently large diffusion for \(U_{2}\) with respect to those of \(U_{1}\) and S.

For graphical verification of obtained analyticaly results and to observe the effects of the immunity delay on the stability of the system, some numerical computations have been presented by taking particular set of parametric values. We have systematically justifies all the analytical conditions.

As we know that the educational awareness programs related to treatment may play a major role in protecting the individuals against use of drug. Therefore, the present study provides an opportunity for further extension of the work via incorporating of public awareness factor for treatment and to observe the effect of public awareness on the eradication of using heroin and other drugs.