1 Introduction

Heroin is an opiate drug that is synthesized from morphine [1, 2]. It not only causes somatic and psychological effects for heroin users, but also brings social panic and economic loss to the entire human society. Specially, it is one of the most important modes of transmitting infectious diseases such as Human Immunodeficiency Virus (HIV) and Hepatitis C Virus (HCV) [3,4,5,6]. In recent years, it has been established that heroin spreads in a population like an epidemic disease. Based on this, some mathematical models have been formulated to describe the epidemic dynamics of heroin users. In [7], Mackintosh and Stewart proposed an exponential model based on the infectious disease model of Kermack and Mckendrick to describe how the use of heroin spreads in an epidemic fashion. White and Comiskey [8] formulated a heroin epidemic model for treating heroin users, and it involves susceptibles, heroin users, and heroin users undergoing treatment, three classes of people. Later, Mulone and Straughan [9] showed that the steady states of the model proposed by White and Comiskey [8] are stable. However, they assumed that the total population is a constant, which is not reasonable in reality. Thus, Wang et al. [10] proposed a heroin model with the bilinear law incidence instead of the standard incidence and studied its stability. Considering the effects of distributed time delay on the dynamics of the heroin model, Samanta et al. [11,12,13,14] investigated different forms of heroin models with distributed delays. Motivated by the work of Samanta et al. [11], Abdurahman et al. [15] derived a discretized heroin epidemic model with a distributed time delay and studied its stability and permanence. As stated in [16], all the heroin models above assume that all individuals have the same level of susceptibility. This is not consistent with the reality, because the individuals at different stages have different levels of susceptibility. Thus, Fang et al. [16, 17] investigated the heroin model with age-dependent susceptibility. In addition, there are also some heroin models with nonlinear incidence rate that have received much attention from scholars at home and abroad [18,19,20].

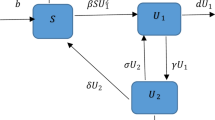
Obviously, most of the heroin models above assume that the treatment rate of heroin users not in treatment is proportional to the number of them. However, it is only possible to treat a limited number of heroin users at a given time, especially when the medical resources are scarce. Thus, it is more realistic to investigate the heroin model with nonlinear treatment function. To this end, Wangari and Stone [21] formulated the following heroin model with a saturated treatment function:

$$ \textstyle\begin{cases} \frac{dS(t)}{dt}=A-\beta U_{1}(t)S(t)-\mu S(t), \\ \frac{dU_{1}(t)}{dt}=\beta U_{1}(t)S(t)+pU_{2}(t)-(\mu +\delta _{1}+ \varepsilon ) U_{1}(t) \\ \hphantom{\frac{dU_{1}(t)}{dt}=}{}-\frac{\alpha U_{1}(t)}{1+\eta U_{1}(t)}, \\ \frac{dU_{2}(t)}{dt}=\frac{\alpha U_{1}(t)}{1+\eta U_{1}(t)}-(p+ \sigma +\delta _{2}+\mu )U_{2}(t), \\ \frac{dU_{3}(t)}{dt}=\sigma U_{2}(t)+\varepsilon U_{1}(t)-\mu U_{3}(t), \end{cases} $$
(1)

where \(S(t)\) denotes the number of susceptibles at time t; \(U_{1}(t)\), \(U_{2}(t)\), and \(U_{3}(t)\) denote the numbers of heroin users not in treatment, heroin users undergoing treatment, and individuals successfully treated from heroin use at time t, respectively. A is the constant input rate of the susceptibles through immigration and birth; β is the contact rate of the susceptibles with heroin users; p is the rate at which the heroin users undergoing treatment relapse; \(\delta _{1}\) and \(\delta _{2}\) are the heroin-induced death rates of heroin users not in treatment and heroin users undergoing treatment, respectively; ε is the self-cure rate of heroin users not in treatment; σ is the successful treatment rate of heroin users undergoing treatment; α is the rate at which heroin users are treated; η accounts for the extent of saturation of heroin users; μ is the natural death rate of all the subpopulations. Wangari and Stone [21] studied the stability and backward bifurcations of system (1).

It should be pointed out that Wangari and Stone [21] assume that the heroin users are cured instantaneously, which is not consistent with reality. As stated in [15], it needs some time to become a heroin user for a susceptible one. In exactly the same way, it should also take a period to cure drug users. Therefore, it is more realistic to incorporate the time delay due to the period used to cure heroin users into system (1). We assume that heroin users begin to be treated at \(t-\tau \) and they are cured at t. Thus, we can obtain the following delayed heroin model:

$$ \textstyle\begin{cases} \frac{dS(t)}{dt}=A-\beta U_{1}(t)S(t)-\mu S(t), \\ \frac{dU_{1}(t)}{dt}=\beta U_{1}(t)S(t)+pU_{2}(t)-(\mu +\delta _{1}) U_{1}(t) \\ \hphantom{\frac{dU_{1}(t)}{dt}=}{} -\varepsilon U_{1}(t-\tau )-\frac{\alpha U_{1}(t)}{1+\eta U_{1}(t)}, \\ \frac{dU_{2}(t)}{dt}=\frac{\alpha U_{1}(t)}{1+\eta U_{1}(t)}-(p+ \delta _{2}+\mu )U_{2}(t)-\sigma U_{2}(t-\tau ), \\ \frac{dU_{3}(t)}{dt}=\sigma U_{2}(t-\tau )+\varepsilon U_{1}(t- \tau )-\mu U_{3}(t), \end{cases} $$
(2)

where τ is the period used to cure heroin users. We mainly focus on the effect of the time delay on system (2).

The organization of this paper is as follows. In Sect. 2, we study local stability and existence of Hopf bifurcation, and sufficient conditions for local stability and existence of Hopf bifurcation are established. Section 3 deals with direction of the Hopf bifurcation, stability, and period of the bifurcating periodic solutions. Computer simulations of the model are performed in Sect. 4. Section 5, which is the last one, contains the conclusions.

2 Local stability and existence of Hopf bifurcation

Based on the analysis in [21], we can conclude that if condition \((H_{1})\): \(R_{0}>1\) and \(L_{1}<0\) holds, then system (2) has a unique endemic equilibrium \(E_{*}(S_{*}, U_{1*}, U_{2*}, U_{3*})\), where

$$\begin{aligned}& S_{*} =\frac{A}{\beta U_{1*}+\mu }, \\& U_{2*} =\frac{\alpha U_{1*}}{(p+\sigma +\delta _{2}+\mu )(1+\eta U _{1*})}, \\& U_{3*} =\frac{\alpha \sigma U_{1*}+\varepsilon (p+\sigma +\delta _{2}+ \mu )(1+\eta U_{1*})U_{1*}}{\mu (p+\sigma +\delta _{2}+\mu )(1+\eta U _{1*})}, \end{aligned}$$

and \(U_{1*}\) is the positive root of Eq. (3)

$$ L_{2}U_{1*}^{2}+L_{1}U_{1*}+L_{0}=0, $$
(3)

where

$$\begin{aligned}& L_{2} =(\mu +\delta _{1}+\varepsilon ) (p+\sigma +\delta _{2}+\mu ) \beta \eta , \\& L_{1} =(p+\sigma +\delta _{2}+\mu )\bigl[(\mu +\delta _{1}+\varepsilon ) ( \beta +\mu \eta )-A\beta \eta \bigr] +\alpha \beta (\sigma +\delta _{2}+\mu ), \\& L_{0} =\bigl[\mu (\mu +\delta _{1}+\varepsilon ) (p+\sigma +\delta _{2}+ \mu )+\alpha \mu (\sigma +\delta _{2}+\mu ) \bigr](1-R_{0}), \end{aligned}$$

with

$$ R_{0}=\frac{\beta A(p+\sigma +\delta _{2}+\mu )}{\mu (\mu +\delta _{1}+ \varepsilon )(p+\sigma +\delta _{2}+\mu )+\mu \alpha (\alpha +\delta _{2}+\sigma )}. $$

The characteristic equation of the linear section of system (2) at \(E_{*}(S_{*}, U_{1*}, U_{2*}, U_{3*})\) is

$$\begin{aligned}& \lambda ^{4}+M_{3}\lambda ^{3} +M_{2}\lambda ^{2}+M_{1}\lambda +M_{0} \\& \quad {}+\bigl(N_{3}\lambda ^{3}+N_{2}\lambda ^{2}+N_{1}\lambda +N_{0}\bigr)e^{-\lambda \tau } \\& \quad {}+\bigl(P_{2}\lambda ^{2}+P_{1}\lambda +P_{0}\bigr)e^{-2\lambda \tau }=0, \end{aligned}$$
(4)

where

$$\begin{aligned}& M_{0} =m_{33}m_{44}(m_{11}m_{22}-m_{12}m_{21})-m_{11}m_{23}m_{32}m _{44}, \\& M_{1} =(m_{12}m_{21}-m_{11}m_{22}) (m_{33}+m_{44})+m_{23}m_{32}(m_{11}+m _{44}) \\& \hphantom{M_{1} =}{}-m_{33}m_{44}(m_{11}+m_{22}), \\& M_{2} =m_{11}m_{22}+m_{33}m_{44}-m_{12}m_{21}-m_{23}m_{32} \\& \hphantom{M_{2} =}{}+(m_{11}+m_{22}) (m_{33}+m_{44}), \\& M_{3} =-(m_{11}+m_{22}+m_{33}+m_{44}), \\& N_{0} =m_{11}m_{44}(m_{33}n_{22}+m_{22}n_{33})-m_{12}m_{21}m_{44}n _{33}, \\& N_{1} =m_{12}m_{21}n_{33}-n_{22}(m_{11}m_{33}+m_{11}m_{44}+m_{33}m _{44}) \\& \hphantom{N_{1} =}{}-n_{33}(m_{11}m_{22}+m_{11}m_{44}+m_{22}m_{44}), \\& N_{2} =n_{22}(m_{11}+m_{33}+m_{44})+n_{33}(m_{11}+m_{22}+m_{44}), \\& N_{3} =-(n_{22}+n_{33}), \qquad P_{0}=m_{11}m_{44}n_{22}n_{33}, \\& P_{1} =-n_{22}n_{33}(m_{11}+m_{44}),\qquad P_{2}=n_{22}n_{33}, \end{aligned}$$

and

$$\begin{aligned}& m_{11} =-(\beta U_{1*}+\mu ),\qquad m_{12}=-\beta S_{*}, \\& m_{21} =\beta U_{1*},\qquad m_{22}=\beta S_{*}-(\mu +\delta _{1})-\frac{ \alpha }{1+\eta U_{1*}}, \qquad m_{23}=p, \\& m_{32} =\frac{\alpha }{1+\eta U_{1*}},\qquad m_{33}=-(p+\delta _{2}+\mu ), \\& m_{42} =-\mu ,\qquad n_{22}=-\varepsilon ,\qquad n_{33}=-\sigma , \qquad n_{42}=\varepsilon ,\qquad n_{43}=\sigma . \end{aligned}$$

Multiplying by \(e^{\lambda \tau }\), Eq. (4) becomes

$$\begin{aligned}& N_{3}\lambda ^{3}+N_{2}\lambda ^{2} +N_{1}\lambda +N_{0} \\& \quad {}+\bigl(\lambda ^{4}+M_{3}\lambda ^{3}+M_{2}\lambda ^{2}+M_{1}\lambda +M_{0}\bigr)e ^{\lambda \tau } \\& \quad {}+\bigl(P_{2}\lambda ^{2}+P_{1}\lambda +P_{0}\bigr)e^{-\lambda \tau }=0. \end{aligned}$$
(5)

When \(\tau =0\), Eq. (5) becomes

$$ \lambda ^{4}+M_{03}\lambda ^{3}+M_{02}\lambda ^{2}+M_{01}\lambda +M_{00}=0, $$
(6)

where

$$\begin{aligned}& M_{00} =M_{0}+N_{0}+P_{0},\qquad M_{01}=M_{1}+N_{1}+P_{1}, \\& M_{02} =M_{2}+N_{2}+P_{2},\qquad M_{03}=M_{3}+N_{3}. \end{aligned}$$

Based on the Routh–Hurwitz theorem, it can be concluded that all the roots of Eq. (6) have negative real parts if \((H_{2})\) holds

$$ (H_{2}): M_{00}>0,\qquad M_{01}>0,\qquad M_{03}>0,\qquad M_{01}M_{02}M_{03}>M_{01}^{2}+M _{03}^{2}M_{00}. $$

For \(\tau >0\), let \(\lambda =i\omega\) (\(\omega >0\)) be a root of Eq. (5). Then

$$ \textstyle\begin{cases} P_{1}(\omega )\cos \tau \omega -P_{2}(\omega )\sin \tau \omega =P_{3}( \omega ), \\ P_{4}(\omega )\sin \tau \omega +P_{5}(\omega )\cos \tau \omega =P_{6}( \omega ), \end{cases} $$

where

$$\begin{aligned}& P_{1}(\omega ) =\omega ^{4}-(M_{2}+P_{2}) \omega ^{2}+M_{0}+P_{0}, \\& P_{2}(\omega ) =(M_{1}-P_{1})\omega -M_{3}\omega ^{3}, \\& P_{3}(\omega ) =N_{2}\omega ^{2}-N_{0}, \\& P_{4}(\omega ) =\omega ^{4}-(M_{2}-P_{2}) \omega ^{2}+M_{0}-P_{0}, \\& P_{5}(\omega ) =(M_{1}+P_{1})\omega -M_{3}\omega ^{3}, \\& P_{6}(\omega ) =N_{3}\omega ^{3}-N_{1} \omega . \end{aligned}$$

Thus, one can obtain

$$\begin{aligned}& \cos \tau \omega =\frac{P_{01}(\omega )}{P_{00}(\omega )}, \\& \sin \tau \omega = \frac{P_{02}(\omega )}{P_{00}(\omega )}, \end{aligned}$$

with

$$\begin{aligned}& P_{00}(\omega ) =\omega ^{8}-2M_{2}\omega ^{6}+\bigl(M_{2}^{2}+2M_{0}-P_{2} ^{2}\bigr)\omega ^{4} \\& \hphantom{P_{00}(\omega ) =}{}+2(P_{0}P_{2}-M_{0}M_{2}) \omega \omega ^{2}+M_{0}^{2}-P_{0}^{2}, \\& P_{01}(\omega ) =(N_{2}-M_{3}N_{3}) \omega ^{6} \\& \hphantom{P_{01}(\omega ) =}{}+\bigl[N_{3}(M_{1}-P_{1})-N_{2}(M_{2}-P_{2})+M_{3}N_{1}-N_{0} \bigr]\omega ^{4} \\& \hphantom{P_{01}(\omega ) =}{}+\bigl[N_{0}(M_{2}-P_{2})-N_{1}(M_{1}-P_{1})+N_{2}(M_{0}-P_{0}) \bigr]\omega ^{2} \\& \hphantom{P_{01}(\omega ) =}{}-N_{0}(M_{0}-P_{0}), \\& P_{02}(\omega ) =N_{3}\omega ^{7}- \bigl[N_{3}(M_{2}+P_{2})+N_{1}\bigr] \omega ^{5} \\& \hphantom{P_{02}(\omega ) =}{}+\bigl[N_{3}(M_{0}+P_{0})-N_{1}(M_{2}+P_{2}) \bigr]\omega ^{3}-N_{1}(M_{0}+P _{0}) \omega . \end{aligned}$$

Then we can obtain the following equation with respect to ω:

$$ P_{01}^{2}(\omega )+P_{02}^{2}( \omega )-P_{00}^{2}(\omega )=0. $$
(7)

Next, we suppose that \((H_{3})\): Eq. (7) has at least one positive root \(\omega _{0}\).

Then Eq. (5) has a pair of purely imaginary roots \(\pm i\omega _{0}\). For \(\omega _{0}\), we can obtain the corresponding critical value of time delay as follows:

$$ \tau _{0}=\frac{1}{\omega _{0}}\arccos \biggl\{ \frac{P_{01}(\omega _{0})}{P _{00}(\omega _{0})} \biggr\} . $$
(8)

In what follows, we differentiate both sides of Eq. (7) with respect to τ and obtain

$$ \biggl[\frac{d\lambda }{d\tau } \biggr]^{-1}=-\frac{G_{1}(\lambda )}{G _{2}(\lambda )}- \frac{\tau }{\lambda }, $$

where

$$\begin{aligned}& G_{1}(\lambda ) =3B_{3}\lambda ^{2}+2B_{2} \lambda +B_{1} \\& \hphantom{G_{1}(\lambda ) =}{}+\bigl(4\lambda ^{3}+3M_{3}\lambda ^{2}+2M_{2}\lambda +M_{1}\bigr)e^{\lambda \tau }+(2P_{2} \lambda +P_{1})e^{-\lambda \tau }, \\& G_{2}(\lambda ) =\lambda \bigl(\lambda ^{4} + M_{3} \lambda ^{3} + M_{2} \lambda ^{2} + M_{1} \lambda + M_{0} \bigr) e^{\lambda \tau } \\& \hphantom{G_{2}(\lambda ) =}{}-\lambda \bigl(P_{2} \lambda ^{2} + P_{1} \lambda + P_{0}\bigr) e^{-\lambda \tau }. \end{aligned}$$

Then we can obtain the expression of \(\operatorname{Re}[\frac{d\lambda }{d\tau } ]^{-1}_{\tau =\tau _{0}}\). Let

$$ \operatorname{Re}\biggl[\frac{d\lambda }{d\tau } \biggr]^{-1}_{\tau =\tau _{0}}= \frac{P _{R}Q_{R}+P_{I}Q_{I}}{Q_{R}^{2} +Q_{I}^{2}}, $$

where

$$\begin{aligned}& P_{R} = N_{1} - 3 N_{3} \omega ^{2} + \bigl(M_{1} + P_{1} - 3 M_{3} \omega ^{2}\bigr) \cos {\tau _{0} \omega _{0}} - 2 \bigl(M_{2} \omega - P_{2} \omega + 2 \omega ^{3} \bigr) \sin {\tau _{0} \omega _{0}}, \\& P_{I} = - 2 N_{2} \omega -2\bigl(M_{2} \omega + P_{2} \omega -2 \omega ^{3}\bigr) \cos {\tau _{0} \omega _{0}} -\bigl(M_{1} -P_{1} -3 M_{3} \omega ^{2}\bigr) \sin {\tau _{0} \omega _{0}}, \\& Q_{R} = \bigl(M_{1} \omega - P_{1} \omega - M_{3} \omega ^{3}\bigr) \cos {\tau _{0} \omega _{0}} +\bigl(M_{0} + P_{0} - M_{2} \omega ^{2} - P_{2} \omega ^{2} + \omega ^{4}\bigr) \sin {\tau _{0} \omega _{0}}, \\& Q_{I} = \bigl(M_{0} - P_{0} - M_{2} \omega ^{2} + P_{2} \omega ^{2} + \omega ^{4}\bigr) \cos {\tau _{0} \omega _{0}} - \bigl(M_{1} \omega +P_{1} \omega - M_{3} \omega ^{3}\bigr) \sin {\tau _{0} \omega _{0}}. \end{aligned}$$

Obviously, if \((H_{4})\): \(P_{R}Q_{R}+P_{I}Q_{I}\neq 0\) holds, then \(\operatorname{Re}[\frac{d\lambda }{d\tau }]^{-1}_{\tau =\tau _{0}}\neq 0\). Based on the discussion above and the Hopf bifurcation theorem in [22], we have the following results.

Theorem 1

For system (2), if conditions \((H_{1})\)–\((H_{4})\) hold, then the positive equilibrium \(E_{*}(S_{*}, U_{1*}, U_{2*}, U_{3*})\) is locally asymptotically stable when \(\tau \in [0, \tau _{0})\); system (2) undergoes a Hopf bifurcation at \(E_{*}(S_{*}, U_{1*}, U_{2*}, U_{3*})\) when \(\tau =\tau _{0}\), and a family of periodic solutions bifurcate from \(E_{*}(S_{*}, U_{1*}, U_{2*}, U_{3*})\).

3 Direction and stability of Hopf bifurcation

In this section, the formulae for determining the direction and stability of the Hopf bifurcation of system (2) at \(\tau =\tau _{0}\) are presented. Let \(\tau =\tau _{0}+\mu _{0}\), \(\mu _{0} \in R\), so that \(\mu _{0} = 0\) is the Hopf bifurcation value for the system. Define the space of continuous real-valued functions as \(C=C([-1, 0], R^{4})\). Let \(u_{1}(t)=S(t)-S_{*}\), \(u_{2}(t)=U_{1}(t)-U _{1*}\), \(u_{3}(t)=U_{2}(t)-U_{2*}\), \(u_{4}(t)=U_{3}(t)-U_{3*}\), and normalize time delay with the scaling \(t\rightarrow (t/\tau )\). Then the delay system (2) transforms to a functional differential equation in C as follows:

$$ \dot{u}(t)=L_{\mu _{0}}(u_{t})+F(\mu _{0}, u_{t}), $$
(9)

where \(u(t)=(u_{1}, u_{2}, u_{3}, u_{4})^{T} \in C=C([-1, 0], R^{4})\) and \(L_{\mu }\): \(C\rightarrow R^{4}\) and F: \(R\times C\rightarrow R ^{4}\) are given as follows:

$$ L_{\mu _{0}}\phi =(\tau _{0}+\mu _{0}) \bigl(M_{\max }\phi (0)+N_{\max }\phi (-1)\bigr) $$

and

F( μ 0 ,ϕ)=( τ 0 + μ 0 ) ( 0 m 25 ϕ 2 2 ( 0 ) + m 26 ϕ 2 3 ( 0 ) + ⋯ m 35 ϕ 2 2 ( 0 ) + m 36 ϕ 2 3 ( 0 ) + ⋯ 0 )

with

M max = ( m 11 m 12 0 0 m 21 m 22 m 23 0 0 m 32 m 33 0 0 0 0 m 44 ) , N max = ( 0 0 0 0 0 n 22 0 0 0 0 n 33 0 0 n 42 n 43 0 )

and

$$\begin{aligned}& \begin{aligned}&m_{25} =\frac{\alpha \eta }{(1+\eta U_{1*})^{3}}, \qquad m_{26}=- \frac{ \alpha \eta ^{2}}{(1+\eta U_{1*})^{4}}, \\ &m_{35} =-\frac{\alpha \eta }{(1+\eta U_{1*})^{3}},\qquad m_{36}= \frac{ \alpha \eta ^{2}}{(1+\eta U_{1*})^{4}}. \end{aligned} \end{aligned}$$
(10)

By the Riesz representation theorem, there exists a function \(\eta (\theta ,\mu _{0})\) for \(\theta \in [-1,0]\) such that

$$ L_{\mu _{0}}\phi = \int _{-1}^{0}\,d\eta (\theta , \mu _{0}) \phi (\theta ) $$
(11)

for \(\phi \in C\). In fact, we choose

$$ \eta (\theta , \mu _{0})=(\tau _{0}+\mu _{0}) \bigl(M_{\max }\delta (\theta )+N _{\max }\delta (\theta +1)\bigr), $$

where \(\delta (\theta )\) is the Dirac delta function.

For \(\phi \in C([-1,0], R^{4})\), define

$$ A(\mu _{0})\phi =\textstyle\begin{cases} \frac{d\phi (\theta )}{d\theta }, & {-}1\leq \theta < 0, \\ \int _{-1}^{0}\,d\eta (\theta , \mu _{0})\phi (\theta ), & \theta =0, \end{cases} $$

and

$$ R(\mu _{0})\phi =\textstyle\begin{cases} 0, & {-}1\leq \theta < 0, \\ F(\mu _{0}, \phi ), & \theta =0. \end{cases} $$

Then system (9) is equivalent to

$$ \dot{u}(t)=A(\mu _{0})u_{t}+R(\mu _{0})u_{t}. $$
(12)

For \(\varphi \in C^{1}([0, 1], (R^{4})^{*})\), the adjoint operator \(A^{*}\) of \(A(0)\) is defined as follows:

$$ A^{*}(\varphi )=\textstyle\begin{cases} -\frac{d\varphi (s)}{ds}, & 0< s\leq 1, \\ \int _{-1}^{0}d{\eta }^{T}(s,0)\varphi (-s), & s=0. \end{cases} $$

Next, we define the bilinear inner form for A and \(A^{*}\):

$$ \bigl\langle \varphi (s),\phi (\theta )\bigr\rangle =\bar{\varphi }(0)\phi (0)- \int _{\theta =-1}^{0} \int _{\xi =0}^{\theta }\bar{\varphi }(\xi - \theta )\,d\eta ( \theta )\phi (\xi )\,d\xi , $$
(13)

where \(\eta (\theta )=\eta (\theta , 0)\).

Suppose that \(q(\theta )=(1, q_{2}, q_{3}, q_{4})^{T}e^{i\omega _{0} \tau _{0}\theta }\) is the eigenvector of \(A(0)\) corresponding to \(i\omega _{0}\tau _{0}\) and \(q^{*}(s)=D(1, q_{2}^{*}, q_{3}^{*}, q_{4} ^{*})^{T}e^{i\tau _{0}\omega _{0}s}\) is the eigenvector of \(A^{*}(0)\) corresponding to \(-i\tau _{0}\omega _{0}\). Then we can obtain

$$\begin{aligned}& q_{2} =\frac{i\omega _{0}-m_{11}}{m_{12}}, \\& q_{3} =\frac{i\omega _{0}-m_{22}-n_{22}e^{-i\tau _{0}\omega _{0}}}{m _{23}}, \\& q_{4} =\frac{n_{42}q_{2}+n_{43}q_{3}}{i\omega _{0}-m_{44}}, \\& q_{2}^{*} =-\frac{i\omega _{0}+m_{11}}{m_{21}}, \\& q_{3}^{*} =\frac{\Delta _{2}-m_{42}e^{i\tau _{0}\omega _{0}}}{m_{32}}, \\& q_{4}^{*} =-\frac{m_{23}m_{32}q_{2}}{\Delta _{1}(\Delta _{2}-n_{42}e ^{i\tau _{0}\omega _{0}})+m_{32}n_{43}e^{i\tau _{0}\omega _{0}}}, \\& \Delta _{1} =i\omega _{0}+m_{33}+n_{33}e^{i\tau _{0}\omega _{0}}, \\& \Delta _{2} =-\bigl(i\omega _{0}+m_{22}+n_{22}e^{i\tau _{0}\omega _{0}} \bigr)q_{2}-m _{12}. \end{aligned}$$

From Eq. (13), we can obtain

$$\begin{aligned} \bar{D} =&\bigl[1+q_{2}q_{2}^{*}+q_{3} \bar{q}_{3}^{*}+q_{4}\bar{q}_{4}^{*} \\ &{}+\tau _{0}e^{-i\tau _{0}\omega _{0}}\bigl(q_{2} \bigl(n_{22}\bar{q}_{2}^{*}+n_{42} \bar{q}_{4}^{*}\bigr)+q_{3}\bigl(n_{33} \bar{q}_{3}^{*}+n_{43}\bar{q}_{4}^{*} \bigr)\bigr)\bigr]^{-1} \end{aligned}$$

such that \(\langle q^{*}, q\rangle =1\) and \(\langle q^{*}, \bar{q} \rangle =0\).

Next, based on the algorithms in [22] and a computation process similar to that in [23,24,25], we can obtain

$$\begin{aligned}& g_{20} =2\bar{D}\tau _{0}\bigl(m_{25} \bar{q}_{2}^{*}q_{2}^{2}+m_{35} \bar{q}_{3}^{*}q_{2}^{2}\bigr), \\& g_{11} =2\bar{D}\tau _{0}q_{2} \bar{q}_{2}\bigl(m_{25}\bar{q}_{2}^{*}+m_{35} \bar{q}_{3}^{*}\bigr), \\& g_{02} =2\bar{D}\tau _{0}\bigl(m_{25} \bar{q}_{2}^{*}\bar{q}_{2}^{2}+m_{35} \bar{q}_{3}^{*}\bar{q}_{2}^{2}\bigr), \\& g_{21} =2\bar{D}\tau _{0}\bigl[\bar{q}_{2}^{*} \bigl(m_{25}\bigl(2W_{11}^{(2)}(0)q _{2}+W_{20}^{(2)}(0)\bar{q}_{2} \bigr)+3m_{26}q_{2}^{2}\bar{q}_{2}\bigr) \\& \hphantom{g_{21} =}{}+\bar{q}_{3}^{*}\bigl(m_{35} \bigl(2W_{11}^{(2)}(0)q_{2}+W_{20}^{(2)}(0) \bar{q}_{2}\bigr)+3m_{36}q_{2}^{2} \bar{q}_{2}\bigr)\bigr], \end{aligned}$$

with

$$\begin{aligned}& W_{20}(\theta ) =\frac{ig_{20}q(0)}{\tau _{0}\omega _{0}}e^{i\tau _{0} \omega _{0}\theta }+ \frac{i\bar{g}_{02}\bar{q}(0)}{3\tau _{0}\omega _{0}}e^{-i\tau _{0}\omega _{0}\theta }+E_{1}e^{2i\tau _{0}\omega _{0}\theta }, \\& W_{11}(\theta ) =-\frac{ig_{11}q(0)}{\tau _{0}\omega _{0}}e^{i\tau _{0} \omega _{0}\theta }+ \frac{i\bar{g}_{11}\bar{q}(0)}{\tau _{0}\omega _{0}}e ^{-i\tau _{0}\omega _{0}\theta }+E_{2}. \end{aligned}$$

\(E_{1}\) and \(E_{2}\) can be obtained by the following two equations:

E 1 = 2 ( 2 i ω 0 − m 11 − m 12 0 0 − m 21 m 22 ′ − m 23 0 0 − m 32 m 33 ′ 0 0 − n 42 e − 2 i τ 0 ω 0 − n 43 e − 2 i τ 0 ω 0 2 i ω 0 − m 44 ) − 1 × ( 0 m 25 q 2 2 m 35 q 2 2 0 ) , E 2 = − ( m 11 m 12 0 0 m 21 m 22 + n 22 m 23 0 0 m 32 m 33 + n 33 0 0 n 42 n 43 m 44 ) − 1 × ( 0 2 m 25 q 2 q ¯ 2 2 m 35 q 2 q ¯ 2 0 ) ,

with

$$\begin{aligned}& m_{22}^{\prime } =2i\omega _{0}-m_{22}-n_{22}e^{-2i\tau _{0}\omega _{0}}, \\& m_{33}^{\prime } =2i\omega _{0}-m_{33}-n_{33}e^{-2i\tau _{0}\omega _{0}}. \end{aligned}$$

Then one can obtain

$$ \begin{aligned} &C_{1}(0)=\frac{i}{2\tau _{0}\omega _{0}} \biggl(g_{11}g_{20}-2 \vert g_{11} \vert ^{2}-\frac{ \vert g _{02} \vert ^{2}}{3} \biggr)+\frac{g_{21}}{2} \\ &\mu _{2} =-\frac{\operatorname{Re}\{C_{1}(0)\}}{\operatorname{Re}\{\lambda '(\tau _{0}) \}}, \\ &\beta _{2}=2{\operatorname{Re}\bigl\{ C_{1}(0)\bigr\} }, \\ &T_{2}=-\frac{\operatorname{Im}\{C_{1}(0)\}+\mu _{2}\operatorname{Im}\{\lambda '(\tau _{0})\}}{\tau _{0}\omega _{0}}. \end{aligned} $$
(14)

In conclusion, we have the following results.

Theorem 2

For system (2), if \(\mu _{2}>0\) (\(\mu _{2}<0\)), then the Hopf bifurcation is supercritical (subcritical); if \(\beta _{2}<0\) (\(\beta _{2}>0\)), then the bifurcating periodic solutions are stable (unstable); if \(T_{2}>0\) (\(T_{2}<0\)), then the period of the bifurcating periodic solutions increases (decreases).

4 Numerical simulation

In this section, some numerical simulations are performed to verify analytically obtained results. We choose the same set of parameters as those in [21]: \(A=3\), \(P=0.46\), \(\alpha =0.9\), \(\beta =0.001\), \(\delta _{1}=0.002\), \(\delta _{2}=0.001\), \(\sigma =0,1\), \(\varepsilon =0.015\), \(\eta =0.15\), and \(\mu =0.01\). Then we obtain the following specific case of system (2):

$$ \textstyle\begin{cases} \frac{dS(t)}{dt}=3-0.001 U_{1}(t)S(t)-0.01 S(t), \\ \frac{dU_{1}(t)}{dt}=0.001 U_{1}(t)S(t)+0.46U_{2}(t)-0.012 U_{1}(t) \\ \hphantom{\frac{dU_{1}(t)}{dt}=}{}-0.015 U_{1}(t-\tau )-\frac{0.9 U_{1}(t)}{1+0.15 U_{1}(t)}, \\ \frac{dU_{2}(t)}{dt}=\frac{0.9 U_{1}(t)}{1+0.15 U_{1}(t)}-0.471U _{2}(t)-0.1 U_{2}(t-\tau ), \\ \frac{dU_{3}(t)}{dt}=0.1 U_{2}(t-\tau )+0.015 U_{1}(t-\tau )-0.01 U _{3}(t). \end{cases} $$
(15)

Then we obtain \(R_{0}=1.4885>1\) and Eq. (3) becomes of the following form:

$$ 2.3126e-006U_{1*}^{2}-1.1851e-004U_{1*}-5.5986e-004=0, $$
(16)

from which one can obtain that system (15) has a unique positive equilibrium \(E_{*}(45.7321, 55.5995,9.3976,177.3752)\). Further, we can verify that \(E_{*}(45.7321, 55.5995, 9.3976, 177.3752)\) is locally asymptotically stable when \(\tau =0\).

For \(\tau >0\), by using Matlab software package, we obtain \(\omega _{0}=0.0368\), \(\tau _{0}=40.1285\), \(P_{R}Q_{R}+P_{I}Q_{I}=0.0082>0\). In other words, the conditions for the occurrence of the Hopf bifurcation are satisfied for system (15). According to Theorem 1, we can conclude that the unique positive equilibrium \(E_{*}(45.7321, 55.5995, 9.3976,177.3752)\) is locally asymptotically stable when \(\tau \in [0, \tau _{0}=40.1285)\). This can be illustrated by Figs. 1–2. System (2) undergoes a Hopf bifurcation at \(E_{*}(45.7321, 55.5995, 9.3976,177.3752)\) when \(\tau =\tau _{0}=40.1285\) and a family of periodic solutions bifurcate from \(E_{*}(45.7321, 55.5995, 9.3976,177.3752)\), which can be shown as in Figs. 3–4. The bifurcation phenomenon can be also illustrated by the bifurcation diagrams in Fig. 5. Moreover, by some complex computations, we obtain \(C_{1}(0)=-0.0462+0.0029i\), \(\lambda ^{\prime }(\tau _{0})=0.3729-0.1846i\), \(\mu _{2}=0.1239>0\), \(\beta _{2}=-0.0924<0\), and \(T_{2}=0.0135>0\). Based on Theorem 2, we know that the Hopf bifurcation is supercritical, the periodic solutions are stable and increase.

Figure 1
figure 1

Time plots of S, \(U_{1}\), \(U_{2}\) and \(U_{3}\) with \(\tau = 37.45 < \tau_{0} =40.1285\)

Full size image
Figure 2
figure 2

Phase portrait of system (15) with \(\tau = 37.45 < \tau_{0} =40.1285\): (a) \(S - U_{1} -U_{2}\), (b) \(S - U_{1} -U_{3}\), (c) \(S - U_{2} -U_{3}\), (d) \(U_{1} -U_{2}-U_{3}\)

Full size image
Figure 3
figure 3

Time plots of S, \(U_{1}\), \(U_{2}\) and \(U_{3}\) with \(\tau = 45.25 > \tau_{0} =40.1285\)

Full size image
Figure 4
figure 4

Phase portrait of system (15) with \(\tau = 45.25 > \tau_{0} =40.1285\): (a) \(S - U_{1} -U_{2}\), (b) \(S - U_{1} -U_{3}\), (c) \(S - U_{2} -U_{3}\), (d) \(U_{1} -U_{2}-U_{3}\)

Full size image
Figure 5
figure 5

Bifurcation diagram of system (15) with respect to τ: (a) S, (b) \(U_{1}\), (c) \(U_{2}\), (d) \(U_{3}\)

Full size image

In addition, according to numerical simulations, we find that: (i) the number of susceptibles decreases and the numbers of the other three populations increase when the number of A or β in system (15) increases; this can be demonstrated by Figs. 6–7. (ii) the numbers of susceptibles and heroin users not in treatment decrease; nevertheless, the numbers of heroin users undergoing treatment and individuals successfully treated from heroin use increase when the number of α in system (15) increases, which can be illustrated by Fig. 8. (iii) the number of heroin users not in treatment increases and the numbers of the other three populations decrease when the number of η in system (15) increases. This phenomenon can be shown as in Fig. 9.

Figure 6
figure 6

Effect of A on all classes for \(\tau= 35.25\): (a) S, (b) \(U_{1}\), (c) \(U_{2}\), (d) \(U_{3}\)

Full size image
Figure 7
figure 7

Effect of β on all classes for \(\tau= 35.25\): (a) S, (b) \(U_{1}\), (c) \(U_{2}\), (d) \(U_{3}\)

Full size image
Figure 8
figure 8

Effect of α on all classes for \(\tau= 25.25\): (a) S, (b) \(U_{1}\), (c) \(U_{2}\), (d) \(U_{3}\)

Full size image
Figure 9
figure 9

Effect of η on all classes for \(\tau= 28.25\): (a) S, (b) \(U_{1}\), (c) \(U_{2}\), (d) \(U_{3}\)

Full size image

5 Conclusions

In this paper, a delayed heroin model with saturated treatment function in the form of \(\frac{\alpha U_{1}}{1+\eta U_{1}}\) is discussed, which is different from the model in [21]. In our model, we assume that the heroin users cannot be cured instantaneously and it needs a period to cure heroin users, which is more in line with truth. Compared with the work by Wangari and Stone in [21], we mainly focus on the effect of the time delay on the proposed model in the present paper.

It has been shown that the time delay may destabilize the positive equilibrium of the model and cause the population to fluctuate if certain conditions are satisfied. When the value of the time delay is below the threshold \(\tau _{0}\), then the positive equilibrium of the model is locally asymptotically stable. In this case, the heroin abuse among the populations can be controlled. However, when the value of the time delay passes through the threshold \(\tau _{0}\), the model will lose its stability and a Hopf bifurcation occurs and a family of periodic solutions bifurcate from the positive equilibrium. In this case, the populations in the model will oscillate in the vicinity of \(E_{*}(S _{*}, U_{1*}, U_{2*}, U_{3*})\). Namely, the heroin abuse in the populations will be out of control. Furthermore, properties of the Hopf bifurcation are investigated with the aid of the normal form theory and center manifold theorem. Finally, numerical simulations are presented to verify the analytical predictions.

It has been observed in our simulations that the number of heroin users not in treatment increases when the number of A increases. Thus, the input rate of the susceptibles in a community should be controlled properly, especially the input rate through immigration. Similarly, it is strongly recommended that people should exercise self-control so as to protect themselves from drugs, since the number of heroin users not in treatment increases when the number of β increases. The number of heroin users not in treatment decreases when the number of α increases, which suggests that populations in a community should periodically go to hospital for physical examination and early recognition, treatment. Also, the number of heroin users not in treatment decreases when the number of η increases. This gives us a suggestion that we should improve medical facilities continuously and ensure that medical resources are sufficient and available.