1 Introduction

A computer worm is a self-contained program that can spread functional copies of itself or its segments to other systems without depending on another program to host its code [1, 2]. With the development of information technology and the increase of network complexity, the problem of computer worms has become the focus with its tremendous destruction. So, it is of considerable interest to understand the law governing spread of the worms in a network. Enlightened by the fact that propagation of the worms in a network could be compared with infectious diseases in a population, many mathematical models have been established to predict the spread of worms [3–7].

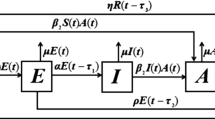
The quarantine strategy is an effective method on controlling disease. Inspired of this, many researchers introduce the quarantine strategy into mathematical models to investigate the spread of the worms in a network [8–10]. In order to describe the dynamics of worm propagation in a network, Kumar et al. proposed the following SEIQRS-V model in [10]:

$$ \textstyle\begin{cases} \frac{dS(t)}{dt} = A-\beta S(t)I(t)-d S(t)-\rho S(t)+\theta R(t)+\chi V(t), \\ \frac{dE(t)}{dt} = \beta S(t)I(t)-dE(t)-\gamma E(t), \\ \frac{dI(t)}{dt} = \gamma E(t)-dI(t)-\alpha I(t)-\delta I(t)-\eta I(t), \\ \frac{dQ(t)}{dt} = \delta I(t)-dQ(t)-\alpha Q(t)-\varepsilon Q(t), \\ \frac{dR(t)}{dt} = \varepsilon Q(t)-dR(t)-\theta R(t)+\eta I(t), \\ \frac{dV(t)}{dt} = \rho S(t)-dV(t)-\chi V(t), \end{cases} $$
(1)

where \(S(t)\), \(E(t)\), \(I(t)\), \(Q(t)\), \(R(t)\) and \(V(t)\) are the numbers of the uninfected computers which have no immunity, the exposed computers which are susceptible to infection, the infected computers which have to be cured, the infected computers which are quarantined, the uninfected computers which have temporary immunity and the vaccinated computers which have susceptibility to infection at time t, respectively. A is the rate at which the new computers are attached to the network; d is the natural death rate of the computers in the network; α is the death rate of computers in the network due to the attack of the worms; β, γ, δ, η, ε, θ, ρ and χ are the state transition rates of system (1).

Clearly, system (1) neglects the delays during the propagation process of the worms in the network. It is well known that delays of one type or another have been incorporated into worm propagation models due to latent period, temporary immunization period or other reasons. Worm propagation models with delay have been investigated by some scholars at home or broad in recent years [11–15]. Delays can play a complicated role in the dynamics of the dynamical models, especially they can cause Hopf bifurcation in the predator-prey models [16–19], epidemic models [20–24] and economic models [25–27]. For worm propagation models, the occurrence of a Hopf bifurcation means that the state of the worm propagation changes from an equilibrium to a limit cycle and this phenomenon makes the propagation of worms out of control. Therefore, it is of substantial importance to investigate the effect of delays on the worm propagation models. Based on this and considering the fact that one of the typical features of worms is its latent characteristic, we incorporate the latent period delay into system (1) and get the following worm propagation model with quarantine strategy and time delay:

$$ \textstyle\begin{cases} \frac{dS(t)}{dt} = A-\beta S(t)I(t)-d S(t)-\rho S(t)+\theta R(t)+\chi V(t), \\ \frac{dE(t)}{dt} = \beta S(t)I(t)-dE(t)-\gamma E(t-\tau), \\ \frac{dI(t)}{dt} = \gamma E(t-\tau)-dI(t)-\alpha I(t)-\delta I(t)-\eta I(t), \\ \frac{dQ(t)}{dt} = \delta I(t)-dQ(t)-\alpha Q(t)-\varepsilon Q(t), \\ \frac{dR(t)}{dt} = \varepsilon Q(t)-dR(t)-\theta R(t)+\eta I(t), \\ \frac{dV(t)}{dt} = \rho S(t)-dV(t)-\chi V(t), \end{cases} $$
(2)

where τ is the latent period delay.

The rest of the present paper is organized as follows. In Section 2, we analyze the local stability of the endemic equilibrium and the threshold of a Hopf bifurcation. Section 3 is devoted to the explicit formulas determining direction of the Hopf bifurcation and stability of the bifurcating periodic solutions. In Section 4, a simulation example is presented and the simulation results match well with our obtained theoretical results. Finally, Section 5 draws the conclusions.

2 Analysis of Hopf bifurcation

By a direct computation, we can know that if \(AR_{0}(d+\chi)>d^{2}+(\rho +\chi)d\) and \(\beta(d+\theta)(d+\alpha+\varepsilon)>R_{0}\theta \varepsilon\delta+R_{0}\theta\eta(d+\alpha+\varepsilon)\), then system (2) has a unique endemic equilibrium \(P_{*}(S_{*}, E_{*}, I_{*}, Q_{*}, R_{*}, V_{*})\), where

$$\begin{aligned}& S_{*} = \frac{(d+\gamma)(d+\alpha+\delta+\eta)}{\beta\gamma}=\frac {1}{R_{0}}, \quad\quad E_{*}=\frac{d+\alpha+\delta+\eta}{\gamma}I_{*}, \\& R_{*} = \frac{\varepsilon\delta+\eta(d+\alpha+\varepsilon )}{(d+\theta)(d+\alpha+\varepsilon)}I_{*},\quad\quad V_{*}=\frac{\rho}{(d+\chi )R_{0}}, \\& Q_{*} = \frac{\delta}{d+\alpha+\varepsilon}I_{*}, \quad\quad I_{*}=\frac{(d+\theta )(d+\alpha+\varepsilon)[d^{2}+(\rho+\chi)d-AR_{0}(d+\chi)]}{(d+\chi )[R_{0}\theta\varepsilon\delta+(d+\alpha+\varepsilon)(R_{0}\theta\eta -\beta d-\beta\theta)]}, \\& R_{0} = \frac{\beta\gamma}{(d+\gamma)(d+\alpha+\delta+\eta)}. \end{aligned}$$

The linearized system of system (2) at \(P_{*}(S_{*}, E_{*}, I_{*}, Q_{*}, R_{*}, V_{*})\) can be given by

$$ \begin{gathered} \frac{dS(t)}{dt} = a_{11}S(t)+a_{13}I(t)+a_{15}R(t)+a_{16}V(t), \\ \frac{dE(t)}{dt} = a_{21}S(t)+a_{22}E(t)+a_{23}I(t)+b_{22}E(t- \tau ), \\ \frac{dI(t)}{dt} = a_{33}I(t)+b_{32}E(t-\tau), \\ \frac{dQ(t)}{dt} = a_{43}I(t)+a_{44}\,dQ(t), \\ \frac{dR(t)}{dt} = a_{53}I(t)+a_{54}Q(t)+a_{55}R(t), \\ \frac{dV(t)}{dt} = a_{61}S(t)+a_{66}V(t). \end{gathered} $$
(3)

The characteristic equation for system (3) is

$$ \begin{aligned}[b] &\lambda^{6}+r_{5} \lambda^{5}+r_{4}\lambda^{4}+r_{3} \lambda^{3}+r_{2}\lambda ^{2}+r_{1} \lambda+r_{0} \\ &\quad{} +\bigl(s_{5}\lambda^{5}+s_{4} \lambda^{4}+s_{3}\lambda ^{3}+s_{2} \lambda^{2}+s_{1}\lambda+s_{0}\bigr)e^{-\lambda\tau}=0, \end{aligned} $$
(4)

where

$$\begin{aligned}& r_{0}=a_{22}a_{33}a_{44}a_{55}(a_{11}a_{22}-a_{16}a_{61}), \\& \begin{aligned} r_{1}&=a_{16}a_{61} \bigl[a_{22}a_{33}(a_{44}+a_{55})+a_{44}a_{55}(a_{22}+a_{33}) \bigr] \\ &\quad{} -a_{11}a_{22}a_{33}a_{44}(a_{55}+a_{66}) \\ &\quad{} -a_{55}a_{66}\bigl[a_{11}a_{22}(a_{33}+a_{44})+a_{33}a_{44}(a_{11}+a_{22}) \bigr], \end{aligned} \\& \begin{aligned} r_{2}&=(a_{55}+a_{66}) \bigl[a_{11}a_{22}(a_{33}+a_{44})+a_{33}a_{44}(a_{11}+a_{22}) \bigr] \\ &\quad{} +a_{55}a_{66}\bigl[a_{11}a_{22}+a_{33}a_{44}+(a_{11}+a_{22}) (a_{33}+a_{44})\bigr] \\ &\quad{} -a_{16}a_{61}\bigl[a_{22}a_{33}+a_{44}a_{55}+(a_{22}+a_{33}) (a_{44}+a_{55})\bigr] \\ &\quad{} +a_{11}a_{22}a_{33}a_{44}, \end{aligned} \\& \begin{aligned} r_{3}&=a_{16}a_{61}(a_{22}+a_{33}+a_{44}+a_{55})-a_{55}a_{66}(a_{11}+a_{22}+a_{33}+a_{44}) \\ &\quad{} -\bigl[a_{11}a_{22}(a_{33}+a_{44})+a_{33}a_{44}(a_{11}+a_{22}) \bigr] \\ &\quad{} -(a_{55}+a_{66})\bigl[a_{11}a_{22}+a_{33}a_{44}+(a_{11}+a_{22}) (a_{33}+a_{44})\bigr], \end{aligned} \\& \begin{aligned} r_{4}&=a_{11}a_{22}+a_{33}a_{44}+a_{55}a_{66}-a_{16}a_{61}-(a_{11}+a_{22}) (a_{33}+a_{44}) \\ &\quad{}\times (a_{55}+a_{66}) (a_{11}+a_{22}+a_{33}+a_{44}), \end{aligned} \\& r_{5}=-(a_{11}+a_{22}+a_{33}+a_{44}+a_{55}+a_{66}), \\& \begin{aligned} s_{0}&=a_{16}a_{44}a_{55}a_{61}b_{32}(a_{23}-a_{33})+a_{15}a_{21}a_{66}b_{32}(a_{43}a_{54}-a_{44}a_{53}) \\ &\quad{} +a_{11}a_{44}a_{55}a_{66}(a_{33}b_{22}-a_{23}b_{32}), \end{aligned} \\& \begin{aligned} s_{1}&=a_{23}b_{32} \bigl[a_{11}a_{44}(a_{55}+a_{66})+a_{55}a_{66}(a_{11}+a_{44}) \bigr] \\ &\quad{} +a_{15}a_{21}a_{43}b_{32}(a_{44}+a_{66})-a_{13}a_{21}b_{32} \bigl[a_{44}a_{55}+a_{66}(a_{44}+a_{55}) \bigr] \\ &\quad{} -a_{15}a_{21}a_{43}a_{54}b_{32}-a_{16}a_{23}a_{61}b_{32}(a_{44}+a_{55}) \\ &\quad{} +a_{16}a_{61}b_{32}\bigl[a_{33}a_{44}+a_{55}(a_{33}+a_{44}) \bigr]-a_{11}a_{33}a_{44}a_{55}b_{22} \\ &\quad{} -a_{66}b_{22}\bigl[a_{11}a_{33}(a_{44}+a_{55})+a_{44}a_{55}(a_{11}+a_{33}) \bigr], \end{aligned} \\& \begin{aligned} s_{2}&=a_{16}a_{23}a_{61}b_{32}+a_{13}a_{21}b_{32}(a_{44}+a_{55}+a_{66}) \\ &\quad{} +a_{16}a_{61}b_{32}(a_{33}+a_{44}+a_{55})-a_{15}a_{21}a_{53}b_{32} \\ &\quad{} -a_{23}b_{32}\bigl[a_{11}a_{44}+a_{55}a_{66}+(a_{11}+a_{44}) (a_{55}+a_{66})\bigr] \\ &\quad{} +a_{66}b_{22}\bigl[a_{11}a_{33}+a_{44}a_{55}+(a_{11}+a_{33}) (a_{44}+a_{55})\bigr] \\ &\quad{} +b_{22}\bigl[a_{11}a_{33}(a_{44}+a_{55})+a_{44}a_{55}(a_{11}+a_{33}) \bigr], \end{aligned} \\& \begin{aligned} s_{3}&=a_{23}b_{32}(a_{11}+a_{44}+a_{55}+a_{66})+a_{16}a_{61}b_{22}-a_{13}a_{21}b_{32} \\ &\quad{} -b_{22}\bigl[a_{11}a_{33}+a_{44}a_{55}+(a_{11}+a_{33}) (a_{44}+a_{55})\bigr] \\ &\quad{} -a_{66}b_{22}(a_{11}+a_{33}+a_{44}+a_{55}), \end{aligned} \\& s_{4}=b_{22}(a_{11}+a_{33}+a_{44}+a_{55}+a_{66})-a_{23}b_{32}, \quad\quad s_{5}=-b_{22}. \end{aligned}$$

When \(\tau=0\), equation (4) becomes

$$ \lambda^{6}+r_{05}\lambda^{5}+r_{04} \lambda^{4}+r_{03}\lambda ^{3}+r_{02} \lambda^{2}+r_{01}\lambda+r_{00}=0, $$
(5)

with

$$\begin{aligned}& r_{00} = r_{0}+s_{0}, \quad\quad r_{01}=r_{1}+s_{1},\quad\quad r_{02}=r_{2}+s_{2}, \\& r_{03} = r_{3}+s_{3},\quad\quad r_{04}=r_{4}+s_{4},\quad\quad r_{05}=r_{5}+s_{5}. \end{aligned}$$

Obviously, \(D_{1}=r_{05}>0\). Therefore, a set of sufficient conditions for all roots of equation (5) to have a negative real part is given by the Routh-Hurwitz criteria in the following form:

$$\begin{aligned}& D_{2}=\det \left ( \textstyle\begin{array}{@{}cc@{}} r_{05} &{1}\\ r_{03} &r_{04} \end{array}\displaystyle \right )>0, \end{aligned}$$
(6)
$$\begin{aligned}& D_{3}=\det \left ( \textstyle\begin{array}{@{}ccc@{}} r_{05} &{1} &{0}\\ r_{03} &r_{04} &r_{05}\\ r_{01} &r_{02} &r_{03} \end{array}\displaystyle \right )>0, \end{aligned}$$
(7)
$$\begin{aligned}& D_{4}=\det \left ( \textstyle\begin{array}{@{}cccc@{}} r_{05} &{1} &{0} &{0}\\ r_{03} &r_{04} &r_{05} &{1}\\ r_{01} &r_{02} &r_{03} &r_{04}\\ {0} &r_{00} &r_{01} &r_{02} \end{array}\displaystyle \right )>0, \end{aligned}$$
(8)
$$\begin{aligned}& D_{5}=\det \left ( \textstyle\begin{array}{@{}ccccc@{}} r_{05} &{1} &{0} &{0} &{0}\\ r_{03} &r_{04} &r_{05} &{1} &{0}\\ r_{01} &r_{02} &r_{03} &r_{04} &r_{05}\\ {0} &r_{00} &r_{01} &r_{02} &r_{03}\\ {0} &{0} &{0} &r_{00} &r_{01} \end{array}\displaystyle \right )>0, \end{aligned}$$
(9)
$$\begin{aligned}& D_{6}=r_{00}>0. \end{aligned}$$
(10)

Assume that \(\lambda=i\omega(\omega>0)\) is a solution of equation (4). Then one can obtain

$$ \textstyle\begin{cases} (s_{5}\omega^{5}-s_{3}\omega^{3}+s_{1}\omega)\sin\tau\omega+(s_{4}\omega ^{4}-s_{2}\omega^{2}+s_{0})\cos\tau\omega\\ \quad =\omega^{6}-r_{4}\omega^{4}+r_{2}\omega ^{2}-r_{0}, \\ (s_{5}\omega^{5}-s_{3}\omega^{3}+s_{1}\omega)\cos\tau\omega-(s_{4}\omega ^{4}-s_{2}\omega^{2}+s_{0})\sin\tau\omega \\ \quad =r_{3}\omega^{3}-r_{5}\omega ^{5}-r_{1}\omega, \end{cases} $$
(11)

from which it follows that

$$ \omega^{12}+p_{5}\omega^{10}+p_{4} \omega^{8}+p_{3}\omega^{6}+p_{2}\omega ^{4}+p_{1}\omega^{2}+p_{0}=0, $$
(12)

where

$$\begin{aligned}& p_{0} = r_{0}^{2}-s_{0}^{2}, \quad\quad p_{1}=r_{1}^{2}-2r_{0}r_{2}-s_{1}^{2}+2s_{0}s_{2}, \\& p_{2} = r_{2}^{2}+2r_{0}r_{4}-2r_{1}r_{3}+2s_{1}s_{3}-s_{2}^{2}-2s_{0}s_{4}, \\& p_{3} = r_{3}^{2}+2r_{1}r_{5}-2r_{0}-2r_{2}r_{4}-s_{3}^{2}-2s_{1}s_{5}+2s_{2}s_{4}, \\& p_{4} = r_{4}^{2}+2r_{2}-2r_{3}r_{5}+2s_{3}s_{5}-s_{4}^{2}, \quad\quad p_{5}=r_{5}^{2}-s_{5}^{2}-2r_{4}. \end{aligned}$$

If all the coefficients of system (2) are given, we can solve equation (12) by Matlab software package easily. So, we make the following assumption.

\((H_{1})\) :

equation (12) has at least one positive root.

If the condition \((H_{1})\) holds, then there exists \(\omega_{0}>0\) such that equation (4) has a pair of purely imaginary roots \(\pm i\omega_{0}\). For \(\omega_{0}\), one can obtain

$$ \tau_{0}=\frac{1}{\omega_{0}}\times\arccos \biggl\{ \frac{F_{1}(\omega _{0})}{F_{2}(\omega_{0})} \biggr\} , $$
(13)

where

$$\begin{aligned}& \begin{aligned} F_{1}(\omega_{0})&=(s_{4}-s_{5}r_{5}) \omega _{0}^{10}+(s_{5}r_{3}+s_{3}r_{5}-s_{4}r_{4}-s_{2}) \omega_{0}^{8} \\ &\quad{} +(s_{2}r_{4}+s_{4}r_{2}-s_{1}r_{5}-s_{5}r_{1}-s_{3}r_{3}+s_{0}) \omega_{0}^{6} \\ &\quad{} +(s_{3}r_{1}+s_{1}r_{3}-s_{4}r_{0}-s_{2}r_{2}-s_{0}r_{4}) \omega_{0}^{4} \\ &\quad{} +(s_{0}r_{2}+s_{2}r_{0}+s_{1}r_{1}) \omega_{0}^{2}-s_{0}r_{0}, \end{aligned} \\& \begin{aligned} F_{2}(\omega_{0})&=s_{5} \omega_{0}^{10}+\bigl(s_{4}^{2}-2s_{3}s_{5} \bigr)\omega _{0}^{8}+\bigl(s_{3}^{2}+2s_{1}s_{5}-2s_{2}s_{4} \bigr)\omega_{0}^{6} \\ &\quad{} +\bigl(s_{2}^{2}+2s_{0}s_{4}-2s_{1}s_{3} \bigr)\omega_{0}^{4}+\bigl(s_{1}^{2}-2s_{0}s_{2} \bigr)\omega _{0}^{2}+s_{0}^{2}. \end{aligned} \end{aligned}$$

For equation (4), by direct computation we have

$$ \frac{d\lambda}{d\tau}=\frac{G(\lambda)}{H(\lambda)}, $$
(14)

where

$$\begin{aligned}& G(\lambda)=\lambda\bigl(s_{5}\lambda^{5}+s_{4} \lambda^{4}+s_{3}\lambda ^{3}+s_{2} \lambda^{2}+s_{1}\lambda+s_{0}\bigr)e^{-\lambda\tau}, \\& \begin{aligned} H(\lambda)&=6\lambda^{5}+5r_{5} \lambda^{4}+4r_{4}\lambda^{3}+3r_{3} \lambda ^{2}+2r_{2}\lambda+r_{1} \\ &\quad{} +\bigl(5s_{5}\lambda^{4}+4s_{4} \lambda^{3}+3s_{3}\lambda^{2}+2s_{2} \lambda +s_{1}\bigr)e^{-\lambda\tau} \\ &\quad{} -\tau\bigl(s_{5}\lambda^{5}+s_{4} \lambda^{4}+s_{3}\lambda^{3}+s_{2}\lambda ^{2}+s_{1}\lambda+s_{0}\bigr)e^{-\lambda\tau}. \end{aligned} \end{aligned}$$

Then we obtain

$$\begin{aligned} \biggl[\frac{d\lambda}{d\tau} \biggr]^{-1} =&-\frac{6\lambda ^{5}+5r_{5}\lambda^{4}+4r_{4}\lambda^{3}+3r_{3}\lambda^{2}+2r_{2}\lambda +r_{1}}{\lambda(\lambda^{6}+r_{5}\lambda^{5}+r_{4}\lambda^{4}+r_{3}\lambda ^{3}+r_{2}\lambda^{2}+r_{1}\lambda+r_{0})} \\ &{}+\frac{5s_{5}\lambda^{4}+4s_{4}\lambda^{3}+3s_{3}\lambda^{2}+2s_{2}\lambda +s_{1}}{\lambda(s_{5}\lambda^{5}+s_{4}\lambda^{4}+s_{3}\lambda^{3}+s_{2}\lambda ^{2}+s_{1}\lambda+s_{0})}-\frac{\tau}{\lambda}. \end{aligned}$$
(15)

Thus,

$$\begin{aligned} \operatorname {Re}\biggl[\frac{d\lambda}{d\tau} \biggr]^{-1}_{\tau=\tau _{0}}= \frac{f^{\prime}(v_{*})}{(s_{5}\omega_{0}^{5}-s_{3}\omega_{0}^{3}+s_{1}\omega _{0})^{2}+(s_{4}\omega_{0}^{4}-s-2\omega_{0}^{2}+s_{0})^{2}}, \end{aligned}$$
(16)

with \(f(v)=v^{6}+p_{5}v^{5}+p_{4}v^{4}+p_{3}v^{3}+p_{2}v^{2}+p_{1}v+p_{0}\) and \(v_{*}=\omega_{0}^{2}\).

Therefore, if we have the condition \((H_{2})\): \(f^{\prime}(v_{*})\neq0\), then \(\operatorname {Re}[d\lambda/d\tau]_{\tau=\tau_{0}}^{-1}\neq0\). According to the discussion above and the Hopf bifurcation theorem in [28], we can obtain the following.

Theorem 1

For system (2), if the conditions \((H_{1})\)-\((H_{2})\) hold, then the endemic equilibrium \(P_{*}(S_{*}, E_{*}, I_{*}, Q_{*}, R_{*}, V_{*})\) is asymptotically stable for \(\tau\in[0, \tau_{0})\); a Hopf bifurcation occurs at the endemic equilibrium \(P_{*}(S_{*}, E_{*}, I_{*}, Q_{*}, R_{*}, V_{*})\) when \(\tau=\tau_{0}\) and a family of periodic solutions bifurcate from the endemic equilibrium \(P_{*}(S_{*}, E_{*}, I_{*}, Q_{*}, R_{*}, V_{*})\) near \(\tau =\tau_{0}\).

3 Direction and stability of the Hopf bifurcation

Motivated by the ideas of Hassard et al. [28], in this section, we will derive the explicit formulas that determine the direction and stability of the Hopf bifurcation at the critical value \(\tau_{0}\). For the sake of simplicity, let \(\tau=\tau_{0}+\mu\), \(\mu\in R\). Then \(\mu=0\) is the Hopf bifurcation value for system (2). Setting \(u_{1}(t)=S(t)-S_{*}\), \(u_{2}(t)=E(t)-E_{*}\), \(u_{3}(t)=I(t)-I_{*}\), \(u_{4}(t)=Q(t)-Q_{*}\), \(u_{5}(t)=R(t)-R_{*}\), \(u_{6}(t)=V(t)-V_{*}\) and \(t\rightarrow(t/\tau)\). Then system (2) can be transformed into functional differential equations in \(C=C([-1, 0], R^{6})\):

$$ \dot{u}(t)=L_{\mu}u_{t}+f(\mu, u_{t}), $$
(17)

with

$$\begin{aligned}& L_{\mu}\phi=(\tau_{0}+\mu) \bigl(B_{1} \phi(0)+B_{2}\phi(-1)\bigr), \\& f(\mu,\phi)=(\tau_{0}+\mu)\left ( \textstyle\begin{array}{@{}c@{}} -\beta\phi_{1}(0)\phi_{3}(0)\\ \beta\phi_{1}(0)\phi_{3}(0)\\ {0}\\ {0}\\ {0}\\ {0} \end{array}\displaystyle \right ), \end{aligned}$$

and

$$\begin{aligned}& B_{1}=\left ( \textstyle\begin{array}{@{}cccccc@{}} a_{11} &{0} &a_{13} &{0} &a_{15} &a_{16}\\ a_{21} &a_{22} &a_{23} &{0} &{0} &{0}\\ {0} &{0} &a_{33} &{0} &{0} &{0}\\ {0} &{0} &a_{43} &a_{44} &{0} &{0}\\ {0} &{0} &a_{53} &a_{54} &a_{55} &{0}\\ a_{61} &{0} &{0} &{0} &{0} &a_{66} \end{array}\displaystyle \right ), \\& B_{2}=\left ( \textstyle\begin{array}{@{}cccccc@{}} {0} &{0} &{0} &{0} &{0} &{0}\\ {0} &b_{22} &{0} &{0} &{0} &{0}\\ {0} &b_{32} &{0} &{0} &{0} &{0}\\ {0} &{0} &{0} &{0} &{0} &{0}\\ {0} &{0} &{0} &{0} &{0} &{0}\\ {0} &{0} &{0} &{0} &{0} &{0} \end{array}\displaystyle \right ). \end{aligned}$$

Based on the Riesz representation theorem, there exists a bounded variation function \(\eta(\theta, \mu)\) for \(\theta\in[-1, 0]\) such that

$$ L_{\mu}\phi= \int_{-1}^{0}d\eta(\theta,\mu)\phi(\theta),\quad \phi \in C. $$
(18)

In fact, we choose

$$\eta(\theta,\mu)=(\tau_{0}+\mu) \bigl(B_{1}\delta( \theta)+B_{2}\delta (\theta+1)\bigr), $$

where \(\delta(\theta)\) is the Dirac delta function. Next, for \(\phi\in C\), we define

$$A(\mu)\phi= \textstyle\begin{cases} \frac{d\phi(\theta)}{d\theta}, & -1\leq \theta< 0, \\ \int_{-1}^{0}d\eta(\theta,\mu)\phi(\theta),& \theta=0, \end{cases} $$

and

$$R(\mu)\phi= \textstyle\begin{cases} 0, & -1\leq\theta< 0, \\ F(\mu,\phi), & \theta=0. \end{cases} $$

Then system (17) can be transformed into

$$ \dot{u}(t)=A(\mu)u_{t}+R(\mu)u_{t}, $$
(19)

where \(u_{t}=u(t+\theta)\).

In order to construct the coordinates describing the center manifold near \(\mu=0\), we have to define an inner product and the adjoint operator \(A^{*}\) of \(A(0)\). Letting \(C^{*}=C([0, 1], R^{6})\), for \(\varphi \in C^{*}\), \(A^{*}\) is defined by

$$A^{*}(\varphi)= \textstyle\begin{cases} -\frac{d\varphi(s)}{ds}, & 0< s\leq1, \\ \int_{-1}^{0}d{\eta}^{T}(s,0)\varphi(-s), & s=0, \end{cases} $$

where \(\eta^{T}\) is the transpose of η.

For \(\phi\in C\) and \(\varphi\in C^{*}\), an inner product is defined as the following bilinear form:

$$ \bigl\langle \varphi(s),\phi(\theta)\bigr\rangle =\bar{\varphi}(0) \phi (0)- \int_{\theta=-1}^{0} \int_{\xi=0}^{\theta}\bar{\varphi}(\xi -\theta)\,d\eta( \theta)\phi(\xi)\,d\xi, $$
(20)

where \(\eta(\theta)=\eta(\theta, 0)\).

We can see that \(i\omega_{0}\tau_{0}\) is the eigenvalue of \(A(0)\), and \(-i\omega_{0}\tau_{0}\) is that of \(A^{*}\). Assume that \(q(\theta)=(1, q_{2}, q_{3}, q_{4}, q_{5}, q_{6})^{T} e^{i\omega_{0}\tau_{0}\theta}\) is the eigenvector of \(A(0)\) corresponding to \(i\omega_{0}\tau_{0}\) and \(q^{*}(s)=M(1, q_{2}^{*}, q_{3}^{*}, q_{4}^{*}, q_{5}^{*}, q_{6}^{*})e^{i\omega_{0}\tau_{0}s}\) is the eigenvector of \(A^{*}\) corresponding to \(-i\omega_{0}\tau_{0}\). From the definitions of \(A(0)\) and \(A^{*}\), we can obtain

$$\begin{aligned}& q_{2} = \biggl[i\omega_{0}-a_{22}-b_{22}e^{-i\tau_{0}\omega_{0}}- \frac {b_{32}e^{-i\tau_{0}\omega_{0}}}{i\omega_{0}-a_{33}} \biggr]^{-1}\times a_{21}, \\& q_{3} = \frac{b_{32}q_{2}}{(i\omega_{0}-a_{33})e^{i\tau_{0}\omega_{0}}},\quad\quad q_{4}= \frac{a_{43}q_{3}}{i\omega_{0}-a_{44}}, \\& q_{5} = \frac{a_{53}q_{3}+a_{54}q_{4}}{i\omega_{0}-a_{55}}, \quad\quad q_{6}= \frac {a_{61}}{i\omega_{0}-a_{66}}, \\& q_{2}^{*} = \frac{a_{16}a_{61}}{a_{21}(i\omega_{0}+a_{66})}-\frac{i\omega _{0}+a_{11}}{a_{21}}, \\& q_{3}^{*} = -\frac{(i\omega_{0}+a_{22}+b_{22}e^{i\tau_{0}\omega _{0}})q_{2}^{*}}{b_{32}e^{i\tau_{0}\omega_{0}}}, \quad\quad q_{4}^{*}= \frac {a_{15}a_{54}}{(i\omega_{0}+a_{44})(i\omega_{0}+a_{55})}, \\& q_{5}^{*} = -\frac{a_{15}}{i\omega_{0}+a_{55}}, \quad\quad q_{6}^{*}=- \frac {a_{16}}{i\omega_{0}+a_{66}}. \end{aligned}$$

In addition, from equation (20), one can get the expression of M̄:

$$\bar{M}=\bigl[1+q_{2}\bar{q}_{2}^{*}+q_{3} \bar{q}_{3}^{*}+q_{4}\bar{q}_{4}^{*}+q_{5}\bar {q}_{5}^{*}+q_{6}\bar{q}_{6}^{*}+\tau_{0}e^{-i\tau_{0}\omega_{0}} \bigl(b_{22}q_{2}\bar {q}_{2}^{*}+b_{32}q_{2} \bar{q}_{3}^{*}\bigr)\bigr]^{-1}, $$

such that \(\langle q^{*}, \bar{q}\rangle=1\).

Then, following the procedure in [29–33], we can obtain the expressions of \(g_{20}\), \(g_{11}\), \(g_{02}\) and \(g_{21}\) as follows:

$$\begin{aligned}& g_{20} = 2\tau_{0}\bar{M}\beta q_{3}\bigl( \bar{q}_{2}^{*}-1\bigr), \quad\quad g_{11}=\tau_{0} \bar {M}\beta \operatorname {Re}{q_{3}}\bigl(\bar{q}_{2}^{*}-1\bigr), \quad \quad g_{02}=2\tau_{0}\bar{M}\beta \bar{q_{3}}\bigl( \bar{q}_{2}^{*}-1\bigr), \\& g_{21} = 2\tau_{0}\bar{M}\beta\bigl(\bar {q}_{2}^{*}-1\bigr) \biggl(W_{11}^{(1)}(0)q_{3}+ \frac{1}{2}W_{20}^{(1)}(0)\bar {q}_{3}+W_{11}^{(3)}(0)+ \frac{1}{2}W_{20}^{(3)}(0)\biggr), \end{aligned}$$

with

$$\begin{aligned}& W_{20}(\theta) = \frac{ig_{20}q(0)}{\tau_{0}\omega_{0}}e^{i\tau _{0}\omega_{0}\theta}+ \frac{i\bar{g}_{02}\bar{q}(0)}{3\tau_{0}\omega _{0}}e^{-i\tau_{0}\omega_{0}\theta}+E_{1}e^{2i\tau_{0}\omega_{0}\theta}, \\& W_{11}(\theta) = -\frac{ig_{11}q(0)}{\tau_{0}\omega_{0}}e^{i\tau _{0}\omega_{0}\theta}+ \frac{i\bar{g}_{11}\bar{q}(0)}{\tau_{0}\omega _{0}}e^{-i\tau_{0}\omega_{0}\theta}+E_{2}, \end{aligned}$$

and \(E_{1}\) and \(E_{2}\) are given

$$\begin{aligned}& E_{1}=2\left ( \textstyle\begin{array}{@{}cccccc@{}} a_{11}^{*} &{0} &-a_{13} &{0} &-a_{15} &-a_{16}\\ -a_{21} &a_{22}^{*} &-a_{23} &{0} &{0} &{0}\\ {0} &-b_{32}e^{-2i\omega_{0}\tau_{0}} &a_{33}^{*} &{0} &{0} &{0}\\ {0} &{0} &-a_{43} &a_{44}^{*} &{0} &{0}\\ {0} &{0} &-a_{53} &-a_{54} &a_{55}^{*} &{0}\\ -a_{61} &{0} &{0} &{0} &{0} &a_{66}^{*} \end{array}\displaystyle \right )^{-1}\times \left ( \textstyle\begin{array}{@{}c@{}} -\beta q_{3}\\ \beta q_{3}\\ {0}\\ {0}\\ {0}\\ {0} \end{array}\displaystyle \right ), \\& E_{2}=-\left ( \textstyle\begin{array}{@{}cccccc@{}} a_{11} &{0} &a_{13} &{0} &a_{15} &a_{16}\\ a_{21} &a_{22}+b_{22}& a_{23} &{0} &{0} &{0}\\ {0} &b_{32} &a_{33} &{0} &{0} &{0}\\ {0} &{0} &a_{43} &a_{44} &{0} &{0}\\ {0} &{0} &a_{53} &a_{54} &a_{55} &{0}\\ a_{16} &{0} &{0} &{0} &{0} &a_{66} \end{array}\displaystyle \right )^{-1}\times \left ( \textstyle\begin{array}{@{}c@{}} -\beta \operatorname {Re}\{q_{3}\}\\ \beta \operatorname {Re}\{q_{3}\}\\ {0}\\ {0}\\ {0}\\ {0} \end{array}\displaystyle \right ), \end{aligned}$$

where

$$\begin{aligned}& a_{11}^{*} = 2i\omega_{0}-a_{11}, \\& a_{22}^{*} = 2i\omega_{0}-a_{22}-b_{22}e^{-2i\omega_{0}\tau_{0}}, \\& a_{33}^{*} = 2i\omega_{0}-a_{33}, \\& a_{44}^{*} = 2i\omega_{0}-a_{44}, \\& a_{55}^{*} = 2i\omega_{0}-a_{55}, \\& a_{66}^{*} = 2i\omega_{0}-a_{66}. \end{aligned}$$

Then we can get the following coefficients:

$$\begin{aligned} \begin{gathered} C_{1}(0) = \frac{i}{2\tau_{0}\omega_{0}} \biggl(g_{11}g_{20}-2 \vert g_{11} \vert ^{2}-\frac{ \vert g_{02} \vert ^{2}}{3} \biggr)+ \frac{g_{21}}{2}, \\ \mu_{2} = -\frac{\operatorname {Re}\{C_{1}(0)\}}{\operatorname {Re}\{\lambda'(\tau_{0})\} }, \\ \rho_{2} = 2{\operatorname {Re}\bigl\{ C_{1}(0)\bigr\} }, \\ T_{2} = -\frac{\text{Im}\{C_{1}(0)\}+\mu_{2}\text{Im}\{\lambda'(\tau _{0})\}}{\tau_{0}\omega_{0}}. \end{gathered} \end{aligned}$$
(21)

Thus, the properties of the Hopf bifurcation of system (2) can be stated as follows.

Theorem 2

\(\mu_{2}\) determines the direction of the Hopf bifurcation: if \(\mu _{2}>0\) (\(\mu_{2}<0\)), then the Hopf bifurcation is supercritical (subcritical); \(\rho_{2}\) determines the stability of the bifurcating periodic solutions: if \(\rho_{2}<0\) (\(\rho_{2}>0\)), then the bifurcating periodic solutions are stable (unstable); \(T_{2}\) determines the period of the bifurcating periodic solutions: if \(T_{2}>0\) (\(T_{2}<0\)), then the period of the bifurcating periodic solutions increases (decreases).

4 Numerical simulation

This section is concerned with some numerical simulations of system (2) with the aim of verifying the obtained theoretical results. We choose \(A=2\), \(\beta=0.09\), \(d=0.05\), \(\rho =0.65\), \(\theta=0.05\), \(\chi=0.55\), \(\gamma=0.45\), \(\alpha=0.035\), \(\delta=0.1\), \(\eta=0.35\) and \(\varepsilon=0.07\). Then system (2) becomes

$$ \textstyle\begin{cases} \frac{dS(t)}{dt} = 2-0.09S(t)I(t)-0.05S(t)-0.65S(t)+0.05R(t)+0.55 V(t), \\ \frac{dE(t)}{dt} = 0.09S(t)I(t)-0.05E(t)-0.45E(t-\tau), \\ \frac{dI(t)}{dt} = 0.45E(t-\tau)-0.05I(t)-0.035I(t)-0.1I(t)-0.35 I(t), \\ \frac{dQ(t)}{dt} = 0.1I(t)-0.05Q(t)-0.035Q(t)-0.07Q(t), \\ \frac{dR(t)}{dt} = 0.07Q(t)-0.05R(t)-0.05R(t)+0.35I(t), \\ \frac{dV(t)}{dt} = 0.65S(t)-0.05V(t)-0.55V(t). \end{cases} $$
(22)

It is easy to verify that \(R_{0}=0.1514\), \(AR_{0}(d+\chi)=0.1817\), \(d^{2}+(\rho+\chi)d=0.0625\), \(\beta(d+\theta)(d+\alpha+\varepsilon )=0.0014\). Therefore, \(AR_{0}(d+\chi)>d^{2}+(\rho+\chi)d\) and \(\beta (d+\theta)(d+\alpha+\varepsilon)>R_{0}\theta\varepsilon\delta +R_{0}\theta\eta(d+\alpha+\varepsilon)\) is satisfied. Then one can obtain the unique endemic equilibrium \(P_{*}(6.6050, 1.1889, 3.2887, 2.1217, 12.9956, 7.1554)\) of system (22). It can be verified that the conditions for the occurrence of a Hopf bifurcation are also satisfied for system (22).

Then, using Matlab 7.0 software package and by some complicated computations, we obtain \(\omega_{0}=0.3703\), \(\tau_{0}=9.7698\), \(\lambda ^{\prime}(\tau_{0})=3.9225-7.3108i\). We choose \(\tau=9.28<\tau _{0}=9.7698\). Thus, the endemic equilibrium \(P_{*}(6.6050, 1.1889, 3.2887, 2.1217, 12.9956, 7.1554)\) is asymptotically stable when \(\tau<\tau _{0}\), which can be illustrated by computer simulations in Figures 1-2. When τ passes through the critical value \(\tau_{0}=9.7698\), the endemic equilibrium \(P_{*}(6.6050, 1.1889, 3.2887, 2.1217, 12.9956, 7.1554)\) loses its stability and a Hopf bifurcation occurs, i.e., a family of periodic solutions bifurcate from the endemic equilibrium \(P_{*}(6.6050, 1.1889, 3.2887, 2.1217, 12.9956, 7.1554)\). Choosing \(\tau=10.38>\tau_{0}=9.7698\), the computer simulations are as shown in Figures 3-4.

Figure 1
figure 1

The phase plot of the states S , I , R for \(\pmb{\tau=9.28<9.7698=\tau_{0}}\) .

Full size image
Figure 2
figure 2

The phase plot of the states E , Q , V for \(\pmb{\tau=9.28<9.7698=\tau_{0}}\) .

Full size image
Figure 3
figure 3

The phase plot of the states S , I , R for \(\pmb{\tau=10.38>9.7698=\tau_{0}}\) .

Full size image
Figure 4
figure 4

The phase plot of the states E , Q , V for \(\pmb{\tau=10.38>9.7698=\tau_{0}}\) .

Full size image

Further, we have \(C_{1}(0)=-1.9603-0.6585i\), \(\mu_{2}=0.4998>0\), \(\beta _{2}=-3.9206<0\) and \(T_{2}=0.8280>0\). Therefore, according to Theorem 2, the Hopf bifurcation at the critical value \(\tau_{0}=9.7698\) is supercritical; the bifurcating periodic solutions are stable and the period of the bifurcating periodic solutions increases.

5 Conclusions

Based on the fact that one of the significant features of computer viruses is its latent characteristic, we incorporate the latent period delay into the model considered in the literature [10] and obtain the delayed SEIQRS-V model describing the worms propagation in a network. Compared with the work in [10], we mainly focus on effects of the delay on the model.

We obtained the sufficient conditions for the local stability of the endemic equilibrium. The stability criteria in the absence of the delay are no longer enough to guarantee the stability in the presence of the delay, rather there is a critical value \(\tau_{0}\) such that the model is stable for \(\tau<\tau_{0}\) and become unstable for \(\tau>\tau_{0}\). By choosing the latent period delay as a bifurcation parameter, and analyzing the corresponding characteristic equation, it is proved that the latent period delay in the model can destabilize the endemic equilibrium and give rise to a Hopf bifurcation. That is, a family of periodic solutions bifurcate from the endemic equilibrium when the delay passes through the critical value. Therefore, we can conclude that when the value of the latent period delay is suitable small, it is helpful to predict and control the propagation of the worms in system (2). Otherwise, the worms persist in the whole host population. For further research, properties of the Hopf bifurcation such as direction and stability are determined by applying the normal theory and the center manifold theorem. Finally, the results are validated by some numerical simulations.

It should be pointed out that many other factors besides time delay can influence a worm propagation system in a real network environment. For example, network congestion and the network topology are also impact factors to worm propagation. Namely, we will link the results obtained with the model proposed in the present paper with the results coming from the networks theory. They will be a major emphasis of our future research.