1 Introduction

In recent years, many mathematical models such as SIR model [1–3], SEIR model [4, 5], SEIRS model [6] and some other models [7–10] have been proposed to predict propagation of computer viruses. All the computer virus models above neglect delays in the virus spreading process. As is well known, delays have an important effect on dynamical models and they can cause the occurrence of the Hopf bifurcation. Therefore, it is reasonable to investigate dynamics of the dynamical systems with time delay. In [11], Zhang and Yang studied the following SEIRS worm propagation model with time delay:

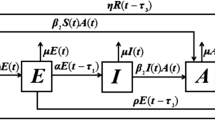
$$ \textstyle\begin{cases} \frac{dS(t)}{dt} = b-\beta I(t)S(t)-pbE(t)-qbI(t)-dS(t)+\zeta R(t-\tau ), \\ \frac{dE(t)}{dt} = \beta I(t)S(t)+pbE(t)+qbI(t)-\varepsilon E(t)-dE(t), \\ \frac{dI(t)}{dt} = \varepsilon E(t)-\gamma I(t-\tau)-dI(t)-\eta I(t), \\ \frac{dR(t)}{dt} = \gamma I(t-\tau)-dR(t)-\zeta R(t-\tau), \end{cases} $$
(1)

where \(S(t)\), \(E(t)\), \(I(t)\), and \(R(t)\) denote numbers of nodes at time t in states susceptible, exposed, infectious, and recovered, respectively. For the specific meanings of b, d, p, q, β, ε, γ, ζ, and η, one can refer to [11]. τ is the period to clean the worms in one node for the antivirus software and the temporary immunity period of the recovered nodes. It should be pointed out that Zhang and Yang assumed that the period to clean the worms in one node for the antivirus software and the temporary immunity period of the recovered nodes are the same [11] for convenience of analysis. In addition, Zhang and Yang neglected the latent period of worms. Based on this and motivated by the work about dynamics of the dynamical system with two or multiple delays in [12–18], we incorporate the time delay due to the latent period of worms in system (1) and obtain the following system with two delays:

$$ \textstyle\begin{cases} \frac{dS(t)}{dt} = b-\beta I(t)S(t)-pbE(t)-qbI(t)-dS(t)+\zeta R(t-\tau _{1}), \\ \frac{dE(t)}{dt} = \beta I(t)S(t)+pbE(t)+qbI(t)-\varepsilon E(t-\tau _{2})-dE(t), \\ \frac{dI(t)}{dt} = \varepsilon E(t-\tau_{2})-\gamma I(t-\tau _{1})-dI(t)-\eta I(t), \\ \frac{dR(t)}{dt} = \gamma I(t-\tau_{1})-dR(t)-\zeta R(t-\tau_{1}), \end{cases} $$
(2)

where \(\tau_{1}\) has the same meaning as that of τ in system (1) and \(\tau_{2}\) is the time delay due to the latent period of worms.

The structure of this paper is as follows. Local stability of the positive equilibrium and existence of the Hopf bifurcation are analyzed in Section 2. The direction and the stability of the Hopf bifurcation when \(\tau_{1}\in(0, \tau_{10})\) and \(\tau_{2}>0\) are determined by means of the normal form theory and center manifold theorem in Section 3. Some numerical simulations are carried out in order to demonstrate the theoretical analysis in Section 4. Conclusions and discussions are also included in the last section.

2 Local stability and local Hopf bifurcation

According to the analysis in [11], we know that if

$$R_{0}=\frac{b\beta\varepsilon+bdq\varepsilon+bdp(d+\gamma+\eta )}{d(d+\varepsilon)(d+\gamma+\eta)}>1 $$

and

$$(d+\varepsilon) (d+\gamma+\eta)>pb(d+\gamma+\eta)+qb\varepsilon $$

system (2) has a unique positive equilibrium \(D_{*}(S_{*}, E_{*}, I_{*}, R_{*})\), with

$$\begin{aligned}& S_{*} = \frac{(d+\varepsilon)(d+\gamma+\eta)-pb(d+\gamma+\eta )-qb\varepsilon}{\beta\varepsilon}, \\& I_{*} = \frac{(d+\zeta)[b\beta\varepsilon+d(pb(d+\gamma+\eta )+qb\varepsilon-(d+\varepsilon)(d+\gamma+\eta))]}{\beta (d+\varepsilon)(d+\zeta)(d+\gamma+\eta)-\beta\gamma\varepsilon \zeta}, \\& E_{*} = \frac{d+\gamma+\eta}{\varepsilon}I_{*},\quad\quad R_{*}=\frac{\gamma}{d+\zeta}I_{*}. \end{aligned}$$

The Jacobian matrix of system (2) at \(D_{*}\) is

$$J(D_{*})=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \lambda-\alpha_{11} &-\alpha_{12} &-\alpha_{13} &-\beta_{14}e^{-\lambda\tau_{1}}\\ -\alpha_{21} &\lambda-\alpha_{22}-\gamma _{22}e^{-\lambda\tau_{2}} &-\alpha_{23} &{0}\\ {0} &-\gamma_{32}e^{-\lambda\tau_{2}} &\lambda-\alpha_{33}-\beta_{33}e^{-\lambda\tau_{1}} &{0}\\ {0} &{0} &-\beta_{43}e^{-\lambda\tau _{1}} &\lambda-\alpha_{44}-\beta_{44}e^{-\lambda\tau_{1}} \end{array}\displaystyle \right ), $$

where

$$\begin{aligned}& \alpha_{11} = -(d+\beta I_{*}), \quad\quad \alpha_{12}=-pb, \quad\quad \alpha _{13}=-(qb+\beta S_{*}), \quad\quad \alpha_{21}=\beta I_{*}, \\& \alpha_{22} = pb-d, \quad\quad \alpha_{23}=qb+\beta S_{*}, \quad\quad \alpha_{33}=-(d+\eta ),\quad\quad \alpha_{44}=-d, \\& \beta_{14} = \zeta, \quad\quad \beta_{33}=-\gamma,\quad\quad \beta_{43}=\gamma,\quad\quad \beta _{44}=-\zeta, \quad\quad \gamma_{22}=- \varepsilon,\quad\quad \gamma_{32}=\varepsilon . \end{aligned}$$

Then we can obtain the characteristic equation of system (2)

$$\begin{aligned}& \lambda^{4}+A_{3}\lambda^{3}+A_{2} \lambda^{2}+A_{1}\lambda+A_{0} \\& \quad{}+ \bigl(B_{3}\lambda^{3}+B_{2} \lambda^{2}+B_{1}\lambda+B_{0} \bigr)e^{-\lambda\tau _{1}} \\& \quad{}+ \bigl(C_{2}\lambda^{2}+C_{1} \lambda+C_{0} \bigr)e^{-2\lambda\tau_{1}} \\& \quad{}+ \bigl(D_{3}\lambda^{3}+D_{2} \lambda^{2}+D_{1}\lambda+D_{0} \bigr)e^{-\lambda(\tau _{1}+\tau_{2})} \\& \quad{}+ \bigl(E_{2}\lambda^{2}+E_{1} \lambda+E_{0} \bigr)e^{-\lambda\tau_{2}}+(F_{1}\lambda +F_{0})e^{-2\lambda\tau_{1}+\tau_{2}}=0, \end{aligned}$$
(3)

where

$$\begin{aligned}& A_{0} = \alpha_{33}\alpha_{44}( \alpha_{11}\alpha_{22}-\alpha _{12} \alpha_{21})+\alpha_{32}\alpha_{44}( \alpha_{13}\alpha _{21}-\alpha_{11} \alpha_{23}), \\& A_{1} = (\alpha_{33}+\alpha_{44}) ( \alpha_{12}\alpha_{21}-\alpha _{11} \alpha_{22})+\alpha_{23}\alpha_{32}( \alpha_{11}+\alpha _{44}) \\& \hphantom{A_{1} =}{} -\alpha_{33}\alpha_{44}( \alpha_{11}+ \alpha_{22})-\alpha _{13} \alpha_{21} \alpha_{32}, \\& A_{2} = (\alpha_{11}+\alpha_{22}) ( \alpha_{33}+\alpha_{44})+\alpha _{11} \alpha_{22}+\alpha_{33}\alpha_{44}- \alpha_{23}\alpha _{32}-\alpha_{12} \alpha_{21}, \\& A_{3} = -(\alpha_{11}+\alpha_{22}+ \alpha_{33}+\alpha_{44}), \\& B_{0} = (\alpha_{11}\alpha_{22}- \alpha_{12}\alpha_{21}) (\alpha _{33} \beta_{44}+\alpha_{44}\beta_{33})+( \alpha_{13}\alpha _{21}-\alpha_{11} \alpha_{23})\alpha_{32}\beta_{44}, \\& B_{1} = (\beta_{33}+\beta_{44}) ( \alpha_{12}\alpha_{21}-\alpha _{11} \alpha_{22})+\alpha_{23}\alpha_{32} \beta_{44} \\& \hphantom{B_{1} =}{} -(\alpha_{11}+\alpha_{22}) ( \alpha_{33} \beta_{44}+\alpha _{44} \beta_{33}), \\& B_{2} = (\alpha_{11}+\alpha_{22}) ( \beta_{33}+\beta_{44})+\alpha _{33} \beta_{44}+\alpha_{44}\beta_{33}, \\& B_{3} = -(\beta_{33}+\beta_{44}), \quad\quad C_{0}= \alpha_{11}\alpha_{22}\beta _{33} \beta_{44}-\alpha_{21}\alpha_{32} \beta_{14}\beta_{43}, \\& C_{1} = -\beta_{33}\beta_{44}( \alpha_{11}+\alpha_{22}), \quad\quad C_{2}=\beta _{33}\beta_{44}, \\& D_{0} = \alpha_{11}\alpha_{33} \gamma_{22}(\alpha_{44}+\beta _{44})+ \alpha_{11}(\alpha_{44}\beta_{33} \gamma_{22}-\alpha _{23}\beta_{44} \gamma_{32}), \\& D_{1} = \alpha_{23}\beta_{44} \gamma_{32}-\beta_{33}\gamma _{22}( \alpha_{11}+\alpha_{44})-\beta_{44} \gamma_{22}(\alpha _{11}+\alpha_{33}) \\& \hphantom{D_{1} =}{} -\alpha_{11}(\alpha_{33}+ \alpha_{44})- \alpha_{33}\alpha _{44}, \\& D_{2} = (\alpha_{11}+\alpha_{22}+ \alpha_{33}+\alpha_{44})\gamma _{22},\quad\quad D_{3}=-\gamma_{22}, \\& E_{0} = \alpha_{44}\gamma _{32}(\alpha _{13}\alpha_{21}-\alpha_{11}\alpha_{23}), \quad\quad E_{1}=\alpha_{23}\gamma _{32}( \alpha_{11}+\alpha_{44})-\alpha_{13} \alpha_{21}\gamma _{32}, \\& E_{2} = -\alpha_{23}\gamma_{32}, \quad\quad F_{0}= \alpha _{11}\beta _{33}\beta_{44} \gamma_{22}-\alpha_{21}\beta_{14} \beta_{43}\gamma _{32}, \quad\quad F_{1}=- \beta_{33} \beta_{44}\gamma_{22}. \end{aligned}$$

Case 1

\(\tau_{1}=\tau_{2}=0\). Equation (3) becomes

$$ \lambda^{4}+A_{13}\lambda^{3}+A_{12} \lambda^{2}+A_{11}\lambda+A_{10}=0, $$
(4)

where

$$\begin{aligned}& A_{10} = A_{0}+B_{0}+C_{0}+D_{0}+E_{0}+F_{0}, \quad\quad A_{11}=A_{1}+B_{1}+C_{1}+D_{1}+E_{1}+F_{1}, \\& A_{12} = A_{2}+B_{2}+C_{2}+D_{2}+E_{2}, \quad\quad A_{13}=A_{3}+B_{3}+D_{3}. \end{aligned}$$

According to Routh-Hurwitz criterion, if the condition (H1) equations (5)-(8) hold, \(D_{*}\) is locally asymptotically stable when \(\tau_{1}=\tau_{2}=0\). We have

$$\begin{aligned}& D_{1}=A_{13}>0, \end{aligned}$$
(5)
$$\begin{aligned}& D_{2}=\det \left ( \textstyle\begin{array}{c@{\quad}c} A_{13} &{1}\\ A_{11} &A_{12} \end{array}\displaystyle \right )>0, \end{aligned}$$
(6)
$$\begin{aligned}& D_{3}=\det \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} A_{13} &{1} &{0}\\ A_{11} &A_{12} &A_{13}\\ {0} &A_{10} &A_{11} \end{array}\displaystyle \right )>0, \end{aligned}$$
(7)
$$\begin{aligned}& D_{4}=\det \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} A_{13} &{1} &{0} &{0}\\ A_{11} &A_{12} &A_{13} &{1}\\ {0} &A_{10} &A_{11} &A_{12}\\ {0} &{0} &{0} &A_{10} \end{array}\displaystyle \right )>0. \end{aligned}$$
(8)

Case 2

\(\tau_{1}>0\), \(\tau_{2}=0\). Equation (3) becomes

$$\begin{aligned}& \lambda^{4}+A_{23}\lambda^{3}+A_{22} \lambda^{2}+A_{21}\lambda +A_{20} \\& \quad{} + \bigl(B_{23}\lambda^{3}+B_{22} \lambda^{2}+B_{21}\lambda+B_{20} \bigr)e^{-\lambda \tau_{1}} \\& \quad{} + \bigl(C_{22}\lambda^{2}+C_{31} \lambda+C_{30} \bigr)e^{-2\lambda\tau_{1}}=0, \end{aligned}$$
(9)

where

$$\begin{aligned}& A_{20} = A_{0}+E_{0},\quad\quad A_{21}=A_{1}+E_{1},\quad\quad A_{22}=A_{2}+E_{2},\quad\quad A_{23}=A_{3}, \\& B_{20} = B_{0}+D_{0},\quad\quad B_{21}=B_{0}+D_{0},\quad\quad B_{22}=B_{2}+D_{2}, \quad\quad B_{23}=B_{3}+D_{3}, \\& C_{20} = C_{0}+F_{0}, \quad\quad C_{21}=C_{1}+F_{1},\quad\quad C_{22}=C_{2}. \end{aligned}$$

Multiplying by \(e^{\lambda\tau_{1}}\), equation (9) becomes

$$\begin{aligned}& B_{23}\lambda^{3}+B_{22} \lambda^{2}+B_{21}\lambda+B_{20} \\& \quad{} + \bigl(\lambda^{4}+A_{23}\lambda^{3}+A_{22} \lambda^{2}+A_{21}\lambda +A_{20} \bigr)e^{\lambda\tau_{1}} \\& \quad{}+ \bigl(C_{22}\lambda^{2}+C_{21} \lambda+C_{20} \bigr)e^{-\lambda\tau_{1}}=0. \end{aligned}$$
(10)

Let \(\lambda=i\omega_{1}\) (\(\omega_{1}>0\)) be a root of equation (10). Then we have

$$\textstyle\begin{cases} (\omega_{1}^{4}-(A_{22}+C_{22})\omega_{1}^{2}+A_{20}+C_{20})\cos\tau _{1}\omega_{1}-((A_{21}-C_{21})\omega_{1}-A_{23}\omega_{1}^{3})\sin\tau _{1}\omega_{1} \\ \quad =B_{2}\omega_{1}^{2}-B_{0}, \\ (\omega_{1}^{4}-(A_{22}-C_{22})\omega_{1}^{2}+A_{20}-C_{20})\sin\tau _{1}\omega_{1}+((A_{21}+C_{21})\omega_{1}-A_{23}\omega_{1}^{3})\cos\tau _{1}\omega_{1} \\ \quad =B_{3}\omega_{1}^{3}-B_{1}\omega_{1}. \end{cases} $$

Then we can get

$$\begin{aligned}& \sin\tau_{1}\omega_{1}=\frac{g_{7}\omega_{1}^{7}+g_{5}\omega_{1}^{5}+g_{3}\omega _{1}^{3}+g_{1}\omega_{1}}{\omega_{1}^{8}+h_{6}\omega_{1}^{6}+h_{4}\omega_{1}^{4}+h_{2}\omega _{1}^{2}+h_{0}}, \\& \cos \tau_{1}\omega_{1}=\frac{g_{6}\omega_{1}^{6}+g_{4}\omega_{1}^{4}+g_{2}\omega _{1}^{2}+g_{0}}{\omega_{1}^{8}+h_{6}\omega_{1}^{6}+h_{4}\omega_{1}^{4}+h_{2}\omega_{1}^{2}+h_{0}}, \end{aligned}$$

where

$$\begin{aligned}& g_{0} = B_{20}(C_{20}-A_{20}),\quad\quad g_{1}=(A_{21}+C_{21})B_{20}-(A_{20}+C_{20})B_{21}, \\& g_{2} = (A_{22}-C_{22})B_{20}+(A_{20}-C_{20})B_{22}+(C_{21}-A_{21})B_{21}, \\& g_{3} = (A_{20}+C_{20})B_{23}-(A_{21}+C_{21})B_{22}+(A_{22}+C_{22})B_{21}-A_{23}B_{20}, \\& g_{4} = (A_{21}-C_{21})B_{23}-(A_{22}-C_{22})B_{22}+A_{23}B_{21}-B_{20}, \\& g_{5} = A_{23}B_{22}-B_{21}-(A_{22}+C_{22})B_{23}, \quad\quad g_{6}=B_{22}-A_{23}B_{23}, \quad \quad g_{7}=B_{23}, \\& h_{0} = A_{20}^{2}-C_{20}^{2}, \quad\quad h_{2}=A_{21}^{2}-C_{21}^{2}-2A_{20}A_{22}+2C_{20}C_{22}, \\& h_{4} = A_{22}^{2}-C_{22}^{2}+2A_{20}-2A_{21}A_{23}, \quad\quad h_{6}=A_{23}^{2}-2A_{22}. \end{aligned}$$

Then one can obtain

$$ \omega_{1}^{16}+e_{27} \omega_{1}^{14}+e_{26}\omega_{1}^{12}+e_{25} \omega _{1}^{10}+e_{24}\omega_{1}^{8}+e_{23} \omega_{1}^{6}+e_{22}\omega _{1}^{4}+e_{21} \omega_{1}^{2}+e_{20}=0, $$
(11)

where

$$\begin{aligned}& e_{20} = h_{0}^{2}-g_{0}^{2}, \quad\quad e_{21}=2h_{0}h_{2}-2g_{0}g_{2}-g_{1}^{2}, \\& e_{22} = h_{2}^{2}+2h_{0}h_{4}-g_{2}^{2}-2g_{0}g_{4}-2g_{1}g_{3}, \\& e_{23} = 2h_{0}h_{6}+2h_{2}h_{4}-g_{3}^{2}-2g_{0}g_{6}-2g_{1}g_{5}-2g_{2}g_{4}, \\& e_{24} = h_{4}^{2}-g_{4}^{2}+2h_{0}+2h_{2}h_{6}-2g_{3}g_{5}-2g_{1}g_{7}-2g_{2}g_{6}, \\& e_{25} = 2h_{2}+2h_{4}h_{6}-g_{5}^{2}-2g_{3}g_{7}-2g_{4}g_{6}, \\& e_{26} = h_{6}^{2}-g_{6}^{2}+2h_{4}-2g_{5}g_{7}, \quad\quad e_{27}=2h_{6}-g_{7}^{2}. \end{aligned}$$

Let \(\omega_{1}^{2}=v_{1}\), then equation (11) becomes

$$ v_{1}^{8}+e_{27}v_{1}^{7}+e_{26}v_{1}^{6}+e_{25}v_{1}^{5}+e_{24}v_{1}^{4}+e_{23}v_{1}^{3}+e_{22}v_{1}^{2}+e_{21}v_{1}+e_{20}=0. $$
(12)

Next, we make the following assumption.

(H21):

Equation (12) has at least one positive root.

If the condition (H21) holds, there exists a positive root \(v_{10}>0\) of equation (12) such that equation (10) has a pair of purely imaginary roots \(\pm i\omega _{10}=\pm i\sqrt{v_{10}}\). Then we can get the corresponding critical value of \(\tau_{1}\) at which a Hopf bifurcation occurs:

$$\tau_{10}=\frac{1}{\omega_{10}}\arccos\frac{g_{6}\omega _{10}^{6}+g_{4}\omega_{10}^{4}+g_{2}\omega_{10}^{2}+g_{0}}{\omega _{10}^{8}+h_{6}\omega_{10}^{6}+h_{4}\omega_{10}^{4}+h_{2}\omega_{10}^{2}+h_{0}}. $$

Differentiating the two sides of equation (10) with respect to \(\tau_{1}\), we get

$$\begin{aligned}& \biggl[\frac{d\lambda}{d\tau_{1}} \biggr]^{-1} \\& \quad =\frac{3B_{23}\lambda ^{2}+2B_{22}\lambda+B_{21}+(2C_{22}\lambda+C_{21})e^{-\lambda\tau _{1}}+(4\lambda^{3}+3A_{23}\lambda^{2}+2A_{22}\lambda+A_{21})e^{\lambda \tau_{1}}}{(C_{22}\lambda^{3}+C_{21}\lambda^{2}+C_{20}\lambda)e^{-\lambda \tau_{1}}-(\lambda^{5}+A_{23}\lambda^{4}+A_{22}\lambda^{3}+A_{21}\lambda ^{2}+A_{20}\lambda)e^{\lambda\tau_{1}}} \\& \quad\quad{} - \frac{\tau_{1}}{\lambda}. \end{aligned}$$

Define

$$\operatorname {Re}\biggl[\frac{d\lambda}{d\tau_{1}} \biggr]^{-1}_{\tau_{1}=\tau _{10}}= \frac{P_{2R}Q_{2R}+P_{2I}Q_{2I}}{Q_{2R}^{2}+Q_{2I}^{2}}. $$

Obviously, if the condition (H22) \(P_{2R}Q_{2R}+P_{2I}Q_{2I}\neq 0\) holds, then \(\operatorname {Re}[\frac{d\lambda}{d\tau_{1}}]^{-1}_{\tau_{1}=\tau_{10}}\neq 0\). Therefore, according to the analysis above and the Hopf bifurcation theorem in [19], we have the following.

Theorem 1

Suppose that the conditions (H21)-(H22) hold. The positive equilibrium \(D_{*}(S_{*}, E_{*}, I_{*}, R_{*})\) is locally asymptotically stable for \(\tau_{1}\in[0,\tau_{10})\) and system (2) undergoes a Hopf bifurcation at the positive equilibrium \(D_{*}(S_{*}, E_{*}, I_{*}, R_{*})\) when \(\tau_{1}=\tau_{10}\).

Case 3

\(\tau_{1}=0\), \(\tau_{2}>0\). Equation (3) becomes

$$ \lambda^{4}+A_{33}\lambda^{3}+A_{32} \lambda^{2}+A_{31}\lambda +A_{30}+ \bigl(D_{33}\lambda^{3}+D_{32}\lambda^{2}+D_{31} \lambda +D_{30} \bigr)e^{-\lambda\tau_{2}}=0, $$
(13)

where

$$\begin{aligned}& A_{30} = A_{0}+B_{0}+C_{0},\quad\quad A_{31}=A_{1}+B_{1}+C_{1},\quad\quad A_{32}=A_{2}+B_{2}+C_{2}, \\& A_{33}=A_{3}+B_{3}, \\& D_{30} = D_{0}+E_{0}+F_{0},\quad\quad D_{31}=D_{1}+E_{1}+F_{1},\quad\quad D_{32}=D_{2}+E_{2},\quad\quad D_{33}=D_{3}. \end{aligned}$$

Let \(\lambda=i\omega_{2}\) (\(\omega_{2}>0\)) be a root of equation (13). Then we get

$$\textstyle\begin{cases} (D_{31}\omega_{2}-D_{33}\omega_{2}^{3})\sin\tau_{2}\omega _{2}+(D_{30}-D_{32}\omega_{2}^{2})\cos\tau_{2}\omega_{2}=A_{32}\omega _{2}^{2}-\omega_{2}^{4}-A_{30}, \\ (D_{31}\omega_{2}-D_{33}\omega_{2}^{3})\cos\tau_{2}\omega _{2}-(D_{30}-D_{32}\omega_{2}^{2})\sin\tau_{2}\omega_{2}=A_{33}\omega _{2}^{3}-A_{31}\omega_{2}, \end{cases} $$

which leads to

$$ \omega_{2}^{8}+e_{33} \omega_{2}^{6}+e_{32}\omega_{2}^{4}+e_{31} \omega_{2}^{2}+e_{30}=0, $$
(14)

where

$$\begin{aligned}& e_{30} = A_{30}^{2}-D_{30}^{2}, \quad\quad e_{31}=A_{31}^{2}-D_{31}^{2}-2A_{30}A_{32}+2D_{30}D_{32}, \\& e_{32} = A_{32}^{2}-D_{32}^{2}-2A_{31}A_{33}+2A_{30}+2D_{31}D_{33}, \quad\quad e_{33}=A_{33}^{2}-D_{33}^{2}-2A_{32}. \end{aligned}$$

The discussion of the distribution of the roots of equation (14) is similar to that in [20]. Thus, we make the following assumption.

(H31):

Equation (14) has at least one positive root.

If the condition (H31) holds, then there exists \(\omega_{20}>0\) such that equation (13) has a pair of purely imaginary roots \(\pm i\omega_{20}\). For \(\omega_{20}\), we have

$$\begin{aligned} \tau_{20} =&\frac{1}{\omega_{20}}\arccos \bigl( \bigl( \bigl(D_{31} \omega _{20}-D_{33} \omega_{20}^{3} \bigr) \times \bigl(A_{33} \omega_{20}^{3}-A_{31} \omega _{20} \bigr)+ \bigl(D_{30}-D_{32} \omega_{20}^{2} \bigr) \\ &{}\times \bigl(A_{32} \omega_{20}^{2}-\omega _{20}^{4}-A_{30} \bigr) \bigr) /{ \bigl( \bigl(D_{31}\omega_{20}-D_{33} \omega _{20}^{3} \bigr)^{2}+ \bigl(D_{30}-D_{32} \omega_{20}^{2} \bigr)^{2} \bigr)} \bigr). \end{aligned}$$

Differentiating the two sides of equation (13) with respect to \(\tau_{2}\), we get

$$\begin{aligned} \biggl[\frac{d\lambda}{d\tau_{2}} \biggr]^{-1} =&-\frac{4\lambda ^{3}+3A_{33}\lambda^{2}+2A_{32}\lambda+A_{31}}{\lambda(\lambda ^{4}+A_{33}\lambda^{3}+A_{32}\lambda^{2}+A_{31}\lambda+A_{30})} \\ &{}+ \frac {2D_{33}\lambda^{2}+2D_{32}\lambda+D_{31}}{\lambda(D_{33}\lambda ^{3}+D_{32}\lambda^{2}+D_{31}\lambda+D_{30})}-\frac{\tau_{2}}{\lambda}. \end{aligned}$$

Further, we get

$$\operatorname {Re}\biggl[\frac{d\lambda}{d\tau_{2}} \biggr]^{-1}_{\tau_{2}=\tau _{20}}= \frac{f_{2}^{\prime}(v_{2*})}{(D_{31}\omega_{20}-D_{33}\omega _{20}^{3})^{2}+(D_{30}-D_{32}\omega_{20}^{2})^{2}}, $$

where \(f_{2}(v_{2})=v_{2}^{4}+e_{33}v_{2}^{3}+e_{32}v_{2}^{2}+e_{31}v_{2}+e_{30}\) and \(v_{2}=\omega_{2}\), \(v_{2*}=\omega_{20}^{2}\).

Obviously, if the condition (H32) \(f_{2}^{\prime}(v_{2*})\neq0\) holds, then \(\operatorname {Re}[\frac{d\lambda}{d\tau_{2}}]^{-1}_{\tau_{2}=\tau_{20}}\neq 0\). Therefore, we have the following.

Theorem 2

Suppose that the conditions (H31)-(H32) hold. The positive equilibrium \(D_{*}(S_{*}, E_{*}, I_{*}, R_{*})\) is locally asymptotically stable for \(\tau_{2}\in[0,\tau_{20})\) and system (2) undergoes a Hopf bifurcation at the positive equilibrium \(D_{*}(S_{*}, E_{*}, I_{*}, R_{*})\) when \(\tau_{2}=\tau_{20}\).

Case 4

\(\tau_{1}=\tau_{2}=\tau>0\). Equation (3) becomes

$$\begin{aligned}& \lambda^{4}+A_{43}\lambda^{3}+A_{42} \lambda^{2}+A_{41}\lambda +A_{40} \\& \quad{} + \bigl(B_{43}\lambda^{3}+B_{42} \lambda^{2}+B_{41}\lambda+B_{40} \bigr)e^{-\lambda \tau} \\& \quad{}+ \bigl(C_{43}\lambda^{3}+C_{42} \lambda^{2}+C_{41}\lambda +C_{40} \bigr)e^{-2\lambda\tau}+(F_{41}\lambda+F_{40})e^{-3\lambda\tau}=0, \end{aligned}$$
(15)

where

$$\begin{aligned}& A_{40} = A_{0},\quad\quad A_{41}=A_{1}, \quad\quad A_{42}=A_{2},\quad\quad A_{43}=A_{3}, \\& B_{40} = B_{0}+E_{0},\quad\quad B_{41}=B_{1}+E_{1},\quad\quad B_{42}=B_{2}+E_{2}, \\& B_{43} = B_{3}, \quad\quad C_{40}=C_{0}+D_{0}, \quad\quad C_{41}=C_{1}+D_{1}, \\& C_{42} = C_{2}+D_{2},\quad\quad C_{43}=D_{3},\quad\quad F_{40}=F_{0}, \quad\quad F_{41}=F_{1}. \end{aligned}$$

Multiplying by \(e^{\lambda\tau}\), equation (15) becomes

$$\begin{aligned}& B_{43}\lambda^{3}+B_{42} \lambda^{2}+B_{41}\lambda+B_{40} \\& \quad{} + \bigl(\lambda^{4}+A_{43}\lambda^{3}+A_{42} \lambda^{2}+A_{41}\lambda +A_{40} \bigr)e^{\lambda\tau} \\& \quad{}+ \bigl(C_{43}\lambda^{3}+C_{42} \lambda^{2}+C_{41}\lambda+C_{40} \bigr)e^{-\lambda \tau} \\& \quad{}+(F_{41}\lambda+F_{40})e^{-2\lambda\tau}=0. \end{aligned}$$
(16)

Let \(\lambda=i\omega\) (\(\omega>0\)) be the root of equation (16), then

$$\textstyle\begin{cases} G_{41}(\omega)\cos\tau\omega-G_{42}(\omega)\sin\tau\omega +G_{43}(\omega)=F_{1}\omega\sin2\tau\omega+F_{0}\cos2\tau\omega , \\ G_{44}(\omega)\sin\tau\omega+G_{45}(\omega)\cos\tau\omega +G_{46}(\omega)=F_{1}\omega\cos2\tau\omega-F_{0}\sin2\tau\omega, \end{cases} $$

where

$$\begin{aligned}& G_{41}(\omega) = \omega^{4}-(A_{42}+C_{42}) \omega ^{2}+A_{40}+C_{40}, \\& G_{42}(\omega) = (A_{41}-C_{41}) \omega-(A_{43}-C_{43})\omega ^{3}, \\& G_{43}(\omega) = B_{40}-B_{42} \omega^{2}, \\& G_{44}(\omega) = \omega^{4}-(A_{42}-C_{42}) \omega ^{2}+A_{40}-C_{40}, \\& G_{45}(\omega) = (A_{41}+C_{41}) \omega-(A_{43}+C_{43})\omega ^{3}, \\& G_{46}(\omega) = B_{41}\omega-B_{43} \omega^{3}. \end{aligned}$$

Thus, we have

$$\begin{aligned}& \bigl(G_{41}(\omega)\cos\tau\omega - G_{42}( \omega)\sin\tau\omega +G_{43}(\omega) \bigr)^{2} \\& \quad{} + \bigl(G_{44}(\omega)\sin\tau\omega+G_{45}(\omega) \cos \tau \omega +G_{46}(\omega) \bigr)^{2}=F_{1}^{2} \omega^{2}+F_{0}^{2}. \end{aligned}$$
(17)

Similar to the analysis in [21], we can obtain the expression of \(\cos \tau\omega\) from equation (17) when \(\sin\tau\omega=\sqrt{1-\cos^{2}\tau\omega}\) and we denote \(f_{41}(\omega)=\cos\tau\omega\) and \(f_{42}(\omega)=\sin\tau \omega\). Thus, we have the following equation with respect to ω:

$$ f_{41}^{2}(\omega)+f_{42}^{2}( \omega)=1. $$
(18)

Next, we assume the following.

(H41):

Equation (18) has at least one positive root.

If the condition (H41) holds, then equation (18) has one root \(\omega_{0*}>0\) such that equation (16) has a pair of purely imaginary roots \(\pm i\omega_{0*}\). For \(\omega _{0*}>0\), we have

$$\tau_{0*}=\frac{1}{\omega_{0*}}\arccos f_{41}( \omega_{0*}). $$

Similarly, we can obtain the expression of \(\cos\tau\omega\) from equation (17) when \(\sin\tau\omega=-\sqrt{1-\cos^{2}\tau\omega}\) and we denote \(f_{43}(\omega)=\cos\tau\omega\) and \(f_{44}(\omega)=\sin\tau \omega\). Thus, we have the equation with respect to ω:

$$ f_{43}^{2}(\omega)+f_{44}^{2}( \omega)=1. $$
(19)

If equation (19) has one positive root \(\omega_{0}^{\prime} \) such that equation (16) has a pair of purely imaginary roots \(\pm i\omega_{0}^{\prime}\), then we can obtain the corresponding critical value of the delay

$$\tau_{0}^{\prime}=\frac{1}{\omega_{0}^{\prime}}\arccos f_{43} \bigl(\omega _{0}^{\prime} \bigr). $$

Let \(\tau_{0}=\text{min}\{\tau_{0*}, \tau_{0}^{\prime}\}\) and let equation (16) have a pair of purely imaginary roots \(\pm i\omega_{0}\) when \(\tau=\tau_{0}\). Taking the derivative with respect to τ on both sides of equation (16), we get

$$\biggl[\frac{d\lambda}{d\tau} \biggr]^{-1}=-\frac{P_{4}(\lambda )}{Q_{4}(\lambda)}- \frac{\tau}{\lambda}, $$

where

$$\begin{aligned}& P_{4}(\lambda) = 3B_{43}\lambda^{2}+2B_{42} \lambda+B_{41}+ \bigl(4\lambda ^{3}+3A_{43} \lambda^{2}+2A_{42}\lambda+A_{41} \bigr)e^{\lambda\tau} \\& \hphantom{P_{4}(\lambda) = }{} +(3C_{43}\lambda2+2C_{42} \lambda+C_{41})e^{-\lambda\tau }+F_{41}e^{-2\lambda\tau}, \\& Q_{4}(\lambda) = \lambda \bigl(C_{43}\lambda^{3}+C_{42} \lambda ^{2}+C_{41}\lambda+C_{40} \bigr)e^{-\lambda\tau}+2\lambda(F_{41}\lambda +F_{40}) \\& \hphantom{Q_{4}(\lambda) =}{} -\lambda \bigl(\lambda^{4}+A_{43} \lambda^{3}+A_{42} \lambda^{2}+A_{41} \lambda +A_{40} \bigr)e^{\lambda\tau}. \end{aligned}$$

Define

$$\operatorname {Re}\biggl[\frac{d\lambda}{d\tau} \biggr]^{-1}_{\tau=\tau _{0}}= \frac{P_{4R}Q_{4R}+P_{4I}Q_{4I}}{Q_{4R}^{2}+Q_{4I}^{2}}. $$

Obviously, if the condition (H42) \(P_{4R}Q_{4R}+P_{4I}Q_{4I}\neq 0\) holds, then \(\operatorname {Re}[\frac{d\lambda}{d\tau}]^{-1}_{\tau=\tau_{0}}\neq0\). Therefore, we have the following results according to the Hopf bifurcation theorem in [19].

Theorem 3

Suppose that the conditions (H41)-(H42) hold. The positive equilibrium \(D_{*}(S_{*}, E_{*}, I_{*}, R_{*})\) is locally asymptotically stable for \(\tau\in[0,\tau_{0})\) and system (2) undergoes a Hopf bifurcation at the positive equilibrium \(D_{*}(S_{*}, E_{*}, I_{*}, R_{*})\) when \(\tau=\tau_{0}\).

Case 5

\(\tau_{1}\in(0, \tau_{10})\), \(\tau_{2}>0\). In this case, we choose \(\tau_{2}\) as a bifurcation parameter with \(\tau_{1}\in (0, \tau_{10})\). Let \(\lambda=i\omega_{2*}\) be the root of equation (3), then

$$\textstyle\begin{cases} G_{51}(\omega_{2*})\sin\tau_{2*}\omega_{2*}+G_{52}(\omega _{2*})\cos\tau_{2*}\omega_{2*}=H_{51}(\omega_{2*}), \\ G_{51}(\omega_{2*})\cos\tau_{2*}\omega_{2*}-G_{51}(\omega _{2*})\sin\tau_{2*}\omega_{2*}=H_{52}(\omega_{2*}), \end{cases} $$

where

$$\begin{aligned}& G_{51}(\omega_{2*}) = E_{1}\omega_{2*}+ \bigl(D_{1}\omega_{2*}-D_{3}\omega _{2*}^{3} \bigr)\cos\tau_{1}\omega_{2*}- \bigl(D_{0}-D_{2}\omega_{2*}^{2} \bigr) \sin \tau _{1}\omega_{2*} \\& \hphantom{G_{51}(\omega_{2*}) =}{} +F_{2}\omega_{2*}\cos2\tau_{1} \omega_{2*}-F_{0}\sin2\tau_{1}\omega _{2*}, \\& G_{52}(\omega_{2*}) = E_{0}-E_{2} \omega_{2*}^{2}+ \bigl(D_{1}\omega_{2*}-D_{3} \omega _{2*}^{3} \bigr)\sin\tau_{1} \omega_{2*}+ \bigl(D_{0}-D_{2}\omega_{2*}^{2} \bigr)\cos\tau _{1}\omega_{2*} \\& \hphantom{G_{52}(\omega_{2*}) =}{} +F_{1}\omega_{2*}\sin2\tau_{1} \omega_{2*}+F_{0}\cos2\tau_{1}\omega _{2*}, \\& H_{51}(\omega_{2*}) = A_{2}\omega_{2*}^{2}- \omega_{2*}^{4}-A_{0}- \bigl(B_{1}\omega _{2*}-B_{3}\omega_{2*}^{3} \bigr)\sin \tau_{1}\omega_{2*}- \bigl(B_{0}-B_{2} \omega _{2*}^{2} \bigr)\cos\tau_{1} \omega_{2*} \\& \hphantom{H_{51}(\omega_{2*}) =}{} -C_{1}\omega_{2*}\sin2\tau_{1} \omega_{2*}- \bigl(C_{0}-C_{2}\omega_{2*}^{2} \bigr)\cos 2\tau_{1}\omega_{2*}, \\& H_{52}(\omega_{2*}) = A_{3}^{3}-A_{1} \omega_{2*}- \bigl(B_{1}\omega_{2*}-B_{3} \omega _{2*}^{3} \bigr)\cos\tau_{1} \omega_{2*}+ \bigl(B_{0}-B_{2}\omega_{2*}^{2} \bigr)\sin\tau _{1}\omega_{2*} \\& \hphantom{H_{52}(\omega_{2*}) = }{} -C_{1}\omega_{2*}\cos2\tau_{1} \omega_{2*}+ \bigl(C_{0}-C_{2}\omega_{2*}^{2} \bigr)\sin 2\tau_{1}\omega_{2*}. \end{aligned}$$

Thus, we can obtain the following equation with respect to ω:

$$ G_{51}^{2}(\omega_{2*})+G_{52}^{2}( \omega_{2*})=H_{51}^{2}(\omega _{2*})+H_{52}^{2}( \omega_{2*}). $$
(20)

Similar to the discussion above, we make the following assumption.

(H51):

Equation (20) has at least one positive root.

If the condition (H51) holds, then there exists \(\omega_{2}^{*}>0\) satisfying equation (20) and equation (3) has a pair of purely imaginary roots \(\pm i\omega_{2}^{*}\). For \(\omega _{2}^{*}\), we have

$$\tau_{20}^{*}=\frac{1}{\omega_{2}^{*}}\arccos\frac{G_{51}(\omega _{2}^{*})\times H_{52}(\omega_{2}^{*})+G_{52}(\omega_{2}^{*})\times H_{51}(\omega_{2}^{*})}{G_{51}^{2}(\omega_{2}^{*})+G_{52}^{2}(\omega_{2}^{*})}. $$

Differentiating the two sides of equation (3) with respect to \(\tau_{2}\), we have

$$\biggl[\frac{d\lambda}{d\tau_{2}} \biggr]^{-1}=\frac{P_{5}(\lambda )}{Q_{5}(\lambda)}- \frac{\tau_{2}}{\lambda}, $$

where

$$\begin{aligned}& P_{5}(\lambda) = 4\lambda^{3}+3A_{3} \lambda^{2}+2A_{2}\lambda+A_{1}- \bigl(B_{3}\tau _{1}\lambda^{3} \\& \hphantom{P_{5}(\lambda) =}{} -(\tau_{1}B_{2}-3B_{3}) \lambda^{2}-( \tau_{1}B_{1}-2B_{2}) \lambda+\tau _{1}B_{0}-B_{1} \bigr)e^{-\lambda\tau_{1}} \\& \hphantom{P_{5}(\lambda) =}{} + \bigl((2C_{2}-2\tau_{1}C_{1}) \lambda+C_{1}-2\tau_{1}C_{0}-2 \tau_{1}C_{2}\lambda ^{2} \bigr)e^{-2\lambda\tau_{1}} \\& \hphantom{P_{5}(\lambda) =}{} + \bigl((3D_{3}-\tau_{1}D_{2}) \lambda^{2}+(2D_{2}-\tau_{1}D_{1}) \lambda-\tau _{1}D_{3}\lambda^{3} \bigr)e^{-\lambda(\tau_{1}+\tau_{2})} \\& \hphantom{P_{5}(\lambda) =}{} +(2E_{2}\lambda+E_{1})e^{-\lambda\tau_{2}}+(F_{1}-2 \tau_{1}F_{0}-2\tau _{1}F_{1})e^{-\lambda(2\tau_{1}+\tau_{2})}, \\& Q_{5}(\lambda) = \bigl(D_{3}\lambda^{3}+D_{2} \lambda^{2}+D_{1}\lambda +D_{0} \bigr)e^{-\lambda(\tau_{1}+\tau_{2})} \\& \hphantom{Q_{5}(\lambda) =}{} + \bigl(E_{2}\lambda^{2}+E_{1} \lambda+E_{0} \bigr)e^{-\lambda\tau_{2}}+(F_{1}\lambda +F_{0})e^{-\lambda(2\tau_{1}+\tau_{2})}. \end{aligned}$$

Define

$$\operatorname {Re}\biggl[\frac{d\lambda}{d\tau_{2}} \biggr]^{-1}_{\tau_{2}=\tau _{20}^{*}}= \frac{P_{5R}Q_{5R}+P_{5I}Q_{5I}}{Q_{5R}^{2}+Q_{5I}^{2}}. $$

Obviously, if the condition (H52) \(P_{5R}Q_{5R}+P_{5I}Q_{5I}\neq 0\) holds, then \(\operatorname {Re}[\frac{d\lambda}{d\tau_{2}}]^{-1}_{\tau_{2}=\tau _{20}^{*}}\neq0\). According to the discussion above, we have the following.

Theorem 4

Suppose that the conditions (H51)-(H52) hold. The positive equilibrium \(D_{*}(S_{*}, E_{*}, I_{*}, R_{*})\) is locally asymptotically stable for \(\tau_{2}\in[0,\tau_{20}^{*})\) and system (2) undergoes a Hopf bifurcation at the positive equilibrium \(D_{*}(S_{*}, E_{*}, I_{*}, R_{*})\) when \(\tau_{2}=\tau_{20}^{*}\).

3 Direction and stability of the Hopf bifurcation

In this section, we shall derive the formulas determining direction and stability of the Hopf bifurcation under the case \(\tau_{1}\in(0, \tau_{10})\) and \(\tau _{2}>0\) by using the normal form theory and the center manifold theorem.

Let \(u_{1}(t)=S(t)-S_{*}\), \(u_{2}(t)=E(t)-E_{*}\), \(u_{3}(t)=I(t)-I_{*}\), \(u_{4}(t)=R(t)-R_{*}\), \(\tau_{2}=\tau_{20}^{*}+\mu\), \(\mu\in R\), and normalize the delay by \(t\rightarrow(t/\tau_{2})\). Throughout this section, we assume that \(\tau_{10}^{*}\in(0, \tau_{10})<\tau_{20}^{*}\). Then system (2) becomes

$$ \dot{u}(t)=L_{\mu}u_{t}+F(\mu, u_{t}), $$
(21)

where \(u_{t}=(u_{1}(t), u_{2}(t), u_{3}(t), u_{4}(t))^{T}\in C=C([-1, 0], R^{4})\) and \(L_{\mu}: C\rightarrow R^{4}\), \(F: R\times C\rightarrow R^{4}\) are given, respectively, by

$$L_{\mu}\phi= \bigl(\tau_{20}^{*}+\mu \bigr) \biggl( \alpha_{mtx}\phi(0)+\beta _{mtx}\phi \biggl(- \frac{\tau_{10}^{*}}{\tau_{20}^{*}} \biggr)+\gamma_{mtx}\phi(-1) \biggr) $$

and

$$F(\mu,\phi)=(\tau_{0}+\mu)\left ( \textstyle\begin{array}{c} -\beta\phi_{1}(0)\phi_{3}(0)\\ \beta\phi_{1}(0)\phi_{3}(0)\\ {0}\\ {0} \end{array}\displaystyle \right ). $$

Here

$$\begin{aligned}& \alpha_{mtx}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \alpha_{11} &\alpha_{12} &\alpha _{13} &{0}\\ \alpha_{21} &\alpha_{22} &\alpha _{23} &{0}\\ {0} &{0} &\alpha_{33} &{0}\\ {0} &{0} &{0} &\alpha_{44} \end{array}\displaystyle \right ),\quad \quad \beta_{mtx}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} {0} &{0} &{0} &\beta_{14}\\ {0} &{0} &{0} &{0}\\ {0} &{0} &\beta_{33} &{0}\\ {0} &{0} &\beta_{43} &\beta_{44} \end{array}\displaystyle \right ), \\& \gamma_{mtx}=\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} {0} &{0} &{0} &{0}\\ {0} &\gamma_{22} &{0} &{0}\\ {0} &\gamma_{32} &{0} &{0}\\ {0} &{0} &{0} &{0} \end{array}\displaystyle \right ). \end{aligned}$$

Thus, there exists a matrix function \(\eta(\theta,\mu):[-1, 0]\rightarrow R^{4}\) such that

$$L_{\mu}\phi= \int_{-1}^{0}d\eta(\theta,\mu)\phi(\theta),\quad \phi \in C. $$

For \(\phi\in C([-1,0], R^{4})\), we define

$$A(\mu)\phi=\textstyle\begin{cases} \frac{d\phi(\theta)}{d\theta}, & -1\leq \theta< 0, \\ \int_{-1}^{0}d\eta(\theta,\mu)\phi(\theta),& \theta=0, \end{cases} $$

and

$$R(\mu)\phi=\textstyle\begin{cases} 0, & -1\leq\theta< 0, \\ F(\mu,\phi),& \theta=0. \end{cases} $$

Then system (21) becomes

$$\dot{u}(t)=A(\mu)u_{t}+R(\mu)u_{t}. $$

Define the adjoint operator \(A^{*}\) of \(A(0)\) as follows:

$$A^{*}(\varphi)=\textstyle\begin{cases} -\frac{d\varphi(s)}{ds}, & 0< s\leq1, \\ \int_{-1}^{0}d{\eta}^{T}(s,0)\varphi(-s),& s=0, \end{cases} $$

and a bilinear form is defined by

$$ \bigl\langle \varphi(s),\phi(\theta) \bigr\rangle =\bar{\varphi}(0) \phi (0)- \int_{\theta=-1}^{0} \int_{\xi=0}^{\theta}\bar{\varphi}(\xi -\theta)\,d\eta( \theta)\phi(\xi)\,d\xi, $$
(22)

where \(\eta(\theta)=\eta(\theta, 0)\).

Let \(\rho(\theta)=(1, \rho_{2}, \rho_{3}, \rho_{4})^{T} e^{i\omega_{2}^{*}\tau_{20}^{*}\theta}\) be the eigenvector of A corresponding to \(i\omega_{0}\tau_{0}\) and \(\rho^{*}(s)=D(1, \rho_{2}^{*}, \rho_{3}^{*}, \rho_{4}^{*})e^{i\omega_{2}^{*}\tau_{20}^{*}s}\) be the eigenvector of \(A^{*}\) corresponding to \(-i\omega_{0}\tau_{0}\). According to the definition of \(A(0)\) and \(A^{*}(0)\), we can get

$$ \begin{aligned} &\rho_{2} = \frac{i\omega_{2}^{*}-\alpha_{33}-\beta_{33}e^{-i\tau _{10}^{*}\omega_{2}^{*}}}{\gamma_{32}e^{-i\tau_{20}^{*}\omega_{2}^{*}}}\rho _{3}, \\ &\rho_{3} = \bigl(i\omega_{2}^{*}-\alpha_{11} \bigr) \times \biggl[\alpha_{13}+\frac {i\omega_{2}^{*}-\alpha_{33}-\beta_{33}e^{-i\tau_{10}^{*}\omega _{2}^{*}}}{\gamma_{32}e^{-i\tau_{20}^{*}\omega_{2}^{*}}} +\frac{\beta_{14}\beta_{43}e^{-2i\tau_{10}^{*}\omega_{2}^{*}}}{i\omega _{2}^{*}-\alpha_{44}-\beta_{44}e^{-i\tau_{10}^{*}\omega _{2}^{*}}} \biggr]^{-1}, \\ &\rho_{4} = \frac{\beta_{43}e^{-i\tau_{10}^{*}\omega_{2}^{*}}}{i\omega _{2}^{*}-\alpha_{44}-\beta_{44}e^{-i\tau_{10}^{*}\omega_{2}^{*}}}\rho _{3}, \\ &\rho_{2}^{*} = -\frac{i\omega_{2}^{*}+\alpha_{11}}{\alpha_{21}}, \\ &\rho_{3}^{*} = \frac{(i\omega_{2}^{*}+\alpha_{11})(i\omega_{2}^{*}+\alpha _{22}+\gamma_{22}e^{i\tau_{20}^{*}\omega_{2}^{*}})}{\alpha_{21}\gamma _{32}e^{i\tau_{20}^{*}\omega_{2}^{*}}}-\frac{\alpha_{12}}{\gamma _{32}e^{i\tau_{20}^{*}\omega_{2}^{*}}}, \\ &\rho_{4}^{*} = -\frac{(i\omega_{2}^{*}+\alpha_{33}+\beta_{33}e^{i\tau _{10}^{*}\omega_{2}^{*}})\rho_{3}^{*}}{\beta_{43}e^{i\tau_{10}^{*}\omega _{2}^{*}}}-\frac{\alpha_{13}+\alpha_{23}\rho_{2}^{*}}{\beta_{43}e^{i\tau _{10}^{*}\omega_{2}^{*}}}. \end{aligned} $$
(23)

From equation (22), we have

$$\begin{aligned} \bigl\langle \rho^{*}, \rho \bigr\rangle =&\bar{D} \bigl[1+\rho_{2}\bar{ \rho}_{2}^{*}+\rho_{3}\bar{\rho }_{3}^{*}+ \rho_{4}\bar{\rho}_{4}^{*}+\tau_{10}^{*}e^{-i\tau_{10}^{*}\omega _{2}^{*}} \rho_{2} \bigl(b_{1}\bar{\rho}_{2}^{*}+b_{2} \bar{\rho}_{3}^{*} \bigr) \\ &{}+\tau _{20}^{*}e^{-i\tau_{20}^{*}\omega_{2}^{*}} \rho_{3} \bigl(c_{1}\bar{\rho}_{3}^{*}+c_{2} \bar { \rho}_{4}^{*} \bigr) \bigr]. \end{aligned}$$

Then we choose

$$\bar{D}= \bigl[1+\rho_{2}\bar{\rho}_{2}^{*}+\rho_{3} \bar{\rho}_{3}^{*}+\rho_{4}\bar {\rho}_{4}^{*}+ \tau_{10}^{*}e^{-i\tau_{10}^{*}\omega_{2}^{*}}\rho_{2} \bigl(b_{1}\bar {\rho}_{2}^{*}+b_{2}\bar{\rho}_{3}^{*} \bigr)+ \tau_{20}^{*}e^{-i\tau_{20}^{*}\omega _{2}^{*}}\rho_{3} \bigl(c_{1} \bar{ \rho}_{3}^{*}+c_{2}\bar{\rho}_{4}^{*} \bigr) \bigr]^{-1}, $$

such that \(\langle\rho^{*}, \rho\rangle=1\), \(\langle\rho^{*}, \bar{\rho}\rangle=0\).

Next, we can obtain the coefficients by using the algorithms in [19] and using the computation process used in [22]:

$$\begin{aligned}& g_{20} = 2\beta\tau_{20}^{*}\bar{D}\rho_{3} \bigl( \bar{\rho }_{2}^{*}-1 \bigr), \\& g_{02} = 2\beta\tau_{20}^{*}\bar{D}\bar{\rho}_{3} \bigl(\bar{\rho }_{2}^{*}-1 \bigr), \\& g_{11} = \beta\tau_{20}^{*}\bar{D}(\rho_{3}+\bar{ \rho}_{3}) \bigl(\bar{\rho }_{2}^{*}-1 \bigr), \\& g_{21} = 2\beta\tau_{20}^{*}\bar{D} \bigl(\bar{\rho }_{2}^{*}-1 \bigr) \biggl(W_{11}^{(1)}(0) \rho_{3}+\frac{1}{2}W_{20}^{(1)}(0)\bar{\rho }_{3} +W_{11}^{(3)}(0)+\frac{1}{2}W_{20}^{(3)}(0) \biggr), \end{aligned}$$

with

$$\begin{aligned}& W_{20}(\theta) = \frac{ig_{20}\rho(0)}{\tau_{20}^{*}\omega _{2}^{*}}e^{i\tau_{20}^{*}\omega_{2}^{*}\theta}+ \frac{i\bar{g}_{02}\bar {\rho}(0)}{3\tau_{20}^{*}\omega_{2}^{*}}e^{-i\tau_{20}^{*}\omega_{2}^{*}\theta }+E_{1}e^{2i\tau_{20}^{*}\omega_{2}^{*}\theta}, \\& W_{11}(\theta) = -\frac{ig_{11}\rho(0)}{\tau_{20}^{*}\omega _{2}^{*}}e^{i\tau_{20}^{*}\omega_{2}^{*}\theta}+ \frac{i\bar{g}_{11}\bar {\rho}(0)}{\tau_{20}^{*}\omega_{2}^{*}}e^{-i\tau_{20}^{*}\omega_{2}^{*}\theta }+E_{2}, \end{aligned}$$

where \(E_{1}\) and \(E_{2}\) can be computed by the following equations, respectively:

$$E_{1}=2\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \alpha_{11}^{\prime} &-\alpha_{12} &-\alpha_{13} &-\beta_{14}e^{-2i\omega_{2}^{*}\tau _{20}^{*}}\\ -\alpha_{21} &\alpha_{22}^{\prime} &-\alpha_{23} &{0}\\ {0} &-\gamma_{32}e^{-2i\omega_{2}^{*}\tau_{20}^{*}} &\alpha_{33}^{\prime} &{0}\\ {0} &{0} &-\beta_{43}e^{-2i\omega_{2}^{*}\tau _{20}^{*}}&\alpha_{44}^{\prime} \end{array}\displaystyle \right )^{-1}\left ( \textstyle\begin{array}{c} E_{1}^{(1)}\\ E_{1}^{(2)}\\ {0}\\ {0} \end{array}\displaystyle \right ), $$
$$E_{2}=-\left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \alpha_{11} &\alpha_{12} &\alpha _{13} &\beta_{14}\\ \alpha_{21} &\alpha_{22}+\gamma_{22} &\alpha_{23} &{0}\\ {0} &\gamma_{32} &\alpha_{33}+\beta _{33} &{0}\\ {0} &{0} &\beta_{43} &\alpha _{44}+\beta_{44} \end{array}\displaystyle \right )^{-1}\left ( \textstyle\begin{array}{c} E_{2}^{(1)}\\ E_{2}^{(2)}\\ {0}\\ {0} \end{array}\displaystyle \right ), $$

with

$$\begin{aligned}& \alpha_{11}^{\prime} = 2i\omega_{2}^{*}- \alpha_{11}, \\& \alpha_{22}^{\prime} = 2i\omega_{2}^{*}- \alpha_{22}-\gamma _{22}e^{-2i\omega_{2}^{*}\tau_{20}^{*}}, \\& \alpha_{33}^{\prime} = 2i\omega_{2}^{*}- \alpha_{33}-\beta _{33}e^{-2i\omega_{2}^{*}\tau_{10}^{*}}, \\& \alpha_{44}^{\prime} = 2i\omega_{2}^{*}- \alpha_{44}-\beta _{44}e^{-2i\omega_{2}^{*}\tau_{10}^{*}} \\& E_{1}^{(1)} = -\beta\rho_{3}, \quad\quad E_{1}^{(2)}= \beta\rho_{3}, \\& E_{2}^{(1)} = -\beta(\rho_{3}+\bar{ \rho}_{3}), \quad\quad E_{2}^{(2)}=\beta( \rho_{3}+ \bar{\rho}_{3}). \end{aligned}$$

Therefore, we can obtain the following values:

$$ \begin{aligned} &C_{1}(0)=\frac{i}{2\tau_{20}^{*}\omega _{2}^{*}} \biggl(g_{11}g_{20}-2\vert g_{11}\vert ^{2}-\frac{\vert g_{02}\vert ^{2}}{3} \biggr)+\frac {g_{21}}{2}, \\ &\mu_{2} =-\frac{\operatorname {Re}\{C_{1}(0)\}}{\operatorname {Re}\{\lambda'(\tau _{20}^{*})\}}, \\ &\beta_{2}=2{\operatorname {Re}\bigl\{ C_{1}(0) \bigr\} }, \\ &T_{2}=-\frac{\operatorname {Im}\{C_{1}(0)\}+\mu_{2}\operatorname {Im}\{\lambda'(\tau _{20}^{*})\}}{\tau_{20}^{*}\omega_{2}^{*}}. \end{aligned} $$
(24)

Therefore we have the following result.

Theorem 5

For system (2), if \(\mu_{2}>0\) (\(\mu_{2}<0\)), the Hopf bifurcation is supercritical (subcritical). If \(\beta_{2}<0\) (\(\beta_{2}>0\)) the bifurcating periodic solutions are stable (unstable). If \(T_{2}>0\) (\(T_{2}<0\)), the period of the bifurcating periodic solutions increases (decreases).

4 Numerical simulations

In order to verify the obtained results above, we present a numerical example in this section. We choose the same values of the parameters in [11]. That is, \(b=0.7\), \(d=0.06\), \(p=0.02\), \(q=0.01\), \(\beta=0.1\), \(\varepsilon=0.2\), \(\gamma=0.05\), \(\eta=0.01\), \(\zeta=0.1\). We obtain the following case of system (2):

$$ \textstyle\begin{cases} \frac{dS(t)}{dt} = 0.7-0.1I(t)S(t)-0.014E(t)-0.007I(t)-0.06S(t)+0.1 R(t-\tau_{1}), \\ \frac{dE(t)}{dt} = 0.1I(t)S(t)+0.014E(t)+0.007I(t)-0.2E(t-\tau _{2})-0.06E(t), \\ \frac{dI(t)}{dt} = 0.2E(t-\tau_{2})-0.05I(t-\tau _{1})-0.06I(t)-0.01I(t), \\ \frac{dR(t)}{dt} = 0.05I(t-\tau_{1})-0.06R(t)-0.1R(t-\tau_{1}). \end{cases} $$
(25)

According to the analysis in [11], we know that system (25) has a unique positive equilibrium \(D_{*}(1.4050, 1.5422, 4.9350, 2.9610)\) and system (25) is locally asymptotically stable when \(\tau_{1}=\tau_{2}=0\).

For \(\tau_{1}>0\), \(\tau_{2}=0\). We have \(\omega_{10}=0.1245\), \(\tau_{10}=13.6109\), and \(\lambda^{\prime}(\tau _{10})=0.0073+0.0299i\). Thus, according to Theorem 1, \(D_{*}\) is asymptotically stable when \(\tau_{1}\in [0, 13.6109)\) and unstable when \(\tau_{1}>13.6109\) and a Hopf bifurcation occurs when \(\tau_{1}=\tau _{10}=13.6109\). This property can be illustrated by the numerical simulations in Figures 1-2. Similarly, we have \(\omega_{20}=0.6322\), \(\tau_{20}=11.9776\). The corresponding waveforms are shown in Figures 3-4.

Figure 1
figure 1

The track of the states S , E , I , R for \(\pmb{\tau_{1}=10.055<13.6109=\tau_{10}}\) .

Full size image
Figure 2
figure 2

The track of the states S , E , I , R for \(\pmb{\tau_{1}=14.965>13.6109=\tau_{10}}\) .

Full size image
Figure 3
figure 3

The track of the states S , E , I , R for \(\pmb{\tau_{2}=11.068<11.9776=\tau_{20}}\) .

Full size image
Figure 4
figure 4

The track of the states S , E , I , R for \(\pmb{\tau_{2}=13.076>11.9776=\tau_{20}}\) .

Full size image

For \(\tau_{1}=\tau_{2}=\tau>0\). We can obtain \(\omega_{0}=1.0091\) and \(\tau_{0}=8.8645\) by some complex computations. That is, when τ increases from zero to \(\tau_{0}\), \(D_{*}\) is asymptotically stable when \(\tau\in[0, 8.8645)\). However, when \(\tau>\tau_{0}=8.8645\), \(D_{*}\) will lose its stability and a Hopf bifurcation occurs, which can be verified by the numerical simulations in Figures 5-6.

Figure 5
figure 5

The track of the states S , E , I , R for \(\pmb{\tau=7.862<8.8645=\tau_{0}}\) .

Full size image
Figure 6
figure 6

The track of the states S , E , I , R for \(\pmb{\tau=9.667>8.8645=\tau_{0}}\) .

Full size image

Finally, we have \(\omega_{2}^{*}=0.6582\) and \(\tau_{20}^{*}=7.855\) for the case when \(\tau_{1}=10.25\in(0, \tau_{10})\), \(\tau_{2}>0\). From Theorem 4, we can conclude that \(D_{*}\) is asymptotically stable when \(\tau_{2}\in[0, 7.855)\) and it will become unstable once \(\tau_{2}\) pass through the critical value \(\tau_{20}^{*}\). This can be illustrated by Figures 7-8. Furthermore, we obtain \(C_{1}(0)=-0.2966-1.0665i\), \(\mu _{2}=0.2206>0\), \(\beta_{2}=-0.5932<0\), \(T_{2}=0.1821>0\). Therefore, by Theorem 5, we know that the Hopf bifurcation is supercritical. The bifurcating periodic solutions are stable and the period of the periodic solutions increases.

Figure 7
figure 7

The track of the states S , E , I , R for \(\pmb{\tau_{2}=7.650<7.855=\tau_{20}^{*}}\) and \(\pmb{\tau_{1}=10.25\in(0, \tau_{10})}\) .

Full size image
Figure 8
figure 8

The track of the states S , E , I , R for \(\pmb{\tau_{2}=9.352>7.855=\tau_{20}^{*}}\) and \(\pmb{\tau_{1}=10.25\in(0, \tau_{10})}\) .

Full size image

5 Conclusions

In the present paper, we devote our attention to the stability and Hopf bifurcation of an SEIRS epidemic model which describes the transmission of worms in the network through vertical transmission with two delays based on the work in the literature [11]. By regarding the different combinations of the two delays as the Hopf bifurcation parameter, the corresponding critical value of the delay is obtained. When the value of the delay is smaller than the corresponding critical value, the positive equilibrium is asymptotically stable and the propagation of the worms in the network can be predicted and controlled easily in this case. However, a local Hopf bifurcation occurs and a branch of periodic solutions bifurcate from the positive equilibrium when the value of the delay is bigger than the corresponding critical value. Thus, the propagation of the worms becomes unstable and out of control. Therefore, we should take some measures to postpone the onset of the Hopf bifurcation.

It should be noted that the model investigated in this paper assumes that the latent computers have no infection ability. This is not consistent with reality. Therefore, it is more realistic to investigate the dynamics of the following worm propagation model with graded rates:

$$ \textstyle\begin{cases} \frac{dS(t)}{dt} = b-\beta_{1} I(t)S(t)-\beta_{2} E(t)S(t)-pbE(t)-qbI(t)-dS(t)+\zeta R(t-\tau_{1}), \\ \frac{dE(t)}{dt} = \beta_{1} I(t)S(t)+\beta_{2} E(t)S(t)+pbE(t)+qbI(t)-\varepsilon E(t-\tau_{2})-dE(t), \\ \frac{dI(t)}{dt} = \varepsilon E(t-\tau_{2})-\gamma I(t-\tau _{1})-dI(t)-\eta I(t), \\ \frac{dR(t)}{dt} = \gamma I(t-\tau_{1})-dR(t)-\zeta R(t-\tau_{1}), \end{cases} $$
(26)

where \(\beta_{1}\) and \(\beta_{2}\) are the transmission rates of the infective computers and the latent computers, respectively. We leave this as our future work.