A diffusive predator-prey system with prey refuge and gestation delay

Abstract

The dynamics of a diffusive predator-prey system with prey refuge and gestation delay is investigated in this paper. For a non-delay system, global stability, Turing instability and Hopf bifurcation are studied. For a delay system, time delay induced instability and Hopf bifurcation are discussed. By the theory of normal form and the center manifold method, the direction and stability of the bifurcating periodic solution are discussed.

1 Introduction

Population biology is an important subject in both ecology and mathematical ecology. And predator-prey model is one of the most interesting and popular areas in population biology. Many scholars have done a lot of work in it and derived some important results [1–6].

Generally, prey-predator models can be written as the following form:

$$ \textstyle\begin{cases} \frac{du}{dt}= uf(u)-g(u,v)v, \\ \frac{dv}{dt}=cg(u,v)v-\theta v, \end{cases} $$

(1.1)

where $u(t)$ and $v(t)$ represent prey and predator densities at time t, respectively. $f(u)$ represents the prey growth law in the absence of predators, and $g(u, v)$ is the functional response of predators to prey density (the average feeding rate of a predator). Parameters c and d represent the conversion rate from prey to predator and the death rate of predator.

In predator-prey models, the functional response of predators to prey density is essential, and it can enrich the dynamics of predator-prey systems. In ecology, many factors, such as prey escape ability, predator hunting ability and the structure of the prey habitat, can affect functional responses [7, 8]. Generally, functional responses can be divided into the following types: prey-dependent (such as Holling I-III [9]) and prey-predator-dependent (such as Beddington-DeAngelis [10], Crowley-Martin [11], Hassel-Varley [12]).

Recently, more and more researchers have suggested that prey-predator-dependent functional responses are more suitable and can enrich the dynamics of predator-prey systems [13–15]. Hsu et al. studied the global property of a general predator-prey model with Hassell-Varley type functional response [16]. Cantrell and Cosner discussed some dynamical properties of predator-prey models with Beddington-DeAngelis functional response [17]. Tripathi et al. considered the permanence, non-permanence, local asymptotic stability and global asymptotic stability of equilibria of delayed predator-prey models with Crowley-Martin functional response [18]. Skalski and Gilliam suggest that Beddington-DeAngelis or Hassell-Varley functional responses are suitable for the case where predator feeding rate becomes independent of predator density at high prey density, and Crowley-Martin model is suitable for the case where predator feeding rate is decreased by higher predator density even when prey density is high [19].

In predator-prey models, prey refuge is one of the important factors, and many researchers have studied it. In [20], Sharma and Samanta studied a Leslie-Gower model with disease and refuge in prey, including the positivity and boundedness of solutions, and the stability of equilibria. In [21], Tripathi et al. considered a delayed predator-prey model with Beddington-DeAngelis functional response and prey refuge. They studied local and global asymptotic stability of various equilibria and time delay induced Hopf bifurcation. In [22], Chen et al. investigated the effect of prey refuge on a Leslie-Gower predator-prey model. They suggest that prey refuge has no influence on the persistent property of this model, but it can affect the prey and predator densities. Most of works suggest that prey refuge has a stabilizing effect on the prey-predator model [23–25]. In [26], Tripathi et al. studied a predator-prey model with Beddington-DeAngelis type functional response incorporating a prey refuge, that is,

$$ \textstyle\begin{cases} \frac{du}{dt}= u ( 1-u-\frac{a(1-m) v}{1+b(1-m) u+c v} ), \\ \frac{dv}{dt}=v ( \frac{e(1-m) u}{1+b(1-m) u+c v}-\theta), \end{cases} $$

(1.2)

with the initial conditions $u(0)=u_{0}>0$, $v(0)=v_{0}>0$, which are biologically meaningful. m is the prey refuge rate. Tripathi et al. studied local and global stability of various boundary equilibria and coexisting equilibria. Using some data, they also discussed the inverse problem of estimation of a model parameter.

In recent years, since predators and their preys distribute inhomogeneously in different spatial locations at time t, many researchers have studied predator-prey systems with diffusion term. Predator-prey systems with diffusion term may exhibit richer dynamical properties, including Turing instability, pattern formation, spatially inhomogeneous periodic solutions etc. [27–31]. In [30], Tang and Song considered a delayed diffusive predator-prey model with herd behavior and analyzed the stability and Hopf bifurcation. In [31] the authors considered the spatial, temporal and spatiotemporal patterns of diffusive predator-prey models with mutual interference. In [29], Jia and Xue discussed the effects of the self- and cross-diffusion on positive steady states for a generalized predator-prey system. In this paper, we will study the effect of diffusion on system (1.2).

Motivated by above, we propose the following system:

$$ \textstyle\begin{cases} \frac{\partial{u(x,t)}}{\partial{t}}=d_{1} \Delta u +u ( 1-u-\frac{a(1-m) v}{1+b(1-m) u+c v} ),\quad x\in\Omega, t>0, \\ \frac{\partial{v(x,t)}}{\partial{t}}=d_{2}\Delta v +s v ( \frac {(1-m) u(t-\tau)}{1+b(1-m) u(t-\tau)+c v(t-\tau)}-d ),\quad x\in\Omega, t>0, \\ u_{x}(x,t)=0,\qquad v_{x}(x,t)=0,\quad x\in\partial{\Omega}, t>0, \\ u(x,t)=u_{0}(x,t)\geq0,\qquad v(x,t)=v_{0}(x,t)\geq0,\quad x\in \Omega, t \in[-\tau,0], \end{cases} $$

(1.3)

where $s=e$, $d=\theta/e$, $\Omega=(0,l\pi)$, ($l>0$). In system (1.3), we assume that the region Ω is closed, with no prey and predator species entering and leaving the region at the boundary. We also assume that the reproduction of predator population after predating the prey will not be instantaneous. There is a time delay τ required for gestation of predator.

The rest of this paper is arranged as follows. We study the stability property of the non-delayed system in the next section and discuss the delayed system in Section 3. Then we give some numerical simulations. At last, we end this paper with a brief conclusion.

2 Stability analysis of the non-delayed system

Without delay, system (1.3) becomes

$$ \textstyle\begin{cases} \frac{\partial{u}}{\partial{t}}=d_{1} \Delta u +u ( 1-u-\frac{a(1-m) v}{1+b(1-m) u+c v} ), \quad x\in(0,l\pi), t>0, \\ \frac{\partial{v}}{\partial{t}}=d_{2} \Delta v +s v ( \frac{(1-m) u}{1+b(1-m) u+c v}-d), \quad x\in(0,l\pi), t>0, \\ u_{x}(0,t)=v_{x}(0,t)=0,\qquad u_{x}(l\pi,t)=v_{x}(l\pi,t)=0, \quad t> 0, \\ u(x,0)=u_{0}(x,t)\geq0,\qquad v(x,0)=v_{0}(x,t)\geq0, \quad x\in[0,l\pi]. \end{cases} $$

(2.1)

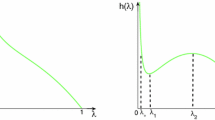
Obviously, system (1.3) has a trivial equilibrium $(0,0)$ and a predator-free axial equilibrium $(1,0)$. If $E_{*}(u_{*},v_{*})$ is a coexisting equilibrium of system (1.3), then it is easy to obtain that $v_{*}=\frac{u_{*} (1-u_{*})}{a d}$. Then $u_{*}\in(0,1)$ and is a root of

$$ h(u)=c u^{2}+ \bigl(a (1-b d) (1-m)-c \bigr) u-a d=0. $$

(2.2)

Obviously, $h(0)=-a d<0$ and $h(1)=a[(1-b d) (1-m)-d]$. If $d<(1-b d) (1-m)$, then $h(1)>0$ implies that system (1.3) has at least one coexisting equilibrium.

In this paper, we just suppose system (1.3) has a coexisting equilibrium point $E_{*}(u_{*},v_{*})$.

2.1 Local stability analysis of the model without diffusion

If $d_{1}=d_{2}=0$, the Jacobian matrix at $E_{*}(u_{*},v_{*})$ is

$$J = \left ( \begin{matrix}a_{11} & a_{12} \\ s a_{21} & s a_{22} \end{matrix} \right ), $$

where

$$\begin{aligned}& a_{11}=b d (1-u_{*})-u_{*},\qquad a_{12}=d \bigl(c (1-u_{*})/(1-m)-a \bigr), \\& a_{21}=(1-b d) (1-u_{*})/a,\qquad a_{22}=-c d (1-u_{*})/a (1-m). \end{aligned}$$

Obviously, $a_{22}<0$. The characteristic equation is

$$ \lambda^{2}-\mathit{tr}_{0} \lambda+ \Delta_{0}=0. $$

(2.3)

The characteristic roots are $\lambda_{1,2}=\frac{1}{2}[\mathit{tr}_{0}\pm\sqrt{ \Delta_{0}}]$. If

$$\mathit{tr}_{0} = a_{11} + sa_{22} < 0 \quad \mbox{and} \quad \Delta_{0}= s(a_{11} a _{22} - a_{12} a_{21}) > 0, $$

then the characteristic roots have negative real parts. Make the following hypothesis:

If ($\mathrm {H}_{1}$) holds, then $E_{*}(u_{*},v_{*})$ is locally asymptotically stable if and only if $a_{11} + sa_{22} < 0$. Meanwhile, if $a_{11}>0$ when s near $-a_{11}/a_{22}$, Eq. (2.3) has a pair of complex eigenvalues $\alpha(s)\pm i\omega(s)$, where

$$\alpha(s)=\frac{1}{2}(a_{11} + sa_{22}),\qquad \omega(s)=\frac{1}{2}\sqrt{s(a _{11} a_{22} - a_{12} a_{21})} $$

and

$$\alpha(-a_{11}/a_{22})=0,\qquad \alpha'(-a_{11}/a_{22})=a_{22}/2, \qquad \omega(-a_{11}/a_{22})>0. $$

Theorem 2.1

When $d_{1}=d_{2}=0$, assume ($\mathrm {H}_{1}$) holds.

• (i) If $a_{11}+sa_{22} < 0$, then $P(u_{*},v_{*})$ is locally asymptotically stable;

• (ii) If $a_{11}>0$, Hopf bifurcation occurs at $P(u_{*},v_{*})$ when $s=-a_{11}/a_{22}$.

2.2 Turing instability and Hopf bifurcation

For system (2.1), the characteristic equation at $E_{*}(u _{*},v_{*})$ is

$$ \lambda^{2}- \mathit{tr}_{n}\lambda+ \Delta_{n}(r)=0, \quad n \in\mathbb{N}_{0}, $$

(2.4)

where

$$ \textstyle\begin{cases} \mathit{tr}_{n}=\mathit{tr}_{0}-\frac{n^{2}}{l^{2}}(d_{1}+d_{2}), \\ \Delta_{n}=\Delta_{0}-\frac{n^{2}}{l^{2}}(d_{2}a_{11}+d_{1}sa_{22})+d _{1}d_{2}\frac{n^{4}}{l^{4}}, \end{cases} $$

(2.5)

and the eigenvalues are

$$ \lambda_{1,2}^{(n)}(r)=\frac{\mathit{tr}_{n}\pm \sqrt{ \mathit{tr}^{2}_{n}-4\Delta_{n}}}{2},\quad n \in \mathbb{N}_{0}. $$

(2.6)

Notice that $a_{11}+sa_{22}<0$ implies that $\mathit{tr}_{n}<0$ for $n \in \mathbb{N}_{0}$. Suppose ($\mathrm {H}_{1}$) holds, then the eigenvalues of (2.4) have negative real parts if $\Delta_{n}>0$ guaranteed by

$$ d_{2}a_{11}+d_{1}sa_{22} \leq0, $$

(2.7)

or

$$ d_{2}a_{11}+d_{1}sa_{22}>0, \quad \mbox{and}\quad (d_{2}a_{11}+d_{1}sa_{22})^{2}-4d _{1}d_{2}\Delta_{0}< 0. $$

(2.8)

If

$$ d_{2}a_{11}+d_{1}sa_{22}>0, \quad \mbox{and}\quad (d_{2}a_{11}+d_{1}sa_{22})^{2}-4d _{1}d_{2}\Delta_{0}>0 $$

(2.9)

hold, and there exists $k\in\mathbb{N}$ such that $\Delta_{k}<0$, then the eigenvalues of (2.4) have a positive real part $\lambda ^{(k)}(s)$, which implies that $E_{*}(u_{*},v_{*})$ is unstable for system (2.1).

Assume ($\mathrm {H}_{1}$) holds and $a_{11}>0$. When

$$ s=s_{n}:=-\frac{1}{a_{22}} \biggl[a_{11}- \frac{n^{2}}{l^{2}}(d_{1}+d_{2}) \biggr], \quad n\in \mathbb{N}_{0} $$

(2.10)

and $\Delta_{n}(s_{n})>0$, Eq. (2.4) has purely imaginary values. Obviously, $\Delta_{0}(s_{0})=-\frac{a_{11}}{a_{22}} ( a_{11}a _{22}-a_{12}a_{21} ) >0$. From (2.5), we know that there exists $n^{*}\geq1\in\mathbb{N}$ such that $\Delta_{n}(s_{n})>0$ for $n=0,1,\ldots, n^{*}-1$. Let

$$\lambda_{n}(s)=\alpha_{n}(s)\pm i\omega_{n}(s), \quad n=0,1, \ldots, n ^{*}-1 $$

be the roots of Eq. (2.4) satisfying

$$\alpha_{n}(s_{n})=0, \qquad \omega_{n}(s_{n})= \sqrt{\Delta_{n}(s_{n})}. $$

When s is near $s_{n}$,

$$\alpha_{n}(s)=\frac{\mathit{tr}_{n}(s)}{2},\qquad \omega_{n}(s)= \sqrt{\Delta_{n}- \alpha_{n}^{2}(s)}. $$

From (2.5), we know that

$$ \alpha'_{n}(s_{n})= \frac{a_{22}}{2}< 0. $$

(2.11)

Theorem 2.2

Assume ($\mathrm {H}_{1}$) holds.

• (i) If $a_{11}+sa_{22}<0$ and (2.7) (or (2.8)) hold, then $E_{*}(u_{*},v_{*})$ is locally asymptotically stable;

• (ii) If $a_{11}+sa_{22}<0$ and (2.9) hold, and $\Delta_{k}>0$ for $k\in\mathbb{N}$, then $E_{*}(u_{*},v_{*})$ is locally asymptotically stable;

• (iii) If $a_{11}+sa_{22}<0$ and (2.9) hold, and $\Delta_{k}<0$ for $k\in\mathbb{N}$, then $E_{*}(u_{*},v_{*})$ is Turing unstable;

• (iv) Hopf bifurcation occurs at $E_{*}(u_{*},v_{*})$ when $s=s_{n}$, for $0\leq n \leq n^{*}-1$.

Similarly, we can obtain that for system (2.1), $(0,0)$ is unstable and $(1,0)$ is locally stable under condition $d>(1-b d) (1-m)$.

2.3 Global stability of $(1,0)$ and $(u_{*},v_{*})$

Theorem 2.3

When $d>(1-b d) (1-m)$, $(1,0)$ is globally asymptotically stable.

Proof

From (2.1), we can obtain that

$$\frac{\partial{u}}{\partial{t}}-d_{1}\frac{\partial^{2}{u}}{\partial {x^{2}}}= u \biggl( 1-u- \frac{a(1-m) v}{1+b(1-m) u+c v} \biggr) \leq u(1-u). $$

Use the comparison principle, then

$$\lim_{t \to+\infty} \max_{x\in[0,l\pi]}u(x,t)\leq1. $$

From (2.1), we can obtain

$$\frac{\partial{v}}{\partial{t}}-d_{1}\frac{\partial^{2}{v}}{\partial {x^{2}}}= s v \biggl( \frac{1-m}{(1+c v)/u+b(1-m)}-d \biggr). $$

When $d>(1-b d) (1-m)$,

$$s v \biggl( \frac{1-m}{(1+c v)/u+b(1-m)}-d \biggr) \leq s v \biggl( \frac{1-m}{1+b(1-m)}-d \biggr) < 0. $$

For an arbitrary constant $\epsilon>0$, there exists $T>0$ such that $v(x,t)\le\epsilon$ for $t>T$. Then

$$\frac{\partial{u}}{\partial{t}}-d_{1}\frac{\partial^{2}{u}}{\partial {x^{2}}}= u \biggl( 1-u- \frac{a(1-m) v}{1+b(1-m) u+c v} \biggr) \ge u \biggl( 1-u-\frac{a(1-m) \epsilon}{1+b(1-m) u+c \epsilon} \biggr). $$

So $\lim_{t\to+\infty}u(x,t)=1$ and $\lim_{t\to+\infty}v(x,t)=0$ for $x\in[0,l\pi]$. □

For the sake of completeness, we give the following theorem about the global stability of $E(u_{*},v_{*})$ by the proof process similar to that in [26].

Theorem 2.4

When $b(1-m)(1-u_{*})\leq1$, $E(u_{*},v_{*})$ is globally asymptotically stable.

Proof

Let $u(x,t)$, $v(x,t)$ be a positive solution of system (2.1) and define the following Lyapunov function:

$$W(t)= \int_{\Omega} \bigl[V_{1}(u)+AV_{2}(v) \bigr] \,dx $$

with $V_{1}(u)=u-u_{*}-u_{*}\ln\frac{u}{u_{*}}$, $V_{2}(v)=v-v_{*}-v _{*} \ln\frac{v}{v_{*}}$ and $A=\frac{a ( 1+b(1-m) u_{*} ) }{s ( 1+c v_{*} ) }>0$ is a positive constant. Denote $p(u,v)=(1+b(1-m) u_{*}+c v_{*})(1+b(1-m) u+c v)>0$. By simple computation, it follows that

$$\begin{aligned} W'(t) = &-I(t)+ \int_{\Omega} \biggl\{ \frac{(u-u_{*})}{u}u_{t}+A \frac{(v-v_{*})}{v}v_{t} \biggr\} \,dx \\ = &-I(t)+ \int_{\Omega} \biggl\{ ( u-u_{*} ) \biggl(- ( u-u_{*} ) +\frac{a(1-m) v_{*}}{1+b(1-m) u_{*}+c v_{*}}-\frac{a(1-m) v}{1+b(1-m) u+c v} \biggr) \\ &{}+A s ( v-v_{*} ) \biggl(\frac{(1-m) u}{1+b(1-m) u+c v}-\frac{(1-m) u_{*}}{1+b(1-m) u_{*}+c v_{*}} \biggr) \biggr\} \,dx \\ = &-I(t)+ \int_{\Omega} \biggl\{ ( u-u_{*} ) \biggl[ - ( u-u_{*} ) +a(1-m)\frac{- ( v-v_{*} ) +b(1-m) ( u v _{*}-u_{*}v) }{p(u,v)} \biggr] \\ &{}+A s ( v-v_{*} ) (1-m)\frac{ ( u-u_{*} ) +c ( u v_{*}-u_{*}v) }{p(u,v)} \biggr\} \,dx \\ = &-I(t)+ \int_{\Omega} \biggl\{ ( u-u_{*} ) \\ &{}\times \biggl[ - ( u-u_{*} ) +a(1-m)\frac{- ( v-v_{*} ) +b(1-m) [ ( u-u_{*} ) v_{*}-u_{*} ( v-v_{*} ) ] }{p(u,v)} \biggr] \\ &{}+A s ( v-v_{*} ) (1-m)\frac{ ( u-u_{*} ) +c [ ( u-u_{*} ) v_{*}-u_{*} ( v-v_{*} ) ] }{p(u,v)} \biggr\} \,dx \\ = &-I(t)+ \int_{\Omega} \biggl\{ - ( u-u_{*} ) ^{2}+a b(1-m)^{2} v _{*}\frac{ ( u-u_{*} ) ^{2}}{p(u,v)}-A s c (1-m)u_{*}\frac{ ( v-v_{*} ) ^{2}}{p(u,v)} \\ &{}+\frac{ ( u-u_{*} ) ( v-v_{*} ) }{p(u,v)} \bigl[ A s ( 1+c v_{*} ) -a \bigl( 1+b(1-m) u_{*} \bigr) \bigr] (1-m) \biggr\} \,dx \\ = &-I(t)+ \int_{\Omega} \biggl\{ - \biggl( 1-\frac{a b(1-m)^{2} v_{*}}{p(u,v)} \biggr) ( u-u_{*} ) ^{2}-A s c (1-m)u_{*}\frac{ ( v-v_{*} ) ^{2}}{p(u,v)} \biggr\} \,dx \end{aligned}$$

with $I(t)=\int_{\Omega}[d_{1}\frac{u_{*}}{u^{2}}\vert \nabla u\vert ^{2}+Ad _{2}\frac{v_{*}}{v^{2}}\vert \nabla v\vert ^{2}]\,dx\ge0$. In addition,

$$\begin{aligned} 1-\frac{a b(1-m)^{2} v_{*}}{p(u,v)} =&1-\frac{a b(1-m)^{2} v_{*}}{ ( 1+b(1-m) u_{*}+c v_{*} ) (1+b(1-m) u+c v)} \\ \geq&1-\frac{a b(1-m)^{2} v_{*}}{ ( 1+b(1-m) u_{*}+c v_{*} ) } \\ =&1-b(1-m) (1-u_{*})\geq0 \end{aligned}$$

under condition $b(1-m)(1-u_{*})\leq1$. Thus $W'(t)\leq0$, which implies the desired assertion since the equality holds only when $(u,v)=(u_{*},v_{*})$. □

3 Stability analysis of the delayed system

3.1 Stability analysis and the existence of Hopf bifurcation

For simplification of notations, use $u(t)$, $v(t)$, $u(t-\tau)$, $v(t-\tau)$ for $u(x,t)$, $v(x,t)$, $u(x,t-\tau)$, $v(x,t-\tau)$, respectively. Linear system (1.3) at $P=(u_{*},v_{*})$:

$$\left(\begin{array}{c}\frac{\partial u}{\partial t}\\ \frac{\partial v}{\partial t}\end{array}\right)=\mathbb{D}\mathrm{\Delta }\left(\begin{array}{c}u(t)\\ v(t)\end{array}\right)+L_1\left(\begin{array}{c}u(t)\\ v(t)\end{array}\right)+L_2\left(\begin{array}{c}u(t-\tau )\\ v(t-\tau )\end{array}\right),$$

(3.1)

where

$$\mathbb{D}=\left(\begin{array}{cc}{d}_1& 0\\ 0& d_2\end{array}\right),L_1=\left(\begin{array}{cc}{a}_{11}& a_{12}\\ 0& 0\end{array}\right),L_2=\left(\begin{array}{cc}0& 0\\ s{a}_{21}& s{a}_{22}\end{array}\right).$$

The characteristic equation is

$$\operatorname{det}\bigl(\lambda I-M_{n}-L_{1}-L_{2}e^{-\lambda\tau} \bigr)=0, $$

where I is the $2 \times2$ identity matrix and $M_n=-n^2/l^2\mathbb{D}$, $n \in\mathbb{N}_{0}$. Then we have

$$ \lambda^{2}+ \lambda A_{n} +B_{n} +s (C_{n}-\lambda a_{22}) e^{- \lambda\tau} =0, $$

(3.2)

where

$$\begin{aligned}& A_{n}=(d_{1}+d_{2}) \frac{n^{2}}{l^{2}}-a_{11}, \\& B_{n}=d_{1} d_{2}\frac{n^{4}}{l^{4}}-d_{2} a_{11} \frac{n^{2}}{l^{2}}, \\& C_{n}=-d_{1} a_{22} \frac{n^{2}}{l^{2}}+a_{11} a_{22}-a_{12} a_{21}. \end{aligned}$$

Let iω ($\omega>0$) be a solution of Eq. (3.2), then

$$- \omega^{2}+i \omega A_{n}+B_{n}+s (C_{n}-i \omega a_{22}) (\cos \omega\tau-i \sin \omega\tau) =0. $$

Then we obtain

$$\textstyle\begin{cases} -\omega^{2}+B_{n}+s C_{n} \cos \omega\tau-a_{22} s \omega \sin \omega \tau=0, \\ A_{n} \omega-C_{n} s \sin \omega\tau-a_{22} s \omega \cos \omega \tau=0. \end{cases}$$

Then

$$ \omega^{4}+ \bigl[ A_{n}^{2}-2 B_{n}-a_{22}^{2} s^{2} \bigr] \omega ^{2}+B_{n}^{2}-C_{n}^{2} s^{2}=0. $$

(3.3)

Denote $z = \omega^{2}$, then (3.3) becomes

$$ z^{2}+ \bigl[A_{n}^{2}-2 B_{n}-a_{22}^{2} s^{2} \bigr]z+B_{n}^{2}-C_{n}^{2} s^{2}=0=0, $$

(3.4)

and the roots are

$$ z^{\pm}=\frac{1}{2} \Bigl[- \bigl(A_{n}^{2}-2 B_{n}-a_{22}^{2} s^{2} \bigr) \pm\sqrt { \bigl(A _{n}^{2}-2 B_{n}-a_{22}^{2} s^{2} \bigr)^{2}-4 \bigl(B_{n}^{2}-C_{n}^{2} s^{2} \bigr)} \Bigr]. $$

(3.5)

Assume ($\mathrm {H}_{1}$) and condition (i) or (ii) in Theorem 2.2 holds. Then

$$\begin{aligned}& B_{n}+sC_{n}=\Delta_{n}>0, \\& A_{n}^{2}-2 B_{n}-a_{22}^{2} s^{2}= \biggl( d_{1} \frac{n^{2}}{l^{2}}- a _{11} \biggr) ^{2}+d_{2}^{2} \frac{n^{4}}{l^{4}}-a_{22}^{2} s^{2}, \end{aligned}$$

and

$$B_{n}-sC_{n}=d_{1} d_{2} \frac{n^{4}}{l^{4}}+\frac{n^{2}}{l^{2}} (a _{22} d_{1} s-a_{11} d_{2})-s(a_{11} a_{22}-a_{12} a_{21}). $$

Denote

$$\mathbb{S}=\{n\vert B_{n}-sC_{n}< 0, n\in \mathbb{N}_{0} \}. $$

Then $\mathbb{S}$ is a finite set since $\lim_{n\rightarrow\infty} B _{n}-sC_{n} \rightarrow+\infty$.

Lemma 3.1

Assume ($\mathrm {H}_{1}$) and condition (i) or (ii) in Theorem  2.2 holds. Then Eq. (3.2) has a pair of purely imaginary roots $\pm i\omega_{n}$ ($n\in\mathbb{S}$) at $\tau^{j}_{n}=\tau^{0}_{n}+ \frac{2j\pi}{\omega_{n}}$, $j \in \mathbb{N}_{0}$, where

$$ \tau^{0}_{n}=\frac{1}{\omega_{n}} \arccos \frac{C_{n} \omega^{2}-B _{n} C_{n}+a_{22} A_{n} \omega^{2}}{s ( C_{n}^{2}+a_{22}^{2} \omega^{2} ) }, \quad \textit{and}\quad \omega_{n}= \sqrt{z^{+}}\quad (\textit{given in }(3.5)). $$

(3.6)

Lemma 3.2

Assume ($\mathrm {H}_{1}$) and condition (i) or (ii) in Theorem  2.2 holds. Then $\operatorname{Re}\lambda'_{n}(\tau^{j}_{n})>0$ for $n\in\mathbb{S}$ and $j \in\mathbb{N}_{0}$.

Proof

Differentiating two sides of (3.2) with respect to τ, we have

$$\biggl(\frac{d \lambda}{d \tau} \biggr)^{-1}= \frac{2 \lambda+A_{n}-s a_{22} e ^{- \lambda\tau}}{s (C_{n}-\lambda a_{22}) \lambda e^{- \lambda \tau}}- \frac{\tau}{\lambda}. $$

Then

$$\begin{aligned} \biggl[\operatorname{Re}\biggl(\frac{d \lambda}{d \tau} \biggr)^{-1} \biggr]_{\tau=\tau^{j}_{n}} =&\operatorname{Re}\biggl[\frac{2 \lambda+A_{n}-s a_{22} e^{- \lambda\tau}}{s (C_{n}-\lambda a_{22}) \lambda e^{- \lambda\tau}}- \frac{\tau}{\lambda} \biggr] \\ =&\frac{1}{\Lambda} \omega^{2} \bigl(2 \omega^{2}+A_{n}^{2}-2 B_{n}-a _{22}^{2} s^{2} \bigr) \\ =&\frac{1}{\Lambda} \omega^{2} \sqrt{ \bigl(A_{n}^{2}-2 B_{n}-a_{22} ^{2} s^{2} \bigr)^{2}-4 \bigl(B_{n}^{2}-C_{n}^{2} s^{2} \bigr)}>0, \end{aligned}$$

where $\Lambda=C_{n}^{2} s^{2} \omega^{2}+a_{22}^{2} s^{2} \omega ^{4}>0$. Therefore $\operatorname{Re}\lambda'_{n}(\tau^{j}_{n})>0$. □

Denote $\tau^{0}_{*}=\min_{ i \in\mathbb{S}}\{\tau^{0}_{i}\}$. According to the above analysis, we have the following theorem.

Theorem 3.1

Assume ($\mathrm {H}_{1}$) and condition (i) or (ii) in Theorem  2.2 holds.

• (i) $E_{*}(u_{*},v_{*})$ is locally asymptotically stable for $\tau\in[0,\tau^{0}_{*})$.

• (ii) $E_{*}(u_{*},v_{*})$ is unstable for $\tau>\tau^{0}_{*}$.

• (iii) $\tau=\tau^{j}_{n}$ ($n\in\mathbb{S}$, $j \in\mathbb{N}_{0}$) are Hopf bifurcation values of system (1.3).

3.2 Stability and direction of Hopf bifurcation

We give detailed computation about Hopf bifurcation using the method in [32, 33]. For fixed $j\in\mathbb{N}_{0}$ and $n\in\mathbb{S}$, we denote $\tilde{\tau}=\tau^{j}_{n}$. Let $\bar{u}(x,t)=u(x,\tau t)-u_{*}$ and $\bar{v}(x,t)=v(x,\tau t)-v_{*}$. For convenience, we drop the bar. Then (1.3) can be written as

$$ \textstyle\begin{cases} \frac{\partial{u}}{\partial{t}}=\tau [d_{1} \Delta u +(u+u_{*}) ( (1-u-u_{*})- \frac{a(1-m) (v+v_{*})}{1+b(1-m) (u+u_{*})+c (v+v _{*})} ) ], \\ \frac{\partial{v}}{\partial{t}}=\tau [d_{2} \Delta v +s (v+v_{*}) ( \frac{(1-m) (u(t-1)+u_{*})}{1+b(1-m) (u(t-1)+u_{*})+c (v(t-1)+v _{*})}-d ) ]. \end{cases} $$

(3.7)

Let

$$\begin{aligned}& \tau=\tilde{\tau}+\mu,\qquad u_{1}(t)=u(\cdot,t), \\& u_{2}(t)=v( \cdot,t) \quad \mbox{and}\quad U=(u_{1},u_{2})^{T}. \end{aligned}$$

In the phase space $\mathscr{C}_{1}:=C([-1,0],X)$, (3.7) can be rewritten as

$$ \frac{dU(t)}{dt}=\tilde{\tau}D\Delta U(t)+L_{\tilde{\tau }}(U_{t})+F(U _{t},\mu), $$

(3.8)

where $L_{\mu}(\phi)$ and $F(\phi,\mu)$ are given respectively by

$$\begin{aligned}& L_{\mu}(\phi)=\mu \left ( \begin{matrix} a_{11} \phi_{1}(0)+a_{12} \phi_{2}(0) \\ s a_{21}\phi_{1}(-1)+s a_{22}\phi_{2}(-1) \end{matrix} \right ), \\& F(\phi,\mu)=\mu D\Delta\phi+L_{\mu}(\phi)+f(\phi,\mu), \end{aligned}$$

with

$$\begin{aligned}& f(\phi,\mu) =(\tilde{\tau}+\mu) \bigl(F_{1}( \phi, \mu),F_{2}(\phi, \mu) \bigr)^{T}, \\& \begin{aligned} F_{1}(\phi,\mu) ={}& \bigl(\phi_{1}(0)+u_{*} \bigr) \biggl( \bigl(1-\phi_{1}(0)-u_{*} \bigr)- \frac{a(1-m) (\phi_{2}(0)+v_{*})}{1+b(1-m) (\phi _{1}(0)+u_{*})+c (\phi_{2}(0)+v_{*})} \biggr) \\ &{} -a_{11}\phi_{1}(0)-a_{12} \phi_{2}(0), \end{aligned} \\& \begin{aligned} F_{2}(\phi,\mu) ={}&s \bigl(\phi_{2}(0)+v_{*} \bigr) \biggl( \frac{(1-m) (\phi _{1}(-1)+u_{*})}{1+b(1-m) (\phi_{1}(-1)+u_{*})+c (\phi_{2}(-1)+v_{*})}-d \biggr) \\ & {}-s a_{21}\phi_{1}(-1)-s a_{22} \phi_{2}(-1) \end{aligned} \end{aligned}$$

for $\phi=(\phi_{1}, \phi_{2})^{T} \in\mathscr{C}_{1}$.

Consider the linear equation

$$ \frac{dU(t)}{dt}=\tilde{\tau} D \Delta U(t)+L_{\tilde {\tau}}(U_{t}). $$

(3.9)

From the previous discussion, we know that $\pm i \omega_{n}$ are simply purely imaginary characteristic values of the linear functional differential equation

$$ \frac{dz(t)}{dt}=-\tilde{\tau} D\frac{n^{2}}{l^{2}} z(t)+L_{ \tilde{\tau}}(z_{t}). $$

(3.10)

From the Riesz representation theorem, there exists a bounded variation function $\eta^{n}(\sigma, \tilde{\tau})-1\le\sigma\le0$ such that $-\tilde{\tau} D\frac{n^{2}}{l^{2}} \phi(0)+L_{\tilde{\tau}}( \phi)= \int_{-1}^{0}\,d\eta^{n}(\sigma, \tau) \phi(\sigma)$ for $\varphi \in C([-1,0],{\mathbb{R}}^2)$.

In fact, we can choose

$$ \eta^{n}(\sigma, \tau)=\textstyle\begin{cases} \tau E, & \sigma=0, \\ 0, & \sigma\in(-1,0), \\ - \tau F, & \sigma=-1, \end{cases} $$

(3.11)

where

$$ E= \left ( \begin{matrix} a_{11}-d_{1}\frac{n^{2}}{l^{2}} & a_{12} \\ 0 & -d_{2}\frac{n^{2}}{l^{2}} \end{matrix} \right ),\qquad F= \left ( \begin{matrix} 0 & 0 \\ s a_{21} & s a_{22} \end{matrix} \right ). $$

(3.12)

Let $A(\tilde{\tau})$ denote the infinitesimal generators of a semigroup included by the solutions of Eq. (3.10) and $A^{*}$ be the formal adjoint of $A(\tilde{\tau})$ under the bilinear pairing

$$\begin{aligned} (\psi,\phi) =&\psi(0) \phi(0)- \int_{-1}^{0} \int_{\xi=0}^{\sigma } \psi(\xi-\sigma)\,d \eta^{n}(\sigma, \tilde{\tau}) \phi(\xi)\,d\xi \\ =&\psi(0) \phi(0)+ \tilde{\tau} \int_{-1}^{0} \psi(\xi+1) F \phi(\xi)\,d\xi \end{aligned}$$

(3.13)

for $\varphi \in C([-1,0],{\mathbb{R}}^2)$, $\psi \in C([-1,0],{\mathbb{R}}^2)$. $\pm i \omega_{n} \tilde{\tau}$ is a pair of simple purely imaginary eigenvalues of $A(\tilde{\tau})$ and $A^{*}$. Let P and $P^{*}$ be the center subspace, that is, the generalized eigenspace of $A(\tilde{\tau})$ and $A^{*}$ associated with $\pm i \omega_{n}$, respectively. Then $P^{*}$ is the adjoint space of P and $\operatorname{dim}P=\operatorname{dim}P^{*}=2$.

Let $p_{1}(\theta)=(1,\xi)^{T}e^{i\omega_{n} \tilde{\tau} \sigma }$ ($\sigma\in[-1,0]$), $q_{1}(r)=(1,\eta)e^{-i\omega_{n} \tilde{\tau} r}$ ($r \in[0,1]$) be the eigenfunctions of $A(\tilde{\tau})$ and $A^{*}$ corresponding to $i \omega_{n} \tilde{\tau}$, $-i \omega_{n} \tilde{\tau}$, respectively. By direct calculations, we chose

$$\xi=\frac{1}{a_{12}} \biggl( i \omega_{n} -a_{11}+d_{1} \frac{n^{2}}{l ^{2}} \biggr),\qquad \eta=\frac{-e^{-i \tau\omega_{n} }}{s a_{21}} \biggl( i \omega_{n} +a_{11}-d_{1} \frac{n^{2}}{l^{2}} \biggr). $$

Let $\Phi=(\Phi_{1},\Phi_{2})$ and $\Psi^{*}=(\Psi^{*}_{1},\Psi^{*} _{2})^{T}$ with

$$\begin{aligned}& \Phi_{1}(\sigma)=\frac{p_{1}(\sigma)+p_{2}(\sigma )}{2}=\left ( \begin{matrix} {\operatorname{Re}} ( e^{i\omega_{n} \tilde{\tau} \sigma} ) \\ \operatorname{Re}( \xi e^{i\omega_{n} \tilde{\tau} \sigma} ) \end{matrix} \right ), \\& \Phi_{2}(\sigma)= \frac{p_{1}(\sigma)-p_{2}(\sigma)}{2i}=\left ( \begin{matrix} {\operatorname{Im}} ( e^{i\omega_{n} \tilde{\tau} \sigma} ) \\ \operatorname{Im}( \xi e^{i\omega_{n} \tilde{\tau}\sigma} ) \end{matrix} \right ) \end{aligned}$$

for $\theta\in[-1,0]$, and

$$\begin{aligned}& \Psi^{*} _{1}(r)= \frac{q_{1}(r)+q_{2}(r)}{2}=\left ( \begin{matrix} {\operatorname{Re}} ( e^{-i\omega_{n} \tilde{\tau}r } ) \\ \operatorname{Re}(\eta {e}^{-i\omega_{n} \tilde{\tau} r } ) \end{matrix} \right ), \\& \Psi^{*} _{2}(r)=\frac{q_{1}(r)-q_{2}(r)}{2i}= \left ( \begin{matrix} {\operatorname{Im}} ( e^{-i\omega_{n} \tilde{\tau}r } ) \\ \operatorname{Im}( \eta e^{-i\omega_{n} \tilde{\tau}r } ) \end{matrix} \right ) \end{aligned}$$

for $r \in[0,1]$. Then we can compute by (3.13)

$$D^{*}_{1}:= \bigl(\Psi^{*} _{1}, \Phi_{1} \bigr),\qquad D^{*}_{2}:= \bigl( \Psi^{*} _{1},\Phi _{2} \bigr),\qquad D^{*}_{3}:= \bigl( \Psi^{*} _{2}, \Phi_{1} \bigr),\qquad D^{*}_{4}:= \bigl( \Psi^{*} _{2}, \Phi_{2} \bigr). $$

Define $(\Psi^{*},\Phi)=(\Psi^{*} _{j},\Phi_{k})= \bigl ({\scriptsize\begin{matrix}{} D^{*}_{1} & D^{*}_{2} \cr D^{*}_{3} & D^{*}_{4} \end{matrix}} \bigr )$ and construct a new basis Ψ for $P^{*}$ by

$$\Psi=(\Psi_{1},\Psi_{2})^{T}= \bigl( \Psi^{*},\Phi \bigr)^{-1}\Psi^{*}. $$

Then $(\Psi,\Phi)=I_{2}$. In addition, define $f_{n}:=(\beta^{1} _{n},\beta^{2}_{n})$, where

$$\beta^{1}_{n}=\left ( \begin{matrix} \cos \frac{n}{l}x \\ 0 \end{matrix} \right ), \qquad \beta^{2}_{n}= \left ( \begin{matrix} 0 \\ \cos \frac{n}{l}x \end{matrix} \right ). $$

We also define

$$c\cdot f_{n}=c_{1} \beta^{1}_{n}+c_{2} \beta^{2}_{n},\quad \mbox{for } c=(c _{1},c_{2})^{T} \in\mathscr{C}_{1}. $$

Thus the center subspace of linear equation (3.9) is given by $P_{CN} \mathscr{C}_{1} \oplus P_{S} \mathscr{C}_{1}$, and $P_{S} \mathscr{C}_{1}$ denotes the complement subspace of $P_{CN} \mathscr{C}_{1}$ in $\mathscr{C}_{1}$,

$$\langle u,v\rangle :=\frac{1}{l\pi} \int_{0}^{l\pi}u_{1} \overline{v_{1}} \,dx+ \frac{1}{l \pi} \int_{0}^{l\pi}u_{2} \overline{v_{2}} \,dx $$

for $u=(u_{1},u_{2})$, $v=(v_{1},v_{2})$, $u,v\in X$ and $\langle \phi,f_{0}\rangle =(\langle \phi,f^{1}_{0}\rangle , \langle \phi,f^{2}_{0}\rangle )^{T}$.

Let $A_{\tilde{\tau}}$ denote the infinitesimal generator of an analytic semigroup induced by the linear system (3.9), and Eq. (3.7) can be rewritten as the following abstract form:

$$ \begin{aligned} \frac{dU(t)}{dt}=A_{\tilde{\tau}} U_{t}+R(U_{t},\mu), \end{aligned} $$

(3.14)

where

$$ R(U_{t},\mu)=\textstyle\begin{cases} 0, & \theta\in[-1,0); \\ F(U_{t},\mu), & \theta=0. \end{cases} $$

(3.15)

By the decomposition of $\mathscr{C}_{1}$, the solution above can be written as

$$ U_{t}=\Phi \left ( \begin{matrix} x_{1} \\ x_{2} \end{matrix} \right ) f_{n}+h(x_{1},x_{2}, \mu), $$

(3.16)

where

$$\left ( \begin{matrix} x_{1} \\ x_{2} \end{matrix} \right ) = \bigl(\Psi, \langle U_{t},f_{n}\rangle \bigr), $$

and

$$h(x_{1},x_{2},\mu) \in P_{S} \mathscr{C}_{1},\qquad h(0,0,0)=0,\qquad Dh(0,0,0)=0. $$

In particular, the solution of (3.8) on the center manifold is given by

$$ U_{t}=\Phi \left ( \begin{matrix} x_{1}(t) \\ x_{2}(t) \end{matrix} \right ) f_{n}+h(x_{1},x_{2},0). $$

(3.17)

Let $z=x_{1}-i x_{2}$, and notice that $p_{1}=\Phi_{1}+i\Phi_{2}$. Then we have

$$\Phi \left ( \begin{matrix} x_{1} \\ x_{2} \end{matrix} \right ) f_{n}= ( \Phi_{1},\Phi_{2}) \left ( \begin{matrix}{} \frac{z+\overline{z}}{2} \\ \frac{i(z-\overline{z})}{2} \end{matrix} \right ) f_{n} = \frac{1}{2}(p_{1}z+ \overline{p_{1}} \overline{z})f _{n} $$

and

$$h(x_{1},x_{2},0)=h \biggl(\frac{z+\overline{z}}{2}, \frac{i(z-\overline{z})}{2},0 \biggr). $$

Hence, Eq. (3.17) can be transformed into

$$\begin{aligned} U_{t} =&\frac{1}{2}(p_{1}z+ \overline{p_{1}} \overline{z})f_{n}+ h \biggl( \frac{z+ \overline{z}}{2},\frac{i(z-\overline{z})}{2},0 \biggr) \\ =&\frac{1}{2}(p_{1}z+ \overline{p_{1}} \overline{z})f_{n}+ W(z, \overline{z}), \end{aligned}$$

(3.18)

where

$$W(z,\overline{z})=h \biggl(\frac{z+\overline{z}}{2}, \frac{i(z-\overline{z})}{2},0 \biggr). $$

From [32], z satisfies

$$ \begin{aligned} \dot{z}=i\omega_{n} \tilde{ \tau} z +g(z,\overline{z}), \end{aligned} $$

(3.19)

where

$$ \begin{aligned} g(z,\overline{z})= \bigl( \Psi_{1}(0)-i \Psi_{2}(0) \bigr) \bigl\langle F(U_{t},0),f_{n} \bigr\rangle . \end{aligned} $$

(3.20)

Let

$$\begin{aligned}& W(z,\overline{z})=W_{20} \frac{z^{2}}{2}+W_{11} z \overline{z} +W_{02} \frac{\overline{z}^{2}}{2}+\cdots, \end{aligned}$$

(3.21)

$$\begin{aligned}& g(z,\overline{z})=g_{20} \frac{z^{2}}{2}+g_{11} z \overline{z} +g_{02} \frac{\overline{z}^{2}}{2}+\cdots, \end{aligned}$$

(3.22)

from Eqs. (3.18) and (3.21), we have

$$\begin{aligned}& u_{t}(0)=\frac{1}{2} (z+\overline{z})\cos \biggl( \frac{n x}{l} \biggr) +W^{(1)}_{20}(0) \frac{z^{2}}{2}+W^{(1)}_{11}(0) z\overline{z}+W^{(1)} _{02}(0) \frac{\overline{z}^{2}}{2}+\cdots, \\& v_{t}(0)=\frac{1}{2} (\xi+\overline{\xi}\overline{z})\cos \biggl( \frac{n x}{l} \biggr) +W^{(2)}_{20}(0) \frac{z^{2}}{2}+W^{(2)}_{11}(0) z\overline{z}+W^{(2)}_{02}(0) \frac{\overline{z}^{2}}{2}+\cdots, \\& u_{t}(-1)=\frac{1}{2} \bigl(z e^{-i\omega_{n} \tilde{\tau}}+\overline {z} e ^{i\omega_{n} \tilde{\tau}} \bigr)\cos \biggl(\frac{n x}{l} \biggr)+W^{(1)}_{20}(-1) \frac{z ^{2}}{2}+W^{(1)}_{11}(-1)z \overline{z}+W^{(1)}_{02}(-1) \frac{ \overline{z}^{2}}{2}+\cdots, \\& \begin{aligned} v_{t}(-1)={}&\frac{1}{2} \bigl(\xi z e^{-i\omega_{n} \tilde{\tau }}+\overline{ \xi} \overline{z} e^{i\omega_{n} \tilde{\tau}} \bigr)\cos \biggl( \frac{n x}{l} \biggr)+W ^{(2)}_{20}(-1) \frac{z^{2}}{2} \\ &{}+W^{(2)}_{11}(-1)z \overline{z}+W^{(2)} _{02}(-1)\frac{\overline{z}^{2}}{2}+\cdots, \end{aligned} \end{aligned}$$

and

$$\begin{aligned}& \begin{aligned} \overline{F}_{1}(U_{t},0) ={}& \frac{1}{\tilde{\tau}}F_{1}=\frac{1}{2} f _{uu} u_{t}^{2}(0)+f_{uv}u_{t}(0) v_{t}(0)+\frac{1}{2} f_{vv}v_{t} ^{2}(0) +\frac{1}{6}f_{uuu}u_{t}^{3}(0) \\ &{}+\frac{1}{2}f_{uuv}u_{t}^{2}(0) v_{t}(0)+\frac{1}{2}f_{uvv} u_{t}(0) v_{t}^{2}(0)+\frac{1}{6}f_{vvv} v_{t}^{3}(0)+O(4), \end{aligned} \\& \begin{aligned} \overline{F}_{2}(U_{t},0) ={}& \frac{1}{\tilde{\tau}}F_{2}=\frac{1}{2} g _{uu} u_{t}^{2}(-1)+ g_{uv} u_{t}(-1)v_{t}(-1)+ \frac{1}{2} g_{vv} v _{t}^{2}(-1) + \frac{1}{6}g_{uuu}u_{t}^{3}(-1) \\ &{}+\frac{1}{2}g_{uuv}u_{t}^{2}(-1) v_{t}(-1)+\frac{1}{2}g_{uvv} u_{t}(-1) v_{t}^{2}(-1)+\frac{1}{6}g_{vvv} v_{t}^{3}(-1)+O(4), \end{aligned} \end{aligned}$$

with

$$\begin{aligned}& f_{uu}=-\frac{2 a (m-1)^{2} v_{*} (b+b c v_{*})}{(-1-b u_{*}+b m u _{*}-c v_{*})^{3}}-2, \\& f_{uv}=\frac{a (m-1) (-1-c v_{*}+b (m-1) u_{*} (1+2 c v_{*}))}{(-1+b (m-1) u_{*}-c v_{*})^{3}}, \\& f_{vv}=-\frac{2 a c (m-1) u_{*} (-1+b (m-1) u_{*})}{(-1+b (m-1) u _{*}-c v_{*})^{3}}, \qquad f_{uuu}= \frac{6 a b^{2} (m-1)^{3} v_{*} (1+c v_{*})}{(1+b (u_{*}-m u _{*})+c v_{*})^{4}}, \\& f_{uuv}=-\frac{a b (m-1)^{2} ( -1+c^{2} v_{*}^{2}+b (m-1) u _{*} (1+2 c v_{*})) }{(1+b (u_{*}-m u_{*})+c v_{*})^{4}}, \\& f_{uvv}=\frac{a c (m-1) ( -1+b^{2} (m-1)^{2} u_{*}^{2}-c v_{*}+2 b c (m-1) u_{*} v_{*} ) }{(1+b (u_{*}-m u_{*})+c v_{*})^{4}}, \\& f_{vvv}=-\frac{6 a c^{2} (m-1) u_{*} (-1+b (m-1) u_{*})}{(1+b (u _{*}-m u_{*})+c v_{*})^{4}},\qquad g_{uu}= \frac{2 (m-1)^{2} s v_{*} (b+b c v_{*})}{(-1-b u_{*}+b m u_{*}-c v_{*})^{3}}, \\& g_{uv}=\frac{c (m-1) s v_{*} (1-b u_{*}+b m u_{*}+c v_{*})}{(1+b u _{*}-b m u_{*}+c v_{*})^{3}},\qquad g_{vv}= \frac{2 c^{2} (1-m) s u_{*} v_{*}}{(1+b (1-m) u_{*}+c v_{*})^{3}}, \\& g_{uuu}=-\frac{6 b^{2} (m-1)^{3} s v_{*} (1+c v_{*})}{(1+b (u_{*}-m u_{*})+c v_{*})^{4}},\qquad g_{uuv}= \frac{b c (m-1)^{2} s v_{*} (2+b (m-1) u_{*}+2 c v_{*})}{(1+b (u_{*}-m u_{*})+c v_{*})^{4}}, \\& g_{uvv}=-\frac{c^{2} (m-1) s v_{*} (1+2 b (m-1) u_{*}+c v_{*})}{(1+b (u_{*}-m u_{*})+c v_{*})^{4}},\qquad g_{vvv}=- \frac{6 c^{3} (1-m) s u_{*} v_{*}}{(1+b (1-m) u_{*}+c v_{*})^{4}}. \end{aligned}$$

Hence,

$$\begin{aligned}& \begin{aligned} \overline{F}_{1}(U_{t},0)={}& \cos^{2} \biggl(\frac{n x}{l} \biggr) \biggl(\frac{z^{2}}{2} \chi_{20} +z\overline{z}\chi_{11} +\frac{\overline{z}^{2}}{2} \overline{ \chi}_{20} \biggr) \\ &{}+\frac{z^{2}\overline{z}}{2}\cos \frac{nx}{l} \kappa_{11} + \frac{z^{2}\overline{z}}{2}\cos^{3} \frac{nx}{l} \kappa_{12} + \cdots, \end{aligned} \\& \begin{aligned} \overline{F}_{2}(U_{t},0)={}& \cos^{2} \biggl(\frac{n x}{l} \biggr) \biggl(\frac{z^{2}}{2} \varsigma_{20} +z\overline{z}\varsigma_{11} + \frac{\overline{z}^{2}}{2}\overline{\varsigma}_{20} \biggr) \\ &{} +\frac{z^{2} \overline{z}}{2} \cos\frac{nx}{l}\kappa_{21} + \frac{z^{2}\overline{z}}{2} \cos^{3} \frac{nx}{l}\kappa_{22} + \cdots, \end{aligned} \\& \begin{aligned} \bigl\langle F(U_{t},0),f_{n} \bigr\rangle = {}&\tilde{\tau} \bigl( \overline{F}_{1}(U_{t},0)f^{1}_{n}+ \overline{F}_{2}(U_{t},0)f^{2}_{n} \bigr) \\ = {}&\frac{z^{2}}{2}\tilde{\tau} \left ( \begin{matrix}{} \chi_{20} \\ \varsigma_{20} \end{matrix} \right ) \Gamma+z \overline{z}\tilde{\tau} \left ( \begin{matrix} \chi_{11} \\ \varsigma_{11} \end{matrix} \right ) \Gamma+\frac{\overline{z}^{2}}{2} \tilde{\tau} \left ( \begin{matrix}{} \overline{\chi}_{20} \\ \overline{\varsigma}_{20} \end{matrix} \right ) \Gamma+\frac{z^{2}\overline{z}}{2}\tilde{ \tau} \left ( \begin{matrix} \kappa_{1} \\ \kappa_{2} \end{matrix} \right ) +\cdots \end{aligned} \end{aligned}$$

with

$$\begin{aligned}& \Gamma=\frac{1}{l\pi} \int_{0}^{l\pi}\cos^{3} \biggl( \frac{n x}{l} \biggr)\,dx, \\& \kappa_{1}= \kappa_{11} \frac{1}{l\pi} \int_{0}^{l\pi}\cos^{2} \biggl( \frac{n x}{l} \biggr)\,dx +\kappa_{12}\frac{1}{l\pi} \int_{0}^{l\pi}\cos^{4} \biggl( \frac{n x}{l} \biggr)\,dx, \\& \kappa_{2}= \kappa_{21} \frac{1}{l\pi} \int_{0}^{l\pi}\cos^{2} \biggl( \frac{n x}{l} \biggr)\,dx +\kappa_{22}\frac{1}{l\pi} \int_{0}^{l\pi}\cos^{4} \biggl( \frac{n x}{l} \biggr)\,dx \end{aligned}$$

and

$$\begin{aligned}& \chi_{20}=\frac{1}{4} \bigl( f_{uu}+ \xi( 2 f_{uv}+\xi f_{vv} ) \bigr), \qquad \chi_{11}= \frac{1}{4} \bigl( f_{uu}+(\overline{\xi} + \xi) f_{uv}+\overline{ \xi} \xi f_{vv} \bigr), \\& \begin{aligned} \kappa_{11}={}&W^{(1)}_{11}(0) ( f_{uu}+\xi f_{uv} ) +W^{(2)} _{11}(0) ( f_{uv}+\xi f_{vv} ) \\ &{} +\frac{1}{2} W^{(1)}_{20}(0) ( f_{uu}+ \overline{\xi} f_{uv} ) +\frac{1}{2} W^{(2)}_{20}(0) ( f_{uv}+\overline{\xi} f_{vv} ),\end{aligned} \\& \kappa_{12}=\frac{1}{24} \bigl( 3 f_{uuu}+(\overline{ \xi} +2 \xi) f_{uuv}+\xi \bigl( (2 \overline{\xi} +\xi) f_{uvv}+3 \overline{ \xi} \xi f_{vvv} \bigr) \bigr), \\& \varsigma_{20}=\frac{1}{4} e^{-2 i \tau\omega_{n}} \bigl( g_{uu}+ \xi( 2 g_{uv}+\xi g_{vv} ) \bigr),\qquad \varsigma_{11}=\frac{1}{4} \bigl( g_{uu}+(\overline{ \xi } +\xi) g _{uv}+\overline{\xi} \xi g_{vv} \bigr), \\& \begin{aligned} \kappa_{21}={}&e^{-i \tau\omega_{n}} W^{(1)}_{11}(-1) ( g_{uu}+ \xi g_{uv} ) +e^{-i \tau\omega_{n}}W^{(2)}_{11}(-1) ( g_{uv}+ \xi g_{vv} ) \\ &{} +\frac{1}{2} e^{i \tau\omega_{n}} W^{(1)}_{20}(-1) ( g_{uu}+\overline{ \xi} g_{uv} ) +\frac{1}{2} e^{i \tau\omega_{n}}W^{(2)}_{20}(-1) ( g_{uv}+ \overline{\xi} g_{vv} ), \end{aligned} \\& \kappa_{22}=\frac{1}{24} e^{-i \tau\omega_{n}} \bigl( 3 g_{uuu}+(\overline{ \xi} +2 \xi) g_{uuv}+\xi \bigl( (2 \overline{\xi} +\xi) g_{uvv}+3 \overline{\xi} \xi g_{vvv} \bigr) \bigr). \end{aligned}$$

Denote

$$\Psi_{1}(0)-i\Psi_{2}(0):=(\gamma_{1}\quad \gamma_{2}). $$

Notice that

$$\frac{1}{l\pi} \int_{0}^{l\pi}\cos^{3} \frac{n x}{l} \,dx=0,\quad n=1,2,3, \ldots, $$

and we have

$$\begin{aligned}& \bigl(\Psi_{1}(0) -i \Psi_{2}(0) \bigr) \bigl\langle F(U_{t},0),f_{n} \bigr\rangle \\& \quad =\frac{z^{2}}{2} (\gamma_{1}\chi_{20} + \gamma_{2}\varsigma_{20}) \Gamma\tilde{\tau} +z\overline{z}( \gamma_{1}\chi_{11} + \gamma_{2} \varsigma_{11})\Gamma\tilde{\tau} +\frac{\overline{z}^{2}}{2}( \gamma_{1}\overline{\chi}_{20} + \gamma_{2} \overline{\varsigma}_{20}) \Gamma\tilde{\tau} \\& \qquad {}+\frac{z^{2}\overline{z}}{2}\tilde{\tau} [\gamma_{1} \kappa_{1} + \gamma_{2} \kappa_{2} ]+\cdots. \end{aligned}$$

(3.23)

By (3.20), (3.22) and (3.23), we obtain that $g_{20}=g_{11}=g_{02}=0$, for $n=1,2,3,\ldots$ . If $n=0$, we have

$$g_{20}=\gamma_{1}\tilde{\tau} \chi_{20} + \gamma_{2}\tilde{\tau} \varsigma_{20}, \qquad g_{11}= \gamma_{1}\tilde{\tau}\chi_{11}+ \gamma_{2}\tilde{ \tau} \varsigma_{11},\qquad g_{02}=\gamma_{1}\tilde{\tau }\overline{\chi}_{20} + \gamma_{2} \tilde{\tau}\overline{ \varsigma}_{20}. $$

And for $n\in\mathbb{N}_{0}$, $g_{21}=\tilde{\tau}( \gamma_{1} \kappa_{1} +\gamma_{2} \kappa_{2})$.

From [32], we have

$$\begin{aligned}& \dot{W}(z,\overline{z})=W_{20}z\dot{z}+W_{11}\dot{z} \overline{z} +W _{11} z \dot{\overline{z}} +W_{02}\overline{z} \dot{\overline{z}}+ \cdots, \\& A_{\tilde{\tau}} W(z,\overline{z})=A_{\tilde{\tau}} W_{20} \frac{z ^{2}}{2}+A_{\tilde{\tau}} W_{11} z \overline{z} + A_{\tilde{\tau}} W _{02} \frac{\overline{z}^{2}}{2}+\cdots, \end{aligned}$$

and $W(z,\overline{z})$ satisfies

$$\dot{W}(z,\overline{z})= A_{\tilde{\tau}} W+H(z,\overline{z}), $$

where

$$\begin{aligned} H(z,\overline{z}) =&H_{20} \frac{z^{2}}{2}+W_{11} z \overline{z} +H _{02} \frac{\overline{z}^{2}}{2}+\cdots \\ =&X_{0}F(U_{t},0)-\Phi \bigl(\Psi, \bigl\langle X_{0}F(U_{t},0),f_{n} \bigr\rangle \cdot f_{n} \bigr). \end{aligned}$$

(3.24)

Hence, we have

$$ (2i\omega_{n} \tilde{\tau}- A_{\tilde{\tau}})W_{20}=H_{20},\qquad -A_{\tilde{\tau}}W_{11}=H_{11}, \qquad (-2i\omega_{n} \tilde{\tau}- A_{\tilde{\tau}})W_{02}=H_{02}, $$

(3.25)

that is,

$$\begin{aligned}& \begin{aligned} &W_{20}=(2i \omega_{n} \tilde{ \tau}- A_{\tilde{\tau}})^{-1}H_{20}, \qquad W_{11}=-A_{\tilde{\tau}} ^{-1} H_{11}, \\ &W_{02}=(-2i\omega_{n} \tilde{\tau}- A_{\tilde{\tau}})^{-1}H_{02}. \end{aligned} \end{aligned}$$

(3.26)

By (3.23), we obtain that for $\theta\in[-1,0)$,

$$\begin{aligned} H(z, \overline{z}) =&-\Phi(0) \Psi(0) \bigl\langle F(U_{t},0),f_{n} \bigr\rangle \cdot f_{n} \\ = &- \biggl(\frac{p_{1}(\theta)+p_{2}(\theta)}{2},\frac{p_{1}(\theta)-p _{2}(\theta)}{2i} \biggr) \left ( \begin{matrix} \Phi_{1}(0) \\ \Phi_{2}(0) \end{matrix} \right ) \bigl\langle F(U_{t},0),f_{n} \bigr\rangle \cdot f_{n} \\ = &-\frac{1}{2} \bigl[p_{1}(\theta) \bigl( \Phi_{1}(0)-i \Phi_{2}(0) \bigr)+p_{2}(\theta) \bigl(\Phi_{1}(0)+i \Phi_{2}(0) \bigr) \bigr] \bigl\langle F(U_{t},0),f_{n} \bigr\rangle \cdot f_{n} \\ = &-\frac{1}{2} \biggl[ \bigl(p_{1}(\theta)g_{20}+p_{2}( \theta)\overline{g}_{02} \bigr)\frac{z ^{2}}{2} + \bigl(p_{1}(\theta)g_{11}+p_{2}(\theta) \overline{g}_{11} \bigr)z \overline{z} \\ &{} + \bigl(p_{1}(\theta )g_{02}+p_{2}(\theta) \overline{g}_{20} \bigr) \frac{ \overline{z}^{2}}{2} \biggr]+\cdots. \end{aligned}$$

Therefore by (3.24), for $\theta\in[-1,0)$,

$$\begin{aligned}& H_{20}(\theta)= \textstyle\begin{cases} 0, & n\in\mathbb{N}, \\ -\frac{1}{2}(p_{1}(\theta)g_{20}+p_{2}(\theta)\overline{g}_{02}) \cdot f_{0}, & n=0, \end{cases}\displaystyle \\& H_{11}(\theta)= \textstyle\begin{cases} 0, & n\in\mathbb{N}, \\ -\frac{1}{2}(p_{1}(\theta)g_{11}+p_{2}(\theta)\overline{g}_{11}) \cdot f_{0}, & n=0, \end{cases}\displaystyle \\& H_{02}(\theta)= \textstyle\begin{cases} 0, & n\in\mathbb{N}, \\ -\frac{1}{2}(p_{1}(\theta)g_{02}+p_{2}(\theta)\overline{g}_{20}) \cdot f_{0}, & n=0, \end{cases}\displaystyle \end{aligned}$$

and

$$H(z,\overline{z}) (0)=F(U_{t},0)-\Phi \bigl(\Psi, \bigl\langle F(U_{t},0),f_{n} \bigr\rangle \bigr)\cdot f_{n}, $$

where

$$\begin{aligned}& H_{20}(0)=\textstyle\begin{cases} \tilde{\tau} \bigl({\scriptsize\begin{matrix}{} \chi_{20} \\ \varsigma_{20} \end{matrix}} \bigr) \cos^{2} ( \frac{n x}{l} ), & n\in\mathbb{N}, \\ \tilde{\tau} \bigl({\scriptsize\begin{matrix}{} \chi_{20} \\ \varsigma_{20} \end{matrix}} \bigr) - \frac{1}{2} (p_{1}(0)g_{20}+p_{2}(0) \overline{g}_{02} )\cdot f _{0}, & n=0,\end{cases}\displaystyle \\& H_{11}(0)=\textstyle\begin{cases} \tilde{\tau} \bigl({\scriptsize\begin{matrix}{} \chi_{11} \\ \varsigma_{11} \end{matrix}} \bigr) \cos^{2} (\frac{n x}{l} ), & n\in \mathbb{N}, \\ \tilde{\tau} \bigl({\scriptsize\begin{matrix}{} \chi_{11} \\ \varsigma_{11} \end{matrix}} \bigr) - \frac{1}{2} (p_{1}(0)g_{11}+p_{2}(0) \overline{g}_{11} )\cdot f _{0}, & n=0. \end{cases}\displaystyle \end{aligned}$$

(3.27)

From $A_{\tilde{\tau}}$ and (3.25), we obtain that

$$\dot{W}_{20}=A_{\tilde{\tau}}W_{20}=2i\omega_{n} \tilde{\tau} W_{20}+ \frac{1}{2} \bigl(p_{1}( \theta)g_{20}+p_{2}(\theta)\overline{g}_{02} \bigr) \cdot f_{n},\quad -1\le\theta< 0. $$

That is,

$$W_{20}(\theta)=\frac{i}{2i\omega_{n} \tilde{\tau}} \biggl(g_{20} p_{1}( \theta)+\frac{\overline{g}_{02}}{3}p_{2}(\theta) \biggr)\cdot f_{n} +E_{1} e^{2i\omega_{n} \tilde{\tau} \theta}, $$

where

$$E_{1}=\textstyle\begin{cases} W_{20}(0), & n=1,2,3,\ldots, \\ W_{20}(0)-\frac{i}{2i\omega_{n} \tilde{\tau}}(g_{20} p_{1}(\theta )+\frac{ \overline{g}_{02}}{3}p_{2}(\theta))\cdot f_{0}, & n=0. \end{cases} $$

From $A_{\tilde{\tau}}$ and (3.25), we obtain that for $-1\le\theta<0$,

$$\begin{aligned}& - \biggl(g_{20}p_{1}(0)+ \frac{\overline{g}_{02}}{3}p_{2}(0) \biggr)\cdot f_{0} +2i \omega_{n} \tilde{\tau} E_{1}-A_{\tilde{\tau}} \biggl( \frac{i}{2\omega_{n} \tilde{\tau}} \biggl(g_{20}p_{1}(0)+ \frac{\overline{g}_{02}}{3}p_{2}(0) \biggr) \cdot f_{0} \biggr) \\& \qquad {}-A_{\tilde{\tau}} E_{1}-L_{\tilde{\tau}} \biggl( \frac{i}{2\omega_{n} \tilde{\tau}} \biggl(g_{20} p_{1}(0)+ \frac{\overline{g}_{02}}{3} p_{2}(0) \biggr) \cdot f_{n}+ E_{1} e^{2i\omega_{n} \tilde{\tau} \theta} \biggr) \\& \quad =\tilde{\tau} \left ( \begin{matrix} \chi_{20} \\ \varsigma_{20} \end{matrix} \right ) - \frac{1}{2} \bigl(p_{1}(0)g_{20}+p_{2}(0) \overline{g}_{02} \bigr)\cdot f _{0}. \end{aligned}$$

As

$$A_{\tilde{\tau}} p_{1}(0)+L_{\tilde{\tau}}(p_{1} \cdot f_{0})=i \omega_{0} p_{1}(0) \cdot f_{0}, $$

and

$$A_{\tilde{\tau}} p_{2}(0)+L_{\tilde{\tau}}(p_{2} \cdot f_{0})=-i \omega_{0} p_{2}(0) \cdot f_{0}, $$

we have

$$2i\omega_{n} E_{1}-A_{\tilde{\tau}} E_{1}-L_{\tilde{\tau}} E_{1} e ^{2i\omega_{n}} =\tilde{\tau }\left ( \begin{matrix} \chi_{20} \\ \varsigma_{20} \end{matrix} \right ) \cos^{2} \biggl( \frac{n x}{l} \biggr),\quad n \in \mathbb{N}_{0}. $$

That is,

$$E_{1}=\tilde{\tau}E \left ( \begin{matrix} \chi_{20} \\ \varsigma_{20} \end{matrix} \right ) \cos^{2} \biggl(\frac{n x}{l} \biggr), $$

where

$$E=\left ( \begin{matrix} 2i \omega_{n} \tilde{\tau}+ d_{1} \frac{n^{2}}{l^{2}} a_{11} & -a _{12} \\ -s a_{21} e^{-2i \omega_{n} \tilde{\tau}} & 2i \omega_{n} \tilde{\tau}+ d_{2} \frac{n^{2}}{l^{2}}-s a_{21} e^{-2i \omega_{n} \tilde{\tau}} \end{matrix} \right ) ^{-1}. $$

Similarly, from (3.26), we have

$$-\dot{W}_{11}=\frac{i}{2\omega_{n} \tilde{\tau}} \bigl(p_{1}( \theta)g_{11}+p _{2}(\theta)\overline{g}_{11} \bigr) \cdot f_{n},\quad -1\le\theta< 0. $$

That is,

$$W_{11}(\theta)=\frac{i}{2i\omega_{n} \tilde{\tau}} \bigl(p_{1}(\theta) \overline{g}_{11}-p_{1}(\theta)g_{11} \bigr)+E_{2}. $$

Similarly, we have

$$E_{2}=\tilde{\tau}E^{*} \left ( \begin{matrix} \chi_{11} \\ \varsigma_{11} \end{matrix} \right ) \cos^{2} \biggl(\frac{n x}{l} \biggr), $$

where

$$E^{*}=\left ( \begin{matrix} d_{1} \frac{n^{2}}{l^{2}} -a_{11} & -a_{12} \\ -s a_{21} & d_{2} \frac{n^{2}}{l^{2}} -s a_{22} \end{matrix} \right ) ^{-1}. $$

Thus, we can obtain the following quantities which determine the property of Hopf bifurcation:

$$\begin{aligned}& \begin{aligned} &c _{1}(0)= \frac{i}{2\omega_{n} \tilde{\tau}} \biggl(g_{20}g_{11}-2\vert g_{11}\vert ^{2}- \frac{\vert g_{02}\vert ^{2}}{3} \biggr) + \frac{1}{2}g_{21},\qquad \mu_{2}=-\frac{\operatorname{Re}(c_{1}(0))}{\operatorname{Re}(\lambda' (\tau^{j}_{n}))}, \\ &T _{2}=-\frac{1}{\omega_{n} \tilde{\tau}} \bigl[\operatorname{Im}\bigl(c_{1}(0) \bigr)+ \mu_{2} \operatorname{Im}\bigl( \lambda' \bigl( \tau^{j}_{n} \bigr) \bigr) \bigr], \qquad \beta_{2}= 2 \operatorname{Re}\bigl(c_{1}(0) \bigr). \end{aligned} \end{aligned}$$

(3.28)

Theorem 3.2

For any critical value $\tau^{j}_{n}$, we have the following results.

• (i) When $\mu_{2}>0$ (resp. <0), the Hopf bifurcation is forward (resp. backward).

• (ii) When $\beta_{2}<0$ (resp. >0), the bifurcating periodic solutions on the center manifold are orbitally asymptotically stable (resp. unstable).

• (iii) When $T_{2}>0$ (resp. $T_{2}<0$), the period increases (resp. decreases).

4 Numerical simulations

4.1 The case of $\tau=0$

Consider the following system:

$$ \textstyle\begin{cases} \frac{\partial{u}}{\partial{t}}=0.1 \Delta u +u ( 1-u- \frac{0.4(1-m) v}{1+9(1-m) u+0.1 v} ), \\ \frac{\partial{v}}{\partial{t}}=5 \Delta v +15 v ( \frac{(1-m) u}{1+9(1-m) u+0.1 v}-0.05 ), \end{cases} $$

(4.1)

where $\Omega=1.5\pi$. To study the effect of prey refuge, vary the parameter m in system (4.1). The stabilities of $E_{*}(u_{*},v _{*})$ for system (4.1) are shown in Table 1. It suggests that prey refuge has a stabilizing effect on system (4.1) without and with diffusion. But when $m=0.15, 0.2$, there are differences in these two kinds of systems.

Table 1 Stability of $\pmb{E_{*}(u_{*},v_{*})}$ for system ( 4.1 )

Now, fix $m=0.2$, vary the parameter s in system (4.1). $E_{*}(0.2069,8.2033)$ is the unique positive equilibrium, and

$$a_{11}\approx0.1501>0,\qquad a_{11}a_{22}-a_{12}a_{21} \approx0.0145 >0, $$

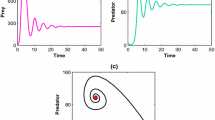
then ($\mathrm {H}_{1}$) holds. If $d_{1}=d_{2}=0$ and $a_{11}+s a_{22} < 0$, then $E_{*}(u_{*},v_{*})$ is locally asymptotically stable, and the system undergoes Hopf bifurcation at $E_{*}(u_{*},v_{*})$ when $s=-a_{11}/a_{22}$ (shown in Figure 1). For system (4.1), if we choose $s =15$, then by Theorem 2.2(iii), $E_{*}(u_{*},v_{*})$ is Turing unstable, this is shown in Figure 2. For system (4.1), by Theorem 2.2(v), Hopf bifurcation occurs when $s=-a_{11}/a_{22}$, this is shown in Figure 3.

Figure 1

Phase portraits of system ( 4.1 ) when $\pmb{d_{1}=d_{2}=0}$ . Left: $s =10$, and the initial condition $(0.5,8.2)$. Right: $s =15$ and the initial condition $(0.5,8.2)$.

Figure 2

For system ( 4.1 ), $\pmb{s=15}$ and the initial condition is $\pmb{(0.5,8.2)}$ . Left component: $u(x,t)$ (Turing unstable). Right component: $v(x,t)$ (Turing unstable).

Figure 3

For system ( 4.1 ), $\pmb{s=10}$ and the initial condition is $\pmb{(0.5,8.2)}$ . Left component: $u(x,t)$ (Stable). Right component: $v(x,t)$ (Stable).

4.2 The case of $\tau\neq0$

Consider the following system:

$$ \textstyle\begin{cases}\frac{\partial{u}}{\partial{t}}=0.1 \Delta u +u ( 1-u- \frac{0.4(1-0.1) v}{1+5(1-0.1) u+0.5 v} ), \\ \frac{\partial{v}}{\partial{t}}=0.2 \Delta v +0.5 v ( \frac {(1-0.1) u(t-\tau)}{1+5(1-0.1) u(t-\tau)+0.5 v(t-\tau)}-0.05 ), \end{cases} $$

(4.2)

where $\Omega=2\pi$. System (1.3) has a unique coexistent equilibrium $E_{*}(0.5348,12.4395)$. It is easy to obtain that $E_{*}(u_{*},v_{*})$ is locally stable when $\tau=0$, this is shown in Figure 4. By computation, we obtain $\tau_{*}\approx9.1937$. By Theorem 3.1, we know that if $\tau\in[0,\tau_{*})$, then $E_{*}(u _{*},v_{*})$ is locally asymptotically stable, this is shown in Figure 5. By Theorem 3.1, Hopf bifurcation occurs at the $E_{*}(u_{*},v _{*})$ when $\tau=\tau_{*}$. By Theorem 3.2, we have $\mu_{2} \approx 1708.45>0$, suggesting that the bifurcating periodic solution exists when $\tau>\tau_{*}$ (shown in Figure 6).

Figure 4

For system ( 4.2 ), $\pmb{\tau=0}$ and the initial condition is $\pmb{(0.5,12)}$ . Left component: $u(x,t)$ (Stable). Right component: $v(x,t)$ (Stable).

Figure 5

For system ( 1.3 ), $\pmb{\tau=8}$ and the initial condition is $\pmb{(0.5,12)}$ . Left component: $u(x,t)$ (Stable). Right component: $v(x,t)$ (Stable).

Figure 6

For system ( 1.3 ), $\pmb{\tau=9.2}$ and the initial condition is $\pmb{(0.5,12)}$ . Left component: $u(x,t)$ (Periodic solution). Right component: $v(x,t)$ (Periodic solution).

5 Conclusion

In this paper, a diffusive predator-prey system with prey refuge and gestation delay is investigated. For a non-delay system, the conditions inducing Turing instability and Hopf bifurcation are given. The global stabilities of equilibria $(1,0)$ and $(u_{*},v_{*})$ are also considered. By numerical simulation, we conclude that prey refuge has a stabilizing effect on the reaction-diffusion system similar to the ODE system. But, when prey refuge is equal to some values, Turing instability may occur. For a delayed system, time induced instability and Hopf bifurcation are investigated. We conclude that time delay τ may affect the stability of the positive equilibrium. When it is smaller than the critical value $\tau_{*}$, then prey and predator will coexist and tend to the interior equilibrium $E_{*}(u_{*},v_{*})$. When the delay passes through some critical values, the positive equilibrium loses its stability and Hopf bifurcations occur. Then prey and predator will exhibit oscillatory behavior.