Skip to main content
SpringerLink
Log in

Turing–Hopf bifurcation analysis of a predator–prey model with herd behavior and cross-diffusion

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

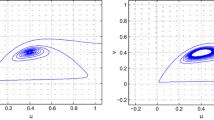
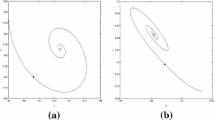
Abstract

In this paper, we consider a predator–prey model with herd behavior and cross-diffusion subject to homogeneous Neumann boundary condition. Firstly, the existence and priori bound of a solution for the model without cross-diffusion are shown. Then, by computing and analyzing the normal form on the center manifold associated with the Turing–Hopf bifurcation, we find a wealth of spatiotemporal dynamics near the Turing–Hopf bifurcation point under suitable conditions. Furthermore, some numerical simulations to illustrate the theoretical analysis are carried out.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Volterra, V.: Sui tentutive di applicazione delle mathematiche alle seienze biologiche e sociali. Ann. Radioelectr. Univ. Romandes 23, 436–458 (1901)

    Google Scholar 

  2. Volterra, V.: Variazione e fluttuazini del numero dindividui in specie animali conviventi. Mem. R. Accad. Naz. dei Lincei 2, 31–113 (1926)

    Google Scholar 

  3. Zhang, T., Zang, H.: Delay-induced Turing instability in reaction–diffusion equations. Phys. Rev. E 90, 052908 (2014)

    Article  Google Scholar 

  4. Zhang, T., Xing, Y., Zang, H., Han, M.: Spatio-temporal patterns in a predator–prey model with hyperbolic mortality. Nonlinear Dyn. 78, 265–277 (2014)

    Article  MathSciNet  Google Scholar 

  5. Song, Y., Zou, X.: Bifurcation analysis of a diffusive ratio-dependent predator–prey model. Nonlinear Dyn. 78, 49–70 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  6. Peng, Y., Zhang, T.: Turing instability and pattern induced by cross-diffusion in a predator–prey system with Allee effect. Appl. Math. Comput. 275, 1–12 (2016)

    MathSciNet  Google Scholar 

  7. Freedman, H.I., Wolkowicz, G.S.K.: Predator–prey systems with groups defence: the paradox of enrichment revisited. Bull. Math. Biol. 48, 493–508 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  8. Andrews, J.F.: A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates. Biotechnol. Bioeng. 10, 707–723 (1968)

    Article  Google Scholar 

  9. Ajraldi, V., Pittavino, M., Venturino, E.: Modeling herd behavior in population systems. Nonlinear Anal. RWA 12, 2319–2338 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  10. Braza, P.A.: Predator–prey dynamics with square root functional responses. Nonlinear Anal. RWA 13, 1837–1843 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  11. Tang, X., Song, Y.: Stability, Hopf bifurcations and spatial patterns in a delayed diffusive predator–prey model with herd behavior. Appl. Math. Comput. 254, 375–391 (2015)

    MathSciNet  Google Scholar 

  12. Turing, A.: The chemical basis of morphogenesis. Philos. Trans. R. Soc. B 237, 37–72 (1952)

    Article  MathSciNet  Google Scholar 

  13. Murray, J.D.: Mathematical Biology of Biomathematics Texts, vol. 19, 2nd edn. Springer, Berlin (2002)

    Google Scholar 

  14. Wang, M.: Stationary patterns for a prey–predator model with prey-dependent and ratio-dependent functional responses and diffusion. Phys. D 196, 172–192 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  15. Wang, M.: Stability and Hopf bifurcation for a predator–prey model with prey-stage structure and diffusion. Math. Biosci. 212, 149–160 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  16. Yi, F., Wei, J., Shi, J.: Bifurcation and spatiotemporal patterns in a homogeneous diffusion predator–prey system. J. Differ. Equ. 246, 1944–1977 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  17. Wang, W., Zhang, L., Wang, H., Li, Z.: Pattern formation of a predator–prey system with Ivlev-type functional response. Ecol. Model. 221, 131–140 (2010)

    Article  Google Scholar 

  18. Zhang, J., Li, W., Yan, X.: Hopf bifurcation and Turing instability in spatial homogeneous and inhomogeneous predator–prey models. Appl. Math. Comput. 218, 1883–1893 (2011)

    MathSciNet  MATH  Google Scholar 

  19. Tang, X., Song, Y.: Bifurcation analysis and Turing instability in a diffusive predator–prey model with herd behavior and hyperbolic mortality. Chaos Solitons Fract. 81, 303–314 (2015)

    Article  MathSciNet  Google Scholar 

  20. Sun, G., Zhang, G., Jin, Z., Li, L.: Predator cannibalism can give rise to regular spatial pattern in a predator–prey system. Nonlinear Dyn. 58, 75–84 (2009)

    Article  MATH  Google Scholar 

  21. Sun, G., Jin, Z., Li, L., Li, B.: Self-organized wave pattern in a predator–prey model. Nonlinear Dyn. 60, 265–275 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  22. Zhang, X., Sun, G., Jin, Z.: Spatial dynamics in a predator–prey model with Beddington–DeAngelis functional response. Phys. Rev. E 85, 021924 (2012)

    Article  Google Scholar 

  23. Upadhyay, R.K., Roy, P., Datta, J.: Complex dynamics of ecological systems under nonlinear harvesting: Hopf bifurcation and Turing instability. Nonlinear Dyn. 79(4), 2251–2270 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  24. Sun, G., Wu, Z., Wang, Z., Jin, Z.: Influence of isolation degree of spatial patterns on persistence of populations. Nonlinear Dyn. 83, 811–819 (2016)

    Article  MathSciNet  Google Scholar 

  25. Gunaratne, G.H., Ouyang, Q., Swinney, H.L.: Pattern formation in the presence of symmetries. Phys. Rev. E 50, 2802–2820 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  26. Penńa, B., Pérez-García, C.: Stability of Turing patterns in the Brusselator model. Phys. Rev. E 64, 056213 (2001)

    Article  MathSciNet  Google Scholar 

  27. Wei, M., Wu, J., Guo, G.: Turing structures and stability for the 1-D Lengyel–Epstein system. J. Math. Chem. 50, 2374–2396 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  28. Guo, G., Li, B., Wei, M., Wu, J.: Hopf bifurcation and steady-state bifurcation for an autocatalysis reaction–diffusion model. J. Math. Anal. Appl. 391, 265–277 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  29. Gambino, G., Lombardo, M.C., Sammartino, M., Sciacca, V.: Turing pattern formation in the Brusselator system with nonlinear diffusion. Phys. Rev. E 88(4), 042925 (2013)

    Article  Google Scholar 

  30. Gambino, G., Lombardo, M.C., Sammartino, M.: Turing instability and pattern formation for the Lengyel–Epstein system with nonlinear diffusion. Acta Appl. Math. 132, 283–294 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  31. Sun, G., Jin, Z., Liu, Q., Li, L.: Pattern formation in a spatial S–I model with non-linear incidence rates. J. Stat. Mech. Theory Exp. 11, P11011 (2007)

    Article  Google Scholar 

  32. Sun, G., Jin, Z., Liu, Q., Li, L.: Spatial pattern in an epidemic system with cross diffusion of the susceptible. J. Biol. Syst. 17, 141–152 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  33. Wang, W., Cai, Y., Wu, M., Wang, K., Li, Z.: Complex dynamics of a reaction–diffusion epidemic model. Nonlinear Anal. RWA 13, 2240–2258 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  34. Li, J., Sun, G., Jin, Z.: Pattern formation of an epidemic model with time delay. Phys. A 403, 100–109 (2014)

    Article  MathSciNet  Google Scholar 

  35. Zhao, H., Huang, X., Zhang, X.: Turing instability and pattern formation of neural networks with reaction–diffusion terms. Nonlinear Dyn. 76(1), 115–124 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  36. Zheng, Q., Shen, J.: Dynamics and pattern formation in a cancer network with diffusion. Commun. Nonlinear Sci. Numer. Simul. 27, 93–109 (2015)

    Article  MathSciNet  Google Scholar 

  37. Ma, J., Xu, Y., Ren, G., Wang, C.: Prediction for breakup of spiral wave in a regular neuronal network. Nonlinear Dyn. 84(2), 1–13 (2015)

    MathSciNet  Google Scholar 

  38. Song, X., Wang, C., Ma, J., Ren, G.: Collapse of ordered spatial pattern in neuronal network. Phys. A 451, 95–112 (2016)

    Article  MathSciNet  Google Scholar 

  39. Yuan, S., Xu, C., Zhang, T.: Spatial dynamics in a predator–prey model with herd behavior. Chaos 23, 0331023 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  40. Xu, Z., Song, Y.: Bifurcation analysis of a diffusive predator–prey system with a herd behavior and quadratic mortality. Math. Methods Appl. Sci. 38(4), 2994–3006 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  41. Shukla, J., Verma, S.: Effects of convective and dispersive interactions on the stability of 2 species. Bull. Math. Biol. 43, 593–610 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  42. Kerner, E.H.: A statistical mechanics of interacting biological species. Bull. Math. Biol. 19, 121–146 (1957)

    MathSciNet  Google Scholar 

  43. Shigesada, N., Kawasaki, K., Teramoto, E.: Spatial segregation of interacting species. J. Theor. Biol. 79, 83–99 (1979)

    Article  MathSciNet  Google Scholar 

  44. Tian, C., Lin, Z., Pedersen, M.: Instability induced by cross-diffusion in reaction–diffusion systems. Nonlinear Anal. RWA 11, 1036–1045 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  45. Xue, L.: Pattern formation in a predator-prey model with spatial effect. Phys. A 391, 5987–5996 (2012)

    Article  Google Scholar 

  46. Guin, L.N.: Existence of spatial patterns in a predator–prey model with self- and cross-diffusion. Appl. Math. Comput. 226, 320–335 (2014)

    MathSciNet  Google Scholar 

  47. Zhang, J., Yan, G.: Lattice Boltzmann simulation of pattern formation under cross-diffusion. Comput. Math. Appl. 69, 157–169 (2015)

    Article  MathSciNet  Google Scholar 

  48. Sun, G., Jin, Z., Li, L., Haque, M., Li, B.: Spatial patterns of a predator-prey model with cross diffusion. Nonlinear Dyn. 69, 1631–1638 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  49. Sun, G., Wang, S., Ren, Q., Jin, Z., Wu, Y.: Effects of time delay and space on herbivore dynamics: linking inducible defenses of plants to herbivore outbreak. Sci. Rep. 5, 11246 (2015)

  50. Kumar, N., Horsthemke, W.: Effects of cross diffusion on Turing bifurcations in two-species reaction-transport systems. Phys. Rev. E 83, 036105 (2011)

    Article  MathSciNet  Google Scholar 

  51. Berenstein, I., Beta, C.: Cross-diffusion in the two-variable oregonator model. Chaos: an interdisciplinary. J. Nonlinear Sci. 23(3), 033119 (2013)

    Google Scholar 

  52. Fanelli, D., Cianci, C., Patti, F.: Turing instabilities in reaction–diffusion systems with cross diffusion. Eur. Phys. J. B 86(4), 142 (2013)

    Article  MathSciNet  Google Scholar 

  53. Baurmann, M., Gross, T., Feudel, U.: Instabilities in spatially extended predator–prey systems: spatio-temporal patterns in the neighborhood of Turing–Hopf bifurcations. J. Theor. Biol. 245, 220–229 (2007)

    Article  MathSciNet  Google Scholar 

  54. Meixner, M., De Wit, A., Bose, S., Scholl, E.: Generic spatiotemporal dynamics near codimension-two Turing–Hopf bifurcations. Phys. Rev. E 55(3), 6690–6697 (1997)

    Article  MathSciNet  Google Scholar 

  55. Rodrigues, L.A.D., Mistro, D.C., Petrovskii, S.: Pattern formation, long-term transients, and the Turing–Hopf bifurcation in a space-and time-discrete predator–prey system. Bull. Math. Biol. 73, 1812–1840 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  56. Song, Y., Zou, X.: Spatiotemporal dynamics in a diffusive ratio-dependent predator–prey model near a Hopf–Turing bifurcation point. Comput. Math. Appl. 67, 1978–1997 (2014)

    Article  MathSciNet  Google Scholar 

  57. Song, Y., Zhang, T., Peng, Y.: Turing–Hopf bifurcation in the reaction–diffusion equations and its applications. Commun. Nonlinear Sci. Numer. Simul. 33, 229–258 (2016)

    Article  MathSciNet  Google Scholar 

  58. Tang, X., Song, Y.: Cross-diffusion induced spatiotemporal patterns in a predator–prey model with herd behavior. Nonlinear Anal. RWA 24, 36–49 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  59. Pao, C.: Nonlinear Parabolic and Elliptic Equations. Plenum Press, New York (1992)

    MATH  Google Scholar 

  60. Ye, Q., Li, Z.: Introduction to Reaction–Diffusion Equations. Science Press, China (1994). (in Chinese)

    Google Scholar 

  61. Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York (1983)

    Book  MATH  Google Scholar 

Download references

Acknowledgments

The authors highly appreciate the anonymous reviewers and editor for providing valuable suggestions which helped us to improve the manuscript. The work is supported by the National Natural Science Foundation of China (No. 11571257) and the Science and Technology Project of Department of Education of Jiangxi Province (No. GJJ150771).

Author information

Authors and Affiliations

  1. Department of Mathematics, Tongji University, Shanghai, 200092, People’s Republic of China

    Xiaosong Tang & Yongli Song

  2. College of Mathematics and Physics, Jinggangshan University, Ji’an, 343009, People’s Republic of China

    Xiaosong Tang

  3. Department of Mathematics, Swinburne University of Technology, Hawthorn, VIC, 3122, Australia

    Tonghua Zhang

Authors
  1. Xiaosong Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yongli Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tonghua Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yongli Song.

Appendix: calculation of \(B_{210}, B_{102}, B_{111}\) and \(B_{003}\)

Appendix: calculation of \(B_{210}, B_{102}, B_{111}\) and \(B_{003}\)

$$\begin{aligned} B_{210}= & {} C_{210}+\frac{3}{2}\left( D_{210}+E_{210}\right) ,\\ B_{102}= & {} C_{102}+\frac{3}{2}\left( D_{102}+E_{102}\right) ,\\ B_{111}= & {} C_{111}+\frac{3}{2}\left( D_{111}+E_{111}\right) ,\\ B_{003}= & {} C_{003}+\frac{3}{2}\left( D_{003}+E_{003}\right) , \end{aligned}$$

where

$$\begin{aligned} C_{210}= & {} \frac{1}{\pi }q_{0}^\mathrm{T}F_{210},\quad C_{102}=\frac{1}{\pi }q_{0}^\mathrm{T}F_{102},\\ C_{111}= & {} \frac{1}{\pi }q_{k_{*}}^\mathrm{T}F_{111},\quad C_{003}=\frac{3}{2\pi }q_{k_{*}}^\mathrm{T}F_{003}, \end{aligned}$$

with

$$\begin{aligned} F_{210}= & {} \frac{1}{2}\left( f_{3000}\left| p_{01}\right| ^2p_{01} +f_{0300}\left| p_{02}\right| ^2p_{02}\right. \\&+\,f_{2100}\left( p_{01}^{2} \overline{p}_{02} +2 \left| p_{01}\right| ^2p_{02}\right) \\&\left. +\,f_{1200}\left( p_{02}^2 \overline{p}_{01}+2 \left| p_{02}\right| ^2p_{01}\right) \right) ,\\ F_{102}= & {} \frac{1}{2}\left( f_{3000} p_{01}p_{k_{*}1}^{2}+f_{0300} p_{02} p_{k_{*}2}^{2}\right. \\&+\,f_{2100}\left( p_{02} p_{k_{*}1}^{2}+2 p_{01}p_{k_{*}1} p_{k_{*}2}\right) \\&\left. +\,f_{1200}\left( p_{01} p_{k_{*}2}^{2}+2 p_{02}p_{k_{*}1} p_{k_{*}2}\right) \right) ,\\ F_{111}= & {} \left( f_{3000} \left| p_{01}\right| ^{2}p_{k_{*}1}+f_{0300} \left| p_{02}\right| ^{2}p_{k_{*}2}\right. \\&+\,f_{2100}\left( \left| p_{01}\right| ^{2}p_{k_{*}2}+2p_{k_{*}1}\text{ Re }\left\{ p_{01}\overline{p}_{02}\right\} \right) \\&\left. +\,f_{1200}\left( \left| p_{02}\right| ^{2}p_{k_{*}1} +2p_{k_{*}2}\text{ Re }\left\{ p_{02}\overline{p}_{01}\right\} \right) \right) ,\\ F_{003}= & {} \frac{1}{3!}\left( f_{3000} p_{k_{*}1}^{3}+f_{0300} p_{k_{*}2}^{3}\right) \\&+\,\frac{1}{2}\left( f_{2100}p_{k_{*}1}^{2}p_{k_{*}2}+ f_{1200} p_{k_{*}1} p_{k_{*}2}^{2}\right) ,\\ D_{210}= & {} \frac{1}{3\pi \omega _{c} i }\left( -\left( q_{0}^\mathrm{T}F_{200}\right) \left( q_{0}^\mathrm{T}F_{110}\right) \right. \nonumber \\&\left. +\,\frac{1}{3}\left| q_{0}^\mathrm{T}F_{020}\right| ^{2}+2\left| q_{0}^\mathrm{T}F_{110}\right| ^{2}\right) , \\ D_{102}= & {} \frac{1}{3\pi \omega _{c} i}\left( -\left( q_{0}^\mathrm{T}F_{200}\right) \left( q_{0}^\mathrm{T}F_{002}\right) +\left( q_{0}^\mathrm{T}F_{110}\right) \right. \\&\left. \left( \overline{q}_{0}^\mathrm{T}F_{002}\right) +2\left( q_{0}^\mathrm{T}F_{002}\right) \left( q_{k_{*}}^\mathrm{T}F_{101}\right) \right) , \\ D_{111}= & {} -\frac{4}{3\pi \omega _{c}} \text{ Im }\left\{ \left( q_{0}^\mathrm{T}F_{110}\right) \left( q_{k_{*}}^\mathrm{T}F_{101} \right) \right\} ,\\ D_{003}= & {} -\frac{2}{3\pi \omega _{c} } \text{ Im }\left\{ \left( q_{0}^\mathrm{T}F_{002}\right) \left( q_{k_{*}}^\mathrm{T}F_{101}\right) \right\} , \end{aligned}$$

and

$$\begin{aligned} E_{210}= & {} \frac{1}{3\sqrt{\pi }}q_{0}^\mathrm{T}\left( \left( p_{01}f_{2000}+p_{02}f_{1100} \right) h^{(1)}_{0110}\right. \\&+\left( p_{02}f_{0200}+p_{01}f_{1100} \right) h^{(2)}_{0110} \\&+\left( \overline{p}_{01}f_{2000}+\overline{p}_{02}f_{1100} \right) h^{(1)}_{0200}\\&\left. +\left( \overline{p}_{02}f_{0200}+\overline{p}_{01}f_{1100} \right) h^{(2)}_{0200} \right) ,\\ E_{102}= & {} \frac{1}{3\sqrt{\pi }}q_{0}^\mathrm{T}\left( \left( p_{01}f_{2000}+p_{02}f_{1100} \right) h^{(1)}_{0002}\right. \\&+\left( p_{02}f_{0200}+p_{01}f_{1100} \right) h^{(2)}_{0002}\\&+\left( p_{k_{*}1}f_{2000}+p_{k_{*}2}f_{1100} \right) h^{(1)}_{k_{*}101}\nonumber \\&\left. +\left( p_{k_{*}2}f_{0200}+p_{k_{*}1}f_{1100} \right) h^{(2)}_{k_{*}101} \right) ,\\ E_{111}= & {} \frac{1}{3\sqrt{\pi }}q_{k_{*}}^\mathrm{T}\left( \left( p_{01}f_{2000}+p_{02}f_{1100}\right) h^{(1)}_{k_{*}011}\right. \\&+\left( p_{02}f_{0200}+p_{01}f_{1100}\right) h^{(2)}_{k_{*}011} \\&\left( \overline{p}_{01}f_{2000}+\overline{p}_{02}f_{1100} \right) h^{(1)}_{k_{*}101}\\&\left. +\left( \overline{p}_{02}f_{0200}+\overline{p}_{01}f_{1100} \right) h^{(2)}_{k_{*}101}\right) \\&+q_{k_{*}}^\mathrm{T}\left( \left( p_{k_{*}1}f_{2000}+p_{k_{*}2}f_{1100}\right) \right. \\&\left( \frac{1}{3\sqrt{\pi }}h_{0110}^{(1)}+ \frac{1}{3\sqrt{2\pi }}h_{(2k_{*})110}^{(1)}\right) \\&+\left( p_{k_{*}2}f_{0200}+p_{k_{*}1}f_{1100}\right) \\&\left. \left( \frac{1}{3\sqrt{\pi }}h_{0110}^{(2)}+ \frac{1}{3\sqrt{2\pi }}h_{(2k_{*})110}^{(2)}\right) \right) ,\\ E_{003}= & {} q_{k_{*}}^\mathrm{T}\left( \left( p_{k_{*}1}f_{2000}+p_{k_{*}2}f_{1100}\right) \right. \\&\left( \frac{1}{3\sqrt{\pi }}h_{0002}^{(1)}+\frac{1}{3\sqrt{2\pi }}h_{(2k_{*})002}^{(1)}\right) \\&+\left( p_{k_{*}2}f_{0200}+p_{k_{*}1}f_{1100}\right) \\&\left. \left( \frac{1}{3\sqrt{\pi }}h_{0002}^{(2)}+\frac{1}{3\sqrt{2\pi }}h_{(2k_{*})002}^{(2)}\right) \right) . \end{aligned}$$

where \(h^{(i)}_{jm_{1}m_{2}m_{3}}, (i=1,2, j=0, 2k_{*}, m_{l}=1, 2, l=1, 2,3)\) are given by

$$\begin{aligned}&h_{0200}=\frac{1}{\sqrt{\pi }}\left( 2i\omega _{c}I-\mathscr {M}_0\right) ^{-1}\\&\left( F_{200}-\left( q_{0}^\mathrm{T}F_{200}p_{0}+\bar{q}_{0}^\mathrm{T}F_{200}\bar{p}_{0}\right) \right) ,\\&h_{0020}=\frac{1}{\sqrt{\pi }}\left( -2i\omega _{c}I-\mathscr {M}_0\right) ^{-1}\\&\left( F_{020}-\left( q_{0}^\mathrm{T}F_{020}p_{0}+\bar{q}_{0}^\mathrm{T}F_{020}\bar{p}_{0}\right) \right) ,\\&h_{0002}=-\frac{1}{\sqrt{\pi }}\mathscr {M}_{0}^{-1}\\&\left( F_{002}-\left( q_0^\mathrm{T}F_{002}p_0+\bar{q}_0^\mathrm{T}F_{002}\bar{p}_{0}\right) \right) ,\\&h_{0110}=-\frac{2}{\sqrt{\pi }}\mathscr {M}_{0}^{-1}\\&\left( F_{110}-\left( q_0^\mathrm{T}F_{110}p_0+\bar{q}_0^\mathrm{T}F_{110}\bar{p}_{0}\right) \right) ,\\&h_{k_{*}101}=\frac{2}{\sqrt{\pi }}\\&\left( i\omega _{c}I-\mathscr {M}_{k_{*}}\right) ^{-1}\left( F_{101}-q_{k_{*}}^\mathrm{T}F_{101}p_{k_{*}}\right) ,\\&h_{k_{*}011}=\frac{2}{\sqrt{\pi }}\left( -i\omega _{c}I-\mathscr {M}_{k_{*}}\right) ^{-1}\\&\left( F_{011}-q_{k_{*}}^\mathrm{T}F_{011}p_{k_{*}}\right) ,\\&h_{(2k_{*})002}=-\frac{1}{\sqrt{2\pi }}\mathscr {M}_{2k_{*}}^{-1}F_{002},\,h_{(2k_{*})110}=(0, 0)^\mathrm{T}. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tang, X., Song, Y. & Zhang, T. Turing–Hopf bifurcation analysis of a predator–prey model with herd behavior and cross-diffusion. Nonlinear Dyn 86, 73–89 (2016). https://doi.org/10.1007/s11071-016-2873-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-2873-3

Keywords

Search

Navigation