1 Introduction

The dynamic relationship between predators and their preys has long been and will continue to be one of the dominant themes in both ecology and mathematical ecology due to its universal existence and importance. One of the familiar factors affecting the dynamics of predator-prey models is the functional response, which relates the single predator’s prey consumption rate to the prey population density. In general, functional response can be classified as: (1) prey-dependent, when the prey density alone determines the response [1, 2]; (2) predator-dependent, when both predator and prey populations affect the response [3, 4]; (3) multispecies-dependent, when species other than the focal predator and its prey species influence the functional response [5].

It is well known that delay differential equations exhibit much more complicated dynamics than ordinary differential equations since a time delay can induce various oscillations and periodic solutions. A great deal of research have been devoted to the delay models (see, e.g., [6–13] and references therein).

In nature, there are many species whose individual members have a life history that takes them through two stages, immature and mature. The single-species model with stage structure was studied by Aiello and Freedman [14]. Xu et al. [2] considered a ratio-dependent predator-prey model with stage structure for the prey. By constructing appropriate Lyapunov functions sufficient conditions are obtained for the global asymptotic stability of nonnegative equilibria of the model.

Motivated by the works of Chen and Jing [15], Wangersky and Cunningham [13], and Xu et al. [2, 16], we consider the following predator-prey model with Holling type-IV functional response

$$ \left \{ \textstyle\begin{array}{l} \dot{x}_{1}(t)=ax_{2}(t)-bx_{1}(t)-d_{1}x_{1}(t), \\ \dot{x}_{2}(t)= bx_{1}(t)-b_{1}x_{2}^{2}(t)-d_{2}x_{2}(t)-\frac {a_{1}x_{2}(t)y(t)}{m+x_{2}^{2}(t)}, \\ \dot{y}(t)= \frac{a_{2}x_{2}(t-\tau)y(t-\tau)}{m+x_{2}^{2}(t-\tau)}-dy(t). \end{array}\displaystyle \right . $$
(1.1)

In system (1.1), \(x_{1}(t)\) and \(x_{2}(t)\) represent the densities of the immature and mature preys at time t, respectively, and \(y(t)\) represents the density of the predator at time t.

The initial conditions for system (1.1) take the form

$$\begin{aligned}& x_{1}(\theta)=\phi_{1}(\theta),\qquad x_{2}(\theta)=\phi_{2}(\theta),\qquad y(\theta )=\psi( \theta), \\& \phi_{1}(\theta)\geq0,\qquad \phi_{2}(\theta)\geq0,\qquad \psi(\theta)\geq0,\quad \theta\in [-\tau,0], \\& \phi_{1}(0)>0,\qquad \phi_{2}(0)>0,\qquad \psi(0)>0, \end{aligned}$$
(1.2)

where \((\phi_{1}(\theta),\phi_{2}(\theta),\psi(\theta))\in C([-\tau ,0),{\mathrm{R}}^{3}_{+})\), the Banach space of continuous functions mapping the interval \([-\tau,0]\) into \({\mathrm{R}}^{3}_{+}=\{ (x_{1},x_{2},x_{3}):x_{i}\geq0,i = 1,2,3\}\).

By the fundamental theory of functional differential equations [17] we know that there is a unique solution \((x_{1}(t), x_{2}(t),y(t))\) to system (1.1) with initial conditions (1.2).

The organization of this paper is as follows. In Section 2, we give the stability analysis of feasible equilibria and find the existence of a Hopf bifurcation at the coexistence equilibrium. The stability and direction of periodic solutions bifurcating from Hopf bifurcations are established in Section 3. Finally, in order to illustrate the validity of the theoretical result, some numerical simulations are included.

2 Local stability and Hopf bifurcation

In this section, we consider the stability of all feasible equilibria and the existence of a Hopf bifurcation occurring at the coexistence equilibrium.

We denote \(A=\frac{2d[ab-d_{2}(b+d_{1})]}{b_{1}(b+d_{1})}\) and \(B=\sqrt {a_{2}^{2}-4d^{2}m}\). Then the equilibria of system (1.1) are as follows:

  1. (1)

    System (1.1) always has a trivial equilibrium \(E_{0}(0,0,0)\).

  2. (2)

    If

    $$ ab>d_{2}(b+d_{1}), $$
    (2.1)

    then system (1.1) has a predator-extinction equilibrium \(E_{1}(x_{1}^{0},x_{2}^{0},0)\), where

    $$x_{1}^{0}=\frac{a(ab-d_{2}(b+d_{1}))}{b_{1}(b+d_{1})^{2}},\qquad x_{2}^{0}= \frac{ab-d_{2}(b+d_{1})}{b_{1}(b+d_{1})}. $$
  3. (3)

    If in addition to condition (2.1),

    $$ a_{2}^{2}-4d^{2}m>0,\qquad A-B< a_{2}< A+B, $$
    (2.2)

    then system (1.1) has a unique coexistence equilibrium \(E^{\ast }(x_{1}^{\ast},x_{2}^{\ast},y^{\ast})\), where

    $$x_{1}^{\ast}=\frac{ax_{2}^{\ast}}{b+d_{1}}, \qquad x_{2}^{\ast}= \frac {a_{2}-\sqrt{a_{2}^{2}-4d^{2}m}}{2d},\qquad y^{\ast}=\frac{a_{2}x_{2}^{\ast}}{a_{1}d}\biggl( \frac {ab}{b+d_{1}}-d_{2}-b_{1}x_{2}^{\ast} \biggr). $$

Now, by analyzing the characteristic equations we begin to discuss the geometric properties of the equilibria of system (1.1).

Theorem 2.1

For system (1.1), we have the following:

  1. (i)

    If \(ab< d_{2}(b+d_{1})\), then the trivial equilibrium \(E_{0}\) is locally asymptotically stable; if (2.1) hold, then \(E_{0}\) is unstable.

  2. (ii)

    If (2.1) holds and

    $$ 2a_{2}A-A^{2}< 4d^{2}m, $$
    (2.3)

    then the predator-extinction equilibrium \(E_{1}\) is locally asymptotically stable; if (2.1) holds and

    $$ 2a_{2}A-A^{2}>4d^{2}m, $$
    (2.4)

    then \(E_{1}\) is unstable.

Proof

(i) For equilibrium \(E_{0}(0,0,0)\), the characteristic equation of system (1.1) is

$$ (\lambda+d)\bigl[\lambda^{2}+(b+d_{1}+d_{2}) \lambda+d_{2}(b+d_{1})-ab\bigr]=0. $$
(2.5)

The characteristic roots are \(\lambda_{1}=-d\), \(\lambda_{2}\), \(\lambda _{3}\), and \(\lambda_{2}+\lambda_{3}=-(b+d_{1}+d_{2})<0\), \(\lambda_{2}\lambda_{3}=d_{2}(b+d_{1})-ab\). It is easy to show that if \(ab< d_{2}(b+d_{1})\), then \(\lambda _{2}<0\), \(\lambda_{3}<0\); hence, \(E_{0}\) is locally asymptotically stable; if \(ab>d_{2}(b+d_{1})\), then Eq. (2.5) has one positive real root, and therefore \(E_{0}\) is unstable.

(ii) The characteristic equation of system (1.1) at the predator-extinction equilibrium \(E_{1}\) is given by

$$ \bigl[\lambda^{2}+\bigl(b+d_{1}+d_{2}+2b_{1}x_{2}^{0} \bigr)\lambda+ab-d_{2}(b+d_{1})\bigr] \biggl(\lambda+d- \frac{a_{2}x_{2}^{0}e^{-\lambda\tau }}{m+(x_{2}^{0})^{2}}\biggr)=0. $$
(2.6)

If (2.1) holds, then the equation

$$\lambda^{2}+\bigl(b+d_{1}+d_{2}+2b_{1}x_{2}^{0} \bigr)\lambda+ab-d_{2}(b+d_{1})=0 $$

has two roots with negative real parts, and other roots of (2.6) are given by the roots of \(g(\lambda)=\lambda+d-\frac{a_{2}x_{2}^{0}e^{-\lambda\tau }}{m+(x_{2}^{0})^{2}}=0\).

From (2.1) and (2.3) we have

$$g(0)=\frac{-1}{m+(x_{2}^{0})^{2}}\frac{2a_{2}A-A^{2}-4d^{2}m}{4d}< 0 \quad \mbox{and}\quad \lim _{\lambda\rightarrow+\infty} g(\lambda)=+\infty. $$

It follows from the continuity of the function g that the equation \(g(\lambda)=0\) has at least one positive real root. So \(E_{1}\) is unstable.

If (2.1) and (2.4) hold, then it is easy to show that \(g(0)>0\). By Theorem 3.2.1 in [12] we know that the equilibrium \(E_{1}\) is locally asymptotically stable for all \(\tau \geq0\). This completes the proof of Theorem 2.1. □

Theorem 2.2

Assume that (2.1) and (2.2) hold and that \((p_{2}+q_{2})(p_{1}+q_{1})>p_{0}+p_{0}\). If \(p_{0}>q_{0}\). Then the coexistence equilibrium \(E^{\ast}\) is locally asymptotically stable for all \(\tau>0\); if \(p_{0}< q_{0}\), then there exists a positive number \(\tau_{0}>0\) such that \(E^{\ast}\) is locally asymptotically stable if \(\tau\in[0,\tau_{0})\) and is unstable if \(\tau>\tau_{0}\). Further, system (1.1) undergoes a Hopf bifurcation at \(E^{\ast}\) when \(\tau=\tau_{0}\).

Proof

The characteristic equation of system (1.1) at \(E^{\ast}\) is

$$ \lambda^{3}+p_{2}\lambda^{2}+p_{1} \lambda+p_{0}+\bigl(q_{2}\lambda ^{2}+q_{1} \lambda+q_{0}\bigr)e^{-\lambda\tau}=0, $$
(2.7)

where

$$\begin{aligned}& p_{0}= d\biggl[(b+d_{1}) \biggl(d_{2}+2b_{1}x_{2}^{\ast}+ \frac{a_{1}y^{\ast }(m-(x_{2}^{\ast})^{2})}{(m+(x_{2}^{\ast})^{2})^{2}}-ab\biggr)\biggr], \\& p_{1}= d\biggl(b+d_{1}+d_{2}+2b_{1}x_{2}^{\ast}+ \frac{a_{1}y^{\ast }(m-(x_{2}^{\ast})^{2})}{(m+(x_{2}^{\ast})^{2})^{2}}\biggr) \\& \hphantom{p_{1}={}}{} +(b+d_{1}) \biggl(d_{2}+2b_{1}x_{2}^{\ast}+ \frac{a_{1}y^{\ast}(m-(x_{2}^{\ast })^{2})}{(m+(x_{2}^{\ast})^{2})^{2}}\biggr)-ab, \\& p_{2}= b+d_{1}+d_{2}+2b_{1}x_{2}^{\ast}+ \frac{a_{1}y^{\ast }(m-(x_{2}^{\ast})^{2})}{(m+(x_{2}^{\ast})^{2})^{2}}+d, \\& q_{0}= -d\bigl((b+d_{1}) \bigl(d_{2}+2b_{1}x_{2}^{\ast} \bigr)-ab\bigr), \\& q_{1}= -d\bigl(b+d_{1}+d_{2}+2b_{1}x_{2}^{\ast} \bigr), \qquad q_{2}=-d. \end{aligned}$$

When \(\tau=0\), (2.7) reduces to

$$\lambda^{3}+(p_{2}+q_{2})\lambda^{2}+(p_{1}+q_{1}) \lambda+p_{0}+p_{0}=0. $$

From (2.2) we derive that

$$\begin{aligned}& p_{0}+q_{0}=\frac{a_{1}dy^{\ast}(m-(x_{2}^{\ast })^{2})(b+d_{1})}{(m+(x_{2}^{\ast})^{2})^{2}}>0, \\& p_{2}+q_{2}=b+d_{1}+d_{2}+2b_{1}x_{2}^{\ast}+ \frac{a_{1}y^{\ast }(m-(x_{2}^{\ast})^{2})}{(m+(x_{2}^{\ast})^{2})^{2}}>0. \end{aligned}$$

By the Routh-Hurwitz criterion we see that the equilibrium \(E^{\ast}\) is locally asymptotically stable when \(\tau=0\).

When \(\tau>0\), let \(\lambda=i\omega\) (\(\omega>0\)) be a root of Eq. (2.7). Substituting it into Eq. (2.7) and separating real and imaginary parts yield

$$ \begin{aligned} &\omega^{3}-p_{1}\omega= \bigl(q_{2}\omega^{2}-q_{0}\bigr)\sin\omega\tau +q_{1}\omega\cos\omega\tau, \\ &{-}p_{2}\omega^{2}+p_{0}=\bigl(q_{2} \omega^{2}-q_{0}\bigr)\cos\omega\tau -q_{1}\omega \sin\omega\tau, \end{aligned} $$
(2.8)

which implies

$$ \omega^{6}+\bigl(p_{2}^{2}-2p_{1}-q_{2}^{2} \bigr)\omega^{4} +\bigl(p_{1}^{2}-2p_{0}p_{2}+2q_{0}q_{2}-q_{1}^{2} \bigr)\omega ^{2}+p_{0}^{2}-q_{0}^{2}=0. $$
(2.9)

Noting that

$$\begin{aligned}& p_{0}-q_{0}=d(b+d_{1})\biggl[2 \biggl(d_{2}+2b_{1}x_{2}^{\ast}- \frac{ab}{b+d_{1}}\biggr) +\frac{a_{1}y^{\ast}(m-(x_{2}^{\ast})^{2})}{(m+(x_{2}^{\ast })^{2})^{2}}\biggr], \\& p_{2}^{2}-2p_{1}-q_{2}^{2}=2ab+(b+d_{1})^{2}+ \frac {[(d_{2}+2b_{1}x_{2}^{\ast})(m+(x_{2}^{\ast})^{2})^{2} +a_{1}y^{\ast}(m-(x_{2}^{\ast})^{2})]^{2}}{(m+(x_{2}^{\ast})^{2})^{4}}, \end{aligned}$$

we have

$$\begin{aligned}& p_{1}^{2}-2p_{0}p_{2}+2q_{0}q_{2}-q_{1}^{2} \\& \quad = \biggl[(b+d_{1}) \biggl(d_{2}+2b_{1}x_{2}^{\ast} +\frac{a_{1}y^{\ast}(m-(x_{2}^{\ast})^{2})}{(m+(x_{2}^{\ast })^{2})^{2}}-ab\biggr)\biggr]^{2} \\& \qquad {}+\frac{d^{2}a_{1}y^{\ast}(m-(x_{2}^{\ast})^{2})}{(m+(x_{2}^{\ast })^{2})^{2}}\biggl[2\bigl(d_{2}+2b_{1}x_{2}^{\ast} \bigr) +\frac{a_{1}y^{\ast}(m-(x_{2}^{\ast})^{2})}{(m+(x_{2}^{\ast})^{2})^{2}}\biggr]. \end{aligned}$$

Therefore, if \(p_{0}>q_{0}\), then (2.9) has no positive real roots. By Theorem 3.4.1 in [12] we know that \(E^{\ast}\) is locally asymptotically stable for all \(\tau \geq0\). If \(p_{0}< q_{0}\), then (2.9) has a unique positive root \(\omega_{0}\), that is, (2.9) has a pair of purely imaginary roots \(i\omega_{0}\).

Denote

$$ \tau_{n}=\frac{1}{\omega_{0}}\arccos\frac{q_{1}\omega_{0}^{2}(\omega _{0}^{2}-p_{1}) +(q_{2}\omega_{0}^{2}-q_{0})(p_{0}-p_{2}\omega _{0}^{2})}{q_{1}^{2}\omega_{0}^{2} +(q_{2}\omega_{0}^{2}-q_{0})^{2}}+ \frac{2n\pi}{\omega_{0}},\quad n=0,1,2,\ldots. $$
(2.10)

By Theorem 3.4.1 in [12] we see that \(E^{\ast}\) is stable for \(\tau<\tau_{0}\).

Next, we turn to show that

$${\biggl.\frac{\mathrm{d}\operatorname{Re}\lambda}{\mathrm{d}\tau}\biggr|_{\tau=\tau_{0}}}>0. $$

This will signify that there exists at least one eigenvalue with a positive real part for \(\tau>\tau_{0}\). Differentiating (2.7) with respect to τ, we get

$$\biggl(\frac{\mathrm{d}\lambda}{\mathrm{d}\tau}\biggr)^{-1} =\frac{3\lambda^{2}+2p_{2}\lambda+p_{1}}{-\lambda(\lambda ^{3}+p_{2}\lambda^{2}+p_{1}\lambda+p_{0})} + \frac{2q_{2}\lambda+q_{1}}{\lambda(q_{2}\lambda^{2}+q_{1}\lambda +q_{0})}-\frac{\tau}{\lambda}. $$

By direct calculation we get that

$$\begin{aligned}& \operatorname{sgn} \biggl\{ \frac{\mathrm{d}\operatorname{Re}\lambda}{\mathrm{d}\tau}\biggr\} _{\lambda=i\omega_{0}} \\& \quad = \operatorname{sgn}\biggl\{ \operatorname{Re}\biggl(\frac{\mathrm{d}\lambda}{\mathrm{d}\tau} \biggr)^{-1}\biggr\} _{\lambda=i\omega_{0}} \\& \quad = \operatorname{sgn}\biggl\{ -\frac{(p_{1}-3\omega_{0}^{2})(\omega _{0}^{2}-p_{1})+2p_{2}(p_{0}-p_{2}\omega_{0}^{2})}{ (\omega_{0}^{3}-p_{1}\omega_{0})^{2}+(p_{0}-p_{2}\omega_{0}^{2})^{2}}- \frac{q_{1}^{2}-2q_{2}(q_{0}-q_{2}\omega_{0}^{2})}{(q_{0}-q_{2}\omega _{0}^{2})^{2}+q_{1}^{2}\omega_{0}^{2}}\biggr\} . \end{aligned}$$

Noting that

$$\bigl(\omega_{0}^{3}-p_{1}\omega_{0} \bigr)^{2}+\bigl(p_{0}-p_{2}\omega _{0}^{2}\bigr)^{2}=\bigl(q_{0}-q_{2} \omega_{0}^{2}\bigr)^{2}+q_{1}^{2} \omega_{0}^{2}, $$

it follows that

$$\operatorname{sgn}\biggl\{ \frac{\mathrm{d}\operatorname{Re}\lambda}{\mathrm{d}{\tau}}\biggr\} _{\lambda=i\omega_{0}} = \operatorname{sgn}\biggl\{ \frac{3\omega_{0}^{4}+2(p_{2}^{2}-2p_{1}-q_{2}^{2})\omega _{0}^{2}+p_{1}^{2} -2p_{0}p_{2}+2q_{0}q_{2}-q_{1}^{2}}{(q_{0}-q_{2}\omega _{0}^{2})^{2}+q_{1}^{2}\omega_{0}^{2}}\biggr\} >0. $$

Therefore, the transversal condition holds, and a Hopf bifurcation occurs at \(\omega=\omega_{0}\), \(\tau=\tau_{0}\). This completes the proof of Theorem 2.2. □

3 Stability of bifurcated periodic solutions

As pointed out in [18], it is interesting to determine the direction and stability of periodic solutions bifurcating from the positive equilibrium \(E^{*}\). In this section, we shall derive explicit formulae for determining the properties of the Hopf bifurcation at \(\tau_{0}\) by using the normal form theory and the center manifold theorem introduced by Hassard et al. [18].

Let \(\bar{x}_{1}(t)=x_{1}(t)-x_{1}^{\ast}\), \(\bar {x}_{2}(t)=x_{2}(t)-x_{2}^{\ast}\), \(\bar{y}(t)=y(t)-y^{\ast}\). Then system (1.1) becomes

$$ \left \{ \textstyle\begin{array}{l} \dot{\bar{x}}_{1}(t)= -(b+d_{1})\bar{x}_{1}(t)+a\bar{x}_{2}(t), \\ \dot{\bar{x}}_{2}(t)= b\bar{x}_{1}(t)+a_{21}\bar{x}_{2}(t)+a_{22}\bar{y}(t) +a_{23}\bar{x}_{2}^{2}(t)+a_{24}a_{1}\bar{x}_{2}^{3}(t) \\ \hphantom{\dot{\bar{x}}_{2}(t)={}}{} +a_{25}a_{1}\bar{x}_{2}(t)\bar{y}(t)+a_{26}a_{1}\bar{x}_{2}^{2}(t)\bar {y}(t), \\ \dot{\bar{y}}(t)= -d\bar{y}(t)+d\bar{y}(t-\tau)+a_{31}\bar {x}_{2}(t-\tau) +a_{32}\bar{x}_{2}^{2}(t-\tau)-a_{24}a_{2}\bar{x}_{2}^{3}(t-\tau) \\ \hphantom{\dot{\bar{y}}(t)={}}{} -a_{25}a_{2}\bar{x}_{2}(t-\tau)\bar{y}(t-\tau)-a_{26}a_{2}\bar {x}_{2}^{2}(t-\tau)\bar{y}(t-\tau), \end{array}\displaystyle \right . $$
(3.1)

where

$$\left \{ \textstyle\begin{array}{l} a_{21}=-c_{1}-\frac{a_{1}c_{3}}{c_{2}^{3}},\qquad a_{22}=\frac{-da_{1}}{a_{2}},\qquad a_{23}=-b_{1}+\frac{2c_{3}a_{1}x_{2}^{\ast}}{c_{2}^{4}} +\frac{a_{1}x_{2}^{\ast}y^{\ast}}{c_{2}^{3}}(c_{2}+4x_{2}^{\ast}), \\ a_{24}=\frac{2x_{2}^{\ast}y^{\ast}}{c_{2}^{3}}-(\frac{4(x_{2}^{\ast })^{2}}{c_{2}^{5}} -\frac{1}{c_{2}^{4}})c_{3}-\frac{2(x_{2}^{\ast})^{2}y^{\ast }}{c_{2}^{4}}(c_{2}+4x_{2}^{\ast}), \\ a_{25}=-\frac{m-(x_{2}^{\ast})^{2}}{c_{2}^{2}},\qquad a_{26}=\frac{x_{2}^{\ast}}{c_{2}^{2}}+\frac{2x_{2}^{\ast}(m-(x_{2}^{\ast })^{2})}{c_{2}^{3}}, \\ a_{31}=\frac{2a_{2}x_{2}^{\ast}y^{\ast}}{c_{2}^{2}}+\frac {a_{2}c_{3}}{c_{2}^{3}},\qquad a_{32}=-\frac{2a_{2}c_{3}x_{2}^{\ast}}{c_{2}^{4}}-\frac{a_{2}x_{2}^{\ast }y^{\ast}(c_{2}+4x_{2}^{\ast})}{c_{2}^{3}} \\ c_{1}=d_{2}+2b_{1}x_{2}^{\ast}+\frac{2a_{1}x_{2}^{\ast}y^{\ast }}{c_{2}^{2}},\qquad c_{2}=m+(x_{2}^{\ast})^{2}, \\ c_{3}=y^{\ast}(m^{2}-(x_{2}^{\ast})^{4}-2mx_{2}^{\ast}-2(x_{2}^{\ast})^{3}). \end{array}\displaystyle \right . $$

Let \(t=s\tau\), \(\bar{x}_{1}(s\tau)=\hat{x}_{1}(s)\), \(\bar{x}_{2}(s\tau )=\hat{x}_{2}(s)\), \(\bar{y}(s\tau)=\hat{y}(s)\), \(\tau=\tau_{0}+\mu\), \(\mu\in{\mathrm{R}}\), where \(\tau_{0}\) is defined by (2.10). We drop the hats for simplification of notation. Then system (3.1) is transformed into the following FDE in \(C=C([-1,0],{\mathrm{R}}^{3})\):

$$\left \{ \textstyle\begin{array}{l} \dot{x_{1}}(t)= (\tau_{0}+\mu)[-(b+d_{1})x_{1}(t)+ax_{2}(t)], \\ \dot{x_{2}}(t)= (\tau_{0}+\mu )[bx_{1}(t)+a_{21}x_{2}(t)+a_{22}y(t)+a_{23}x_{2}^{2}(t)+a_{24}a_{1}x_{2}^{3}(t) \\ \hphantom{\dot{x_{2}}(t)={}}{}+a_{25}a_{1}x_{2}(t)y(t)+a_{26}a_{1}x_{2}^{2}(t)y(t)], \\ \dot{y}(t)= (\tau_{0}+\mu )[-dy(t)+dy(t-1)+a_{31}x_{2}(t-1)+a_{32}x_{2}^{2}(t-1) \\ \hphantom{\dot{y}(t)={}}{}-a_{24}a_{2}x_{2}^{3}(t-1)-a_{25}a_{2}x_{2}(t-1)y(t-1)-a_{26}a_{2}x_{2}^{2}(t-1)y(t-1)]. \end{array}\displaystyle \right . $$

We rewrite this system in the matrix form

$$ \dot{x}(t)=L_{\mu}x_{t}+f(\mu,x_{t}). $$
(3.2)

where \(x(t)=(x_{1}(t),x_{2}(t),y(t))^{\mathrm{T}}\in{\mathrm{R}}^{3}\), and \(L_{\mu }:C\rightarrow{\mathrm{R}}^{3}\), \(f:{\mathrm{R}}\times C\rightarrow{\mathrm{R}}^{3}\) are given, respectively, as follows: for \(\phi(t)=(\phi_{1}(t),\phi_{2}(t),\phi_{3}(t))^{\mathrm{T}}\in C([-\tau ,0],{\mathrm{R}}^{3})\), we define

$$ L_{\mu}\phi=D_{1}\phi(0)+D_{2}\phi(-1) $$
(3.3)

and

$$ f(\mu,\phi)=(\tau_{0}+\mu)M, $$
(3.4)

where

$$ \begin{aligned} &D_{1}=(\tau_{0}+\mu)\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} -(b+d_{1}) & a & 0\\ b & a_{21} & a_{22}\\ 0 & 0 & -d \end{array}\displaystyle \right ), \qquad D_{2}=(\tau_{0}+ \mu)\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & a_{31}& d \end{array}\displaystyle \right ), \\ &M=\left ( \textstyle\begin{array}{@{}c@{}} 0\\ a_{23}\phi_{2}^{2}(0)+a_{24}a_{1}\phi_{2}^{3}(0)+a_{25}a_{1}\phi _{2}(0)\phi_{3}(0)+a_{26}a_{1}\phi_{2}^{2}(0)\phi_{3}(0)\\ a_{32}\phi_{2}^{2}(-1)-a_{24}a_{2}\phi_{2}^{3}(-1)-a_{25}a_{2}\phi _{2}(-1)\phi_{3}(-1)-a_{26}a_{2}\phi_{2}^{2}(-1)\phi_{3}(-1) \end{array}\displaystyle \right ). \end{aligned} $$
(3.5)

By the Riesz representation theorem there exists a matrix function \(\eta (\cdot,\mu):[-1,0] \rightarrow{\mathrm{R}}^{3}\) such that

$$ L_{\mu}(\phi)= \int_{-1}^{0}\mathrm{d}\eta(\theta,\mu)\phi(\theta) \quad \mbox{for } \phi\in C. $$
(3.6)

In fact, we can choose

$$ \eta(\theta,\mu)=D_{1}\delta(\theta)+D_{2}\delta(\theta+1), $$
(3.7)

where δ is the Dirac delta function. For \(\phi\in C^{1}([-1,0],{\mathrm{R}}^{3})\), define

$$ A(\mu)\phi(\theta)= \left \{ \textstyle\begin{array}{l@{\quad}l} \frac{\mathrm{d}\phi(\theta)}{\mathrm{d}\theta}, &-1\leq\theta< 0, \\ \int_{-1}^{0}\mathrm{d}\eta(s,\mu)\phi(s), &\theta=0 \end{array}\displaystyle \right . $$

and

$$ R(\mu)\phi(\theta)= \left \{ \textstyle\begin{array}{l@{\quad}l} 0, &-1\leq\theta< 0, \\ f(\mu,\theta), &\theta=0. \end{array}\displaystyle \right . $$

Hence, system (3.2) is equivalent to the operator equation

$$\dot{x}_{t}=A(\mu)x_{t}+R(\mu)x_{t}, $$

where \(x_{t}(t)=x(t+\theta)\) for \(\theta\in[-1,0]\).

For \(\psi\in C([-1,0],({\mathrm{R}}^{3})^{\ast})\), define

$$ A^{\ast}(\mu)\psi(s)= \left \{ \textstyle\begin{array}{l@{\quad}l} -\frac{\mathrm{d}\psi(s)}{\mathrm{d} s}, & 0< s\leq1, \\ \int_{-1}^{0}\mathrm{d}\eta(s,\mu)\psi(-s), & s=0, \end{array}\displaystyle \right . $$

and the bilinear inner product

$$ \langle\phi,\psi\rangle=\bar{\psi}^{\mathrm{T}}(0)\phi(0)- \int_{-1}^{0} \int_{\xi=0}^{\theta}\bar{\psi}^{\mathrm{T}}(\xi-\theta)\, \mathrm{d}\eta(\theta)\phi (\xi)\, \mathrm{d}\xi, $$
(3.8)

where \(\eta(\theta)=\eta(\theta,0)\). Then \(A(0)\) and \(A^{\ast}\) are adjoint operators.

By the discussion in Section 2 we know that \(\pm i\omega_{0}\tau_{0}\) are eigenvalues of \(A(0)\). Hence, they are also eigenvalues of \(A^{\ast}\).

Assume that \(q(\theta)=(1, q_{1}, q_{2})^{\mathrm{T}}e^{i\omega_{0}\tau _{0}\theta}\) is the eigenvector of \(A(0)\) corresponding to \(i\omega_{0}\tau_{0}\). Then \(A(0)q(\theta)=i\omega_{0}\tau_{0}q(\theta )\). From the definition of \(A(0)\) and from (3.3), (3.6), and (3.7), for \(q(-1)=q(0)e^{-i\omega_{0}\tau_{0}}\), we have

$$\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} -(b+d_{1}) & a & 0\\ b & a_{21} & a_{22}\\ 0 & 0 & -d \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} 1\\ q_{1}(0)\\ q_{2}(0) \end{array}\displaystyle \right ) =i\omega_{0}\tau_{0}\left ( \textstyle\begin{array}{@{}c@{}} 1\\ q_{1}(0)\\ q_{2}(0) \end{array}\displaystyle \right ). $$

Then we obtain

$$q_{1}=\frac{b+d_{1}+i\omega_{0}}{a},\qquad q_{2}=\frac{-a_{31}e^{-i\omega_{0}\tau_{0}}(b+d_{1}+i\omega _{0})}{a[de^{-i\omega_{0}\tau_{0}}-(d+i\omega_{0})]}. $$

Similarly, we can calculate the eigenvector \(q^{*}(s)=D(1,q_{1}^{*}, q_{2}^{*})^{\mathrm{T}}e^{i\omega_{0}\tau_{0}}\) of A corresponding to \(-i\omega_{0}\tau_{0}\), where

$$q^{\ast}_{1}=\frac{b+d_{1}-i\omega_{0}}{b},\qquad q^{\ast}_{2}= \frac{-a_{22}(b+d_{1}-i\omega_{0})}{b[de^{i\omega_{0}\tau _{0}}-(d-i\omega_{0})]}. $$

We normalize q and \(q^{*}\) by the condition \(\langle q^{*}(s), q(\theta)\rangle=1\). Clearly, \(\langle q^{*}(s), {q}(\theta)\rangle=0\). In order to ensure that \(\langle q^{*}(s), q(\theta)\rangle=1\), we need to determine the value of D. By (3.8) we can choose

$$\bar{D}=\bigl[1+q_{1}\bar{q}^{\ast}_{1}+q_{2} \bar{q}^{\ast }_{2}+\bigl(a_{31}q_{1} \bar{q}^{\ast}_{2} +dq_{2}\bar{q}^{\ast}_{2} \bigr)\tau_{0}e^{-i\omega_{0}\tau_{0}}\bigr]^{-1}. $$

In the following, we use the same notation as in [18], and using a computation similar to that of Wei and Ruan [19], we can obtain the coefficients that will be used for determining the important qualities:

$$\left \{ \textstyle\begin{array}{l} g_{20}=2\tau_{0}\bar{D}(k_{11}\bar{q}^{\ast}_{1}+k_{21}\bar{q}^{\ast}_{2}),\qquad g_{11}=\tau_{0}\bar{D}(k_{12}\bar{q}^{\ast}_{1}+k_{22}\bar{q}^{\ast }_{2}), \\ g_{02}=2\tau_{0}\bar{D}(k_{13}\bar{q}^{\ast}_{1}+k_{23}\bar{q}^{\ast}_{2}),\qquad g_{21}=2\tau_{0}\bar{D}(k_{14}\bar{q}^{\ast}_{1}+k_{24}\bar{q}^{\ast }_{2}), \end{array}\displaystyle \right . $$

where

$$\begin{aligned}& k_{11}= a_{23}q_{1}^{2}+a_{25}a_{1}q_{1}q_{2}, \\& k_{12}= 2a_{23}q_{1}\bar{q}_{1}+a_{25}a_{1}(q_{1} \bar{q}_{2}+q_{2}\bar {q}_{1}), \\& k_{13}= a_{23}\bar{q}_{1}^{2}+a_{25}a_{1} \bar{q}_{1}\bar{q_{2}}, \\& k_{14}= a_{23}\bigl[\bar {q}_{1}W_{20}^{(2)}(0)+2q_{1}W_{11}^{(2)}(0) \bigr]+3a_{24}a_{1}q_{1}^{2} \bar{q}_{1} +a_{26}a_{1}\bigl(q_{1}^{2} \bar{q}_{2}+2q_{1}q_{2}\bar{q}_{1}\bigr) \\& \hphantom{k_{14}={}}{} +a_{25}a_{1}\biggl[\frac{1}{2} \bar{q}_{2}W_{20}^{(2)}(0)+q_{2}W_{11}^{(2)}(0) +\frac{1}{2}\bar{q}_{1}W_{20}^{(3)}(0)+q_{1}W_{11}^{(3)}(0) \biggr], \\& k_{21}= \bigl(a_{32}q_{1}^{2}-a_{25}a_{2}q_{1}q_{2} \bigr)e^{-2i\omega_{0}\tau _{0}}, \\& k_{22}= \bigl[2a_{32}q_{1}\bar{q}_{1}-a_{25}a_{2}(q_{1} \bar {q}_{2}+q_{2}\bar{q_{1}})\bigr]e^{-2i\omega_{0}\tau_{0}}, \\& k_{23}= \bigl(a_{32}\bar{q}_{1}^{2}-a_{25}a_{2} \bar{q}_{1}\bar {q}_{2}\bigr)e^{-2i\omega_{0}\tau_{0}}, \\& k_{24}= a_{32}\bigl[\bar {q}_{1}W_{20}^{(2)}(-1)+2q_{1}W_{11}^{(2)}(-1) \bigr]e^{-i\omega_{0}\tau_{0}} -3a_{24}a_{2}q_{1}^{2} \bar{q}_{1}e^{-3i\omega_{0}\tau_{0}} \\& \hphantom{k_{24}={}}{} -a_{26}a_{2}\bigl(q_{1}^{2} \bar{q}_{2}+2q_{1}q_{2}\bar{q}_{1} \bigr)e^{-3i\omega _{0}\tau_{0}} \\& \hphantom{k_{24}={}}{} -a_{25}a_{2}\biggl[\frac{1}{2}W_{20}^{(2)}(-1) \bar{q}_{2}+q_{2}W_{11}^{(2)}(-1) + \frac{1}{2}\bar {q}_{1}W_{20}^{(3)}(-1)+q_{1}W_{11}^{(3)}(-1) \biggr]e^{-i\omega_{0}\tau_{0}} \end{aligned}$$

and

$$\left \{ \textstyle\begin{array}{l} W_{20}(\theta)=\frac{ig_{20}}{\omega_{0}\tau_{0}}q(0)e^{i\omega_{0}\tau _{0}\theta} +\frac{i\bar{g}_{02}}{3\omega_{0}\tau_{0}}\bar{q}(0)e^{-i\omega_{0}\tau _{0}\theta} +E_{1}e^{2i\omega_{0}\tau_{0}\theta}, \\ W_{11}(\theta)=-\frac{ig_{11}}{\omega_{0}\tau_{0}}q(0)e^{i\omega _{0}\tau_{0}\theta} +\frac{i\bar{g}_{11}}{\omega_{0}\tau_{0}}\bar{q}(0)e^{-i\omega_{0}\tau _{0}\theta}+E_{2}. \end{array}\displaystyle \right . $$

Moreover \(E_{1}\) and \(E_{2}\) satisfy the following equations:

$$\begin{aligned}& \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 2i\omega_{0}+(b+d_{1}) & -a & 0\\ -b & 2i\omega_{0}-a_{21} & -a_{22}\\ 0 & -a_{31}e^{-2i\omega_{0}\tau_{0}} & 2i\omega_{0}-d-de^{-2i\omega _{0}\tau_{0}} \end{array}\displaystyle \right )E_{1}=2\left ( \textstyle\begin{array}{@{}c@{}} 0\\ k_{11}\\ k_{21} \end{array}\displaystyle \right ), \\& \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} b+d_{1} & -a & 0\\ -b & -a_{21} & -a_{22}\\ 0 & -a_{31} & 0 \end{array}\displaystyle \right )E_{2}=\left ( \textstyle\begin{array}{@{}c@{}} 0\\ k_{12}\\ k_{22} \end{array}\displaystyle \right ). \end{aligned}$$

Furthermore, \(g_{ij}\) is expressed by the parameters and delay in (1.1). Thus, we can compute the following values:

$$ \left \{ \textstyle\begin{array}{l} C_{1}(0)=\frac{i}{2\omega_{0}\tau_{0}}(g_{20}g_{11}-2|g_{11}|^{2}-\frac {|g_{02}|^{2}}{3})+\frac{g_{21}}{2}, \\ \mu_{2}=-\frac{\operatorname{Re}\{C_{1}(0)\}}{\operatorname{Re}\{\frac{\mathrm{d}\lambda (\tau_{0})}{\mathrm{d}\tau}\}}, \\ \beta_{2}=2\operatorname{Re}\{C_{1}(0)\}, \\ T_{2}=\frac{\operatorname{Im}\{C_{1}(0)\}+\mu_{2}\operatorname{Im}\{\frac{\mathrm{d}\lambda (\tau_{0})}{\mathrm{d}\tau}\}}{\omega_{0}\tau_{0}},\quad k=0,1,2,\ldots. \end{array}\displaystyle \right . $$
(3.9)

By the result of Hassard et al. [18] we have the following theorem.

Theorem 3.1

In view of (3.9), the following results hold:

  1. (i)

    the sign of \(\mu_{2}\) determines the directions of the Hopf bifurcation: if \(\mu_{2}>0\) (\(\mu_{2}<0\)), then the Hopf bifurcation is supercritical (subcritical) and the bifurcating periodic solutions exist for \(\tau>\tau^{*}\) (\(\tau<\tau_{0}\));

  2. (ii)

    the sign of \(\beta_{2}\) determines the stability of the bifurcating periodic solutions: the bifurcating periodic solutions are stable (unstable) if \(\beta _{2}<0\) (\(\beta_{2}>0\));

  3. (iii)

    the sign of \(T_{2}\) determines the period of the bifurcating periodic solutions: the period is increasing (decreasing) if \(\beta_{2}>0\) (\(\beta_{2}<0\)).

4 Computer simulations

In this section, we present some numerical results for system (1.1).

In (1.1), let \(a=9\), \(b=1/2\), \(a1=22\), \(a2=20\), \(b1=8\), \(d1=d2=1/8\), \(d=1/3\), \(m=8\). It is easy to show that (2.1) and (2.2) hold. Hence, system (1.1) has a unique coexistence equilibrium \(E^{\ast}(1.9243,0.1336,2.1889)\).

By calculation we have \(\tau_{0}\approx3.13\), \(C_{1}(0)\approx0.0030 - 0.0758i\), \(\mu_{2}\approx-0.00016215<0\), \(\beta_{2}\approx0.0060>0\), \(T_{2}\approx0.0871>0\).

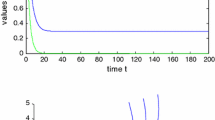
By Theorem 2.2, \(E^{\ast}\) is locally asymptotically stable if \(0<\tau <\tau_{0}\) and is unstable if \(\tau>\tau_{0}\), and system (1.1) undergoes a Hopf bifurcation at \(E^{\ast}\). When \(\tau =\tau_{0}\), we know that the bifurcation is subcritical and the bifurcating periodic solution is unstable (see Figure 1). With the increase of the delays, system (1.1) shows complicated dynamical behaviors. A numerical simulation illustrates this fact (see Figure 2).

Figure 1
figure 1

\(\pmb{\tau=3<\tau_{0}}\) , \(\pmb{E^{\ast}}\) is locally asymptotically stable.

Full size image
Figure 2
figure 2

\(\pmb{\tau=3.2>\tau_{0}}\) , \(\pmb{E^{\ast}}\) is unstable.

Full size image