An inertial extrapolation method for multiple-set split feasibility problem

Abstract

In this paper, we propose an iterative algorithm with inertial extrapolation to approximate the solution of multiple-set split feasibility problem. Based on Lopez et al. (Inverse Probl. 28(8):085004, 2012), we have developed a self-adaptive technique to choose the stepsizes such that the implementation of our algorithm does not need any prior information about the operator norm. We then prove the strong convergence of a sequence generated by our algorithm. We also present numerical examples to illustrate that the acceleration of our algorithm is effective.

1 Introduction

Throughout the paper, unless otherwise stated, we assume $H_{1}$ and $H_{2}$ are two real Hilbert spaces, and $A:H_{1}\rightarrow H_{2}$ is a bounded linear operator.

The split feasibility problem (SFP) is a problem of finding a point x̄ with a property

$$ \bar{x}\in C\quad \text{such that } A\bar{x}\in Q, $$

(1)

where C and Q are nonempty closed convex subsets of $H_{1}$ and $H_{2}$, respectively. The SFP was first introduced in 1994 by Censor and Elfving [2] for modeling inverse problems in finite-dimensional Hilbert spaces which arise from phase retrievals and in medical image reconstruction. Many projection methods have been developed for solving the SFP, see [3–7] and the references therein. The SFP has broad theoretical applications in many fields such as approximation theory [8], control [9], etc., and it plays an important role in the study of signal processing, image reconstruction, intensity-modulated radiation therapy, etc. [3, 4, 10, 11].

The original algorithm by Censor and Elfving [2] involves the computation of the inverse of A per each iteration assuming the existence of the inverse of A, and thus has not become popular. A seemingly more popular algorithm that solves the SFP is the CQ algorithm by Byrne [11] which is found to be a gradient-projection method (GPM) in convex minimization. It is also a special case of the proximal forward–backward splitting method [12]. The CQ algorithm starts with any $x_{1}\in H_{1}$ and generates a sequence $\{x_{n}\}$ through the iteration

$$ x_{n+1}=P_{C}\bigl(I-\gamma _{n} A^{*}(I-P_{Q})A\bigr)x_{n}, $$

where $\gamma _{n}\in (0,\frac{2}{\|A\|^{2}})$ (where $\|A\|^{2}$ is the the spectral radius of the operator $A^{*}A$), $P_{C}$ and $P_{Q}$ denote the metric projections of $H_{1}$ and $H_{2}$ onto C and Q, respectively, $A^{*}$ denotes the adjoint operator of A, and I stands for the identity mapping in $H_{1}$ and $H_{2}$. Many of the SFP findings are continuation of the study on the CQ algorithm, see, for example, [3, 4, 13–17]. An important advantage of the CQ algorithm by Byrne [11] and its continuation of studies is that computation of inverse of A (matrix inverses) is not necessary, but the implementation of the algorithm requires prior knowledge of the operator norm. However, operator norm is a global invariant and is often difficult to estimate, see, for example, a theorem of Hendrickx and Olshevsky in [18]. Moreover, the computation of a projection onto a closed convex subset is generally difficult. To overcome this difficulty, Fukushima [19] suggested a way to calculate the projection onto a level set of a convex function by computing a sequence of projections onto half-spaces containing the original level set. This idea is applied to solve SFPs in the finite-dimensional and infinite-dimensional Hilbert space setting by Yang [20] and Lopez et al. [1], respectively, and see more recent split type problems in this direction, for example, [21, 22] and the references therein. They considered SFPs in which the involved sets C and Q are given as sublevel sets of convex functions, i.e.,

$$ C=\bigl\{ x\in H_{1}:c(x)\leq 0\bigr\} \quad \text{and} \quad Q=\bigl\{ y\in H_{2}:q(y)\leq 0\bigr\} , $$

(2)

where $c:H_{1}\rightarrow \mathbb{R}$ and $q:H_{2}\rightarrow \mathbb{R}$ are convex and subdifferentiable functions on $H_{1}$ and $H_{2}$, respectively, and that ∂c and ∂q are bounded operators (i.e., bounded on bounded sets). Yang introduced a relaxed CQ algorithm

$$ x_{n+1}=P_{C_{n}}\bigl(x_{n}-\gamma _{n} A^{*}(I-P_{Q_{n}})A(x_{n})\bigr), $$

(3)

where $\gamma _{n}=\gamma \in (0,\frac{2}{L})$, L denotes the largest eigenvalue of matrix $A^{*}A$, for each $n\in \mathbb{N}$ the set $C_{n}$ is given by

$$ C_{n}=\bigl\{ x\in H_{1}:c(x_{n}) \leq \langle \xi _{n},x_{n}-x\rangle \bigr\} $$

(4)

for $\xi _{n}\in \partial c(x_{n})$, and the set $Q_{n}$ is given by

$$ Q_{n}=\bigl\{ y\in H_{2}:q(Ax_{n}) \leq \langle \varepsilon _{n},Ax_{n}-y \rangle \bigr\} $$

(5)

for $\varepsilon _{n}\in \partial q(Ax_{n})$. Obviously, $C_{n}$ and $Q_{n}$ are half-spaces and $C\subset C_{n}$ and $Q\subset Q_{n}$ for every $n\geq 1$. More important, since the projections onto $C_{n}$ and $Q_{n}$ have closed form, the relaxed CQ algorithm is now easily implemented. The specific form of the metric projections onto $C_{n}$ and $Q_{n}$ can be found in [23]. Moreover, Lopez et al. [1] introduced a new way of selecting the stepsizes for solving SFP (1) such that the information of operator norm is not necessary. To be precise, Lopez et al. [1] replaced the parameter $\gamma _{n}$ which appeared in (3) by

$$ \gamma _{n}=\frac{\rho _{n}f(x_{n})}{ \Vert \nabla f(x_{n}) \Vert ^{2}}, \quad \forall n\geq 1, $$

where $\rho _{n}\in (0,4)$, $f(x_{n})=\frac{1}{2}\|(I-P_{Q_{n}})Ax_{n}\|^{2}$ and $\nabla f(x_{n})=A^{*}(I-P_{Q_{n}})Ax_{n}$.

The most recent and prototypical split problem is presented by Censor et al. [24] and is called the split inverse problem (SIP) formulated as follows:

$$\begin{aligned}& \text{find a point } \bar{x}\in X \text{ that solves (IP1)} \\& \text{such that} \\& \text{the point } \bar{y}=A(\bar{x})\in Y \text{ solves (IP2)}, \end{aligned}$$

where IP1 is a problem set in space X, IP2 is a problem set in space Y and $A:X\rightarrow Y$ is a bounded linear mapping. Many inverse problems can be modeled in this framework by choosing different problems for IP1 and IP2, and numerous results in this area were developed in the recent decades, for example, see [25–30] and the references therein.

In this paper, we are concerned with a problem in the framework of SIP, called multiple-set split feasibility problem (MSSFP), which was introduced by Censor et al. [27] and is formulated as a problem of finding a point

$$ \bar{x}\in \bigcap_{i=1}^{N}C_{i} \quad \text{such that } A\bar{x}\in \bigcap_{j=1}^{M}Q_{j}, $$

(6)

where $\{C_{1},\ldots , C_{N}\}$ and $\{Q_{1},\ldots , Q_{M}\}$ are nonempty closed convex subsets of $H_{1}$ and $H_{2}$, respectively. Denote by Ω the set of solutions for (6). The MSSFP (6) with $N=M=1$ is the SFP (1). For solving the MSSFP (6), many methods have been developed, see, for example, in [27, 31–42] and the references therein.

Inspired by Yang [20] and Lopez et al. [1], we are interested in solving MSSFP in which the involved sets $C_{i}$ ($i\in \{1,\ldots ,N\}$) and $Q_{j}$ ($j\in \{1, \ldots ,M\}$) are given as sublevel sets of convex functions, i.e.,

$$ C_{i}=\bigl\{ x\in H_{1}:c_{i}(x) \leq 0\bigr\} \quad \text{and}\quad Q_{j}=\bigl\{ y\in H_{2}:q_{j}(y) \leq 0\bigr\} , $$

(7)

where $c_{i}:H_{1}\rightarrow \mathbb{R}$ and $q_{j}:H_{2}\rightarrow \mathbb{R}$ are convex functions for all $i\in \{1,\ldots ,N\}$, $j\in \{1,\ldots ,M\}$. We assume that both $c_{i}$ and $q_{j}$ are subdifferentiable on $H_{1}$ and $H_{2}$, respectively, and that $\partial c_{i}$ and $\partial q_{j}$ are bounded operators (i.e., bounded on bounded sets). In what follows, we define $N+M$ half-spaces at point $x_{n}$ by

$$ C_{i,n}=\bigl\{ x\in H_{1}:c_{i}(x_{n}) \leq \langle \xi _{i,n},x_{n}-x \rangle \bigr\} , $$

(8)

where $\xi _{i,n}\in \partial c_{i}(x_{n})$, and

$$ Q_{j,n}=\bigl\{ y\in H_{2}:q_{j}(Ax_{n}) \leq \langle \varepsilon _{j,n},Ax_{n}-y \rangle \bigr\} , $$

(9)

where $\varepsilon _{j,n}\in \partial q_{j}(Ax_{n})$.

In various disciplines, for example, in economics and control theory [43, 44], problems arise in infinite-dimensional spaces. In such problems, norm convergence is often much more desirable than weak convergence, for it translates the physically tangible property that the energy $\|x_{n}-p\|$ of the error between the iterate $x_{n}$ and a solution p eventually becomes arbitrarily small. More about the importance of strong convergence in a minimization problem via the proximal-point algorithm is underlined in [45].

The classical iteration can only provide weak convergence within an infinite-dimensional space. But strong convergence is the one that’s most wanted. Since it plays a key role in the strong convergence, we put the viscosity term for iteration, see, for example, [46]. It is well known that the inertial method greatly enhances algorithm efficiency and has good convergence properties [38, 47–49].

This paper contributes a strongly convergent iterative algorithm for MSSFP with inertial effect (extrapolated point $x_{n}+\alpha _{n}(x_{n}-x_{n-1})$, rather than $x_{n}$ itself) in the direction of half-space relaxation (assuming $C_{i}$ and $Q_{j}$ are given as sublevel sets of convex functions (7)) where the projection onto half-spaces (8) and (9) is computed in parallel and a priori knowledge of the operator norm is not required. For this purpose, we introduce the extended form of the way of selecting stepsize used by Lopez et al. [1], to work for MSSFP framework, and we analyze the strong convergence of our proposed algorithm.

2 Preliminary

In this paper, the symbols “⇀” and “→” stand for the weak and strong convergence, respectively.

Let C be a nonempty closed convex subset of a real Hilbert space H. The metric projection on C is a mapping $P_{C} : H\rightarrow {C}$ defined by

$$ P_{C}(x) =\arg \min \bigl\{ \Vert y-x \Vert :y\in {C}\bigr\} , \quad x\in H. $$

Lemma 2.1

Let C be a closed convex subset of H. Given $x\in H$ and a point $z\in C$, $z=P_{C}(x)$ if and only if

$$ \langle x-z, y-z\rangle \leq 0, \quad \forall y\in C. $$

More properties of the metric projection can be found in [50].

Definition 2.2

The mapping $T:H\rightarrow H$ is said to be

• (i) γ-contraction if there exists a constant $\gamma \in [0,1)$ such that

  $$ \bigl\Vert T(x)-T(y) \bigr\Vert \leq \gamma \Vert x-y \Vert , \quad \forall x,y\in H; $$

• (ii) firmly nonexpansive if

  $$ \Vert Tx-Ty \Vert ^{2}\leq \Vert x-y \Vert ^{2}- \bigl\Vert (I-T)x-(I-T)y \bigr\Vert ^{2}, \quad \forall x,y\in H, $$

  which is equivalent to

  $$ \Vert Tx-Ty \Vert ^{2}\leq \langle Tx-Ty,x-y\rangle , \quad \forall x,y\in H. $$

If T is firmly nonexpansive, $I-T$ is also firmly nonexpansive. The metric projection $P_{C}$ on a closed convex subset C of H is firmly nonexpansive.

Definition 2.3

The subdifferential of a convex function $f:H\rightarrow \mathbb{R}$ at $x\in H$, denoted by $\partial f(x)$, is defined by

$$ \partial f(x)=\bigl\{ \xi \in H:f(z)\geq f(x)+\langle \xi ,z-x \rangle , \forall z\in H\bigr\} . $$

If $\partial f(x)\neq \emptyset$, f is said to be subdifferentiable at x. If the function f is continuously differentiable, then $\partial f(x)=\{\nabla f(x)\}$, this is the gradient of f.

Definition 2.4

The function $f:H\rightarrow \mathbb{R}$ is called weakly lower semicontinuous at $x_{0}$ if for a sequence $\{x_{n}\}$ weakly converging to $x_{0}$ one has

$$ \liminf_{n\rightarrow \infty }f(x_{n})\geq f(x_{0}). $$

A function which is weakly lower semicontinuous at each point of H is called weakly lower semicontinuous on H.

Lemma 2.5

([3, 51])

Let $H_{1}$ and $H_{2}$ be real Hilbert spaces and $f:H_{1}\rightarrow \mathbb{R}$ be given by $f(x)=\frac{1}{2}\|(I-P_{Q})Ax\|^{2}$ where Q is a closed convex subset of $H_{2}$ and $A:H_{1}\rightarrow H_{2}$ is a bounded linear operator. Then

• (i) the function f is convex and weakly lower semicontinuous on $H_{1}$;

• (ii) $\nabla f(x)=A^{*}(I-P_{Q})Ax$, for $x\in H_{1}$;

• (iii) ∇f is $\|A\|^{2}$-Lipschitz, i.e., $\|\nabla f(x)-\nabla f(y)\|\leq \|A\|^{2}\|x-y\|$, $\forall x,y\in H_{1}$.

Lemma 2.6

([52])

Let H be a real Hilbert space. Then, for all $x,y\in H$ and $\alpha \in \mathbb{R,}$, we have

• (i) $\|\alpha x+(1-\alpha )y\|^{2}=\alpha \|x\|^{2}+(1-\alpha )\|y\|^{2}- \alpha (1-\alpha )\|x-y\|^{2}$;

• (ii) $\|x+y\|^{2}=\|x\|^{2}+\|y\|^{2}+2\langle x,y \rangle$;

• (iii) $\|x+y\|^{2}\leq \|x\|^{2}+2\langle y,x+y \rangle$;

• (iv) $\langle x,y\rangle = \frac{1}{2}\|x\|^{2}+ \frac{1}{2}\|y\|^{2}-\frac{1}{2}\|x-y\|^{2}$, $\forall x,y\in H$.

Lemma 2.7

([53, 54])

Let $\{c_{n}\}$ and $\{\alpha _{n}\}$ be a sequences of nonnegative real numbers, $\{\beta _{n}\}$ be a sequences of real numbers such that

$$ c_{n+1}\leq (1-\alpha _{n})c_{n}+\beta _{n}, \quad n\geq 1, $$

where $0<\alpha _{n}< 1$.

• (i) If $\beta _{n}\leq \alpha _{n}L$ for some $L\geq 0$, then $\{c_{n}\}$ is a bounded sequence.

• (ii) If $\sum \alpha _{n}=\infty$ and $\limsup_{n\rightarrow \infty }\frac{\beta _{n}}{\alpha _{n}} \leq 0$, then $c_{n}\rightarrow 0$ as $n\rightarrow \infty$.

Definition 2.8

Let $\{\Gamma _{n}\}$ be a real sequence. Then, $\{\Gamma _{n}\}$ decreases at infinity if there exists $n_{0}\in \mathbb{N}$ such that $\Gamma _{n+1}\leq \Gamma _{n}$ for $n\geq n_{0}$. In other words, the sequence $\{\Gamma _{n}\}$ does not decrease at infinity, if there exists a subsequence $\{\Gamma _{n_{t}}\}_{t\geq 1}$ of $\{\Gamma _{n}\}$ such that $\Gamma _{n_{t}}<\Gamma _{n_{t}+1}$ for all $t\geq 1$.

Lemma 2.9

([55])

Let $\{\Gamma _{n}\}$ be a sequence of real numbers that does not decrease at infinity. Also consider the sequence of integers $\{\varphi (n)\}_{n\geq n_{0}}$ defined by

$$ \varphi (n)=\max \{k\in \mathbb{N}:k\leq n,\Gamma _{k}\leq \Gamma _{k+1} \}. $$

Then $\{\varphi (n)\}_{n\geq n_{0}}$ is a nondecreasing sequence verifying $\lim_{n\rightarrow \infty }\varphi (n)=\infty$, and for all $n\geq n_{0}$, the following two estimates hold:

$$ \Gamma _{\varphi (n)}\leq \Gamma _{\varphi (n)+1}\quad \textit{and}\quad \Gamma _{n}\leq \Gamma _{\varphi (n)+1}. $$

3 Main result

Motivated by Lopez et al. [1], we introduce the following setting. For $x\in H_{1}$,

• (1) for each $i\in \{1,\ldots ,N\}$ and $n\geq 1$, define

  $$ g_{i,n}(x)=\frac{1}{2} \bigl\Vert (I-P_{C_{i,n}})x \bigr\Vert ^{2}\quad \text{and}\quad \nabla g_{i,n}(x)=(I-P_{C_{i,n}})x, $$

• (2) $g_{n}(x)$ and $\nabla g_{n}(x)$ are defined as $g_{n}(x)=g_{i_{x},n}(x)$ and so $\nabla g_{n}(x)=\nabla g_{i_{x},n}(x)$ where $i_{x}\in \{1,\ldots ,N\}$ is such that for each $n\geq 1$,

  $$ i_{x}\in \arg \max \bigl\{ g_{i,n}(x): i\in \{1,\ldots ,N\} \bigr\} , $$

• (3) for each $j\in \{1,\ldots ,M\}$ and $n\geq 1$, define

  $$ f_{j,n}(x)=\frac{1}{2} \bigl\Vert (I-P_{Q_{j,n}})Ax \bigr\Vert ^{2}\quad \text{and}\quad \nabla f_{j,n}(x)=A^{*}(I-P_{Q_{j,n}})Ax. $$

We can easily see that the functions (see Aubin [51]) $g_{i,n}$ and $f_{j,n}$ are convex, weakly lower semicontinuous and differentiable for each $i\in \{1,\ldots ,N\}$ and $j\in \{1,\ldots ,M\}$. Using the definitions of $\nabla g_{i,n}$, $g_{i,n}$, $g_{n}$, $\nabla g_{n}$, $f_{j,n}$, and $\nabla f_{j,n}$ given in (1)–(3), we are now in a position to introduce our algorithm and, assuming that the solution set Ω of the MSSFP (6) is nonempty, we analyze the strong convergence of our Algorithm 1.

Algorithm 1

Algorithm for solving the MSSFP

Remark 3.1

In Algorithm 1, if $\|\nabla g_{n}(y_{n})+\nabla f_{j,n}(y_{n})\|=0$ and $y_{n}=x_{n}$, $j\in \{1,\ldots ,M\}$, then $x_{n}$ is the solution of the MSSFP (6) and the iterative process stops, otherwise, we set $n:=n+1$ and repeat the iteration.

Theorem 3.2

If the parameters $\{\delta _{j,n}\}$ ($j\in \{1,\ldots ,M\}$), $\{\rho _{n}\}$, $\{\alpha _{n}\}$, $\{\theta _{n}\}$ in Algorithm 1 satisfy the following conditions:

• (C1) $0<\liminf_{n\rightarrow \infty } \delta _{j,n}\leq \limsup_{n\rightarrow \infty } \delta _{j,n}< 1$ for $j\in \{1,\ldots ,M\}$ and $\sum_{j=1}^{M}\delta _{j,n}=1$,

• (C2) $0<\alpha _{n}<1$, $\lim_{n\rightarrow \infty }\alpha _{n}=0$ and $\sum_{n=1}^{\infty }\alpha _{n}=\infty$,

• (C3) $0\leq \theta _{n}\leq \theta <1$ and $\lim_{n\rightarrow \infty }\frac{\theta _{n}}{\alpha _{n}}\|x_{n}-x_{n-1} \|=0$,

• (C4) $0<\rho _{n}<4$ and $\liminf_{n\rightarrow \infty }\rho _{n}(4-\rho _{n})>0$,

then the sequence $\{x_{n}\}$ generated by Algorithm 1 converges strongly to $\bar{x}\in \Omega$.

Proof

Let $\bar{x}\in \Omega$. Since $I-P_{C_{i,n}}$ and $I-P_{Q_{j,n}}$ are firmly nonexpansive, and since x̄ verifies (6), we have for all $x\in H_{1}$,

$$\begin{aligned} \bigl\langle \nabla g_{i,n}(x),x-\bar{x} \bigr\rangle {}=&\bigl\langle (I-P_{C_{i,n}})x,x-\bar{x} \bigr\rangle \\ {}\geq & \bigl\Vert (I-P_{C_{i,n}})x \bigr\Vert ^{2}=2g_{i,n}(x) \end{aligned}$$

(10)

and

$$\begin{aligned} \bigl\langle \nabla f_{j,n}(x),x-\bar{x} \bigr\rangle {}=&\bigl\langle A^{*}(I-P_{Q_{j,n}})Ax,x- \bar{x} \bigr\rangle \\ {}=&\bigl\langle (I-P_{Q_{j,n}})Ax,Ax-A\bar{x} \bigr\rangle \\ {}\geq & \bigl\Vert (I-P_{Q_{j,n}})Ax \bigr\Vert ^{2}=2f_{j,n}(x). \end{aligned}$$

(11)

Now from the definition of $y_{n}$, we get

$$\begin{aligned} \Vert y_{n}-\bar{x} \Vert =& \bigl\Vert x_{n}+\theta _{n}(x_{n}-x_{n-1})- \bar{x} \bigr\Vert \\ \leq & \Vert x_{n}-\bar{x} \Vert +\theta _{n} \Vert x_{n}-x_{n-1} \Vert . \end{aligned}$$

(12)

Using definition of $z_{n}$ and Lemma 2.6 (ii), we have

$$ \begin{aligned} \Vert z_{n}-\bar{x} \Vert ^{2}&= \Biggl\Vert y_{n}-\sum _{j=1}^{M} \biggl\{ \delta _{j,n}\rho _{n} \frac{f_{j,n}(y_{n})+g_{n}(y_{n})}{d_{j}^{2}(y_{n})}\bigl(\nabla g_{n}(y_{n})+ \nabla f_{j,n}(y_{n})\bigr) \biggr\} -\bar{x} \Biggr\Vert ^{2} \\ &\leq \Vert y_{n}-\bar{x} \Vert ^{2}+ \Biggl\Vert \sum_{j=1}^{M} \biggl\{ \delta _{j,n} \rho _{n}\frac{f_{j,n}(y_{n})+g_{n}(y_{n})}{d_{j}^{2}(y_{n})}\bigl(\nabla g_{n}(y_{n})+ \nabla f_{j,n}(y_{n})\bigr) \biggr\} \Biggr\Vert ^{2} \\ &\quad{} -2 \Biggl\langle \sum_{j=1}^{M} \biggl\{ \delta _{j,n}\rho _{n} \frac{f_{j,n}(y_{n})+g_{n}(y_{n})}{d_{j}^{2}(y_{n})}\bigl(\nabla g_{n}(y_{n})+ \nabla f_{j,n}(y_{n}) \bigr) \biggr\} ,y_{n}-\bar{x} \Biggr\rangle . \end{aligned} $$

(13)

Using the convexity of $\|\cdot \|^{2}$, we have

$$\begin{aligned} & \Biggl\Vert \sum _{j=1}^{M} \biggl\{ \delta _{j,n}\rho _{n} \frac{f_{j,n}(y_{n})+g_{n}(y_{n})}{d_{j}^{2}(y_{n})}\bigl(\nabla g_{n}(y_{n})+ \nabla f_{j,n}(y_{n})\bigr) \biggr\} \Biggr\Vert ^{2} \\ &\quad \leq \sum_{j=1}^{M} \biggl\{ \delta _{j,n} \biggl(\rho _{n} \frac{f_{j,n}(y_{n})+g_{n}(y_{n})}{d_{j}^{2}(y_{n})} \biggr)^{2} \bigl\Vert \nabla g_{n}(y_{n})+ \nabla f_{j,n}(y_{n}) \bigr\Vert ^{2} \biggr\} \\ &\quad \leq \sum_{j=1}^{M} \biggl\{ \delta _{j,n} \biggl(\rho _{n} \frac{f_{j,n}(y_{n})+g_{n}(y_{n})}{d_{j}^{2}(y_{n})} \biggr)^{2}d_{j}^{2}(y_{n}) \biggr\} \\ &\quad =\rho _{n}^{2}\sum_{j=1}^{M} \delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})}. \end{aligned}$$

(14)

From (10) and (11), we have

$$\begin{aligned} & \Biggl\langle \sum_{j=1}^{M} \biggl\{ \delta _{j,n}\rho _{n} \frac{f_{j,n}(y_{n})+g_{n}(y_{n})}{d_{j}^{2}(y_{n})}\bigl(\nabla g_{n}(y_{n})+ \nabla f_{j,n}(y_{n}) \bigr) \biggr\} ,y_{n}-\bar{x} \Biggr\rangle \\ &\quad =\sum_{j=1}^{M} \biggl\{ \delta _{j,n}\rho _{n} \frac{f_{j,n}(y_{n})+g_{n}(y_{n})}{d_{j}^{2}(y_{n})} \bigl\langle \nabla g_{n}(y_{n})+\nabla f_{j,n}(y_{n}),y_{n}- \bar{x} \bigr\rangle \biggr\} \\ &\quad =\sum_{j=1}^{M} \biggl\{ \delta _{j,n}\rho _{n} \frac{f_{j,n}(y_{n})+g_{n}(y_{n})}{d_{j}^{2}(y_{n})}\bigl(\bigl\langle \nabla g_{n}(y_{n}),y_{n}- \bar{x} \bigr\rangle +\bigl\langle \nabla f_{j,n}(y_{n}),y_{n}-\bar{x}\bigr\rangle \bigr) \biggr\} \\ &\quad \geq \sum_{j=1}^{M} \biggl\{ \delta _{j,n}\rho _{n} \frac{f_{j,n}(y_{n})+g_{n}(y_{n})}{d_{j}^{2}(y_{n})}\bigl(2g_{n}(y_{n})+2 f_{j,n}(y_{n})\bigr) \biggr\} \\ &\quad \geq 2\rho _{n}\sum_{j=1}^{M} \delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}(y_{n})}. \end{aligned}$$

(15)

In view of (13), (14), and (15), we have

$$\begin{aligned} \Vert z_{n}-\bar{x} \Vert ^{2} \leq & \Vert y_{n}-\bar{x} \Vert ^{2}+\rho _{n}^{2}\sum_{j=1}^{M} \delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})} \\ &{}-4\rho _{n}\sum_{j=1}^{M} \delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})} \\ =& \Vert y_{n}-\bar{x} \Vert ^{2}+\rho _{n}(\rho _{n}-4)\sum_{j=1}^{M} \delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})} \\ =& \Vert y_{n}-\bar{x} \Vert ^{2}-\rho _{n}(4-\rho _{n})\sum_{j=1}^{M} \delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})}. \end{aligned}$$

(16)

Next, we show that the sequences $\{x_{n}\}$, $\{y_{n}\}$, and $\{z_{n}\}$ are bounded.

From (16) and (C4), we have

$$ \Vert z_{n}-\bar{x} \Vert \leq \Vert y_{n}-\bar{x} \Vert . $$

(17)

Using (12), (17), and the definition of $x_{n+1}$, we get

$$\begin{aligned} \Vert x_{n+1}-\bar{x} \Vert =& \bigl\Vert \alpha _{n}V(y_{n})+(1-\alpha _{n})z_{n}- \bar{x} \bigr\Vert \\ =& \bigl\Vert (1-\alpha _{n}) (z_{n}-\bar{x})+\alpha _{n}\bigl(V(y_{n})-V(\bar{x})\bigr)+ \alpha _{n} \bigl(V(\bar{x})-\bar{x}\bigr) \bigr\Vert \\ \leq& (1-\alpha _{n}) \Vert z_{n}-\bar{x} \Vert + \alpha _{n} \bigl\Vert V(y_{n})-V(\bar{x}) \bigr\Vert + \alpha _{n} \bigl\Vert V(\bar{x})-\bar{x} \bigr\Vert \\ \leq& (1-\alpha _{n}) \Vert z_{n}-\bar{x} \Vert + \alpha _{n}\gamma \Vert y_{n}- \bar{x} \Vert +\alpha _{n} \bigl\Vert V(\bar{x})-\hat{x} \bigr\Vert \\ \leq& \bigl(1-\alpha _{n}(1-\gamma )\bigr) \Vert y_{n}-\bar{x} \Vert +\alpha _{n} \bigl\Vert V( \bar{x})-\bar{x} \bigr\Vert \\ \leq& \bigl(1-\alpha _{n}(1-\gamma )\bigr) \Vert x_{n}- \bar{x} \Vert +\bigl(1-\alpha _{n}(1- \gamma )\bigr)\theta _{n} \Vert x_{n}-x_{n-1} \Vert \\ &{} +\alpha _{n} \bigl\Vert V(\bar{x})-\bar{x} \bigr\Vert \\ =&\bigl(1-\alpha _{n}(1-\gamma )\bigr) \Vert x_{n}- \bar{x} \Vert \\ &{} +\alpha _{n}(1-\gamma ) \biggl\{ \frac{(1-\alpha _{n}(1-\gamma ))}{1-\gamma } \frac{\theta _{n}}{\alpha _{n}} \Vert x_{n}-x_{n-1} \Vert + \frac{ \Vert V(\bar{x})-\bar{x} \Vert }{1-\gamma } \biggr\} . \end{aligned}$$

(18)

Observe that by (C2) and (C3),

$$ \lim_{n\rightarrow \infty } \frac{(1-\alpha _{n}(1-\gamma ))}{1-\gamma } \frac{\theta _{n}}{\alpha _{n}} \Vert x_{n}-x_{n-1} \Vert =0. $$

Let

$$ K=2\max \biggl\{ \frac{ \Vert V(\bar{x})-\bar{x} \Vert }{1-\gamma },\sup_{n\geq 1} \frac{(1-\alpha _{n}(1-\gamma ))}{1-\gamma } \frac{\theta _{n}}{\alpha _{n}} \Vert x_{n}-x_{n-1} \Vert \biggr\} . $$

Then, (18) becomes

$$ \Vert x_{n+1}-\bar{x} \Vert \leq \bigl(1-\alpha _{n}(1- \gamma )\bigr) \Vert x_{n}-\bar{x} \Vert + \alpha _{n}(1-\gamma )K. $$

Thus, by Lemma 2.7, the sequence $\{x_{n}\}$ is bounded. As a consequence, $\{y_{n}\}$, $\{V(y_{n})\}$, and $\{z_{n}\}$ are also bounded.

Claim 1: There exists a unique $\bar{x}\in H_{1}$ such that $\bar{x}=P_{\Omega }V(\bar{x})$ .

As a result of

$$ \bigl\Vert P_{\Omega }V(x)-P_{\Omega }V(y) \bigr\Vert \leq \bigl\Vert V(x)-V(y) \bigr\Vert \leq \gamma \Vert x-y \Vert , \quad \forall x,y\in H_{1}, $$

the mapping $P_{\Omega }V$ is a contraction mapping of $H_{1}$ into itself. Hence, by the Banach contraction principle, there exists a unique element $\bar{x}\in H_{1}$ such that $\bar{x}=P_{\Omega }V(\bar{x})$. Clearly, $\bar{x}\in \Omega$, and we have

$$ \bar{x}=P_{\Omega }V(\bar{x})\quad \Leftrightarrow\quad \bigl\langle \bar{x}-V( \bar{x}),y- \bar{x}\bigr\rangle \geq 0, \quad \forall y\in \Omega . $$

Claim 2: The sequence $\{x_{n}\}$ converges strongly to $\bar{x}\in \Omega$ where $\bar{x}=P_{\Omega }V(\bar{x})$ .

Let $\bar{x}\in \Omega$ where $\bar{x}=P_{\Omega }V(\bar{x})$. Now

$$\begin{aligned} \Vert y_{n}-\bar{x} \Vert ^{2} =& \bigl\Vert x_{n}+\theta _{n}(x_{n}-x_{n-1})- \bar{x} \bigr\Vert ^{2} \\ =& \Vert x_{n}-\bar{x} \Vert ^{2}+\theta ^{2}_{n} \Vert x_{n}-x_{n-1} \Vert ^{2} \\ &{}+2\theta _{n} \langle x_{n}-\bar{x},x_{n}-x_{n-1} \rangle . \end{aligned}$$

(19)

From Lemma 2.6 (iv), we have

$$ \langle x_{n}-\bar{x},x_{n}-x_{n-1} \rangle =\frac{1}{2} \Vert x_{n}- \bar{x} \Vert ^{2}-\frac{1}{2} \Vert x_{n-1}-\bar{x} \Vert ^{2}+\frac{1}{2} \Vert x_{n}-x_{n-1} \Vert ^{2}. $$

(20)

From (19) and (20), and since $0\leq \theta _{n}<1$, we get

$$\begin{aligned} \Vert y_{n}-\bar{x} \Vert ^{2} =& \Vert x_{n}-\bar{x} \Vert ^{2}+\theta ^{2}_{n} \Vert x_{n}-x_{n-1} \Vert \\ &{}+\theta _{n}\bigl( \Vert x_{n}-\bar{x} \Vert ^{2}- \Vert x_{n-1}-\bar{x} \Vert ^{2}+ \Vert x_{n}-x_{n-1} \Vert ^{2}\bigr) \\ \leq & \Vert x_{n}-\bar{x} \Vert ^{2}+2\theta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2}+ \theta _{n}\bigl( \Vert x_{n}-\bar{x} \Vert ^{2}- \Vert x_{n-1}-\bar{x} \Vert ^{2}\bigr). \end{aligned}$$

(21)

Using the definition of $x_{n+1}$ and Lemma 2.6 (iii), together with (21), we have

$$\begin{aligned} \Vert x_{n+1}-\bar{x} \Vert ^{2} =& \bigl\Vert \alpha _{n}V(y_{n})+(1-\alpha _{n})z_{n}-\bar{x} \bigr\Vert ^{2} \\ =& \bigl\Vert \alpha _{n}\bigl(V(y_{n})-\bar{x} \bigr)+(1-\alpha _{n}) (z_{n}-\bar{x}) \bigr\Vert ^{2} \\ \leq &(1-\alpha _{n}) \Vert z_{n}-\bar{x} \Vert ^{2}+2\alpha _{n}\bigl\langle V(y_{n})- \bar{x},x_{n+1}-\bar{x}\bigr\rangle \\ \leq & \Vert z_{n}-\bar{x} \Vert ^{2}+2\alpha _{n}\bigl\langle V(y_{n})-\bar{x},x_{n+1}- \bar{x} \bigr\rangle \\ \leq & \Vert y_{n}-\bar{x} \Vert ^{2}+2\alpha _{n}\bigl\langle V(y_{n})-\bar{x},x_{n+1}- \bar{x} \bigr\rangle \\ &{} +\rho _{n}(\rho _{n}-4)\sum _{j=1}^{M}\delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})} \\ \leq & \Vert x_{n}-\bar{x} \Vert ^{2}+2\theta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2} \\ &{} +\theta _{n}\bigl( \Vert x_{n}-\bar{x} \Vert ^{2}- \Vert x_{n-1}-\bar{x} \Vert ^{2}\bigr) \\ &{} +2\alpha _{n}\bigl\langle V(y_{n})- \bar{x},x_{n+1}-\bar{x}\bigr\rangle \\ &{} +\rho _{n}(\rho _{n}-4)\sum _{j=1}^{M}\delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})}. \end{aligned}$$

(22)

Since the sequences $\{x_{n}\}$ and $\{V(y_{n})\}$ are bounded, there exists $K_{1}$ such that $2\langle V(y_{n})-\bar{x},x_{n+1}-\bar{x}\rangle \leq K_{1}$ for all $n\geq 1$. Thus, from (22), we obtain

$$ \begin{aligned} \Vert x_{n+1}-\bar{x} \Vert ^{2}&\leq \Vert x_{n}-\bar{x} \Vert ^{2}+2\theta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2}+\theta _{n}\bigl( \Vert x_{n}- \bar{x} \Vert ^{2}- \Vert x_{n-1}-\bar{x} \Vert ^{2}\bigr) \\ &\quad{} +\alpha _{n}K_{1}+\rho _{n}(\rho _{n}-4)\sum_{j=1}^{M} \delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})}. \end{aligned} $$

(23)

Let us distinguish the following two cases related to the behavior of the sequence $\{\Gamma _{n}\}$ where

$$ \Gamma _{n}= \Vert x_{n}-\bar{x} \Vert ^{2}. $$

Case 1: Suppose the sequence $\{\Gamma _{n}\}$ decrease at infinity. Thus, there exists $n_{0}\in \mathbb{N}$ such that $\Gamma _{n+1}\leq \Gamma _{n}$ for $n\geq n_{0}$. Then, $\{\Gamma _{n}\}$ converges and $\Gamma _{n}-\Gamma _{n+1}\rightarrow 0$ as $n\rightarrow 0$.

From (23), we have

$$ \begin{aligned} \rho _{n}(4-\rho _{n})\sum_{j=1}^{M}\delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})}&\leq ( \Gamma _{n}-\Gamma _{n+1})+\alpha _{n}K_{1}+\theta _{n}( \Gamma _{n}- \Gamma _{n-1}) \\ &\quad{} +2\theta _{n} \Vert x_{n}-x_{n-1} \Vert ^{2}. \end{aligned} $$

(24)

Since $\Gamma _{n}-\Gamma _{n+1}\rightarrow 0$ ($\Gamma _{n-1}- \Gamma _{n}\rightarrow 0$) and using (C2) and (C3) (noting $\alpha _{n}\rightarrow 0$, $0<\alpha _{n}<1$, $\theta _{n}\|x_{n}-x_{n-1}\|\leq \frac{\theta _{n}}{\alpha _{n}}\|x_{n}-x_{n-1} \|\rightarrow 0$ and $\{x_{n}\}$ is bounded), we have from (24)

$$ \rho _{n}(4-\rho _{n})\sum _{j=1}^{M}\delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})} \rightarrow 0, \quad n\rightarrow \infty . $$

(25)

The conditions (C4) and (25) yield

$$ \sum_{j=1}^{M}\delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})} \rightarrow 0, \quad n\rightarrow \infty . $$

(26)

In view of (26) and the restriction condition imposed on $\delta _{j,n}$ in (C1), we have

$$ \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d^{2}_{j}(y_{n})} \rightarrow 0, \quad n\rightarrow \infty , $$

(27)

for all $j\in \{1,\ldots ,M\}$.

Now, using the definition of $z_{n}$ and the convexity of $\|\cdot \|^{2}$, we have

$$\begin{aligned} \Vert y_{n}-z_{n} \Vert ^{2} =& \Biggl\Vert \sum_{j=1}^{M} \biggl\{ \delta _{j,n}\rho _{n} \frac{f_{j,n}(y_{n})+g_{n}(y_{n})}{d_{j}^{2}(y_{n})}\bigl(\nabla g_{n}(y_{n})+ \nabla f_{j,n}(y_{n}) \bigr) \biggr\} \Biggr\Vert ^{2} \\ \leq &\sum_{j=1}^{M} \biggl\{ \delta _{j,n} \biggl(\rho _{n} \frac{f_{j,n}(y_{n})+g_{n}(y_{n})}{d_{j}^{2}(y_{n})} \biggr)^{2} \bigl\Vert \nabla g_{n}(y_{n})+ \nabla f_{j,n}(y_{n}) \bigr\Vert ^{2} \biggr\} \\ \leq &\rho _{n}^{2} \sum_{j=1}^{M} \delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})} \\ \leq &16\sum_{j=1}^{M}\delta _{j,n} \frac{(f_{j,n}(y_{n})+g_{n}(y_{n}))^{2}}{d_{j}^{2}(y_{n})}. \end{aligned}$$

(28)

Thus, (28) together with (26) gives

$$ \Vert y_{n}-z_{n} \Vert \rightarrow 0, \quad n\rightarrow \infty . $$

(29)

Now, using the definition of $y_{n}$ and (C3) ($\theta _{n}\|x_{n}-x_{n-1} \|\leq \frac{\theta _{n}}{\alpha _{n}}\|x_{n}-x_{n-1}\|\rightarrow 0$), we have

$$ \Vert x_{n}-y_{n} \Vert = \bigl\Vert x_{n}-x_{n}-\theta _{n}(x_{n}-x_{n-1}) \bigr\Vert =\theta _{n} \Vert x_{n}-x_{n-1} \Vert \rightarrow 0, \quad n\rightarrow \infty . $$

(30)

By (29) and (30), we get

$$ \Vert x_{n}-z_{n} \Vert \leq \Vert x_{n}-y_{n} \Vert + \Vert y_{n}-z_{n} \Vert \rightarrow 0, \quad n\rightarrow \infty . $$

(31)

Using the definition of $x_{n+1}$, (C2), and noting that $\{V(y_{n})\}$ and $\{z_{n}\}$ are bounded, we have

$$ \Vert x_{n+1}-z_{n} \Vert =\alpha _{n} \bigl\Vert V(y_{n})-z_{n} \bigr\Vert \rightarrow 0, \quad n\rightarrow \infty . $$

(32)

Results from (31) and (32) give

$$ \Vert x_{n+1}-x_{n} \Vert \leq \Vert x_{n+1}-z_{n} \Vert + \Vert z_{n}-x_{n} \Vert \rightarrow 0, \quad n\rightarrow \infty . $$

(33)

Since $\{x_{n}\}$ is bounded, there exists a subsequence $\{x_{n_{k}}\}$ of $\{x_{n}\}$ which converges to p for some $p\in H_{1}$. Next, we show that $p\in \Omega$.

For each $i\in \{1,\ldots ,N\}$ and for each $j\in \{1,\ldots ,M\}$, $\nabla f_{j,n}(\cdot )$ and $\nabla g_{i,n}(\cdot )$ are Lipschitz continuous with constant $\|A\|^{2}$ and 1, respectively. Since the sequence $\{z_{n}\}$ is bounded and

$$\begin{aligned}& \bigl\Vert \nabla f_{j,n}(y_{n}) \bigr\Vert = \bigl\Vert \nabla f_{j,n}(y_{n})-\nabla f_{j,n}( \bar{x}) \bigr\Vert \leq \Vert A \Vert ^{2} \Vert y_{n}-\bar{x} \Vert , \quad \forall j\in \{1,\ldots ,M\}, \\& \bigl\Vert \nabla g_{i,n}(y_{n}) \bigr\Vert = \bigl\Vert \nabla g_{i,n}(y_{n})-\nabla g_{i,n}( \bar{x}) \bigr\Vert \leq \Vert y_{n}-\bar{x} \Vert , \quad \forall i\in \{1,\ldots ,N\}, \end{aligned}$$

we have that the sequences $\{\|\nabla g_{i,n}(y_{n})\|\}_{n=1}^{\infty }$ and $\{\|\nabla f_{j,n}(y_{n})\|\}_{n=1}^{\infty }$ are bounded. Hence, we have $\{d_{j}(y_{n})\}_{n=1}^{\infty }$ is bounded and hence $\{d_{j}(y_{n_{k}})\}_{k=1}^{\infty }$ is bounded. Consequently, by (27), we have

$$ \lim_{k\rightarrow \infty }f_{j,n_{k}}(y_{n_{k}})= \lim_{k\rightarrow \infty }g_{n_{k}}(y_{n_{k}})=0, \quad \forall j \in \{1,\ldots ,M\}. $$

(34)

From the definition of $g_{n_{k}}(y_{n_{k}})$, we get

$$ g_{i,n_{k}}(y_{n_{k}})\leq g_{n_{k}}(y_{n_{k}}), \quad \forall i\in \{1,\ldots ,N\}. $$

(35)

Therefore, (34) and (35) give

$$ \lim_{k\rightarrow \infty }f_{j,n_{k}}(y_{n_{k}})=\lim _{k\rightarrow \infty }g_{i,n_{k} }(y_{n_{k}})=0, \quad \forall i\in \{1,\ldots ,N\},\forall j\in \{1,\ldots ,M\}. $$

That is, for all $i\in \{1,\ldots ,N\}$, $j\in \{1,\ldots ,M\}$, we have

$$ \lim_{k\rightarrow \infty } \bigl\Vert (I-P_{Q_{j,n_{k}}})Ay_{n_{k}} \bigr\Vert = \lim_{k\rightarrow \infty } \bigl\Vert (I-P_{C_{i,n_{k}}})y_{n_{k}} \bigr\Vert =0. $$

(36)

Therefore, since $\{y_{n}\}$ is bounded and from the boundedness assumption of the subdifferential operator $\partial q_{j}$, the sequence $\{\varepsilon _{j,n}\}_{n=1}^{\infty }$ is bounded. In view of this and (36), for all $j\in \{1,\ldots ,M\}$, we have

$$ \begin{aligned} q_{j}(Ay_{n_{k}})& \leq \bigl\langle \varepsilon _{j,n_{k}},Az_{n_{k}}-P_{Q_{j,n_{k}}}(Ay_{n_{k}}) \bigr\rangle \\ &\leq \Vert \varepsilon _{j,n_{k}} \Vert \bigl\Vert (I-P_{Q_{j,n_{k}}})Ay_{n_{k}} \bigr\Vert \rightarrow 0, \quad k \rightarrow \infty . \end{aligned} $$

(37)

Similarly, from the boundedness of $\{\xi _{i,n}\}_{n=1}^{\infty }$ and (36), for all $i\in \{1,\ldots ,N\}$, we obtain

$$ \begin{aligned} c_{i}(y_{n_{k}})& \leq \bigl\langle \xi _{i,n_{k}},y_{n_{k}}-P_{C_{i,n_{k}}}(y_{n_{k}}) \bigr\rangle \\ &\leq \Vert \xi _{i,n_{k}} \Vert \bigl\Vert (I-P_{C_{i,n_{k}}})y_{n_{k}} \bigr\Vert \rightarrow 0, \quad k\rightarrow \infty . \end{aligned} $$

(38)

Since $x_{n_{k}}\rightharpoonup p$, by using (30), we have $y_{n_{k}}\rightharpoonup p$. Hence $Ay_{n_{k}}\rightharpoonup Ap$.

The weak lower semicontinuity of $q_{j}(\cdot )$ and (37) imply that

$$ q_{j}(Ap)\leq \liminf_{k\rightarrow \infty }q_{j}(Ay_{n_{k}}) \leq \limsup_{k\rightarrow \infty }q_{j}(Ay_{n_{k}})\leq 0, \quad \forall j\in \{1,\ldots ,M\}. $$

That is, $Ap\in Q_{j}$ for all $j\in \{1,\ldots ,M\}$.

Likewise, the weak lower semicontinuity of $c_{i}(\cdot )$ and (38) imply that

$$ c_{i}(p)\leq \liminf_{k\rightarrow \infty }c_{i }(y_{n_{k}}) \leq 0, \quad \forall i\in \{1,\ldots ,N\}. $$

That is, $p\in C_{i}$ for all $i\in \{1,\ldots ,N\}$. Hence, $p\in \Omega$.

Next, we show that $\limsup_{n\rightarrow \infty }\langle (I-V)\bar{x},\bar{x}-x_{n} \rangle \leq 0$. Indeed, since $\bar{x}=P_{\Omega }V(\bar{x})$ and $p\in \Omega$, we obtain that

$$\begin{aligned} \limsup_{n\rightarrow \infty }\bigl\langle (I-V) \bar{x},\bar{x}-x_{n} \bigr\rangle =&\lim _{k\rightarrow \infty }\bigl\langle (I-V)\bar{x},\bar{x}-x_{n_{k}} \bigr\rangle \\ =&\bigl\langle (I-V)\bar{x},\bar{x}-p\bigr\rangle \leq 0. \end{aligned}$$

(39)

Since $\|x_{n+1}-x_{n}\|\rightarrow 0$, from (33) and by (39), we have

$$ \limsup_{n\rightarrow \infty }\bigl\langle (I-V)\bar{x}, \bar{x}-x_{n+1} \bigr\rangle \leq 0. $$

Using (17), we have

$$\begin{aligned} \Vert x_{n+1}-\bar{x} \Vert ^{2} =&\bigl\langle \alpha _{n}V(y_{n})+(1-\alpha _{n})z_{n}- \bar{x},x_{n+1}-\bar{x} \bigr\rangle \\ =& \alpha _{n}\bigl\langle V(y_{n})-V( \bar{x}),x_{n+1}-\bar{x}\bigr\rangle +(1- \alpha _{n})\langle z_{n}-\bar{x},x_{n+1}-\bar{x}\rangle \\ &{} +\alpha _{n}\bigl\langle V(\bar{x})-\bar{x},x_{n+1}- \bar{x} \bigr\rangle \\ \leq& \gamma \alpha _{n} \Vert y_{n}-\bar{x} \Vert \Vert x_{n+1}-\bar{x} \Vert +(1- \alpha _{n}) \Vert z_{n}-\bar{x} \Vert \Vert x_{n+1}-\bar{x} \Vert \\ &{} +\alpha _{n}\bigl\langle V(\bar{x})-\bar{x},x_{n+1}- \bar{x} \bigr\rangle \\ \leq& \bigl(1-\alpha _{n}(1-\gamma )\bigr) \Vert y_{n}-\bar{x} \Vert \Vert x_{n+1}-\bar{x} \Vert \\ &{} +\alpha _{n}\bigl\langle V(\bar{x})-\bar{x},x_{n+1}- \bar{x} \bigr\rangle \\ \leq& \bigl(1-\alpha _{n}(1-\gamma )\bigr) \biggl( \frac{ \Vert y_{n}-\bar{x} \Vert ^{2}}{2}+ \frac{ \Vert x_{n+1}-\bar{x} \Vert ^{2}}{2} \biggr) \\ &{} +\alpha _{n}\bigl\langle V(\bar{x})-\bar{x},x_{n+1}- \bar{x} \bigr\rangle . \end{aligned}$$

(40)

Therefore, from (40), we have

$$\begin{aligned} \Vert x_{n+1}-\bar{x} \Vert ^{2} \leq& \frac{1-\alpha _{n}(1-\gamma )}{1+\alpha _{n}(1-\gamma )} \Vert y_{n}- \bar{x} \Vert ^{2}+\frac{2\alpha _{n}}{1+\alpha _{n}(1-\gamma )}\bigl\langle V( \bar{x})-\bar{x},x_{n+1}- \bar{x} \bigr\rangle \\ =& \biggl(1-\frac{2\alpha _{n}(1-\gamma )}{1+\alpha _{n}(1-\gamma )} \biggr) \Vert y_{n}-\bar{x} \Vert ^{2}+\frac{2\alpha _{n}}{1+\alpha _{n}(1-\gamma )} \bigl\langle V(\bar{x})- \bar{x},x_{n+1}-\bar{x} \bigr\rangle . \end{aligned}$$

(41)

Combining (41) and

$$ \Vert y_{n}-\bar{x} \Vert = \bigl\Vert x_{n}+\theta _{n}(x_{n}-x_{n-1})-\bar{x} \bigr\Vert \leq \Vert x_{n}- \bar{x} \Vert +\theta _{n} \Vert x_{n}-x_{n-1} \Vert , $$

it holds that

$$\begin{aligned} \Vert x_{n+1}-\bar{x} \Vert ^{2} \leq& \biggl(1- \frac{2\alpha _{n}(1-\gamma )}{1+\alpha _{n}(1-\gamma )} \biggr) \bigl( \Vert x_{n}- \bar{x} \Vert +\theta _{n} \Vert x_{n}-x_{n-1} \Vert \bigr)^{2} \\ &{} +\frac{2\alpha _{n}}{1+\alpha _{n}(1-\gamma )}\bigl\langle V(\bar{x})- \bar{x},x_{n+1}- \bar{x} \bigr\rangle \\ =& \biggl(1-\frac{2\alpha _{n}(1-\gamma )}{1+\alpha _{n}(1-\gamma )} \biggr) \bigl( \Vert x_{n}-\bar{x} \Vert ^{2}+\theta _{n}^{2} \Vert x_{n}-x_{n-1} \Vert ^{2} \\ &{} +2\theta _{n} \Vert x_{n}-\bar{x} \Vert \Vert x_{n}-x_{n-1} \Vert \bigr) \\ &{} +\frac{2\alpha _{n}}{1+\alpha _{n}(1-\gamma )}\bigl\langle V(\bar{x})- \bar{x},x_{n+1}- \bar{x} \bigr\rangle \\ \leq& \biggl(1-\frac{2\alpha _{n}(1-\gamma )}{1+\alpha _{n}(1-\gamma )} \biggr) \Vert x_{n}-\bar{x} \Vert ^{2}+\theta _{n}^{2} \Vert x_{n}-x_{n-1} \Vert ^{2} \\ &{} +2\theta _{n} \Vert x_{n}-\bar{x} \Vert \Vert x_{n}-x_{n-1} \Vert \\ &{} +\frac{2\alpha _{n}}{1+\alpha _{n}(1-\gamma )}\bigl\langle V(\bar{x})- \bar{x},x_{n+1}- \bar{x} \bigr\rangle . \end{aligned}$$

(42)

Since $\{x_{n}\}$ is bounded, there exists $K_{2}>0$ such that $\|x_{n}-\bar{x}\|\leq K_{2}$ for all $n\geq 1$. Thus, in view of (42), we have

$$\begin{aligned} \Gamma _{n+1} \leq & \biggl(1- \frac{2\alpha _{n}(1-\gamma )}{1+\alpha _{n}(1-\gamma )} \biggr)\Gamma _{n}+ \theta _{n} \Vert x_{n}-x_{n-1} \Vert \bigl(\theta _{n} \Vert x_{n}-x_{n-1} \Vert +2K_{2}\bigr) \\ &{} + \frac{2\alpha _{n}}{1+\alpha _{n}(1-\gamma )}\bigl\langle V(\bar{x})- \bar{x},x_{n+1}- \bar{x} \bigr\rangle \\ =& (1-\sigma _{n} )\Gamma _{n}+\sigma _{n} \vartheta _{n}, \end{aligned}$$

(43)

where $\sigma _{n}=\frac{2\alpha _{n}(1-\gamma )}{1+\alpha _{n}(1-\gamma )}$ and

$$ \begin{aligned} \vartheta _{n}&=\frac{1+\alpha _{n}(1-\gamma )}{2(1-\gamma )} \biggl( \frac{\theta _{n}}{\alpha _{n}} \Vert x_{n}-x_{n-1} \Vert \biggr) \bigl\{ \theta _{n} \Vert x_{n}-x_{n-1} \Vert +2K_{2} \bigr\} \\ &\quad{} +\frac{1}{1-\gamma }\bigl\langle V(\bar{x})-\bar{x},x_{n+1}- \bar{x} \bigr\rangle . \end{aligned} $$

From (40), (C2), and (C3), we have $\sum_{n=1}^{\infty }\sigma _{n}=\infty$ and $\limsup_{n\rightarrow \infty }\vartheta _{n}\leq 0$. Thus, using Lemma 2.7 and (43), we get $\Gamma _{n}\rightarrow 0$ as $n\rightarrow \infty$. Hence, $x_{n}\rightarrow \bar{x}$ as $n\rightarrow \infty$.

Case 2: Assume that $\{\Gamma _{n}\}$ does not decrease at infinity. Let $\varphi :\mathbb{N}\rightarrow \mathbb{N}$ be a mapping for all $n\geq n_{0}$ (for some $n_{0}$ large enough) defined by

$$ \varphi (n)=\max \{k\in \mathbb{N}:k\leq n,\Gamma _{k}\leq \Gamma _{k+1} \}. $$

By Lemma 2.9, $\{\varphi (n)\}_{n=n_{0}}^{\infty }$ is a nondecreasing sequence, $\varphi (n)\rightarrow \infty$ as $n\rightarrow \infty$, and

$$ \Gamma _{\varphi (n)}\leq \Gamma _{\varphi (n)+1} \quad \text{and}\quad \Gamma _{n}\leq \Gamma _{\varphi (n)+1}, \quad \forall n \geq n_{0}. $$

(44)

In view of $\|x_{\varphi (n)}-\bar{x}\|^{2}-\|x_{\varphi (n)+1}-\bar{x}\|^{2}= \Gamma _{\varphi (n)}-\Gamma _{\varphi (n)+1}\leq 0$ for all $n\geq n_{0}$ and (23), we have for all $n\geq n_{0}$,

$$\begin{aligned} &\rho _{\varphi (n)}(4-\rho _{\varphi (n)})\sum _{j=1}^{M} \delta _{j,\varphi (n)} \frac{(f_{j,\varphi (n)}(y_{\varphi (n)})+g_{\varphi (n)}(y_{\varphi (n)}))^{2}}{d_{j}^{2}(y_{\varphi (n)})} \\ &\quad \leq (\Gamma _{\varphi (n)}-\Gamma _{\varphi (n)+1})+\alpha _{ \varphi (n)}K_{1}+\theta _{\varphi (n)}(\Gamma _{\varphi (n)}- \Gamma _{ \varphi (n)-1}) \\ &\qquad{} +2\theta _{\varphi (n)} \Vert x_{\varphi (n)}-x_{\varphi (n)-1} \Vert ^{2} \\ &\quad \leq \alpha _{\varphi (n)}K_{1}+\theta _{\varphi (n)}(\Gamma _{ \varphi (n)}-\Gamma _{\varphi (n)-1})+2\theta _{\varphi (n)} \Vert x_{ \varphi (n)}-x_{\varphi (n)-1} \Vert ^{2} \\ &\quad \leq \alpha _{\varphi (n)}K_{1}+\theta _{\varphi (n)} \Vert x_{\varphi (n)}-x_{ \varphi (n)-1} \Vert (\sqrt{\Gamma _{\varphi (n)}}+ \sqrt{\Gamma _{ \varphi (n)-1}} ) \\ &\qquad{} +2\theta _{\varphi (n)} \Vert x_{\varphi (n)}-x_{\varphi (n)-1} \Vert ^{2}. \end{aligned}$$

(45)

Thus, from (45) together with (C2) and (C3), we have for each $j\in \{1,\ldots ,M\}$,

$$ \frac{(f_{j,\varphi (n)}(y_{\varphi (n)})+g_{\varphi (n)}(y_{\varphi (n)}))^{2}}{d_{j}^{2}(y_{\varphi (n)})} \rightarrow 0, \quad n\rightarrow \infty . $$

(46)

Using a similar procedure as above in Case 1, we have

$$ \lim_{n\rightarrow \infty } \Vert x_{\varphi (n)}-y_{\varphi (n)} \Vert = \lim_{n\rightarrow \infty } \Vert x_{\varphi (n)+1}-x_{\varphi (n)} \Vert =0. $$

Since $\{x_{\varphi (n)}\}$ is bounded, there exists a subsequence of $\{x_{\varphi (n)}\}$, still denoted by $\{x_{\varphi (n)}\}$, which converges weakly to p. By a similar argument as above in Case 1, we conclude immediately that $p\in \Omega$. In addition, by the similar argument as above in Case 1, we have $\limsup_{n\rightarrow \infty }\langle (I-V)\bar{x},\bar{x}-x_{ \varphi (n)}\rangle \leq 0$. Since $\lim_{n\rightarrow \infty }\|x_{\varphi (n)+1}-x_{\varphi (n)} \|=0$, we get $\limsup_{n\rightarrow \infty }\langle (I-V)\bar{x},\bar{x}-x_{ \varphi (n)+1}\rangle \leq 0$. From (43), we have

$$ \Gamma _{\varphi (n)+1}\leq (1-\sigma _{\varphi (n)} ) \Gamma _{ \varphi (n)}+\sigma _{\varphi (n)}\vartheta _{\varphi (n)}, $$

(47)

where $\sigma _{\varphi (n)}= \frac{2\alpha _{\varphi (n)}(1-\gamma )}{1+\alpha _{\varphi (n)}(1-\gamma )}$ and

$$ \begin{aligned} \vartheta _{\varphi (n)}&= \frac{1+\alpha _{\varphi (n)}(1-\gamma )}{2(1-\gamma )} \biggl( \frac{\theta _{\varphi (n)}}{\alpha _{\varphi (n)}} \Vert x_{\varphi (n)}-&x_{ \varphi (n)-1} \Vert \biggr) \bigl\{ \theta _{\varphi (n)} \Vert x_{\varphi (n)}-x_{ \varphi (n)-1} \Vert +2K_{2} \bigr\} \\ &\quad{} +\frac{1}{1-\gamma }\bigl\langle V(\bar{x})-\bar{x},x_{\varphi (n)+1}- \bar{x} \bigr\rangle . \end{aligned} $$

Using $\Gamma _{\varphi (n)}-\Gamma _{\varphi (n)+1}\leq 0$ for all $n\geq n_{0}$ and $\vartheta _{\varphi (n)}>0$, (47) gives

$$ 0\leq -\sigma _{\varphi (n)}\Gamma _{\varphi (n)}+\sigma _{\varphi (n)} \vartheta _{\varphi (n)}. $$

Since $\sigma _{\varphi (n)}>0$, we obtain $\|x_{\varphi (n)}-\bar{x}\|^{2}=\Gamma _{\varphi (n)}\leq \vartheta _{ \varphi (n)}$. Moreover, since $\limsup_{n\rightarrow \infty }\vartheta _{\varphi (n)}\leq 0$, we have $\lim_{n\rightarrow \infty }\|x_{\varphi (n)}-\bar{x}\|=0$. Thus, $\lim_{n\rightarrow \infty }\|x_{\varphi (n)}-\bar{x}\|=0$ together with $\lim_{n\rightarrow \infty }\|x_{\varphi (n)+1}-x_{\varphi (n)} \|=0$, gives $\lim_{n\rightarrow \infty }\Gamma _{\varphi (n)+1}=0$. Therefore, from (44), we obtain $\lim_{n\rightarrow \infty }\Gamma _{n}=0$, that is, $x_{n}\rightarrow \bar{x}$ as $n\rightarrow \infty$. This completes the proof. □

Remark 3.3

Take a real number $\beta \in [0,1)$ and a real sequence $\{\varepsilon _{n}\}$ such that $\varepsilon _{n}>0$ and $\varepsilon _{n}=o(\alpha _{n})$. Then given the iterates $x_{n-1}$ and $x_{n}$ ($n\geq 1$), choose $\theta _{n}$ such that $0\leq \theta _{n}\leq \bar{\theta }_{n}$ where

$$ \bar{\theta }_{n}:= \textstyle\begin{cases} \min \{\theta ,\frac{\varepsilon _{n}}{ \Vert x_{n-1}-x_{n} \Vert } \},& \text{if } x_{n-1}\neq x_{n}, \\ \theta , & \text{otherwise}. \end{cases} $$

Under this setting, condition (C3) of Theorem 3.2 is satisfied.

It is worth mentioning that our approach also works for approximation of solution of split feasibility problem (1) where C and Q are given as sublevel sets of convex functions given as (2). Set $g_{n}(x)=\frac{1}{2}\|(I-P_{C_{n}})x\|^{2}$ and $\nabla g_{n}(x)=(I-P_{C_{n}})x$, $f_{n}(x)=\frac{1}{2}\|(I-P_{Q_{n}})Ax\|^{2}$ and $\nabla f_{n}(x)=A^{*}(I-P_{Q_{n}})Ax$, where $C_{n}$ and $Q_{n}$ are half-spaces containing C and Q given by (4) and (5), respectively. Thus, the following corollary is an immediate consequence of Theorem 3.2.

Corollary 3.4

Consider the iterative algorithm

$$ \textstyle\begin{cases} x_{0},x_{1}\in H_{1}, \\ y_{n}=x_{n}+\theta _{n}(x_{n}-x_{n-1}), \\ d(y_{n})=\max \{ 1, \Vert \nabla g_{n}(y_{n})+\nabla f_{n}(y_{n}) \Vert \}, \\ z_{n}=y_{n}-\rho _{n}\frac{f_{n}(y_{n})+g_{n}(y_{n})}{d^{2}(y_{n})}( \nabla g_{n}(y_{n})+\nabla f_{n}(y_{n})), \\ x_{n+1}=\alpha _{n}V(y_{n})+(1-\alpha _{n})z_{n}, \end{cases} $$

(48)

where $\{\rho _{n}\}$, $\{\alpha _{n}\}$, and $\{\theta _{n}\}$ are real parameter sequences. If the parameters $\{\alpha _{n}\}$, $\{\theta _{n}\}$, and $\{\rho _{n}\}$ in the iterative algorithm (48) satisfy the following conditions:

• (C1) $0<\alpha _{n}<1$, $\lim_{n\rightarrow \infty }\alpha _{n}=0$ and $\sum_{n=1}^{\infty }\alpha _{n}=\infty$;

• (C2) $0\leq \theta _{n}\leq \theta <1$ and $\lim_{n\rightarrow \infty }\frac{\theta _{n}}{\alpha _{n}}\|x_{n}-x_{n-1} \|=0$,

• (C3) $0<\rho _{n}<4$ and $\liminf_{n\rightarrow \infty }\rho _{n}(4-\rho _{n})>0$,

then the sequence $\{x_{n}\}$ generated by (48) converges strongly to $\bar{x}\in \bar{\Omega }=\{\bar{x}\in C: A\bar{x}\in Q\}$.

4 Numerical results

Example 4.1

Consider MSSFP for $H_{1}=\mathbb{R}^{s}$, $H_{2}=\mathbb{R}^{t}$, $A:\mathbb{R}^{s}\rightarrow \mathbb{R}^{t}$ given by $A(x)=G_{t\times s} (x)$, where $G_{t\times s}$ is a $t\times s$ matrix, the closed convex subsets $C_{i}$ ($i\in \{1,\ldots ,N\}$) of $\mathbb{R}^{s}$ are s-dimensional ellipsoids centered at $b_{i}=(b_{i}^{(1)},b_{i}^{(2)},\ldots ,b_{i}^{(s)})$ given by

$$ C_{i}= \Biggl\{ x=(x_{1},\ldots ,x_{s})^{T} \in \mathbb{R}^{s}:\sum_{l=1}^{s} \frac{(x_{l}-b_{i}^{(l)})^{2}}{(w_{i}^{(l)})^{2}}-1 \leq 0 \Biggr\} , $$

where

$$b_{i}^{(l)}= \textstyle\begin{cases} i-1, &\text{if } l=1, \\ 0, &\text{if } l=2,\ldots ,s,\end{cases} $$

and

$$w_{i}^{(l)}= \textstyle\begin{cases} 2v, &\text{if } l=1, \\ v+i, &\text{otherwise,} \end{cases} $$

for $v\in \mathbb{N}$, and the closed convex subsets $Q_{j}$ ($j\in \{1,\ldots ,M\}$) of $\mathbb{R}^{t}$ are t-dimensional balls centered at $p_{j}=(p^{(1)}_{j},p^{(2)}_{j},\ldots ,p^{(t)}_{j})$ given by

$$ Q_{j}= \bigl\{ y=(y_{1},\ldots ,y_{t})^{T} \in \mathbb{R}^{t}: \Vert y-p_{j} \Vert ^{2}-r_{j}^{2} \leq 0 \bigr\} , $$

where $r_{j}=2v\varrho _{j}-\varrho _{j}$ and

$$p^{(k)}_{j}= \textstyle\begin{cases} \varrho _{j}, &\text{if } k=j, \\ 0, &\text{otherwise. } \end{cases} $$

Now, we take randomly generated $t\times s$ matrix $G_{t\times S}$ given by

$$ G_{t\times s}= (a_{ij} )_{t\times s}, $$

where $a_{j,1}=\varrho _{j}$. Note that

• $$\bigcap_{i=1}^{N}C_{i}= \textstyle\begin{cases} \emptyset , &\text{if } N>4v+1, \\ \{(2v,0,0,\ldots ,0)\}, &\text{if } N=4v+1, \\ D \text{ with }\mathrm{card}(D)>1, &\text{if } N< 4v+1, \end{cases} $$

• $A((2v,0,0,\ldots ,0))=(2v\varrho _{1},2v\varrho _{2},\ldots ,2v \varrho _{t})$,

• $(2v\varrho _{1},2v\varrho _{2},\ldots ,2v\varrho _{t})\in \bigcap_{j=1}^{M}Q_{j}$.

In our experiment we take $N\leq 4v+1$ for each choice of $v\in \mathbb{N}$ and hence we have $\Omega =\{(s,0,0,\ldots ,0)\}$.

We illustrate and compare the numerical results of Algorithm 1 in view of the number of iterations ($\operatorname{Iter}(n)$) and the time of execution in seconds (CPUt) using the following data:

• Data I: $G_{t\times s}$ is a randomly generated $t\times s$ matrix and starting points $x_{0}$ and $x_{1}$ are also randomly generated.

• Parameters for Data I: $\delta _{j,n}=\frac{j}{\sum_{t=1}^{M}t}$, $\alpha _{n}=\frac{1}{\sqrt{n+1}}$, $\rho _{n}=1$ and $\theta _{n}=0.8$.

• Stopping Criterion: $\frac{\|x_{n+1}-x_{n}\|}{\|x_{2}-x_{1}\|}\leq TOL$.

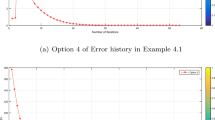
The numerical results are showed in Fig. 1, Tables 1 and 2. In Fig. 1, the x-axis represents the number of iterations n while the y-axis gives the value of $\|x_{n+1}-x_{n}\|$ generated by each iteration n.

Figure 1

Comparison of Algorithm 1 with GPM, PPM, and SAPM for $s=t=10$ and randomly generated starting points $x_{0}$ and $x_{1}$.

Table 1 Algorithm 1 for $v=1$, $N=5$, $M=1$, $s=4=t$, $\varrho _{1}=-2$, $\varrho _{2}=4$, $\varrho _{3}=2$, $\varrho _{4}=-2.5$, and $TOL=10^{-3}$

Table 2 For $\varrho _{j}=j$ for each $j=1,\ldots ,M$

We compare Algorithm 1 with the gradient projection method (GPM) by Censor et al. [27, Algorithm 1], the perturbed projection method (PPM) by Censor et al. [32, Algorithm 5], and the self-adaptive projection method (SAPM) by Zhao and Yang [34, Algorithm 3.2].

In view of Fig. 1 and Table 2, it is easy to observe that our algorithm has better performance than GPM, PPM, and SAPM. It appears in most cases our algorithm needed fewer iterations and converged more quickly than GPM, PPM, and SAPM.

Example 4.2

([41])

Consider the Hilbert space $H_{1} = H_{2} = L^{2}([0, 1])$ with norm $\|x||: = \sqrt{\int _{0}^{1} |x(s)|^{2}\,ds}$ and the inner product given by $\langle x| y\rangle = \int _{0}^{1}x(s)y(s)\,ds$. The two nonempty, closed, and convex sets are $C = \{x\in L^{2}([0, 1]): \langle x(s), 3s^{2}\rangle = 0\}$ and $Q = \{x\in L^{2}([0, 1]): \langle x, \frac{s}{3}\rangle \geq -1\}$, and the linear operator is given as $(Ax)(s) = x(s)$, i.e., $\|A\| = 1$ or $A = I$ is the identity. The orthogonal projections onto C and Q have explicit formulas (see, for example, [56]):

$$\begin{aligned}& P_{C}\bigl(v(s)\bigr)= \textstyle\begin{cases} v(s)- \frac{\langle v(s), 3s^{2}\rangle }{ \Vert 3s^{2} \Vert ^{2}_{L^{2}}}3s^{2}, &\text{if } \langle v(s), 3s^{2}\rangle \neq 0, \\ v(s),&\text{if } \langle v(s), 3s^{2}\rangle = 0, \end{cases}\displaystyle \end{aligned}$$

(49)

$$\begin{aligned}& P_{Q}\bigl(v(s)\bigr)= \textstyle\begin{cases} v(s)- \frac{\langle v(s), \frac{-s}{3}\rangle -1}{ \Vert \frac{-s}{3} \Vert ^{2}_{L^{2}}}( \frac{-s}{3}), &\text{if } \langle v(s), \frac{-s}{3}\rangle < -1, \\ v(s),&\text{if } \langle v(s), \frac{-s}{3}\rangle \geq -1. \end{cases}\displaystyle \end{aligned}$$

(50)

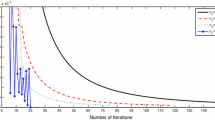
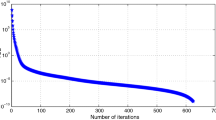
Now, we consider the SFP (1). It is clear that problem (1) has a nonempty solution set Ω since $0\in \Omega$. In this example, we compare scheme (48) with the strong convergence result of SFP proposed by Shehu [57]. In the iterative scheme (48), for $x_{0}, x_{1} \in C$, we take $\rho _{n}=3.5$, $\theta _{n}=0.75$, and $\alpha _{n}= \frac{1}{\sqrt{n+1}}$. The iterative scheme (27) in [57] for $u, x_{1}\in C$, with $\alpha _{n}=\frac{1}{n+1}$, $\beta _{n}=\frac{n}{2(n+1)}=\gamma _{n}$, and $t_{n}=\frac{1}{\|A\|^{2}}$ was reduced into the following form:

$$ \textstyle\begin{cases} y_{n}=[x_{n}-\frac{1}{ \Vert A \Vert ^{2}}A^{*}(Ax_{n}-P_{Q_{n}}(Ax_{n}))], \\ x_{n+1}=P_{C} (\frac{u}{n+1}+\frac{nx_{n}}{2(n+1)}+ \frac{ny_{n}}{2(n+1)} ),\quad n\geq 1. \end{cases} $$

(51)

We see here that our iterative scheme can be implemented to solve problem (1) considered in this example. We use $\|x_{n+1}-x_{n}\|< 10^{-4}$ as a stopping criterion for both schemes, and the outcome of the numerical experiment is reported in Figs. 2–5.

Figure 2

Comparison of schemes (48) and (51) for $x_{0}=u=e^{3s}$, and $x_{1}=e^{s}$.

Figure 3

Comparison of schemes (48) and (51) for $x_{0}=u=s$, and $x_{1}=e^{s}$.

Figure 4

Comparison of schemes (48) and (51) for $x_{0}=u=\sin (s)$, and $x_{1}=s$.

Figure 5

Comparison of schemes (48) and (51) for $x_{0}=u=se^{s}$, and $x_{1}=s^{2}+1$.

5 Conclusions

In this paper, we have presented a strongly convergent iterative algorithm with an inertial extrapolation to approximate the solution of MSSFP. A self-adaptive technique has been developed to choose the stepsizes such that the implementation of our algorithm does not need to know the prior operator norm. Some numerical experiments are given to illustrate the efficiency of the proposed iterative algorithm. Algorithm 1 is compared with the gradient projection method (GPM) by Censor et al. [27, Algorithm 1], the perturbed projection method (PPM) by Censor et al. [32, Algorithm 5], and the self-adaptive projection method (SAPM) by Zhao and Yang [34, Algorithm 3.2]. The numerical results show Algorithm 1 has a better performance than GPM, PPM, and SPM. In addition, scheme (48) is compared with scheme (51). It can be observed from Figs. 2–5 that, for different choices of u, $x_{0}$, and $x_{1}$, scheme (48) is faster in terms of the number of iterations and CPU-run time than scheme (51).