1 Introduction

Let \(H_{1}\) and \(H_{2}\) be real Hilbert spaces, \(t\geq 1\) and \(r\geq 1\) be integers, \(\{C_{i}\}_{i=1}^{t}\) and \(\{Q_{j}\}_{j=1}^{r}\) be the nonempty, closed, and convex subsets of \(H_{1}\) and \(H_{2}\).

In this paper, we study the multiple-sets split feasibility problem (MSSFP). This problem is to find a point \(x^{*}\) such that

$$\begin{aligned} x^{*}\in C=\bigcap_{i=1}^{t} C_{i},\qquad Ax^{*}\in Q=\bigcap_{j=1}^{r} Q_{j}, \end{aligned}$$
(1.1)

where \(A:H_{1}\rightarrow H_{2}\) is a given bounded linear operator and \(A^{*}\) is the adjoint operator of A. Censor et al. [6] first proposed this problem in finite-dimensional Hilbert spaces, mainly based on the inverse problem modeling in the intensity modulation radiation treatment modeling, the signal processing, and image reconstruction. Because of these implements, there are many algorithms that are proposed to work out the multiple-sets split feasibility problem, such as [24, 25, 28–30]. If \(t=r=1\), the multiple-sets split feasibility problem turns into the split feasibility problem, see [5].

It is well known that the split feasibility problem amounts to the following minimization problem:

$$\begin{aligned} \operatorname{min} \frac{1}{2} \bigl\Vert x-P_{C}(x) \bigr\Vert ^{2} + \frac{1}{2} \bigl\Vert Ax-P_{Q}(Ax) \bigr\Vert ^{2}, \end{aligned}$$
(1.2)

where \(P_{C}\) is the metric projection on C and \(P_{Q}\) is the metric projection on Q. It is important to note that since a projection on an ordinary closed convex set has not closed form method, it is difficult to calculate its projection. Fukushima [11] proposed a new relaxation projection formula to overcome this difficulty. Specifically, he calculated a projection on a convex functions level set by calculating a series of projections onto half-spaces containing the general level set. Yang [26] proposed a relaxed CQ algorithm for working out the split feasibility problem in the context of a finite-dimensional Hilbert space, in which closed convex subsets C and Q are the level sets of convex functions, which are proposed as follows:

$$\begin{aligned} C = \bigl\{ x \in H_{1}:c(x) \leq 0 \bigr\} \quad\text{and}\quad Q = \bigl\{ y \in H_{2} :q(y) \leq 0 \bigr\} , \end{aligned}$$
(1.3)

where \(c:H_{1}\rightarrow R\) and \(q:H_{2}\rightarrow R\) are convex functions which are weakly lower semi-continuous. Meanwhile, they assumed that c is subdifferentiable on \(H_{1}\) and ∂c is a bounded operator in any bounded subset of \(H_{1}\). Similarly, q is subdifferentiable on \(H_{2}\) and ∂q is also a bounded operator in any bounded subset of \(H_{2}\). Then two sets are defined at point \(x_{n}\) as follows:

$$\begin{aligned} C_{n} = \bigl\{ x \in H_{1}:c(x_{n}) \leq \langle \xi _{n},x_{n}-x\rangle \bigr\} , \end{aligned}$$
(1.4)

where \(\xi _{n}\in \partial {c(x_{n})}\), and

$$\begin{aligned} Q_{n} = \bigl\{ y \in H_{2}:q(Ax_{n}) \leq \langle \zeta _{n},Ax_{n}-y \rangle \bigr\} , \end{aligned}$$
(1.5)

where \(\zeta _{n}\in \partial {q(Ax_{n})}\). We can easily see that \(C_{n}\) and \(Q_{n}\) are half-spaces. For all \(n \geq 1\), we easily know that \(C_{n} \supset C\) and \(Q_{n}\supset Q\). Under this framework, the projection can be simply computed because of the particular form of the metric projection of the sets \(C_{n}\) and \(Q_{n}\), for details, please see [18]. Using this framework, Yang [26] built a new relaxed CQ algorithm, which was used to solve the split feasibility problem by using the semi-spaces \(C_{n}\) and \(Q_{n}\), rather than the sets C and Q. Whereafter, Shehu [19] came up with a relaxed CQ method with alternating inertial extrapolation step, which was used to solve the split feasibility problem by using the half spaces \(C_{n}\) and \(Q_{n}\). At the same time, they verified their convergence in certain appropriate step size.

In this paper, we consider a class of multiple-sets split feasibility problem (1.1), where the convex sets are defined by

$$\begin{aligned} C_{i} = \bigl\{ x \in H_{1}:c_{i}(x) \leq 0\bigr\} \quad \text{and} \quad Q_{j} = \bigl\{ y \in H_{2}:q_{j}(y) \leq 0\bigr\} , \end{aligned}$$
(1.6)

where \(c_{i}:H_{1}\rightarrow R\ (i=1,2,\ldots,t)\) and \(q_{j}:H_{2}\rightarrow R\ (j=1,2,\ldots,r)\) are the convex functions which are weakly lower semi-continuous. Meanwhile, it is assumed that \(c_{i}\ (i=1,2,\ldots,t)\) are subdifferentiable on \(H_{1}\) and \(\partial c_{i}\ (i=1,2,\ldots,t)\) are the bounded operators in any bounded subsets of \(H_{1}\). Similarly, \(q_{j}\ (j=1,2,\ldots,r)\) are subdifferentiable on \(H_{2}\) and \(\partial q_{j}\ (j=1,2,\ldots,r)\) are the bounded operators in any bounded subsets of \(H_{2}\). In the whole study, we represent the solution set of the multiple-sets split feasibility problem (1.1) by S, when it is consistent. Censor et al. [6] invented the following distance function:

$$\begin{aligned} f(x) = \frac{1}{2} \sum_{i=1}^{t} l_{i} \bigl\Vert x-P_{C_{i}}(x) \bigr\Vert ^{2} + \frac{1}{2} \sum_{j=1}^{r} \lambda _{j} \bigl\Vert Ax-P_{Q_{j}}(Ax) \bigr\Vert ^{2}, \end{aligned}$$
(1.7)

where \(l_{i}\ (i=1,2,\ldots,t)\) and \(\lambda _{j}\ (j=1,2,\ldots,r)\) are positive constants such that \(\sum_{i=1}^{t} l_{i}+\sum_{j=1}^{r} \lambda _{j}=1\). Then we know that

$$\begin{aligned} \nabla f(x) = \sum_{i=1}^{t} l_{i}\bigl(x-P_{C_{i}}(x)\bigr) + \sum _{j=1}^{r} \lambda _{j} A^{*}(I-P_{Q_{j}})Ax. \end{aligned}$$
(1.8)

They proposed the following algorithm:

$$\begin{aligned} x_{n+1} = P_{\Omega }\bigl(x_{n} - {\rho \nabla f_{n}(x_{n})}\bigr), \end{aligned}$$
(1.9)

where \(\Omega \subseteq R^{N}\) is the auxiliary brief nonempty closed convex set satisfying \(\Omega \cap S\neq \emptyset \) and \(\rho >0\). When L was the Lipschitz constant of \(\nabla f(x)\) and \(\rho \in (0,2/L)\), they proved that the sequence \(\{x_{n}\}\) produced by (1.9) converged to a solution of the multiple-sets split feasibility problem.

In order to improve the practicability of the method, in allusion to the split convex programming problem, Nesterov [17] proposed the next iterative process.

$$\begin{aligned} \begin{aligned} &{y_{n}}={x_{n}}+{ \theta _{n}(x_{n} - x_{n-1})}, \\ &x_{n+1}=y_{n}-\lambda _{n} \nabla f(y_{n}),\quad n\geq 1, \end{aligned} \end{aligned}$$
(1.10)

where \(\lambda _{n}\) is a positive array and \(\theta _{n}\in [0,1)\) is an inertial element. Besides that, there are many other correlative algorithms, for example, the inertial forward-backward splitting method, the inertial Mann method, and the moving asymptotes method, for details, please see [1–4, 10, 12, 14–16].

Under the motivation of the above study, we provide a relaxed CQ algorithm to solve the multiple-sets split feasibility problem by using an alternating inertial step. In this algorithm, the stepsize is determined by line search. Hence, it avoids the calculation of the operators norms. Furthermore, we prove the weak convergence of the algorithm under some mild conditions. In addition, the inertial factor of the controlling parameters \(\beta _{n}\) can be selected as far as possible to close to the one, such as [7–9, 20–23, 27].

The structure of the paper is as follows. The basic concepts, definitions, and related results are described in Sect. 2. The third section presents the algorithm and its proof, and the fourth section provides the corresponding numerical experiment, which verifies the validity and stability of the algorithm. The final summarization is offered in Sect. 5.

2 Preliminaries

In this section, we give some basic concepts and relevant conclusions. Suppose that H is a Hilbert space.

Look back upon that a mapping T: \(H \rightarrow H\) is called

  1. (a)

    nonexpansive if \(\Vert {Tx-Ty}\Vert \leq \Vert {x-y}\Vert \) for all \(x,y\in H\);

  2. (b)

    firmly nonexpansive if \(\Vert {Tx-Ty}\Vert ^{2} \leq \Vert {x-y}\Vert ^{2}-\Vert {(I-T)x-(I-T)y} \Vert ^{2}\) for all \(x,y\in H\). Equivalently, for all \(x,y\in H\), \(\Vert {Tx-Ty}\Vert ^{2} \leq \langle x-y,Tx-Ty\rangle \).

As we all know, T is firmly nonexpansive if and only if \(I-T\) is firmly nonexpansive.

For a point \(u\in H\) and C is a nonempty, closed, and convex set of H, there is a unique point \(P_{C}u\in C\) such that

$$\begin{aligned} \Vert {u-P_{C}u} \Vert \leq \Vert {u-y} \Vert , \quad \forall y\in C, \end{aligned}$$
(2.1)

where \(P_{C}\) is the metric projection of H on C. The following is a list of the significant quality of the metric projection. It is well known that \(P_{C}\) is the firmly nonexpansive mapping on C. Meanwhile, \(P_{C}\) possesses

$$\begin{aligned} \langle x-y,P_{C}x-P_{C}y\rangle \geq \Vert {P_{C}x-P_{C}y} \Vert ^{2},\quad \forall x,y \in H. \end{aligned}$$
(2.2)

Moreover, the characteristic of the \(P_{C}x\) is

$$\begin{aligned} P_{C}x\in C \quad\text{and}\quad \langle x-P_{C}x,P_{C}x-y \rangle \geq 0, \quad \forall y\in C. \end{aligned}$$
(2.3)

This representation means that

$$\begin{aligned} \Vert {x-y} \Vert ^{2} \geq \Vert {x-P_{C}x} \Vert ^{2}+ \Vert {y-P_{C}x} \Vert ^{2}, \quad\forall x\in H, \forall y\in C. \end{aligned}$$
(2.4)

Suppose that a function \(f:H\rightarrow R\), the element \(g\in H\) is thought to be the \(subgradient\) of f on a point x if

$$\begin{aligned} f(y) \geq f(x)+\langle y-x,g\rangle,\quad \forall y\in H. \end{aligned}$$
(2.5)

Besides, \(\partial f(x)\) is the subdifferential of f at the point x which is described by

$$\begin{aligned} \partial f(x)=\bigl\{ g\in H:f(y)\geq f(x)+\langle y-x,g\rangle, \forall y\in H\bigr\} . \end{aligned}$$
(2.6)

The function \(f:H\rightarrow R\) is thought to be weakly lower semi-continuous on a point x if \(\{x_{n}\}\) converges weakly to x. It means that

$$\begin{aligned} f(x)\leq \liminf_{n \to \infty } f(x_{n}). \end{aligned}$$
(2.7)

Lemma 2.1

([23])

Suppose that \(\{C_{i}\}_{i=1}^{t}\) and \(\{Q_{j}\}_{j=1}^{r}\) are the closed and convex subsets of \(H_{1}\) and \(H_{2}\), and \(A:H_{1}\rightarrow H_{2}\) is the bounded linear operator. At the same time, suppose that \(f(x)\) is a function described by (1.7). Then \(\nabla f(x)\) is Lipschitz continuous with \(L=\sum_{i=1}^{t} l_{i}+\Vert A\Vert ^{2} \sum_{j=1}^{r} \lambda _{j}\) as a Lipschitz constant.

Lemma 2.2

([19])

Suppose \(x,y\in H\). Then

(i) \(\Vert x+y\Vert ^{2} = \Vert x\Vert ^{2}+2\langle x,y \rangle +\Vert y\Vert ^{2}\);

(ii) \(\Vert x+y\Vert ^{2} \leq \Vert x\Vert ^{2}+2\langle y,x+y \rangle \);

(iii) \(\Vert \alpha x+\beta y\Vert ^{2} = \alpha (\alpha +\beta ) \Vert x\Vert ^{2}+\beta (\alpha +\beta )\Vert y\Vert ^{2}-\alpha \beta \Vert x-y\Vert ^{2}, \forall \alpha,\beta \in R\).

Lemma 2.3

([18])

Suppose that the half-spaces \(C_{k}\) and \(Q_{k}\) are defined as (1.4) and (1.5). Then the projections onto them from the points x and y are given as follows, respectively:

$$\begin{aligned} P_{C_{k}}(x)= \textstyle\begin{cases} x- \frac{c(x^{k})+\langle \xi ^{k},x-x^{k}\rangle }{ \Vert \xi _{k} \Vert ^{2}} \xi _{k} & \textit{if } c(x^{k})+\langle \xi ^{k},x-x^{k}\rangle >0; \\ x & \textit{if } c(x^{k})+\langle \xi ^{k},x-x^{k}\rangle \leq 0; \end{cases}\displaystyle \end{aligned}$$

and

$$\begin{aligned} P_{Q_{k}}(y)= \textstyle\begin{cases} y- \frac{q(y^{k})+\langle \zeta ^{k},y-y^{k}\rangle }{ \Vert \zeta _{k} \Vert ^{2}} \zeta _{k} & \textit{if } q(y^{k})+\langle \zeta ^{k},y-y^{k}\rangle >0; \\ y & \textit{if } q(y^{k})+\langle \zeta ^{k},y-y^{k}\rangle \leq 0. \end{cases}\displaystyle \end{aligned}$$

3 The algorithm and convergence analysis

For \(n \geq 1\), define

$$\begin{aligned} C_{i}^{n} = \bigl\{ x \in H_{1}:c_{i}(x_{n}) \leq \bigl\langle \xi _{i}^{n},x_{n}-x \bigr\rangle \bigr\} , \end{aligned}$$
(3.1)

where \(\xi _{i}^{n}\in \partial {c_{i}(x_{n})}\) for \(i=1,2,\ldots,t\), and

$$\begin{aligned} Q_{j}^{n} = \bigl\{ y \in H_{2}:q_{j}(Ax_{n}) \leq \bigl\langle \zeta _{j}^{n},Ax_{n}-y \bigr\rangle \bigr\} , \end{aligned}$$
(3.2)

where \(\zeta _{j}^{n}\in \partial {q_{j}(Ax_{n})}\) for \(j=1,2,\ldots,r\). We can easily see that \(C_{i}^{n}\ (i=1,2,\ldots,t)\) and \(Q_{j}^{n}\ (j=1,2,\ldots,r)\) are half-spaces. It is easy to see that, for all \(n \geq 1\), \(C_{i}^{n} \supset C_{i}\ (i=1,2,\ldots,t)\) and \(Q_{j}^{n}\supset Q_{j}\ (j=1,2,\ldots,r)\). We define

$$\begin{aligned} f_{n}(x) = \frac{1}{2} \sum _{i=1}^{t} l_{i} \bigl\Vert x-P_{C_{i}^{n}}(x) \bigr\Vert ^{2} + \frac{1}{2} \sum _{j=1}^{r} \lambda _{j} \bigl\Vert Ax-P_{Q_{j}^{n}}(Ax) \bigr\Vert ^{2}, \end{aligned}$$
(3.3)

where \(C_{i}^{n}\ (i=1,2,\ldots,t)\) and \(Q_{j}^{n}\ (j=1,2,\ldots,r)\) are respectively given by (3.1) and (3.2). Then we know

$$\begin{aligned} \nabla f_{n}(x) = \sum_{i=1}^{t} l_{i}\bigl(x-P_{C_{i}^{n}}(x)\bigr) + \sum _{j=1}^{r} \lambda _{j} A^{*}(I-P_{Q_{j}^{n}})Ax, \end{aligned}$$
(3.4)

where \(A^{*}\) denotes the adjoint operator of A. And \(l_{i}\ (i=1,2,\ldots,t)\) and \(\lambda _{j}\ (j=1,2,\ldots,r)\) are positive constants such that \(\sum_{i=1}^{t} l_{i}+\sum_{j=1}^{r} \lambda _{j}=1\).

Now, we propose an algorithm for solving the multiple-sets split feasibility problem (1.1), where \(C_{i}\ (i=1,2,\ldots,t)\) and \(Q_{j}\ (j=1,2,\ldots,r)\) are as shown in (1.6).

Algorithm 3.1

(The inertial relaxed algorithm with Armijo-type line search)

Step 1: Given \(\gamma > 0\), \(l \in (0,1)\), \(\mu \in (0,1)\), select the parameter \(\beta _{n}\) such that

$$\begin{aligned} {0} \leq {\beta _{n}} < {\frac{1 - \mu }{1 + \mu }}. \end{aligned}$$
(3.5)

Select starting points \(x_{0}, x_{1} \in H_{1}\) and set \(n = 1\).

Step 2: For the iterations \(x_{n}, x_{n-1}\), calculate

$$\begin{aligned} {y_{n}}= \textstyle\begin{cases} {x_{n}}& \textit{$n =\textit{ eve}n$}, \\ {x_{n}} + {\beta _{n}(x_{n} - x_{n-1})}& \textit{$n = \textit{ odd}$.} \end{cases}\displaystyle \end{aligned}$$
(3.6)

Step 3: Calculate

$$\begin{aligned} z_{n} = P_{\Omega }\bigl(y_{n} - {\tau _{n} \nabla f_{n}(y_{n})}\bigr), \end{aligned}$$
(3.7)

where \(\tau _{n} = \gamma l^{m_{n}}\) and \(m_{n}\) is the smallest nonnegative integer such that

$$\begin{aligned} \tau _{n} \bigl\Vert { \nabla f_{n}(y_{n}) - \nabla f_{n}(z_{n})} \bigr\Vert \leq {\mu \Vert {y_{n}-z_{n}} \Vert }. \end{aligned}$$

Step 4: Compute the new iterate point

$$\begin{aligned} x_{n+1} = P_{\Omega }\bigl(y_{n} - {\tau _{n} \nabla f_{n}(z_{n})}\bigr). \end{aligned}$$
(3.8)

Step 5: Set \(n \leftarrow n+1\), and go to Step 2.

In the following, we prove the convergence of Algorithm 3.1.

Lemma 3.1

Suppose that the solution set of MSSFP is nonempty, that is, \(S \neq \emptyset \) and {\(x_{n}\)} is any sequence generated by Algorithm 3.1. Then {\(x_{2n}\)} is Fejer monotone with respect to S (i.e., \(\Vert x_{2n+2}-z \Vert \leq \Vert x_{2n}-z \Vert, \forall z \in S\)).

Proof

Choose a point z in S. We have

$$\begin{aligned} & { \Vert x_{2n+2}-z \Vert ^{2}} \\ &\quad= \bigl\Vert {P_{\Omega }\bigl(y_{2n+1}-{ \tau _{2n+1}\nabla f_{2n+1}(z_{2n+1})}\bigr)- z} \bigr\Vert ^{2} \\ &\quad\leq { \bigl\Vert {(y_{2n+1}- z)-{\tau _{2n+1} \nabla f_{2n+1}(z_{2n+1})}} \bigr\Vert ^{2}} \\ &\qquad{}- { \bigl\Vert {x_{2n+2}-y_{2n+1}+{\tau _{2n+1}\nabla f_{2n+1}(z_{2n+1})}} \bigr\Vert ^{2}} \\ &\quad = { \Vert {y_{2n+1}- z} \Vert ^{2}}-{2\tau _{2n+1} \bigl\langle \nabla f_{2n+1}(z_{2n+1}), y_{2n+1}- z\bigr\rangle }-{ \Vert {x_{2n+2}- y_{2n+1}} \Vert ^{2}} \\ &\qquad{}- {2\tau _{2n+1} \bigl\langle \nabla f_{2n+1}(z_{2n+1}), x_{2n+2}- y_{2n+1}\bigr\rangle } \\ &\quad = { \Vert {y_{2n+1}- z} \Vert ^{2}}-{2\tau _{2n+1} \bigl\langle \nabla f_{2n+1}(z_{2n+1}), z_{2n+1}- z\bigr\rangle } \\ &\qquad{}-{2\tau _{2n+1} \bigl\langle \nabla f_{2n+1}(z_{2n+1}), y_{2n+1}- z_{2n+1}\bigr\rangle }-{ \Vert {x_{2n+2}- y_{2n+1}} \Vert ^{2}} \\ \begin{aligned} &\qquad{}-{2\tau _{2n+1} \bigl\langle \nabla f_{2n+1}(z_{2n+1}), x_{2n+2}- y_{2n+1}\bigr\rangle } \\ &\quad= { \Vert {y_{2n+1}- z} \Vert ^{2}}-{2\tau _{2n+1} \bigl\langle \nabla f_{2n+1}(z_{2n+1}), z_{2n+1}- z\bigr\rangle } \end{aligned} \\ &\qquad{}-{2\tau _{2n+1} \bigl\langle \nabla f_{2n+1}(z_{2n+1}), x_{2n+2}- z_{2n+1}\bigr\rangle } \\ &\qquad{}-{ \Vert {x_{2n+2}- z_{2n+1}+ z_{2n+1}- y_{2n+1}} \Vert ^{2}} \\ &\quad= { \Vert {y_{2n+1}- z} \Vert ^{2}}-{2\tau _{2n+1} \bigl\langle \nabla f_{2n+1}(z_{2n+1}), z_{2n+1}- z\bigr\rangle } \\ &\qquad{}-{2\tau _{2n+1} \bigl\langle \nabla f_{2n+1}(z_{2n+1}), x_{2n+2}- z_{2n+1}\bigr\rangle }-{ \Vert x_{2n+2}- z_{2n+1} \Vert ^{2}} \\ &\qquad{}-{2\langle x_{2n+2}-z_{2n+1}, z_{2n+1}-y_{2n+1} \rangle }-{ \Vert z_{2n+1}- y_{2n+1} \Vert ^{2}} \\ &\quad= { \Vert {y_{2n+1}- z} \Vert ^{2}}-{ \Vert x_{2n+2}- z_{2n+1} \Vert ^{2}}-{ \Vert z_{2n+1}- y_{2n+1} \Vert ^{2}} \\ &\qquad{}-{2\bigl\langle {z_{2n+1}-y_{2n+1}+\tau _{2n+1}\nabla f_{2n+1}(z_{2n+1})}, x_{2n+2}-z_{2n+1}\bigr\rangle } \\ &\qquad{}-{2\tau _{2n+1} \bigl\langle \nabla f_{2n+1}(z_{2n+1}), z_{2n+1}- z\bigr\rangle }. \end{aligned}$$
(3.9)

Due to the fact that \(z_{2n+1} \in \Omega \), we have

$$\begin{aligned} \begin{aligned} &\bigl\langle {z_{2n+1}-y_{2n+1}+ \tau _{2n+1}\nabla f_{2n+1}(y_{2n+1})}, x_{2n+2}-z_{2n+1}\bigr\rangle \\ &\quad =\bigl\langle {P_{\Omega }\bigl(y_{2n+1}- \tau _{2n+1}\nabla f_{2n+1}(y_{2n+1})\bigr)-y_{2n+1}+ \tau _{2n+1}\nabla f_{2n+1}(y_{2n+1})}, \\ &\qquad x_{2n+2}-P_{\Omega }\bigl(y_{2n+1}-\tau _{2n+1} \nabla f_{2n+1}(y_{2n+1})\bigr) \bigr\rangle \geq 0. \end{aligned} \end{aligned}$$
(3.10)

As a result,

$$\begin{aligned} \begin{aligned} &{-}2\bigl\langle {z_{2n+1}-y_{2n+1}+\tau _{2n+1}\nabla f_{2n+1}(z_{2n+1})}, x_{2n+2}-z_{2n+1}\bigr\rangle \\ &\quad\leq 2\bigl\langle {y_{2n+1}-z_{2n+1}-\tau _{2n+1} \nabla f_{2n+1}(z_{2n+1})}, x_{2n+2}-z_{2n+1} \bigr\rangle \\ &\qquad{}+2\bigl\langle {z_{2n+1}-y_{2n+1}+\tau _{2n+1}\nabla f_{2n+1}(y_{2n+1})}, x_{2n+2}-z_{2n+1} \bigr\rangle \\ &\quad=2\bigl\langle {\tau _{2n+1}\nabla f_{2n+1}(y_{2n+1})- \tau _{2n+1}\nabla f_{2n+1}(z_{2n+1})}, x_{2n+2}-z_{2n+1}\bigr\rangle \\ &\quad\leq 2\tau _{2n+1} \bigl\Vert \nabla f_{2n+1}(y_{2n+1})- \nabla f_{2n+1}(z_{2n+1}) \bigr\Vert \Vert x_{2n+2}-z_{2n+1} \Vert \\ &\quad\leq \tau _{2n+1}^{2} \bigl\Vert \nabla f_{2n+1}(y_{2n+1})- \nabla f_{2n+1}(z_{2n+1}) \bigr\Vert ^{2} + \Vert x_{2n+2}-z_{2n+1} \Vert ^{2} \\ &\quad \leq \mu ^{2} \Vert y_{2n+1}-z_{2n+1} \Vert ^{2}+ \Vert x_{2n+2}-z_{2n+1} \Vert ^{2}. \end{aligned} \end{aligned}$$
(3.11)

As \({I-P_{C_{i}^{2n+1}}}\) and \({I-P_{Q_{j}^{2n+1}}}\) are firmly-nonexpansive and \(\nabla f_{2n+1}(z_{2n+1})=0\), then

$$\begin{aligned} & 2\tau _{2n+1} \bigl\langle \nabla f_{2n+1}(z_{2n+1}), z_{2n+1}- z\bigr\rangle \\ &\quad =2\tau _{2n+1} \bigl\langle \nabla f_{2n+1}(z_{2n+1})- \nabla f_{2n+1}(z), z_{2n+1}- z\bigr\rangle \\ &\quad = 2\tau _{2n+1} \Biggl\langle \sum _{i=1}^{t} l_{i}(I-P_{C_{i}^{2n+1}})z_{2n+1} + \sum_{j=1}^{r} \lambda _{j} A^{*}(I-P_{Q_{j}^{2n+1}})Az_{2n+1} \\ &\qquad{}-\sum_{i=1}^{t} l_{i}(I-P_{C_{i}^{2n+1}})z - \sum_{j=1}^{r} \lambda _{j} A^{*}(I-P_{Q_{j}^{2n+1}})Az, z_{2n+1} - z\Biggr\rangle \\ &\quad= 2\tau _{2n+1}\Biggl[\Biggl\langle \sum _{i=1}^{t} l_{i}(I-P_{C_{i}^{2n+1}})z_{2n+1}- \sum_{i=1}^{t} l_{i}(I-P_{C_{i}^{2n+1}})z, z_{2n+1}- z\Biggr\rangle \\ &\qquad{}+\Biggl\langle \sum_{j=1}^{r} \lambda _{j}(I-P_{Q_{j}^{2n+1}})Az_{2n+1}- \sum _{j=1}^{r} \lambda _{j}(I-P_{Q_{j}^{2n+1}})Az, Az_{2n+1}- Az\Biggr\rangle \Biggr] \\ &\quad\geq 2\tau _{2n+1}\Biggl[\sum_{i=1}^{t} l_{i} \bigl\Vert (I-P_{C_{i}^{2n+1}})z_{2n+1}-(I-P_{C_{i}^{2n+1}})z \bigr\Vert ^{2} \\ &\qquad{}+\sum_{j=1}^{r} \lambda _{j} \bigl\Vert (I-P_{Q_{j}^{2n+1}})Az_{2n+1}-(I-P_{Q_{j}^{2n+1}})Az \bigr\Vert ^{2}\Biggr] \\ &\quad\geq \frac{2\mu l}{ \Vert A \Vert ^{2}} \Biggl[\sum_{i=1}^{t} l_{i} \bigl\Vert (I-P_{C_{i}^{2n+1}})z_{2n+1} \bigr\Vert ^{2}+ \sum_{j=1}^{r} \lambda _{j} \bigl\Vert (I-P_{Q_{j}^{2n+1}})Az_{2n+1} \bigr\Vert ^{2}\Biggr]. \end{aligned}$$
(3.12)

Putting (3.10), (3.11), (3.12) into (3.9), one has

$$\begin{aligned} \begin{aligned} & { \Vert x_{2n+2}-z \Vert ^{2}} \\ &\quad\leq \Vert y_{2n+1}-z \Vert ^{2}-\bigl(1-\mu ^{2}\bigr) \Vert y_{2n+1}-z_{2n+1} \Vert ^{2} \\ &\qquad{} -\frac{2\mu l}{ \Vert A \Vert ^{2}} \Biggl[ \sum_{i=1}^{t} l_{i} \bigl\Vert (I-P_{C_{i}^{2n+1}})z_{2n+1} \bigr\Vert ^{2}+\sum_{j=1}^{r} \lambda _{j} \bigl\Vert (I-P_{Q_{j}^{2n+1}})Az_{2n+1} \bigr\Vert ^{2}\Biggr]. \end{aligned} \end{aligned}$$
(3.13)

Similar to the discussion of (3.13), we can know

$$\begin{aligned} \begin{aligned}& { \Vert x_{2n+1}-z \Vert ^{2}} \\ &\quad\leq \Vert y_{2n}-z \Vert ^{2}-\bigl(1-\mu ^{2}\bigr) \Vert y_{2n}-z_{2n} \Vert ^{2} \\ &\qquad{}-\frac{2\mu l}{ \Vert A \Vert ^{2}} \Biggl[ \sum_{i=1}^{t} l_{i} \bigl\Vert (I-P_{C_{i}^{2n}})z_{2n} \bigr\Vert ^{2}+ \sum_{j=1}^{r} \lambda _{j} \bigl\Vert (I-P_{Q_{j}^{2n}})Az_{2n} \bigr\Vert ^{2}\Biggr] \\ &\quad = \Vert x_{2n}-z \Vert ^{2}- \bigl(1-\mu ^{2}\bigr) \Vert y_{2n}-z_{2n} \Vert ^{2} \\ &\qquad{}-\frac{2\mu l}{ \Vert A \Vert ^{2}} \Biggl[ \sum_{i=1}^{t} l_{i} \bigl\Vert (I-P_{C_{i}^{2n}})z_{2n} \bigr\Vert ^{2}+\sum_{j=1}^{r} \lambda _{j} \bigl\Vert (I-P_{Q_{j}^{2n}})Az_{2n} \bigr\Vert ^{2}\Biggr] . \end{aligned} \end{aligned}$$
(3.14)

According to (3.6), we obtain

$$\begin{aligned} \begin{aligned} &\Vert y_{2n+1}-z \Vert ^{2} \\ &\quad= \bigl\Vert {x_{2n+1}} + {\beta _{2n+1}(x_{2n+1} - x_{2n})}-z \bigr\Vert ^{2} \\ &\quad= \bigl\Vert {x_{2n+1}}-\beta _{2n+1}z+\beta _{2n+1}z + {\beta _{2n+1}(x_{2n+1} - x_{2n})}-z \bigr\Vert ^{2} \\ &\quad= \bigl\Vert (1+\beta _{2n+1}) (x_{2n+1}-z)-\beta _{2n+1}(x_{2n}-z) \bigr\Vert ^{2} \\ &\quad=(1+\beta _{2n+1}) \Vert x_{2n+1}-z \Vert ^{2} - \beta _{2n+1} \Vert x_{2n}-z \Vert ^{2} \\ &\qquad{}+\beta _{2n+1}(1+\beta _{2n+1}) \Vert x_{2n+1}-x_{2n} \Vert ^{2}. \end{aligned} \end{aligned}$$
(3.15)

Substituting (3.14) and (3.15) into (3.13), one has

$$\begin{aligned} \begin{aligned} &{ \Vert x_{2n+2}-z \Vert ^{2}} \\ &\quad\leq \Vert x_{2n}-z \Vert ^{2}-(1+\beta _{2n+1}) \bigl(1-\mu ^{2}\bigr) \Vert y_{2n}-z_{2n} \Vert ^{2} \\ &\qquad{}-(1+\beta _{2n+1})\frac{2\mu l}{ \Vert A \Vert ^{2}} \Biggl[ \sum _{i=1}^{t} l_{i} \bigl\Vert (I-P_{C_{i}^{2n}})z_{2n} \bigr\Vert ^{2}+ \sum _{j=1}^{r} \lambda _{j} \bigl\Vert (I-P_{Q_{j}^{2n}})Az_{2n} \bigr\Vert ^{2}\Biggr] \\ &\qquad{}-\bigl(1-\mu ^{2}\bigr) \Vert y_{2n+1}-z_{2n+1} \Vert ^{2}+\beta _{2n+1}(1+ \beta _{2n+1}) \Vert x_{2n+1}-x_{2n} \Vert ^{2} \\ &\qquad{}-\frac{2\mu l}{ \Vert A \Vert ^{2}} \Biggl[ \sum_{i=1}^{t} l_{i} \bigl\Vert (I-P_{C_{i}^{2n+1}})z_{2n+1} \bigr\Vert ^{2}+\sum_{j=1}^{r} \lambda _{j} \bigl\Vert (I-P_{Q_{j}^{2n+1}})Az_{2n+1} \bigr\Vert ^{2}\Biggr]. \end{aligned} \end{aligned}$$
(3.16)

Note that

$$\begin{aligned} \begin{aligned} &\Vert x_{2n+1}-x_{2n} \Vert \\ &\quad\leq \Vert x_{2n+1}-z_{2n} \Vert + \Vert z_{2n}-x_{2n} \Vert \\ &\quad= \bigl\Vert P_{\Omega }\bigl(y_{2n} - {\tau _{2n} \nabla f_{2n}(z_{2n})}\bigr)-z_{2n} \bigr\Vert + \Vert x_{2n}-z_{2n} \Vert \\ &\quad\leq \bigl\Vert y_{2n} - {\tau _{2n} \nabla f_{2n}(z_{2n})}-y_{2n}+{\tau _{2n} \nabla f_{2n}(y_{2n})} \bigr\Vert + \Vert x_{2n}-z_{2n} \Vert \\ &\quad=\tau _{2n} \bigl\Vert \nabla f_{2n}(y_{2n})- \nabla f_{2n}(z_{2n}) \bigr\Vert + \Vert x_{2n}-z_{2n} \Vert \\ &\quad\leq (1+\mu ) \Vert x_{2n}-z_{2n} \Vert . \end{aligned} \end{aligned}$$
(3.17)

Combining (3.16) and (3.17), we have

$$\begin{aligned} \begin{aligned} &{ \Vert x_{2n+2}-z \Vert ^{2}} \\ &\quad\leq \Vert x_{2n}-z \Vert ^{2}-\bigl(1-\mu ^{2}\bigr) \Vert y_{2n+1}-z_{2n+1} \Vert ^{2} \\ &\qquad{}-(1+\beta _{2n+1})\frac{2\mu l}{ \Vert A \Vert ^{2}} \Biggl[ \sum _{i=1}^{t} l_{i} \bigl\Vert (I-P_{C_{i}^{2n}})z_{2n} \bigr\Vert ^{2}+ \sum _{j=1}^{r} \lambda _{j} \bigl\Vert (I-P_{Q_{j}^{2n}})Az_{2n} \bigr\Vert ^{2}\Biggr] \\ &\qquad{}-\bigl[ (1+\beta _{2n+1}) \bigl(1-\mu ^{2}\bigr)-\beta _{2n+1}(1+\beta _{2n+1}) (1+ \mu )^{2}\bigr] \Vert y_{2n}-z_{2n} \Vert ^{2} \\ &\qquad{}-\frac{2\mu l}{ \Vert A \Vert ^{2}} \Biggl[ \sum_{i=1}^{t} l_{i} \bigl\Vert (I-P_{C_{i}^{2n+1}})z_{2n+1} \bigr\Vert ^{2}+\sum_{j=1}^{r} \lambda _{j} \bigl\Vert (I-P_{Q_{j}^{2n+1}})Az_{2n+1} \bigr\Vert ^{2}\Biggr] \\ &\quad\leq \Vert x_{2n}-z \Vert ^{2}, \end{aligned} \end{aligned}$$
(3.18)

where \(\mu \in (0,1)\), \(\beta _{2n+1}\in [0,\frac{1-\mu }{1+\mu }]\), so \((1-\mu ^{2})>0\), \((1+\beta _{2n+1})(1-\mu ^{2})-\beta _{2n+1}(1+\beta _{2n+1})(1+\mu )^{2}>0\), \(1+\beta _{2n+1}>0\), \(\frac{2\mu l}{\Vert A \Vert ^{2}}>0\).

Hence,

$$\begin{aligned} \Vert x_{2n+2}-z \Vert \leq \Vert x_{2n}-z \Vert . \end{aligned}$$

 □

Theorem 3.1

Suppose that \(S \neq \emptyset \) and {\(x_{n}\)} is any sequence generated by Algorithm 3.1. Then {\(x_{n}\)} converges weakly to a point in S.

Proof

According to Lemma 3.1, it is easy to know that \(\lim_{n \to \infty }\Vert x_{2n+2}-z \Vert \) exists. This means that {\(x_{2n}\)} is bounded. In addition, from (3.18), we conclude that

$$\begin{aligned} \lim_{n \to \infty }\Biggl[ \sum_{i=1}^{t} l_{i} \bigl\Vert (I-P_{C_{i}^{2n}})z_{2n} \bigr\Vert + \sum_{j=1}^{r} \lambda _{j} \bigl\Vert (I-P_{Q_{j}^{2n}})Az_{2n} \bigr\Vert \Biggr]=0. \end{aligned}$$

That is to say,

$$\begin{aligned} \lim_{n \to \infty } \bigl\Vert (I-P_{C_{i}^{2n}})z_{2n} \bigr\Vert =0\quad (i=1,2,\ldots,t) \end{aligned}$$
(3.19)

and

$$\begin{aligned} \lim_{n \to \infty } \bigl\Vert (I-P_{Q_{j}^{2n}})Az_{2n} \bigr\Vert =0\quad (j=1,2,\ldots,r). \end{aligned}$$
(3.20)

Besides,

$$\begin{aligned} \lim_{n \to \infty } \Vert x_{2n}-z_{2n} \Vert =0. \end{aligned}$$
(3.21)

Owing to \({I-P_{C_{i}^{2n}}}\) and \({I-P_{Q_{j}^{2n}}}\) are nonexpansive, then

$$\begin{aligned} \begin{aligned} & \bigl\Vert (I-P_{C_{i}^{2n}})x_{2n} \bigr\Vert \\ &\quad\leq \bigl\Vert (I-P_{C_{i}^{2n}})x_{2n}-(I-P_{C_{i}^{2n}})z_{2n} \bigr\Vert + \bigl\Vert (I-P_{C_{i}^{2n}})z_{2n} \bigr\Vert \\ &\quad\leq \Vert x_{2n}-z_{2n} \Vert + \bigl\Vert (I-P_{C_{i}^{2n}})z_{2n} \bigr\Vert \quad(i=1,2,\ldots,t) \end{aligned} \end{aligned}$$
(3.22)

and

$$\begin{aligned} \begin{aligned} & \bigl\Vert (I-P_{Q_{j}^{2n}})Ax_{2n} \bigr\Vert \\ &\quad\leq \bigl\Vert (I-P_{Q_{j}^{2n}})Ax_{2n}-(I-P_{Q_{j}^{2n}})Az_{2n} \bigr\Vert + \bigl\Vert (I-P_{Q_{j}^{2n}})Az_{2n} \bigr\Vert \\ &\quad\leq \Vert Ax_{2n}-Az_{2n} \Vert + \bigl\Vert (I-P_{Q_{j}^{2n}})Az_{2n} \bigr\Vert \\ &\quad\leq \Vert A \Vert \Vert x_{2n}-z_{2n} \Vert + \bigl\Vert (I-P_{Q_{j}^{2n}})Az_{2n} \bigr\Vert \quad(j=1,2,\ldots,r). \end{aligned} \end{aligned}$$
(3.23)

According to (3.19) and (3.21), from (3.22), we conclude that

$$\begin{aligned} \lim_{n \to \infty } \bigl\Vert (I-P_{C_{i}^{2n}})x_{2n} \bigr\Vert =0\quad (i=1,2,\ldots,t). \end{aligned}$$
(3.24)

According to (3.20) and (3.21), from (3.23), we conclude that

$$\begin{aligned} \lim_{n \to \infty } \bigl\Vert (I-P_{Q_{j}^{2n}})Ax_{2n} \bigr\Vert =0\quad (j=1,2,\ldots,r). \end{aligned}$$
(3.25)

Similar to the discussion in (3.24) and (3.25), we know

$$\begin{aligned} \begin{aligned} &\lim_{n \to \infty } \bigl\Vert (I-P_{C_{i}^{2n+1}})x_{2n+1} \bigr\Vert =0\quad (i=1,2,\ldots,t), \\ &\lim_{n \to \infty } \bigl\Vert (I-P_{Q_{j}^{2n+1}})Ax_{2n+1} \bigr\Vert =0\quad (j=1,2,\ldots,r). \end{aligned} \end{aligned}$$
(3.26)

As \(\partial {c_{i}}\) for \(i=1,2,\ldots,t\) are bounded on bounded sets, we have a constant \(\xi > 0\) such that \(\Vert \xi _{i}^{2n}\Vert \leq \xi\ (i=1,2,\ldots,t)\). On account of \(P_{C_{i}^{2n}}x_{2n}\in C_{i}^{2n}\), we obtain from the algorithm and (3.24) that

$$\begin{aligned} \begin{aligned} c_{i}(x_{2n}) &\leq \bigl\langle \xi _{i}^{2n},y_{2n}-P_{C_{i}^{2n}}x_{2n} \bigr\rangle =\bigl\langle \xi _{i}^{2n},(I-P_{C_{i}^{2n}})x_{2n} \bigr\rangle \\ &\leq \xi \bigl\Vert (I-P_{C_{i}^{2n}})x_{2n} \bigr\Vert \longrightarrow 0,\quad n \longrightarrow +\infty. \end{aligned} \end{aligned}$$
(3.27)

As {\(x_{2n}\)} is bounded, there exists a weakly convergent subsequence \(\{x_{2n_{k}}\}\subset \{x_{2n}\}, k\in N\), such that \(x_{2n_{k}}\rightharpoonup x^{*}, x^{*}\in H_{1}\). According to \(c_{i}\ (i=1,2,\ldots,t)\) being continuous and (3.27), we have

$$\begin{aligned} c_{i}\bigl(x^{*}\bigr)\leq \liminf _{k \to \infty } c_{i}(x_{2n_{k}}) \leq 0,\quad i=1,2,\ldots,t. \end{aligned}$$
(3.28)

So \(x^{*} \in C_{i}\) for \(i=1,2,\ldots,t\).

As \(\partial {q_{j}}\) for \(j=1,2,\ldots,r\) are bounded on bounded sets, we have a constant \(\zeta > 0\) such that \(\Vert \zeta _{j}^{2n}\Vert \leq \zeta \ (j=1,2,\ldots,r)\). On account of \(P_{Q_{j}^{2n}}x_{2n}\in Q_{j}^{2n}\), we obtain from the algorithm and (3.25) that

$$\begin{aligned} \begin{aligned} q_{j}(Ax_{2n}) & \leq \bigl\langle \zeta _{j}^{2n},Ay_{2n}-P_{Q_{j}^{2n}}Ax_{2n} \bigr\rangle =\bigl\langle \zeta _{j}^{2n},(I-P_{Q_{j}^{2n}})Ax_{2n} \bigr\rangle \\ &\leq \zeta \bigl\Vert (I-P_{Q_{j}^{2n}})Ax_{2n} \bigr\Vert \longrightarrow 0, \quad n \longrightarrow +\infty. \end{aligned} \end{aligned}$$
(3.29)

According to \(q_{j}\) for \(j=1,2,\ldots,r\) are continuous and (3.29), we have

$$\begin{aligned} q_{j}\bigl(Ax^{*}\bigr)\leq \liminf _{k \to \infty } q_{j}(Ax_{2n_{k}}) \leq 0,\quad j=1,2, \ldots,r. \end{aligned}$$
(3.30)

So \(Ax^{*} \in Q_{j}\) for \(j=1,2,\ldots,r\).

Thus, \(x^{*}\in S\).

Now, we are going to prove that {\(x_{2n+1}\)} converges to \(x^{*}\). Just for the sake of convenience, we are still going to use {\(x_{2n+1}\)} for the proof. According to \(\lim_{n \to \infty }\Vert x_{2n}-x^{*}\Vert \) exists and \(\lim_{n \to \infty }\Vert x_{2n_{k}}-x^{*}\Vert =0\), these mean that \(\lim_{n \to \infty }\Vert x_{2n}-x^{*}\Vert =0\). Thus, \(x^{*}\) is sole.

Using the same discussion in (3.9)–(3.13), we can know that

$$\begin{aligned} \begin{aligned} &{ \bigl\Vert x_{2n+1}-x^{*} \bigr\Vert ^{2}} \\ &\quad= \bigl\Vert {P_{\Omega }\bigl(y_{2n}-{\tau _{2n} \nabla f_{2n}(z_{2n})}\bigr)- x^{*}} \bigr\Vert ^{2} \\ &\quad \leq { \bigl\Vert {y_{2n}- x^{*}} \bigr\Vert ^{2}}-{ \Vert x_{2n+1}- z_{2n} \Vert ^{2}}-{ \Vert z_{2n}- y_{2n} \Vert ^{2}} \\ &\qquad{}-{2\bigl\langle {z_{2n}-y_{2n}+\tau _{2n}\nabla f_{2n}(z_{2n})}, x_{2n+1}-z_{2n}\bigr\rangle } \\ &\qquad{}-{2\tau _{2n} \bigl\langle \nabla f_{2n}(z_{2n}), z_{2n}- x^{*}\bigr\rangle } \\ &\quad\leq \bigl\Vert y_{2n}-x^{*} \bigr\Vert ^{2}-\bigl(1-\mu ^{2}\bigr) \Vert y_{2n}-z_{2n} \Vert ^{2} \\ &\qquad{}-\frac{2\mu l}{ \Vert A \Vert ^{2}} \Biggl[ \sum_{i=1}^{t} l_{i} \bigl\Vert (I-P_{C_{i}^{2n}})z_{2n} \bigr\Vert ^{2}+ \sum_{j=1}^{r} \lambda _{j} \bigl\Vert (I-P_{Q_{j}^{2n}})Az_{2n} \bigr\Vert ^{2}\Biggr] \\ &\quad\leq \bigl\Vert y_{2n}-x^{*} \bigr\Vert ^{2}. \end{aligned} \end{aligned}$$
(3.31)

Thus,

$$\begin{aligned} { \bigl\Vert x_{2n+1}-x^{*} \bigr\Vert ^{2}} \leq \bigl\Vert y_{2n}-x^{*} \bigr\Vert ^{2}= \bigl\Vert x_{2n}-x^{*} \bigr\Vert ^{2}. \end{aligned}$$
(3.32)

Consequently,

$$\begin{aligned} \lim_{n \to \infty } \bigl\Vert x_{2n+1}-x^{*} \bigr\Vert =0. \end{aligned}$$
(3.33)

To sum up,

$$\begin{aligned} \lim_{n \to \infty } x_{n}=x^{*}. \end{aligned}$$

 □

4 Numerical examples

As in Example 4.1, we will provide the results in this section. The whole codes are written in Matlab R2012a. All the numerical results are carried out on a personal Lenovo Thinkpad computer with Intel(R) Core(TM) i7-3517U CPU 2.40 GHz and RAM 8.00GB. Firstly, we are going to come up with some different \(x_{0},x_{1}\) in our Algorithm 3.1. These results are provided in Table 1 and Fig. 1. Secondly, we contrast Algorithm 3.1 in this paper and Algorithm 3.1 in [23]. From the numerical results of Example 1 in [23], it is better than the results in [13]. So our algorithm is compared to Algorithm 3.1 in [23]. These results are provided in Table 2. Lastly, we check the stability of the iteration number for Algorithm 3.1 in this paper comparing with Algorithm 3.1 in [23]. These results are provided in Figs. 2–4.

Figure 1
figure 1

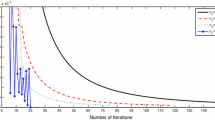
Error history in Example 4.1

Full size image
Figure 2
figure 2

The iteration number of Algorithm 3.1 in this paper and Algorithm 3.1 in [23]

Full size image
Table 1 Algorithm 3.1 in this paper under diverse options of \(x_{0}\) and \(x_{1}\)
Full size table
Table 2 Comparison of Algorithm 3.1 in this paper and Algorithm 3.1 in [23]
Full size table

Example 4.1

([13])

Suppose that \(H_{1}=H_{2}=R^{3}\), \(r=t=2\), and \(l_{1}=l_{2}=\lambda _{1}=\lambda _{2}=\frac{1}{4}\). We give that

$$\begin{aligned} \begin{aligned}& C_{1} = \bigl\{ x=(a,b,c)^{T} \in R^{3}:a+b^{2}+2c\leq 0\bigr\} , \\ &C_{2} = \biggl\{ x=(a,b,c)^{T} \in R^{3}: \frac{a^{2}}{16}+\frac{b^{2}}{9}+ \frac{c^{2}}{4}-1\leq 0\biggr\} , \\ &Q_{1} = \bigl\{ x=(a,b,c)^{T} \in R^{3}:a^{2}+b-c \leq 0\bigr\} , \\ &Q_{2} = \biggl\{ x=(a,b,c)^{T} \in R^{3}: \frac{a^{2}}{4}+\frac{b^{2}}{4}+ \frac{c^{2}}{9}-1\leq 0\biggr\} , \end{aligned} \end{aligned}$$
(4.1)

and

$$A= \begin{pmatrix} 2&-1&3 \\ 4&2&5 \\ 2&0&2\end{pmatrix}. $$

To find \(x^{*}\in C_{1}\cap C_{2}\) such that \(Ax^{*}\in Q_{1}\cap Q_{2}\).

In the first place, let \(\gamma =2\), \(l=0.5\), \(\mu =0.95\), and \(\beta _{n}=\frac{1}{n+1}\). Next, we study the iteration number required for the convergence of the sequence under different initial values. The condition for stopping the iteration is

$$\begin{aligned} E_{n}=\frac{1}{2}\sum_{i=1}^{2} \bigl\Vert x_{n}-P_{C_{i}^{n}}(x_{n}) \bigr\Vert ^{2} + \frac{1}{2}\sum_{j=1}^{2} \bigl\Vert Ax_{n}-P_{Q_{j}^{n}}(Ax_{n}) \bigr\Vert ^{2}< 10^{-4}. \end{aligned}$$
(4.2)

We select diverse options of \(x_{0}\) and \(x_{1}\) as follows.

  1. Option 1:

    \(x_{0}=(1,1,5)^{T}\) and \(x_{1}=(5,-3,2)^{T}\);

  2. Option 2:

    \(x_{0}=(-4,3,-2)^{T}\) and \(x_{1}=(-5,2,1)^{T}\);

  3. Option 3:

    \(x_{0}=(7,5,1)^{T}\) and \(x_{1}=(7,-3,-1)^{T}\);

  4. Option 4:

    \(x_{0}=(1,-6,-4)^{T}\) and \(x_{1}=(-4,1,6)^{T}\);

  5. Option 5:

    \(x_{0}=(-4,-2,-3)^{T}\) and \(x_{1}=(-5,-2,-3)^{T}\);

  6. Option 6:

    \(x_{0}=(-5.34,-7.36,-3.21)^{T}\) and \(x_{1}=(0.23,-2.13,3.56)^{T}\);

  7. Option 7:

    \(x_{0}=(-2.345,2.431,1.573)^{T}\) and \(x_{1}=(1.235,-1.756,-4.234)^{T}\);

  8. Option 8:

    \(x_{0}=(5.32,2.33,7.75)^{T}\) and \(x_{1}=(3.23,3.75,-3.86)^{T}\).

From Table 1, we can see the iteration number and running time of Algorithm 3.1 in this paper for diverse options of \(x_{0}\) and \(x_{1}\).

In Algorithm 3.1, if we choose \(x_{0}\) and \(x_{1}\) as Option 4 and Option 5, the compartment of the error \(E_{n}\) is gradually converging, for details, please see Fig. 1. For other options, they are also gradually converging, which we do not show here.

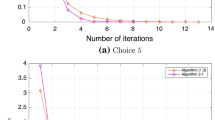
Now, we compare Algorithm 3.1 in this paper and Algorithm 3.1 in [23]. The results are as shown in Table 2. Furthermore, in order to test the stability of the iteration number, 500 diverse initial value points are randomly selected for the experiment in the context of Algorithm 3.1 in this paper, for instance,

$$\begin{aligned} &x_{0}=\operatorname{rand}(3,1),\qquad x_{1}=\operatorname{rand}(3,1)*10, \\ &x_{0}=\operatorname{rand}(3,1),\qquad x_{1}=\operatorname{rand}(3,1)*50, \\ &x_{0}=\operatorname{rand}(3,1),\qquad x_{1}=\operatorname{rand}(3,1)*100, \end{aligned}$$

the consequences are separately shown in Fig. 2(a), Fig. 3(a), and Fig. 4(a).

Figure 3
figure 3

The iteration number of Algorithm 3.1 in this paper and Algorithm 3.1 in [23]

Full size image
Figure 4
figure 4

The iteration number of Algorithm 3.1 in this paper and Algorithm 3.1 in [23]

Full size image

In the same way, we also offer 500 experiments for diverse initial value points which are randomly selected in the context of Algorithm 3.1 in [23]. For \(\forall n\in N\), let \(\alpha _{n}=\frac{1}{n+1}\), \(\rho _{n}=3.95\), and \(\omega _{n}=\frac{1}{{1+n}^{1.2}}\). Suppose \(\beta =0.5\) and \(\beta _{n}=\beta \), for instance,

$$\begin{aligned} \begin{aligned} &u=\operatorname{rand}(3,1), \qquad x_{0}=\operatorname{rand}(3,1),\qquad x_{1}=\operatorname{rand}(3,1)*10, \\ &u=\operatorname{rand}(3,1),\qquad x_{0}=\operatorname{rand}(3,1),\qquad x_{1}=\operatorname{rand}(3,1)*50, \\ &u=\operatorname{rand}(3,1),\qquad x_{0}=\operatorname{rand}(3,1), \qquad x_{1}=\operatorname{rand}(3,1)*100, \end{aligned} \end{aligned}$$

the consequences are separately shown in Fig. 2(b), Fig. 3(b), and Fig. 4(b).

From Tables 1–2 and Figs. 1–4, we can obtain the following conclusions.

1. Algorithm 3.1 in this paper is efficient for some different options and has a nice convergence speed and lower iteration number.

2. As you can see, for every option of \(x_{0}\) and \(x_{1}\), there is no important difference in CPU running times or iteration number. Therefore, our preliminary speculation is that the different options of \(x_{0}\) and \(x_{1}\) have negligible influence on the convergence of this algorithm.

3. With regard to Table 2, for some different options of \(x_{0}\) and \(x_{1}\), our Algorithm 3.1 clearly outperforms Algorithm 3.1 in [23].

4. According to Figs. 2–4, we conclude that the iteration number of Algorithm 3.1 in this paper is stable. Moreover, we can see the iteration number of Algorithm 3.1 in this paper is lower than that of Algorithm 3.1 in [23]. For example, in Fig. 4, the iteration number of Algorithm 3.1 in this paper is basically stable at about 50. However, Algorithm 3.1 in [23] is basically stable at about 150.

5 Conclusions

In this paper, we propose the inertial relaxed CQ algorithm for solving the convex multiple-sets split feasibility problem. And the global convergence conclusions are obtained. Our consequences generalize and produce some existing associated outcomes. Moreover, the preliminary numerical conclusions reveal that our presented algorithm is superior to some existing relaxed CQ algorithms in some cases about solving the convex multiple-sets split feasibility problem.