Skip to main content
SpringerLink
Log in

Iterative Regularization Methods for the Multiple-Sets Split Feasibility Problem in Hilbert Spaces

  • Published:
Acta Applicandae Mathematicae Aims and scope Submit manuscript

Abstract

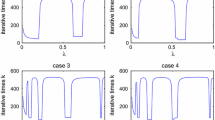
In this paper, we introduce iterative regularization methods for solving the multiple-sets split feasibility problem, that is to find a point closest to a family of closed convex subsets in one space such that its image under a bounded linear mapping will be closest to another family of closed convex subsets in the image space. We consider the cases, when the families are either finite or infinite. We also give two numerical examples for illustrating our main method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alber, Y., Ryazantseva, I.P.: Nonlinear Ill-Posed Problems of Monotone Type. Springer, Berlin (2006)

    MATH  Google Scholar 

  2. Bakushinsky, A.B.: Methods for solving monotonic variational inequalities based on the principle of iterative regularization. Comput. Math. Math. Phys. 17, 12–24 (1977)

    Google Scholar 

  3. Bakushinsky, A.B., Goncharsky, A.: Ill-Posed Problems: Theory and Applications. Kluwer Academic, Dordrecht (1989)

    Google Scholar 

  4. Bruck, R.E.: Properties of fixed point sets of nonexpansive mappings in Banach spaces. Trans. Am. Math. Soc. 179, 251–262 (1973)

    MathSciNet  MATH  Google Scholar 

  5. Bruck, R.E.: A strong convergent iterative method for the solution \(0\in Ux\) for a maximal monotone operator \(U\) in Hilbert spaces. J. Math. Anal. Appl. 48, 114–126 (1974)

    MathSciNet  Google Scholar 

  6. Buong, Ng., Duong, L.Th.Th.: An explicit iterative algorithm for a class of variational inequalities. J. Optim. Theory Appl. 151, 513–524 (2011)

    MathSciNet  MATH  Google Scholar 

  7. Buong, Ng., Quynh, V.X., Thuy, Ng.Th.Th.: A steepest-descent Krasnosel’skii–Mann algorithm for a class of variational inequalities in Banach spaces. J. Fixed Point Theory Appl. 18, 519–532 (2016)

    MathSciNet  MATH  Google Scholar 

  8. Buong, Ng., Ha Ng.S., Thuy, Ng.Th.Th.: A new explicit iteration method for a class of variational inequalities. Numer. Algorithms 72, 467–481 (2016)

    MathSciNet  MATH  Google Scholar 

  9. Byrne, C.: Iterative oblique projections onto convex subsets and the split feasibility problem. Inverse Probl. 18, 441–453 (2002)

    MATH  Google Scholar 

  10. Byrne, C.: A unified treatment of some iterative methods in signal processing and image reconstruction. Inverse Probl. 20, 103–120 (2004)

    MATH  Google Scholar 

  11. Ceng, L.C., Ansari, Q.H., Yao, J.Ch.: Relaxed extragradient methods for finding minimum-norm solutions of the split feasibility problem. Nonlinear Anal. 75, 2116–2125 (2012)

    MathSciNet  MATH  Google Scholar 

  12. Censor, Y., Elfving, T.: A multiprojection algorithm using Bregman projections in a product spaces. Numer. Algorithms 8, 221–239 (1994)

    MathSciNet  MATH  Google Scholar 

  13. Censor, Y., Elfving, T., Knop, N., Bortfeld, T.: The multiple-sets split feasibility problem and its applications for inverse problems. Inverse Probl. 21, 2071–2084 (2005)

    MathSciNet  MATH  Google Scholar 

  14. Censor, Y., Bortfeld, T., Martin, B., Trofimov, A.: A unified approach for inverse problems in intensity-modulated radiation therapy. Phys. Med. Biol. 51, 2353–2365 (2006)

    Google Scholar 

  15. Censor, Y., Motova, A., Segal, A.: Perturbed projections and subgradient projections for the multiple-sets split feasibility problem. J. Math. Anal. Appl. 327, 1244–1256 (2007)

    MathSciNet  MATH  Google Scholar 

  16. Censor, Y., Segal, A.: Iterative projection methods in biomedical inverse problems. In: Censor, Y., Jiang, M., Louis, A.K. (eds.) Mathematical Methods in Biomedical Imaging and Intensity-Modulated Radiation Therapy (IMRT), pp. 65–96. Edizioni della Normale, Pisa (2008)

    Google Scholar 

  17. Chen, Y., Guo, Y., Yu, Y., Chen, R.: Self-adaptive and relaxed self-adaptive projection methods for solving the multiple-sets split feasibility problem. Abstr. Appl. Anal. 2012, 958040 (2012), 11 pages

    MathSciNet  MATH  Google Scholar 

  18. Chuang, Ch.Sh.: Strong convergence theorems for the split variational inclusion problem in Hilbert spaces. Fixed Point Theory Appl. 2013, 350 (2013)

    MathSciNet  MATH  Google Scholar 

  19. Dang, Y., Gao, Y.: The strong convergence of a KM-CQ-like algorithm for a split feasibility problem. Inverse Probl. 27, 015007 (2011), 9 pages

    MathSciNet  MATH  Google Scholar 

  20. Dong, Q.L., He, S.: On two projection algorithms for the multiple-sets split feasibility problems. J. Appl. Math. 2013, 347401 (2013), 5 pages

    MathSciNet  MATH  Google Scholar 

  21. Goebel, K., Kirk, W.A.: Topics in Metric Fixed Point Theory, vol. 28. Cambridge University Press, Cambridge (1990)

    MATH  Google Scholar 

  22. He, S., Zhao, Z., Luo, B.: A relaxed self-adaptive CQ algorithm for the multiple-sets split feasibility problem. Optimization 64(9), 1907–1918 (2015)

    MathSciNet  MATH  Google Scholar 

  23. Jung, J.S.: Iterative algorithms on the hybrid steepest descent method for the split feasibility problem. J. Nonlinear Sci. Appl. 9, 4214–4225 (2016)

    MathSciNet  MATH  Google Scholar 

  24. López, G., Marquez, V.M., Wang, F., Xu, H.K.: Solving the split feasibility problem without prior knowledge of matrix norms. Inverse Probl. 28, 085004 (2012), 18 pages

    MathSciNet  MATH  Google Scholar 

  25. Maingé, P.E.: Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization. Set-Valued Var. Anal. 16, 899–912 (2008)

    MathSciNet  MATH  Google Scholar 

  26. Polyak, P.T.: Introduction for Optimization, Optimization Software, New York (1987)

    MATH  Google Scholar 

  27. Schopfer, F., Schuster, T., Luis, A.K.: An iterative regularization method for the solution of the split feasibility problem in Banach spaces. Inverse Probl. 24(5), 055008 (2008), 20 pages

    MathSciNet  MATH  Google Scholar 

  28. Shehu, Y.: Strong convergence theorem for multiple sets split feasibility problem in Banach spaces. Numer. Funct. Anal. Optim. 37(8), 1021–1036 (2016)

    MathSciNet  MATH  Google Scholar 

  29. Tang, Y., Zhu, Ch., Yu, H.: Iterative for solving the multiple-sets split feasibility problem with splitting self-adaptive step size. Fixed Point Theory Appl. 2015, 178 (2015). https://doi.org/10.1186/s13663-015-0430-2

    Article  MathSciNet  MATH  Google Scholar 

  30. Wang, L.: An iterative method for nonexpansive mapping in Hilbert spaces. Fixed Point Theory Appl. 2007, 28619 (2007). https://doi.org/10.1155/2007/28619

    Article  MATH  Google Scholar 

  31. Wang, F., Xu, H.K.: Cyclic algorithms for split feasibility problem in Hilbert spaces. Nonlinear Anal. 74, 4105–4111 (2011)

    MathSciNet  MATH  Google Scholar 

  32. Wen, M., Peng, J., Tang, Y.: A cyclic and simultaneous iterative method for solving the multiple-sets split feasibility problem. J. Optim. Theory Appl. 166, 844–860 (2015)

    MathSciNet  MATH  Google Scholar 

  33. Xu, H.K.: An iterative approach to quadratic optimization. J. Optim. Theory Appl. 116, 659–678 (2003)

    MathSciNet  MATH  Google Scholar 

  34. Xu, H.K.: A variable Krasnosel’skii–Mann algorithm and multiple set split feasibility problem. Inverse Probl. 22, 2021–2034 (2006)

    MATH  Google Scholar 

  35. Xu, H.K.: Iterative methods for the split feasibility problem in infinite-dimensional Hilbert spaces. Inverse Probl. 26, 1005018 (2010), 17 pages

    MathSciNet  Google Scholar 

  36. Xu, H.K.: Averaged mappings and the gradient-projection algorithm. J. Optim. Theory Appl. 150, 360–378 (2011)

    MathSciNet  MATH  Google Scholar 

  37. Yamada, I.: The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings. Butnariu, D., Censor, Y., Reich, S. (eds.) Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications, pp. 473–504. North-Holland, Amsterdam (2001)

    Google Scholar 

  38. Yao, Y., Jiang, W., Liou, Y.C.: Regularized methods for the split feasibility problem. Abstr. Appl. Anal. 2012, 140679 (2012). https://doi.org/10.1155/2012/140679

    Article  MathSciNet  MATH  Google Scholar 

  39. Yu, X., Shahzad, N., Yao, Y.: Implicit and explicit algorithms for solving the split feasibility problem. Optim. Lett. 6, 1447–1462 (2012)

    MathSciNet  MATH  Google Scholar 

  40. Zhang, W., Han, D., Li, Zh.: A self-adaptive projection method for solving the multiple-sets split feasibility problem. Inverse Probl. 25, 115001 (2009), 16 pages

    MathSciNet  MATH  Google Scholar 

  41. Zhao, J., Yang, Q.: A simple projection method for solving the multiple-sets split feasibility problem. Inverse Probl. Sci. Eng. 21(3), 537–546 (2013)

    MathSciNet  MATH  Google Scholar 

  42. Zhao, J., Zhang, Y., Yang, Q.: Modified projection methods for the split feasibility problem and the multiple-sets split feasibility problem. Appl. Math. Comput. 219, 1644–1653 (2012)

    MathSciNet  MATH  Google Scholar 

  43. Zhou, H., Wang, P.: Adaptively relaxed algorithm for solving the multiple-sets split feasibility problem. J. Inequal. Appl. 2014, 448 (2014)

    MATH  Google Scholar 

  44. Zhou, H., Wang, P.: A simpler explicit iterative algorithm for a class of variational inequalities in Hilbert spaces. J. Optim. Theory Appl. 161, 716–727 (2014)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are extremely grateful to the referees for their useful comments, which helped to improve this paper. This work was supported by the Vietnam National Foundation for Science and Technology Development under grant number 101.02-2017.305.

Author information

Authors and Affiliations

  1. Duy Tan University, 13 Quang Trung, Da Nang, Vietnam

    Nguyen Buong

  2. Vietnam Academy of Science and Technology, Institute of Information Technology, 18, Hoang Quoc Viet, Hanoi, Vietnam

    Nguyen Buong

  3. Vietnam Maritime University, Hai Phong, Vietnam

    Pham Thi Thu Hoai

  4. Banking Academy, Hanoi, Vietnam

    Khuat Thi Binh

Authors
  1. Nguyen Buong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pham Thi Thu Hoai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Khuat Thi Binh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nguyen Buong.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Buong, N., Hoai, P.T.T. & Thi Binh, K. Iterative Regularization Methods for the Multiple-Sets Split Feasibility Problem in Hilbert Spaces. Acta Appl Math 165, 183–197 (2020). https://doi.org/10.1007/s10440-019-00249-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10440-019-00249-1

Keywords

Mathematics Subject Classification

Search

Navigation