The scalar $f_0(500)$, $f_0(980)$, and $a_0(980)$ resonances and vector mesons in the single Cabibbo-suppressed decays $\Lambda _c \rightarrow p K^+K^-$ and $p\pi ^+\pi ^-$

Abstract

In the chiral unitary approach, we have studied the single Cabibbo-suppressed decays $\Lambda _c\rightarrow pK^+K^-$ and $\Lambda _c \rightarrow p \pi ^+\pi ^-$ by taking into account the s-wave meson–meson interaction as well as the contributions from the intermediate vectors $\phi$ and $\rho ^0$. Our theoretical results for the ratios of the branching fractions of $\Lambda _c\rightarrow p {\bar{K}}^{*0}$ and $\Lambda _c\rightarrow p \omega$ with respect to the one of $\Lambda _c\rightarrow p \phi$ are in agreement with the experimental data. Within the picture that the scalar resonances $f_0(500)$, $f_0(980)$, and $a_0(980)$ are dynamically generated from the pseudoscalar-pseudoscalar interactions in s-wave, we have calculated the $K^+K^-$ and $\pi ^+\pi ^-$ invariant mass distributions respectively for the decays $\Lambda _c\rightarrow pK^+K^-$ and $\Lambda _c\rightarrow p\pi ^+\pi ^-$. One can find a broad bump structure for the $f_0(500)$ and a narrow peak for the $f_0(980)$ in the $\pi ^+\pi ^-$ invariant mass distribution of the decay $\Lambda _c\rightarrow p\pi ^+\pi ^-$. For the $K^+K^-$ invariant mass distribution, in addition to the narrow peak for the $\phi$ meson, there is an enhancement structure near the $K^+K^-$ threshold mainly due to the contribution from the $f_0(980)$. Both the $\pi ^+\pi ^-$ and $K^+K^-$ invariant mass distributions are compatible with the BESIII measurement. We encourage our experimental colleagues to measure these two decays, which would be helpful to understand the nature of the $f_0(500)$, $f_0(980)$, and $a_0(980)$.

1 Introduction

The non-leptonic decays of the lightest charmed baryon $\Lambda _c$ play an important role in the study of strong and weak interactions [1,2,3,4,5,6]. In the last decades, lots of the information about the $\Lambda _c$ decays has been accumulated [7,8,9,10,11], which provides a good platform to investigate the possible final state interference effects where some resonances can be dynamically generated [12,13,14,15,16,17].

Recently, the BESIII Collaboration has reported the branching fractions of the $\Lambda _c\rightarrow p K^+K^-, \,p\pi ^+\pi ^-$,

$$\begin{aligned} \frac{{\mathcal {B}}(\Lambda _c \rightarrow p \phi )}{{\mathcal {B}}(\Lambda _c \rightarrow p K^-\pi ^+)}= & {} (1.81\pm 0.33\pm 0.13)\%, \end{aligned}$$

(1)

$$\begin{aligned} \frac{{\mathcal {B}}(\Lambda _c \rightarrow p K^+K^-)_{\mathrm{non}-\phi }}{{\mathcal {B}}(\Lambda _c \rightarrow p K^-\pi ^+)}= & {} (9.36\pm 2.22\pm 0.71)\%, \end{aligned}$$

(2)

$$\begin{aligned} \frac{{\mathcal {B}}(\Lambda _c \rightarrow p \pi ^+\pi ^-)}{{\mathcal {B}}(\Lambda _c \rightarrow p K^-\pi ^+)}= & {} (6.70\pm 0.48\pm 0.25)\%, \end{aligned}$$

(3)

and also measured the $\pi ^+\pi ^-$ and $K^+K^-$ invariant mass distributions, respectively [18], where one can find a broad bump around 500 MeV for the scalar resonance $f_0(500)$ and a narrow peak around 980 MeV for the scalar resonance $f_0(980)$ in the $\pi ^+\pi ^-$ invariant mass distribution, in addition to the peak for the $\rho ^0$ meson. Later, the LHCb Collaboration has also reported these ratios using the proton-proton collision data [11],

$$\begin{aligned} \frac{{\mathcal {B}}(\Lambda _c \rightarrow p K^+K^-)}{{\mathcal {B}}(\Lambda _c \rightarrow p K^-\pi ^+)}= & {} (1.70\pm 0.03\pm 0.03)\%, \end{aligned}$$

(4)

$$\begin{aligned} \frac{{\mathcal {B}}(\Lambda _c \rightarrow p \pi ^+\pi ^-)}{{\mathcal {B}}(\Lambda _c \rightarrow p K^-\pi ^+)}= & {} (7.44\pm 0.08\pm 0.18)\%. \end{aligned}$$

(5)

Before the BESIII and LHCb results, the above two decay modes have also been observed by the NA32 [19], E687 [20], CLEO [21], and Belle Collaborations [7].

Within the chiral unitary approach, the scalar resonances $f_0(500)$, $f_0(980)$, $a_0(980)$, and $K^*_0(700)$ [known as $\kappa (800)$] appear as composite states of meson-meson, automatically dynamically generated by the interaction of pseudoscalar-pseudoscalar where the kernel for the Bethe-Salpter equation is taken from the chiral Lagrangians [22,23,24,25,26,27]. The productions of $f_0(500)$, $f_0(980)$, and $a_0(980)$ have been recently studied with the chiral unitary approach and the final state interactions in the decays of the $D^0$ [28], $D^+_s$ [29], ${\bar{B}}$ and ${\bar{B}}_s$ [30,31,32,33], $\chi _{c1}$ [34, 35], $\tau ^-$ [36], and $J/\psi$ [37].

In this work, we perform the calculations for the decays $\Lambda _c \rightarrow p K^+K^-$ and $\Lambda _c \rightarrow p \pi ^+\pi ^-$ taking into account the meson-meson interaction in coupled channels and also the contributions from the intermediate vector mesons $\phi$ and $\rho ^0$. The final states interaction of the pseudoscalar-pseudoscalar in the decay $\Lambda _c \rightarrow p \pi ^+\pi ^-$ can propagate in s-wave, which will generate the $f_0(500)$ and $f_0(980)$ resonances, and for the decay $\Lambda _c \rightarrow p K^+K^-$, the $f_0(980)$ and $a_0(980)$ resonances dynamically generated from the s-wave final state interaction will result in an enhancement structure close to the $K^+K^-$ threshold.

The paper is organized as follows. In Sect. 2, we present the formalism and ingredients for the decays of the $\Lambda _c \rightarrow p K^+ K^-$ and $p\pi ^+ \pi ^-$ decays. Numerical results for the $K^+K^-$ and $\pi ^+ \pi ^-$ invariant mass distributions and discussions are given in Sect. 3, followed by a short summary in the last section.

2 Formalism

In this section, we will present the formalism for the decays $\Lambda _c \rightarrow p K^+ K^-$ and $\Lambda _c \rightarrow p \pi ^+ \pi ^-$. For the three-body decays of $\Lambda _c$, the s-wave final state interactions of $\pi ^+\pi ^-$ or $K^+K^-$ will dynamically generate the scalar resonances $f_0(500)$, $f_0(980)$, and $a_0(980)$. In addition, the three-body decays can happen via the intermediate vector mesons $\rho ^0$ or $\phi$. We first introduce the formalism for the mechanism of final state interactions of $\pi ^+\pi ^-$ or $K^+K^-$ in s-wave in Sect. 2.1, then we show the details for the mechanism of the $\Lambda _c$ decays via the intermediate vector mesons $\rho ^0$ and $\phi$ in Sect 2.2.

2.1 $s$-wave final state interactions of $K^+ K^-$ and $\pi ^+\pi ^-$

Fig. 1

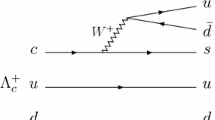
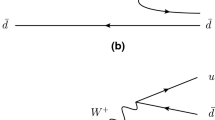
The diagrams of the decays $\Lambda _c\rightarrow pK^+K^-$ and $p\pi ^+\pi ^-$, a the internal W emission for $\Lambda _c \rightarrow p K^+K^-$, b the internal W emission for $\Lambda _c \rightarrow p \pi ^+\pi ^-$, c the external W emission for $\Lambda _c \rightarrow p K^+K^-$, and d the external W emission for $\Lambda _c \rightarrow p \pi ^+\pi ^-$

Following Refs. [38,39,40,41], we take the decay mechanism of the internal W emission mechanism for the decays $\Lambda _c \rightarrow p K^+K^-$ and $\Lambda _c \rightarrow p \pi ^+ \pi ^-$ as depicted in Fig. 1a, b. For the weak decays of $\Lambda _c$, the c quark decays into a $W^+$ boson and an s (or d) quark, then the $W^+$ boson decays into an ${\bar{s}}u$ (or ${\bar{d}}u$) pair. In order to give rise to the final states of $p K^+K^-$ (or $p \pi ^+\pi ^-$), the $s{\bar{s}}$ (or $d{\bar{d}}$) quark pair need to hadronize together with the ${\bar{q}}q$ ($={\bar{u}}u+{\bar{d}}d+{\bar{s}}s$) produced in the vacuum, which are given by,

$$\begin{aligned} H^{(a)}= & {} V^{(a)} s({\bar{u}}u+{\bar{d}}d \nonumber \\&+{\bar{s}}s){\bar{s}} u\frac{1}{\sqrt{2}}(ud-du) = V^{(a)} \left( M^2\right) _{33}p, \end{aligned}$$

(6)

$$\begin{aligned} H^{(b)}= & {} V^{(b)} d({\bar{u}}u+{\bar{d}}d \nonumber \\&+{\bar{s}}s){\bar{d}} u\frac{1}{\sqrt{2}}(ud-du) = V^{(b)}\left( M^2\right) _{22}p, \end{aligned}$$

(7)

where $V^{(a)}$ and $V^{(b)}$ are the weak interaction strengths. We use $\left| p\right\rangle =\frac{1}{\sqrt{2}}\left| u(ud-du)\right\rangle$, and $\left| \Lambda _c\right\rangle =\frac{1}{\sqrt{2}}\left| c(ud-du)\right\rangle$. M is the $q{\bar{q}}$ matrix,

$$\begin{aligned} M=\left( \begin{array}{ccc} u{\bar{u}} &{} u{\bar{d}} &{} u{\bar{s}}\\ d{\bar{u}} &{} d{\bar{d}} &{} d{\bar{s}} \\ s{\bar{u}} &{} s{\bar{d}} &{} s{\bar{s}} \end{array} \right) . \end{aligned}$$

The matrix M in terms of pseudoscalar mesons can be written as,

$$\begin{aligned} M\Rightarrow P= \left( \begin{array}{ccc} \frac{\pi ^0}{\sqrt{2}} + \frac{\eta }{\sqrt{3}}+\frac{\eta '}{\sqrt{6}}&{} \pi ^+ &{} K^+\\ \pi ^-&{} -\frac{1}{\sqrt{2}}\pi ^0 + \frac{\eta }{\sqrt{3}}+ \frac{\eta '}{\sqrt{6}}&{} K^0\\ K^-&{} {\bar{K}}^0 &{} -\frac{\eta }{\sqrt{3}}+ \frac{2\eta '}{\sqrt{6}} \end{array} \right) . \nonumber \\ \end{aligned}$$

(8)

Then, we have,

$$\begin{aligned} H^{(a)}= & {} V^{(a)} \left( M^2\right) _{33} p \nonumber \\= & {} V_P V_{cs}V_{us} \left( K^-K^+ +K^0{\bar{K}}^0 +\frac{1}{3}\eta \eta \right) p, \end{aligned}$$

(9)

$$\begin{aligned} H^{(b)}= & {} V^{(b)} \left( M^2\right) _{22} p \nonumber \\= & {} V_P V_{cd}V_{ud} \left( \pi ^+\pi ^-+\frac{1}{2}\pi ^0\pi ^0\right. \nonumber \\&\left. +\frac{1}{3}\eta \eta -\frac{2}{\sqrt{6}}\pi ^0\eta +K^0{\bar{K}}^0\right) p, \end{aligned}$$

(10)

where we neglect the $\eta '$ because of its large mass. $V_P$ is the strength of the production vertex, and contains all dynamical factors, which is assumed to be same for Fig. 1a, b within the SU(3) flavor symmetry. In the following, we will see that this hypothesis is also reasonable by comparing the predicted ratios of the two body decays of $\Lambda _c$ with the experimental measurements. In this work we take $V_{cd}=V_{us}= -0.22534$, $V_{cs}=V_{ud}=0.97427$ [42].

On the other hand, the decays $\Lambda _c \rightarrow p K^+ K^-$ and $\Lambda _c \rightarrow p \pi ^+ \pi ^-$ can also proceed with the color favored external W emission mechanism: (i) the charmed quark turns into $W^+$ and the s (or d) quark, with the $K^+$ or $\pi ^+$ emission from the $W^+$; (ii) the remaining quarks s (or d) and ud in the $\Lambda _c$, together with the $u{\bar{u}}$ pair created from the vacuum, hadronize to the $K^- p$ (or $\pi ^- p$), as depicted in Fig. 1c, d respectively. Thus, we have,

$$\begin{aligned} H^{(c)}= & {} V^{\mathrm{(c)}}(u{\bar{s}})s{\bar{u}}u\frac{1}{\sqrt{2}}(ud-du)=C\times V_P V_{cs}V_{us} K^+K^-p,\nonumber \\ \end{aligned}$$

(11)

$$\begin{aligned} H^{(d)}= & {} V^{\mathrm{(d)}}(u{\bar{d}})d{\bar{u}}u\frac{1}{\sqrt{2}}(ud-du)= C\times V_P V_{cd}V_{ud}\pi ^+\pi ^-p,\nonumber \\ \end{aligned}$$

(12)

where we take the same normalization factor $V_P$ as Eqs. (9) and (10), the color factor C accounts for the relative weight of the external emission mechanism with respect to the one of the internal emission mechanism [41, 43]. The value of C should be around 3, because the quarks from the W decay in the external emission diagram (for example, the u and ${\bar{s}}$ of Fig. 1c) have three choices of the colors (we take $N_c=3$), while the quarks from the W decay in the internal emission diagram (for example, the u and ${\bar{s}}$ of Fig. 1a) have the fixed colors. We will keep this factor in the following formalism, and present our results by varying its value in Sect. 3.

Fig. 2

The mechanisms of the decay $\Lambda _c \rightarrow p K^+K^-$, left) tree diagram, right) the s-wave final state interactions

Fig. 3

The mechanisms of the decay $\Lambda _c \rightarrow p \pi ^+\pi ^-$, left) tree diagram, right) the s-wave final state interactions

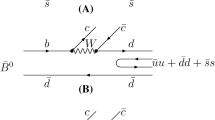
After the production of a meson-meson pair, the final state interaction in the s-wave between the mesons takes place, as shown in Figs. 2 and 3 for the decays $\Lambda _c\rightarrow p K^+K^-$ and $\Lambda _c\rightarrow p \pi ^+\pi ^-$. Since the isospin of $\pi ^+\pi ^-$ system is $I=0$, we will take into account the contributions from all the mechanisms of Fig. 1, except the $\pi ^0\eta p$ states of Eq. (10) because of the isospin violation, and the amplitude is given by,

$$\begin{aligned}&t^{s-\mathrm{wave}}_{\Lambda _c\rightarrow p\pi ^+\pi ^-}= t^{(a)}_{\Lambda _c\rightarrow p\pi ^+\pi ^-}+t^{(b)}_{\Lambda _c\rightarrow p\pi ^+\pi ^-}\nonumber \\&\qquad +t^{(c)}_{\Lambda _c\rightarrow p\pi ^+\pi ^-}+t^{(d)}_{\Lambda _c\rightarrow p\pi ^+\pi ^-} \nonumber \\&\quad = V_PV_{cs}V_{us} \left[ G_{K^+K^-}t_{K^+K^-\rightarrow \pi ^+\pi ^-}\right. \nonumber \\&\qquad \left. + G_{K^0{\bar{K}}^0}t_{K^0{\bar{K}}^0\rightarrow \pi ^+\pi ^-} +\frac{1}{3}\times 2\times \frac{1}{2} G_{\eta \eta }{\tilde{t}}_{\eta \eta \rightarrow \pi ^+\pi ^-} \right] \nonumber \\&\qquad + V_PV_{cs}V_{us} \left[ 1 +G_{\pi ^+\pi ^-}t_{\pi ^+\pi ^-\rightarrow \pi ^+\pi ^-}\right. \nonumber \\&\qquad \left. + \frac{1}{2}\times 2\times \frac{1}{2} G_{\pi ^0\pi ^0}{\tilde{t}}_{\pi ^0\pi ^0\rightarrow \pi ^+\pi ^-} \right. \nonumber \\&\qquad \left. +\frac{1}{3}\times 2 \times \frac{1}{2} G_{\eta \eta }{\tilde{t}}_{\eta \eta \rightarrow \pi ^+\pi ^-} + G_{K^0{\bar{K}}^0}t_{K^0{\bar{K}}^0\rightarrow \pi ^+\pi ^-} \right] \nonumber \\&\qquad + C\times V_PV_{cs}V_{us} \left[ G_{K^+K^-}t_{K^+K^-\rightarrow \pi ^+\pi ^-}\right] \nonumber \\&\qquad + C\times V_p V_{cs}V_{us} \left[ 1+ G_{\pi ^+\pi ^-}t_{\pi ^+\pi ^-\rightarrow \pi ^+\pi ^-}\right] \nonumber \\&\quad = V_P V_{cs}V_{us} \left[ (1+C) +(1+C) G_{K^+K^-}t_{K^+K^-\rightarrow \pi ^+\pi ^-}\right. \nonumber \\&\qquad \left. + 2 G_{K^0{\bar{K}}^0}t_{K^0{\bar{K}}^0\rightarrow \pi ^+\pi ^-} + (1+C) G_{\pi ^+\pi ^-}t_{\pi ^+\pi ^-\rightarrow \pi ^+\pi ^-} \right. \nonumber \\&\qquad \left. + \frac{1}{2} G_{\pi ^0\pi ^0}{\tilde{t}}_{\pi ^0\pi ^0\rightarrow \pi ^+\pi ^-} +\frac{2}{3}G_{\eta \eta }{\tilde{t}}_{\eta \eta \rightarrow \pi ^+\pi ^-} \right] . \end{aligned}$$

(13)

For the decay $\Lambda _c\rightarrow p K^+K^-$, the amplitude is given by,

$$\begin{aligned}&t^{s-\mathrm{wave}}_{\Lambda _c\rightarrow pK^+K^-}= t^{(a)}_{\Lambda _c\rightarrow pK^+K^-}\nonumber \\&\qquad + t^{(b)}_{\Lambda _c\rightarrow pK^+K^-}+ t^{(c)}_{\Lambda _c\rightarrow pK^+K^-}+ t^{(d)}_{\Lambda _c\rightarrow pK^+K^-} \nonumber \\&\quad = V_PV_{cs}V_{us}\biggl [1+ G_{K^+K^-}t_{K^+K^-\rightarrow K^+K^-}\nonumber \\&\qquad + G_{K^0{\bar{K}}^0}t_{K^0{\bar{K}}^0\rightarrow K^+K^-}\nonumber \\&\qquad +\frac{1}{3}\times 2\times \frac{1}{2} G_{\eta \eta }{\tilde{t}}_{\eta \eta \rightarrow K^+K^-} \biggr ] \nonumber \\&\qquad + V_P V_{cs}V_{us}\biggl [G_{\pi ^+\pi ^-}t_{\pi ^+\pi ^-\rightarrow K^+K^-}\nonumber \\&\qquad + \frac{1}{2}\times 2\times \frac{1}{2} G_{\pi ^0\pi ^0}{\tilde{t}}_{\pi ^0\pi ^0\rightarrow K^+K^-}\nonumber \\&\qquad +\frac{1}{3}\times 2 \times \frac{1}{2} G_{\eta \eta }{\tilde{t}}_{\eta \eta \rightarrow K^+K^-} \nonumber \\&\qquad - \frac{2}{\sqrt{6}} G_{\pi ^0\eta }t_{\pi ^0\eta \rightarrow K^+K^-} + G_{K^0{\bar{K}}^0}t_{K^0{\bar{K}}^0\rightarrow K^+K^-} \biggr ] \nonumber \\&\qquad + C\times V_P V_{cs}V_{us}\biggl [1+G_{K^+K^-}t_{K^+K^-\rightarrow K^+K^-}\biggr ]\nonumber \\&\qquad + C\times V_p V_{cs}V_{us} \biggl [ G_{\pi ^+\pi ^-}t_{\pi ^+\pi ^-\rightarrow K^+K^-}\biggr ] \nonumber \\&\quad = V_PV_{cs}V_{us} \biggl [ (1+C)+ G_{K^+K^-}t_{K^+K^-\rightarrow K^+K^-}\nonumber \\&\qquad + G_{K^0{\bar{K}}^0}t_{K^0{\bar{K}}^0\rightarrow K^+K^-} + (1+C) G_{\pi ^+\pi ^-}t_{\pi ^+\pi ^-\rightarrow K^+K^-} \nonumber \\&\qquad +\frac{1}{2} G_{\pi ^0\pi ^0}{\tilde{t}}_{\pi ^0\pi ^0\rightarrow K^+K^-} + \frac{2}{3}G_{\eta \eta }{\tilde{t}}_{\eta \eta \rightarrow K^+K^-}\biggr ] \nonumber \\&\qquad + V_PV_{cs}V_{us}\biggl [ C\times G_{K^+K^-}t_{K^+K^-\rightarrow K^+K^-}\nonumber \\&\qquad + G_{K^0{\bar{K}}^0}t_{K^0{\bar{K}}^0\rightarrow K^+K^-} - \frac{2}{\sqrt{6}} G_{\pi ^0\eta }t_{\pi ^0\eta \rightarrow K^+K^-} \biggr ], \end{aligned}$$

(14)

where the first term only contains the contribution from isospin $I=0$, and the second term has the contributions of $I=0$ and $I=1$ from the mechanisms of Fig. 1b, c. It is easily done taking $G_{K^0{\bar{K}}^0}=G_{K^+K^-}$, and rewriting $t_{K^+K^-\rightarrow K^+K^-}$ and $t_{K^0{\bar{K}}^0\rightarrow K^+K^-}$ from the mechanisms of Fig. 1b, c as done in Ref. [32],

$$\begin{aligned}&G_{K^0{\bar{K}}^0}t_{K^0{\bar{K}}^0\rightarrow K^+K^-}+ C\times G_{K^+K^-}t_{K^+K^-\rightarrow K^+K^-} \nonumber \\&\quad = G_{K^0{\bar{K}}^0}\left[ \frac{1+C}{2} \left( t_{K^0{\bar{K}}^0\rightarrow K^+K^-} +t_{K^+K^-\rightarrow K^+K^-} \right) \right. \nonumber \\&\qquad \left. +\frac{1-C}{2} \left( t_{K^0{\bar{K}}^0\rightarrow K^+K^-} -t_{K^+K^-\rightarrow K^+K^-} \right) \right] , \end{aligned}$$

(15)

where the first two terms are in $I=0$ while the last two terms are in $I=1$.

Thus, the amplitude of Eq. (14) can be rewritten as,

$$\begin{aligned}&t^{s-\mathrm{wave}}_{\Lambda _c\rightarrow pK^+K^-} = V_P V_{cs}V_{us}\left\{ \left[ (1+C) \right. \right. \nonumber \\&\qquad \left. \left. + \frac{3+C}{2}G_{K^0{\bar{K}}^0} \left( t_{K^0{\bar{K}}^0\rightarrow K^+K^-} +t_{K^+K^-\rightarrow K^+K^-} \right) \right. \right. \nonumber \\&\qquad \left. + (1+C) G_{\pi ^+\pi ^-}t_{\pi ^+\pi ^-\rightarrow K^+K^-}\right. \nonumber \\&\qquad \left. +\frac{1}{2} G_{\pi ^0\pi ^0}{\tilde{t}}_{\pi ^0\pi ^0\rightarrow K^+K^-} +\frac{2}{3}G_{\eta \eta }{\tilde{t}}_{\eta \eta \rightarrow K^+K^-} \right] \nonumber \\&\qquad \left. +\left[ \frac{1-C}{2} G_{K^0{\bar{K}}^0}\left( t_{K^0{\bar{K}}^0\rightarrow K^+K^-} -t_{K^+K^-\rightarrow K^+K^-}\right) \right. \right. \nonumber \\&\qquad \left. \left. - \frac{2}{\sqrt{6}} G_{\pi ^0\eta }t_{\pi ^0\eta \rightarrow K^+K^-} \right] \right\} \nonumber \\&\quad = t^{I=0} + t^{I=1} , \end{aligned}$$

(16)

where the terms $t^{I=0}$ and $t^{I=1}$ correspond to the contributions from the $I=0$ and $I=1$, respectively.

In Eqs. (13) and (14), we include a factor of 2 from the two way to match the two identical particles of the operators in Eqs. (9) and (10) with the two mesons ($\pi ^0\pi ^0$ and $\eta \eta$) produced, and a factor 1/2 in the intermediate loops involving a pair of identical mesons [30, 32]. The scattering matrix $t_{i\rightarrow j}$ has been calculated within the chiral unitary approach in Refs. [22, 28, 31, 44, 45], and we take ${\tilde{t}}_{\eta \eta \rightarrow i}=\sqrt{2}t_{\eta \eta \rightarrow i}$, ${\tilde{t}}_{\pi ^0\pi ^0\rightarrow j}=\sqrt{2} t_{\pi ^0\pi ^0\rightarrow j}$ for the two identical particles [44]. $G_l$ is the loop function for the two mesons propagator in the lth channel, which is given as follows after the integration in $dq^0$,

$$\begin{aligned}&G_l =i\int \frac{d^4q}{(2\pi )^4}\frac{1}{(p-q)^2-m^2_1+i\epsilon }\frac{1}{q^2-m^2_2+i\epsilon }\nonumber \\&\quad = \int \frac{d^3\mathbf {q}}{(2\pi )^3}\frac{\omega _1+\omega _2}{\omega _1 \omega _2}\frac{1}{(\sqrt{s}+\omega _1+\omega _2)(\sqrt{s}-\omega _1-\omega _2+i\epsilon )},\nonumber \\ \end{aligned}$$

(17)

where $\sqrt{s}$ is the invariant mass of the meson-meson pair, and the meson energies $\omega _i=\sqrt{(\mathbf {q}\,)^2+m_i^2}$ ($i=1,2$). The integral on $\mathbf {q}$ in Eq. (17) is performed with a cutoff $|\mathbf {q}_{\mathrm{max}}|=600$ MeV, as used in Refs. [28, 31, 44]. The transition amplitude $t_{ij}$ is obtained by solving the Bethe–Salpeter equation in coupled channels,

$$\begin{aligned} T=[1-VG]^{-1}V, \end{aligned}$$

(18)

where five channels $\pi ^+\pi ^-$ (1), $\pi ^0\pi ^0$ (2), $K^+K^-$ (3), $K^0{\bar{K}}^0$ (4), and $\eta \eta$ (5) are included for $I=0$, and three channels $K^+K^-$ (1), $K^0{\bar{K}}^0$, (2) and $\pi ^0\eta$ (3) are included for $I=1$. The elements of the diagonal matrix G are given by the loop function of Eq. (17), and V is the matrix of the interaction kernel corresponding to the tree level transition amplitudes obtained from phenomenological Lagrangians [22]. The explicit expressions for $I=0$ can be expressed as [44],

$$\begin{aligned}&V_{\pi ^+\pi ^-\rightarrow \pi ^+\pi ^-}=-\frac{1}{2f^2}s,~~~V_{\pi ^+\pi ^-\rightarrow \pi ^0\pi ^0}\nonumber \\&\quad =-\frac{1}{\sqrt{2}f^2}(s-m^2_\pi ),~~~V_{\pi ^+\pi ^-\rightarrow K^+K^-}=-\frac{1}{4f^2}s, \nonumber \\&\qquad V_{\pi ^+\pi ^-\rightarrow K^0{\bar{K}}^0}=-\frac{1}{4f^2}s,~~~V_{\pi ^+\pi ^-\rightarrow \eta \eta }\nonumber \\&\quad =-\frac{1}{3\sqrt{2}f^2}m^2_\pi ,~~~V_{\pi ^0\pi ^0 \rightarrow \pi ^0\pi ^0}=-\frac{1}{2f^2}m^2_\pi ,\nonumber \\&\qquad V_{\pi ^0\pi ^0 \rightarrow K^+K^-}=-\frac{1}{4\sqrt{2} f^2}s,~~~V_{\pi ^0\pi ^0 \rightarrow K^0{\bar{K}}^0}\nonumber \\&\quad =-\frac{1}{4\sqrt{2} f^2}s,~~~V_{\pi ^0\pi ^0 \rightarrow \eta \eta }=-\frac{1}{6f^2}m^2_\pi , \nonumber \\&\qquad V_{K^+K^- \rightarrow K^+K^-}=-\frac{1}{2f^2}s,~~~V_{K^+K^-\rightarrow K^0{\bar{K}}^0}\nonumber \\&\quad =-\frac{1}{4f^2}s,~~~V_{K^+K^- \rightarrow \eta \eta }\nonumber \\&\quad =-\frac{1}{12\sqrt{2}f^2}(9s-6m^2_\eta -2m^2_\pi ),\nonumber \\&\qquad V_{K^0{\bar{K}}^0 \rightarrow K^0{\bar{K}}^0}=-\frac{1}{2f^2}s,~~~V_{K^0{\bar{K}}^0\rightarrow \eta \eta }\nonumber \\&\quad =-\frac{1}{12\sqrt{2}f^2}(9s-6m^2_\eta -2m^2_\pi ),\nonumber \\&\qquad V_{\eta \eta \rightarrow \eta \eta }=-\frac{1}{18f^2}(16m^2_K-7m^2_\pi ), \end{aligned}$$

(19)

and the ones for $I=1$ are [28],

$$\begin{aligned}&V_{K^+K^- \rightarrow K^+K^-}=-\frac{1}{2f^2}s,~~~V_{K^+K^-\rightarrow K^0{\bar{K}}^0}=-\frac{1}{4f^2}s,\nonumber \\&\qquad V_{K^+K^-\rightarrow \pi ^0\eta }=\frac{-\sqrt{3}}{12f^2}\left( 3s-\frac{8}{3}m^2_K-\frac{1}{3}m^2_\pi -m^2_\eta \right) ,\nonumber \\&\qquad V_{K^0{\bar{K}}^0-\rightarrow K^0{\bar{K}}^0 }=-\frac{1}{2f^2}s,~~~V_{K^0{\bar{K}}^0-\rightarrow \pi ^0\eta }\nonumber \\&\quad =-V_{K^+K^- \rightarrow \pi ^0\eta },~~~V_{\pi ^0\eta \rightarrow \pi ^0\eta }=-\frac{m^2_\pi }{3f^2}, \end{aligned}$$

(20)

where $f=f_\pi =93$ MeV is the pion decay constant, and $m_\pi$, $m_K$, and $m_\eta$ are the averaged masses of the pion, kaon, and $\eta$ mesons, respectively [42].

With the amplitudes of Eqs. (14) and (13), we can write the differential decay width for the decays $\Lambda _c\rightarrow p K^+K^-$ and $\Lambda _c\rightarrow p \pi ^+\pi ^-$ in s-wave,

$$\begin{aligned} \frac{d\Gamma ^{s-\mathrm{wave}}}{dM_\mathrm{inv}}=\frac{1}{(2\pi )^3}\frac{p_p {\tilde{k}}}{4M^2_{\Lambda _c}}\left| t^{s-\mathrm{wave}}_{\Lambda _c\rightarrow pK^+K^-,\, p \pi ^+\pi ^-}\right| ^2, \end{aligned}$$

(21)

where $M_{\mathrm{inv}}$ is the invariant mass of the $K^+K^-$ or $\pi ^+\pi ^-$, $p_p$ is the momentum of the proton in the $\Lambda _c$ rest frame, and ${\tilde{k}}$ is the momentum of the $K^+$ (or $\pi ^+$) in the rest frame of the $K^+K^-$ (or $\pi ^+\pi ^-$) system,

$$\begin{aligned}&p_p=\frac{\lambda ^{1/2}\left( M^2_{\Lambda _c}, M^2_p, M^2_{\mathrm{inv}} \right) }{2M_{\Lambda _c}},\nonumber \\&\qquad {\tilde{k}} = \frac{\lambda ^{1/2}\left( M^2_{\mathrm{inv}}, m^2_{K^+/\pi ^+}, m^2_{K^-/\pi ^-} \right) }{2M_{\mathrm{inv}}}, \end{aligned}$$

(22)

with the Källen function $\lambda (x,y,z)=x^2+y^2+z^2-2xy-2yz-2zx$. The masses of the baryons and mesons involved in our calculations are taken from PDG [42].

2.2 $\Lambda _c$ decays via the intermediate vector mesons $\phi$ and $\rho ^0$

In this section, we will present the formalism for the decays $\Lambda _c\rightarrow p K^+K^-$ and $\Lambda _c\rightarrow p \pi ^+\pi ^-$ via the intermediate mesons $\phi$ and $\rho ^0$. The quark level diagrams for the two-body decays of $\Lambda _c$ into a proton and a vector meson are shown in Fig. 4.

Fig. 4

The quark level diagrams for the two-body decays of $\Lambda _c$, a $\Lambda _c \rightarrow p \rho ^0$, and $p\omega$, b $\Lambda _c \rightarrow p \phi$, and c $\Lambda _c \rightarrow p {\bar{K}}^{*0}$

At the quark level, the quark components of the vector mesons are,

$$\begin{aligned} \rho ^0= & {} \frac{1}{\sqrt{2}}(u{\bar{u}}-d {\bar{d}}),~~~\phi =s{\bar{s}}, \nonumber \\ \omega= & {} \frac{1}{\sqrt{2}}(u{\bar{u}}+d {\bar{d}}), ~~{\bar{K}}^{*0}= s{\bar{d}}. \end{aligned}$$

(23)

The amplitudes can be written as,

$$\begin{aligned} t_{\Lambda _c\rightarrow p\rho ^0}= & {} -\frac{1}{\sqrt{2}} V'_P V_{cd}V_{ud}, ~~~~~~~~~ t_{\Lambda _c\rightarrow p\phi } = V'_P V_{cs}V_{us}, \end{aligned}$$

(24)

$$\begin{aligned} t_{\Lambda _c\rightarrow p\omega }= & {} \frac{1}{\sqrt{2}} V'_P V_{cd}V_{ud}, ~~~~~~~~~ t_{\Lambda _c\rightarrow p {\bar{K}}^{*0}} = V'_P V_{cs}V_{ud}, \end{aligned}$$

(25)

where $V'_P$ is a normalization factor for the $\Lambda _c$ decay into proton and a vector meson. The factor of $1/\sqrt{2}$ in the above amplitudes comes from the quark component of the $\rho ^0$ and $\omega$. With those amplitudes, the decay width for the two-body decay of $\Lambda _c$ into proton and a vector meson in s-wave is,

$$\begin{aligned} \Gamma _{\Lambda _c\rightarrow p V} = \frac{\lambda ^{1/2}\left( M^2_{\Lambda _c}, m^2_V, M^2_p \right) }{16\pi M^3_{\Lambda _c}} \left| t_{\Lambda _c\rightarrow p V}\right| ^2 , \end{aligned}$$

(26)

where V stands for the vector mesons $\rho ^0$, $\phi$, $\omega$, and ${\bar{K}}^{*0}$.

The $K^+K^-$ and $\pi ^+\pi ^-$ invariant mass distributions respectively for the $\phi$ and $\rho ^0$ mesons can be obtained by converting the total rate for vector production into a mass distribution as Refs. [30, 46],

$$\begin{aligned} \frac{d\Gamma _{\Lambda _c\rightarrow p \rho ^0, \rho ^0 \rightarrow \pi ^+ \pi ^-}}{dM_{\mathrm{inv}}}= & {} \frac{2m^2_\rho }{\pi } \frac{{{\tilde{\Gamma }}}_\rho {\tilde{\Gamma }}_{\Lambda _c\rightarrow p \rho ^0}}{(M^2_{\mathrm{inv}}-m^2_\rho )^2 + m^2_\rho {{\tilde{\Gamma }}}^2_\rho } , \end{aligned}$$

(27)

$$\begin{aligned} \frac{d\Gamma _{\Lambda _c\rightarrow p \phi , \phi \rightarrow K^+ K^-}}{dM_{\mathrm{inv}}}= & {} \frac{m^2_\phi }{\pi } \frac{{{\tilde{\Gamma }}}_\phi {\tilde{\Gamma }}_{\Lambda _c\rightarrow p \phi }}{(M^2_{\mathrm{inv}}-m^2_\phi )^2 + m^2_\phi {{\tilde{\Gamma }}}^2_\phi } , \end{aligned}$$

(28)

where we have considered that the $K^+ K^-$ decay accounts for 1/2 of the $K{\bar{K}}$ decay width of the $\phi$ meson. Since $\rho ^0 \rightarrow \pi ^+\pi ^-$ and $\phi \rightarrow K^+ K^-$ are in p-wave, we take

$$\begin{aligned} {{\tilde{\Gamma }}}_\rho= & {} \Gamma _{\rho ^0} \left( \frac{ \sqrt{M^2_{\mathrm{inv}} - 4m^2_\pi } }{ \sqrt{m^2_\rho - 4m^2_\pi } } \right) ^3, \nonumber \\ {{\tilde{\Gamma }}}_\phi= & {} \Gamma _{\phi } \left( \frac{ \sqrt{M^2_{\mathrm{inv}} - 4m^2_K} }{ \sqrt{m^2_\phi - 4m^2_K} } \right) ^3, \end{aligned}$$

(29)

and

$$\begin{aligned} {{\tilde{\Gamma }}}_{\Lambda _c\rightarrow p V}= & {} \Gamma _{\Lambda _c\rightarrow p V} \frac{\lambda ^{1/2}\left( M^2_{\Lambda _c}, M^2_{\mathrm{inv}}, M^2_{p} \right) }{\lambda ^{1/2}\left( M^2_{\Lambda _c}, m^2_V, M^2_{p} \right) } \frac{m_V}{M_{\mathrm{inv}}}. \end{aligned}$$

(30)

For the processes $\Lambda _c\rightarrow p K^+K^-$ and $\Lambda _c\rightarrow p \pi ^+\pi ^-$, the contributions from the vector mesons $\phi$ and $\rho ^0$, which respectively decay into $K^+K^-$ and $\pi ^+\pi ^-$ in p-wave, should be added to Eq. (21) incoherently.

3 Results and discussion

With Eqs. (24-26), the ratios of the branching fractions of the decays $\Lambda _c\rightarrow p {\bar{K}}^{*0}$, $\Lambda _c\rightarrow p \omega$, $\Lambda _c\rightarrow p \rho ^0$ with respect to the decay $\Lambda _c\rightarrow p \phi$ can be obtained with Eq. (26),

$$\begin{aligned} R^{\mathrm{th}}_1= & {} \frac{{\mathcal {B}}(\Lambda _c\rightarrow p {\bar{K}}^{*0})}{{\mathcal {B}}(\Lambda _c\rightarrow p \phi )}=\frac{\Gamma _{\Lambda _c\rightarrow p {\bar{K}}^{*0}}}{\Gamma _{\Lambda _c\rightarrow p \phi }} \nonumber \\= & {} \frac{\lambda ^{1/2}\left( M^2_{\Lambda _c}, m^2_{{\bar{K}}^{*0}}, M^2_p \right) \left| t_{\Lambda _c\rightarrow p {\bar{K}}^{*0}}\right| ^2}{\lambda ^{1/2}\left( M^2_{\Lambda _c}, m^2_{\phi }, M^2_p \right) \left| t_{\Lambda _c\rightarrow p \phi }\right| ^2}\nonumber \\= & {} \frac{\lambda ^{1/2}\left( M^2_{\Lambda _c}, m^2_{K^{*0}}, M^2_p \right) V^2_{ud}}{\lambda ^{1/2}\left( M^2_{\Lambda _c}, m^2_{\phi }, M^2_p \right) V^2_{us}}=21.6, \end{aligned}$$

(31)

and analogously,

$$\begin{aligned} R^{\mathrm{th}}_2= & {} \frac{{\mathcal {B}}(\Lambda _c\rightarrow p \omega )}{{\mathcal {B}}(\Lambda _c\rightarrow p \phi )}=0.636, \nonumber \\ R^{\mathrm{th}}_3= & {} \frac{{\mathcal {B}}(\Lambda _c\rightarrow p \rho ^0)}{{\mathcal {B}}(\Lambda _c\rightarrow p \phi )}=0.640, \end{aligned}$$

(32)

and one can find that $R^{\mathrm{th}}_1$ and $R^{\mathrm{th}}_2$ are consistent with the experimental results [42],

$$\begin{aligned} R^{\mathrm{exp}}_1= & {} \frac{{\mathcal {B}}(\Lambda _c\rightarrow p {\bar{K}}^{*0})}{{\mathcal {B}}(\Lambda _c\rightarrow p \phi )}\nonumber \\= & {} \frac{(1.94\pm 0.27) \%}{(1.06\pm 0.14)\times 10^{-3}}=18.3\pm 3.5, \end{aligned}$$

(33)

$$\begin{aligned} R^{\mathrm{exp}}_2= & {} \frac{{\mathcal {B}}(\Lambda _c\rightarrow p \omega )}{{\mathcal {B}}(\Lambda _c\rightarrow p \phi )}\nonumber \\= & {} \frac{(9\pm 4)\times 10^{-4}}{(1.06\pm 0.14)\times 10^{-3}}=0.85\pm 0.39, \end{aligned}$$

(34)

which implies that it is reasonable to take the same value of $V'_P$ for the mechanisms of Fig. 4. By fitting to the branching fractions of the decays $\Lambda _c\rightarrow p {\bar{K}}^{*0}$, $\Lambda _c\rightarrow p \phi$, and $\Lambda _c\rightarrow p \omega$, we can obtain the $(V'_P)^2/\Gamma _{\Lambda _c}=(4.5 \pm 0.4)\times 10^3$ MeV. With this value, the branching fraction of the decay $\Lambda _c\rightarrow p \rho ^0$ is estimated to be ${\mathcal {B}}(\Lambda _c\rightarrow p \rho ^0)=(6.3 \pm 0.6)\times 10^{-4}$, and the $K^+K^-$ and $\pi ^+\pi ^-$ invariant mass distribution of the decays $\Lambda _c\rightarrow p \phi \rightarrow p K^+K^-$ and $\Lambda _c\rightarrow p \rho \rightarrow p \pi ^+\pi ^-$ are easily calculated as shown in Figs. 5 and 6, respectively.

Fig. 5

The $K^+K^-$ invariant mass distribution of the decay $\Lambda _c \rightarrow p\phi \rightarrow pK^+K^-$ with $(V'_P)^2/\Gamma _{\Lambda _c}=4.5\times 10^3$ MeV

Fig. 6

The $\pi ^+\pi ^-$ invariant mass distribution of the decay $\Lambda _c \rightarrow p\rho \rightarrow p\pi ^+\pi ^-$ with $(V'_P)^2/\Gamma _{\Lambda _c}=4.5\times 10^3$ MeV

Fig. 7

The $K^+K^-$ invariant mass distribution of the decay $\Lambda _c \rightarrow pK^+K^-$ in s-wave with different values of $C=3,2,-2,-3$ and an arbitrary normalization factor $V_P$. The curves labeled as ‘both’, ‘$I=0$’, and ‘$I=1$’ correspond to the contributions from the term of $t^{\mathrm{s-wave}}_{\Lambda _c\rightarrow pK^+K^-}$, $t^{I=0}$, and $t^{I=1}$, respectively

In addition to the factor $V_P$, we have also the free parameter C, the relative weight of the external emission mechanism with respect to the internal emission mechanisms. The value of C should be around 3 because we take the number of the colors $N_c=3$, and the relative sign of C is not fixed. We present the $K^+K^-$ and $\pi ^+\pi ^-$ invariant mass distributions with different values of $C=3,2,-2,-3$ in Figs. 7 and 8, respectively. In the $K^+K^-$ invariant mass distribution, one can see that the contributions from the isospin $I=1$ are much smaller than the ones of the isospin $I=0$ for the positive values of C, while both contributions from the isospin $I=0$ and $I=1$ are comparable for the negative values of C. This is because the coefficients of the terms $t^{I=0}$ and $t^{I=1}$ have the opposite sign before the C, and the contributions from the $\pi ^0\eta$ and $(K{\bar{K}})_{I=1}$ [see Eq. (16)] have the negative interference for positive values of C. In both cases, one can find an enhancement structure close to the threshold, which is stronger for the positive values of C and weaker for the negative values of C. For the $\pi ^+\pi ^-$ invariant mass distribution of Fig. 8, we can see a clear bump structure around 500 MeV, and a sharp peak around 980 MeV, which correspond to the $f_0(500)$ and $f_0(980)$, respectively. Both the signals are clearer for the positive value of C, and weaker for the negative value of C.

Fig. 8

The $\pi ^+\pi ^-$ invariant mass distribution of the decay $\Lambda _c \rightarrow p\pi ^+\pi ^-$ in s-wave with different values of $C=3,2,-2,-3$ and an arbitrary normalization factor $V_P$

It should be stressed that although the BESIII Collaboration has reported the $K^+K^-$ and $\pi ^+\pi ^-$ invariant mass distributions, we can not fit our model to to BESIII data which contain the background in the sideband region [18]. In addition, we must bear in mind that the chiral unitary approach only makes reliable predictions up to 1100-1200 MeV. With the value of $(V'_P)^2/\Gamma _{\Lambda _c}=4.5\times 10^3$ MeV obtained above, we present the $K^+K^-$ and $\pi ^+\pi ^-$ invariant mass distributions by summing the contributions from the decays in s-wave and the intermediate vector mesons incoherently, as shown in Figs. 9 and 10, respectively. For comparison, the BESIII data [18] have been adjusted to the strength of our theoretical calculations. We take the parameter $C=2$ and $(V_P)^2/\Gamma _{\Lambda _c}=0.2$ MeV$^{-1}$, in order to give rise to the sizeable signals of the $f_0(500)$ and $f_0(980)$ ¹. Both the parameters can be obtained by fitting to the experimental data, when more precise measurement of the processes is available in future. For the $K^+K^-$ invariant mass distribution, our model produces an enhancement structure close to the threshold mainly due to the resonance $f_0(980)$, and a clear peak of the $\phi$, which are in good agreement with the BESIII data. It is worth mentioning that, in the $K^+K^-$ invariant mass distribution of the decay $\chi _{cJ}\rightarrow p{\bar{p}}K^+K^-$ measured by the BESIII Collaboration [47], one can find an enhancement structure close to the threshold, which can be associated to the resonance $f_0(980)$ and $a_0(980)$. A similar structure can also be found in the decay $D^+_s \rightarrow K^+K^-\pi ^+$ measured by the BABAR Collaboration [48].

Fig. 9

The $K^+K$ invariant mass distribution of the $\Lambda _c \rightarrow pK^+K^-$ decay compared with the experimental data from Ref. [18]. The green dotted curve stands for the contribution from the meson-meson interaction in s-wave, the blue dashed curve corresponds to the results for the intermediate vector $\phi$, and the red solid line shows the total contributions

For the $\pi ^+\pi ^-$ invariant mass distribution of the decay $\Lambda _c\rightarrow p \pi ^+\pi ^-$ as shown in Fig. 10, one can see a clear peak around 770 MeV, corresponding to the vector meson $\rho ^0$, and a broad peak around 500 MeV, which can be associated to the scalar meson $f_0(500)$, dynamically generated from the meson-meson interactions in s-wave. In addition, there is a narrow sharp peak around 980 MeV for the scalar state $f_0(980)$. We can see that the broad peak for $f_0(500)$, the peak for $\rho ^0$, and a narrow sharp one for $f_0(980)$ ² of our results are compatible with the BESIII measurement [18].

From Figs. 9 and 10, one can find that the results with $C=2$ are in reasonable agreement with the BESIII measurements [18], which implies that the W external emission mechanism is more important than the W internal emission mechanism. According to the topological classification of the weak decays in Refs. [49, 50], the strength of W external emission is larger than the one of W internal emission. It should be stressed that our results strongly depend on the sign of C, and the present measurements of the BESIII Collaboration favor $C=2$ and a much smaller contribution from the $a_0(980)$. Indeed, if there is a sizeable contribution from the $a_0(980)$ in $\Lambda _c \rightarrow p K^+K^-$, it implies that we can observe the process $\Lambda _c\rightarrow p \pi ^0 \eta$, and the signal of the $a_0(980)$ in the $\pi ^0\eta$ mass distribution experimentally, however there are no any report about this process [42].

Fig. 10

The $\pi ^+\pi ^-$ invariant mass distributions of the $\Lambda _c \rightarrow p \pi ^+ \pi ^-$ decay compared with the experimental data from Ref. [18]. The green dotted curve stands for the contribution from the meson–meson interaction in s-wave, the blue dashed curve corresponds to the results for the intermediate vector $\rho ^0$, and the red solid line shows the total contributions

4 Conclusions

In this work, we have studied the decays $\Lambda _c\rightarrow p K^+K^-$ and $\Lambda _c\rightarrow p \pi ^+\pi ^-$, by taking into account contributions of the intermediate vector mesons, and the s-wave meson–meson interactions within the chiral unitary approach, where the $f_0(500)$, $f_0(980)$, and $a_0(980)$ resonances are dynamically generated.

The $K^+K^-$ and $\pi ^+\pi ^-$ invariant mass distributions for these two decays are calculated. In the $K^+K^-$ invariant mass distribution, one can find a narrow peak for the $\phi$, and an enhancement structure close to the $K^+K^-$ threshold, which should be the reflection of the $f_0(980)$ and $a_0(980)$ resonances. For the $\Lambda _c\rightarrow p \pi ^+\pi ^-$ mass distribution, in addition to the broad peak of the $\rho ^0$, one can find a bump structure around 500 MeV for the $f_0(500)$, and a narrow sharp peak around 980 MeV for the $f_0(980)$, in agreement with the BESIII measurement.

According to our calculations, the present measurements of the BESIII Collaboration favor a much smaller contribution from the $a_0(980)$. As we discussed, if there is a sizeable contribution from the $a_0(980)$ in $\Lambda _c \rightarrow p K^+K^-$, it implies that we can observe the process $\Lambda _c\rightarrow p \pi ^0 \eta$, and the signal of the $a_0(980)$ in the $\pi ^0\eta$ mass distribution experimentally, however there are no any report about this process [42].

We encourage our experimental colleagues to measure these two decays, which can be used to test the molecular nature of the scalar resonances $f_0(500)$, $f_0(980)$, and $a_0(980)$.