The $a_0(980)$ and $\Lambda (1670)$ in the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay

Abstract

We propose to study the $a_0(980)$ and the $\Lambda (1670)$ resonances in the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay via the final-state interactions of the $\pi ^+ \eta$ and $\eta \Lambda$ pairs. The weak interaction part proceeds through the c quark decay process: $c(ud) \rightarrow (s + u + \bar{d})(ud)$, while the hadronization part takes place in two mechanisms, differing in how the quarks from the weak decay combines into $\pi ^+\eta \Lambda$ with a $q\bar{q}$ with the quantum numbers of the vacuum. Because the final $\pi ^+ \eta$ and $\eta \Lambda$ states are in pure isospin $I = 1$ and $I=0$ combinations, the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay can be an ideal process to study the $a_0(980)$ and $\Lambda (1670)$ resonances. Describing the final-state interaction in the chiral unitary approach, we find that the $\pi ^+ \eta$ and $\eta \Lambda$ invariant mass distributions, up to an arbitrary normalization, show clear cusp and peak structures, which can be associated with the $a_0(980)$ and $\Lambda (1670)$ resonances, respectively. The proposed mechanism can provide valuable information on the nature of these resonances and can in principle be tested by facilities such as BEPCII.

1 Introduction

Understanding the nature of mesons and baryons has always been one of the most challenging topics in hadron physics. The new observations [1–7] have challenged the conventional wisdom that mesons are made of quark–antiquark pairs and baryons are composed of three quarks at low energies. In this respect, it is not surprising that both the $a_0(980)$ state and the $\Lambda (1670)$ have generated a lot of interests in their true nature. The $a_0(980)$ has been suggested of being either a $q \bar{q}$, a tetraquark state, a meson–meson molecule, a glueball, or a dynamically generated state [8]. Similarly, the $\Lambda (1670)$ has been found to be consistent with both a naive three-quark picture and a molecular picture dynamically generated from $\eta \Lambda$ and $\bar{K}N$ interactions.

In the chiral unitary approach, the $a_0(980)$ state was shown to be dynamically generated from the interaction of $\bar{K} K$ and $\pi \eta$ treated as coupled channels in isospin $I = 1$ [9, 10]. It decays into $\pi \eta$ in s-wave with a total decay width around 170 MeV. The pole of the $a_0(980)$ is strongly tied to the coupled channels and it disappears if either the $\pi \eta$ or the $K\bar{K}$ channel is discarded. The closeness of its pole to the $K\bar{K}$ threshold and its strong coupling to $K\bar{K}$ have led to the suggestion that the $a_0(980)$ state might be a cusp effect [9, 10]. As a result, the $a_0(980)$ total decay width increases very fast as its mass increases. For instance, Ref. [11] has claimed a large width for the $a_0(980)$ around 200 MeV, where the $a_0(980)$ state was studied within a realistic meson-exchange model for the $\pi \pi$ and $\pi \eta$ interactions.

On the other hand, in Ref. [12], it was claimed that both the $a_0(980)$ and the $a_0(1450)$ resonance emerge from a single $q \bar{q}$ seed state. This state interacts with other mesons, giving rise to meson–meson (MM) loop contributions to the corresponding mass. These contributions shift the pole of the seed state to higher energies, turning into the $a_0(1450)$. For the $a_0(980)$, the meson cloud eats up the original seed, becoming the largest component [12] (see also Refs. [13–16]). By now it is commonly accepted that the $a_0(980)$ is not a standard $q \bar{q}$ state but an extraordinary state [17].

For the $\Lambda (1670)$ hyperon resonance, based on the analysis of the available high precision data on $K^- p \rightarrow \eta \Lambda$ reaction, it was argued to be a three-quark state [18]. Such a conclusion is also supported in the study of the $K^- p \rightarrow \pi ^0 \Sigma ^0$ reaction at low energies within the chiral quark model [19]. However, in the chiral unitary approach, the $\Lambda (1670)$ resonance can be dynamically generated from the s-wave meson baryon interaction in the strangeness $S=-1$ sector [20, 21]. Experimentally, the $\Lambda (1670)$ resonance is known to have a strong coupling to the $\eta \Lambda$ channel [22]. Hence, it is expected that the $\eta \Lambda$ production is dominated by formation of the intermediate $\Lambda (1670)$ resonance.

In recent years, it has been shown that the selection of particular modes is possible in the nonleptonic weak decays of heavy hadrons [23]. In particular, the nonleptonic weak decays of charmed baryons can be useful tools to study hadronic resonances, some of which are subjects of intense debate about their nature [8, 24, 25]. In addition, those weak decays are also helpful to investigate final-state interactions and hence have the potential to bring further light into the nature of some puzzling hadrons [23]. For instance, the $\Lambda ^0_b \rightarrow J/\psi \Lambda (1405)$ decay was studied in Refs. [26, 27], where the $\Lambda (1405)$ state is generated in the final-state interaction of the ground state pseudoscalar mesons and octet baryons (MB). In Ref. [28], the work of Refs. [26, 27] on the $\Lambda ^0_b \rightarrow J/\psi \mathrm{MB}$ weak decays was extended to the $\Lambda ^+_c \rightarrow \pi ^+ \mathrm{MB}$ weak decays. It is shown there that these weak decays might be ideal processes to study the $\Lambda (1405)$ and $\Lambda (1670)$ resonances, because they are dominated by the $I = 0$ contribution. In Ref. [29], the $\pi \Sigma$ mass distribution was studied in the $\Lambda ^+_c \rightarrow \pi ^+ \pi \Sigma$ decays with the aim of extracting the $\pi \Sigma$ scattering lengths. In a recent work [30] the role of the exclusive $\Lambda ^+_c$ decays into a neutron in testing the flavor symmetry and final-state interaction was investigated. It was shown that the three-body nonleptonic decays are of great interest to explore the final-state interaction in $\Lambda _c^+$ decays.

Along this line, in the present work, we revisit the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay taking into account not only the $\eta \Lambda$ final-state interaction, but also the final-state interaction of $\pi ^+ \eta$, which gives the line shape of the $a_0(980)$ state. The pure $I = 1$ nature of the $\pi ^+ \eta$ channel is particularly beneficial to the study of the $a_0(980)$ state.

This article is organized as follows. In Sect. 2, we present the theoretical formalism of the weak $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay, explaining in detail the hadronization and final-state interactions of the $\eta \Lambda$ and $\pi ^+\eta$ pairs. Numerical results and discussions are presented in Sect. 3, followed by a short summary in the last section.

2 Formalism

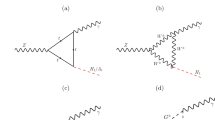
As shown in Ref. [28], a way for the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ to proceed is the following: in the first step the charmed quark in $\Lambda ^+_c$ turns into a strange quark with a $u \bar{d}$ pair by the weak decay shown in Fig. 1. The next step consists in introducing a new $\bar{q} q$ pair with the quantum numbers of the vacuum, $\bar{u} u + \bar{d} d + \bar{s} s$, to form a meson (baryon) from the s quark (ud diquark) or MM from the $u \bar{d}$ pair with $\Lambda$ from the sud cluster. Finally, the final-state interactions of the MM or $\mathrm{MB}$ will lead to dynamical generation of the $a_0(980)$ and $\Lambda (1670)$. In the following, we discuss the $\eta \Lambda$ and $\pi ^+ \eta$ final-state interactions separately.

Fig. 1

The dominant diagram at the quark level for $\Lambda ^+_c$ decaying into a $u \bar{d}$ pair and a su d cluster. The solid lines and the wiggly line stand for the quarks and the $W^+$ boson, respectively

In addition to the c quark decay process descried above, in principle one can also have contributions from internal W exchange ($c+d \rightarrow s + u$). As discussed in Refs. [28, 31], these contributions are smaller than the c decay process. Furthermore, including such contributions, the decay amplitudes would become more complex due to additional parameters from the weak interaction, and we cannot determine or constrain these parameters. Hence, we will leave these contributions to future studies when more experimental data become available.

2.1 Final-state interaction of meson–baryon

We first discuss the decay of $\Lambda ^+_c\rightarrow \pi ^+\eta \Lambda$ where the $\pi ^+$ is formed from the $u \bar{d}$ pair and the sud cluster hadronizes into a meson–baryon pair. To create the $\mathrm{MB}$ final state, we must proceed to hadronize the sud cluster by creating an extra $\bar{q} q$ pair as depicted in Fig. 2. In this process, the ud diquark in $\Lambda ^+_c$ is the spectator, and the sud cluster is combined into a pure $I = 0$ state,

$$\begin{aligned} \frac{1}{\sqrt{2}} |s(ud -du)\rangle . \end{aligned}$$

(1)

As in Refs. [26, 28], one can straightforwardly obtain the meson–baryon states after the $\bar{q} q$ pair production as

$$\begin{aligned} |\mathrm{MB}\rangle = |K^-p\rangle + |\bar{K}^0 n\rangle - \frac{\sqrt{2}}{3} |\eta \Lambda \rangle , \end{aligned}$$

(2)

where the flavor states of the baryons are as follows:

$$\begin{aligned}&|p\rangle = \frac{1}{\sqrt{2}} |u(ud - du)\rangle , \end{aligned}$$

(3)

$$\begin{aligned}&|n\rangle = \frac{1}{\sqrt{2}} |d(ud - du)\rangle , \end{aligned}$$

(4)

$$\begin{aligned} |\Lambda \rangle= & {} \frac{1}{\sqrt{12}} |(usd - dsu) + (dsu - uds) \nonumber \\&+\, 2(sud - sdu)\rangle . \end{aligned}$$

(5)

Fig. 2

Hadronization of the su d cluster into one meson and one baryon for the $\Lambda ^+_c \rightarrow \pi ^+ \mathrm{MB}$ decay with the $\pi ^+$ emission from the $u \bar{d}$ pair

After the production of a meson–baryon pair, the final-state interaction between the meson and the baryon takes place, which can be parameterized by the rescattering shown in Fig. 3 at the hadronic level for the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay. In Fig. 3, we also show the tree level diagram for the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay.

Fig. 3

The diagram for the meson-baryon final-state interaction for the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay

According to Eq. (2), we can write down the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay amplitude of Fig. 3 as [32]:

$$\begin{aligned} T^{\mathrm{MB}}= & {} V_P \Big ( -\frac{\sqrt{2}}{3} + G_{K^- p} (M_{\eta \Lambda }) t_{K^- p \rightarrow \eta \Lambda } (M_{\eta \Lambda }) \nonumber \\&+\, G_{\bar{K}^0 n} (M_{\eta \Lambda }) t_{\bar{K}^0 n \rightarrow \eta \Lambda } (M_{\eta \Lambda }) \nonumber \\&-\frac{\sqrt{2}}{3} G_{\eta \Lambda } (M_{\eta \Lambda }) t_{\eta \Lambda \rightarrow \eta \Lambda } (M_{\eta \Lambda }) \Big ), \end{aligned}$$

(6)

where $V_P$ expresses the weak and hadronization strength, which is assumed to be independent of the final-state interaction.¹ In the above equation, $G_{\mathrm{MB}}$ denotes the one-meson–one-baryon loop function, which depends on the invariant mass of the final $\eta \Lambda$ system, $M_{\eta \Lambda }$. The meson–baryon scattering amplitudes $t_{\mathrm{MB} \rightarrow \eta \Lambda }$ are those obtained in the chiral unitary approach, which depend also on $M_{\eta \Lambda }$. Details can be found in Refs. [20, 21, 34].

2.2 Final-state interaction of meson–meson

Next, we discuss the decay of $\Lambda ^+_c$ where the $\Lambda$ originates from the sud cluster and the $u \bar{d}$ pair undergoes hadronization to form a meson–meson pair. The hadronization is now realized combining an extra $\bar{q} q$ pair from the vacuum with the $u \bar{d}$ pair,² as shown in Fig. 4. In this process, the $I = 0$ sud cluster will form the $\Lambda$ state:

$$\begin{aligned} \frac{1}{\sqrt{2}} |s(ud -du)\rangle ~~ \Rightarrow ~~ \frac{\sqrt{6}}{3} |\Lambda \rangle . \end{aligned}$$

(7)

Fig. 4

The hadronization of the $u \bar{d}$ pair into two mesons

In the following, we explain in detail which mesons are produced in the hadronization of the $u \bar{d}$ pair. We first introduce the $q \bar{q}$ matrix,

$$\begin{aligned} M = \left( \begin{array}{c@{\quad }c@{\quad }c} u\bar{u} &{} u \bar{d} &{} u\bar{s} \\ d\bar{u} &{} d\bar{d} &{} d\bar{s} \\ s\bar{u} &{} s\bar{d} &{} s\bar{s} \\ \end{array} \right) = \left( \begin{array}{c} u \\ d \\ s \\ \end{array} \right) \left( \begin{array}{c@{\quad }c@{\quad }c} \bar{u}&\bar{d}&\bar{s} \end{array} \right) , \end{aligned}$$

(8)

which has the following property:

$$\begin{aligned} M \cdot M = M \times (\bar{u} u + \bar{d} d + \bar{s} s). \end{aligned}$$

(9)

Next, we rewrite the $\bar{q} q$ matrix M in terms of meson components and, as a result, M can be identified with the matrix $\phi$ [36–38]

$$\begin{aligned} \phi = \left( \begin{array}{c@{\quad }c@{\quad }c} \frac{\eta }{\sqrt{3}} + \frac{\pi ^0}{\sqrt{2}} + \frac{\eta '}{\sqrt{6}} &{} \pi ^+ &{} K^{+} \\ \pi ^- &{}\frac{\eta }{\sqrt{3}} - \frac{\pi ^0}{\sqrt{2}} + \frac{\eta '}{\sqrt{6}} &{} K^{0} \\ K^{-} &{} \bar{K}^{0} &{} - \frac{\eta }{\sqrt{3}} + \sqrt{\frac{2}{3}}\eta ' \\ \end{array} \right) , \end{aligned}$$

(10)

which incorporates the standard $\eta$ and $\eta '$ mixing [36].

Then, in terms of mesons, the hadronized $u \bar{d}$ pair is given by

$$\begin{aligned} u \bar{d} (\bar{u} u +\bar{d} d +\bar{s} s)\equiv & {} (M \cdot M)_{12} \equiv (\phi \cdot \phi )_{12} \nonumber \\= & {} \frac{2}{\sqrt{3}} \pi ^+ \eta + K^+ \bar{K}^{0}, \end{aligned}$$

(11)

where we have omitted the $\eta '$ term because of its large mass. Taking into account the $\Lambda$ production of Fig. 5 and the weight of Eq. (7), we obtain the meson–meson production with a $\Lambda$ baryon as

$$\begin{aligned} |\mathrm{MM}\rangle = \frac{2\sqrt{2}}{3} \pi ^+ \eta + \frac{\sqrt{6}}{3} K^+ \bar{K}^0, \end{aligned}$$

(12)

where the rescattering of $\pi ^+ \eta$ and $K^+ \bar{K}^0$ will give the line shape of the $a_0(980)$ state.

Fig. 5

The diagram for the meson–meson final-state interaction for the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay

More specifically the transition amplitude is of the following form [32]:

$$\begin{aligned} T^{\mathrm{MM}}= & {} V'_P \left( \frac{2\sqrt{2}}{3} + \frac{2\sqrt{2}}{3} G_{\pi ^+ \eta } (M_{\pi ^+ \eta }) t_{\pi ^+ \eta \rightarrow \pi ^+ \eta } (M_{\pi ^+ \eta })\right. \nonumber \\&\left. + \frac{\sqrt{6}}{3}G_{K^+ \bar{K}^0} (M_{\pi ^+ \eta }) t_{K^+ \bar{K}^0 \rightarrow \pi ^+ \eta } (M_{\pi ^+ \eta }) \right) , \end{aligned}$$

(13)

where $G_\mathrm{MM}$ is the loop function of the two intermediate meson propagators [9] and $t_{\mathrm{MM} \rightarrow \pi ^+ \eta }$ are the meson–meson scattering amplitudes obtained in Ref. [9], which depend on the invariant mass $M_{\pi ^+ \eta }$ of the $\pi ^+ \eta$ system. In general, the factor $V'_P$ should be different from the factor $V_P$ in Eq. (6).

2.3 Invariant mass distributions of the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay

With all the ingredients obtained in the previous section, one can write down the invariant mass distributions for the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay as [22]

$$\begin{aligned} \frac{\mathrm{d}^2 \Gamma _{\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda }}{\mathrm{d} M^2_{\pi ^+ \eta } \mathrm{d} M^2_{\eta \Lambda }}= & {} \frac{1}{(2\pi )^3} \frac{M_{\Lambda }}{8 M^2_{\Lambda ^+_c}} \left|T (M_{\pi ^+ \eta }, M_{\eta \Lambda }) \right|^2 , \end{aligned}$$

(14)

where T is the total decay amplitude for the decay of $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ depending on the invariant $\pi ^+ \eta$ and $\eta \Lambda$ masses. The $\Lambda _c^+$ decay is a three-body decay and the invariant mass distribution with respect to any of the two invariant masses is evaluated by integrating over the other invariant mass. For a given value of $M_{\pi ^+ \eta }$, the range of $M_{\eta \Lambda }$ is fixed as

$$\begin{aligned} M^\mathrm{max}_{\eta \Lambda } \!= & {} \! \sqrt{ \left( E_{\eta } + E_{\Lambda } \right) ^2-\left( \sqrt{E^{2}_{\eta } - m^2_{\eta }} - \sqrt{E^{2}_{\Lambda } - m^2_{\Lambda }} \right) ^2 }, \\ M^\mathrm{min}_{\eta \Lambda } \!= & {} \! \sqrt{ \left( E_{\eta } + E_{\Lambda } \right) ^2 - \left( \sqrt{E^{2}_{\eta } - m^2_{\eta }} + \sqrt{E^{2}_{\Lambda } - m^2_{\Lambda }} \right) ^2 }, \end{aligned}$$

where $E_{\eta } = (M^2_{\pi ^+ \eta } - m^2_{\pi ^+} + m^2_{\eta })/2M_{\pi ^+ \eta }$ and $E_{\Lambda } = (M^2_{\Lambda ^+_c} - M^2_{\pi ^+ \eta } - m^2_{\Lambda })/2M_{\pi ^+ \eta }$ are the energies of $\eta$ and $\Lambda$ in the $\pi ^+ \eta$ rest frame. Similarly, for a given value of $M_{\eta \Lambda }$, we can easily obtain the range of invariant masses allowed for the $\pi ^+\eta$, namely $M_{\pi ^+ \eta }$.

Taking $M_{\pi ^+ \eta } = 980$ MeV, we obtain

$$\begin{aligned} M^\mathrm{max}_{\eta \Lambda }= & {} 2043 ~\mathrm{MeV}, \\ M^\mathrm{min}_{\eta \Lambda }= & {} 1680 ~\mathrm{MeV}, \end{aligned}$$

which indicates that the meson–meson final-state interaction to form the $a_0(980)$ state only contributes to $\eta \Lambda$ invariant masses beyond the peak around 1670 MeV. Noting the fact that the obtained peak of the $\Lambda (1670)$ resonance is narrow [20, 21], we expect that the meson–meson final state interaction will not affect much the peak structure of the $\Lambda (1670)$ resonance in the $\eta \Lambda$ invariant mass distribution.

Similarly, if we take $M_{\eta \Lambda } = 1670$ MeV, we obtain

$$\begin{aligned} M^\mathrm{max}_{\pi ^+ \eta }= & {} 1104 ~\mathrm{MeV}, \\ M^\mathrm{min}_{\pi ^+ \eta }= & {} 1011 ~\mathrm{MeV}, \end{aligned}$$

which seems to imply that the meson–baryon final-state interaction to form the $\Lambda (1670)$ state contributes to the $\pi ^+ \eta$ invariant masses beyond the peak/cusp in the $\pi ^+ \eta$ mass around 980 MeV of the $a_0(980)$ state. However, we will see that the meson–baryon final-state interaction does affect the $a_0(980)$ structure in the invariant $\pi ^+ \eta$ mass distribution.

Because the factors $V_P$ and $V'_P$ are unknown in our model, and the relative phase between $T^{\mathrm{MB}}$ and $T^{\mathrm{MM}}$ is unknown either, we will study three models: Model A takes into account only the meson–baryon final-state interaction; Model B includes only the meson–meson final-state interaction; Model C considers both meson–baryon and meson–meson final-state interactions. Because the relative strong phase, $\delta$, between these two decay mechanisms is unknown, in Model C, we take $\delta$ as a free parameter. For these three models, we can write the total decay amplitude T as

$$\begin{aligned} T= & {} T^{\mathrm{MB}}, ~~~ \mathrm{for~ Model~ A}, \end{aligned}$$

(15)

$$\begin{aligned} T= & {} T^{\mathrm{MM}}, ~~~ \mathrm{for~ Model~ B}, \end{aligned}$$

(16)

$$\begin{aligned} T= & {} T^{\mathrm{MB}} + T^{\mathrm{MM}} e^{i\delta }, ~~~ \mathrm{for~ Model~ C}. \end{aligned}$$

(17)

On the other hand, since the values of $V_P$ and $V'_P$ are unknown, we impose a constraint on the values of $V_P$ and $V'_P$ such that

$$\begin{aligned} \Gamma ^\mathrm{Model ~A}_{\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda } = \Gamma ^\mathrm{Model ~B}_{\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda }. \end{aligned}$$

(18)

In this respect, we assume that the strengths of the two decay mechanisms shown in Figs. 2 and 4 are equal. This is a reasonable assumption, since any proposed mechanism should first explain the experimental decay width, and then the corresponding invariant mass distributions will allow one to distinguish between different decay mechanisms. At present, neither the decay width nor the invariant mass distribution of the $\Lambda _c\rightarrow \pi ^+\eta \Lambda$ is known experimentally. From Eq. (18), we obtain³

$$\begin{aligned} V'_P = 0.38 V_P. \end{aligned}$$

(19)

Table 1 Masses and spin-parities of the particles studied in the present work

3 Numerical results and discussion

In this section, we show the numerical results for the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay using the formalism described in the previous section with the masses and spin-parities of the involved particles listed in Table 1 with values taken from PDG [22]. First we show $\frac{\mathrm{d}\Gamma }{\mathrm{d}M_{\eta \Lambda }}$ in Fig. 6. The dashed and dotted curves represent the numerical results obtained with Model A and B, respectively, while the black-solid, red-solid, and green-solid lines stand for the results obtained with Model C and the relative strong phase $\delta = \pi /2$, 0, and $\pi$, respectively. The meson–baryon amplitudes are taken from Ref. [20, 21] and the meson–meson amplitudes from Ref. [9]. In Fig. 6, a peak corresponding to the $\Lambda (1670)$ resonance can be clearly seen as in Ref. [28], regardless of the value of $\delta$. The interference between $T^{\mathrm{MB}}$ and $T^{\mathrm{MM}}$ is destructive and constructive with $\delta = 0$ and $\delta = \pi$, respectively. From Fig. 6, it is clear that, for the $\eta \Lambda$ invariant mass distribution, particularly regarding the $\Lambda (1670)$, the effect from the meson–meson final-state interaction is small and can be safely neglected, supporting the assumption made in Ref. [28]. We expect that the $\Lambda (1670)$ resonance can be seen and studied from the weak decay of $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ in future experiments.

Fig. 6

(Color online) Invariant $\eta \Lambda$ mass distribution for the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay. The dashed, dotted, and solid lines represent the results obtained with Model A, B, and C, respectively.

Next we turn to the $\pi ^+ \eta$ distribution shown in Fig. 7. From the numerical results of Model B, we see a clear peak/cusp around $M_{\pi ^+\eta } = 980$ MeV which corresponds to the $a_0(980)$ state. In addition, the effect of the meson–baryon final-state interaction broadens the line shape of the $\pi ^+ \eta$ mass distribution. Nevertheless, the peak/cusp structure of the $a_0(980)$ state is still visible. Hence, additional experimental information on $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay can be used to investigate the nature of the $a_0(980)$ state. It should be noted that the visibility of the $a_0(980)$ in Model C is tied to the assumption we made for the interference of the two hadronization amplitudes and their relative coupling strengths. An experimental measurement of the line shape will ultimately allow one to extract such information.

Fig. 7

(Color online) Invariant $\pi ^+ \eta$ mass distribution for the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay. The dashed, dotted, and solid lines represent the results obtained with Model A, B, and C, respectively

4 Conclusions

In the present work we have studied the $\pi ^+ \eta$ and $\eta \Lambda$ invariant mass distributions in the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay to understand better the $a_0(980)$ and $\Lambda (1670)$ resonances. The weak interaction part is dominated by the c quark decay process: $c(ud) \rightarrow (s + u + \bar{d})(ud)$, while the hadronization part can take place in two different mechanisms. In the first one, the sud cluster picks up a $q\bar{q}$ pair from the vacuum and hadronizes into a meson–baryon pair, while the $u\bar{d}$ pair from the weak decay turns into a $\pi ^+$. In the second mechanism, the sud cluster hadronizes into a $\Lambda$, while the $u\bar{d}$ pair from the weak process hadronizes into a meson–meson pair together with a $q\bar{q}$ pair with the quantum numbers of the vacuum. The following final-state interactions of the meson–meson and baryon–baryon pairs are described in the chiral unitary model that dynamically generates the $a_0(980)$ and $\Lambda (1670)$ states. From the line shapes of the invariant mass distributions, the $a_0(980)$ and $\Lambda (1670)$ states are clearly seen.

On the experimental side, the decay mode $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ has been observed [22, 39] and the branching ratio $\mathrm {Br}(\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda )$ is determined to be $(2.4 \pm 0.5)\%$, which is one of the dominant decay modes of the $\Lambda ^+_c$ state. For the decay of $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$, the final $\pi ^+ \eta$ and $\eta \Lambda$ states are in pure isospin $I = 1$ and $I=0$ combinations, respectively. Hence, the $\Lambda ^+_c \rightarrow \pi ^+ \eta \Lambda$ decay might be an ideal process to study the $a_0(980)$ and $\Lambda (1670)$ resonances. Future experimental measurements of the invariant mass distributions studied in the present work will be very helpful in illuminating the nature of the $a_0(980)$ and $\Lambda (1670)$ resonances. For example, a corresponding experimental measurement could in principle be done at BESIII [40].