The decays of $\bar{B}^0$, $\bar{B}^0_s$ and $B^-$ into $\eta _c$ plus a scalar or vector meson

Abstract

We investigate the decays of $\bar{B}^0_s$, $\bar{B}^0$ and $B^-$ into $\eta _c$ plus a scalar or vector meson in a theoretical framework by taking into account the dominant process for the weak decay of $\bar{B}$ meson into $\eta _c$ and a $q\bar{q}$ pair. After hadronization of this $q\bar{q}$ component into pairs of pseudoscalar mesons we obtain certain weights for the pseudoscalar meson-pseudoscalar meson components. In addition, the $\bar{B}^0$ and $\bar{B}^0_s$ decays into $\eta _c$ and $\rho ^0$, $K^*$ are evaluated and compared to the $\eta _c$ and $\phi$ production. The calculation is based on the postulation that the scalar mesons $f_0(500)$, $f_0(980)$ and $a_0(980)$ are dynamically generated states from the pseudoscalar meson-pseudoscalar meson interactions in S-wave. Up to a global normalization factor, the $\pi \pi$, $K \bar{K}$ and $\pi \eta$ invariant mass distributions for the decays of $\bar{B}^0_s \rightarrow \eta _c \pi ^+ \pi ^-$, $\bar{B}^0_s \rightarrow \eta _c K^+ K^-$, $\bar{B}^0 \rightarrow \eta _c \pi ^+ \pi ^-$, $\bar{B}^0 \rightarrow \eta _c K^+ K^-$, $\bar{B}^0 \rightarrow \eta _c \pi ^0 \eta$, $B^- \rightarrow \eta _c K^0 K^-$ and $B^- \rightarrow \eta _c \pi ^- \eta$ are predicted. Comparison is made with the limited experimental information available and other theoretical calcualtions. Further comparison of these results with coming LHCb measurements will be very valuable to make progress in our understanding of the nature of the low lying scalar mesons, $f_0(500), f_0(980)$ and $a_0(980)$.

1 Introduction

In addition to the measurement of the $B^0_s \rightarrow J/\psi \pi ^+ \pi ^-$ decay [1], the branching fractions $\mathrm{Br}(B^0_s \rightarrow \eta _c \pi ^+ \pi ^-) = (1.76 \pm 0.59 \pm 0.12 \pm 0.29) \times 10^{-4}$ and $\mathrm{Br}(B^0_s \rightarrow \eta _c \phi ) = (5.01 \pm 0.53 \pm 0.27 \pm 0.63) \times 10^{-4}$ are recently measured by the LHCb collaboration [2]. The $f_0(980)$ is produced in the $\bar{B}^0_s$ decays into $J/\psi$ and $\pi ^+ \pi ^-$ and no trace of the $f_0(500)$ is seen [1], while in the $\bar{B}^0 \rightarrow J/\psi \pi ^+ \pi ^-$ decay, the main contribution is from the $f_0(500)$ with a small fraction for the $f_0(980)$ [3, 4]. The new measurement in Ref. [2], suggests also that the $\pi ^+ \pi ^-$ pair in $B^0_s \rightarrow \eta _c \pi ^+ \pi ^-$ arises from the contribution of $f_0(980)$. To understand the new experimental measurements and search for some hints about involved physics, corresponding theoretical studies are needed.

Estimations of the branch ratios for some of these decays have been done by employing the perturbative QCD factorization approach [5, 6]. Also, in Ref. [7] the decay widths of $B^0_s \rightarrow \eta _c f_0(980)$ and $B^0_s \rightarrow \eta _c \phi$ were evaluated in the light-front quark model. The conclusions of Ref. [7] are that the mostly dominant contribution for the $B^0_s \rightarrow \eta _c \pi ^+ \pi ^-$ decay is from the $f_0(980)$ and the $f_0(980)$ should be a $K\bar{K}$ molecule or a tetraquark state, at least the pure quark-antiquark component of $f_0(980)$ is small.

For the $B^0_s \rightarrow J/\psi \pi ^+ \pi ^-$ decay, a simple theoretical method based on the final state interaction of mesons provided by the chiral unitary approach has been applied in Ref. [8], where the theoretical results are in agreement with the data. The work of Ref. [8] isolates the dominant weak decay mechanism into $J/\psi$ and a $q\bar{q}$ pair. Then, the $q\bar{q}$ pair is hadronized and meson-meson pairs are formed with a certain weight. The final state interaction of the meson-meson components, described in terms of chiral unitary approach, gives rise to the $f_0(980)$ and $f_0(500)$ resonances. The approach of Ref. [8] was successfully extended to study other weak B and D decays in Refs. [9,10,11,12,13,14,15,16] (see also Ref. [17] for an extensive review). Other theoretical work has also been done within the perturbative QCD approach in Ref. [18]. Recently, another approach has been used in Ref. [19] using effective Hamiltonians, transversity form factors and implementing the meson-meson final sate interaction. In addition to the $\pi ^+ \pi ^-$ production, the $\bar{B}^0_s$ decay into $J/\psi$ and $K^+ K^-$ is also studied in Ref. [19] and compared to experimental measurements. In Ref. [20], the work of Ref. [19] on the $\bar{B}^0_s$ decay was extended to the $\bar{B}^0$ decay, where the $\bar{B}^0 \rightarrow J/\psi \pi \eta$ and $J/\psi K\bar{K}$ were investigated. It was found that the crucial information on $\pi \eta$ scattering can be deduced from the $\bar{B}^0 \rightarrow J/\psi \pi \eta$ and $J/\psi K\bar{K}$ decays [20].

Following this line of research, the purpose of this paper is to investigate the reactions of $\bar{B}^0$, $\bar{B}^0_s$ and $B^-$ decaying into $\eta _c$ plus a scalar or vector meson. We evaluate the $\pi ^+ \pi ^-$ and $K^+ K^-$ invariant mass distributions in the $\bar{B}^0_s$ decays into $\eta _c \pi ^+ \pi ^-$ and $\eta _c K^+ K^-$ and the $\pi ^+ \pi ^-$, $K^+ K^-$ and $\pi \eta$ production in the $\bar{B}^0$ decay into $\eta _c$ and this pair of mesons through scalar of vector meson. At the same time, we investigate also the $B^- \rightarrow \eta _c K^0 K^-$ and $B^- \rightarrow \eta _c \pi ^- \eta$ decays. Up to a global factor, one can compare the strength of those invariant mass distributions.

To end this introduction, we would like to mention that, up to an arbitrary normalization, one can obtain the invariant mass distributions and relate the different mass distributions with no parameters fitted to the data. This is due to the unified picture that the chiral unitary approach provides for the final state interaction of mesons. In this sense, predictions on the coming measurements should be most welcome, and if supported by experiment, it can give us more information about the nature of these low lying scalar mesons, $f_0(500)$, $f_0(980)$ and $a_0(980)$, which are dynamically generated states from the interaction of pseudoscalar mesons using a meson-meson interaction derived from the chiral Lagrangians [21, 22].

This article is organized as follows. In Sect. 2, we present the theoretical formalism of the decays of $\bar{B}^0$, $\bar{B}^0_s$ and $B^-$ decays into $\eta _c$ plus a scalar meson, explaining in detail the hadronization and final state interactions of the meson-meson pairs. Numerical results and discussions are presented in Sect. 3, followed by a summary in the last section.

2 Formalism and ingredients

2.1 Scalar meson production

The leading contributions to the decays of $\bar{B}^0_s$, $\bar{B}^0$ and $B^-$ into $\eta _c$ plus a scalar meson is the Cabibbo favored $b \rightarrow c \bar{c} s$ process and the Cabibbo suppressed $b \rightarrow c\bar{c}d$ process. In the following we will discuss the production mechanisms for these decays.

In addition to the charm quark decay process described above, in principle one should consider also the diagrams in which the $q\bar{q}$ pair in the final state annihilate into gluons which can then hadronize into pseudoscalar meson pairs. However, these contributions are smaller than the charm quark decay process, because these disconnected diagrams should be suppressed according to the Okubo-Zeig-Iizuka (OZI) rule. On the other hand, including such contributions, the decay amplitudes would become more complex due to additional parameters and we cannot determine or constrain these parameters because of the scarce information about them. Hence, we will leave these contributions to a future work when more experimental data become available.

Fig. 1

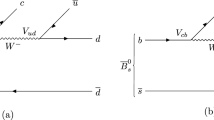
Diagrams for the decay of $\bar{B}^0$, $\bar{B}^0_s$ and $B^-$ into $\eta _c$ ($c\bar{c}$) and a primary $q\bar{q}$ pair, $s\bar{s}$ for $\bar{B}^0_s$ (a), $d \bar{d}$ for $\bar{B}^0$ (b), and $d \bar{u}$ for $B^-$ (c). The schematic representation of the hadronization $\bar{q}q \rightarrow \bar{q}q(\bar{u}u + \bar{d}d + \bar{s}s)$ is also shown

Following Refs. [8, 23], in Fig. 1 we show the diagrams at the quark level that are responsible for the $\bar{B}^0_s$, $\bar{B}^0$, and $B^-$ decays into $\eta _c$ and another pair of quarks: $s \bar{s}$ in the case of the $\bar{B}^0_s$ decay (Fig. 1a), $d \bar{d}$ in the case of $\bar{B}^0$ decay (Fig. 1b), and $d \bar{u}$ for the $B^-$ decay (Fig. 1c). The $\bar{B}^0_s$ decay involves the $V_{cs}$, Cabibbo favored Cabibbo-Kobayashi-Maskawa matrix element, and the $\bar{B}^0$ and $B^-$ decays involves the $V_{cd}$ Cabibbo suppressed one, which makes the widths large in the $\bar{B}^0_s$ case compared to the $\bar{B}^0$ and $B^-$ decays.¹

Fig. 2

Diagrammatic representations of the production of $\pi ^+ \pi ^-$, $\pi ^0 \eta$, $K^+ K^-$, $\pi ^- \eta$, and $K^-K^0$ via direct plus re-scattering mechanisms in $\bar{B}^0$ (a), $\bar{B} ^0_s$ (b) and $B^-$ (c) decays

In order to produce two mesons, the $q \bar{q}$ pair has to hadronize, which one can implement adding an extra $\bar{q} q$ pair with the quantum numbers of the vacuum, $\bar{u} u+ \bar{d} d+ \bar{s} s$, as shown also in Fig. 1. Next step corresponds to writing the $q\bar{q} (\bar{u} u+ \bar{d} d+ \bar{s} s)$ combination in terms of pairs of mesons. Following the work of Refs. [8, 17] we obtain²

$$\begin{aligned} d\bar{d} (\bar{u} u +\bar{d} d +\bar{s} s)\equiv & {} \pi ^- \pi ^+ +\frac{1}{2}\pi ^0 \pi ^0 +\frac{1}{3}\eta \eta \nonumber \\&-\frac{2}{\sqrt{6}}\pi ^0 \eta +\bar{K}^0 K^0 , \end{aligned}$$

(1)

$$\begin{aligned} s\bar{s} (\bar{u} u + \bar{d} d +\bar{s} s)\equiv & {} K^- K^+ + \bar{K}^0 K^0 +\frac{1}{3}\eta \eta , \end{aligned}$$

(2)

$$\begin{aligned} d\bar{u} (\bar{u} u +\bar{d} d +\bar{s} s)\equiv & {} \frac{2}{\sqrt{3}}\pi ^- \eta + K^0 K^- , \end{aligned}$$

(3)

where the $\eta '$ terms have been neglected because the $\eta '$ has large mass and has very small effect here. It is worth to mention that these results shown in Eqs. (1)–(3) can be also obtained with the scalar form factors [24, 25].

After the production of a meson-meson (MM) pair, the final state interaction between the mesons takes place, which can be parameterized by the re-scattering shown in Fig. 2 at the hadronic level. Since we consider only the S-wave interaction between the pseudo-scalar meson and pseudo-scalar meson, we will have the contributions from only the scalar mesons. In Fig. 2, we also show the tree level diagrams for the $\pi \pi$, $K \bar{K}$ and $\pi \eta$ production.

The decay amplitudes for a final production of the different meson pairs are given by [26]

$$\begin{aligned}&T(\bar{B}^0_s \rightarrow \eta _c \pi ^+ \pi ^-) = V_P V_{cs} ( G_{K^+ K^-} t_{K^+ K^- \rightarrow \pi ^+ \pi ^-} \nonumber \\&\quad + G_{K^0 \bar{K}^0} t_{K^0 \bar{K}^0 \rightarrow \pi ^+ \pi ^-} + \frac{1}{3} G_{\eta \eta } t_{\eta \eta \rightarrow \pi ^+ \pi ^-} ), \end{aligned}$$

(4)

$$\begin{aligned}&T(\bar{B}^0_s \rightarrow \eta _c K^+ K^-) = V_P V_{cs} ( 1+ G_{K^+ K^-} t_{K^+ K^- \rightarrow K^+ K^-} \nonumber \\&\quad + G_{K^0 \bar{K}^0} t_{K^0 \bar{K}^0 \rightarrow K^+ K^-} + \frac{1}{3} G_{\eta \eta } t_{\eta \eta \rightarrow K^+ K^-} ), \end{aligned}$$

(5)

for $\bar{B}^0_s$ decays, and

$$\begin{aligned}&T(\bar{B}^0 \rightarrow \eta _c \pi ^+ \pi ^-) = V_P V_{cd} ( 1+G_{\pi ^+ \pi ^-} t_{\pi ^+ \pi ^- \rightarrow \pi ^+ \pi ^-} \nonumber \\&\quad + \frac{1}{2} G_{\pi ^0 \pi ^0} t_{\pi ^0 \pi ^0 \rightarrow \pi ^+ \pi ^-} + G_{K^0 \bar{K}^0} t_{K^0 \bar{K}^0 \rightarrow \pi ^+ \pi ^-} \nonumber \\&\quad + \frac{1}{3} G_{\eta \eta } t_{\eta \eta \rightarrow \pi ^+ \pi ^-} ), \end{aligned}$$

(6)

$$\begin{aligned}&T(\bar{B}^0 \rightarrow \eta _c \pi ^0 \eta ) = V_P V_{cd} \left( -\frac{2}{\sqrt{6}}-\frac{2}{\sqrt{6}} G_{\pi ^0 \eta } t_{\pi ^0 \eta \rightarrow \pi ^0 \eta } \right. \nonumber \\&\quad \left. \phantom {\left( -\frac{2}{\sqrt{6}}-\frac{2}{\sqrt{6}} G_{\pi ^0 \eta } t_{\pi ^0 \eta \rightarrow \pi ^0 \eta } \right. }+ G_{K^0 \bar{K}^0} t_{K^0 \bar{K}^0\rightarrow \pi ^0 \eta } \right) , \end{aligned}$$

(7)

$$\begin{aligned}&T(\bar{B}^0 \rightarrow \eta _c K^+ K^-) = V_P V_{cd} ( G_{\pi ^+ \pi ^-} t_{\pi ^+ \pi ^- \rightarrow K^+ K^-} \nonumber \\&\quad + \frac{1}{2} G_{\pi ^0 \pi ^0} t_{\pi ^0 \pi ^0 \rightarrow K^+ K^-} + \frac{1}{3} G_{\eta \eta } t_{\eta \eta \rightarrow K^+ K^-} \nonumber \\&\quad -\frac{2}{\sqrt{6}} G_{\pi ^0 \eta } t_{\pi ^0 \eta \rightarrow K^+ K^-} +G_{K^0 \bar{K}^0} t_{K^0 \bar{K}^0\rightarrow K^+ K^-} ), \end{aligned}$$

(8)

for $\bar{B}^0$ decays, and

$$\begin{aligned}&T(B^- \rightarrow \eta _c \pi ^- \eta ) = V_P V_{cd} \left( \frac{2}{\sqrt{3}}+\frac{2}{\sqrt{3}} G_{\pi ^- \eta } t_{\pi ^- \eta \rightarrow \pi ^- \eta } \right. \nonumber \\&\quad \left. +G_{K^0 K^-} t_{K^0 K^- \rightarrow \pi ^- \eta } \phantom {\frac{2}{\sqrt{3}}}\right) , \end{aligned}$$

(9)

$$\begin{aligned}&T(B^- \rightarrow \eta _c K^0 K^-) = V_P V_{cd} \left( \phantom {\frac{2}{\sqrt{3}}}1+G_{K^0 K^-} t_{K^0 K^- \rightarrow K^0 K^-} \right. \nonumber \\&\quad \left. + \frac{2}{\sqrt{3}} G_{\pi ^- \eta } t_{\pi ^- \eta \rightarrow K^0 K^-} \right) , \end{aligned}$$

(10)

for $\bar{B}^-$ decays.

In Eqs. (4)–(10), $V_P$ is the production vertex which contains all dynamical factors common to all the above seven decays. We shall assume $V_P$ as constant and fit it to the experimental date. The $G_{\mathrm{MM}}$ are the loop functions of two meson propagators. The $t_{\mathrm{MM}\rightarrow \mathrm{MM}}$ are the scattering matrices and they are calculated in Ref. [8] following Ref. [27]. Note that we can easily obtain $t_{\pi ^- \eta \rightarrow \pi ^- \eta }$, $t_{K^0 K^- \rightarrow K^0 K^-}$ and $t_{\pi ^- \eta \rightarrow K^0 K^-}$ using isospin symmetry,

$$\begin{aligned} t_{\pi ^- \eta \rightarrow \pi ^- \eta }= & {} t_{\pi ^0 \eta \rightarrow \pi ^0 \eta }, \end{aligned}$$

(11)

$$\begin{aligned} t_{K^0 K^- \rightarrow \pi ^- \eta }= & {} -\sqrt{2}~ t_{K^0 \bar{K}^0 \rightarrow \pi ^0 \eta }, \end{aligned}$$

(12)

$$\begin{aligned} t_{K^0 K^- \rightarrow K^0 K^-}= & {} t_{K^+ K^- \rightarrow K^+ K^-} - t_{K^+ K^- \rightarrow K^0 \bar{K}^0}. \end{aligned}$$

(13)

With all the ingredients obtained above, one can write down the invariant mass distributions for those decays as follows [29]

$$\begin{aligned} \frac{d \Gamma }{d M_{\mathrm{inv}}} = \frac{1}{(2\pi )^3}\frac{1}{4M_{\bar{B}_j}^2} p_{\eta _c} \tilde{p}_{\mathrm{M}} \sum \left| T \right| ^2, \end{aligned}$$

(14)

where $M_{\bar{B}_j}$ is the mass of $\bar{B}^0$, $\bar{B}^0_s$, or $B^-$, while $M_{\mathrm{inv}}$ is the invariant mass of the final $\mathrm{MM}$ pair. The $p_{\eta _c}$ is the $\eta _c$ momentum in the rest frame of $\bar{B}_j$ and $\tilde{p}_{M}$ is the momentum of one pseudo-scalar meson in the rest frame of $\mathrm{MM}$ pair, which are,

$$\begin{aligned} p_{\eta _c}= & {} \frac{\lambda ^{1/2}(M^2_{\bar{B}_j}, M^2_{\eta _c}, M^2_{\mathrm{inv}})}{2M_{\bar{B}_j}}, \end{aligned}$$

(15)

$$\begin{aligned} \tilde{p}_{\mathrm{M}}= & {} \frac{\lambda ^{1/2}(M^2_{\mathrm{inv}}, m^2_1, m^2_2)}{2M_{\mathrm{inv}}}, \end{aligned}$$

(16)

where $\lambda$ is the Källen function with $\lambda (x,y,z) = (x-y-z)^2 - 4yz$, and $m_1$ and $m_2$ are the masses of the two mesons of the MM pair, respectively.

2.2 Vector meson production

The B meson decays weakly into $\eta _c$ meson in addition to a vector meson. At the quark level, this process is illustrated in Fig. 1 without the $q\bar{q}$ hadronzition to two mesons. According to this figure, the $c \bar{c}$ quark pair converts into an $\eta _c$, while the remaining $q \bar{q}$ can be related to the vector mesons, $\rho ^0$, $\phi$ or $K^{*0}$, which are largely $q \bar{q}$ states [28, 29]. Therefore, in terms of quarks the vector mesons are given by: $\rho ^0 = \frac{1}{\sqrt{2}} (u\bar{u} - d\bar{d})$, $\phi = s\bar{s}$, and $K^{^*0} = d \bar{s}$. Then the decay amplitudes for the vector mesons production are

$$\begin{aligned} T(\bar{B}^0_s \rightarrow \eta _c \phi )= & {} V'_P V_{cs} p_\phi \mathrm{cos{\theta }}, \end{aligned}$$

(17)

$$\begin{aligned} T(\bar{B}^0_s \rightarrow \eta _c K^{*0})= & {} V'_P V_{cd} p_{K^{*0}} \mathrm{cos{\theta }}, \end{aligned}$$

(18)

$$\begin{aligned} T(\bar{B}^0 \rightarrow \eta _c \rho ^0)= & {} - V'_P \frac{1}{\sqrt{2}} V_{cd} p_{\rho ^0} \mathrm{cos{\theta }}, \end{aligned}$$

(19)

$$\begin{aligned} T(\bar{B}^0 \rightarrow \eta _c \bar{K}^{*0})= & {} V'_P V_{cs} p_{\bar{K}^{*0}} \mathrm{cos{\theta }}, \end{aligned}$$

(20)

where $p_V$ (V = $\phi$, $\rho ^0$, $K^{*0}$ or $\bar{K}^{*0}$) is the vector momentum in the rest frame of $\bar{B}_j$,

$$\begin{aligned} p_{V}= & {} \frac{\lambda ^{1/2}(M^2_{\bar{B}_j}, M^2_{\eta _c}, m^2_{V})}{2M_{\bar{B}_j}}. \end{aligned}$$

(21)

As in Refs. [8, 9], in a $0^- \rightarrow 0^- 1^-$ transition, we shall need an $L'=1$ orbital angular momentum for the vector meson to match angular momentum conservation. Hence, we assume the vertex as $V'_Pp_V \mathrm{cos}\theta$ and we also assume $V'_P$ to be constant. Then we can determine ratios of vector mesons production with respect to the $\phi$ production which was measured by the LHCb collaboration [2],

$$\begin{aligned} \frac{\mathrm{Br}(\bar{B}^0_s \rightarrow \eta _c K^{*0})}{\mathrm{Br}(\bar{B}^0_s \rightarrow \eta _c \phi )}= & {} \frac{V^2_{cd}}{V^2_{cs}} \frac{p^3_{K^{*0}}}{p^3_\phi } = 0.058, \end{aligned}$$

(22)

$$\begin{aligned} \frac{\mathrm{Br}(\bar{B}^0 \rightarrow \eta _c \bar{K}^{*0})}{\mathrm{Br}(\bar{B}^0_s \rightarrow \eta _c \phi )}= & {} \frac{\Gamma _{\bar{B}^0_s} M^2_{\bar{B}^0_s}}{\Gamma _{\bar{B}^0} M^2_{\bar{B}^0}} \frac{p^3_{\bar{K}^{*0}}}{p^3_\phi } = 1.0, \end{aligned}$$

(23)

$$\begin{aligned} \frac{\mathrm{Br}(\bar{B}^0 \rightarrow \eta _c \rho ^{0})}{\mathrm{Br}(\bar{B}^0_s \rightarrow \eta _c \phi )}= & {} \frac{\Gamma _{\bar{B}^0_s} M^2_{\bar{B}^0_s}V^2_{cd}}{2\Gamma _{\bar{B}^0} M^2_{\bar{B}^0} V^2_{cs}} \frac{p^3_{\rho ^{0}}}{p^3_\phi } = 0.029. \end{aligned}$$

(24)

The above values are obtained with $V_{cs} = 0.97427$, $V_{cd} = -\,0.22534$, $M_{\bar{B}^0} = 5279.58$ MeV, $M_{\bar{B}^0_s} = 5366.77$ MeV, $\Gamma _{\bar{B}^0} = 4.33 \times 10^{-10}$ MeV, and $\Gamma _{\bar{B}^0_s} = 4.37 \times 10^{-10}$ MeV as in Ref. [29].

Then we obtain the branching ratios by taking $\mathrm{Br} (\bar{B}^0_s \rightarrow \eta _c \phi ) = (5.01 \pm 0.87) \times 10^{-4}$ [2] as input,

$$\begin{aligned} \mathrm{Br} (\bar{B}^0_s \rightarrow \eta _c K^{*0})= & {} (2.9 \pm 0.5) \times 10^{-5}, \end{aligned}$$

(25)

$$\begin{aligned} \mathrm{Br} (\bar{B}^0 \rightarrow \eta _c \bar{K}^{*0})= & {} (5.0 \pm 0.9) \times 10^{-4}, \end{aligned}$$

(26)

$$\begin{aligned} \mathrm{Br} (\bar{B}^0 \rightarrow \eta _c \rho ^{0})= & {} (1.4 \pm 0.2) \times 10^{-5}, \end{aligned}$$

(27)

where the errors are from the experimental branching ratio of $\mathrm{Br} (\bar{B}^0_s \rightarrow \eta _c \phi )$.

The experimental result for $\mathrm{Br} (\bar{B}^0 \rightarrow \eta _c \bar{K}^{*0})$ is $(6.3 \pm 0.9) \times 10^{-4}$ [29], from where we can see that the agreement between our theoretical calculation and the experiment is good within error. There are no experimental results for the branching ratios of $\mathrm{Br} (\bar{B}^0_s \rightarrow \eta _c K^{*0})$ and $\mathrm{Br} (\bar{B}^0 \rightarrow \eta _c \rho ^{0})$. Our predictions here will be tested by the future LHCb and Belle-II experiment.

We next come to the $\bar{B}^0 \rightarrow \eta _c \rho ^0 \rightarrow \eta _c \pi ^+\pi ^-$ decay comparing with $\bar{B}^0 \rightarrow \eta _c f_0 [f_0 \equiv f_0(500), f_0(980)] \rightarrow \eta _c \pi ^+ \pi ^-$. For this purpose, we multiply the partial decay width of $\bar{B}^0 \rightarrow \eta _c \rho ^0$ by the spectral function of

$$\begin{aligned}&\frac{d\Gamma (\bar{B}^0 \rightarrow \eta _c \rho ^0 \rightarrow \eta _c \pi ^+ \pi ^-)}{dM_{\mathrm{inv}}} \nonumber \\&\quad = -\frac{2m_{\rho }}{\pi } \mathrm{Im} \left( \frac{1}{M^2_{\mathrm{inv}} -m^2_\rho + i m_\rho \Gamma _\rho } \right) \Gamma _{\bar{B}^0 \rightarrow \eta _c \rho ^0}, \end{aligned}$$

(28)

where

$$\begin{aligned} \Gamma _\rho= & {} \Gamma _0 \left( \frac{\tilde{p}_\pi }{p_\pi } \right) ^3, \end{aligned}$$

(29)

$$\begin{aligned} \tilde{p}_\pi= & {} \frac{\sqrt{M^2_{\mathrm{inv}} - 4m^2_\pi }}{2}, \end{aligned}$$

(30)

$$\begin{aligned} p_\pi= & {} \frac{\sqrt{m^2_{\rho } - 4m^2_\pi }}{2}, \end{aligned}$$

(31)

with $M_{\mathrm{inv}}$ the invariant mass of $\pi ^+ \pi ^-$ system. We will take $m_\rho = 775.26$ MeV and $\Gamma _0 = 149.1$ MeV in this work as in Ref. [29].

3 Numerical results and discussions

Same to the $\bar{B}^0_s \rightarrow J/\psi \pi ^+ \pi ^-$ decay [8], the $\bar{B}^0_s \rightarrow \eta _c \pi ^+ \pi ^-$ decay is also dominated by $f_0(980)$. In Ref. [5], the fraction for the $f_0(980)$ contribution in the $\bar{B}^0_s \rightarrow \eta _c \pi ^+ \pi ^-$ decay is around $70\%$. Thus, we assume³

$$\begin{aligned} \frac{\mathrm{Br} [\bar{B}^0_s \rightarrow \eta _c f_0(980) \rightarrow \eta _c \pi ^+ \pi ^-]}{\mathrm{Br}(\bar{B}^0_s \rightarrow \eta _c \pi ^+ \pi ^-)} = (80 \pm 10)\%, \end{aligned}$$

from where we get $\mathrm{Br} [\bar{B}^0_s \rightarrow \eta _c f_0(980) \rightarrow \eta _c \pi ^+ \pi ^-] = (1.41 \pm 0.56) \times 10^{-4}$, where we have added in quadrature the three sets of errors quoted in Ref. [2].

On the other hand, if we integrated Eq. (14), up to one free parameter $V_P$, we can extract the contribution from $f_0(980)$ for the decay of $\bar{B}^0_s \rightarrow \eta _c \pi ^+ \pi ^-$, since, in our production mechanism, the main contribution for this decay is $f_0(980)$. Then, one can determine $V_P$ as

$$\begin{aligned} V_P = (3.44 \pm 0.68) \times 10^{-6}. \end{aligned}$$

(32)

In Fig. 3, we show the $\pi ^+ \pi ^-$ and $K^+ K^-$ invariant mass distributions for the $\bar{B}^0_s \rightarrow \eta _c \pi ^+ \pi ^-$ and $\bar{B}^0_s \rightarrow \eta _c K^+ K^-$, respectively. As one can see, the $f_0(980)$ production is clearly dominant while there is no evident signal for the $f_0(500)$. For the $\bar{B}^0_s \rightarrow \eta _c K^+ K^-$ decay, the $K^+ K^-$ distribution gets maximum strength just above the $K^+ K^-$ threshold and then falls down gradually. This is due to the effect of the $f_0(980)$ resonance below the $K\bar{K}$ threshold.⁴ Starting from the dominant weak decay process shown in Fig. 1 we have $\eta _c$ and $s\bar{s}$ production in the $\bar{B}^0_s$ decay. Because the $s \bar{s}$ pair has isospin zero, and the strong interaction hadronization conserves it, even if the $K^+ K^-$ system can have $I=0$ or 1, the process of formation guarantees that this is an $I=0$ state and the shape of the $K^+ K^-$ distribution is due to the $f_0(980)$ with $I = 0$.

Fig. 3

$\pi ^+ \pi ^-$ and $K^+ K^-$ invariant mass distributions for $\bar{B}_s^0 \rightarrow \eta _c \pi ^+ \pi ^-$ and $\eta _c K^+ K^-$

The strength for the $K^+ K^-$ distribution is small compared to the one of the $f_0(980)$ at its peak for the $\pi ^+ \pi ^-$ distribution, but the integrated strength over the invariant mass of $K^+ K^-$ is of the same order of magnitude as that for the strength below the peak of the $f_0(980)$ going to $\pi ^+ \pi ^-$. It is interesting to compare this with experiment. First by integrating the strength of the $K^+ K^-$ invariant mass distribution over its invariant mass, up to $M_{\mathrm{inv}}(K^+ K^-) = 1200$ MeV,⁵ we find a ratio

$$\begin{aligned} \frac{\mathrm{Br} [ \bar{B}^0_s \rightarrow \eta _c f_0(980) \rightarrow \eta _c K^+ K^-]}{\mathrm{Br} [\bar{B}^0_s \rightarrow \eta _c f_0(980) \rightarrow \eta _c \pi ^+ \pi ^- ]} = 0.4. \end{aligned}$$

(33)

Here, we should mention that we are calculating only the S-wave contribution of the $K^+ K^-$ invariant mass distribution, hence, contributions from higher waves, such as $\phi$ (P-wave), $f'_2(1525)$ (D-wave) etc, are not included.

Secondly, if we stick to a band of energies around the $\phi$ meson peak, $990<M_{\mathrm{inv}}(K^+K^-) <1050$ MeV, as done in Ref. [34] for the $\bar{B}^0_s \rightarrow J/\psi K^+K^-$, we get the S-wave fraction

$$\begin{aligned} \frac{\mathrm{Br}[\bar{B}^0_s \rightarrow \eta _c K^+ K^-] (S\mathrm{-wave})}{\mathrm{Br} [\bar{B}^0_s \rightarrow \eta _c \phi \rightarrow \eta _c K^+ K^- ]}= (13 \pm 6) \times 10^{-2} , \end{aligned}$$

(34)

where $\mathrm{Br} [\bar{B}^0_s \rightarrow \eta _c \phi ] = (5.01 \pm 0.87) \times 10^{-4}$ [2] and the branching fraction of 0.489 for $\phi$ decay into $K^+ K^-$ has been taken [29]. This value, one of our model predictions, could be tested by future experiment.

On the other hand, for the case of $J/\psi$ production, the experimental result for the S-wave fraction is $(1.1 \pm 0.1 ^{+0.2}_{-0.1})\%$ [34], while the theoretical calculation for this value in Ref. [19] is about $(1.1 \sim 1.95)\%$ and the value of $(1.7 \pm 0.3)\%$ was obtained in Ref. [12]. The decays of $\bar{B}^0_s$ into $\eta _c$ plus a scalar meson is in S-wave and thus we should expect the S-wave fraction for the $\bar{B}^0_s \rightarrow \eta _c f_0(980)$ reasonably bigger than for $\bar{B}^0_s \rightarrow J/\psi f_0(980)$.

We come back now to the decays of the $\bar{B}^0$. In Fig. 4 we show the theoretical results for the $\pi ^+ \pi ^-$, $K^+ K^-$ and $\pi ^0 \eta$ invariant mass distributions for $\bar{B}^0 \rightarrow \eta _c \pi ^+ \pi ^-$, $\eta _c K^+ K^-$, and $\eta _c \pi ^0 \eta$. In the $\bar{B}^0$ decays into $\eta _c$ plus a scalar meson, we had the hadronization of a $d \bar{d}$ pair, which contains $I=0$ and 1. But, the $\pi ^+ \pi ^-$ in S-wave can only be in $I=0$, hence the peaks for the $\pi ^+ \pi ^-$ distribution due to the $f_0(500)$ and $f_0(980)$ excitation. While for the $\rho ^0$ vector meson production, we see that the $\rho ^0$ contribution peaks around 770 MeV, and has larger strength than the $f_0(500)$ contribution, but at invariant masses around 500 MeV and bellow, the strength of the $f_0(500)$ dominates over the one of the $\rho ^0$ meson. The strength of the peak of $\rho ^0$ distribution is about a factor 2 larger than that of the $f_0(500)$ distribution. For the $K^+ K^-$ production in the $\bar{B}^0$ decay, we have considered both the $I=0$ [$f_0(980)$] and $I=1$ [$a_0(980)$] contribution. This makes the line shape of $K^+K^-$ invariant mass distributions different with the one shown in Fig. 3 for the $\bar{B}_s^0$ decay.

Fig. 4

$\pi ^+ \pi ^-$, $\pi ^0 \eta$, and $K^+ K^-$ invariant mass distributions for $\bar{B}^0 \rightarrow \eta _c \pi ^+ \pi ^-$, $\eta _c K^+ K^-$, and $\eta _c \pi ^0 \eta$, respectively

One can see that, from Fig. 4, the strength of the $f_0(980)$ excitation is very small compared to that of the $f_0(500)$ (the broad peak to the left). Note that because of the experimental resolution the $f_0(980)$ peak would not appear so narrow in the experiments. As done in Refs. [8, 10], we can extract the $f_0(500)$ contribution to the branching ratio by assuming a smooth background below the $f_0(980)$ peak, we find

$$\begin{aligned} \mathrm{Br} [\bar{B}^0 \rightarrow \eta _c f_0(500) \rightarrow \eta _c \pi ^+ \pi ^-] = (1.2 \pm 0.5) \times 10^{-5},\nonumber \\ \end{aligned}$$

(35)

with error from the uncertainty of $V_P$ shown in Eq. (32). Then we find ratios, $R_1$ and $R_2$

$$\begin{aligned} R_1= & {} \frac{\mathrm{Br} [ \bar{B}^0 \rightarrow \eta _c f_0(500) \rightarrow \eta _c \pi ^+ \pi ^-]}{\mathrm{Br} [\bar{B}^0_s \rightarrow \eta _c f_0(980) \rightarrow \eta _c \pi ^+ \pi ^- ]} \nonumber \\= & {} ( 9 \pm 5) \times 10^{-2}, \end{aligned}$$

(36)

$$\begin{aligned} R_2= & {} \frac{\mathrm{Br} [ \bar{B}^0 \rightarrow \eta _c \rho ^0 \rightarrow \eta _c \pi ^+ \pi ^-]}{\mathrm{Br} [\bar{B}^0 \rightarrow \eta _c f_0(500) \rightarrow \eta _c \pi ^+ \pi ^- ]} \nonumber \\= & {} 1.2 \pm 0.6, \end{aligned}$$

(37)

which is consistent with the ones obtained in Refs. [5, 6]: $R_1 = (3 \sim 8) \times 10^{-2}$ in Breit-Wigner model and $(4 \sim 12) \times 10^{-2}$ in Bugg model, while $R_2 = 2.6$ in Breit-Wigner model and 1.7 in Bugg model.⁶ However, the branch ratio, $\mathrm{Br} [\bar{B}^0 \rightarrow \eta _c f_0(500) \rightarrow \eta _c \pi ^+ \pi ^-]$ obtained here, is larger than the one, $1.53^{+0.76}_{-0.35} \times 10^{-6}$ in Breit-Wigner model and $2.31^{+0.96}_{-0.48} \times 10^{-6}$ in Bugg model, obtained in Ref. [5] with the perturbative QCD factorization approach. We hope that the future experimental measurements can clarify this issue.

Fig. 5

$\pi ^- \eta$ and $K^0 K^-$ invariant mass distributions for $B^- \rightarrow \eta _c \pi ^- \eta$ and $B^- \rightarrow \eta _c K^0 K^-$

In Fig. 4, the $\pi ^0 \eta$ invariant mass distribution has a sizeable strength, bigger than that for the S-wave $\pi ^+ \pi ^-$ and $K^+ K^-$ distributions. As one can see, we get the typical cusp structure of the $a_0(980)$. This prediction is tied exclusively to the weights of the starting meson meson channels in Eq. (1) and the final state interaction in Eqs. (6), (7), and (8). Hence, this is a prediction of this approach, not tied to any experimental input.

Next, we show the results for $B^-$ decay in Fig. 5, where the strength for the $\pi ^- \eta$ invariant mass distribution is two times as big as the one of $\bar{B}^0 \rightarrow \eta _c \pi ^0 \eta$ shown in Fig. 4. For the $K^0 K^-$ mass distribution we see that the position of the peak has moved to higher invariant masses compared to the $K^+ K^-$ invariant mass spectrum of the $\bar{B}^0 \rightarrow \eta _c K^+ K^-$ or $\bar{B}_s^0 \rightarrow \eta _c K^+ K^-$ decays. In fact, the $K^0 K^-$ invariant mass distribution in the $B^-$ decay due to the $a_0(980)$, which is seen in the figures, is much wider than that of the $f_0(980)$. It would be most instructive to see all these features in future experiments, such as LHCb and Belle-II.

4 Summary

We have performed a study of the $\pi \pi$, $\pi \eta$ and $K \bar{K}$ invariant mass distributions for $\bar{B}^0_s \rightarrow \eta _c \pi ^+ \pi ^-$, $\bar{B}^0_s \rightarrow \eta _c K^+ K^-$, $\bar{B}^0 \rightarrow \eta _c \pi ^+ \pi ^-$, $\bar{B}^0 \rightarrow \eta _c K^+ K^-$, $\bar{B}^0 \rightarrow \eta _c \pi ^0 \eta$, $B^- \rightarrow \eta _c \pi ^- \eta$, and $B^- \rightarrow \eta _c K^0 K^-$. We take the dominant mechanism for the weak decay of the B meson, going to $\eta _c$ and a $q\bar{q}$ pair that, upon hadronization, leads to $\pi \pi$, $\pi \eta$, and $K\bar{K}$ in the final state, and this interaction is basically mediated by the scalar mesons, $f_0(500)$, $f_0(980)$, and $a_0(980)$. In addition, we have also studied the decay of these B mesons into $\eta _c$ plus a vector meson, $\rho ^0$, $\phi$, $\bar{K}^{*0}$, and $K^{*0}$.

Up to a global factor,⁷ which is determined to the experimental measurement, we can compare the strength of the $\pi \pi$, $\pi \eta$ and $K \bar{K}$ invariant mass distributions. For the $\bar{B}^0_s \rightarrow \eta _c K^+ K^-$, only the $f_0(980)$ resonance contributes to the $K^+K^-$ mass distribution, but in the case of the $\bar{B}^0 \rightarrow \eta _c K^+ K^-$, both the $f_0(980)$ and $a_0(980)$ resonances contribute to its strength. The strength of the $K \bar{K}$ invariant mass distribution in the $\bar{B}^0_s$ decay is much larger than the one in $\bar{B}^0$ decay, which is because the $\bar{B}^0_s$ decay is Cabibbo favored process, while the $\bar{B}^0$ decay is the Cabibbo suppressed process. In the case of the $\bar{B}^0 \rightarrow \eta _c \pi ^0 \eta$, one finds a cusp structure for the $a_0(980)$ and its strength is much larger than the one for the $\bar{B}^0 \rightarrow \eta _c \pi ^+ \pi ^-$ decay around the $f_0(980)$ peak. We also have made predictions for $\eta _c \rho ^0$, $\eta _c K^{*0}$, and $\eta _c \bar{K}^{*0}$ productions that can be tested in a future partial wave analysis of these decays. In particular, we find that the $\rho ^0$ production is bigger then the $f_0(500)$ production in $\bar{B}^0$ decay by a factor 2.

Our theoretical results shown here are predictions for ongoing experiments at LHCb and Belle-II, and comparison of the observed results with our predictions will be most useful to make progress in our understanding of the meson-meson interaction and the nature of the low lying scalar mesons. We would suggest the experimentalists carry out a more precise measurements on the invariant mass distributions of $\pi \pi$ and $K \bar{K}$ of $\bar{B}^0_s$ and $\bar{B}^0$ decays.