Drag force of Anisotropic plasma at finite U(1) chemical potential

Abstract

We perform the calculation of the drag force acting on a massive quark moving through an anisotropic $\mathcal{N}=4$ SU(N) Super Yang–Mills plasma in the presence of a U(1) chemical potential. We present the numerical results for any value of the anisotropy and arbitrary direction of the quark velocity with respect to the direction of the anisotropy. We find the effect of the chemical potential or charge density will enhance the drag force for our charged solution.

1 Introduction

The experimental data in the Relativistic Heavy Ion Collider (RHIC) [1, 2] show that the quark gluon plasma (QGP), as deconfined phase of QCD at high temperature and high number density, is a strongly coupled fluid rather than a weakly coupled gas of quarks and gluons. Thus perturbative QCD is no longer reliable and we should explore the non-perturbative methods of QCD.

Fig. 1

The metric functions for $a=1.86$, $Q=6.23$ (left) and $a=64.06$, $Q=9.76$ (middle), with $u_H=1$

Fig. 2

Drag force in x-direction $F_x$ as a function $\Theta$ at $v=0.5$. The four graphs denote $a/T=1.38$, $a/T=4.41$, $a/T=12.2$, $a/T=86$, respectively, where the color lines denote $Q=5$ (green), $Q=2$ (brown), $Q=1$ (red), $Q=0$ (blue)

Fig. 3

Drag force in x-direction $F_x$ as a function $\Theta$ at $v=0.9$. The four graphs denote $a/T=1.38$, $a/T=4.41$, $a/T=12.2$, $a/T=86$, respectively, where the color lines denote $Q=5$ (green), $Q=2$ (brown), $Q=1$ (red), $Q=0$ (blue)

Fig. 4

Drag force in z-direction $F_z$ as a function $\Theta$ at $v=0.5$. The four graphs denote $a/T=1.38$, $a/T=4.41$, $a/T=12.2$, $a/T=86$, respectively, where the color lines denote $Q=5$ (green), $Q=2$ (brown), $Q=1$ (red), $Q=0$ (blue)

The AdS/CFT correspondence [3–5] provides a powerful tool to investigate the strongly coupled system in condensed matter physics (for reviews, see [6, 7]) like superconductors [8–10], Lifshitz fixed point [11–14], quantum chromodynamics [15, 16] and heavy ion collisions like photon production [17, 18], elliptic flow [19], drag force [20, 21], jet quenching [22, 23], Langevin coefficients [24], and anomalous transport [25–28]. Using the AdS/CFT correspondence, we can study the strongly coupled $\mathcal{N} = 4$ Super Yang–Mills plasma through considering IIB supergravity in $\mathrm{AdS}_5\times S^5$. One significant result is the calculation of the ratio of the shear viscosity to the entropy density of QGP; this ratio is universal and equal to $1/4\pi$ [29], which matches the experimental data very well. This indicates the QGP is a strongly coupled system and the AdS/CFT presents a useful method to investigate the properties of QGP at least at a qualitative level.

Fig. 5

Drag force in z-direction $F_z$ as a function $\Theta$ at $v=0.9$. The four graphs denote $a/T=1.38$, $a/T=4.41$, $a/T=12.2$, $a/T=86$, respectively, where the color lines denote $Q=5$ (green), $Q=2$ (brown), $Q=1$ (red), $Q=0$ (blue)

Fig. 6

Drag force F as a function $\Theta$ at $v=0.5$. The four graphs denote $a/T=1.38$, $a/T=4.41$, $a/T=12.2$, $a/T=86$ respectively, where the color lines denote $Q=5$ (green), $Q=2$ (brown), $Q=1$ (red), $Q=0$ (blue)

Fig. 7

Drag force F as a function $\Theta$ at $v=0.9$. The four graphs denote $a/T=1.38$, $a/T=4.41$, $a/T=12.2$, $a/T=86$, respectively, where the color lines denote $Q=5$ (green), $Q=2$ (brown), $Q=1$ (red), $Q=0$ (blue)

Fig. 8

The drag force F as a function of velocity for a quark moving through the plasma with $Q=0$ (i.e. chargeless). The four graphs correspond to $a/T=1.38, a/T=4.42, a/T=12.2, a/T=86$ respectively, in which five lines denotes (from the top to down) $\Theta =0$, $\Theta =\pi /6$, $\Theta =\pi /4$, $\Theta =\pi /3$, $\Theta =\pi /2$

It is well known that the most important quantities of QGP are the drag force and the jet-quenching parameter. In the context of AdS/CFT [20, 21], the moving heavy quark in the thermal medium is dual to a probe open string with infinite mass, which is attached to the boundary of the bulk spacetime and stretches to the black hole horizon. So the dynamics of the string can give us the effects of $\mathcal{N} = 4$ Super Yang–Mills plasma in which quark is moving. The similar study for jet quenching for $\mathcal{N} = 4$ SYM plasma can be found in [22, 23], where the jet-quenching parameter was obtained by calculating the expectation value of a closed light-like Wilson loop in the dipole approximation.

In this paper, we will study the moving quark in the anisotropic QGP with chemical potential, since the QGP after creation in a short time is anisotropic and real experiments are done at finite baryon potential.¹ Our motivations come from the facts that significant observation of the RHIC and the LHC experiments is that the plasma created is anisotropic and non-equilibrium during the period of time $\tau _\mathrm{out}$ after the collision, i.e. it is locally anisotropic at the time $\tau _\mathrm{out} <\tau <\tau _\mathrm{iso}$, a configuration to be described by the hydrodynamics with the anisotropic energy-momentum tensor.

Another motivation comes from the fact that in condensed matter physics, some materials are anisotropic, with different properties in different directions. For example, for high-temperature cuprates, the crystal structure of such superconductors shows a multi-layer of $\mathrm{CuO}_2$ planes with superconductivity taking place between these layers. The electric transport perpendicular to the $\mathrm{CuO}_2$ plane is more difficult than the electric transport in the $\mathrm{CuO}_2$ plane [30]. It is natural to investigate the drag force in an anisotropic system at finite chemical potential and compare the results with those isotropic cases.

From the point of view of holography, the anisotropic plasma with chemical potential is dual to an anisotropic charged black brane [31, 32], hence, to compute the drag force experienced by an infinitely massive quark, we should consider a string in an anisotropic charged black brane. We will show the results analytically and numerically, respectively. The discussion for a chargeless anisotropic plasma, shear viscosity–entropy density ratio, and its energy loss in the framework of AdS/CFT can be found in [18, 33–39].

This paper is organized as follows. In Sect. 2, we briefly describe the construction of the anisotropic charged black brane solution. In Sect. 3, we calculate the drag force acting on a massive quark moving through the plasma. Furthermore, in the small anisotropy and high-temperature limit, we can perform the calculation of the drag force analytically. In Sect. 4, we show our numerical results for prolate anisotropy. In Sect. 5, we conclude with a brief summary of our results.

Note: When this paper was in preparation, Ref. [40] appeared, which has some overlap with this paper. The difference between our paper and [40] is that we consider the drag force for the large charge case in particular.

2 Anisotropic charged black brane solution

The five-dimensional axion–dilaton–Maxwell–gravity bulk action reduced from type IIB supergravity is given by [31, 32]

$$\begin{aligned} S&=\frac{1}{2\kappa ^2}\bigg [\int \mathrm{d}^5 x \sqrt{-g} \Big ( R +12-\frac{1}{2} (\partial \phi )^2 - \frac{1}{2} \mathrm{e}^{2\phi } (\partial \chi )^2\nonumber \\&\quad -\frac{1}{4} F_{\mu \nu }F^{\mu \nu }\Big )-2\int \mathrm{d}^4x \sqrt{-\gamma }K \bigg ], \end{aligned}$$

(1)

where we have set the AdS radius $L=1$, and $\kappa ^2=8\pi G=\frac{4\pi ^2}{N^2_c}$. The $\mathrm{AdS}_5$ part of a ten-dimensional anisotropic IIB supergravity solution in an Einstein frame is given by [32],²

$$\begin{aligned}&\mathrm{d}s^2 = \frac{\mathrm{e}^{-\frac{1}{2}\phi }}{u^2}\left( -\mathcal{F}\mathcal{B}\, \mathrm{d}t^2+\mathrm{d}x^2+\mathrm{d}y^2+ \mathcal{H}dz^2 +\frac{ du^2}{\mathcal{F}}\right) ,\end{aligned}$$

(2)

$$\begin{aligned}&A=A_t(u) \mathrm{d}t,\quad \mathrm{{and}} \quad \chi =az, \end{aligned}$$

(3)

which was obtained by dimensional reduction on $S^5$ from the ten-dimensional metric. So we have ignored the metric of the $S^5$ part that will play no role in the following discussions and our treatment is in agreement with a ten-dimensional framework. Note that the anisotropy is introduced through deforming the SYM theory by a $\theta$-parameter of the form $\theta \propto z$, which acts as an isotropy-breaking external source that forces the system into an anisotropic equilibrium state [34]. The $\theta$-parameter is dual to the type IIB axion $\chi$ with the form $\chi = a z$.

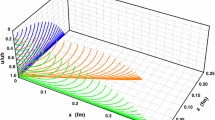
The spacetime is required to be anisotropic but homogeneous, so that the functions $\phi$, $\mathcal{F}$, $\mathcal{B}$, and $\mathcal{H}=\mathrm{e}^{-\phi }$ should only depend on the radial coordinate u. The electric potential $A_t$ in this metric is expressed as $A_{t}(u)=-\int ^u_{u_\text {H}}\mathrm{d}u Q\sqrt{\mathcal{B}}\mathrm{e}^{\frac{3}{4}\phi }u$ from the Maxwell equations, where Q is an integral constant related to the charge density. Note that the electric potential has a contribution from the anisotropy through the dilatonic field $\phi$. The horizon is at $u=u_\text {H}$ and the boundary is at $u=0$, respectively. The asymptotic AdS boundary requires $\mathcal{F}=\mathcal{B}=\mathcal{H}=1$. We plot the numerical solutions in Fig. 1 [32].

In the small anisotropy and charge limits, we can obtain the high-temperature solution,

$$\begin{aligned}&\mathcal{F}=1-\bigg (\frac{u}{u_H}\bigg )^4+\bigg [\bigg (\frac{u}{u_H}\bigg )^6-\bigg (\frac{u}{u_H}\bigg )^4\bigg ]q^2\nonumber \\&\qquad +\,a^2 \mathcal{F}_2(u)+\mathcal {O}(a^4),\nonumber \\&\mathcal{B}=1+a^2 \mathcal{B}_2(u)+\mathcal {O}(a^4),\nonumber \\&\mathcal{H}=\mathrm{e}^{-\phi (u)}, \quad {~\mathrm {with}~} \phi (u)=a^2 \phi _2(u)+\mathcal {O}(a^4), \end{aligned}$$

(4)

where $\mathcal{F}_2(u)=\hat{\mathcal{F}_0}(u)+\hat{\mathcal{F}_2}(u) q^2+{O}(q^4), \mathcal{B}_2(u)=\hat{\mathcal{B}_0}(u)+\hat{\mathcal{B}_2}(u) q^2+{O}(q^4)$, and $\phi _2(u)=\hat{\phi _0}(u)+\hat{\phi _2}(u)q^2+{O}(q^4)$ with

$$\begin{aligned} \hat{\mathcal{F}}_0(u)= & {} \frac{1}{24 u_\text {H}^2}\left[ 8 u^2( u_\text {H}^2-u^2)-10 u^4\log 2 \right. \nonumber \\&\left. +(3 u_\text {H}^4+7u^4)\log \left( 1+\frac{u^2}{u_\text {H}^2}\right) \right] , \nonumber \\ \hat{\mathcal{B}}_0(u)= & {} -\frac{u_\text {H}^2}{24}\left[ \frac{10 u^2}{u_\text {H}^2+u^2} +\log \left( 1+\frac{u^2}{u_\text {H}^2}\right) \right] , \nonumber \\ \hat{\phi }_0(u)= & {} -\frac{u_\text {H}^2}{4}\log \left( 1+\frac{u^2}{u_\text {H}^2}\right) \,, \end{aligned}$$

(5)

and

$$\begin{aligned} \hat{\mathcal{F}}_2(u)= & {} \frac{1}{24 u_\text {H}^4(u^2+u_\text {H}^2)} \left[ 7u^8+6u^2u_\text {H}^6+u^4u_\text {H}^4(25\log 2-12),\right. \nonumber \\&+\,u^6u_\text {H}^2(25\log 2-1)\nonumber \\&\left. -\,(u^2+u_\text {H}^2)(12u^6+7u^4u_\text {H}^2+6u_\text {H}^6)\log \Bigg (1+\frac{u^2}{u_\text {H}^2}\Bigg ) \right] , \nonumber \\ \hat{\mathcal{B}}_2(u)= & {} \frac{1}{24}\left[ -\frac{u^2(11u^4+3u^2u_\text {H}^2+2u_\text {H}^4)}{(u^2+u_\text {H}^2)^2}+2u_\text {H}^2\log \left( 1+\frac{u^2}{u_\text {H}^2}\right) \right] , \nonumber \\ \hat{\phi }_2(u)= & {} \frac{1}{4}\left[ -2u^2+\frac{u^4}{u^2+u_\text {H}^2}+2u_\text {H}^2\log \left( 1+\frac{u^2}{u_\text {H}^2}\right) \right] , \end{aligned}$$

(6)

where we have used the dimensionless parameter $q=\frac{u_\text {H}^3Q}{2\sqrt{3}}$. Here we would like to justify the usage of the small anisotropy and charge limits. The analytic solution for the non-perturbative charge was given in [31, 32]. Unfortunately, for the analytic computation of the drag force, it is too difficult to determine some critical parameters.

We can easily obtain the temperature:

$$\begin{aligned} T= -\frac{\mathcal{F}'(u_\text {H}) \sqrt{\mathcal{B}(u_\text {H})}}{4\pi }. \end{aligned}$$

(7)

Note that the temperature cannot be zero unless $a^2\le 0$, which corresponds to oblate anisotropy. In contrast, $a^2>0$ corresponds to prolate anisotropy. On the dual quantum field theory side, an imaginary a looks like a nonunitary deformation and could lead to a negative field coupling. In this sense, the oblate black brane solution with $a^2<0$ could give unphysical results. In the following discussions, we mainly focus on the prolate case.

3 Drag force

On the anisotropic charged brane background, the Nambo–Goto action which governs the dynamics of a probe string in string frame is given by

$$\begin{aligned} S = -T_0 \int \mathrm{d}^2 \sigma \, \mathrm{e}^{\phi /2}\sqrt{-\det g_{\alpha \beta }}, \end{aligned}$$

(8)

where $g_{\alpha \beta } \equiv G_{\mu \nu } \partial _\alpha X^\mu \partial _\beta X^\nu$ is the induced metric on the two-dimensional world sheet. $X^\mu (\sigma ^\alpha )$ are the embedding equations of the world sheet in spacetime. In the following, we generalize the calculations in [37, 38] to the charged plasma case and find the additional contribution to the drag force from the chemical potential. We will work in the static gauge, i.e. $\sigma =u$ and $\tau =t$. Since the plasma is anisotropic, we consider the motions of the string in two different directions, x and z, which corresponds to the quark moving at constant velocity v. It is convenient to set the configuration of the string as [37]

$$\begin{aligned} x(u,t)= & {} x(u)\sin \theta +v t ~ \sin \theta \nonumber \\ z(u,t)= & {} z(u)\cos \theta +v t ~ \cos \theta . \end{aligned}$$

(9)

Obviously $\theta$ is the angle between the z-axis and the velocity.

Fig. 9

The drag force F as a function of velocity for a quark moving through the plasma with $Q=2$. The four graphs correspond to $a/T=1.38, a/T=4.42,a/T=12.2,a/T=86$, respectively, in which five lines denotes (from the top to down) $\Theta =0$, $\Theta =\pi /6$, $\Theta =\pi /4$, $\Theta =\pi /3$, $\Theta =\pi /2$

Fig. 10

The drag force F as a function of velocity for a quark moving through the plasma with $Q=5$. The four graphs correspond to $a/T=1.38, a/T=4.42,a/T=12.2,a/T=86$, respectively, in which five lines denotes (from the top to down) $\Theta =0$, $\Theta =\pi /6$, $\Theta =\pi /4$, $\Theta =\pi /3$, $\Theta =\pi /2$

Fig. 11

The drag force F as a function of velocity for a quark moving through the plasma with $Q=10$. The four graphs correspond to $a/T=1.38, a/T=4.42,a/T=12.2,a/T=86$, respectively, in which five lines denote (from the top to down) $\Theta =0$, $\Theta =\pi /6$, $\Theta =\pi /4$, $\Theta =\pi /3$, $\Theta =\pi /2$

Fig. 12

Drag force in x direction as a function a / T at $v=0.5$ (left) and $v=0.7$ (right), where the red, green, blue lines represent $Q=0$, $Q=1$, $Q=2$, respectively

Fig. 13

Drag force in z direction as a function a / T at $v=0.5$ (left) and $v=0.7$ (right), where the red, green, blue lines represent $Q=0$, $Q=1$, $Q=2$, respectively

The determinant of $g_{\alpha \beta }$ satisfies

$$\begin{aligned} -g e^{\phi }=\frac{-v^2\left( \sin ^2\theta +\big (1+\mathcal{F}\sin ^2\theta (x'-z')^2\big )\mathcal{H}\cos ^2\theta \right) +\mathcal{B}\mathcal{F}\left( 1+\mathcal{F}(x'^2\sin ^2\theta +\mathcal{H}z'^2\cos ^2\theta )\right) }{u^4\mathcal{F}}, \end{aligned}$$

(10)

so the Lagrangian $\mathcal{L}=-T_0 e^{\phi /2}\sqrt{-g}$ gives the canonical momenta density to the string as

$$\begin{aligned}&\Pi ^\sigma _x=\frac{\partial \mathcal L}{\partial x'}=-T_0 \mathrm{e}^{-\phi /2}\frac{x'\mathcal{B}\mathcal{F}+v^2\mathcal{H}(z'-x')\cos ^2\theta }{u^4\sqrt{-g}}\sin \theta , \nonumber \\&\Pi ^\sigma _z=\frac{\partial \mathcal L}{\partial z'}=-T_0 \mathrm{e}^{-\phi /2}\frac{z'\mathcal{B}\mathcal{F}+v^2\mathcal{H}(x'-z')\sin ^2\theta }{u^4\sqrt{-g}}\cos \theta ,\nonumber \\ \end{aligned}$$

(11)

where the prime denotes the derivative with respect to u. Then the equations of motion following from the Nambu–Goto action are

$$\begin{aligned} \partial _u\left( -T_0 \mathrm{e}^{-\phi /2}\frac{x'\mathcal{B}\mathcal{F}+v^2\mathcal{H}(z'-x')\cos ^2\theta }{u^4\sqrt{-g}}\sin \theta \right) =0,\nonumber \\ \partial _u\left( -T_0 \mathrm{e}^{-\phi /2}\frac{z'\mathcal{B}\mathcal{F}+v^2\mathcal{H}(x'-z')\sin ^2\theta }{u^4\sqrt{-g}}\cos \theta \right) =0.\nonumber \\ \end{aligned}$$

(12)

Note that in the string configuration (9), the time part of the E.O.M vanishes because of the time independence. Then after integration of (12), we have

$$\begin{aligned} -T_0\mathrm{e}^{-\phi /2}\frac{x'\mathcal{B}\mathcal{F}+v^2\mathcal{H}(z'-x')\cos ^2\theta }{u^4\sqrt{-g}}\sin \theta =C, \nonumber \\ -T_0\mathrm{e}^{-\phi /2}\frac{z'\mathcal{B}\mathcal{F}+v^2\mathcal{H}(x'-z')\sin ^2\theta }{u^4\sqrt{-g}}\cos \theta =D, \end{aligned}$$

(13)

which involve

$$\begin{aligned}&x'=\frac{\mathrm{e}^{\phi /2}u^4\csc \theta \sqrt{-g}\left( v^2(C+D \cot \theta )-C\mathcal{B}\mathcal{F}\csc ^2\theta \right) }{T_0\mathcal{B}\mathcal{F}\left( \mathcal{B}\mathcal{F}\csc ^2\theta -v^2(1+\mathcal{H}\cot ^2\theta )\right) },\nonumber \\&z'=\frac{e^{\phi /2}u^4\csc \theta \sqrt{-g}\sec \theta \left( v^2\mathcal{H}(D\csc \theta +C\sec \theta )-D\mathcal{B}\mathcal{F}\csc \theta \sec ^2\theta \right) }{T_0\mathcal{B}\mathcal{F}\mathcal{H}\left( 4\mathcal{B}\mathcal{F}\csc ^22\theta -v^2(\mathcal{H}\csc ^2\theta +\sec ^2\theta )\right) },\nonumber \\ \end{aligned}$$

(14)

where the constants C and D are integral constants corresponding to the momenta in the two directions. Taking (14) back to (10), we can solve the determinant of the induced metric as

$$\begin{aligned} -g \mathrm{e}^{\phi }=-\frac{2T_0\mathcal{B}\mathcal{H}(\mathcal{B}\mathcal{F}-v^2(\cos ^2\theta \mathcal{H}+\sin ^2\theta ))^2}{I(u)}, \end{aligned}$$

(15)

with

$$\begin{aligned} I(u)= & {} u^4\Big [-2T_0^2\mathcal{B}^2\mathcal{F}^2\mathcal{H}\nonumber \\&+\,\mathcal{B}\mathcal{F}\left( 2D^2u^4+\mathcal{H}(2C^2u^4+T_0^2v^2 \right. \nonumber \\&\left. +\,T_0^2v^2\cos 2\theta (\mathcal{H}-1)+T_0^2v^2\mathcal{H})\right) \nonumber \\&-\,2u^4v^2\mathcal{H}(D\cos \theta +C\sin \theta )^2\Big ]. \end{aligned}$$

(16)

The positiveness of the determinant requires [37]

$$\begin{aligned} \mathcal{B}(u)=\frac{v^2(\mathcal{H}(u)\cos ^2\theta +\sin ^2\theta )}{\mathcal{F}(u)}, \end{aligned}$$

(17)

at $u=u_c$ where the denominator I(u) vanishes, which implies that the integral constants satisfy

$$\begin{aligned} D=C\mathcal{H}(u)\cot \theta , \end{aligned}$$

(18)

at $u=u_c$. So the determinant of the induced metric can be simplified to

$$\begin{aligned} -g \mathrm{e}^{\phi }=\frac{T_0^2\mathcal{B}\left( -\mathcal{B}\mathcal{F}+v^2(\cos ^2\theta \mathcal{H}+\sin ^2\theta )\right) }{-T_0^2u^4\mathcal{B}\mathcal{F}+C^2u^8(1+\cot ^2\theta \mathcal{H})}, \end{aligned}$$

(19)

with the choices of

$$\begin{aligned} C=\pm \frac{T_0v \sin \theta }{u_c^2},\quad D=\pm \frac{T_0\mathcal{H}(u_c)v\cos \theta }{u_c^2}. \end{aligned}$$

(20)

Then the drag forces along the x-direction and z-direction on the string are

$$\begin{aligned} F_x=\frac{T_0v \sin \theta }{u_c^2},\quad F_z=\frac{T_0\mathcal{H}(u_c)v\cos \theta }{u_c^2}. \end{aligned}$$

(21)

4 Numerical analysis

In a charged anisotropic plasma, the angle dependence of the drag force in the x-direction in units of the isotropic drag force are shown in Figs. 2 and 3. From the first three plots of Fig. 2, we can see that $F_x$ is a monotonically increasing function of $\Theta$ when $a\ll T$ and $a\sim T$. However, the last plot of Fig. 2 illustrates that $F_x$ is no longer a monotonic function of $\Theta$ when $a\gg T$. By contrast, Fig. 3 shows that the $F_x$ at $v=0.9$ is no longer a monotonic function of $\Theta$ when $a/T=12.2$. We also find that for a charged plasma, with fixed v, $F_x$ can be larger than $F_{iso}\equiv F_{iso}(q=0)$ for some interval of $\Theta$ which depends on Q and a / T; by contrast, $F_x$ is always smaller than $F_{iso}$ for a chargeless anisotropic plasma. Note that the non-monotonic behavior shown in Fig. 3 is consistent with the result given in [37], where the authors did not show $F_x$. This is because if we write down the general expression for F, we can obtain the same ansatz as that given in [37] in the zero-chemical potential limit. Similarly, we can plot the angle dependence of the drag force in the z-direction in Figs. 4 and 5, while $F_z$ is always a monotonically decreasing function of $\Theta$.

Figures 6 and 7 illustrate the $\Theta$ dependence of the drag force F in units of the isotropic drag force at fixed v and a / T. It is easy to see that F is a monotonically decreasing function of $\Theta$, and when a / T is greater, the falloff of F is faster.

In Figs. 8, 9, 10, and 11, we can see that the drag force F in units of the isotropic drag force diverges in the ultra-relativistic limit, $v\rightarrow 1$, for any $\Theta \ne \pi /2$. We can see that F in a charged plasma diverges faster than in a chargeless plasma. So the anisotropic drag force is arbitrarily larger than the isotropic case in the ultra-relativistic limit. More interestingly, in the large Q limit, the behavior of the drag force F coincides for different angles $\Theta$.

To exhibit the temperature dependence of the drag force more explicitly, we plot the drag force as a function of a / T with different Q in Figs. 12 and 13. We can see that, unlike an anisotropic neutral plasma, in which the drag force in the transverse direction $F_x$ ($\Theta =\frac{\pi }{2}$) is a monotonically decreasing function of a / T, $F_x$ in anisotropic charged plasma is no longer a monotonically function: In the region with $a/T < 1$, $F_x$ increases as a / T increases, but in the region $a/T > 1$, $F_x$ decreases as a / T increases. This means that for a non-zero charge Q, the force changes non-monotonically. However, as shown in the plot of $F_z$ ($\Theta =0$) in Fig. 13, the drag force along the longitudinal direction is always a monotonically increasing function for both neutral plasma and charged plasma.

5 Summary

By using the AdS/CFT correspondence we have performed the calculations of the drag force exerted on a massive quark moving through a charged, anisotropic $\mathcal{{N}}=4$ SU(N) Super Yang–Mills plasma. We used the anisotropic charged black brane solution, which is dual to anisotropic QGP with a chemical potential. For a complete study of the drag force in an anisotropic background, we carried out an analytic calculation first and obtained some general expressions for the drag force. Different from the isotropic case, where the drag force in a charged plasma is always larger than in a neutral plasma at the same temperature, for our anisotropic case, we will find that it will be dependent on the explicit value of q and a, which can be seen in the numerical analysis. For arbitrary anisotropy and charge, we presented the numerical results for any prolate anisotropy and arbitrary direction of the quark velocity with respect to the direction of the anisotropy. We find the effect of the chemical potential or charge density is to enhance the drag force for the prolate solution.

Appendix: High temperature analysis

In this appendix, we calculate the drag forces in the limit of high temperature. We consider the high-temperature solution (4). First, plugging Eq. (4) into (17), it is easy to obtain $u_c$ to order $a^2$:

$$\begin{aligned} u_c=u_0+u_1a^2, \end{aligned}$$

(22)

with

$$\begin{aligned} u_0= & {} \left( u_\text {H}^2\sqrt{1-v^2}-\frac{u_\text {H}^2(-1+v^2+\sqrt{1-v^2})}{2}q^2\right) ^{1/2},\nonumber \\ u_1= & {} \frac{u_\text {H}^3\left( 1-\sqrt{1-v^2}-5\log 2+5\log (1+\sqrt{1-v^2})-v^2(1-5\log 2+(4+3\cos ^2\theta )\log (1+\sqrt{1-v^2}))\right) }{48(1-v^2)^{3/4}}\nonumber \\&+\,\frac{u_\text {H}^3}{384(1-v^2)^{5/4}(1+\sqrt{1-v^2})}\Big (10(1-v^2)(8(1+\sqrt{1-v^2})\log 2-v^2(8\sqrt{1-v^2}+(8-7\sqrt{1-v^2})\log 2))\nonumber \\&+(-80(1+\sqrt{1-v^2})+v^4(-86+13\sqrt{1-v^2})+2v^2(83+38\sqrt{1-v^2}))\log (1+\sqrt{1-v^2})\nonumber \\&+9v^2\cos 2\theta (2(v^2-1)(1+\sqrt{1-v^2})+(v^2(-2+\sqrt{1-v^2})+2(1+\sqrt{1-v^2}))\log (1+\sqrt{1-v^2}))\Big )q^2. \end{aligned}$$

(23)

So, by the use of (7) and (21), we are able to derive the drag force,

$$\begin{aligned} F_x= & {} \frac{\pi \sqrt{\lambda }T^2v}{2}\left( \sqrt{\frac{1}{1-v^2}}-\frac{q^2}{2}\left( 1-\frac{3}{\sqrt{1-v^2}}\right) \right) \nonumber \\&+\frac{v\sqrt{\lambda }a^2}{48\pi }\Big (\frac{1-v^2+\sqrt{1-v^2}+(4v^2-5)\log (1+\sqrt{1-v^2})}{(1-v^2)^{3/2}}\nonumber \\&+\,\frac{q^2}{2(1-v^2)^2(1+\sqrt{1-v^2})},\big (-(1+\sqrt{1-v^2})\nonumber \\&\times \,(13+30\log 2)+v^2(23+29\sqrt{1-v^2}\nonumber \\&+\,15(4+\sqrt{1-v^2})\log 2)+v^4(15\sqrt{1-v^2}\log 2\nonumber \\&-\,2(5+8\sqrt{1-v^2}+15\log 2))\nonumber \\&+\,(20(1+\sqrt{1-v^2})+v^4(17+5\sqrt{1-v^2})\nonumber \\&-v^2(37+22\sqrt{1-v^2}))\log (1+\sqrt{1-v^2})\big )\Big ),\nonumber \\ F_z= & {} \frac{\pi \sqrt{\lambda }T^2v}{2}\left( \sqrt{\frac{1}{1-v^2}}-\frac{q^2}{2}\big (1-\frac{3}{\sqrt{1-v^2}}\big )\right) \nonumber \\&+\,\frac{v\sqrt{\lambda }a^2}{48\pi }\Big (\frac{1-v^2+\sqrt{1-v^2}+(1+v^2)\log (1+\sqrt{1-v^2})}{(1-v^2)^{3/2}}\nonumber \\&+\,\frac{q^2}{2(v^2-1)^2(1+\sqrt{1-v^2})}\big (v^4(-1-7\sqrt{1-v^2}\nonumber \\&-15(2-\sqrt{1-v^2})\log 2)\nonumber \\&+\,v^2(2(-2+\sqrt{1-v^2})+15(4+\sqrt{1-v^2})\log 2)\nonumber \\&-\,5(1+\sqrt{1-v^2})(-1+6\log 2)\nonumber \\&-\,(v^2(1+v^2)(-2+\sqrt{1-v^2})\nonumber \\&+\,4(1+\sqrt{1-v^2}))\log (1+\sqrt{1-v^2})\big )\Big ), \end{aligned}$$

(24)

where we have used $\theta =\pi /2$ and $\theta =0$, which correspond to the x-direction and the z-direction, respectively. Note that the first part of the right hand side of (24) is an isotropic force in the charged plasma $F_\mathrm{iso}$:

Table 1 Critical velocity for different q

$$\begin{aligned} F_\mathrm{iso}(q)=\frac{\pi \sqrt{\lambda }T^2v}{2}\left( \sqrt{\frac{1}{1-v^2}}-\frac{q^2}{2}\left( 1-\frac{3}{\sqrt{1-v^2}}\right) \right) ,\nonumber \\ \end{aligned}$$

(25)

and, when $q=0$, we can get the drag forces in the plasma for zero chemical potential, which coincides with the result of [37]. We can see from (25) that, in the isotropic case, the drag force in the charged plasma is always larger than in a neutral plasma at the same temperature. In [38], the author obtained a critical velocity $v_c \approx 0.909$ for anisotropic neutral case independent of the temperature and anisotropy. The critical velocity turns out to be charge dependent and $v_c$ increases as q increases (Table 1).

In the absence of a chemical potential, Eq. (24) recover the analytical expressions for the transverse and parallel drag forces given in [38].