1 Introduction

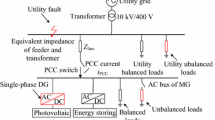
At present, the three-phase four-wire power supply network has been widely used in the 380 V low-voltage power supply system [1, 2], in which each phase can operate independently. If there is no effective compensation, unbalanced grid currents will emerge because of a single-phase load or unbalanced loads, and these will cause a zero sequence current flow in the neutral line of the grid side. The more unbalanced the loads are, the greater neutral line current is. Usually, the neutral line of the grid side is selected as a reference ground for both the power and control circuit in a three-phase four-wire system. The neutral potential is not zero when a larger current flows through the neutral line, and this will lead to an offset over the reference ground. As a result of this ground offset, the control precision and performance of the overall UPQC will be deteriorated, and then three-phase load voltages become unbalanced. Each phase voltage may be above or below the rated voltage to a different extent, and this will tend to cause damage to the electrical equipment [3].

To overcome the influence of unbalanced loads on the grid side neutral potential shift, it is necessary to control the three-phase grid currents to keep them in a sinusoidal and balanced state under unbalanced loads. The unified power quality conditioner (UPQC) [4,5,6,7,8,9,10,11,12,13] has the ability to compensate for unbalanced load currents and to realize the balance control of the grid currents.

In terms of grid current control, three independent H-bridges are used to form a parallel active power filter, and the single-phase p-q theory is employed to control the grid currents, so as to keep them in a balanced state [4, 5]. However, in this structure six more IGBTs are needed compared with a three-phase half-bridge inverter, and this will increase the control complexity and the cost. In [6], the grid current and load voltage references in both dq and αβ coordinates are calculated, and then hysteresis control is used to achieve grid current balance. However, the switching frequency of hysteresis control is not constant, and in [6] the design of appropriate LC filters is not considered. In [7], the grid currents are controlled as balanced sinusoidal currents in the positive and negative sequence double synchronous rotating coordinates under unbalanced loads. However, the implementation of this method requires multiple coordinate transformations, and the number of controllers in the closed-loop control is relatively larger, so control complexity is increased. The reactive power compensation and admittance calculation method are used to realize grid current balance control based on the balanced component method [8, 9]. In using this method, the unbalanced loads need to be decomposed, and the admittance calculation is also necessary. This makes the calculation rather complicated.

In a direct control scheme [10, 11] for UPQC, the DC bus voltage will be involved in the generation process of the grid current reference. The output result of the DC bus voltage loop is directly used as the grid current reference generation in [12, 13]. However, the DC bus voltage will produce a larger fluctuation under unbalanced loads, and this may cause the current reference to be distorted and thus the sine and balance degrees of the grid currents to be poor. Because of the low bandwidth and slow response of the DC bus voltage loop, the DC bus voltage will produce a large transient drop with a load step-up, exacerbating the deterioration of the control effect of the grid currents. To overcome the above shortcomings, a matching-ratio compensation algorithm (MCA) for the fundamental active component of load currents is proposed to calculate the grid current reference, so as to optimize the sine and balance degrees of the grid currents, reduce the steady-state fluctuation of the DC bus voltage, and improve the dynamic response speed of the DC bus loop. At the same time, the mutual influence between DC bus voltage fluctuations and unbalanced grid currents can also be weakened.

When a system is controlled in the three-phase stationary coordinate, the traditional proportional-integral (PI) controller [14] cannot achieve the zero steady-state error control. Therefore, a resonant (R) controller is employed to achieve zero steady-state error in [15]. The nonlinear loads may cause the output voltages of the inverter to be distorted, and thus multi-resonant (MR) controllers are employed to effectively control several low-order harmonics with high content in the nonlinear load currents in [16], so as to improve the waveform quality of the inverter voltage. In this paper, the UPQC is controlled in the three-phase stationary coordinate. The references of both converters are the fundamental sine quantities, considering the influence of the nonlinear loads, the PI + MR control method is employed to improve the waveform qualities of the grid currents and load voltages for the UPQC.

This paper aims to realize the balance control of three-phase grid currents under unbalanced loads. Compared with the aforementioned control strategies in [4,5,6,7,8,9,10,11,12,13], the control strategy based on the proposed MCA possesses a better control performance and can be realized more easily.

This paper is organized as follows. After this introduction and in Section 2, the mathematical model of UPQC is established, and the mechanism of DC bus voltage fluctuation is analyzed thoroughly; then the control strategy based on the MCA is given under the three-phase stationary coordinate, and the essence of the mutual influence between the DC bus voltage fluctuations and the unbalanced grid currents is revealed. To reduce the steady-state errors of PI controllers in the three-phase stationary coordinate, the MR controllers are added to the control loop of the two converters. Considering the most serious unbalanced loads (a single-phase load), the operation state of UPQC is thoroughly described and three important conclusions are obtained in Section 3. Finally, experimental results show that three-phase grid currents can be maintained in a sinusoidal and balanced state under the single-phase resistive and nonlinear load by using the proposed MCA strategy. The neutral line current on the grid side fluctuates slightly around zero. The steady-state fluctuation and the transient drop of the DC bus voltage can be reduced. The correctness of the theoretical analysis and the feasibility of the given strategy are verified by experiment results.

2 Theoretical analysis

The three-phase four-wire UPQC mainly consists of two bidirectional converters connected back-to-back sharing a common DC bus, as shown in Fig. 1.

Fig. 1
figure 1

Three-phase four-wire UPQC topology

Full size image

It should be noted that Sabc are turned on at the positive and negative half cycles of the grid voltage. Once the grid short circuit, Sabc can cut off the connection between the UPQC and grid in time, so as to prevent the UPQC from generating a large short circuit current to feed back to the grid. The primary and secondary sides of Trabc are connected to the grid and series converter, with turn ratio n = N1:N2 = 1:5.

The direct control scheme [10, 11] employed is described as follows: (a) The series converter is controlled to operate as a sinusoidal current source. It has the current source characteristic with impedance high enough for harmonic voltages, and thus mutual pollution between the source and load can be avoided [17]. The grid currents are controlled by the series converter to be sinusoidal, balanced and always in phase with the grid voltages, and the DC bus voltage is stabilized at a desired level; (b) The parallel converter is controlled to operate as a sinusoidal voltage source. It has the voltage source characteristic with impedance small enough to harmonic currents, and it provides the reactive power and harmonic currents for loads [11]. The load voltages are controlled by the parallel converter to be sinusoidal, balanced and in phase with the grid voltages.

2.1 Modeling and control of series converter

  1. 1)

    Mathematical model of series converter

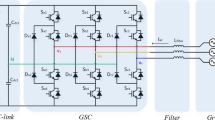
The series converter topology is shown in Fig. 2, where idco2 is the zero sequence current generated by the unbalanced loads and load voltages, and iso is the zero sequence current generated by the output currents of the series converter iserabc. Since the grid currents iSabc are controlled by the currents iserabc, the current iso is equivalent to the neutral current of the grid side iSN.

Fig. 2
figure 2

Series converter topology

Full size image

The main reason for the unbalanced grid currents is the DC bus voltage fluctuations caused by the unbalanced loads. Therefore, it is necessary to establish the mathematical model of the series converter and analyze the mechanism of DC bus voltage fluctuations.

Let Lserabc = Lser, and the state space average model of the series converter is as follows:

$$\left\{ \begin{aligned} u_{{ 1 {\text{a}}}} = L_{\text{ser}} \frac{{{\text{d}}i_{\text{sera}} }}{{{\text{d}}t}} + R_{\text{ser}} i_{\text{sera}} + u_{\text{cna}} \hfill \\ u_{{ 1 {\text{b}}}} = L_{\text{ser}} \frac{{{\text{d}}i_{\text{serb}} }}{{{\text{d}}t}} + R_{\text{ser}} i_{\text{serb}} + u_{\text{cnb}} \hfill \\ u_{{ 1 {\text{c}}}} = L_{\text{ser}} \frac{{{\text{d}}i_{\text{serc}} }}{{{\text{d}}t}} + R_{\text{ser}} i_{\text{serc}} + u_{\text{cnc}} \hfill \\ \end{aligned} \right.$$
(1)

where Rser is the equivalent resistance of Lser.

The relationship among the secondary side voltages of series transformers ucnabc, grid voltages uSabc and load voltages uLabc is:

$$\left\{ \begin{aligned} u_{\text{cna}} = {{(u_{\text{La}} - u_{\text{Sa}} )} \mathord{\left/ {\vphantom {{(u_{\text{La}} - u_{\text{Sa}} )} n}} \right. \kern-0pt} n} \hfill \\ u_{\text{cnb}} = {{(u_{\text{Lb}} - u_{\text{Sb}} )} \mathord{\left/ {\vphantom {{(u_{\text{Lb}} - u_{\text{Sb}} )} n}} \right. \kern-0pt} n} \hfill \\ u_{\text{cnc}} = {{(u_{\text{Lc}} - u_{\text{Sc}} )} \mathord{\left/ {\vphantom {{(u_{\text{Lc}} - u_{\text{Sc}} )} n}} \right. \kern-0pt} n} \hfill \\ \end{aligned} \right.$$
(2)

If output currents of the series converter iserabc are unbalanced, they can be expressed as:

$$i_{\text{sera}} + i_{\text{serb}} + i_{\text{serc}} = i_{\text{so}}$$
(3)

The zero sequence current idco2 generated by the unbalanced loads ZLabc and load voltage uLo can be expressed as:

$$i_{\text{dco2}} = i_{\text{LN}} + i_{\text{co}} = (i_{\text{para}} + i_{\text{parb}} + i_{\text{parc}} ) + \frac{3}{{C_{\text{par}} }}\frac{{{\text{d}}u_{\text{Lo}} }}{{{\text{d}}t}}$$
(4)

The switching states of the series converter are represented by the switching function S1j: (1) S1j = 1 when jth leg upper switch is turned on and jth leg lower switch is turned off, (2) S1j = − 1 when jth leg lower switch is turned on and jth leg upper switch is turned off.

$$S_{1j} = \left\{ \begin{aligned} 1 \, \hfill \\ - 1 \, \hfill \\ \end{aligned} \right.\quad \quad j = {\text{a, b, c}}$$
(5)

where subscript 1 represents the series converter.

Based on (5), the three-leg voltages of the series converter u1abc can be expressed as:

$$\left\{ {\begin{array}{*{20}c} {u_{{ 1 {\text{a}}}} = u_{{{\text{dc}} + }} \frac{{S_{{ 1 {\text{a}}}} + 1}}{2} + u_{{{\text{dc}} - }} \frac{{S_{{ 1 {\text{a}}}} - 1}}{2}} \\ {u_{{1{\text{b}}}} = u_{{{\text{dc}} + }} \frac{{S_{{ 1 {\text{b}}}} + 1}}{2} + u_{{{\text{dc}} - }} \frac{{S_{{ 1 {\text{b}}}} - 1}}{2}} \\ {u_{{ 1 {\text{c}}}} = u_{{{\text{dc}} + }} \frac{{S_{{ 1 {\text{c}}}} + 1}}{2} + u_{{{\text{dc}} - }} \frac{{S_{{ 1 {\text{c}}}} - 1}}{2}} \\ \end{array} } \right.$$
(6)

The positive and negative DC bus currents idc± can be expressed as:

$$\left\{ \begin{aligned} &i_{{{\text{dc}}1 + }} = i_{\text{sera}} \frac{{S_{{ 1 {\text{a}}}} + 1}}{2} + i_{\text{serb}} \frac{{S_{{ 1 {\text{b}}}} + 1}}{2} + i_{\text{serc}} \frac{{S_{{ 1 {\text{c}}}} + 1}}{2} \hfill \\ &i_{{{\text{dc}}1 - }} = i_{\text{sera}} \frac{{S_{{ 1 {\text{a}}}} - 1}}{2} + i_{\text{serb}} \frac{{S_{{ 1 {\text{b}}}} - 1}}{2} + i_{\text{serc}} \frac{{S_{{ 1 {\text{c}}}} - 1}}{2} \hfill \\ &i_{{{\text{dc}}1 + }} - i_{{{\text{dc}}1 - }} = i_{\text{so}} + i_{\text{dco2}} = i_{\text{dco}} \hfill \\ \end{aligned} \right.$$
(7)

Based on the instantaneous power theory [18], ignoring the inductance resistance Rser, an energy expression is derived from (1) to (7):

$$\begin{aligned} & u_{\text{cna}} i_{\text{sera}} + u_{\text{cnb}} i_{\text{serb}} + u_{\text{cnc}} i_{\text{serc}} \\ & \quad = u_{{{\text{dc}} + }} i_{{{\text{dc1}} + }} + u_{{{\text{dc}} - }} i_{{{\text{dc1}} - }} - \frac{{L_{\text{ser}} }}{2}\frac{{{\text{d}}a_{1} }}{{{\text{d}}t}} \\ \end{aligned}$$
(8)

where \(a_{ 1} = i_{\text{sera}}^{2} + i_{\text{serb}}^{2} + i_{\text{serc}}^{2}\).

The left side of (8) is the instantaneous output power of the series converter pser, and it can be expressed as:

$$p_{\text{ser}} = u_{\text{cna}} i_{\text{sera}} + u_{\text{cnb}} i_{\text{serb}} + u_{\text{cnc}} i_{\text{serc}}$$
(9)

The positive and negative DC capacitor currents idc1± can be expressed as:

$$\left\{ \begin{aligned} i_{\text{dc1 + }} = C_{\text{dc + }} \frac{{{\text{d}}u_{\text{dc + }} }}{{{\text{d}}t}} \hfill \\ i_{\text{dc1 - }} = C_{\text{dc - }} \frac{{{\text{d}}u_{\text{dc - }} }}{{{\text{d}}t}} \hfill \\ \end{aligned} \right.$$
(10)

Substituting (9) and (10) into (8), pser can be further expressed as:

$$p_{\text{ser}} = \frac{{C_{{{\text{dc}} + }} }}{2}\frac{{{\text{d}}u_{{{\text{dc}} + }}^{2} }}{{{\text{d}}t}} + \frac{{C_{{{\text{dc}} - }} }}{2}\frac{{{\text{d}}u_{{{\text{dc}} - }}^{2} }}{{{\text{d}}t}} - \frac{{L_{\text{ser}} }}{2}\frac{{{\text{d}}a_{1} }}{{{\text{d}}t}}$$
(11)

The expressions of positive and negative DC bus voltages udc± can be derived from (10):

$$\left\{ {\begin{array}{*{20}c} {u_{{{\text{dc}} + }} = \frac{1}{{C_{{{\text{dc}} + }} }}\int_{0}^{t} {i_{{{\text{dc1}} + }} } {\text{d}}t + U_{{{\text{dco}} + }} } \\ {u_{{{\text{dc}} - }} = \frac{1}{{C_{{{\text{dc}} - }} }}\int_{0}^{t} {i_{{{\text{dc1}} - }} } {\text{d}}t + U_{{{\text{dco}} - }} } \\ \end{array} } \right.$$
(12)

where Udco+ and Udco− are the initial voltages of capacitors Cdc+ and Cdc− respectively.

Let Cdc+ = Cdc− = Cdc and Udco+ = Udco− = Udco, the difference of udc+ and udc− can be derived from (12):

$$u_{{{\text{dc}} + }} - u_{{{\text{dc}} - }} = \frac{1}{{C_{\text{dc}} }}\int_{0}^{t} {i_{\text{dco}} } {\text{d}}t$$
(13)

It can be derived from (11) that:

$$u_{{{\text{dc}} + }}^{2} + u_{{{\text{dc}} - }}^{2} = \frac{2}{{C_{\text{dc}} }}\int_{0}^{t} {p_{\text{ser}} {\text{d}}t + } \frac{{L_{\text{ser}} a_{1} }}{{C_{\text{dc}} }} + \frac{{W_{\text{o}} }}{{C_{\text{dc}} }}$$
(14)

where Wo is the initial energy stored on the capacitor Cdc.

The total DC bus voltage udc can be obtained based on (13) and (14):

$$\begin{aligned}& u_{\text{dc}} = u_{{{\text{dc}} + }} + u_{{{\text{dc}} - }} \hfill \\ &\quad= \sqrt {\frac{{2W_{\text{o}} }}{{C_{\text{dc}} }} + \frac{4}{{C_{\text{dc}} }}\int_{0}^{t} {p_{\text{ser}} {\text{d}}t + } \frac{{2L_{\text{ser}} a_{1} }}{{C_{\text{dc}} }} - \frac{1}{{C_{\text{dc}}^{ 2} }}(\int_{0}^{t} {i_{\text{dco}} } {\text{d}}t)^{2} } \hfill \\ \end{aligned}$$
(15)

From (13) and (15), the expressions of positive and negative DC bus voltages udc± can be rewritten as:

$$\left\{ {\begin{array}{l} {u_{{{\text{dc}} + }} = \frac{{u_{\text{dc}} }}{2} + \frac{1}{{2C_{\text{dc}} }}\int_{0}^{t} {i_{\text{dco}} {\text{d}}t} } \\ {u_{{{\text{dc}} - }} = \frac{{u_{\text{dc}} }}{2} - \frac{1}{{2C_{\text{dc}} }}\int_{0}^{t} {i_{\text{dco}} {\text{d}}t} } \\ \end{array} } \right.$$
(16)

The mechanism of DC bus voltage fluctuations can be revealed by (15) and (16). That is, the DC bus voltage udc and udc± will fluctuate with the changes of the power pser, currents iserabc and neutral current idco.

However, udc will be involved in the generation process of the grid current reference. If the fluctuation of udc is larger than a certain level, it will deteriorate with the sine and balance degrees of the grid currents, leading to increasing the neutral current iSN, which exacerbates the DC bus voltage fluctuation in turn. Thus, based on the above analysis, it can be clearly seen that there is a mutual influence between the DC bus voltage fluctuation and the neutral currents. In addition, in the topology proposed, the neutral current of the load side flows into the neutral point of the positive and negative DC capacitors, resulting in a larger DC bus voltage fluctuation which is proportional to the load unbalance degree.

  1. 2)

    Control strategy of series converter

To overcome the adverse influence of DC bus voltage fluctuation on the balance control of grid currents, this paper proposes the MCA to calculate the grid current reference. Three ways for improvement are presented: (a) it can suppress influence of the DC bus voltage fluctuation on the sine and balance degrees of the grid currents; (b) it can reduce the steady-state fluctuation of the DC bus voltage; (c) it can improve the response speed of the DC bus voltage loop, so as to reduce a large transient drop of DC bus voltage with a load step-up. Considering (a), (b) and (c), the MCA can finally reduce the mutual influence between the DC bus voltage fluctuation and unbalanced grid currents.

The proposed MCA is described as follows: First the grid voltages uSabc, load voltages uLabc and load currents iLabc are transformed by dq transformation:

$$u_{\text{Sd}} = \bar{u}_{\text{Sd}} + \tilde{u}_{\text{Sd}}$$
(17)
$$u_{\text{Ld}} = \bar{u}_{\text{Ld}} + \tilde{u}_{\text{Ld}}$$
(18)
$$i_{\text{Ld}} = \bar{i}_{\text{Ld}} + \tilde{i}_{\text{Ld}}$$
(19)

where \(\bar{u}_{\text{Sd}}\), \(\bar{u}_{\text{Ld}}\) and \(\bar{i}_{\text{Ld}}\) are the DC components, and they represent the fundamental active components. \(\tilde{u}_{\text{Sd}}\), \(\tilde{u}_{\text{Ld}}\) and \(\tilde{i}_{\text{Ld}}\) are the AC components, and they represent the harmonic components.

Generally, certain harmonics and imbalance usually exist in the grid voltages, so the AC component \(\tilde{u}_{\text{Sd}}\) obtained after dq transformation is not zero. In addition, the load voltages and currents after dq transformation must contain the ac components \(\tilde{u}_{\text{Ld}}\) and \(\tilde{i}_{\text{Ld}}\) with the nonlinear loads. The above ac components will bring in an error during the grid current reference calculation process, and to solve this problem, low pass filters (LPFs) are employed to eliminate these ac components.

In (17), (18) and (19), \(\bar{u}_{\text{Sd}}\), \(\bar{u}_{\text{Ld}}\) and \(\bar{i}_{\text{Ld}}\) represent the fundamental amplitude of grid voltages, load voltages and load currents, respectively, and they can be obtained by filtering uSd, uLd and iLd with LPFs.

According to the instantaneous power theory, ignoring the system loss, the fundamental active powers on the grid side and load side are equal, as follows:

$$\bar{P}_{\text{Sd}} = \bar{P}_{\text{Ld}} = \bar{u}_{\text{Sd}} \bar{i}_{\text{Sd}} = \bar{u}_{\text{Ld}} \bar{i}_{\text{Ld}}$$
(20)

The proposed MCA for load fundamental active current can be expressed as:

$$\bar{i}_{\text{Sd}} = \frac{{\bar{u}_{\text{Ld}} }}{{\bar{u}_{\text{Sd}} }}\bar{i}_{\text{Ld}}$$
(21)

It can be seen from (21) that \(\bar{i}_{\text{Sd}}\) can adjust the magnitude of the grid current with the changes of the load active power \(\bar{u}_{\text{Ld}} \bar{i}_{\text{Ld}}\) and the grid voltage \(\bar{u}_{\text{Sd}}\), and thus \(\bar{i}_{\text{Sd}}\) has adaptability to grid voltages.

Based on the proposed MCA and mathematical model of the series converter, the control block diagram of the series converter in a three-phase stationary coordinate is given, as shown in Fig. 3. It can be seen that there is a mutual influence between the DC bus voltage fluctuation and unbalanced grid currents.

Fig. 3
figure 3

Control block diagram of the series converter

Full size image

The DC bus voltage loop can compensate for the UPQC internal loss, and is also a link of cooperative work between serial and parallel converters.

The transfer function of PI controller Gdc(s) for the DC voltage loop can be expressed as:

$$G_{\text{dc}} (s) = k_{\text{dcp}} + {{k_{\text{dci}} } \mathord{\left/ {\vphantom {{k_{\text{dci}} } s}} \right. \kern-0pt} s}$$
(22)

where kdcp and kdci are the proportional and integral coefficient of Gdc(s), respectively.

The output signal of the DC voltage loop \(\Delta i_{\text{d}}^{ * }\) can be expressed as:

$$\Delta i_{\text{d}}^{ * } = (U_{\text{dcref}} - u_{\text{dc + }} - u_{{{\text{dc}} - }} )G_{\text{dc}} (s)$$
(23)

The grid current reference amplitude is obtained by adding the value of \(\bar{i}_{\text{Sd}}\) calculated by the MCA and the output signal \(\Delta i_{\text{d}}^{ * }\):

$$I_{\text{dref}} = \bar{i}_{\text{Sd}} + \Delta i_{\text{d}}^{ * }$$
(24)

In contrast, there is no the MCA part in [12, 13], and the reference Idref is implemented only by the output signal of the DC bus voltage loop, i.e. Idref = \(\Delta i_{d}^{ * }\). The DC bus voltage udc with a larger fluctuation will make the grid currents iSabc unbalanced or even distorted, but after adding the MCA, it can be found that the reference Idref is shared by \(\bar{i}_{\text{Sd}}\) and \(\Delta i_{\text{d}}^{ * }\), where \(\bar{i}_{\text{Sd}}\) takes most of the current reference from (21) and (24), so as to reduce the influence of the DC bus voltage fluctuation on iSabc.

The a-phase of the series converter is designed as an example. Its control block diagram is shown in Fig. 4, where kPWM is the equivalent gain of the converter, Gsam(s) is the current sampling link and isera_s is the sampling value of the current isera.

Fig. 4
figure 4

Control block diagram of current loop

Full size image

The current sampling link can be equivalent to a first-order inertia link, and its transfer function Gsam(s) is:

$$G_{\text{sam}} (s) = {{k_{{{\text{sam\_ser}}}} } \mathord{\left/ {\vphantom {{k_{{{\text{sam\_ser}}}} } {(T_{{{\text{sam\_ser}}}} s + 1)}}} \right. \kern-0pt} {(T_{{{\text{sam\_ser}}}} s + 1)}}$$
(25)

where ksam_ser and Tsam_ser are the current isera sampling coefficient and filter delay time (s), respectively.

The current loop of the series converter is controlled by the PI + MR controllers, where the PI controller can correct the current loop to a type II system to improve the system’s anti-jamming performance; the MR controllers are used to control the fundamental and harmonics components to improve the control accuracy of the series converter and the waveform qualities of the grid currents.

With the increase of the harmonic order, the harmonic components will decrease rapidly, and thus the influence of the high harmonic components on the load voltages is limited. Therefore, the MR controllers mainly control for the lower harmonics. Taking into account the cost of digital control computation, the fundamental and 3th, 5th and 7th harmonics are selected in this paper.

The transfer function of PI + MR controllers GPIMR(s) can be expressed as:

$$\begin{aligned} G_{\text{PIMR}} (s) & = G_{\text{PI}} (s) + G_{\text{MR}} (s) \\ & = (k_{\text{serp}} + \frac{{k_{\text{seri}} }}{s}) + \sum\limits_{h = 1,3,5,7} {\frac{{2k_{\text{r}} \omega_{\text{c}} s}}{{s^{2} + 2\omega_{\text{c}} s{ + (}h\omega_{\text{o}} )^{2} }}} \\ \end{aligned}$$
(26)

where kserp and kseri are the proportional and integral coefficient, respectively. kr is the resonant coefficient, ωc is the cut-off frequency (rad/s), ωo is the resonant frequency ωo = 100π (rad/s), and h is the harmonic order.

The design method of MR controllers can be found in [16]. The parameters of the GMR(s) controller are as follows: kr = 50 and ωc = 5rad/s.

Figure 5 is the bode plot of GPIMR(s). The gain of the low frequency-band is determined by the gain of the PI controller. The PI controller plays a major role in the overall regulation process. The MR controllers will generate a large gain at the desired resonant points, and the performance of the PI controller is reflected at other frequency-bands outside the resonant points, so the parameters of GPI(s) will be designed accordingly.

Fig. 5
figure 5

Bode plot of GPIMR(s)

Full size image

The design process of the PI controller in [14] is now applied. Let the shear frequency of the current loop ωseri_cut = 3340π rad/s (1/10 of the switching frequency 16.7 kHz), and then the turning frequency Rser/Lser is much smaller than ωseri_cut, so the resistor Rser can be ignored in Fig.4. The current loop is corrected to a type II system, and the transfer function of the current open-loop Gop_seri(s) can be expressed as:

$$G_{{{\text{op\_seri}}}} (s) = \frac{{k_{\text{PWM}} }}{{L_{\text{ser}} s}}G_{\text{PI}} (s)G_{\text{sam}} (s) = k_{{{\text{op\_ser}}}} \frac{{k_{\text{serp}} s + k_{\text{seri}} }}{{s^{2} (T_{{{\text{sam\_ser}}}} s + 1)}}$$
(27)

where the current open-loop gain kop_seri = kPWM ksam_ser/Lser.

The turning frequency of the zero point of Gop_seri(s) is 1/5 of ωseri_cut, and thus the relation between kserp and kseri can be expressed as:

$${{k_{\text{seri}} } \mathord{\left/ {\vphantom {{k_{\text{seri}} } {k_{\text{serp}} }}} \right. \kern-0pt} {k_{\text{serp}} }} = k_{\upomega} \omega_{{{\text{seri\_cut}}}} = {{\omega_{{{\text{seri\_cut}}}} } \mathord{\left/ {\vphantom {{\omega_{{{\text{seri\_cut}}}} } 5}} \right. \kern-0pt} 5}$$
(28)

The modulus of the transfer function Gop_seri(s) at the shear frequency ωseri_cut is equal to 1, and the following equation can be obtained:

$$k_{\text{serp}} = \frac{{\omega_{{{\text{seri\_cut}}}} L_{\text{ser}} }}{{k_{{{\text{sam\_ser}}}} k_{\text{PWM}} }}\sqrt {\frac{{1 + T_{{{\text{sam\_ser}}}}^{2} \omega_{{{\text{seri\_cut}}}}^{2} }}{{1 + k_{\omega }^{2} }}}$$
(29)

According to (28) and (29), the parameters of GPI(s) are as follows: kserp = 6.43 and kseri = 819.

The modulation signals of the series converter \(u_{\text{serabc}}^{ * }\)can be expressed as:

$$\left\{ \begin{aligned} u_{\text{sera}}^{ * } = (i_{\text{refa}} - i_{{{\text{sera\_s}}}} )G_{\text{PIMR}} (s) + u_{\text{cna}} \hfill \\ u_{\text{serb}}^{ * } = (i_{\text{refb}} - i_{{{\text{serb\_s}}}} )G_{\text{PIMR}} (s) + u_{\text{cnb}} \hfill \\ u_{\text{serc}}^{ * } = (i_{\text{refc}} - i_{{{\text{serc\_s}}}} )G_{\text{PIMR}} (s) + u_{\text{cnc}} \hfill \\ \end{aligned} \right.$$
(30)

The three-phase grid current references irefabc can be derived from the grid current reference amplitude using the inverse dq transformation:

$$\left\{ \begin{aligned} i_{\text{refa}} &= I_{\text{dref}} \sin \omega t \hfill \\ i_{\text{refb}} &= I_{\text{dref}} \sin (\omega t - 2\pi /3) \hfill \\ i_{\text{refc}} &= I_{\text{dref}} \sin (\omega t + 2\pi /3) \hfill \\ \end{aligned} \right.$$
(31)

where ωt is obtained by a phase-locked loop (PLL) [19].

Under the control of the series converter, the neutral current of the grid side iSN is equal to zero.

2.2 Modeling and control of parallel converter

  1. 1)

    Mathematical model of parallel converter

The main task of the parallel converter is to ensure that the load voltages uLabc are sinusoidal and balanced, and also to provide the required harmonic and reactive currents for loads. The parallel converter topology is shown in Fig. 6.

Fig. 6
figure 6

Parallel converter topology

Full size image

The modeling process of the parallel converter is the similar as that of the series converter, and the mathematical model expressions of the DC bus voltage in the parallel converter are given directly in this section.

The state space average model of the parallel converter is as follows:

$$\left\{ {\begin{array}{*{20}c} {u_{{ 2 {\text{a}}}} = L_{\text{par}} \frac{{{\text{d}}i_{{ 2 {\text{a}}}} }}{{{\text{d}}t}} + R_{\text{par}} i_{{ 2 {\text{a}}}} + u_{\text{La}} } \\ {u_{{ 2 {\text{b}}}} = L_{\text{par}} \frac{{{\text{d}}i_{{ 2 {\text{b}}}} }}{{{\text{d}}t}} + R_{\text{par}} i_{{ 2 {\text{b}}}} + u_{\text{Lb}} } \\ {u_{{ 2 {\text{c}}}} = L_{\text{par}} \frac{{{\text{d}}i_{{ 2 {\text{c}}}} }}{{{\text{d}}t}} + R_{\text{par}} i_{{ 2 {\text{c}}}} + u_{\text{Lc}} } \\ \end{array} } \right.$$
(32)
$$\left\{ {\begin{array}{*{20}c} {i_{{ 2 {\text{a}}}} = i_{\text{ca}} + i_{\text{para}} = C_{\text{par}} \frac{{{\text{d}}u_{\text{La}} }}{{{\text{d}}t}} + i_{\text{La}} - i_{\text{Sa}} } \\ {i_{{ 2 {\text{b}}}} = i_{\text{cb}} + i_{\text{parb}} = C_{\text{par}} \frac{{{\text{d}}u_{\text{Lb}} }}{{{\text{d}}t}} + i_{\text{Lb}} - i_{\text{Sb}} } \\ {i_{{ 2 {\text{c}}}} = i_{\text{cc}} + i_{\text{parc}} = C_{\text{par}} \frac{{{\text{d}}u_{\text{Lc}} }}{{{\text{d}}t}} + i_{\text{Lc}} - i_{\text{Sc}} } \\ \end{array} } \right.$$
(33)

where Rpar is the equivalent resistance of inductor Lpar.

The parallel converter will output a zero sequence current iLN under the unbalanced loads:

$$i_{\text{para}} + i_{\text{parb}} + i_{\text{parc}} = i_{\text{LN}}$$
(34)

The total DC bus voltage udc can be expressed as:

$$\begin{aligned} & u_{\text{dc}} = u_{{{\text{dc}} + }} + u_{{{\text{dc}} - }} \\ & = \sqrt {\frac{{2W_{\text{o}} }}{{C_{\text{dc}} }} + \frac{4}{{C_{\text{dc}} }}\int_{0}^{t} {p_{\text{par}} {\text{d}}t + } \frac{{2L_{\text{par}} b_{1} }}{{C_{\text{dc}} }} + \frac{{2C_{\text{par}} b_{2} }}{{C_{\text{dc}} }} - \frac{1}{{C_{\text{dc}}^{ 2} }}(\int_{0}^{t} {i_{\text{dco}} } {\text{d}}t)^{2} } \\ \end{aligned}$$
(35)

where \(b_{ 1} = i_{{ 2 {\text{a}}}}^{2} + i_{{ 2 {\text{b}}}}^{2} + i_{{ 2 {\text{c}}}}^{2}\) and \(b_{2} = u_{\text{La}}^{2} + u_{\text{Lb}}^{2} + u_{\text{Lc}}^{2}\).

The expressions of positive and negative DC bus voltages udc± can be expressed as:

$$\left\{ {\begin{array}{*{20}c} {u_{{{\text{dc}} + }} = \frac{{u_{\text{dc}} }}{2} + \frac{1}{{2C_{\text{dc}} }}\int_{0}^{t} {i_{\text{dco}} {\text{d}}t} } \\ {u_{{{\text{dc}} - }} = \frac{{u_{\text{dc}} }}{2} - \frac{1}{{2C_{\text{dc}} }}\int_{0}^{t} {i_{\text{dco}} {\text{d}}t} } \\ \end{array} } \right.$$
(36)

It can be seen from (35) and (36) that the DC bus voltage udc and udc± will fluctuate with the changes of the power ppar, currents i2abc, voltages uLabc and neutral current idco.

The unbalanced load voltages will also cause fluctuations in the DC bus voltage, and thus the control objective of the parallel converter is to keep the three-phase load voltages sinusoidal and balanced, so as to minimize the impact of the load voltages on the DC bus voltage.

  1. 2)

    Control strategy of parallel converter

Based on the mathematical model of the parallel converter, a double closed-loop control strategy for the parallel converter under three-phase stationary coordinate is given, as shown in Fig. 7, where i2a_s and uLa_s are the sampling values of i2a and uLa, respectively. To reduce the steady-state errors of PI controllers, MR controllers are added in the voltage outer-loop.

Fig. 7
figure 7

Control block diagram of the parallel converter

Full size image

The control block diagram of the current inner-loop is shown in Fig. 8. To eliminate the disturbance of the load voltage to the current loop, the load voltage (uLa) feedforward control is added to the current inner-loop.

Fig. 8
figure 8

Control block diagram of the current inner-loop

Full size image

The transfer function of the current sampling Gsami(s) in the parallel converter can be expressed as:

$$G_{\text{sami}} (s) = {{k_{{{\text{sam\_pari}}}} } \mathord{\left/ {\vphantom {{k_{{{\text{sam\_pari}}}} } {(T_{{{\text{sam\_pari}}}} s + 1)}}} \right. \kern-0pt} {(T_{{{\text{sam\_pari}}}} s + 1)}}$$
(37)

where ksam_pari and Tsam_pari are the sampling coefficient and filter delay time (s) of the current i2a, respectively.

The current inner-loop represents the tracking performance, so it is designed as a type I system. A PI controller is employed by the current inner-loop, and its transfer function GPIi(s) can be expressed as:

$$G_{\text{PIi}} (s) = k_{\text{parip}} + {{k_{\text{parii}} } \mathord{\left/ {\vphantom {{k_{\text{parii}} } s}} \right. \kern-0pt} s}$$
(38)

where kparip and kparii are the proportional and integral coefficient of GPIi(s), respectively.

After the zero point of GPIi(s) and the pole point of 1/(Lpars + Rpar) cancellation, the transfer function of the current open-loop Gop_pari(s) can be expressed as:

$$G_{{{\text{op\_pari}}}} (s) = \frac{{k_{\text{PWM}} }}{{L_{\text{par}} s + R_{\text{par}} }}G_{\text{PIi}} (s)G_{\text{sami}} (s) = \frac{{k_{{{\text{op\_pari}}}} }}{{s(T_{{{\text{sam\_pari}}}} s + 1)}}$$
(39)

where the current open-loop gain kop_pari = kPWM ksam_pari km, and the proportional relationship km = kparip / Lpar = kparii / Rpar.

The parameter calculation of GPIi(s) is the same as that of the series converter. Let the shear frequency of the current loop ωpari_cut = 3340π rad/s, and the parameters of GPIi(s) are: kparip = 0.96 and kparii = 319.

The transfer function of the current closed-loop Gcl_pari(s) can be expressed as:

$$G_{{{\text{cl\_pari}}}} (s) = \frac{{k_{\text{PWM}} k_{\text{m}} }}{{T_{{{\text{sam\_pari}}}} s^{2} + s + k_{{{\text{op\_pari}}}} }}$$
(40)

Ignoring the higher order term Tsam_paris2 in (40), Gcl_pari(s) can be reduced order to:

$$G_{{{\text{cl\_pari}}}} (s) = \frac{{k_{\text{PWM}} k_{\text{m}} }}{{s + k_{\text{op - pari}} }}$$
(41)

The control block diagram of the voltage outer-loop is shown in Fig. 9, where the PI + MR controllers are employed for the load voltages, and their transfer function is shown in (26).

Fig. 9
figure 9

Control block diagram of the voltage outer-loop

Full size image

The transfer function of the voltage sampling Gsamu(s) can be expressed as:

$$G_{\text{samu}} (s) = {{k_{{{\text{sam\_paru}}}} } \mathord{\left/ {\vphantom {{k_{{{\text{sam\_paru}}}} } {(T_{{{\text{sam\_paru}}}} s + 1)}}} \right. \kern-0pt} {(T_{{{\text{sam\_paru}}}} s + 1)}}$$
(42)

where ksam_paru and Tsam_paru are the sampling coefficient and filter delay time (s) of the voltage uLa, respectively.

The PI controller transfer function of the voltage outer-loop GPIu(s) can be expressed as:

$$G_{\text{PIu}} (s) = k_{\text{parup}} + {{k_{\text{parui}} } \mathord{\left/ {\vphantom {{k_{\text{parui}} } s}} \right. \kern-0pt} s}$$
(43)

where kparup and kparui are the proportional and integral coefficient of GPIu(s), respectively.

The transfer function of the voltage open-loop Gop_paru(s) can be expressed as:

$$G_{{{\text{op\_paru}}}} (s) = \frac{{k_{{{\text{op\_paru}}}} (k_{\text{parup}} s + k_{\text{parui}} )}}{{s^{2} (T_{{\sum {\text{par}}}} s + 1)}}$$
(44)

where the voltage open-loop gain kop_paru = ksam_paru / (ksam_pari Cpar), and the sum of the small inertia time constants T∑paru = Tsam_paru + 1/ (kop_pari).

Let the shear frequency of the voltage loop ωparu_cut = 668π rad/s (1/5 of ωpari_cut), and the parameters of GPIu(s) are as follows: kparup = 0.16 and kparui = 77.6.

The load voltage references urefabc can be expressed as:

$$\left\{ \begin{aligned} u_{\text{refa}} &= U_{\text{ref}} \sin \omega t \hfill \\ u_{\text{refb}} &= U_{\text{ref}} \sin (\omega t - 2\pi /3) \hfill \\ u_{\text{refc}} &= U_{\text{ref}} \sin (\omega t + 2\pi /3) \hfill \\ \end{aligned} \right.$$
(45)

where Uref is the desired amplitude of load voltages.

The current loop references \(i_{\text{refabc}}^{ * }\) can be expressed as:

$$\left\{ \begin{aligned} \hfill i_{\text{refa}}^{ * } = (u_{\text{refa}} - u_{{{\text{La\_s}}}} )G_{\text{PIMR}} (s) \\ \hfill i_{\text{refb}}^{ * } = (u_{\text{refb}} - u_{{{\text{Lb\_s}}}} )G_{\text{PIMR}} (s) \\ \hfill i_{\text{refc}}^{ * } = (u_{\text{refc}} - u_{{{\text{Lc\_s}}}} )G_{\text{PIMR}} (s) \\ \end{aligned} \right.$$
(46)

The modulation signals of the series converter \(u_{\text{parabc}}^{ * }\) can be expressed as:

$$\left\{ \begin{aligned} u_{\text{para}}^{ * } = (i_{\text{refa}}^{ * } - i_{{ 2 {\text{a\_s}}}} )G_{\text{PIi}} (s) + {{u_{\text{La}} } \mathord{\left/ {\vphantom {{u_{\text{La}} } {k_{\text{PWM}} }}} \right. \kern-0pt} {k_{\text{PWM}} }} \hfill \\ u_{\text{parb}}^{ * } = (i_{\text{refb}}^{ * } - i_{{ 2 {\text{b\_s}}}} )G_{\text{PIi}} (s) + {{u_{\text{Lb}} } \mathord{\left/ {\vphantom {{u_{\text{Lb}} } {k_{\text{PWM}} }}} \right. \kern-0pt} {k_{\text{PWM}} }} \hfill \\ u_{\text{parc}}^{ * } = (i_{\text{refc}}^{ * } - i_{{ 2 {\text{c\_s}}}} )G_{\text{PIi}} (s) + {{u_{\text{Lc}} } \mathord{\left/ {\vphantom {{u_{\text{Lc}} } {k_{\text{PWM}} }}} \right. \kern-0pt} {k_{\text{PWM}} }} \hfill \\ \end{aligned} \right.$$
(47)

3 Case analysis of single-phase load

By employing the proposed control strategies, UPQC can compensate for unbalanced load currents caused by unbalanced loads, so that the grid currents can be kept in sinusoidal and balanced state. Here we take the most serious unbalanced loads (100% unbalanced load) as an example to do some analysis. To better illustrate the compensation effect of the UPQC for the unbalanced load current, the operation schematic and phasor diagram only with a-phase load are shown in Fig. 10.

Fig. 10
figure 10

Operating principle of UPQC with a-phase load

Full size image

Under the control of the series converter, the a-phase load fundamental active current iLa can be evenly distributed to each phase on the grid side, so the three-phase grid currents iSabc are still maintained in a sinusoidal and balanced state. Seen from the grid side, the whole system is in a three-phase balanced state. iSabc can be expressed as:

$$i_{\text{Sabc}} = {{i_{\text{La}} } \mathord{\left/ {\vphantom {{i_{\text{La}} } 3}} \right. \kern-0pt} 3}$$
(48)

From (48), each phase grid current is equal to 1/3 of the load fundamental active current.

Under the control of parallel converter, the a-phase current of the parallel converter ipara is in phase with the a-phase grid current iSa, and provides the 2/3 load current iLa for the load. The b- and c-phase grid currents iSb, iSc are absorbed by the b- and c-phase of the parallel converter. Therefore, the a-phase load current iLa is jointly provided by the grid and parallel converter.

The output currents of the parallel converter iparabc can be expressed as:

$$\left\{ \begin{aligned} i_{\text{para}} &= 2i_{\text{La}} /3 \hfill \\ i_{\text{parb}} &= - i_{\text{Sb}} \hfill \\ i_{\text{parc}} &= - i_{\text{Sc}} \hfill \\ \end{aligned} \right.$$
(49)

The three-phase load currents iLabc can be expressed as:

$$\left\{ \begin{aligned} i_{\text{La}} &= i_{\text{Sa}} + i_{\text{para}} \hfill \\ i_{\text{Lb}} &= i_{\text{Lc}} = 0 \hfill \\ \end{aligned} \right.$$
(50)

The neutral currents on both the grid and load side iSN, iLN can be obtained as:

$$\left\{ \begin{aligned} i_{\text{SN}} &= 0 \hfill \\ i_{\text{LN}} &= i_{\text{La}} \hfill \\ \end{aligned} \right.$$
(51)

Thus the following conclusions can be drawn on unbalanced loads: (1) Each phase grid current is 1/3 of the sum of three-phase load fundamental active currents; (2) The neutral current on the grid side is zero, whereas the neutral current on the load side is equal to the load unbalanced currents; (3) The parallel converter absorbs and converts the grid currents to ensure the operation of unbalanced loads.

4 Experimental validation

Two DSPs (TMS320F28335) are used as the controllers of the series and parallel converters. Experimental parameters are: the rms values of grid and load voltage are 220 V, their frequencies are 50 Hz; the switching frequencies of the two converters are 16.7 kHz; the positive and negative DC bus voltages are ±400 V; the a-phase rated load power is 9.35 kW; the a-phase rated load is 5.18 Ω.

The experimental results of the a-phase resistance load with the MCA are shown in Fig. 11. To verify the aforementioned important functions of the proposed MCA, the comparative experiments are carried out in terms of the sine and balance degrees of the grid currents, the neutral current of the grid side and the steady-state fluctuation and the transient drop of the DC bus voltage, as shown in Fig. 12.

Fig. 11
figure 11

Experimental results of the a-phase resistance load with MCA

Full size image
Fig. 12
figure 12

Experimental results of the a-phase resistance load without MCA

Full size image

The grid voltages uSabc, grid currents iSabc, load voltages uLabc and load currents iLabc are shown in Fig. 11a–d. The percentage of unbalanced load is 100% only with a-phase rated load. It can be seen from Fig. 11b, c that three-phase grid currents iSabc and load voltages uLabc remain in a good sinusoidal and balanced state under the proposed control strategies. Moreover, the grid currents iSabc with the system loss are controlled to be in phase with the grid voltages, and their rms values are 16.9 A, 16.6 A and 16.5 A, respectively, which are approximately 1/3 of the a-phase load current iLa (42.6 A rms). Compared with Fig. 12a, because of the influence of the DC bus voltage fluctuations (as described in Section 2.1), the sine and balance degrees of the grid currents iSabc without the proposed MCA are obviously poorer, and the rms values of the currents iSabc are 18.6 A, 19.7 A and 20.5 A, respectively.

The output currents of parallel converter iparabc are shown in Fig. 11e. The a-phase current ipara is in phase with the a-phase grid voltage uSa, indicating that the a-phase of the parallel converter supplies 2/3 of the load current for the a-phase load. The b- and c-phase currents iparb, iparc are reversed with the b- and c-phase grid voltage uSb, uSc, indicating that the b- and c-phase of the parallel converter absorb 1/3 of load current from the grid side.

The neutral current of the load side iSN is equal to the a-phase load current iLa in Fig. 11f. Under the control of series and parallel converters, the neutral current of the grid side iSN is very small, fluctuating in a small range around the zero axis, and its rms value is 2.72 A, which is much smaller than the neutral current of the load side iLN (44.8 A rms). Compared with Fig. 12b, the neutral current of the grid side iSN (4.77 A rms) without MCA is larger than that with MCA.

The steady-state positive and negative DC bus voltages udc± are shown in Fig. 11g. It should be noted that the neutral current of the load side flows into the neutral point of the positive and negative DC capacitors Cdc±, and this will result in the DC bus voltage fluctuations. The fluctuation frequencies of the positive and negative DC bus voltages are 50 Hz, which coincides with the a-phase load current frequency, and the fluctuation frequency of the total DC bus voltage is twice the fundamental frequency. Compared with Fig. 12c, the positive and negative DC bus voltage fluctuations without the MCA are larger than those with the MCA because of the increased unbalanced degree of the grid currents.

The grid currents iSabc cannot immediately respond to the sudden change of a-phase load from empty-load to full-load in Fig. 11h, so a certain adjustment time is needed. During this adjustment time, the positive or negative DC bus capacitor provides energy for the a-phase load, and thus the total DC bus voltage udc experiences a large drop. Fig. 11i is an enlarged view of Fig. 11h. Compared with Fig. 12d, it can be seen that the DC bus voltage transient drop without MCA is much larger.

The experimental results in Fig. 12 also prove that there is a mutual influence between the DC bus voltage fluctuation and the neutral current of the grid side.

To verify the robustness of the UPQC based on the proposed MCA control strategy, the experimental results of the a-phase nonlinear load (diode bridge rectifier with a capacitive load) are added in this section, as shown in Fig. 13. The sine degree of the grid currents iSbac will be deteriorated, as shown in Fig. 13a, but the UPQC is still able to control iSbac to be balanced, and the rms values of iSabc are 7.06 A, 7.27 A and 7.07 A. The a-phase load voltage uLa appears to be distorted because of the influence of the a-phase nonlinear load, as shown in Fig. 13b. Figure 13c shows the three-phase load currents iLabc, where the a-phase load current iLa has the characteristics of periodic load and no-load. The a-phase of the parallel converter provides a part of the fundamental active current and all of the harmonic currents ipara for the nonlinear load. Meanwhile the b- and c-phase absorb the grid currents, as shown in Fig. 13d. The neutral current iSN is obviously smaller than the current iLN, as shown in Fig. 13e. The unbalanced grid currents and the larger neutral current of the load side will cause the fluctuations in the DC bus voltage, as shown in Fig. 13f.

Fig. 13
figure 13

Experimental results of the a-phase nonlinear load with MCA

Full size image

5 Conclusion

Tackling the problem of three-phase grid currents imbalance caused by three-phase unbalanced loads, first the mathematical model of a three-phase four-wire UPQC is established. The mechanism of DC bus voltage fluctuations is analyzed in detail, and the mutual influence between the DC bus voltage fluctuations and the unbalanced grid currents is described. Then the control strategy based on the MCA is given under a three-phase stationary coordinate. The experimental results show that:

  1. 1)

    The balance control of the grid currents with 100% unbalanced load can be realized by the given control strategy based on the proposed MCA;

  2. 2)

    The neutral current of the grid side fluctuates in a small range around zero;

  3. 3)

    The steady-state fluctuation and the transient drop of the DC bus voltage can also be restrained;

  4. 4)

    The system has a greater robustness under the single-phase nonlinear load.

Therefore, the correctness of the theoretical analysis and the feasibility of the control strategy based on the MCA are verified. On the basis of the theoretical analysis, we believe this paper also draws important conclusions, which are of significance to related academic research as well as engineering.