1 Introduction

Distributed generation (DG) units such as wind turbines and solar cell panels are integrated into distribution networks by power electronic switches [1, 2]. As a consequence of the increasing penetration of DG units in local grids, the concept of microgrid has gained popularity. Microgrid has ability to operate in both islanded and grid-connected modes [3–5]. The former, droop control methods [5, 6] are used to guarantee the accuracy of power sharing among DG units. The latter, current control schemes with maximum power-point tracking (MPPT) algorithms are implemented to maximize power supply to the grid [7–9].

The L and LCL filters are widely used in grid-connected inverters, while the LC filter is mostly applied in uninterruptible power supplies or islanded microgrids [10, 11]. The LCL filter performs a better ability to attenuate high-order harmonics than the L filter. Nevertheless, the LCL filter has an inherent resonance peak which significantly magnifies the harmonic current around its peak frequency. Therefore, active damping methods should be used to reduce the current distortion. The most common control structures which include active damping can be categorized into: ➀ cascaded dual-loop [12], consisting of a grid-side-current outer loop and an inner active-damping loop; ➁ single loop with inner feedback [13–15], consisting of a grid-side-current outer loop and an active-damping inner feedback loop.

In the dual-loop control system, the closed-loop stability can be guaranteed by sophisticatedly designing the inner and outer loop parameters. However, these parameters are coupled with each other. Thus, it makes the tuning procedure more difficult. To completely decouple the control parameters, the control structure of single loop with inner feedback is a feasible solution. By this way, the control parameters without coupling can be easily to acquire. For the inner feedback, the filter-capacitor current is more favorable than the inverter-side current [15]. The latter equals to place virtual impedance connecting in series with inverter-side inductor, which will deteriorate the frequency dynamics of output filter.

The resonance phenomena among multi-parallel inverters are more complicated than the case of single one [16]. To explaining the coupling resonance phenomena, the parallel and series resonances should be investigated as a whole. For this reason, a simplified explanation of these resonances among multi-parallel inverters is presented in [17]. And the discussion about series and parallel resonances in wideband frequency domain is presented in [18].

In this paper, an equivalent coupling resonance model of multi-parallel inverters in microgrid operating in grid-connected mode is presented, and the coupling resonance phenomena are explicitly investigated through the mathematical approach. To attenuate coupling resonance, an active damping control parameter design method is proposed. The rest of the paper is organized as follows. Firstly, an equivalent coupling resonance model is built, and the resonance peaks among multi-parallel inverters are explicitly investigated through the mathematical approach in Sect. 2. Secondly, the intrinsic and extrinsic resonances in the different number of inverters are analyzed in detail in Sect. 3. Then, an active damping control parameter design method is proposed to attenuate coupling resonance, and the optimal range of the damping parameter can be easily located through an initiatively graphic method in Sect. 4. Finally, simulations and experimental results verify the correctness of the modeling and also confirm the feasibility of the proposed approach in Sect. 5. Some conclusions are given out in Sect. 6.

2 Equivalent coupling modeling of multiple-parallel inverters

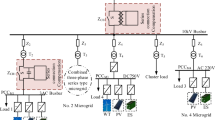
Figure 1 shows the power stage and control diagram of multiple-parallel inverters in the microgrid operating in grid-connected mode. Each DG unit consists of several photovoltaic panels, a DC/DC boost converter, an H-bridge inverter, and a LCL filter.

Fig. 1
figure 1

Power stage and control diagram of a cluster of photovoltaic inverters

Full size image

Subscript n is the n th inverter; Superscript * is the reference of a signal; u dc is the DC link voltage; u inv is the inverter output voltage; R 1, R 2 are the inverter-side and grid-side equivalent resistances of the filter; Cf is the filter capacitor; L 1, L 2 are the inverter-side and grid-side inductors of filter; i 1, i 2, i c are the inverter-side current, grid-side inductor current, and filter-capacitor current, respectively; i ref is the inverter reference current; u pcc is the point of common coupling (PCC) voltage; u g is the grid voltage; i g is the grid current; R g, L g are the equivalent resistance and inductance of the grid.

To simplify the analysis, the photovoltaic panel and its DC/DC boost converter can be regarded as a DC voltage source. The block of reference current calculation in Fig. 1, is used to obtain i ref. For the interested reader, further discussion on how to obtain the value of i ref can be found in [8, 9], and will not be repeated in this paper.

Figure 2 shows the block diagram of current control and active damping from Fig. 1. The control structure consists of grid-side-current outer loop and filter-capacitor-current inner feedback. K pwm is the inverter switch gain and K pwm = u dc/u tri, where u tri is the amplitude of triangular carrier. To enhance the control accuracy, as well as improve attenuation ability of low-order harmonics, the proportional resonant (PR) controller takes account of the fundamental, 3rd, 5th, 7th, 9th, and 11th harmonic currents. The objective of the inner feedback loop is to guarantee the active damping effect on the inherent resonance of the filter, and K C is the coefficient of damping feedback.

Fig. 2
figure 2

Block diagram of current control and active damping

Full size image

The Norton equivalent model of inverter control system can be deduced from Fig. 1, and expressed as

$$I_{2} \left( s \right) = G_{\rm cs} (s)I_{\rm ref} \left( s \right) - Y_{\rm cs} U_{\rm pcc} \left( s \right)$$
(1)

where G cs(s) and Y cs(s) are the equivalent current source coefficient and equivalent admittance, and expressed as follows.

$$\frac{{I_{2} \left( s \right)}}{{I_{\rm ref} \left( s \right)}} = G_{\rm cs} \left( s \right) = \frac{{K_{\rm PWM} G_{\rm PR} G_{1} G_{\rm c} G_{2} }}{{1 + H_{\rm d} G_{\rm c} + G_{1} G_{\rm c} + G_{\rm c} G_{2} + K_{\rm PWM} G_{\rm PR} G_{1} G_{\rm c} G_{2} }}$$
(2)
$$\frac{{I_{2} \left( s \right)}}{{U_{\rm pcc} \left( s \right)}} = Y_{\rm cs} \left( s \right) = - \frac{{G_{2} + H_{\rm d} G_{\rm c} G_{2} + G_{1} G_{\rm c} G_{2} }}{{1 + H_{\rm d} G_{\rm c} + G_{1} G_{\rm c} + G_{\rm c} G_{2} + K_{\rm PWM} G_{\rm PR} G_{1} G_{\rm c} G_{2} }}$$
(3)

where H d = K PWM K C C f/L 1; G 1 = 1/(sL 1+R 1); G c = 1/sC f; G 2 = 1/(sL 2 + R 2); G PR is the transfer function of PR controller, and expressed as

$$G_{\rm PR} = K_{p} + \sum\limits_{h = 1,3,5,7,9,11} {\frac{{2k_{\rm i,h} \omega_{\rm c} s}}{{s^{2} + 2\omega_{\rm c} s + h^{2} \omega_{\rm n}^{2} }}}$$
(4)

where K p and k i,h are the proportional and the h th resonant gains of the PR controller; ω c is the cut-off frequency; ω n is the fundamental frequency; h is the harmonic order.

Figure 3 shows the equivalent circuit of multi-parallel inverters. Y g is the grid equivalent admittance.

Fig. 3
figure 3

Equivalent circuit of multi-parallel inverters in microgrid operating in grid-connected mode

Full size image

The voltage equation associated with the node of U pcc in Fig. 3 can be written as

$$\left( {Y_{\rm cs,1} + \cdots + Y_{\rm cs,n} } \right)U_{\rm pcc} + Y_{\rm g} U_{\rm pcc} = \left( {G_{\rm cs,1} I_{\rm ref,1} + \cdots + G_{\rm cs,n} I_{\rm ref,n} } \right) + Y_{\rm g} U_{\rm g}$$
(5)

As far as the m th inverter (1≤m≤n) is considered, (1) can be rewritten as

$$I_{2,m} \left( s \right) = G_{{\rm cs},m} (s)I_{{\rm ref},m} \left( s \right) - Y_{{\rm cs},m} U_{\rm pcc} \left( s \right)$$
(6)

By substituting (6) into (5), I 2,m can be explained as

$$I_{2,m} = \varPhi_{{\rm ind},m} I_{{\rm ref},m} - \sum\limits_{i = 1,\;i \ne m}^{n} {\varPhi_{{\rm para},m,i} I_{{\rm ref},i} } - \varPhi_{{\rm series},m} U_{g}$$
(7)

where the subscripts i and m are the i th and m th inverter; Φind,m is the relationship between I 2,m and I ref,m ; Φpara,m,i is the relationship between I 2,m and I ref,i ; Φseries,m is the relationship between I 2,m and U g.

$$\begin{aligned} \varPhi_{{\rm ind},}m = &\, \frac{{K_{{\rm PWM},m} G_{{\rm PR},m} G_{1,m} G_{{\rm c},m} G_{2,m} }}{{1 + H_{{\rm d},m} G_{{\rm c},m} + G_{1,m} G_{{\rm c},m} + G_{{\rm c},m} G_{2,m} + K_{{\rm PWM},m} G_{{\rm PR},m} G_{1,m} G_{{\rm c},m} G_{2,m} }} \bullet \\ & \sum\limits_{i = 1}^{n} {\left( \begin{aligned} 1 - \frac{{1 + H_{{\rm d},i} G_{{\rm c},i} + G_{1,i} G_{{\rm c},i} + G_{{\rm c},i} G_{2,i} + K_{{\rm PWM},i} G_{{\rm PR},i} G_{1,i} G_{{\rm c},i} G_{2,i} }}{{G_{2,i} + H_{{\rm d},i} G_{{\rm c},i} G_{2,i} + G_{1,i} G_{{\rm c},i} G_{2,i} + Y_{\rm g} \left( {1 + H_{{\rm d},i} G_{{\rm c},i} + G_{1,i} G_{{\rm c},i} + G_{{\rm c},i} G_{2,i} + K_{{\rm PWM},i} G_{{\rm PR},i} G_{1,i} G_{{\rm c},i} G_{2,i} } \right)}} \bullet \hfill \\ \frac{{G_{2,m} + H_{d,m} G_{c,m} G_{2,m} + G_{1,m} G_{c,m} G_{2,m} }}{{1 + H_{{\rm d},m} G_{{\rm c},m} + G_{1,m} G_{{\rm c},m} + G_{{\rm c},m} G_{2,m} + K_{{\rm PWM},m} G_{{\rm PR},m} G_{1,m} G_{{\rm c},m} G_{2,m} }} \hfill \\ \end{aligned} \right)} \\ \end{aligned}$$
$$\begin{aligned} \varPhi_{{\rm para},m,i} = \frac{{\frac{{G_{2,m} + H_{{\rm d},m} G_{{\rm c},m} G_{2,m} + G_{1,m} G_{{\rm c},m} G_{2,m} }}{{1 + H_{{\rm d},m} G_{{\rm c},m} + G_{1,m} G_{{\rm c},m} + G_{{\rm c},m} G_{2,m} + K_{{\rm PWM},m} G_{{\rm PR},m} G_{1,m} G_{{\rm c},m} G_{2,m} }}}}{{\sum\limits_{i = 1}^{n} {\frac{{G_{2,i} + H_{{\rm d},i} G_{{\rm c},i} G_{2,i} + G_{1,i} G_{{\rm c},i} G_{2,i} + Y_{g} \left( {1 + H_{{\rm d},i} G_{{\rm c},i} + G_{1,i} G_{{\rm c},i} + G_{{\rm c},i} G_{2,i} + K_{{\rm PWM},i} G_{{\rm PR},i} G_{1,i} G_{{\rm c},i} G_{2,i} } \right)}}{{\left( {1 + H_{{\rm d},i} G_{{\rm c},i} + G_{1,i} G_{{\rm c},i} + G_{{\rm c},i} G_{2,i} + K_{{\rm PWM},i} G_{{\rm PR},i} G_{1,i} G_{{\rm c},i} G_{2,i} } \right)}}} }} \bullet \\ \sum\limits_{i = 1,\;i \ne m}^{n} {\frac{{K_{{\rm PWM},i} G_{{\rm PR},i} G_{1,i} G_{{\rm c},i} G_{2,i} }}{{1 + H_{{\rm d},i} G_{{\rm c},i} + G_{1,i} G_{{\rm c},i} + G_{{\rm c},i} G_{2,i} + K_{{\rm PWM},i} G_{{\rm PR},i} G_{1,i} G_{{\rm c},i} G_{2,i} }}I_{{\rm ref},i} } \\ \end{aligned}$$
$$\begin{aligned} \varPhi_{{\rm series},m} =&\, \frac{{G_{2,m} + H_{{\rm d},m} G_{{\rm c},m} G_{2,m} + G_{1,m} G_{{\rm c},m} G_{2,m} }}{{1 + H_{{\rm d},m} G_{{\rm c},m} + G_{1,m} G_{{\rm c},m} + G_{{\rm c},m} G_{2,m} + K_{{\rm PWM},m} G_{{\rm PR},m} G_{1,m} G_{{\rm c},m} G_{2,m} }} \bullet \\& \sum\limits_{i = 1}^{\rm n} {\frac{{Y_{\rm g} \left( {1 + H_{{\rm} d,i} G_{{\rm c},i} + G_{1,i} G_{{\rm c},i} + G_{{\rm c},i} G_{2,i} + K_{{\rm PWM},i} G_{{\rm PR},i} G_{1,i} G_{{\rm c},i} G_{2,i} } \right)}}{{G_{2,i} + H_{{\rm d},i} G_{{\rm c},i} G_{2,i} + G_{1,i} G_{{\rm c},i} G_{2,i} + Y_{\rm g} \left( {1 + H_{{\rm d},i} G_{{\rm c},i} + G_{1,i} G_{{\rm c},i} + G_{{\rm c},i} G_{2,i} + K_{{\rm PWM},i} G_{{\rm PR},i} G_{1,i} G_{{\rm c},i} G_{2,i} } \right)}}} \\ \end{aligned}$$

Seen from (7), three factors impact directly grid-side current of an inverter, including ➀ its own inverter reference current; ➁ the reference currents of other inverters; ➂ the grid voltage.

Figure 4 shows the equivalent coupling circuit of multi-parallel inverters.

Fig. 4
figure 4

Equivalent coupling circuit of multi-parallel inverters in microgrid operating in grid-connected mode

Full size image

Taking I 2,1 for example, Fig. 4 indicates that I 2,1 is produced by the currents superposition from n+1 branches, i.e., ➀ Φind,1 I ref,1; ➁ Φpara,m,i I ref,i (i = 2,3,…,n); ➂ Φseries,1.

3 Analysis and distributions of coupling resonance peaks considering three factors impact

It is reasonable to suppose that each DG unit is equivalent. Therefore, the elements in (7) can be expressed as reduced-order forms, and rewritten as

$$\begin{aligned} \varPhi_{{{\text{ind,}}m}} & = \frac{{K_{{{\text{PWM,}}m}} G_{{{\text{PR,}}m}} G_{1,m} G_{{{\text{c}},m}} G_{2,m} }}{{1 + H_{{{\text{d}},m}} G_{{{\text{c}},m}} + G_{1,m} G_{{{\text{c}},m}} + G_{{{\text{c}},m}} G_{2,m} + K_{{{\text{PWM,}}m}} G_{{{\text{PR,}}m}} G_{1,m} G_{\text{c,m}} G_{2,m} }} \bullet \\ & \left( {n - \frac{{n(G_{2,m} + H_{{{\text{d}},m}} G_{\text{c,m}} G_{2,m} + G_{1,m} G_{{{\text{c}},m}} G_{2,m} )}}{{(G_{2,m} + H_{{{\text{d}},m}} G_{{{\text{c}},m}} G_{2,m} + G_{1,m} G_{{{\text{c}},m}} G_{2,m} + Y_{\text{g}} (1 + H_{{{\text{d}},m}} G_{{{\text{c}},m}} + G_{1,m} G_{{{\text{c}},m}} + G_{{{\text{c}},m}} G_{2,m} + K_{{{\text{PWM}},m}} G_{{{\text{PR,}}m}} G_{1,m} G_{{{\text{c}},m}} G_{2,m} ))}}} \right) \\ \end{aligned}$$
(8)
$$\begin{aligned} \varPhi_{{{\text{para,}}m ,i}} & = \frac{{G_{2,m} + H_{{{\text{d}},m}} G_{{{\text{c}},m}} G_{2,m} + G_{1,m} G_{{{\text{c}},m}} G_{2,m} }}{{1 + H_{{{\text{d}},m}} G_{{{\text{c}},m}} + G_{1,m} G_{{{\text{c}},m}} + G_{{{\text{c}},m}} G_{2,m} + K_{{{\text{PWM,}}m}} G_{{{\text{PR}},m}} G_{1,m} G_{\text{c,m}} G_{2,m} }} \bullet \\ & \frac{{K_{{{\text{PWM,}}i}} G_{{{\text{PR}},i}} G_{1,i} G_{{{\text{c}},i}} G_{2,i} }}{{G_{2,i} + H_{{{\text{d}},i}} G_{{{\text{c}},i}} G_{2,i} + G_{1,i} G_{{{\text{c}},i}} G_{2,i} + Y_{\text{g}} (1 + H_{{{\text{d}},i}} G_{{{\text{c}},i}} + G_{1,i} G_{{{\text{c}},i}} + G_{{{\text{c}},i}} G_{2,i} + K_{{{\text{PWM,}}i}} G_{{{\text{PR}},i}} G_{1,i} G_{{{\text{c}},i}} G_{2,i} )}}\,{I_{{\rm ref},i}} \\ \end{aligned}$$
(9)
$$\varPhi_{{\rm series},m} = \frac{{n\left( {G_{2,m} + H_{{\rm d},m} G_{{\rm c},m} G_{2,m} + G_{1,m} G_{{\rm c},m} G_{2,m} } \right)Y_{\rm g} }}{{G_{2,i} + H_{{\rm d},i} G_{{\rm c},i} G_{2,i} + G_{1,i} G_{{\rm c},i} G_{2,i} + Y_{\rm g} \left( {1 + H_{{\rm d},i} G_{{\rm c},i} + G_{1,i} G_{{\rm c},i} + G_{{\rm c},i} G_{2,i} + K_{{\rm PWM},i} G_{{\rm PR},i} G_{1,i} G_{{\rm c},i} G_{2,i} } \right)}}$$
(10)

3.1 Mathematical approach to describe resonance peaks

According to the simulation parameters listed in Table 1, the inherent resonance peak of the filter is around 35th harmonic frequency. The frequency interval chooses within (0, 40ω n].

Table 1 Simulating and experimental parameters of multi-parallel inverters
Full size table

The mathematical approach to search the peak frequencies of the resonances among multi-parallel inverters can be described as finding the local maxima of the functions Φind(jω), Φpara(jω), and Φseries(jω).

According to the first derivative test in calculus, the precise statement of a resonance peak in a specific frequency domain can be described as: Suppose a transfer function Φ(jω) defined on the left-open-right-closed interval of (0, 40ω n]; Further suppose that Φ(jω) is continuous at ω R and differentiable on some open interval containing ω R, except possibly at ω R itself; If there exist a positive number Δω such that for every ω in (ω R -Δω,ω R] we have d|Φ(jω)|/dω≥0, and for every ω in [ω R, ω R+Δω) we have d|Φ(jω)|/dω ≤ 0, then Φ(jω) has a local maximum at ω R. In other words, ω R is a resonance frequency which cause the amplitude-frequency response of Φ(jω) to reach its peak. In addition, according to (7), the resonance phenomena caused by Φind,m , Φseries,m , and Φpara,m,i are individual, parallel, and series resonances, respectively.

Further, supposing that each inverter is equivalent, the value of d|Φind(jω)|/dω, d|Φpara(jω)|/dω, and d|Φseries(jω)|/dω in the frequency domain of (ω n, 40ω n), along with the variation in the number of parallel inverters are depicted in Fig. 5. Obviously, a local maximum of Φ(jω) locates at the position where d|Φ(jω)|/dω drastically switches from a positive to a negative value. The ω R (the harmonic order multiplying by ω n) and n (number of inverters) associated with this local maximum are indicated that the n sets of parallel inverters will have a resonance peak around ω R.

Fig. 5
figure 5

Distribution of resonance peaks

Full size image

Within the frequency interval of [12ω n, 40ω n], if the number of inverters is a constant, the values of d|Φind(jω)|/dω, d|Φpara(jω)|/dω and d|Φseries(jω)|/dω occur 2, 2, and 1 times signum changes, respectively. It indicates that |Φind(jω)|, |Φpara(jω)| and |Φseries(jω)| have 2, 2, and 1 maxima within this frequency interval, respectively. This also indicates that Φind(jω), Φpara(jω), and Φseries(jω) have 2, 2, 1 intrinsic resonance peaks, respectively.

Within the frequency interval of (0, 12ω n), d|Φind(jω)|/dω, d|Φpara(jω)|/dω, and d|Φseries(jω)|/dω obviously occur 6, 6, 1 times sign changes, respectively. It indicates that 6, 6, 1 extrinsic resonance peaks exist in Φind(jω), Φpara(jω), and Φseries(jω) respectively. It should be emphasized that the extrinsic resonances is caused by the outer-loop PR controller which exerts resonance effect on the multi-parallel inverters around the selected frequencies. On the contrary, the intrinsic resonance peaks within the interval of [12ω n, 40ω n] are caused by the coupling effect of the inverter equivalent output impedances. Thus, the intrinsic resonances inherently exist in multi-parallel inverters system, for any current control schemes. To some extent, the analysis of the intrinsic resonance phenomena possesses universal significance, being also one of the focuses of the rest of the paper.

3.2 Distribution of resonance peaks

According to Fig. 5, the frequency distribution of intrinsic resonance peaks for different number of parallel inverters is listed in Table 2. If a single inverter is connected to the grid, the harmonics in u g and i 2 around 1280 Hz will be largely magnified. Furthermore, the individual and series resonance peaks around 1280 Hz will move toward lower frequency domain along with the increasing in the number of parallel inverters. These moving resonance peaks can be defined as non-fixed peaks. Besides, an additionally fixed individual resonance peak around 1740 Hz appears when we have more than one inverter. Further, parallel resonances with a fixed peak and a non-fixed peak only appear in case of multiple-parallel inverters, which present the same frequency distribution as the individual resonance. Series resonances have not fixed peaks.

Table 2 Frequency distribution of intrinsic resonance peaks along with different number of parallel inverters
Full size table

From (7) and Table 2, it can be concluded that the amount of intrinsic resonance peaks of Φind,m (jω), Φpara,m,i (jω), and Φseries,m (jω) of the m th inverter in case of n (n≥2) parallel inverters is 2, 2(n-1), and 1, respectively. Supposing that each inverter is equivalent, the resonance amplitudes of Φind,m (jω), Φpara,m,i (jω), and Φseries,m (jω) in the frequency domain of (ω n, 40ω n) along with the inverters of (1, 20) is depicted in Fig. 6. The simulation parameters are listed in Table 1.

Fig. 6
figure 6

Resonance amplitudes

Full size image

From Fig. 6a and b, a fixed intrinsic peak emerges in both the individual resonance and the parallel resonance around 35th harmonic frequency (1740 Hz). Note that when increasing in the number of inverters, the amplitude of the individual resonance increases, but, by contrast, the parallel resonance decreases. Besides, when the number of inverters increases, the variation of the non-fixed intrinsic peaks in frequency and amplitude for the three kinds of resonances are summarized as follows: the amplitudes of the non-fixed intrinsic peaks decrease, while the peak frequencies are moving towards low-frequency domain, as shown in Fig. 6. Notice that only non-fixed peak exists in series resonance.

4 Active damping control design and damping coefficient optimization

4.1 Active damping control loop design

The inner active damping loop introducing the feedback of filter-capacitor current is to emulate a virtual resistance connecting in parallel with the filter capacitor. In order to quantify this physical equivalence, the block diagram from Fig. 3 can be equivalently modified by substituting the bold-line feedback for a dashed-line feedback, as shown in Fig. 7. The feedback coefficient H d is equal to K PWM K C C f/L 1 when R 1 is neglected.

Fig. 7
figure 7

Equivalent control block of filter-capacitor current feedback loop

Full size image

The inner loop, which is composed by H d and 1/sC f, in Fig. 7 can be simplified as

$$G_{d} = \frac{{\frac{1}{{sC_{\rm f} }}}}{{1 + \frac{{K_{\rm PWM} K_{\rm C} }}{{sL_{1} }}}} = \frac{{\frac{1}{{sC_{\rm f} }}\frac{{L_{1} }}{{K_{\rm PWM} K_{\rm C} C_{\rm f} }}}}{{\frac{1}{{sC_{\rm f} }} + \frac{{L_{1} }}{{K_{\rm PWM} K_{C} C_{\rm f} }}}} = \frac{1}{{sC_{\rm f} }}//\frac{{L_{1} }}{{K_{\rm PWM} K_{\rm C} C_{\rm f} }}$$
(11)

which indicates that the equivalent effect of the active damping loop is to add a virtual resistance equal to L 1/(K PWM K C C f) connecting in parallel with C f. From the frequency response viewpoint, a virtual resistance connecting in parallel with the filter capacitor is considered as a good damping method. The reason is that it has the ability to damp the resonance peak without deteriorating the filter dynamic in low or high frequency domains.

4.2 Chosen an optimal coefficient of damping feedback

Then, an intuitive approach to choose an optimal coefficient of damping feedback K C is proposed. Taking two parallel inverters for example, Fig. 8 shows the amplitude-frequency responses of Φind,1, Φpara,1,2, and Φseries,1 of the 1st inverter in the frequency domain of (ω n, 40ω n) along with the growth in value of K C,1 from 0 to 40. The simulation parameters are listed in the Table 1. As shown in Fig. 8, the most prominent coupling resonance phenomena will occur in two-parallel-inverter system (worst case).

Fig. 8
figure 8

Amplitude-frequency responses

Full size image

According to (11), if K C,1 = 0, the virtual resistance tends to be infinite, which means that the damping effect is in vain. In this case, the most severe intrinsic peaks will appear in the individual, parallel, and series resonances, as shown in Fig. 8. The amplitudes of Φind,1 around the 21st and 35th harmonic frequencies are about 79% and 130%, respectively; the amplitudes of Φpara,1,2 around 21st and 35th harmonic frequencies are about 68% and 129%, respectively; and the amplitude of Φseries,1 around the 21st harmonic frequency is about 96%.

With the growth in value of K C,1, the amplitudes of intrinsic resonance peaks are drastically decreased. If the value of K C,1 increases up to 25.1, all the peak amplitudes of intrinsic resonances reduce to 6% or less, as listed in Table 3.

Table 3 Resonance peak amplitudes of two-parallel-inverter system when K C,1 = 25.1
Full size table

If the value of K C,1 continues increasing (K C,1>25.1), the attenuation of intrinsic resonance peaks around 21st and 35th harmonic frequencies tends to be moderate. Meanwhile, the peak amplitude of Φseries,1 around 13th harmonic frequency gently increases. Further, if K C,1 increases up to 39.6, the amplitude will slightly raise up to 8.6 %. The variation of K C,1 has less influence over the peak amplitudes of the extrinsic resonances, which is a result of the decoupling control effect between the outer-loop PR controller and the inner-loop feedback.

Based on foregoing analysis, K C = 25.1 is the optimal choice for each single inverter in order to fulfill the demand frequency-domain responses.

5 Simulations and experiments

To verify effectiveness of the proposed modeling and method, several cases including 2, 3, and 6 inverters are simulated by MATLAB simulation. To confirm the feasibility of the damping parameter optimization, all the simulation cases are comparatively conducted under two conditions: K C = 1 and K C = 25.1. The rated power of each inverter is 2 kW. The power stage and control parameters are listed in Table 1.

5.1 Individual resonance

In order to show the movement of the individual resonance peak in frequency domain along with the variation in the number of inverters, the cases of 2, 3, and 6 parallel inverters are considered. When the amplitude of the 1st inverter reference current i ref,1 achieves 12 A from 6 A at 0.405 s, the transient waveforms of the 1st inverter’s grid-side current i 2,1 and its frequency spectrum with K C = 1 are depicted in Fig. 9.

Fig. 9
figure 9

Simulation waveforms of the 1st inverter grid-side current and its frequency spectrum during the transient of its amplitude of reference current (K C = 1)

Full size image

There are two individual resonance peaks (a fixed and an unfixed) exist in the case of 2, 3, and 6 parallel inverters, as shown in Fig. 9a–c, and their unfixed peaks are around 22nd (1120 Hz), 20th (1030 Hz), and 18th (901 Hz) harmonic frequency, respectively. Their fixed peaks are permanently located around 35th (1740 Hz) harmonic frequency. The peak movements of the individual resonances shown in Fig. 9 are consistent with the resonance frequencies listed in the Table 2.

Under the condition of K C = 25.1, the 1st inverter grid-side currents i ref,1 during the transient of its amplitude of reference current suddenly changing from 6 A to 12 A at 0.405 s, are depicted in Fig. 10. Compared with the case of K C = 1, the 1st inverter grid-side current i ref,1 depicted in Fig. 10 apparently presents less current distortion associated with high-frequency harmonic during the transient. In other words, the case of K C = 25.1 presents better damping effect.

Fig. 10
figure 10

Simulation waveforms of 1st inverter grid-side current during its amplitude of reference current (K C = 25.1)

Full size image

5.2 Parallel resonance

To show the peak movements of the paralle

l resonance in the frequency domain when the number of inverters change, the cases of 2, 3, and 6 parallel inverters are investigated, respectively. These cases are simulated under the condition of K C = 1. When the amplitude of the 2nd inverter reference current i ref,2 suddenly changes from 6 A to 12 A at 0.405 s, the transient waveforms of the 1st inverter’s grid-side current i ref,1 and its frequency spectrum are depicted in Fig. 11.

Fig. 11
figure 11

Simulation waveforms of the 1st inverter grid-side current and its harmonic spectrum during the transient of the amplitude of the 2nd inverter reference current (K C = 1)

Full size image

Two parallel resonance peaks including a fixed and an unfixed ones exist in the cases of 2, 3, 6 parallel inverters, as shown in Fig. 11a–c. And the unfixed peaks are around 22nd (1120 Hz), 20th (1030 Hz), and 18th (901 Hz) harmonic frequency, respectively. The fixed peaks are permanently located around 35th (1740 Hz) harmonic frequency.

Under the condition of K C = 25.1, the 1st inverter’s grid-side currents i ref,1 during the transient of the amplitude of the 2nd inverter reference current i ref,2 changing from 6 A to 12 A at 0.405 s are depicted in Fig. 12. Compared with the case of K C = 1, the 1st inverter’s grid-side current i ref,1 is hardly influenced during the transient. This decoupling effect is going to enhance with the growth in number of parallel inverters. As shown in Fig. 12, the high-frequency ripples during the transient are going to decrease with the growth in the number of parallel inverters.

Fig. 12
figure 12

Simulation waveforms of the 1st inverter grid-side current during the transient of the amplitude of the 2nd inverter reference current (K C = 25.1)

Full size image

5.3 Series resonance

The output currents of inverters are subjected to fluctuations of power generation, e.g. solar irradiance in case of photovoltaic panels. In order to simulate the practical condition of a parallel system that consists of 6 inverters, the amplitudes of the 1st to the 6th inverter reference currents are 6, 6, 8, 7, 5, 8 A, respectively. A local weak grid containing 0.32% of 21st background harmonic voltage is also simulated.

To simulate the transient of several inverters shutting down by sudden changing the local irradiance, the parallel system operates in the following time sequence: before 0.4 s, 6 inverters operate in parallel; next, the 4th to 6th inverters are shut down at 0.4 s; then, the 3rd inverter is shut-down at 0.44 s; finally, the 2nd inverter is shut-down at 0.48 s, meanwhile, only the 1st inverter is still operating.

The cases are simulated under the condition of K C = 1. The 1st inverter’s grid-side current i ref,1 and its frequency spectrum during the transient are depicted in Fig. 13. According to Table 2, the series resonance peaks in the cases of a single inverter and 2, 3, and 6 parallel inverters are around 1280, 1120, 1030, 901 Hz, respectively. Although, the 1st inverter does connect to the grid during the whole transient period, the high-frequency ripple of its grid-side current i 2,1 occurs significant variation along with the aforementioned time sequence. The reason for this ripple variation is that the peak frequency of series resonance moves toward a higher frequency domain when the number of operating inverters decreases, as shown in Figs. 13. Due to the series resonance peak of 2 parallel inverters around 23rd harmonic frequency, the 21st background harmonic voltage dramatically distorts the 1st inverter’s grid-side current i 2,1 and its THD is up to 19.64%.

Fig. 13
figure 13

Simulation waveforms of the 1st inverter grid-side current and its frequency spectrum during the transient of other inverters shutting down in the time sequence (K C = 1)

Full size image

Figure 14 shows the 1st inverter’s grid-side current i ref,1 during the transient of other inverters shutting down in the same time sequence. Compared with K C = 1, the 1st inverter’s grid-side current i 2,1 is hardly influenced during the transient. Moreover, in this case the grid background harmonic voltage has less influence on the 1st inverter’s grid-side current i ref,1.

Fig. 14
figure 14

Simulated waveform of the 1st inverter grid-side current during the transient of other inverters shutting down in the time sequence (K C = 25.1)

Full size image

5.4 Experimental verification

A prototype of three-parallel-inverter system is built. The rated power of each single-phase inverter is 2 kW. The switching frequency is 12.8 kHz. The grid currents of 3 parallel inverters flow to the grid. The two cases (K C = 5 and K C = 25.1) are comparatively investigated and the parameters are same as in the simulation (see Table 1).

When the amplitude of the 1st inverter’s grid-side current suddenly changes from 6 A to 12 A, the experimental waveforms of the 1st and 2nd inverters’ grid currents and grid voltage, and the frequency spectrum diagrams of the 2nd inverter grid-side current are shown in Fig. 15. In case of K C=5, the two inverters’ grid-side currents apparently contain high-frequency ripples, which significantly increase after the transient. The 2nd inverter’s grid-side current presents severe disturbances at the PCC point where the amplitude of the 1st inverter’s grid-side current step change occurs. The THD of the 2nd inverters’ grid-side current is up to 9.2% after the transient. On the contrary, in case of K C = 25.1, the high-frequency ripples drastically decrease before and during the transient. The 2nd inverter’s grid-side current presents little disturbances caused by the step change of the amplitude of the 1st inverter’s grid-side current. The THD of the 2nd inverters’ grid-side current is only 3.9% after the transient.

Fig. 15
figure 15

Experimental waveforms during the transient of the amplitude of the 1st inverter reference current

Full size image

When the 1st inverter is disconnected, the 1st and 2nd inverter grid-side current and grid voltages during the transient are depicted in Fig. 16. In the case of K C = 5, the 2nd inverter grid-side current contains apparent high-frequency ripples after the 1st inverter shutting down. The current ripples are caused by the grid background harmonic voltage. On the contrary, in the case of K C = 25.1, the transient of the 1st inverter’s shutting down presents less influence over the 2nd inverter grid-side current.

Fig. 16
figure 16

Experimental waveforms during the transient of the 1st inverter shutting down

Full size image

6 Conclusions

The resonances in multi-parallel inverters in microgrid operating in grid-connected mode can be classified into two types: intrinsic resonance and extrinsic resonance. The former exists permanently in the parallel-inverters system, independently from the chosen controller. On the contrary, the extrinsic resonance is caused by the different control modes of the inverters. And the distributions of intrinsic resonances along with the growth in the number of inverters have been explicitly investigated by using mathematical approach. The equivalent coupling circuit of multi-parallel inverters which can explain the coupling resonance phenomena among parallel inverters has been figured out. Besides, the intuitive way to choose an optimal damping parameter has been proposed in this paper, which can easily locate the optimal range of the control parameter. Simulations and experimental results have been performed in order to validate the proposed model and control approaches. The approach is useful to mitigate coupling resonances in multi-parallel inverters in microgrid operating in grid-connected mode.