Abstract
A deterministic inventory model with two levels of storage (own warehouse and rented warehouse) with non-instantaneous deteriorating items is studied. The supplier offers the retailer a trade credit period to settle the amount. Different scenarios based on the deterioration and the trade credit period have been considered. In this article, we have framed two models considering single warehouse (Model-I) and two warehouses (Model-II) for non-instantaneous deteriorating items. The objective of this work is to minimize the total inventory cost and to find the optimal length of replenishment and the optimal order quantity. Mathematical theorems have been developed to determine the existence and the uniqueness of the optimal solution. Computational algorithms for the two different models are designed to find the optimal order quantity and the optimal cycle time. Comparison between the optimal solutions for the two models is also given. Numerical illustrations and managerial insights obtained demonstrate the application and the performance of the proposed theory.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Deterioration plays an essential role in many inventory systems. Deterioration is defined as decay, damage, obsolescence, evaporation, spoilage, loss of utility, or loss of marginal value of a commodity which decreases the original quality of the product. Many researchers such as Ghare and Schrader (1963), Philip (1974), Goyal and Giri (2001), Li and Mao (2009), Geetha and Udayakumar (2015) and Mahata (2015) assume that the deterioration of the items in inventory starts from the instant of their arrival.
However, most of the goods such as medicine, volatile liquids, and blood banks, undergo decay or deterioration over time. Wu et al. (2006) defined the term “non-instantaneous” for such deteriorating items. He gave an optimal replenishment policy for non-instantaneous deteriorating items with stock-dependent demand and partial backlogging. In this direction, researchers have developed their inventory model for a single warehouse which has unlimited capacity. This assumption is not applicable in real-life situation. When an attractive price discount for bulk purchase is available, the management decides to purchase a huge quantity of items at a time. These goods cannot be stored in the existing storage (the owned warehouse with limited capacity). However, to take advantage, it may be profitable for the retailer to hire another storage facility called the rented warehouse. Units are continuously transferred from rented warehouse to owned and sold from owned warehouse. Usually, the holding cost in rented warehouse is higher than that in owned warehouse, due to the non-availability of better preserving facility which results in higher deterioration rate. Hence to reduce the holding cost, it is more economical to consume the goods of rented warehouse at the earliest.
Trade credit is an essential tool for financing growth for many businesses. The number of days for which a credit is given is determined by the company allowing the credit and is agreed on by both the company allowing the credit and the company receiving it. By payment extension date, the company receiving the credit essentially could sell the goods and use the credited amount to pay back the debt. To encourage sales, such a credit is given. During this credit period, the retailer can accumulate and earn interest on the encouraged sales revenue. In case of an extension period, the supplier charges interest on the unpaid balance. Hence, the permissible delay period indirectly reduces the cost of holding cost. In addition, trade credit offered by the supplier encourages the retailer to buy more products. Hence, the trade credit plays a major role in inventory control for both the supplier as well as the retailer. Goyal (1985) developed an EOQ model under the condition of a permissible delay in payments. Aggarwal and Jaggi (1995) then extended Goyal’s model to allow for deteriorating items under permissible delay in payments. Uthayakumar and Geetha (2009) developed a replenishment policy for non-instantaneous deteriorating inventory system with partial backlogging.
In this direction, we have formulated a model for non-instantaneous deteriorating items with two levels of storage and the supplier offers the retailer a trade credit period to settle the amount. The rest of this paper is organized as follows. Literature review carried is given in the “Literature review”. The assumptions and notations which are used throughout the article are presented in “Problem description”. In “Model formulation”, mathematical model to minimize the total cost is formulated and the solution methodology comprising some useful theoretical results to find the optimal solution is given. Computational algorithm is designed to obtain the optimal values in the “Algorithm”. “Numerical examples” is provided to illustrate the theory and the solution procedure. Following this, sensitivity analysis for the major parameters of the inventory system has been analyzed and the comparison between the two models is studied in “Comparative study of the results between the two models”. Managerial implications with respect to the sensitivity analysis were given in “Managerial implication”. Finally, we draw a conclusion in “Conclusion”.
Literature review
During the last few decades, a number of research papers in the inventory area for deteriorating items have been published by several researchers. Mukhopadhyay et al. (2004) considered joint pricing and ordering policy for a deteriorating inventory. Malik and Singh (2011) developed an inventory model for deteriorating items with soft-computing techniques and variable demand. Taleizadeh (2014b) developed an economic-order quantity model with partial backordering and advance payments for an evaporating item. Taleizadeh and Nematollahi (2014) established an inventory control problem for deteriorating items with backordering and financial considerations. Taleizadeh (2014a) developed an economic-order quantity model for deteriorating item in a purchasing system with multiple prepayments. Taleizadeh et al. (2015) gave a joint optimization of price, replenishment frequency, replenishment cycle, and production rate in vendor-managed inventory system with deteriorating items. Tavakoli and Taleizadeh (2017) gave a lot sizing model for decaying item with full advance payment from the buyer and conditional discount from the supplier.
Ouyang et al. (2006) derived an inventory model for non-instantaneous deteriorating items with permissible delay in payments. Liao (2008) discussed an EOQ model with non-instantaneous receipt and exponentially deteriorating items under two-level trade credits. Maihami and Kamal Abadi (2012) gave a joint control of inventory and it is pricing for non-instantaneously deteriorating items under permissible delay in payments and partial backlogging. Soni (2013) established an optimal replenishment policy for non-instantaneous deteriorating items with price and stock-sensitive demand under permissible delay in payment. Tat et al. (2013) developed and EOQ model with non-instantaneous deteriorating items in vendor-managed inventory system. Udayakumar and Geetha (2014) gave an optimal replenishment policy for non-instantaneous deteriorating items with inflation-induced time-dependent demand. Maihami and Karimi (2014) developed pricing and replenishment policy for non-instantaneous deteriorating items with stochastic demand and promotional efforts. Geetha and Udayakumar (2016) developed an optimal lot sizing policy for non-instantaneous deteriorating items with price and advertisement-dependent demand under partial backlogging. Wu et al. (2014) gave a note on optimal replenishment policies for non-instantaneous deteriorating items with price and stock-sensitive demand under permissible delay in payment. Zia and Taleizadeh (2015) gave a lot sizing model with backordering under hybrid linked to order multiple advance payments and delayed payment. Udayakumar and Geetha (2016) developed an economic-ordering policy for non-instantaneous deteriorating items over finite-time horizon. Taleizadeh et al. (2016) developed an imperfect economic production quantity model with up-stream trade credit periods linked to raw material-order quantity and downstream trade credit periods. Heydari et al. (2017) discussed a two-level day in payments contract for supply chain coordination in the case of credit-dependent demand.
In existing literature, Sarma (1987) was the first to develop a deterministic inventory model with two levels of storage and an optimum release rate. Murdeshwar and Sathe (1985) gave some aspects of lot size model with two levels of storage. Pakkala and Achary (1992) developed a deterministic inventory model for deteriorating items with two warehouses and finite-replenishment rates. Goswami and Chaudhuri (1992) established an economic-order quantity model for items with two levels of storage for a linear trend in demand. Benkherouf (1997) established a deterministic-order-level inventory model for deteriorating items with two storage facilities. Bhunia and Maiti (1994, 1998) gave a two-warehouse inventory model for a linear trend in demand. Ray et al. (1998) developed an inventory model with two levels of storage and stock-dependent demand rate. Lee and Ying (2000) derived an optimal inventory policy for deteriorating items with two warehouses and time-dependent demand. Deterministic inventory model with two levels of storage, a linear trend in demand and a fixed time horizon, was derived by Kar et al. (2001). Yang (2004) gave two-warehouse inventory model for deteriorating items with shortages under inflation. Zhou and Yang (2005) derived the model for two warehouses with stock-level-dependent demand. Yang (2006) developed two-warehouse partial backlogging inventory models for deteriorating items under inflation. Lee (2006) investigated two-warehouse inventory model with deterioration under FIFO dispatching policy. Chung and Huang (2007) derived an optimal retailer’s ordering policies for deteriorating items with limited storage capacity under trade credit financing. Hsieh et al. (2007) determined an optimal lot size for a two-warehouse system with deterioration and shortages using net present value. Rong et al. (2008) gave a two-warehouse inventory model for a deteriorating item with partially/fully backlogged shortage and fuzzy lead time. Lee and Hsu (2009) gave a two-warehouse production model for deteriorating inventory items with time-dependent demands. Liang and Zhou (2011) developed the two-warehouse inventory model for deteriorating items under conditionally permissible delay in payment. Agrawal et al. (2013) derived the model with ramp-type demand and partially backlogged shortages for a two-warehouse system. Liao et al. (2012, 2013) developed two-warehouse inventory models under different assumptions. Jaggi et al. (2014) discussed under credit financing in a two-warehouse environment for deteriorating items with price-sensitive demand and fully backlogged shortages. Bhunia and Shaikh (2015) gave an application of PSO in a two-warehouse inventory model for deteriorating item under permissible delay in payment with different inventory policies. Lashgari et al. (2016) considered partial up-stream advanced payment and partial up-stream delayed payment in a three-level supply chain. Lashgari and Taleizadeh (2016) developed an inventory control problem for deteriorating items with backordering and financial considerations under two levels of trade credit linked to order quantity. In the literature, the warehouse owned by the retailer is referred to as owned warehouse OW, while the one hired on rent is referred to as rented warehouse RW. The major assumptions used in the previous articles are summarized in Table 1.
From Table 1, it is clear that, the two-warehouse system for non-instantaneous deteriorating items under trade credit policy with the assumption of \(\alpha > \beta > 0\) has not been considered previously in the literature, represents several practical real-life situations. A typical example of industries that actually operate under the same set of assumptions is the food industry, vegetable markets, fruits stall, supermarkets, etc., and the product may deteriorate after certain time. With longer storage durations, many processed food items require more sophisticated warehousing facilities. Moreover, in the model developed by Liang and Zhou (2011), they considered instantaneous deteriorating items under delay in payment. In the present work, we have made an attempt to investigate the above issues together and derive a model that helps the retailer to reduce the total inventory cost of the inventory system, where permissible delay in payment is offered. The parameters of the proposed model are given in Table 2.
Problem description
To the best of our knowledge, there is no work considering both single-warehouse and two-warehouse models for non-instantaneous deteriorating items with trade credit. To bridge this gap, we have framed two models considering single warehouse (Model-I) and two warehouses (Model-II). Different scenarios based on deterioration time and trade credit period are considered and the theoretical results to find the optimal solution are derived. The main objective of the proposed work is to determine the optimal cycle time and the optimal-order quantity in the above-said situations, such that the total cost is minimized. We consider the different types of storage capacity, so that it will suit to different situations in realistic environment. To develop the mathematical model, the following assumptions are being made.
Assumptions
-
i.
Demand rate is known and constant. Demand is satisfied initially from goods stored in RW and continues with those in OW once inventory stored at RW is exhausted. This implies that \(t_{\text{w}} < T\). The replenishment rate is infinite and the lead time is zero. The time horizon is infinite. Shortages are not allowed.
-
ii.
The owned warehouse OW has limited capacity of W units and the rented warehouse RW has unlimited capacity. For economic reasons, the items of RW are consumed first and next the items of OW.
-
iii.
The items deteriorate at a fixed rate \(\alpha\) in OW and at \(\beta\) in RW, for the rented warehouse offers better facility, so \(\alpha > \beta\), and \(h_{\text{r}} - h_{\text{o}} > c\left( {\alpha - \beta } \right)\) (following Liang and Zhou (2011)). To guarantee that the optimal solution exists, we assume that \(\alpha W < D,\) that is, deteriorating quantity for items in OW is less than the demand rate.
-
iv.
When \(T \ge M\), the account is settled at \(T = M\). Beyond the fixed credit period, the retailer begins paying the interest charges on the items in stock at rate \(I_{\text{p}}\). Before the settlement of the replenishment amount, the retailer can use the sales revenue to earn the interest at annual rate \(I_{\text{e}}\), where \(I_{\text{p}} \ge I_{\text{e}} .\) When \(T \le M\), the account is settled at \(T = M\) and the retailer does not pay any interest charge. Alternatively, the retailer can accumulate revenue and earn interest until the end of the trade credit period.
Notations
In addition, the following notations are used throughout this paper:
- OW:
-
The owned warehouse
- RW:
-
The rented warehouse
- \(D\) :
-
The demand per unit time
- \(k\) :
-
The replenishment cost per order ($/order)
- \(c\) :
-
The purchasing cost per unit item ($/unit)
- \(p\) :
-
The selling price per unit item \(p > c\)
- \(h_{\text{r}}\) :
-
The holding cost per unit per unit time in RW
- \(h_{\text{o}}\) :
-
The holding cost per unit per unit time in OW
- \(\alpha\) :
-
The deterioration rate in OW
- \(\beta\) :
-
The deterioration rate in RW
- \(M\) :
-
Permissible delay in settling the accounts
- \(I_{\text{p}}\) :
-
The interest charged per dollar in stocks per year
- \(I_{\text{e}}\) :
-
The interest earned per dollar per year
- \(t_{\text{d}}\) :
-
The length of time in which the product has no deterioration
- \(I_{0} (t)\) :
-
The inventory level in OW at time t
- \(I_{\text{r}} (t)\) :
-
The inventory level in RW at time t
- \(W\) :
-
The storage capacity of OW
- \(Q\) :
-
The retailer’s order quantity (a decision variable)
- \({\text{TC}}_{i}\) :
-
The total relevant costs
- \(t_{\text{w}}\) :
-
The time at which the inventory level reaches zero in RW
- \(T\) :
-
The length of replenishment cycle (a decision variable)
Model formulation
In this article, we consider two different inventory models, namely, single-warehouse system and two-warehouse system. Based on the values of \(M\), \(t_{\text{d }}\), and \(t_{\text{w }}\), the classification for the two different models is given in Table 3.
Model-I (single-warehouse system)
In this system, two scenarios based on values of \(t_{\text{d}} {\text{and}} T\) arise.
Scenario I: \(t_{\text{d}} < T\)
In this case, demand becomes constant before the inventory level becomes zero. Thus, inventory level at OW decreases because of the increasing demand in the interval \((0,t_{\text{d}} )\) and because of the constant demand and deterioration in the interval \(\left( {t_{\text{d}} ,T} \right)\). The behavior of the model is given in Fig. 1.
Hence, the change in the inventory level in OW at any time t in the interval \((0,T)\) is given by the following differential equations:
with the boundary condition \(I_{02} \left( T \right) = 0.\)
The solutions of the above equation are given, respectively, by
Furthermore, at \(t = t_{\text{d}}\), we get
Based on the assumptions and description of the model, the total annual relevant costs (ordering cost + holding cost + deterioration cost + interest payable − interest earned) is given by
where
Case 1 (\(0 < M \le t_{\text{d}}\))
Case 2 (\(\varvec{ }t_{\text{d}} < M \le T\))
Case 3 (\(M > T\))
Since \(T\) is the decision variable, the necessary condition to find the optimum value of \(T\) to minimize the total cost is \(\frac{{{\text{d}}TC_{1} }}{{{\text{d}}T}} = 0,\quad \frac{{{\text{d}}TC_{2} }}{{{\text{d}}T}} = 0,\quad \frac{{{\text{d}}TC_{3} }}{{{\text{d}}T}} = 0\), which yield
provided they satisfy the sufficient condition \(\frac{{{\text{d}}^{2} {\text{TC}}_{1} (T)}}{{{\text{d}}T^{2} }} > 0\), \(\frac{{{\text{d}}^{2} {\text{TC}}_{2} (T)}}{{{\text{d}}T^{2} }} > 0\), and \(\frac{{{\text{d}}^{2} {\text{TC}}_{3} (T)}}{{{\text{d}}T^{2} }} > 0\).
Scenario II: \(t_{\text{d}} > T\)
In this case, demand becomes constant before the inventory level becomes zero. Thus, inventory level at OW decreases because of the increasing demand in the interval \(\left( {0,T} \right)\) (refer Fig. 2).
Hence, the change in the inventory level in OW at any time t in the interval \((0,T)\) is given by the following differential equation:
with the boundary condition \(I_{01} \left( T \right) = 0.\)
The solution of the above equation is
Based on the assumptions and description of the model, the total annual relevant costs is given by
where
Case 1 (\(M < T\))
Case 2 (\(M > T\))
Since, \(T\) is the decision variable, the necessary condition to find the optimum value of \(T\) to minimize the total cost is \(\frac{{{\text{d}}TC_{4} }}{{{\text{d}}T}} = 0\) and \(\frac{{{\text{d}}TC_{5} }}{{{\text{d}}T}} = 0\), which yield
and
provided that they satisfy the sufficient condition \(\frac{{{\text{d}}^{2} {\text{TC}}_{4} (T)}}{{{\text{d}}T^{2} }} > 0\) and \(\frac{{{\text{d}}^{2} {\text{TC}}_{5} (T)}}{{{\text{d}}T^{2} }} > 0\).
Model-II (two-warehouse system)
There are certain circumstances, where the owned warehouse of the retailer is insufficient to store the goods. In that situation, the retailer may go for rented warehouse. To suit to this case, we develop an inventory model, where there are two warehouses (owned warehouse OW and rented warehouse RW) (refer Table 3).
The inventory system evolves as follows: \(Q\) units of items arrive at the inventory system at the beginning of each cycle. Out of which \(W\) units are kept in OW and the remaining \((Q - W)\) units are stored in RW. The items of OW are consumed only after consuming the goods kept in RW. For the analysis of the inventory system, it is necessary to compare the value of the parameter \(t_{\text{d}}\) and \(M\) with the possible values that the decision variables \(t_{\text{w }}\) and \(T\) can take on. This results in the following three scenarios.
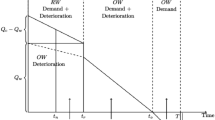
Scenario I: \(t_{\text{d}} < t_{\text{w}} < T\)
During the time interval \((0,t_{\text{d}} )\), the inventory level at RW is decreasing only owing to demand rate. The inventory level is dropping to zero due to demand and deterioration during the time interval \((t_{\text{d}} ,t_{\text{w}} )\). The behavior of the inventory system is depicted in Fig. 3.
Hence, the change in the inventory level in RW at any time t in the interval \((0,t_{\text{w}} )\) is given by the following differential equations:
with the boundary condition \(I_{r2} \left( {t_{\text{w }} } \right) = 0.\)
The solutions of the above equations are given, respectively, by
Furthermore, since \(I_{r1} \left( 0 \right) = Q - W\) and continuity of \(I_{r} \left( t \right)\) at \(t = t_{\text{d}}\), we get
During the interval \((0,t_{\text{d}} )\), there is no change in the inventory level in OW as demand is met from RW. Hence, at any epoch t, the inventory level at OW is
After the time \(t_{\text{d}}\), the inventory level in OW decreases due to deterioration in the interval \((t_{\text{d}} ,t_{\text{w}} )\) and decreases both by demand and by deterioration in the interval \((t_{\text{w}} ,T)\). Hence, the differential equation governing the inventory position is given by
with the boundary condition \(I_{03} \left( T \right) = 0\), and the solution of the above differential equations is given by
Based on the assumptions and description of the model, the total annual cost which is a function of \(t_{\text{w}}\) and \(T\) is given by
where
Theoretical results
To derive the optimal solutions for the proposed model, we need the following lemma.
Lemma 1
Proof
(See Appendix)
Case 1 (\(0 < M \le t_{\text{d }}\))
The necessary conditions for the total annual cost in (11) to be the minimum are \(\frac{{\partial {\text{TC}}_{6} \left( {t_{\text{w}} ,T} \right)}}{{\partial t_{\text{w}} }} = 0\) and \(\frac{{\partial {\text{TC}}_{6} \left( {t_{\text{w}} ,T} \right)}}{\partial T} = 0\), which give
and
From Eqs. (15) and (16), we have the following expressions:
Theorem 1
If \(0 < M \le t_{\text{d }}\), then the total annual cost \({\text{TC}}_{6} \left( {t_{w} ,T} \right)\) is convex and reaches its global minimum at the point \((t_{{{\text{w}}_{6} }}^{*} ,T_{6}^{*} )\), where \((t_{{{\text{w}}_{6} }}^{*} ,T_{6}^{*} )\) is the point which satisfies Eqs. (17) and (18).
Proof
Let \(t_{{{\text{w}}_{6} }}^{*}\) and \(T_{6}^{*}\) be the solution of Eqs. (17) and (18) and \(H_{1} (t_{{{\text{w}}_{6} }}^{*} ,T_{6}^{*} )\) be the Hessian matrix of \({\text{TC}}_{6} \left( {t_{\text{w}} ,T} \right)\) evaluated at \(t_{{{\text{w}}_{6} }}^{*}\) and \(T_{6}^{*}\). It is known that if this matrix is positive definite, then the solution \((t_{{{\text{w}}_{6} }}^{*} ,T_{6}^{*} )\) is an optimal solution. Taking the second derivative of \({\text{TC}}_{6} \left( {t_{\text{w}} ,T} \right)\) with respect to \(t_{\text{w}}\) and \(T\), and then, finding the values of these functions at point \((t_{{{\text{w}}_{6} }}^{*} ,T_{6}^{*} )\), we obtain
Hence, we obtain that
holds, which implies that the matrix \(H_{1} (t_{{{\text{w}}_{6} }}^{*} ,T_{6}^{*} )\) is positive definite and \((t_{{{\text{w}}_{6} }}^{*} ,T_{6}^{*} )\) is the optimal solution of \({\text{TC}}_{6} \left( {t_{\text{w}} ,T} \right).\)
Case 2 (\(\varvec{ }t_{d } < M \le t_{\text{w }}\))
The necessary conditions for the total annual cost in Eq. (12) to be the minimum are \(\frac{{\partial {\text{TC}}_{7} \left( {t_{\text{w}} ,T} \right)}}{{\partial t_{\text{w}} }} = 0\) and \(\frac{{\partial {\text{TC}}_{7} \left( {t_{\text{w}} ,T} \right)}}{\partial T} = 0\), which give
and
From Eqs. (19) and (20), we have the following expressions:
Theorem 2
If \(t_{\text{d }} < M \le t_{\text{w }}\), then the total annual cost \({\text{TC}}_{7} \left( {t_{\text{w}} ,T} \right)\) is convex and reaches its global minimum at the point \((t_{{{\text{w}}_{7} }}^{*} ,T_{7}^{*} )\), where \((t_{{{\text{w}}_{7} }}^{*} ,T_{7}^{*} )\) is the point which satisfies Eqs. (21) and (22).
Proof
(Similar to the proof of Theorem 1).
Case 3 (\(\varvec{ }t_{\text{w }} < M \le T\))
The necessary conditions for the total annual cost in Eq. (13) to be the minimum are \(\frac{{\partial {\text{TC}}_{8} \left( {t_{\text{w}} ,T} \right)}}{{\partial t_{\text{w}} }} = 0\) and \(\frac{{\partial {\text{TC}}_{8} \left( {t_{\text{w}} ,T} \right)}}{\partial T} = 0\), which give
and
Equations (23) and (24) can be written as
Theorem 3
If \(t_{\text{w }} < M \le T\), then the total annual cost \({\text{TC}}_{8} \left( {t_{\text{w}} ,T} \right)\) is convex and reaches its global minimum at the point \((t_{{{\text{w}}_{8} }}^{*} ,T_{8}^{*} )\), where \((t_{{{\text{w}}_{8} }}^{*} ,T_{8}^{*} )\) is the point which satisfies Eqs. (25) and (26).
Proof
(Similar to the proof of Theorem 1).
Case 4 (\(M > T\))
The necessary conditions for the total annual cost in Eq. (14) to be the minimum are \(\frac{{\partial {\text{TC}}_{9} \left( {t_{\text{w}} ,T} \right)}}{{\partial t_{\text{w}} }} = 0\) and \(\frac{{\partial TC_{9} \left( {t_{w} ,T} \right)}}{\partial T} = 0\), which give
and
Equations (27) and (28) can be written as
Theorem 4
If \(M > T\), then the total annual cost \({\text{TC}}_{9} \left( {t_{\text{w}} ,T} \right)\) is convex and reaches its global minimum at the point \((t_{{{\text{w}}_{9} }}^{*} ,T_{9}^{*} )\), where \((t_{{{\text{w}}_{9} }}^{*} ,T_{9}^{*} )\) is the point which satisfies Eqs. (29) and (30).
Proof
(Similar to the proof of Theorem 1).
Scenario II: \(\varvec{ }t_{\text{w}} < t_{\text{d}} < T\)
In this case, during the time interval \((0,t_{\text{w}} )\), the inventory level at RW decreases only owing to demand rate, where \(t_{\text{w}}\) is the epoch at which the inventory level in RW is zero. The inventory level is dropping to zero due to demand and deterioration during the time interval \((t_{\text{d}} ,t_{\text{w}} )\). This case is demonstrated in Fig. 4.
Hence, the change in the inventory level in RW at any time t in the interval \((0,t_{\text{w}} )\) is given by the following differential equations:
with the boundary condition \(I_{{{\text{r}}1}} \left( {t_{\text{w}} } \right) = 0\) and the solution of the above differential equation is given by
Again, during the interval \((0,t_{\text{w}} )\), demand is met from RW alone, and there is no change in the inventory level in OW. Thus, at any instant t, the inventory level \(I_{02} (t)\) at OW is
After time \(t_{\text{w}}\), demand is met from OW. Hence, the inventory level at OW decreases because of the increasing demand rate during the interval \((t_{\text{w}} ,t_{\text{d}} )\) and then because of the demand rate and deterioration during the interval (\(t_{\text{d}} ,T)\). Thus, differential equations governing the inventory level in OW during the interval \((t_{\text{w}} ,T)\) are
with the boundary condition \(I_{03} \left( T \right) = 0\), and the solutions of the above equations are given, respectively, by
Furthermore, since \(I_{02} \left( { t_{\text{w}} } \right) = W\), we get
Based on the assumptions and description of the model, the total annual relevant costs is given by
where
Theoretical results
Case 1 (\(0 < M \le t_{\text{w }}\))
The necessary conditions for the total annual cost in (31) to be the minimum are \(\frac{{\partial {\text{TC}}_{10} \left( {t_{\text{w}} ,T} \right)}}{{\partial t_{\text{w}} }} = 0\) and \(\frac{{\partial {\text{TC}}_{10} \left( {t_{\text{w}} ,T} \right)}}{\partial T} = 0\), which give
From Eqs. (35) and (36), we have the following expressions:
Theorem 5
If \(0 < M \le t_{\text{d }}\), then the total annual cost \({\text{TC}}_{10} \left( {t_{\text{w}} ,T} \right)\) is convex and reaches its global minimum at the point \((t_{{{\text{w}}_{10} }}^{*} ,T_{10}^{*} )\), where \((t_{{{\text{w}}_{10} }}^{*} ,T_{10}^{*} )\) is the point which satisfies Eqs. (37) and (38).
Proof
(Similar to the proof of Theorem 1).
Case 2 (\(\varvec{ }t_{\text{w }} < M \le t_{\text{d }}\))
The necessary conditions for the total annual cost in (32) to be the minimum are \(\frac{{\partial {\text{TC}}_{11} \left( {t_{\text{w}} ,T} \right)}}{{\partial t_{\text{w}} }} = 0\) and \(\frac{{\partial {\text{TC}}_{11} \left( {t_{\text{w}} ,T} \right)}}{\partial T} = 0\), which give
In addition
From Eqs. (39) and (40), we have the following expressions:
Theorem 6
If \(t_{\text{d }} < M \le t_{\text{w }}\), then the total annual cost \({\text{TC}}_{11} \left( {t_{\text{w}} ,T} \right)\) is convex and reaches its global minimum at the point \((t_{11}^{*} , T_{11}^{*} )\), where \((t_{11}^{*} , T_{11}^{*} )\) is the point which satisfies Eqs. (41) and (42).
Proof
(Similar to the proof of Theorem 1).
Case 3 (\(\varvec{ }t_{\text{d }} < M \le T\))
The necessary conditions for the total annual cost in (33) to be the minimum are \(\frac{{\partial {\text{TC}}_{12} \left( {t_{\text{w}} ,T} \right)}}{{\partial t_{\text{w}} }} = 0\) and \(\frac{{\partial {\text{TC}}_{12} \left( {t_{\text{w}} ,T} \right)}}{\partial T} = 0\), which give
In addition
From Eqs. (43) and (44), we have the following expressions:
Theorem 7
If \(t_{\text{d }} < M \le T\), then the total annual cost \({\text{TC}}_{12} \left( {t_{\text{w}} ,T} \right)\) is convex and reaches its global minimum at the point \((t_{{{\text{w}}_{12} }}^{*} , T_{12}^{*} )\), where \((t_{{{\text{w}}_{12} }}^{*} , T_{12}^{*} )\) is the point which satisfies Eqs. (45) and (46).
Proof
(Similar to the proof of Theorem 1).
Case 4 (\(M > T\))
The necessary conditions for the total annual cost in (34) to be the minimum are \(\frac{{\partial {\text{TC}}_{13} \left( {t_{\text{w}} ,T} \right)}}{{\partial t_{\text{w}} }} = 0\) and \(\frac{{\partial {\text{TC}}_{13} \left( {t_{\text{w}} ,T} \right)}}{\partial T} = 0\), which give
From Eqs. (47) and (48), we have the following expressions:
Theorem 8
If \(M > T\), then the total annual cost \({\text{TC}}_{13} \left( {t_{w} ,T} \right)\) is convex and reaches its global minimum at the point \((t_{{{\text{w}}_{13} }}^{*} , T_{13}^{*} )\), where \((t_{{{\text{w}}_{13} }}^{*} , T_{13}^{*} )\) is the point which satisfies Eqs. (49) and (50).
Proof
(Similar to the proof of Theorem 1).
Scenario III: \(\varvec{ }t_{\text{d}} > T\)
In this case, the inventory levels both in RW as well as in OW become zero before the demand stabilises. Thus, the inventory levels at both the warehouses decrease only because of the increasing demand. The case is depicted in Fig. 5.
The inventory level at RW at any epoch t in the time interval \((0,t_{\text{w}} )\) is given by
During the interval \((0,t_{\text{w}} )\), demand is met from RW and there is no change in the inventory level in OW. Thus, at any epoch t, during this interval, the inventory level in OW is
During the interval \((t_{\text{w}} , T)\), the inventory level at OW decreases due to increase in the demand rate. Thus, the differential equation governing the inventory level in OW during the interval \((t_{\text{w}} , T)\) is
Using the boundary condition \(I_{02} \left( T \right) = 0\), the solution of the above equation is given by
Based on the assumptions and description of the model, the total annual relevant costs is given by
where
Theoretical results
Case 1 (\(0 < M \le t_{\text{w}}\))
The necessary conditions for the total annual cost in (51) to be the minimum are \(\frac{{\partial {\text{TC}}_{14} \left( {t_{\text{w}} ,T} \right)}}{{\partial t_{\text{w}} }} = 0\) and \(\frac{{\partial {\text{TC}}_{14} \left( {t_{\text{w}} ,T} \right)}}{\partial T} = 0\), which give
From Eqs. (54) and (55), we have the following expressions:
Theorem 9
If \(0 < M \le t_{\text{w}}\), then the total annual cost \({\text{TC}}_{14} \left( {t_{\text{w}} ,T} \right)\) is convex and reaches its global minimum at the point \((t_{{{\text{w}}_{14} }}^{*} , T_{14}^{*} )\), where \((t_{{{\text{w}}_{14} }}^{*} , T_{14}^{*} )\) is the point which satisfies Eqs. (56) and (57).
Proof
(Similar to the proof of Theorem 1).
Case 2 (\(\varvec{ }t_{\text{w}} < M \le T\))
The necessary conditions for the total annual cost in (52) to be the minimum are \(\frac{{\partial {\text{TC}}_{15} \left( {t_{\text{w}} ,T} \right)}}{{\partial t_{\text{w}} }} = 0\) and \(\frac{{\partial {\text{TC}}_{15} \left( {t_{\text{w}} ,T} \right)}}{\partial T} = 0\), which give
From Eqs. (58) and (59), we have the following expressions:
Theorem 10
If \(t_{\text{w}} < M \le T\), then the total annual cost \({\text{TC}}_{15} \left( {t_{\text{w}} ,T} \right)\) is convex and reaches its global minimum at the point \((t_{{{\text{w}}_{15} }}^{*} , T_{15}^{*} )\), where \((t_{{{\text{w}}_{15} }}^{*} , T_{15}^{*} )\) is the point which satisfies Eqs. (60) and (61).
Proof
(Similar to the proof of Theorem 1).
Case 3 (\(M > T\))
The necessary conditions for the total annual cost in (53) to be the minimum are \(\frac{{\partial {\text{TC}}_{16} \left( {t_{\text{w}} ,T} \right)}}{{\partial t_{\text{w}} }} = 0\) and \(\frac{{\partial {\text{TC}}_{16} \left( {t_{\text{w}} ,T} \right)}}{\partial T} = 0\), which give
From Eqs. (62) and (63), we have the following expressions:
Theorem 11
If \(M > T\), then the total annual cost \({\text{TC}}_{16} \left( {t_{\text{w}} ,T} \right)\) is convex and reaches its global minimum at the point \((t_{{{\text{w}}_{16} }}^{*} , T_{16}^{*} )\), where \((t_{{{\text{w}}_{16} }}^{*} , T_{16}^{*} )\) is the point which satisfies Eqs. (64) and (65).
Proof
(Similar to the proof of Theorem 1).
Algorithm
Based on the above analysis, we state the algorithm which enables us to obtain the overall optimal policy for the single-warehouse system and two-warehouse inventory system.
Algorithm I (single-warehouse system)
Step 1: Input all the parameters of the inventory system.
Step 2: Compare the values of \(M\) and \(t_{\text{d}}\). If \(M < t_{\text{d}}\), then go to step 3, and if \(M > t_{\text{d}}\), go to step 4.
Step 3:
-
(i)
Determine \(T_{1}^{*} ,\) from Eq. (4). If \(t_{\text{d }} < T\), let \(T^{*} = T_{1}^{*}\) and \({\text{TC}}^{*} = {\text{TC}}_{1}^{*}\), otherwise go to step (ii).
-
(ii)
Determine \(T_{4}^{*} ,\) from Eq. (9). If \(T \le t_{\text{d }}\), let \(T^{*} = T_{4}^{*}\) and \({\text{TC}}^{*} = {\text{TC}}_{4}^{*}\); otherwise, go to step (iii).
-
(iii)
Determine \(T_{5}^{*} ,\) from Eq. (10). If \(T < M \le t_{\text{d }}\), let \(T^{*} = T_{5}^{*}\) and \({\text{TC}}^{*} = {\text{TC}}_{5}^{*}\); otherwise, go to step (iv).
-
(iv)
Let \(T^{*}\) = arg min \(\left\{ {{\text{TC}}_{1}^{*} ,{\text{TC}}_{4}^{*} ,{\text{TC}}_{5}^{*} } \right\}\), output the optimal \(T^{*}\) and \({\text{TC}}^{*}\).
Step 4:
-
(i)
Determine \(T_{2}^{*} ,\) from Eq. (5). If \(t_{\text{d }} < T\), let \(T^{*} = T_{2}^{*}\) and \({\text{TC}}^{*} = {\text{TC}}_{2}^{*}\); otherwise, go to step (ii).
-
(ii)
Determine \(T_{3}^{*} ,\) from Eq. (5). If \(M < T \le t_{d }\), let \(T^{*} = T_{3}^{*}\) and \({\text{TC}}^{*} = {\text{TC}}_{3}^{*}\); otherwise, go to step (iii).
-
(iii)
Let \(T^{*}\) = arg min \(\left\{ {{\text{TC}}_{2}^{*} ,{\text{TC}}_{3}^{*} } \right\}\), output the optimal \(T^{*}\) and \({\text{TC}}^{*}\).
Algorithm II (two-warehouse system)
Step 1: Input all the parameters of the inventory system.
Step 2: Compare the values of \(M\) and \(t_{\text{d}}\). If \(M < t_{\text{d}}\), then go to step 3, and if \(M > t_{\text{d}}\), go to step 4.
Step 3:
-
(i)
Determine \(t_{{{\text{w}}_{6} }}^{*}\) and \(T_{6}^{*}\), from Eqs. (15) and (16). If \(t_{{{\text{w}}_{6} }}^{*} < T_{6}^{*}\), let \(t_{\text{w}}^{*} = t_{{{\text{w}}_{6} }}^{*}\), \(T^{*} = T_{6}^{*}\), and \({\text{TC}}^{*} = {\text{TC}}_{6}^{*} (t_{{{\text{w}}_{6} }}^{*} , T_{6}^{*} )\); otherwise, go to step (ii).
-
(ii)
Determine \(t_{{{\text{w}}_{10} }}^{*}\) and \(T_{10}^{*}\), from Eqs. (35) and (36). If \(M < t_{{{\text{w}}_{10} }}^{*} \le t_{\text{d }} < T_{10}^{*}\), let \(t_{\text{w}}^{*} = t_{{{\text{w}}_{10} }}^{*}\), \(T^{*} = T_{10}^{*}\), and \({\text{TC}}^{*} = {\text{TC}}_{10}^{*} (t_{{{\text{w}}_{10} }}^{*} , T_{10}^{*} )\); otherwise, go to step (iii).
-
(iii)
Determine \(t_{{{\text{w}}_{11} }}^{*}\) and \(T_{11}^{*}\), from Eqs. (39) and (40). If \(t_{{{\text{w}}_{11} }}^{*} < T_{11}^{*}\), let \(t_{\text{w}}^{*} = t_{{{\text{w}}_{11} }}^{*}\), \(T^{*} = T_{11}^{*}\), and \({\text{TC}}^{*} = {\text{TC}}_{11}^{*} (t_{{{\text{w}}_{11} }}^{*} , T_{11}^{*} )\); otherwise, go to step (iv).
-
(iv)
Determine \(t_{{{\text{w}}_{14} }}^{*}\) and \(T_{14}^{*}\), from Eqs. (54) and (55). If \(M < t_{{{\text{w}}_{14} }}^{*} < T_{14}^{*} \le t_{\text{d }}\), let \(t_{\text{w}}^{*} = t_{{{\text{w}}_{14} }}^{*}\), \(T^{*} = T_{14}^{*}\), and \({\text{TC}}^{*} = {\text{TC}}_{14}^{*} (t_{{{\text{w}}_{14} }}^{*} , T_{14}^{*} )\); otherwise, go to step (v).
-
(v)
Determine \(t_{{{\text{w}}_{15} }}^{*}\) and \(T_{15}^{*}\), from Eqs. (58) and (59). If \(t_{{{\text{w}}_{15} }}^{*} < M < T_{15}^{*} \le t_{\text{d }}\), let \(t_{\text{w}}^{*} = t_{{{\text{w}}_{15} }}^{*}\), \(T^{*} = T_{15}^{*}\), and \({\text{TC}}^{*} = {\text{TC}}_{15}^{*} (t_{{{\text{w}}_{15} }}^{*} , T_{15}^{*} )\); otherwise, go to step (vi).
-
(vi)
Determine \(t_{{{\text{w}}_{16} }}^{*}\) and \(T_{16}^{*}\), from Eqs. (62) and (63). If \(t_{{{\text{w}}_{16} }}^{*} < T_{16}^{*}\), let \(t_{\text{w}}^{*} = t_{{{\text{w}}_{16} }}^{*} ,\) \(T^{*} = T_{16}^{*}\), and \({\text{TC}}^{*} = {\text{TC}}_{16}^{*} (t_{{{\text{w}}_{16} }}^{*} , T_{16}^{*} )\); otherwise, go to step (vii).
-
(vii)
Let \(\left( {t_{\text{w}}^{*} ,T^{*} } \right)\) = arg min \(\left\{ {{\text{TC}}_{6}^{*} (t_{{{\text{w}}_{6} }}^{*} , T_{6}^{*} ), {\text{TC}}_{10}^{*} (t_{{{\text{w}}_{10} }}^{*} , T_{10}^{*} ),{\text{TC}}_{11}^{*} (t_{{{\text{w}}_{11} }}^{*} , T_{11}^{*} ),{\text{TC}}_{14}^{*} (t_{{{\text{w}}_{14} }}^{*} , T_{14}^{*} ),{\text{TC}}_{15}^{*} (t_{{{\text{w}}_{15} }}^{*} , T_{15}^{*} ),{\text{TC}}_{16}^{*} (t_{{{\text{w}}_{16} }}^{*} , T_{16}^{*} )} \right\}\), output the optimal \(t_{\text{w}}^{*}\), \(T^{*}\) and \({\text{TC}}^{*}\).
Step 4:
-
(i)
Determine \(t_{{{\text{w}}_{7} }}^{*}\) and \(T_{7}^{*}\), from Eqs. (19) and (20). If \(t_{{{\text{w}}_{7} }}^{*} < T_{7}^{*}\), let \(t_{\text{w}}^{*} = t_{{{\text{w}}_{7} }}^{*}\), \(T^{*} = T_{7}^{*}\), and \({\text{TC}}^{*} = {\text{TC}}_{7}^{*} (t_{{{\text{w}}_{7} }}^{*} , T_{7}^{*} )\); otherwise, go to step (ii).
-
(ii)
Determine \(t_{{{\text{w}}_{8} }}^{*}\) and \(T_{8}^{*}\), from Eqs. (23) and (24). If \(t_{{{\text{w}}_{8} }}^{*} < M < T_{8}^{*}\), let \(t_{\text{w}}^{*} = t_{{{\text{w}}_{8} }}^{*}\), \(T^{*} = T_{8}^{*}\), and \({\text{TC}}^{*} = {\text{TC}}_{8}^{*} (t_{{{\text{w}}_{8} }}^{*} , T_{8}^{*} )\); otherwise, go to step (iii).
-
(iii)
Determine \(t_{{{\text{w}}_{9} }}^{*}\) and \(T_{9}^{*}\), from Eqs. (27) and (28). If \(t_{{{\text{w}}_{9} }}^{*} < T_{9}^{*} \le M\), let \(t_{\text{w}}^{*} = t_{{{\text{w}}_{9} }}^{*}\), \(T^{*} = T_{9}^{*}\), and \({\text{TC}}^{*} = {\text{TC}}_{9}^{*} (t_{{{\text{w}}_{9} }}^{*} , T_{9}^{*} )\); otherwise, go to step (iv).
-
(iv)
Determine \(t_{{{\text{w}}_{12} }}^{*}\) and \(T_{12}^{*}\), from Eqs. (43) and (44). If \(t_{{{\text{w}}_{12} }}^{*} < T_{12}^{*}\), let \(t_{\text{w}}^{*} = t_{{{\text{w}}_{12} }}^{*}\), \(T^{*} = T_{12}^{*}\), and \({\text{TC}}^{*} = {\text{TC}}_{12}^{*} (t_{{{\text{w}}_{12} }}^{*} , T_{12}^{*} )\); otherwise, go to step (v).
-
(v)
Determine \(t_{{{\text{w}}_{13} }}^{*}\) and \(T_{13}^{*}\), from Eqs. (47) and (48). If \(t_{{{\text{w}}_{13} }}^{*} < T_{13}^{*} \le {\text{M}}\), let \(t_{\text{w}}^{*} = t_{{{\text{w}}_{13} }}^{*}\), \(T^{*} = T_{13}^{*}\), and \({\text{TC}}^{*} = {\text{TC}}_{13}^{*} (t_{{{\text{w}}_{13} }}^{*} , T_{13}^{*} )\); otherwise, go to step (vi).
-
(vi)
Let \(\left( {t_{\text{w}}^{*} ,T^{*} } \right)\) = arg min \(\left\{ {{\text{TC}}_{7}^{*} (t_{{{\text{w}}_{7} }}^{*} , T_{7}^{*} ), {\text{TC}}_{8}^{*} (t_{{{\text{w}}_{8} }}^{*} , T_{8}^{*} ),{\text{TC}}_{9}^{*} (t_{{{\text{w}}_{9} }}^{*} , T_{9}^{*} ),{\text{TC}}_{12}^{*} (t_{{{\text{w}}_{12} }}^{*} , T_{12}^{*} ),{\text{TC}}_{13}^{*} (t_{{{\text{w}}_{13} }}^{*} , T_{13}^{*} )} \right\}\), output the optimal \(t_{\text{w}}^{*}\), \(T^{*}\) and \({\text{TC}}^{*}\).
Numerical examples
The following examples illustrate our solution procedure when single warehouse (Model-I) is considered.
Example 1 (\(M < t_{\text{d }}\))
Consider an inventory system with the following data: \(k = 450\), \(D = 1000 ,\) \(h_{\text{o}} = 10\), \(c = 20\), \(p = 25\), \(I_{\text{e}} = 0.2\), \(I_{\text{p}} = 0.5\), \(M = 0.0833\), \(\alpha = 0.08\), and \(t_{\text{d}} = 0.1045\), in appropriate units. In this case, we see that \(M < t_{\text{d }} .\) Therefore, applying algorithm I, we get the optimal solutions, \(T^{*} = 0.5554\), the corresponding total cost \({\text{TC}}^{*} = 5092.42\), and the ordering quantity \(Q^{*} = 563.64.\)
Example 2 (\(M > t_{\text{d}}\))
The data are the same as in Example 1 except: \(M = 0.0417\) and \(t_{\text{d}} = 0.0322\), in appropriate units. Here, we see that \(M > t_{\text{d}}\). Therefore, applying algorithm I, we get the optimal solutions, \(T^{*} = 0.2067\), the corresponding total cost \({\text{TC}}^{*} = 3712.26\), and \(Q^{*} = 207.90.\)
Example 3 (\(t_{\text{d}} > T\))
The data are the same as in Example 1 except: \(M = 0.99\) and \(t_{\text{d}} = 0.9984\), in appropriate units. In this case, we see that \(t_{\text{d}} > T\). Therefore, applying algorithm I, we get the optimal solutions, \(T^{*} = 1.0440\), the corresponding total cost \({\text{TC}}^{*} = 8206.40\), and \(Q^{*} = 1044.10.\)
To illustrate the situations, where two warehouses (Model-II) are considered, we have the following set of examples.
Example 4 (\(M < t_{\text{d }}\))
Consider an inventory system with the following data: \(k = 450\), \(D = 1000 , h_{\text{r}} = 15,\) \(h_{\text{o}} = 10\), \(c = 20\), \(p = 25\), \(I_{\text{e}} = 0.2\), \(I_{\text{p}} = 0.5\), \(M = 0.0833\), \(W = 100\), \(\alpha = 0.08\), \(\beta = 0.02\), and \(t_{\text{d}} = 0.1045\), in appropriate units. Here, we see that \(M < t_{\text{d }} .\) Therefore, applying algorithm II, we get the optimal solutions \(t_{\text{w}}^{*} = 0.1179\) and \(T^{*} = 0.2429\), the corresponding total cost \({\text{TC}}^{*} = 2714.80\), and \(Q^{*} = 251.88.\)
Example 5 (\(M > t_{\text{d}}\))
The data are the same as in Example 4 except: \(M = 0.0417\), and \(t_{\text{d}} = 0.0322\), in appropriate units. Here, we see that \(M > t_{\text{d}}\). Therefore, applying algorithm II, we get the optimal solutions \(t_{\text{w}}^{*} = 0.0888\) and \(T^{*} = 0.2502\), the corresponding total cost \({\text{TC}}^{*} = 3505.30\), and \(Q^{*} = 252.51.\)
Example 6 (\(t_{\text{d}} > T\))
The data are the same as in Example 4 except: \(M = 0.99\) and \(t_{\text{d}} = 0.9984\), in appropriate units. Here, we see that \(t_{\text{d}} > T\). Therefore, applying algorithm II, we get the optimal solutions \(t_{\text{w}}^{*} = 0.3548\) and \(T^{*} = 0.9874\), the corresponding total cost \({\text{TC}}^{*} = 1379.60\), and \(Q^{*} = 458.91.\)
Comparative study of the results between the two models
Comparative study with respect to the major parameters for the single and two-warehouse models is done in this section. In this article, we discussed two models. Single warehouse is considered in Model-I and Model-II is framed with two-warehouse system. Different scenarios based on the time in which the product deteriorates is classified. In “Numerical examples”, we have given six numerical data sets for obtaining the solution using the computational algorithms. Example 1, Example 2, and Example 3 represent the single-warehouse model (Model-I) for the various scenarios \(M < t_{\text{d }}\),\(M > t_{\text{d}}\), and \(t_{\text{d}} > T\), respectively. From Example 3, when \(t_{\text{d}} > T\), the total cost of the single-warehouse inventory system is \({\text{TC}}^{*} = 8206.40\) and \(Q^{*} = 1044.10.\) From this, we infer that the retailer should avail the permissible delay in payment before the cycle time, so that the total cost of the inventory system can be reduced when compared to the case \(M < t_{\text{d }}\) and \(M > t_{\text{d}}\). Similarly, from Example 4 (\(M < t_{\text{d }}\)) and Example 5 \(( M > t_{\text{d}} )\) which represent two-warehouse system (Model-II), we see that the total cost of the inventory system in the case \(M < t_{\text{d }}\) is less than the total cost of case \(M > t_{\text{d}}\). In addition, Table 4 infers that the total cost of the inventory system is reduced effectively when the retailer avails the rented warehouse facility, that is, when the retailer adopts two-warehouse storage facilities. For example, under scenario \(M < t_{\text{d }}\), the total cost of the system \({\text{TC}}^{*} = 5092.42\) which is effectively reduced to \({\text{TC}}^{*} = 2714.80\) when the retailer avails the rented warehouse facility. Furthermore, consider the case \(( M > t_{\text{d}} )\), the total cost of the integrated system in single-warehouse model is \({\text{TC}}^{*} = 3712.26\), whereas in two-warehouse model, the total cost is \({\text{TC}}^{*} = 3505.30\) (less = 206.96). In addition when we consider the case \(t_{\text{d}} > T\), the difference between the total cost in two models is very much significant (\(8206.40\) − \(1379.60\) = 6826.80). In all the scenarios, the total cost is effectively reduced in a two-warehouse model comparatively. Furthermore, the comparative study infers that the retailer should order less quantity more frequently in two-warehouse model, but in single-warehouse model, the optimal replenishment policy suggests that more quantity may be ordered less frequently. Therefore, the retailer can gain more profit by improving the storage facility such as warehouses, godowns, and so on to store materials.
Managerial implication
In this section, we perform the sensitivity analysis on the key parameters of Model-II, to study their effect on the inventory system. The results are summarized in Tables 5, 6, 7, and 8 and the graphical representation of the sensitivity analysis is shown in Figs. 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, and 16. Based on the computational results obtained from the sensitivity analysis, the following inferences can be made from managerial view point:
-
When \(k\) increases, the optimal cycle time \(T^{*}\) and the minimum total relevant cost per unit time \({\text{TC}}^{*}\) increase simultaneously. For example, when \(W\) = 50 and \(D\) = 1000, \(k\) increases from 450 to 550 units, \(T^{*}\) increases from 0.2709 to 0.3006, and also \({\text{TC}}^{*}\) increases from 2542.20 to 2892.40. This implies that, from managerial view point, if the ordering cost per order is reduced effectively, then the total cost per unit time could be reduced. The retailer should order more quantity per order when the ordering cost per order is high.
-
When retailer’s warehouse capacity \(W\) is increasing, the optimal replenishment cycle time \(T^{*}\) will decrease, but the relevant total costs \({\text{TC}}^{*}\) will increase. For example, when \(k\) = 450/order and \(D\) = 1000 units, \(W\) increases from 50 to 100 units, \(T^{*}\) decreases from 0.2709 to 0.2429, but \({\text{TC}}^{*}\) increases from 2542.20 to 2714.80. This implies that the retailer should order less frequently to reduce the total inventory cost when warehouse storage capacity is more.
-
When there is an increase in the value of \(M\), the optimal order quantity \(Q^{*}\) increases, whereas the optimal total cost \({\text{TC}}^{*}\) decreases. This shows that the retailer can minimize the total cost if the retailer obtains a longer permissible delay period from the supplier.
-
When the holding cost increases, the length of the cycle time \(T^{*}\) decreases and the total cost \({\text{TC}}^{*}\) increases. If the retailer can effectively reduce the holding cost of the item by improving equipment of storehouse, the total cost will be lowered. When the holding cost increases, the ordering quantity \(Q^{*}\) decreases. From the managerial point of view, when the holding cost for a product is more, the retailer should order less.
-
When the fresh product time increases, the optimal total cost \({\text{TC}}^{*}\) decreases and \(Q^{*}\) increases. Hence, from our model, we suggest that when the fresh product time of a product is more, the retailer should order more quantity. In addition, it shows that the model with non-instantaneous deteriorating items always has smaller total annual inventory cost than with instantaneous deteriorating items. If the retailer can extend effectively the length of time, the product has no deterioration for a few days or months, then the total annual cost will be reduced obviously.
-
When the selling price \(p\) increases, there is a decrease in the optimal order quantity \(Q^{*}\). The larger the value of \(p\), the smaller is the value of the optimal cycle time \(T^{*}\). That is, when the unit selling price is increasing, the retailer will order less quantity more frequently.
Conclusion
The purpose of this article is to frame a model that will help the retailer to determine the optimal replenishment policy for non-instantaneous deteriorating items. The supplier offers a permissible delay in payments with two levels of storage facilities. Our model suits well for the retailer in situations involving unlimited storage space. Thus, the decision maker can easily determine whether it will be financially advantageous to rent a warehouse to hold much more items to obtain a trade credit period. It was assumed that the rented warehouse charges are higher holding cost than the owned warehouse. To reduce the inventory costs, it will be economical to consume the goods of the rented warehouse at the earliest. From the results obtained, we see that the retailer can reduce total annual inventory cost by ordering lower quantity when the supplier provides a permissible delay in payments by improving storage conditions for non-instantaneous deteriorating items. Incorporating more realistic assumptions such as allowable shortages, probabilistic demand, or quantity discounts, this article paves way to extend future research works.
References
Aggarwal SP, Jaggi CK (1995) Ordering policies of deteriorating items under permissible delay in payments. J Oper Res Soc 46:658–662
Agrawal S, Banerjee S, Papachristos S (2013) Inventory model with deteriorating items, ramp-type demand and partially backlogged shortages for a two warehouse system. App Math Modell 37:8912–8929
Benkherouf L (1997) A deterministic order level inventory model for deteriorating items with two storage facilities. Int J Prod Econ 48:167–175
Bhunia AK, Maiti M (1994) A two warehouse inventory model for a linear trend in demand. OPSEARCH 31:318–329
Bhunia AK, Maiti M (1998) A two warehouse inventory model for deteriorating items with a linear trend in demand and shortages. J Oper Res Soc 49:287–292
Bhunia AK, Shaikh AK (2015) An application of PSO in a two-warehouse inventory model for deteriorating item under permissible delay in payment with different inventory policies. App Math and Comp 256:831–850
Chung CJ, Huang TS (2007) The optimal retailer’s ordering policies for deteriorating items with limited storage capacity under trade credit financing. Int J Prod Econ 106:127–145
Geetha KV, Udayakumar R (2015) Optimal replenishment policy for deteriorating items with time sensitive demand under trade credit financing. Am J Math Man Sci 34:197–212
Geetha KV, Udayakumar R (2016) Optimal lot sizing policy for non-instantaneous deteriorating items with price and advertisement dependent demand under partial backlogging. Int J Appl Comp Math 2:171–193
Ghare PM, Schrader GH (1963) A model for exponentially decaying inventory system. Int J Prod Res 21:449–460
Goswami A, Chaudhuri KS (1992) An economic order quantity model for items with two levels of storage for a linear trend in demand. J Oper Res Soc 43:157–167
Goyal SK (1985) Economic order quantity under condition of permissible delay in payments. J Oper Res Soc 36:335–338
Goyal SK, Giri BC (2001) Recent trends in modeling of deteriorating inventory. Euro J Oper Res 134:1–16
Heydari J, Rastegar M, Glock CH (2017) A two level day in payments contract for supply chain coordination: the case of credit-dependent demand. Int J Prod Econ 191:26–36
Hsieh TP, Dye CY, Ouyang LY (2007) Determining optimal lot size for a two warehouse system with deterioration and shortages using net present value. Euro J Oper Res 191:182–192
Jaggi CK, Pareek S, Khanna A, Sharma R (2014) Credit financing in a two warehouse environment for deteriorating items with price-sensitive demand and fully backlogged shortages. App Math Modell 38:5315–5333
Kar S, Bhunia AK, Maiti M (2001) Deterministic inventory model with two levels of storage, a linear trend in demand and a fixed time horizon. Comput Oper Res 28:1315–1331
Lashgari M, Taleizadeh AA (2016) An inventory control problem for deteriorating items with backordering and financial considerations under two levels of trade credit linked to order quantity. J Ind Manag Opt 12(3):1091–1119
Lashgari M, Taleizadeh AA, Ahmadi A (2016) Partial up-stream advanced payment and partial up-stream delayed payment in a three level supply chain. Ann Oper Res 238:329–354
Lee CC (2006) Two-warehouse inventory model with deterioration under FIFO dispatching policy. Euro J Oper Res 174:861–873
Lee CC, Hsu SL (2009) A two-warehouse production model for deteriorating inventory items with time-dependent demands. Euro J Oper Res 194:700–710
Lee CC, Ying C (2000) Optimal inventory policy for deteriorating items with two warehouse and time-dependent demands. Prod Plan Cont Manag Oper 11:689–696
Li J, Mao J (2009) An Inventory model of perishable item with two types of retailers. J Chin Inst Ind Eng 26:176–183
Liang Y, Zhou F (2011) A two-warehouse inventory model for deteriorating items under conditionally permissible delay in payment. App Math Modell 35:2221–2231
Liao J-J (2008) An EOQ model with non-instantaneous receipt and exponentially deteriorating items under two-level trade credit. Int J Prod Econ 113:852–861
Liao JJ, Huang KN, Chung KJ (2012) Lot-sizing decisions for deteriorating items with two ware houses under an order-size-dependent trade credit. Int J Prod Econ 137:102–115
Liao JJ, Chung KJ, Huang KN (2013) A deterministic inventory model for deteriorating items with two warehouses and trade credit in a supply chain system. Int J Prod Econ 146:557–565
Mahata GC (2015) Retailer’s optimal credit period and cycle time in a supply chain for deteriorating items with up-stream and down-stream trade credits. J Ind Eng Int 11:353–366
Maihami R, Kamal Abadi IN (2012) Joint control of inventory and its pricing for non-instantaneously deteriorating items under permissible delay in payments and partial backlogging. Mathe Comp Modell 55(5–6):1722–1733
Maihami R, Karimi B (2014) Optimizing the pricing and replenishment policy for non-instantaneous deteriorating items with stochastic demand and promotional efforts. Comput Oper Res 51:302–312
Malik AK, Singh Y (2011) An inventory model for deteriorating items with soft computing techniques and variable demand. Int J Soft Comp Eng 1(5):317–321
Mukhopadhyay S, Mukherjee RN, Chaudhuri KS (2004) Joint pricing and ordering policy for a deteriorating inventory. Comp Ind Eng 47(4):339–349
Murdeshwar TA, Sathe YS (1985) Some aspects of lot size model with two levels of storage. OPSEARCH 22:255–262
Ouyang LY, Wu KS, Yang CT (2006) A study on an inventory model for non-instantaneous deteriorating items with permissible delay in payments. Comput Ind Eng 51:637–651
Pakkala TP, Achary KK (1992) A deterministic inventory model for deteriorating items with two warehouses and finite replenishment rates. Eur J Oper Res 57:71–76
Philip GC (1974) A generalized EOQ model for items with Weibull distribution. AIIE Trans 6:159–162
Ray J, Goswami A, Chaudhuri KS (1998) On an inventory model with two levels of storage and stock-dependent demand rate. Int J Syst Sci 29(3):249–254
Rong M, Mahapatra NK, Maiti M (2008) A two warehouse inventory model for a deteriorating item with partially/fully backlogged shortage and fuzzy lead time. Eur J Oper Res 189:59–75
Sarma KVS (1987) A deterministic order level inventory model for deteriorating items with two storage facilities. Eur J Oper Res 29:70–73
Soni HN (2013) Optimal replenishment policies for non-instantaneous deteriorating items with price and stock sensitive demand under permissible delay in payment. Int J Prod Econ 146:259–268
Taleizadeh AA (2014a) An economic order quantity model for deteriorating item in a purchasing system with multiple prepayments. App Math Modell 38:5357–5366
Taleizadeh AA (2014b) An economic order quantity model with partial backordering and advance payments for an evaporating item. Int J Prod Econ 155:185–193
Taleizadeh AA, Nematollahi MR (2014) An inventory control problem for deteriorating items with backordering and financial considerations. App Math Model 38:93–109
Taleizadeh AA, Noori-daryan M, Cardenas-Barron LE (2015) Joint optimization of price, replenishment frequency, replenishment cycle and production rate in vendor managed inventory system with deteriorating items. Int J Prod Econ 159:285–295
Taleizadeh AA, Mohsen M, Akram R, Heydari J (2016) Imperfect economic production quantity model with upstream trade credit periods linked to raw material order quantity and downstream trade credit periods. Appl Math Modell 40(19):8777–8793
Tat R, Taleizadeh AA, Esmaeili M (2013) Developing EOQ model with non-instantaneous deteriorating items in vendor-managed inventory system. Int J Syst Sci 46(7):1257–1268
Tavakoli S, Taleizadeh AA (2017) A lot sizing model for decaying item with full advance payment from the buyer and conditional discount from the supplier. Ann Oper Res. doi:10.1007/s10479-017-2510-7
Udayakumar R, Geetha KV (2014) Optimal replenishment policy for items with inflation rate and time dependent demand with salvage value. Art Int Syst Mach Learn 6:193–197
Udayakumar R, Geetha KV (2016) Economic ordering policy for single item inventory model over finite time horizon. Int J Syst Assu Eng Manag. doi:10.1007/s13198-016-0516-1
Uthayakumar R, Geetha KV (2009) A replenishment policy for non-instantaneous deteriorating inventory system with partial backlogging. Tamsui Oxf J Math Sci 25:313–332
Wu KS, Ouyang LY, Yang CT (2006) An optimal replenishment policy for non-instantaneous deteriorating items with stock-dependent demand and partial backlogging. Int J Prod Econ 101:369–384
Wu J, Skouri K, Teng J-T, Ouyang L-Y (2014) A note on optimal replenishment policies for non-instantaneous deteriorating items with price and stock sensitive demand under permissible delay in payment. Int J Prod Econ 155:324–329
Yang HL (2004) Two-warehouse inventory models for deteriorating items with shortages under inflation. Eur J Oper Res 157:344–356
Yang HL (2006) Two-warehouse partial backlogging inventory models for deteriorating items under inflation. Int J Prod Econ 103:362–370
Zhou YW, Yang SL (2005) A two-warehouse inventory model for items with stock-level-dependent demand rate. Int J Prod Econ 95:215–228
Zia NPM, Taleizadeh AA (2015) A lot sizing model with backordering under hybrid linked to order multiple advance payments and delayed payment. Transp Res Part E 82:19–37
Acknowledgements
The authors are grateful to the Editor and the anonymous reviewers for their valuable suggestions and constructive comments which have led to a significant improvement of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof of Lemma 1
Based on the assumptions, we know that \(0 < \beta < \alpha < < 1, \;h_{\text{o}} + c\alpha < h_{\text{r}} + c\beta , \;D - \alpha W > 0\) and \(\beta M\) is sufficiently small.
-
(a)
Let \(f\left( t \right) = D\left( {h_{\text{r}} + c\beta + cI_{\text{p}} {\text{e}}^{{ - \beta t_{\text{d }} }} } \right){\text{e}}^{\beta t} - \alpha W{\left( {h_{\text{r}} + c\beta + cI_{\text{p}} } \right)}{{\text{e}}^{\alpha t} ,\quad t > 0}\), then we have
$$\begin{aligned} f\left( 0 \right) = \, & D\left( {h_{r} + c\beta + cI_{\text{p}} {\text{e}}^{{ - \beta t_{d } }} } \right) - \alpha W\left( {h_{\text{r}} + c\beta + cI_{\text{p}} } \right) \\ = \, & \left( {h_{\text{r}} + c\beta } \right)\left( {D - \alpha W} \right) + cI_{\text{p}} (D{\text{e}}^{{ - \beta t_{\text{d }} }} {-}\alpha W) \\ > \, & \left( {h_{\text{r}} + c\beta } \right)\left( {D - \alpha W} \right) + cI_{\text{p}} (D(1 - \beta t_{\text{d }} ){-}\alpha W) > 0, \\ \end{aligned}$$and \(f^{'} (t) = \beta D\left( {h_{\text{r}} + c\beta + cI_{\text{p}} {\text{e}}^{{ - \beta t_{\text{d }} }} } \right){\text{e}}^{\beta t} + \alpha^{2} W\left( {h_{\text{r}} + c\beta + cI_{\text{p}} } \right){\text{e}}^{\alpha t} ,\;t > 0\).
Hence, \(f\left( t \right)\) is an increasing function and \(f\left( t \right) > 0\) for all \(t > 0.\) As a result, \(D\left( {h_{\text{r}} + c\beta + cI_{\text{p}} {\text{e}}^{{ - \beta t_{\text{d }} }} } \right){\text{e}}^{\beta t} > \alpha W\left( {h_{\text{r}} + c\beta + cI_{\text{p}} } \right){\text{e}}^{\alpha t} > \alpha W\left( {h_{\text{o}} + c\alpha + cI_{\text{p}} } \right){\text{e}}^{\alpha t}\) holds.
-
(b)
Let \(g\left( t \right) = D\left( {h_{\text{r}} + c\beta + cI_{\text{p}} {\text{e}}^{ - \beta M} } \right){\text{e}}^{\beta t} - \alpha W\left( {h_{\text{r}} + c\beta + cI_{\text{p}} } \right){\text{e}}^{\alpha t} ,\;t > 0\), then we have
$$\begin{aligned} g\left( 0 \right) = & D\left( {h_{\text{r}} + c\beta + cI_{\text{p}} {\text{e}}^{ - \beta M} } \right) - \alpha W\left( {h_{\text{r}} + c\beta + cI_{\text{p}} } \right) \\ = & \left( {h_{\text{r}} + c\beta } \right)\left( {D - \alpha W} \right) + cI_{\text{p}} (D{\text{e}}^{ - \beta M} {-}\alpha W) \\ > & \left( {h_{\text{r}} + c\beta } \right)\left( {D - \alpha W} \right) + cI_{\text{p}} (D(1 - \beta M){-}\alpha W) > 0, \\ \end{aligned}$$and \(g^{'} (t) = \beta D\left( {h_{\text{r}} + c\beta + cI_{\text{p}} {\text{e}}^{ - \beta M} } \right){\text{e}}^{\beta t} + \alpha^{2} W\left( {h_{\text{r}} + c\beta + cI_{\text{p}} } \right){\text{e}}^{\alpha t} ,\;t > 0\).
Hence, \(g\left( t \right)\) is an increasing function and \(g\left( t \right) > 0\) for all \(t > 0.\) As a result, \(D\left( {h_{\text{r}} + c\beta + cI_{\text{p}} {\text{e}}^{ - \beta M} } \right){\text{e}}^{\beta t} > \alpha W\left( {h_{\text{r}} + c\beta + cI_{\text{p}} } \right){\text{e}}^{\alpha t} > \alpha W\left( {h_{\text{o}} + c\alpha + cI_{\text{p}} } \right){\text{e}}^{\alpha t}\) holds.
-
(c)
Similarly, let \(h\left( t \right) = D\left( {h_{\text{r}} + c\beta } \right){\text{e}}^{\beta t} - \alpha W\left( {h_{\text{r}} + c\beta } \right){\text{e}}^{\alpha t} ,\;t > 0\), then we have
$$\begin{aligned} h\left( 0 \right) = & D\left( {h_{\text{r}} + c\beta } \right) - \alpha W\left( {h_{\text{r}} + c\beta } \right) \\ = & \left( {h_{\text{r}} + c\beta } \right)\left( {D - \alpha W} \right) > 0, \\ \end{aligned}$$and \(h^{'} (t) = \beta D\left( {h_{\text{r}} + c\beta } \right){\text{e}}^{\beta t} + \alpha^{2} W\left( {h_{\text{r}} + c\beta } \right){\text{e}}^{\alpha t} ,\;t > 0.\)
Hence, \(h\left( t \right)\) is an increasing function and \(h\left( t \right) > 0\) for all \(t > 0.\) As a result, \(D\left( {h_{\text{r}} + c\beta } \right){\text{e}}^{\beta t} > \alpha W\left( {h_{\text{r}} + c\beta } \right){\text{e}}^{\alpha t} > \alpha W\left( {h_{\text{o}} + c\alpha } \right){\text{e}}^{\alpha t}\) holds.
This completes the proof of the lemma.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Udayakumar, R., Geetha, K.V. An EOQ model for non-instantaneous deteriorating items with two levels of storage under trade credit policy. J Ind Eng Int 14, 343–365 (2018). https://doi.org/10.1007/s40092-017-0228-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40092-017-0228-4