Assessment of predictive control performance using fractal measures

Abstract

This paper presents novel approach to the task of control performance assessment. Proposed approach does not require any a priori knowledge on process model and uses control error time series data using nonlinear dynamical fractal persistence measures. Notion of the rescaled range R/S plots with estimation of Hurst exponent is applied. Crossover phenomenon is observed in data being investigated and discussed. Paper starts with industrial engineering rationale. Review of the control error histogram is followed by statistical analysis of probabilistic distribution functions (PDFs). Lévy $\alpha$-stable PDF parameters seem to be best fitted. They directly lead to the fractal analysis using Hurst exponents and R/S plot crossover points. The evaluation aims at performance of the generalized predictive control (GPC) and discusses freshly introduced loop performance quality sensitivity against design parameters of the GPC controller.

1 Introduction

Presented work combines observations from different contexts: CPA [24], model predictive control (MPC) [6], non-Gaussian statistics [19] and fractal nonlinear analysis [36]. The main research interests focus on the subject of control quality for SISO loop using predictive controller (GPC).

Predictive MPC algorithms gain popularity in industrial process control. Although they are more complicated and require specific knowledge, they allow to address issues that are unattained by PID loops. It may coordinate multivariate installations that are subject to delays and technology constraints. Real processes are mostly non-stationary, time-varying complex systems. Application of MPC may significantly improve control quality. It is compensated with more extensive tuning effort due to the larger number of parameters. Additionally, system sensitivity to unmodeled dynamics or internal model misfit increases. It may unexpectedly level down accomplishments. Improper or inexistent maintenance may significantly deteriorate any positive results [39].

Thus, loop quality and control system performance plays crucial role in achieving operational. Improperly selected philosophy of regulation or poor tuning affects or even may fully destroy overall process performance. Control performance monitoring and diagnostic tools are inevitable elements properly designed I&C infrastructure. This subject is even more important in case of advanced process control (APC) solutions.

MPC approach consists of many algorithms being variants of backbone predictive philosophy [28]. It uses embedded model supporting controller with predictions and optimization algorithm to choose optimal scenario. Control evaluation is repeated each step (sampling period). GPC algorithm is one of them. It was introduced in 1987 [9]. Although the algorithm is well established and there are a lot of variants and reported successful implementations, its design, tuning and maintenance are still challenging.

Reviews show that a large number of industrial loops perform poorly with 60% featuring bad tuning and more (85%) facing wrong design [25]. The need for control quality assessment is strong. CPA is closely connected with life cycle of control system. It uses specific indexes allowing measuring and benchmarking. There are several methods to evaluate and further interpret results. Data analysis may be performed with several different approaches starting from time trends, through statistical, minimum variance, frequency domain, orthogonal functions, wavelets, fractals, entropy and many others.

Historically, each control engineer used his own approach to quantify loop quality. They gathered unique knowledge based on personal experience, and it was rarely shared. Increasing quantity of applications accompanied with still limited number of experts forced the need for knowledge sharing. First reported loop performance assessment was applied to paper machine in 1967 [2]. The research continued gaining increased interest in 1989 with minimum variance (MinVar) index [21]. CPA interest grew up fast starting from that moment. Actually research covers almost all aspects of control, i.e., MIMO structures [51], nonlinear processes [23], large-scale systems [30], predictive systems [18, 34].

Moreover, there are developed new methodologies using frequency domain [35], wavelets [29], persistence measures [33], orthonormal functions [25], entropy [50]. It is interesting to notice that soft computing or artificial intelligence approach is rare. Scientific research is accompanied with industrial methods and commercial software packages.

Most methods assumes Gaussian properties. Normal probabilistic distribution function (PDF) approach is the most popular. But there are a lot of other functions offering interesting interpretations. It also appears that properties of many industrial examples are not so unambiguous. Extension of Gaussian approach opens new opportunities. It seems that fat-tail properties exist in the control error data [15]. Stable distributions may address real issues. Lévy $\alpha$-stable PDF seems to be one possible alternative. It is described by several parameters reflecting distribution position, stability, scale and skewness factors. There exist relations between fat-tail properties and a phenomenon of fractality [36].

Thus, there is only single step to apply fractal analysis. Approach was first proposed by Mandelbrot in 70’s [27]. Self-similarity is the underlying concept behind fractals meaning invariance against changes in scale or size [36]. Two other main distinctive properties are Hausdorff dimension larger then topological one and simple recursive definition.

Fractal time series analysis started to be developed in the world of economy. In economy there exists effectiveness hypothesis assuming that if prices reflect all publicly available information, new prices are only caused by new information. Thus, the prices should hold properties of the Brownian motion. It assumes that future is independent on past and the present. However, practice does not reflect it. Information is neither complete nor a priori known. We do not react immediately and simultaneously. Thus, we obtain rather fractional Brownian motion. Research shows that similar behavior and results are observed in many different areas. Fractal methods have found several applications in meteorology, seismology, biology, medicine, telecommunication, networking, etc. Analysis of control engineering time series originating from real complex industrial systems reveals similar properties [15, 17].

Unfortunately, there are only a few reported applications in control engineering. Authors in [41] address the subject of using Hurst exponent in the assessment of PI and PID controller. In [10] scaling exponent is used to assess Kalman filter performance. In the recent works authors [11] perform diagnosis of MIMO control loops with Hurts exponent evaluated through detrended fluctuation analysis (DFA) algorithm using Mahalanobis distance. The same approach is applied also to the disturbed univariate and multivariate systems with disturbances [12]. Methodology investigated in the paper performs comprehensive approach to the fractal methodology analyzing different persistence measures (not only single Hurst exponent).

Research considering performance assessment for predictive control strategies was conducted for several years. First works used knowledge-based system applied to the DMC-like predictive controller [34]. Further works continued in various directions. Model-based approaches [3, 7, 42] are accompanied with minimum variance methods [47, 48] that also require some process knowledge. Statistical approach through correlation analysis of optimal and working controller was proposed in [3], while prediction error benchmarking was used in [49]. Different aspect of economic, not dynamic, controller performance was addressed in [1]. Comprehensive review of various approaches is presented in [18].

We see that some of the previous methods use data-driven approach with covariance analysis. And most of them considers GPC structures. Algorithm proposed in this paper does not require any knowledge on controller neither embedded model and is purely based on historical data without any assumptions on its character. Thus, it may be commonly applied in industrial cases. In fact, it may be used to other control strategies. PID loop assessment is considered in [14].

SISO linear case is considered in paper. Such a selection is intentional. Its applicability has been already observed and effectively used in real industrial cases [17] with nonlinear complex process witnessing strong and unknown disturbances. Simple case enables clear and direct analysis of the investigated phenomena. The goal is to identify method potential and weaknesses. First works have shown approach applicability with simulated PID controllers. This work forms natural next step that (if successful) may be followed by further, in-depth (nonlinear, MIMO, complex) research. It is rather expected that nonlinear cases will be more suitable for fractal approach as it is just nonlinear. Research conducted on real industrial data confirms such a premise. In fact, there is no much difference in approach extension toward MIMO structures. The system uses control error; thus, it may monitor and assess independently all the channels (CVs—controlled variables).

Paper starts with the presentation of GPC algorithm (Sect. 2) and standard CPA approaches (Sect. 3). It is followed by introduction to stable distributions and their connections with fractal and persistence properties. Main part of the paper consists of simulation scenarios including varying GPC configuration (Sect. 4). Paper concludes with Sect. 5 consisting of observations and open issues requiring further attention.

2 Generalized predictive control

2.1 Predictive task formulation

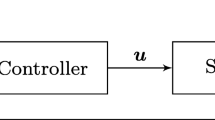
Let assume that process input (MV—manipulated variable) is u and the output (CV—controlled variable) y. Classical PID algorithm calculates only value of manipulated variable at current sampling moment k, i.e., u(k). In contrast, MPC algorithms [6] calculate a whole set of future controls for each consecutive moment k.

$$\begin{aligned} \triangle {\varvec{u}}(k)= & {} \left[ \triangle u(k|k) \ \triangle u(k+1|k)\right. \nonumber \\&\left. \ldots \triangle u(k+N_{\mathrm {u}}-1|k)\right] ^{\mathrm {T}} \end{aligned}$$

(1)

Number of decision variables is defined by control horizon length $N_{\mathrm {u}}$ and increments by:

$$\begin{aligned}&\triangle u(k+p|k)\\&\quad = {\left\{ \begin{array}{ll} u(k|k)-u(k-1) &{} \text {if }p=0\\ u(k+p|k)-u(k+p-1|k) &{} \text {if }p\ge 1 \end{array}\right. } \end{aligned}$$

We assume $\triangle u(k+p|k)=0$ for $p\ge N_{\mathrm {u}}$, i.e., $u(k+p|k)=u(k+N_{\mathrm {u}}-1|k)$ for $p\ge N_{\mathrm {u}}$. Future increments in MV (1) are calculated from optimization, in which predicted control quality is maximized and constraints regarded. Typically, quality is defined as predicted control errors over prediction horizon $N\ge N_{\mathrm {u}}$, i.e., differences between setpoint $y^{\mathrm {sp}}(k+p|k)$ and predicted process output ${\hat{y}}(k+p|k)$ for $p=1,\ldots ,N$.

Constraints are imposed on the range of MV defined by $u^{\min }, u^{\max }$, constraints on MV rate of change MV by $\triangle u^{\min }, \triangle u^{\max }$ and constraints limiting the range of predicted CV are $y^{\min }, y^{\max }$. MPC optimization may be expressed in a vector–matrix notation

$$\begin{aligned}&\min \limits _{\triangle {\varvec{u}}(k)} \Big \{ \left\| {\varvec{y}}^{\mathrm {sp}}(k)-\hat{{\varvec{y}}}(k)\right\| ^{2} +\left\| \triangle {\varvec{u}}(k)\right\| ^{2}_{\varvec{\Lambda }} \Big \} \nonumber \\&\text {subject to}\nonumber \\&{\varvec{u}}^{\min }\le {\varvec{J}}\triangle {\varvec{u}}(k)+ {\varvec{u}}(k-1) \le {\varvec{u}}^{\max }-\triangle {\varvec{u}}^{\max }\nonumber \\&\le \triangle {\varvec{u}}(k) \le \triangle {\varvec{u}}^{\max }{\varvec{y}}^{\min }\le \hat{{\varvec{y}}}(k)\triangle {\varvec{u}} (k)\le {\varvec{y}}^{\max } \end{aligned}$$

(2)

where the norms are defined as $\left\| {\varvec{x}}\right\| ^{2}={\varvec{x}}^{\mathrm {T}}{\varvec{x}}$ and $\left\| {\varvec{x}}\right\| ^{2}_{{\varvec{A}}}={\varvec{x}}^{\mathrm {T}}{\varvec{A}}{\varvec{x}}$, the setpoint trajectory vector is defined as ${\varvec{y}}^{\mathrm {sp}}(k)=\left[ y^{\mathrm {sp}}(k+1|k)\ldots y^{\mathrm {sp}}(k+N|k)\right] ^{\mathrm {T}}$, and the predicted trajectory vector $\hat{{\varvec{y}}}(k)=\left[ {\hat{y}}(k+1|k)\ldots {\hat{y}}(k+N|k)\right] ^{\mathrm {T}}$ and the output constraint vectors ${\varvec{y}}^{\min } =\left[ y^{\min }\ldots y^{\min }\right] ^{\mathrm {T}}, {\varvec{y}}^{\max }=\left[ y^{\max }\ldots y^{\max }\right] ^{\mathrm {T}}$ are of length N. The input constraint vectors ${\varvec{u}}^{\min }=\left[ u^{\min }\ldots u^{\min }\right] ^{\mathrm {T}}, {\varvec{u}}^{\max }=\left[ u^{\max }\ldots u^{\max }\right] ^{\mathrm {T}}, \triangle {\varvec{u}}^{\max }=\left[ \triangle u^{\max }\ldots \triangle u^{\max }\right] ^{\mathrm {T}}$ and the vector ${\varvec{u}}(k-1)=\left[ u(k-1)\ldots u(k-1)\right] ^{\mathrm {T}}$ are of length $N_{\mathrm {u}}$, matrices $\varvec{\Lambda }=\mathrm {diag}(\lambda ,\ldots ,\lambda )$ and ${\varvec{J}}$ are of size $N_{\mathrm {u}}\times N_{\mathrm {u}}$.

Optimization (2) is solved online. Future control increments (1) are calculated, but only first element of the sequence is applied to the process, i.e., $u(k)=\triangle u(k|k)+u(k-1)$. At next moment $k+1$, prediction is shifted one step forward and the procedure is repeated. Second part of the minimized cost function is a penalty term (weight $\lambda >0$), which is used to calm down trajectories (the bigger the value of $\lambda$, the slower the trajectories) and obtain good numerical properties.

2.2 GPC implementation issues

In all MPC algorithms dynamic model of the controlled process is used to predict the future values of the output variable, ${\hat{y}}(k+p|k)$, over the prediction horizon, i.e., for $p=1,\ldots ,N$. In the GPC algorithm process model has the form of a discrete difference equation

$$\begin{aligned} {\varvec{A}}(q^{-1})y(k)={\varvec{B}}(q^{-1})u(k-1)+{\varvec{C}}(q^{-1})\frac{\epsilon (k)}{\triangle } \end{aligned}$$

(3)

with polynomials in the backward shift operator ($q^{-1}$)

$$\begin{aligned} {\varvec{A}}(q^{-1})&=1+a_1 q^{-1}+\cdots +a^1_{n_{\mathrm {A}}}q^{-n_{\mathrm {A}^1}} \end{aligned}$$

(4)

$$\begin{aligned} {\varvec{B}}(q^{-1})&=b_1q^{-1}+\cdots +b_{n_{\mathrm {B}}} q^{-n_{\mathrm {B}}}\end{aligned}$$

(5)

$$\begin{aligned} {\varvec{C}}(q^{-1})&=1+c_1q^{-1}+\cdots +c_{n_{\mathrm {C}}} q^{-n_{\mathrm {C}}} \end{aligned}$$

(6)

Vector of white noises with zero mean is $\epsilon (k)$, and $\triangle =1-q^{-1}$ means backward difference operator ($1/\triangle$ is integration). Model (3) may be called autoregressive integrated moving average with exogenous input (ARIMAX) or controlled autoregressive integrated moving average (CARIMA) [44]. Assuming that the process is affected by integrated white noise, i.e., ${\varvec{C}}(q^{-1})=1$, model (3) becomes

$$\begin{aligned} {\varvec{A}}(q^{-1})y(k)={\varvec{B}}(q^{-1})u(k-1) +\frac{\epsilon (k)}{\triangle } \end{aligned}$$

(7)

Above model is usually applied in practical implementations of the GPC algorithm. Assumption that ${\varvec{C}}(q^{-1})=1$ makes it possible to easily derive prediction equations in comparison with the general case of ${\varvec{C}}(q^{-1})\ne 1$, i.e., when the integrated noise is colored. Model (7) is used to derive the prediction equation [9]

$$\begin{aligned} \hat{{\varvec{y}}}(k)={\varvec{G}} \triangle {\varvec{u}}(k)+{\varvec{y}}^{0}(k) \end{aligned}$$

(8)

where dynamic matrix ${\varvec{G}}$ (calculated once) of dimensionality $N\times N_{\mathrm {u}}$ consists of step response coefficients of model (7) and the free trajectory vector ${\varvec{y}}^0(k)=\left[ y^0(k+1|k)\ldots y^0(k+N|k)\right] ^{\mathrm {T}}$ (calculated at each sampling instant k) is obtained from

$$\begin{aligned} {\varvec{y}}^{0}(k)={\varvec{F}}{\varvec{y}}^{\mathrm {PG}}(k)+{\varvec{G}}^{\mathrm {PG}}\triangle {\varvec{u}}^{\mathrm {PG}}(k). \end{aligned}$$

(9)

The vectors ${\varvec{y}}^{\mathrm {PG}}(k)=\left[ y(k)\ldots y(k-n_{\mathrm {A}})\right] ^{\mathrm {T}}$ and ${\varvec{u}}^{\mathrm {PG}}(k)=\left[ \triangle u(k-1)\ldots \triangle u(k-n_{\mathrm {B}})\right] ^{\mathrm {T}}$ are of length $n_{\mathrm {A}}+1$ and $n_{\mathrm {B}}$, respectively, and the matrices ${\varvec{F}}$ and ${\varvec{G}}^{\mathrm {PG}}$ of size $N \times (n_{\mathrm {A}}+1)$ and $N \times n_{\mathrm {B}}$ are calculated from the model Eq. (7) solving Diophantine equations [44]. From Eqs. (8) and (9), GPC prediction equation is derived

$$\begin{aligned} \hat{{\varvec{y}}}(k)={\varvec{G}}\triangle {\varvec{u}}(k) +{\varvec{F}}{\varvec{y}}^{\mathrm {PG}}(k) +{\varvec{G}}^{\mathrm {PG}} \triangle {\varvec{u}}^{\mathrm {PG}}(k) \end{aligned}$$

(10)

It is necessary to notify that according to the GPC prediction Eq. (10) the future predictions of the controlled variable form linear functions of the calculated decision vector $\triangle {\varvec{u}}(k)$, and the free trajectory depends only on the past. Using Eq. (10), from the general MPC optimization problem (2), one obtains the GPC quadratic optimization task

$$\begin{aligned}&\begin{array}{l} \min \limits _{\triangle {\varvec{u}}(k)} \Big \{ \left\| {\varvec{y}} ^{\mathrm {sp}}(k)-{\varvec{G}}\triangle {\varvec{u}}(k)-{\varvec{F}}{\varvec{y}}^{\mathrm {PG}}(k)-{\varvec{G}}^{\mathrm {PG}}\triangle {\varvec{u}}^{\mathrm {PG}}(k)\right\| ^{2}\\ \quad \quad \quad +\left\| \triangle {\varvec{u}}(k)\right\| ^{2}_{\varvec{\Lambda }} \Big \} \end{array}\nonumber \\&\text {subject to}\nonumber \\&{\varvec{u}}^{\min }\le {\varvec{J}}\triangle {\varvec{u}}(k)+{\varvec{u}}(k-1) \le {\varvec{u}}^{\max }\nonumber \\&-\triangle {\varvec{u}}^{\max }\le \triangle {\varvec{u}}(k)\le \triangle {\varvec{u}}^{\max }\nonumber \\&{\varvec{y}}^{\min }\le {\varvec{G}}\triangle {\varvec{u}}(k)+ {\varvec{F}}{\varvec{y}}^{\mathrm {PG}}(k)+{\varvec{G}}^{\mathrm {PG}} \triangle {\varvec{u}}^{\mathrm {PG}}(k)\triangle {\varvec{u}}(k)\le {\varvec{y}}^{\max } \end{aligned}$$

(11)

In the GPC quadratic optimization problem (11), which is solved online at each sampling instant k to calculate the vector of the increments of the future values of the manipulated variable, i.e., the vector $\triangle {\varvec{u}}(k)$, the minimized cost function is quadratic in terms of $\triangle {\varvec{u}}(k)$ and all the constraints are linear in terms of $\triangle {\varvec{u}}(k)$. That is why it may be solved online very efficiently using the available solvers, e.g., the active set or interior point algorithms. It is important to emphasize that due to the quadratic nature of the GPC optimization problem, the global solution is found at all sampling instants k.

3 Control loop quality measures

Control performance assessment methods that are used in the analysis are described in the following paragraphs.

3.1 Time-domain CPA methods

Time-domain approach is straightforward and is commonly used. It may be based on data gathered from specific test experiment data (like step test) or from normal operation time trends. Step test measures are very informative [40] (area index, output index, R-index, idle index), but they have limited applicability. Industry is not eager to allow dedicated experiments disturbing normal operation, because of lost profits and safety issues. On the other hand, integral indexes based on data from normal operation are widely used. Three of them will be evaluated and compared further:

• Mean square error (MSE):

  $$\begin{aligned} \hbox {MSE} = \frac{1}{N}\sum _{i=1}^{N}\left( y^{*}_{i} - y_{i} \right) ^{2}, \end{aligned}$$

  (12)

  where N-number of samples, $y^{*}$-setpoint (reference signal), y-process output.

• Integral of absolute error (IAE):

  $$\begin{aligned} \hbox {IAE} = \frac{1}{N}\sum _{i=1}^{N}\left| y^{*}_{i} - y_{i} \right| , \end{aligned}$$

  (13)

• And amplitude index (AMP):

  $$\begin{aligned} \hbox {AMP} = \max \left( y^{*}_{i} - y_{i} \right) - \min \left( y^{*}_{i} - y_{i} \right) . \end{aligned}$$

  (14)

MSE and IAE are frequently used alternately. However, they focus on different aspects. It was shown [37] that tuning minimizing MSE punishes large setpoint deviations and generates aggressive control, while IAE has closest relationship to economic considerations [38]. Both of them will be considered in this work.

3.2 Statistical indexes

Statistical factors of Gaussian normal distribution deliver number of KPIs. Mean value $x_{o}$ and standard deviation $\sigma$ are commonly used. They are frequently followed by higher-order statistics [8]. Their meaning and importance are unquestionable, and the majority of researchers and practitioners use them. However, we have to remember that they are valid, while signal properties are Gaussian.

Fig. 1

Histogram fitted with Cauchy PDF

Fig. 2

Histogram fitted with Lévy PDF

It was shown [13] that only small amount ($\approx$6%) of industrial loops holds normal properties. Majority of them have fat-tail characteristics. Mostly Lévy $\alpha$-stable distribution is the best fitted (>60%) (see Fig. 2), with the rest covered by Cauchy distribution (see Fig. 1). Lévy $\alpha$-stable distribution forms feasible alternative for control error fitting. It has more degrees of freedom (15) as it is parametrized by four parameters.

$$\begin{aligned} \varphi _{\alpha ,\beta ,\delta ,\gamma }(t) = \hbox {e}^{i\delta t - \left| \gamma t \right| ^{\alpha } \left( 1-i\beta l(t) \right) }, \end{aligned}$$

(15)

where

$$\begin{aligned} l(t) = \left\{ \begin{array}{ll} \hbox {sgn}(t) tg\left( \frac{\pi \alpha }{2} \right) &{} \text {for }\alpha \ne 1\\ -\hbox {sgn}(t) \frac{2}{\pi }\ln \left| t \right| &{} \text {for }\alpha = 1\\ \end{array} \right. , \end{aligned}$$

$0<\alpha \le 2$ stability index, $\left| \beta \right| \le 1$ skewness, $\delta \in {\mathbb {R}}$ location and $\gamma >0$ scale factor.

Stability parameter $\alpha$ is responsible for long tails. Location $\delta$ keeps information about function position, but it should not be considered identical to the mean value. Additionally, we have two more shaping parameters. $\beta$ informs about distribution skewness, while scale factor $\gamma$ has the meaning very similar to $\gamma$ parameter of Cauchy PDF. There might be different combinations of them. For instance $\alpha =2$ reflects independent realizations. For $\alpha =2 , \beta =0 , \gamma = 1$ and $\delta = 1$ we get exact normal distribution equation.

Lévy distribution has another advantage. Stability parameter $\alpha$ responsible for tails is connected with fractal properties. This aspect will be closely discussed later; however, at that moment we decide to use $\alpha$-stable factors as potential measure. In considered case, $\alpha$-stable fitting uses Koutrouvelis [26] regression approach.

3.3 Nonlinear (fractal) analysis

There are several factors to verify fractal hypothesis. One is to calculate value of the Hurst exponent H measuring persistence. Hurst exponent is defined as the asymptotic property of the rescaled range R/S factor

$$\begin{aligned} \left( \frac{R}{S} \right) _{n}=cn^{H}, n\rightarrow \infty \end{aligned}$$

(16)

where S—standard deviations in time slot n, c—positive constant, n—number of observations, H—Hurst exponent. H is calculated using logarithms

$$\begin{aligned} \ln \ E(R/S)_{n} = \ln \ c\ +\ H\ln \ n \end{aligned}$$

(17)

plotted in double logarithmic scale $E(R/S)_{n}$ from n estimating H as the line slope. Meaning of H value is as follows:

• $H=0.5$ means that all observations are statistically independent and process is stochastically uncorrelated.

• $0<H<0.5$ means anti-persistent time series. Decrease in the past suggests increase in the future and opposite.

• $0.5<H\le 1$ means persistent process, i.e., data increase or decrease in the past implies increase/decrease in future, respectively.

• For higher values, i.e., $H>1$ processes are said to have no dependency in time domain.

R/S plot is the basic approach to estimate H. It enables to evaluate not only single scaling exponent, but also reveals additional features of multiple scales and crossover points. Apart from above Hurst exponent evaluation method, there are other algorithms, as in historical order. Selected ones (among many others) are used: periodogram [20], boxed or modified periodogram method [22], aggregated variance method [5], detrended fluctuation analysis (Peng) [31], absolute value method [43] and differential variance [45].

Finally, there exists hypothesis that Hurst exponent may be equivalent to the inverse of $\alpha$ parameter of the Lévy $\alpha$-stable distribution characteristics equation [32]. There exist several assumptions on data properties limiting validity of this result. The comparison and sensitivities of chosen methods are not the direct goal for this paper, but some such aspects will be addressed.

4 Simulations

4.1 Simulation example

The following continuous-time dynamic system is used:

$$\begin{aligned} G(s)=\frac{K}{(T_1s+1)(T_2s+1)}\hbox {e}^{-T_0s} \end{aligned}$$

(18)

with parameters: $K=2, T_0=4, T_1=3, T_2=10$. During GPC algorithm simulations constraints imposed on the range of MV are taken into account, $u^{\min }=-1, u^{\max }=1$, as well as change rate limits of MV $\triangle u^{\min }=-0.05, \triangle u^{\max }=0.05$. It has been determined that control horizon should be $N_{\mathrm {u}}=3$, prediction horizon should be $N=25$ and penalty term $\lambda =0.5$ [its value is found experimentally, and it leads to no problems with online solution of the quadratic optimization GPC task (11)]. For tuning of the GPC algorithm no plant–model mismatch is assumed, i.e., the model is perfect. Simulation loop diagram is sketched in Fig. 3.

Fig. 3

Closed-loop simulation environment

Simulation control loop is also exposed to disturbances. Disturbance z(t) with $\alpha$-stable properties is added before the process, while Gaussian noise d(t) is added at the process output. In order to investigate how disturbances which affect the process and modeling inaccuracy result in deterioration of control quality, four scenarios are run:

(Sc1):

Seven real process gains are applied: 0.4, 0.8, 1.2, 2.0, 2.8, 3.2 and 3.6.

(Sc2):

GPC applied prediction horizon length different from the tuned one $N=25$. Altogether seven values are considered: 5, 10, 15, 20, 25, 30 and 35.

(Sc3):

Real process delay value differs from that of the model used for GPC design, $T_0=8$. Nine different process delays are used: 4, 5, 6, 7, 8, 9, 10, 11 and 12.

(Sc4):

Real value of time constant, $T_2$ being different from the tuning value $T_2=10$. Seven values are checked: 0.5, 1, 5, 10, 15, 20 and 40.

In addition to above experiments, three different scenarios of disturbances are considered:

• 1. Process is not exposed to any disturbance.

• 2. Control loop is affected by additive input disturbances in the form of random values with normal distribution and amplitude of 0.008.

• 3. Control loop is affected by additive input disturbances in the form of random values. It has a $\alpha$-stable distribution with amplitude of 0.04.

Additionally, nominal GPC loop was simulated with different noise characteristics, i.e., no disturbances, three levels of normal noise (small, medium and large) and stability factors $\alpha = 1.5,\ 1.75,\ 2$ of stable distribution. Those scenarios are used to answer questions and check the following hypotheses:

• (H0) Are the measures independent on disturbance characteristics? Can we evaluate loop quality despite disturbances?

• (H1) Does setpoint impact results of loop quality assessment?

• (H2) Can we identify whether GPC model gain is appropriate?

• (H3) Can we estimate whether GPC horizon is set properly?

• (H4) Can we confirm whether GPC model delay is appropriate?

• (H5) Can we say assess GPC model dynamics?

Simulation scheme, especially applied SISO model, is simple. However, this decision was intentional. Simple model enables disclosure of the possible relations. On the other hand, this model embeds several common features of real process, i.e., different scales in dynamics and significant delays. Complexity and detection difficulties are imposed by selected fat-tail disturbances that may easily and often shadow any detection possibility.

4.2 Results

The main goal is to investigate behavior of fractal measures. However, its analysis without any references would not be comparable. At first all the indexes are simply correlated against each other to see if there is any consistency. This analysis is done on all available data (see Table 1).

Table 1 Correlation table ($H^{RS}$: single memory scale Hurst exponent, $n^\mathrm{(cross)}$: crossover, $H^\mathrm{(short)}$: short-history exponent for two scales, $H^\mathrm{(long)}$: long-history exponent for two scales)

Analysis of correlation data enables to formulate initial observations. We see that crossover point (cross) is rather uncorrelated with other measures. It seems that this factor carries on other information. Also short-history Hurst exponent for two memory scales R/S plot is not correlated. In fractal domain H calculated as $1/\alpha$ is not in line with other Hurst estimates or CPA indexes. We may also notice that Hurst exponents calculated from R/S plot are not strongly correlated with other H measures. Those measures are intercorrelated, and additionally, it seems that they may reflect similar behavior as AMP and integral indexes IAE and MSE. We see that statistical scale factors of non-Gaussian functions are closely coupled. Lévy stability parameter $\alpha$ seems to keep similar information. Thus, for further analysis only two statistical factors of $\alpha$-stable distribution are used, i.e., stability and scale factor.

4.2.1 H0: impact of disturbances

Ability to detect and identify controller tuning goodness despite any disturbances should be one of the main features of perfect loop quality assessment. From that perspective of controller the measure value should be invariant. We consider 13 scenarios of different disturbances (see Table 2).

Table 2 Scenarios for disturbance invariance investigation

Analysis starts with comparison of undisturbed value with mean and variance of disturbed values for any measure. Six different simulations are considered: optimal GPC model with horizons equal to 12 and 25, internal model with too small gain $K=1.6$ for both horizons. Analogously, two simulations are run with too large gain $K=2.4$ for both horizons.

Stability factor $\alpha$ is sketched in Fig. 4 and scaling $\gamma$ in Fig. 5. Very clear separation is visible with worse tuning for both parameters. Unfortunately, GPC regulation with optimal model is not well detected.

Fig. 4

Disturbance impact on factor $\alpha$ of $\alpha$-stable distribution

Fig. 5

Disturbance impact on factor $\gamma$ of $\alpha$-stable distribution

Next fractal measures are presented. For all cases rescaled range R/S plots are prepared. It has been noticed that all of them witness crossover behavior. R/S plot for the best GPC controller (ideal model) with no disturbances is presented in Fig. 6 as an example.

We clearly see two persistence scales separated with single crossover point. Short-memory Hurst exponent is close to the value of uncorrelated process $H^\mathrm{(short)} = 0.544$, while long-memory Hurst exponent (starting after crossover point $n^\mathrm{(cross)} = 504\,s$) is definitely anti-persistent with $H^\mathrm{(long)} = 0.157$. Comparison of plots confirms the same pattern for all considered scenarios.

Above results are very interesting. Short-memory exponent $H^\mathrm{(short)}$ is close to 0.5, i.e., independent stochastic process of Brownian motion. It would confirm hypothesis proposed in [40] that $H=0.5$ is connected with well-fitted controller. It is also suggested that persistent properties reflect sluggish performance, while anti-persistent ones indicate aggressive tuning often characterized by oscillations.

Fig. 6

R/S plot for an ideal case

It is needed to explain strong anti-persistent behavior of long-memory $H^\mathrm{(long)}$ exponent. Control error constitutes of two elements: short-term transient period (probably associated with $H^\mathrm{(short)}$) and long-term steady-state operation (reflected in $H^\mathrm{(long)}$). As GPC controller uses ideal model, $H^\mathrm{(short)}$ is relatively close to 0.5. On the other hand, strong anti-persistent $H^\mathrm{(long)}$ is reflected in semi-flat line of the steady-state control error once system stays on setpoint.

Discussion prepares hypotheses for further analysis. As R/S plot is characterized by two persistence scales separated with single crossover point, the evaluation of single Hurst indexes with other then R/S plot algorithms is not justified. Thus, only parameters of two memory scales R/S plot will be further taken into consideration, i.e., $n^\mathrm{(cross)}, H^\mathrm{(short)}$ and $H^\mathrm{(long)}$.

Crossover phenomenon impact is presented in Fig. 7. We may see that crossover seems to be relatively independent of noise and is worth to be considered in further evaluations.

Fig. 7

Disturbance impact on crossover point

Fig. 8

Disturbance impact on short-memory Hurst exponent

Fig. 9

Disturbance impact on long-memory Hurst exponent

Both Hurst exponents $H^\mathrm{(short)}$ and $H^\mathrm{(long)}$ are sketched on two following plots (Figs. 8, 9). Both present similar properties despite loop disturbances. One may notice from those plots’ behavior similar to the one from non-Gaussian statistics. There is more clear distinction between GPC model fitting for worse controller, rather than for the ideal one.

The analysis presented in that paragraph evaluated potential robustness of the considered loop quality measures against disturbances embedded into the close loop. It seems that the parameters are mostly able to detect controller misfitting despite disturbances. However, there are parameters that are screened by noise with unreliable results, like AMP.

On the other hand, in the group of fractal indexes it has been shown that R/S plot features distinctive crossover behavior. Thus, all single memory Hurst indexes are of no use and their estimation is not useful. Following indexes are further used:

• statistical indexes: Gauss standard deviation $\sigma$ together with $\alpha$ and $\gamma$ of $\alpha$-stable PDF,

• integral indexes of IAE and MSE,

• fractal measures originating from R/S plot: $n^\mathrm{(cross)}, H^\mathrm{(short)}$ and $H^\mathrm{(long)}$.

4.2.2 H1: effect of setpoint shape

During evaluation of above results there has been formulated hypothesis that results may be biased by the shape of setpoint. At first setpoint is in the form of rectangular wave with varying amplitude. Second set of the same experiments is run to exclude that effect with setpoint filtered by first-order inertia. It is to verify hypothesis that setpoint shape may affect results, especially through length of transient period in relation to steady-state time. Minimum, maximum, average and standard deviations of the measure error $\Delta \eta$ for each index are calculated. Results are presented in Table 3.

Table 3 Statistical properties of the measure errors

We see good robust behavior of scale factor $\gamma$. We also observe that stability parameter $\alpha$ has the largest standard deviation (variability). The reason for that may originate from multi-persistent nature of the R’S plot with two distinct scales. Short-memory Hurst exponent $H^\mathrm{(short)}$ is the most robust one from the perspective of robustness. Its value is practically invariant against setpoint shape. It is in clear contrary to the long-memory exponent $H^\mathrm{(long)}$. It somehow confirms hypothesis that long-memory effect is connected with steady state. It is reflected in long-memory Hurst exponent, as setpoint shape affects steady-state operation. Crossover position is indecisive, and it remains for further evaluations, while $H^\mathrm{(long)}$ is excluded.

We main formulated some working hypothesis that detailed analysis of R/S plot may new indications on loop behavior, like for instance about steady-state operation. While $H^\mathrm{(short)}$ holds information about transient period properties, $H^\mathrm{(long)}$ supplements us with steady-state information.

4.2.3 H2: impact of model gain

Experiments to verify hypothesis H2 are organized as follows. We check whether selected measures can detect proper selection of the GPC embedded model gain. Thus, nine different gain values are tested: 0.4, 0.8, 1.2, 1.6, 2.0, 2.4, 2.8, 3.2 and 3.6. For each one three different disturbance scenarios are tested: no disturbances, Gaussian noise added before the process and $\alpha$-stable disturbance after the controller.

Fig. 10

Dependence of Lévy’s $\gamma$ on GPC model gain

Fig. 11

Dependence of Lévy’s $\alpha$ on GPC model gain

Fig. 12

Dependence of R/S crossover $n^\mathrm{(cross)}$ on GPC model gain

Fig. 13

Dependence of Hurst exponent $H^\mathrm{(short)}$ on GPC model gain

As we know the real value of the model gain is 2.0. Thus, the plots should be able detect that value with minimum index value. It is very clearly seen that all but $\alpha$ curves indicate that point. Stability parameter (Fig. 11) fails in this task. Scale factor is exact in detection (Fig. 10). Fractal parameters originating from R/S plot, i.e., crossover point (Fig. 12) and Hurst exponent $H^\mathrm{(short)}$ (Fig. 13), also have similar ability. Crossover indicates exact point, while $H^\mathrm{(short)}$ detect slightly overestimated value of $K=2.4$.

4.2.4 H3: impact of model delay

Similar analysis is used to verify whether selected measures can detect selection of the GPC controller model delay. Thus, nine different delay values are tested: 4, 5, 6, 7, 8, 9, 10, 11 and 12. For each of the delays three disturbance scenarios are tested: no disturbances, Gaussian noise added before the process and $\alpha$-stable disturbance inputted after the controller.

Fig. 14

Dependence of $\gamma$ of Lévy distribution on GPC model delay

Fig. 15

Dependence of $\alpha$ of Lévy distribution on GPC model delay

Real value of the model delay is 8.0. Thus, plots should somehow enable finding out of this value. Unfortunately, in that case detection is not straightforward. It works only in one case, i.e., when there are no disturbances in the loop. It is especially visible for both stable PDF $\gamma$ (Figs. 14, 15) indexes. Curve for undisturbed loop is in compliance with our expectation. First the index diminishes up to ideal value and then starts to rise in linear way. We may clearly find out optimal value of the delay and additionally see that increase in the model delay constantly degrades control. However, simultaneously relations for disturbed loops are just flat. The measures are independent on model delay. It seems that loop disturbances screen effect of model delay misfit.

Fig. 16

Dependence of R/S crossover $n^\mathrm{(cross)}$ on GPC model delay

Fig. 17

Dependence of Hurst exponent $H^\mathrm{(short)}$ on GPC model delay

The curves for fractal measures, i.e., crossover point (Fig. 16) and Hurst exponent $H^\mathrm{(short)}$ (Fig. 17), are indecisive. First of all they show something only for undisturbed loop. Disturbances shadow delay misfit.

They both also degrade with overestimated delay. Thus, they detect to large delay. But they fail to change their value for underestimated model delay. Concluding, we see that appropriate model delay value is hardly detected. Strange behavior is observed in presence of disturbances. All the curves flatten and show nothing.

4.2.5 H4: impact of model dynamics

Next the same methodology is applied to verification whether selected measures can detect proper GPC embedded model dynamics. Seven different values for time constant $T_2$ are tested: 0.5, 1, 5, 10, 15, 20 and 40. Three different disturbance scenarios are tested, i.e., no disturbances, Gaussian noise added before the process and $\alpha$-stable disturbance inputted after the controller for each time constant.

Fig. 18

Dependence of $\gamma$ of Lévy distribution on GPC model time constant $T_2$

Fig. 19

Dependence of $\alpha$ of Lévy distribution on GPC model time constant $T_2$

Real value of the model delay is 10. Thus, the plots should be able to detect that value. Observing the plots we notice two different curve types. First, for stable PDF $\gamma$ (Fig. 18) we see clear ability to show the right value, while $\alpha$ (Fig. 19) totally fails.

Fig. 20

Dependence of R/S crossover $n^\mathrm{(cross)}$ on GPC model time constant $T_2$

Fig. 21

Dependence of Hurst exponent $H^\mathrm{(short)}$ on GPC model time constant $T_2$

We see that too small values of dynamics do not deteriorate control quality significantly (in sense of the measure considered). In contrary, for too high values of $T_2$ indexes rapidly increase suggesting fast degradation of control quality. This behavior is interpreted that underestimated dynamics is not so dangerous for GPC control as a too slow ones.

There is also observed that detection is better for disturbed loops, than for undisturbed ones. This is in contrary to previous scenario (H3: impact of model delay). It seems that more excited trends (due to the disturbances) enable better exposure of dynamics misfit effect.

Curves for parameters originating from R/S plot, crossover point (Fig. 20) and Hurst exponent $H^\mathrm{(short)}$ (Fig. 21) have different properties. Both of them are monotonic. Crossover point decreases, while Hurst exponent has positive slope. They keep the same shape despite loop disturbances.

This effect requires discussion. Some explanations may be proposed for the Hurst exponent. As it was already cited [40], Hurst exponent value shows different kinds of tunings. It changes from anti-persistent $H<0.5$ oscillatory behavior, through neutral Brownian motion with independent stochastic process ($H=0.5$) up to persistent properties ($H>0.5$) reflecting sluggish tuning. From that perspective limiting (min or max) index values does not have to reflect anything. We see that for model gain impact all the $H^\mathrm{(short)}$ values are larger than 0.5, and thus, minimal value is the closest to independent stochastic process $H^\mathrm{(short)} \approx 0.54$. For model delay impact analysis we had similar values for $H^\mathrm{(short)} > 0.5$ with similar minimum of close to independent stochastic process $H^\mathrm{(short)} \approx 0.54$.

Following above, optimal value of the Hurst exponent should not be extremum necessarily. It should lie at the crossing with Hurst exponent optimum value. Its first estimate is 0.5, but other research shows that it does not have to be exactly that value. Thus, lack of extremum does not mean wrong detection. Hurst index is more reach in information showing not only whether control is good or bad, it also give us indication what kind of wrong tuning we are witnessing (sluggish or aggressive). Hypothetically, it might be possible that similar effect is observed on the crossover curve but this hypothesis requires further investigation.

4.2.6 H5: impact of GPC controller horizon

Finally, similar analysis is used to verify whether selected measures can detect proper selection of the GPC controller horizon. Thus, seven different horizon values are tested: 10, 12, 15, 20, 25, 30 and 35. For each of the horizons three different disturbance scenarios are tested: no disturbances, Gaussian noise added before the process and $\alpha$-stable disturbance inputted after the controller.

In this case different kind of results is expected. Theoretical speculations about predictive controller clearly say that the horizon should not be too short against process delay and dominant time constant. We should not loose dynamics. However, there is nothing wrong about overestimated horizon length. It will only result in larger calculation effort without deterioration of control quality.

Fig. 22

Dependence of $\gamma$ of Lévy distribution on GPC controller horizon

Fig. 23

Dependence of $\alpha$ of Lévy distribution on GPC controller horizon

As we look at figures of $\gamma$ (Fig. 22) and $\alpha$ (Fig. 23), we explicitly see expected behavior. First, the measure curve rapidly decreases up to value of ${\sim }20$ and after that saturates. It means that there is no reason to increase further GPC horizon. We are unable to improve control performance behind this value. Additionally, it is detected despite loop disturbances. Proper horizon value is identified despite minor differences for stability index.

Crossover point (Fig. 24) impact analysis does not give us any explicitly clear indication. We see measure value saturation for $\hbox {horizon} > 20$ and tendency for lower values for smaller horizon lengths. These observations are independent on loop disturbances.

Fig. 24

Dependence of R/S plot crossover $n^\mathrm{(cross)}$ on GPC controller horizon

Fig. 25

Dependence of Hurst exponent $H^\mathrm{(short)}$ on GPC controller horizon

Less clear detection is for short-memory exponent $H^\mathrm{(short)}$ (Fig. 25). First of all its values vary in a very narrow range $\left( 0.54 \div 0.58 \right)$. Despite shape disruption for the shortest horizon considered ($\hbox {horizon} = 10$) the shape gives indication. This unexplained behavior for short horizon is not so disturbing for crossover point as it varies in relatively wider range. This effect disturbs proper detection with Hurst exponent. This scenario closes simulation analysis.

4.3 Method application scheme

Applicability of the proposed methods and measures may help to extend current schemes, allowing for more degrees of freedom. We may imagine two possible scenarios:

• 1. the tuning (implementation) of the MPC controller,

• 2. monitoring of the already working MPC algorithm.

The methodology differs in each of the above scenarios. The proposed measures show ability to reflect misfitting in the parameters of the MPC embedded model. But the measures itself do not show direction of the required change. We can investigate it through several tests evaluating the trends of the indexes. Moreover, the changes in measures do not show the source of the results. It is difficult to distinguish between the gain or dynamics misfit. The one possible method of their use is described below. We select three measures for observation: $\alpha$-stable PDF scaling $\gamma$, stability factor $\alpha$ and short-memory Hurst exponent $H^\mathrm{(short)}$.

4.3.1 MPC tuning

The tuning of the MPC controller is not an easy task. The embedded model and the prediction horizon are among the most important settings.

• 1. At first the process model is identified, most often during the process of process parametric tests and a separate identification. This model allows MPC operation; however, its fine tuning is most probably required.

• 2. Next, the horizon should be set. As we are changing only one MPC parameter in a time, we can try to lower the horizon length and observe the according changes in the scaling $\gamma$. We select the shortest horizon length, when the scaling value stops to diminish.

• 3. Model delay is not well reflected by the measures in case of high disturbance ratio. If the disturbances are significant, we have to use other methods or rely on the initially identified value. In case of minor disturbance impact, it can be tuned with the aid of scaling $\gamma$.

• 4. Tuning of the model gain should be done next. We select the gain for the minimum value of the scaling factor $\gamma$.

• 5. We perform the fine tuning of the model dynamics (time constants) in the same way as for the model gain.

• 6. The above steps are using scaling factor $\gamma$ only intentionally. During the whole process the stability $\alpha$ is observed. It is responsible for the fat tails, and its desired value is $\alpha =2$. We use it to distinguish between tunings of the very similar performance (from the perspective of scaling) to select the one with stability closest to 2.

• 7. Finally, the Hurst exponent should be discussed. Actually it is not actively used during the process. But it should be measured continuously and matched with the obtained control qualities, both good, sluggish and aggressive. This relation is used to determine what value of the Hurst exponent relates to the best case tuning.

• 8. Hurst exponent is then used for further process monitoring. We may distinguish between selected “good” operation and undesirable sluggish or aggressive one through observation of its fluctuations.

4.3.2 MPC assessment

During the monitoring of the already operating loop we are facing the situation, when the process fluctuates. It is the most probably associated with the non-stationary variations in the process dynamic characteristics. This causes misfitting in the MPC embedded model.

We need to observe time trends scaling factor $\gamma$ and short-memory Hurst exponent for that purpose. Lasting increase in scaling may indicate the effect of process dynamic fluctuations and MPC embedded model misfit. Simultaneously observing direction of changes in Hurst exponent we may determine, in which direction these changes go, i.e., sluggish or aggressive. It is worth to perform online monitoring activity. This subject is discussed in details in [16].

Following the observations of the online monitoring, the appropriate tuning initiative may be started using the schemes proposed in the description of the MPC tuning.

5 Conclusions and further research issues

This paper presents results of the research on alternative CPA measures applied to control quality assessment for SISO loop with GPC controller. Analysis is based on simulations, even though the subject has appeared and grown up in real, industrial cases. All considered measures have been calculated using control error variable as it is the best loop signal available for analysis. First, its optimal value is zero, so any nonzero mean value at once indicates steady-state error. Any skewness clearly suggests asymmetric control, possibly due to the process nonlinearities or constraints. Finally, it should not be subject to any external trends, like for instance process output variable. Thus, no detrending is required.

Investigation starts with comparison of three CPA measures’ groups: statistical ones (both Gaussian and non-Gaussian), integral indexes based on time trends and fractal persistence measures using Hurst exponent. The goal is to find indexes invariant to loop external environment (disturbances, setpoint, etc.). Analysis enables selection of four promising indexes: two parameters of $\alpha$-stable distribution (stability and scale factor), $n^\mathrm{(cross)}$—crossover point of the R/S plot for the control error and $H^\mathrm{(short)}$—short-memory Hurst exponent.

The approach to the estimation of Hurst exponent is general. It does not assumes whether we face single or multiple persistence scales. It may work in case of any loop performance, like oscillation. Its deficiency lies in fact that it is not automatic. Close visual inspection of rescaled range plots is required, at least at the early stage of assessment. However, in opinion of authors, it is advantage as such review may disclose aspects otherwise omitted.

Next, they are used to verify ability to detect tuning quality of the GPC controller: impact of model gain, effect of model delay, influence of model dynamics and impact of GPC controller horizon. Comparison of results shows that:

• 1. Gaussian standard deviation is biased by the character of setpoint signal. The same effect happens with stability parameter $\alpha$. In contrary scale factor of the $\alpha$-stable distribution seems to be robust as control error histogram is strongly fat-tailed.

• 2. Fractal analysis through rescaled range R/S plot and Hurst exponents show that it has crossover properties with two strict Hurst exponents: short and long memory. Analysis suggests that crossover and short-scale Hurst exponent are invariant and informative. It is proposed that short-range exponent is responsible for transient period performance (controller tuning), while long-range one informs about steady-state stabilization.

• 3. It is not suggested to calculate single Hurst exponent without review od R/S plot.

• 4. Lévy’s $\gamma$ is able to detect model gain, dynamics misfit and GPC horizon length. It only has problems with model delay. In that case any loop disturbance screens detection.

• 5. Short-range Hurst exponent behaves in different way. We are not searching for its minimum, nor maximum value. Its best value is expected to be at values ${\sim }0.5$ with smaller values informing about control loop aggressiveness and higher ones detecting sluggish tuning. Thus, Hurst exponent is more informative. It not only says whether control is better or worse, but indicates the reason. We may also have another degree of freedom. Value 0.5 does not have to be optimal. It depends on control requirements. If we allow overshoot, it may be shifted down and in opposite case biased up.

• 6. Crossover behavior and its detection ability are still open and undecided. It seems to be good indicator, independent on external loop influences. However, its optimal value does not have to be at extremum. It may also hold information about reasons for wrong tuning. As for Hurst exponent the best value may be estimated as uncorrelated stochastic process, it is not evident what value is the best for crossover point.

• 7. Detection ability fails with model delay misfit. It works only in case of no disturbances.

• 8. Stability factor of Lévy distribution is altered by two memory scales in R/S plot and needs more investigation

Above analysis addresses the subject of performance monitoring of a closed-loop dynamic system. The approach originates from process industry needs, when some complex system is controlled. The paper shows that application of chaos-based methods brings benefits. It would be extremely interesting to see whether such persistence and fractal measures may be used to evaluate quality of a control for chaotic systems, like [46].

Analysis reveals open subject that requires closer insight. Delay misfit detection is probably the most important one. It is the only parameter of the GPC controller, for which approximation misfit is hardly detected. Potential hypothesis that it may be caused my disturbance shadowing effect requires attention. Next, statistical properties of the control error signal should be investigated. It would be worth to confront such a simulation analysis with industrial process time trends. Last open issues are associated with fractal properties.

• Crossover phenomenon requires closer attention. Further research will focus on its origins and meaning. It will be analyzed how process complexity affects the number of crossover points and their position, as complex dynamics frequently causes multiple scaling exponents in the same range of scales [4].

• Finally, the paper did not addressed eventual multi-fractal properties of the control error time series. The authors assumed mono-fractal behavior. The data will be analyzed to see, whether multi-fractal properties exist in control time trends data.

Above results and observations are accomplished with simple linear SISO case. It is worth to investigate more complex scenarios, like nonlinear, MIMO and systems with significant delays cases to verify method applicability and effectiveness.