1 Introduction

An extensive system of flood defences has been constructed in the Netherlands to prevent regular floods from the sea, major rivers and lakes. In this system, 53 dike ring areas are distinguished, which are protected by a connected system of dikes, dunes and hydraulic structures. For the design and safety assessment of the flood defences, protection standards per dike ring area are defined in terms of “allowable flood frequencies”. The present protection standards vary from 10−3 to 10−4 per year. The foundation of the flood protection standards was laid by Van Dantzig (1956) and formally established in Delta Committee (1958). The present protection standards are being reconsidered, following the advice of a newly established Delta Committee (2008). The proposed protection standards for safety assessments from 2017 onwards will be based on an advanced cost-benefit analysis (Kind 2013) and on flood fatality risk assessments. Fatality risks are considered from the viewpoint of individuals and from the perspective of society. The framework presented in this paper is developed to assess societal flood fatality risks. However, the concept can also be used to quantify economic flood risks.

Societal flood fatality risk in the Netherlands is defined as the probability of exceedance of a large number of flood fatalities occurring in a single year. This risk is typically quantified with FN-curves (Beckers et al. 2012; De Bruijn et al. 2010; Evans and Verlander 1997; Vrijling et al. 1995), where N is the number of fatalities and F is the associated frequency of exceedance. The FN-curve allows for a differentiated evaluation of events with high probabilities and low numbers of fatalities versus events with low probabilities and high numbers of fatalities. The new protection standards for the Netherlands will be based on the criterion that events with 10*N fatalities are 100 times less tolerable than events resulting in N fatalities. The FN-curve provides the required information to evaluate such criteria.

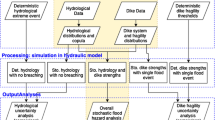
For the analysis of societal flood risk, the potential influence of a dike breach on the flood risk of downstream areas needs to be taken into account. Otherwise, scenarios in which (almost) all dike ring areas are flooded may have a significant effect on the derived FN-curve, even though in reality these scenarios cannot occur. So far, this retention effect has not been taken into account in formal flood risk assessments in the Netherlands. This paper describes the set-up of the Monte Carlo based probabilistic framework for societal flood risk analysis, which takes the retention effects of dike breaches into account. The full framework will only be described briefly, as the main focus of the paper will be on a specific component: the Monte Carlo sampling method. Computation results of the framework and consequences for societal flood risk are discussed in a separate paper (De Bruijn et al. 2014). The main objective of the current paper is to construct a sampling strategy that is efficient in terms of computation times and at the same time provides sufficiently accurate results. The method is applied on the Rhine–Meuse delta in the Netherlands, but can be applied on other river deltas as well.

2 Probabilistic risk modeling framework

2.1 Required capabilities

The modeling framework is developed with the aim to derive societal flood risks for large river deltas. Furthermore, it is required that mitigating measures can be evaluated and also that areas that contribute most to the societal flood risk can be identified. This leads to the following set of requirements:

  1. 1.

    The framework has to be able to quantify the (societal) flood risk of the delta as a whole and the individual polders and floodplains;

  2. 2.

    The main components of the risk chain need to be modeled explicitly, i.e. hydraulic loads, resistance and breaching of flood defences, flooding of polders and flood plains and evacuation response;

  3. 3.

    All relevant uncertainties need to be taken into account;

  4. 4.

    The method has to be able to deal with the combined influence of sea water level and river discharge;

  5. 5.

    The reduction of downstream water levels due to breaching flood defences has to be quantified;

  6. 6.

    The method has to be applicable for systems with a large number (>100) of dike sections and potential breach locations;

  7. 7.

    For practical purposes the runtime should preferably be less than 24 h on a standard personal computer.

2.2 Existing flood risk models in literature

The advantages of probabilistic flood risk methods over more traditional deterministic methods are widely recognized. The increase in computation power has given an impulse to the development of various flood risk models in which the entire ‘chain’ (sources, pathways, receptors) is explicitly modelled, including all relevant uncertainties. This section discusses a number of risk models from literature that are most relevant to our study.

The subject of downstream flood risk reduction due to upstream breaching in the Netherlands was explored in a research project as described by Van Mierlo et al. (2007) and Courage et al. (2013). Courage et al. (2013) successfully quantified the potential effects of dike breaches on downstream water levels and flood risks for a number of dike rings in the Rhine–Meuse delta. In their simulations, flood defences could breach due to the failure mechanisms ‘piping’ and ‘erosion of the inner slope due to wave overtopping’. In case of a dike breach, a detailed 2D flood simulation model was used to compute inundation depths in the protected polders. As a result, their approach was computationally time-consuming: a single flood simulation took about 2–6 days on a standard issue 2 GHz Linux PC.

Apel et al. (2004) and (2009) also quantified the retention effects of breaching on downstream flood frequency curves for stretches of the Lower Rhine River in Germany. They used a Monte Carlo based approach in which upstream discharges were sampled from the derived distribution function and subsequently routed through the river stretch. In their model, flood defences could only breach due to the failure mechanism ‘wave overtopping’. In both studies the retention effects were demonstrated to have significant influences on the flood frequency curves of downstream locations, especially for events with high return periods. Apel et al. (2009) therefore concluded that their approach provides more realistic results than the traditional flood frequency approach in which the retention effect is not taken into account. Vorogushyn et al. (2012) extended the work of Apel et al. (2009) by quantifying additional flood intensity indicators and introducing ‘piping and heave’ and ‘micro-instability’ as additional failure mechanisms in their framework. Their method was applied on a stretch of the Elbe River in Germany. Due to the relatively small storage of the Elbe floodplains, dike breaching was not as influential on downstream flood levels as it was for the lower Rhine in the studies of Apel et al. (2004) and (2009).

Lamb et al. (2010) developed a statistical conditional exceedance model to describe the joint probability of extreme river flows or sea levels at multiple locations. The joint probability method was developed by Keef et al. (2009), based on the earlier works of Heffernan and Tawn (2004). One of the main advantages of this model is that it offers the possibility to handle dependencies of a large set of locations with mutually correlated hydraulic loads. Wyncoll and Gouldby (2013) linked the load model of Lamb et al. (2010) to the consequence model of Gouldby et al. (2008) to develop a fully risk based approach. Gouldby et al. (2008) used fragility curves to describe the resistance of the flood defences, a rapid flood model to derive flood depths and standard depth-damage functions to quantify economic losses. In the models of Lamb et al. (2010) and Wyncoll and Gouldby (2013) the hydraulic loading conditions are assumed to be fully dependent in terms of recurrence interval (return period). Retention effects of breaching flood defences were not taken into account.

Recently, Zhong et al. (2013) have implemented a hydraulic load model for the Rhine–Meuse delta in a Monte Carlo framework. They applied importance sampling functions for the most relevant input variables to speed up the convergence process. The importance sampling procedure used normal distribution functions which were centred around the values that lead to critical water levels for design and safety assessment. They did not report on the efficiency of this sampling strategy compared to crude Monte Carlo, which is the focal point of our study. Dawson and Hal (2006) developed a Monte Carlo based flood risk method in which adaptive importance sampling was applied to speed up the convergence of the sampling process. Fragility curves were used to describe the reliability of the flood defences of a combined coastal/fluvial system in Towyn, North Wales. Five different failure modes, including dune erosion, were taken into account and represented by fragilty curves. A simplified two-dimensional inundation model and standard damages curves were used to compute flood damages for each simulated event. Retention effects were not taken into account. The output of their study consisted of flood risk maps of the study area.

The papers described in this section provide valuable flood risk modeling concepts that can be used for our modeling purposes. However, to our best knowledge there is no model available that has all modeling capabilities as desired for our study (Sect. 2.1). Especially a system that takes the retention effects of dike breaches into account for a tidal river system with combined influences of sea water levels and river discharges does not seem to be available. Therefore a new modeling framework was required that takes these issues into account.

2.3 Framework components

The objective of the probabilistic framework is to quantify FN-curves for river deltas. The computation of FN curves involves dealing with multiple sources of uncertainty. In our framework, uncertainties in the hydraulic loads, the resistance of the flood defences, the evacuation response and the resulting number of flood fatalities from a breach are all taken into account. The different sources of uncertainty are described with probability distribution functions, which are input for the framework. The framework consists of the following components:

  1. [i]

    Generation of synthetic events characterized by load, strength and response variables;

  2. [ii]

    Hydrodynamic modeling of the synthetic events; and

  3. [iii]

    Post-processing for deriving FN-curves.

The generation of synthetic events (component [i]) starts with sampling of hydraulic load variables like river discharge and sea water level from derived distribution functions. Subsequently, the resistance of the flood defences is sampled from fragility curves for potential breach locations. Breaching of flood defences can potentially occur anywhere in the system. The framework, however, requires a finite set of potential breach locations. These breach locations are selected in such a way that all relevant potential flood scenarios are captured. For this purpose, the system of flood defences is subdivided into several stretches, based on the criterion that flood consequences are approximately the same for breaches at any location within a single stretch. For each stretch, a single representative potential breach location was selected. For each potential breach location, fragility curves are derived for all relevant failure mechanisms based on characteristics of the flood defences. Three failure mechanisms are considered that are known to be dominant for riverine flood defences: “erosion of the inner slope”, “piping” and “slope instability”. This means for each simulated event and each location, three breaching levels are sampled from the fragility curves, representing the water levels at which the flood defence will breach due to the corresponding failure mechanism. The lowest of the three breaching levels is the water level at which the flood defence will breach. The final step in component [i] consists of sampling a success rate of the evacuation response, which is used later on to determine the expected number of casualties in a flood event.

Each event is simulated with a hydrodynamic model (component [ii]). The sampled hydraulic load variables like river discharge and sea water level serve as boundary conditions for this model. The sampled breaching levels from the fragility curves are also input to the hydrodynamic model. At each simulation time step, locations are identified for which the water level exceeds the breaching level. For these locations the formation of a breach is simulated and water is abstracted from the river. This leads to a reduction of downstream water levels as well as inundation of the protected polders. As such, the framework is able to take the reducing effect of breaching on downstream water levels and flood probabilities into account. More details on the hydrodynamic model simulation are provided in Sect. 4.3.

In the post-processing procedure (component [iii]), the expected number of fatalities in the simulated events is derived from indicators like the flooded area, the number of inhabitants and the evacuation success rate. These numbers are used to derive FN-curves that show frequencies of exceedance of (large) numbers of flood fatalities. More details on the computation of the FN curves are provided in the following section.

2.4 Probabilistic computation method

To estimate the probability of failure of complex systems, probabilistic computation methods are required. In such computations, generally the probability is computed that the load (S) of the systems exceeds the strength, or resistance (R). For food defences, the load typically consists of a combination of water levels and waves and in some cases currents. The resistance depends on the geometry of the flood defence and soil characteristics. For convenience, a limit state function Z is defined as follows:

$$ Z = R - S $$
(1)

With this definition, Z < 0 refers to “failure” and Z ≥ 0 to the opposite, i.e. “no failure”. This means the failure probability is equal to: P[Z < 0]. This definition of function Z can also be used to quantify exceedance probabilities of e.g. a threshold water level w*. In that case the “load”, S, is taken equal to the actual water level, w, and the “resistance”, R, is taken equal to w*. A value of Z < 0 then corresponds to the situation that w exceeds w*, so again P[Z < 0] is the probability that needs to be quantified.

The limit state function, Z, is a function of a number of random variables representing both load and resistance variables. This means Z is a random variable as well. The probability of failure can be written as follows:

$$ P_{f} = P\left[ {Z < 0} \right] = \int\limits_{{Z\left( {\mathbf{x}} \right) < 0}} {f_{{\mathbf{X}}} \left( {\mathbf{x}} \right)} \,d{\mathbf{x}} $$
(2)

where x is the vector of variables: x = (x 1,…x n) and f X is the joint probability density function of x. To evaluate Z(x), often numerical simulation models are required. This means Eq. (2) is generally too complex to evaluate in an exact, analytical way. Therefore, probabilistic techniques are required to provide an estimate of the failure probability. There are different probabilistic methods available, each with its advantages and disadvantages. Extensive overviews are given in Ditlevsen and Madsen (1996) and Melchers (2002). The “best” choice of the probabilistic method depends on the problem under consideration. Grooteman (2011) identifies the following three selection criteria on which the choice of a computational method should be based: accuracy, efficiency (i.e. computation time) and robustness.

For the existing statutory safety assessment procedure of flood defences in the Rhine–Meuse delta, numerical integration is used to determine probabilities of hydraulic loads (Geerse, 2005). Numerical integration scores high on robustness and accuracy, if grid cells are chosen sufficiently small. However, numerical integration becomes very time-consuming if more than just a few random variables are involved. For the probabilistic model of the statutory safety assessment this poses no problem as it only considers hydraulic loads in order to determine design water levels. The number of random variables is therefore limited. However, in our study the resistance of the flood defences is also considered and the number of random variables is well over a hundred. This makes the application of numerical integration infeasible.

As a potential alternative, FORM (Rackwitz, and Fiessler, 1978) is known to be computationally efficient. This is the reason why this is the preferred method in the computational software that is being developed for the subsequent statutory safety assessment of flood defences in the Netherlands (Den Heijer and Diermanse, 2012). The disadvantage of FORM is that it relies on an iterative procedure which sometimes does not converge. Furthermore, FORM relies on linearization of the Z-function, which means errors are introduced if the actual Z-function is highly non-linear. For application in the framework of the current study, FORM has a further disadvantage that it computes the failure probability (or exceedance probability) at a single location. Since the framework needs to be applicable for systems with large numbers of potential breach locations, the efficiency gain of FORM is easily lost in this case.

Monte Carlo methods do not have the disadvantages of FORM and numerical integration as described above. The required computation time does not increase with increasing number of variables and the failure analysis of multiple locations can be efficiently combined. For this reason it was decided to implement a Monte Carlo based method in the framework. For Monte Carlo methods, the main challenge is provide accurate estimates for cases in which the probability of failure is very small. In those cases, crude Monte Carlo sampling requires a large number of Z-function evaluations for an accurate estimate of the failure probability. If Z-function evaluations are very time-consuming, the number of evaluations will have to be limited from a practical point of view. This will automatically be at the expense of the accuracy of the estimate. Fortunately, the efficiency of Monte Carlo simulation can be enhanced through application of advanced sampling techniques like Latin hypercube sampling (Georgiou 2009; HSU et al. 2011; Olsson et al. 2003; Owen 1994; Ye 1998), directional sampling (Bjerager 1988; Ditlevsen et al. 1990; Grooteman, 2011; Melchers 2002), stratified sampling (May et al. 2010; Keskintürk and Er 2007; Christofides 2003) or importance sampling (Engelund and Rackwitz 1993; Koopman et al. 2009; Sezer 2009; Yuan and Druzdzel 2006). A further efficiency gain may be achieved if these methods are combined with adaptive response surface techniques (Liu et al. 2010; Steenackers et al. 2009 Allaix and Carbone, 2011) which help explore the failure space, Z(x) < 0, at a low computational cost.

For most practical problems, the advanced sampling techniques reduce the required number of Z-function evaluations in comparison with the crude Monte Carlo approach. The efficiency gain of Latin Hypercube sampling is relatively small compared to the other methods in cases where extreme events are relevant, and therefore not appropriate for our purpose. The efficiency of directional sampling decreases if a large number of random variables are involved (Waarts 2000). Furthermore, directional sampling is less efficient in case of a large number of objective functions that need to be evaluated individually. The large number of potential breach locations considered in the current study, brings with it an even larger set of random variables and objective functions in the hydraulic load model, which is why directional sampling is not the preferred option. Stratified sampling and importance sampling are anticipated to be the most efficient Monte Carlo techniques for our framework. We chose to apply importance sampling as it was considered the most practical of the two methods to implement and apply in the test procedure as described in Sect. 4.4

Application of importance sampling means the actual multivariate distribution function, F, of the set, x, of random variables is replaced in the sampling procedure by an alternative distribution function, H, in order to increase the probability of sampling events which are most relevant for the flood risk in the study area. The changes in sampling probabilities need to be corrected for in the Monte Carlo probability estimate by a factor that is equal to c = f(x)/h(x), where f and h are the density functions corresponding to F and H. This correction factor c is determined for each sample of x. The estimated probability of exceedance of a threshold number of N* fatalities is then equal to:

$$ P\left[ {N > N^{*} } \right] = \frac{1}{n}\sum\limits_{i = 1}^{n} {1_{{\left[ {N_{i} > N^{*} } \right]}} } c_{i} $$
(3)

In which n is the number of simulated events, P is the exceedance probability per event, N is the number of fatalities in an event, N* is a possible realization of N, N i is the number of fatalities in event i, 1[..] is an indicator function which is equal to 1 if N i > N* and 0 otherwise and c i is the correction factor for importance sampling for event i. The FN-curve is derived through application of Eq. (3) for a range of values of N*.

The Monte Carlo simulation procedure in our framework uses random variables to model the hydraulic load (river discharge, sea water level, possible failure of a barrier), the resistance of flood defences (fragility curves for potential breach locations) and the rate of success of the evacuation response. In the method, n years are simulated, where n can be selected by the user. The choice of n is generally based on the trade-off between computation time and desired accuracy. The simulated years do not represent a series of n subsequent years, but n possible realizations of a reference year. This is a relevant distinction, because in the first case, the sampling method for resistance variables needs to take the high correlations between samples of subsequent years into account, whereas in the second case the samples for each simulated year can be generated independently.

For each simulated year, two synthetic events are considered: (i) the event in which the annual maximum river discharge occurs and (ii) the event in which the annual maximum sea water level occurs. The motivation is that in a river delta both types of events can cause floods and they generally do not coincide. This means in total 2n synthetic events are generated and simulated according to steps [i] and [ii] of Sect. 2.3. In this approach, the estimated annual probability of exceedance of a threshold number of N* fatalities is equal to:

$$ P\left[ {N > N*} \right] = \frac{1}{n}\sum\limits_{i = 1}^{2n} {1_{{\left[ {N_{i} > N^{*} } \right]}} } c_{i} $$
(4)

In Eq. (4) P refers to the annual exceedance probability, whereas in Eq. (3) P referred to the exceedance probability per event. This explains the number ‘2’ in Eq. (4)which is absent in Eq. (3): there are two simulated events per year.

3 Criteria for selecting importance sampling strategies

The main purpose of this paper is to establish an efficient sampling strategy for the framework as described in the previous section. The optimal strategy usually depends on the case study area. In other words: no sampling strategy can be expected to be efficient for all river deltas in the world. However, our proposed approach to derive the sampling strategy is generic. The method is to iteratively develop and apply various sampling strategies and to test the efficiency. Sampling strategies will be formulated based on test results from previous iterations.

One of the possible approaches to ‘learn’ from previous simulation results is to use adaptive sampling schemes (e.g. Steenackers et al. 2009; Allaix and Carbone 2011). Dawson and Hal (2006) applied such an approach in a flood risk analysis of a combined coastal/fluvial system in Towyn, North Wales. In their method, the sampling density function h(x) is iteratively adapted in such a way that events that were found to contribute most to the flood risk in earlier iterations are given higher sampling densities in subsequent iterations. They demonstrated that such an approach can significantly speed up the convergence of the Monte Carlo simulation procedure. Nevertheless, such an approach was not adopted in our study. The main reason is that for our decision making process not only the flood risk of the entire delta area is required, but also the flood risk of all the individual polder areas that are protected by flood defences. An approach that optimizes the sampling scheme for the flood risk of the delta as a whole may not provide reliable estimates for each individual polder.

For this reason a ‘learn-by-doing’ approach was followed in which sampling schemes are judged based on their ability to provide reliable Monte Carlo estimates at each location in the delta within an acceptable simulation time. This means the sampling scheme needs to be efficient, accurate and robust for all locations. As stated before, importance sampling can increase the efficiency of a Monte Carlo simulation by sampling the vector, x, of random variables from an alternative distribution function, H(x), instead of the actual distribution function, F(x). Function H(x) should be chosen in such a way that the required number of samples to obtain accurate results is reduced as much as possible. The accuracy of the sampling procedure can be verified with the following two criteria for the Monte Carlo estimate:

  1. 1.

    the bias should be equal to 0;

  2. 2.

    the standard deviation should be lower than an acceptable threshold.

The first criterion implies that the Monte Carlo estimate (Eq. (4)) should converge to the correct result if the number of samples, n, goes to infinity. More formally, this criterion can be described as follows: The bias is equal to zero if for any combination of (small) positive values ε 1 and ε 2 there is a value n* for which the following holds if the number of samples, n, is higher than n*:

$$ P\left[ {\varepsilon > \varepsilon_{1} } \right] < \varepsilon_{2} $$
(5)

In which ε is the error in the Monte Carlo estimate. A bias in the estimate will be introduced if, and only if, there are events that result in failure which are awarded a probability of 0 in the importance sampling procedure. The second criterion above can be verified by carrying out the Monte Carlo experiment multiple (M s) times, and to subsequently verify if the standard deviation of the resulting M s estimates is below the acceptable threshold. Note that the choice of the acceptable threshold is subjective. The standard deviation can always be kept as low as possible by increasing the number of samples, n. However, the purpose of importance sampling is to keep this number as low as possible. So, if we assume the number of n to be fixed, notorious contributors to high standard deviations are potential realisations, x, for which Z(x) < 0 and f(x)/h(x) ≫ 1. These are events that contribute to failure, but have a relatively small probability of being sampled in the importance sampling procedure. However, if they are sampled, they have a relatively large contribution to the Monte Carlo estimator because the factor c = f(x)/h(x) is large. Such realisations of x can cause relatively large differences in the successive Monte Carlo estimators and therefore contribute strongly to the standard deviation. This should therefore be avoided, which means the events that contribute to the flood risk in the area should never be awarded a sampling probability that is significantly lower than the actual probability.

The bias and standard deviation are used in the remainder of this paper as criteria to test the accuracy of various importance sampling strategies. Our main objective is to construct a sampling function, H(x), that is efficient (i.e. low number of hydraulic model simulations) and sufficiently accurate (i.e. no bias and acceptably small standard deviations) for all considered locations in the area. Different sampling strategies are tested and mutually compared in terms of bias and standard deviation, in order to obtain an “optimal” sampling strategy.

4 Case study

4.1 Area

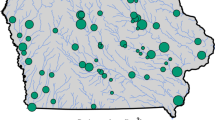
The Rhine–Meuse delta in the Netherlands (see Fig. 1) is a densely populated region that includes the cities of Rotterdam, Utrecht, Arnhem, Nijmegen and Dordrecht. The area is of high economic value, in particular the port of Rotterdam. The protection standards for this region are among the highest in the world: the flood defenses must be able to withstand hydraulic loads associated with a return period of 10,000 years. With respect to the hydraulic characteristics, the area can be subdivided into three regions: a tidal region, where high water levels are caused by high sea water levels; a non-tidal region, where high water levels are caused by high river discharges and a transitional region, where high water levels can be caused by both high sea water levels and high river discharges.

Fig. 1
figure 1

Model area and potential breach locations (red dots)

Full size image

The tidal and transitional regions are protected from high sea water levels by the Maeslant storm surge barrier, near location Maasmond (see Fig. 1). This barrier closes when the water level at Rotterdam is expected to exceed the level of NAP + 3 m,Footnote 1 or if the water level at Dordrecht is expected to exceed a water level of NAP + 2.9 m. A closure request for the barrier due to high storm surges is expected to occur on average approximately once every 10 years. There is an estimated probability of 1 % that the barrier fails to close upon request.

Flood defence breaches can occur at any location in the area and consequences in terms of numbers of fatalities can vary strongly from location to location. The framework, however, requires a finite set of potential breach locations. The potential breach locations of the model are selected in such a way that all relevant potential flood scenarios are captured by the modelling framework. For this purpose, the system of flood defences is subdivided into several stretches, based on the criterion that flood consequences are approximately the same for breaches at any location within a single stretch. In total 171 different stretches were identified by De Bruijn and Van der Doef (2011), varying in length from 400 m to 34 km. Figure 1 shows the corresponding 171 representative breach locations.

4.2 Statistics of hydraulic loads

High water levels in the Rhine–Meuse delta are mainly determined by the discharge of the River Rhine at upstream boundary Lobith, the discharge of the river Meuse at upstream boundary Lith, the sea water level at downstream boundary Maasmond and the functioning of the barrier near Maasmond, which may fail to close upon request. As the focus of the study is on flood risk, statistics of high river discharges and high sea water levels are most relevant. Statistical distribution functions for high rivers discharges and sea water levels have been adopted as much as possible from the probabilistic model that was developed to derive design water levels for the formal safety assessment of flood defences in the Rhine–Meuse delta (see e.g. Geerse 2005 for a description of that model). Statistics of extreme river discharges and sea water levels have been derived by fitting extreme value distribution functions through observed annual maximum water levels and peaks-over-threshold series. Sea water level statistics are described by a conditional Weibull distribution:

$$ P\left( {M \le m|m > \omega } \right) = 1 - \exp \left[ {\left( {{\omega \mathord{\left/ {\vphantom {\omega \sigma }} \right. \kern-0pt} \sigma }} \right)^{\xi } - \left( {{m \mathord{\left/ {\vphantom {m \sigma }} \right. \kern-0pt} \sigma }} \right)^{\xi } } \right], $$
(6)

where M is the annual maximum sea water level, relative to NAP, m a potential realization of M and ω, σ, and ξ are the location, scale and shape parameter respectively. Exceedance frequencies of high sea water levels can be derived by multiplying the probabilities that follow from equation (6) with the frequency of exceedance, λ, of threshold ω. The value of λ is determined by counting the number of peaks above the threshold and dividing by the number of years of record. For location Maasmond, ω = 1.97, λ = 7.24, ξ = 0.57 and σ = 0.0157.

Probabilities of high river discharges in the Rhine and Meuse are described with a Gumbel distribution:

$$ P\left( {Q < q} \right) = \exp \left( { - \exp \left( { - \frac{q - b}{a}} \right)} \right), $$
(7)

where Q is the annual maximum peak discharge, q is a potential realization of Q and a and b are the two parameters of the distribution function, with a = 1,316 m3/s, b = 6,612 m3/s for the Rhine River at Lobith and a = 342 m3/s, b = 1,190 m3/s for the Meuse River at Lith.

These statistical distribution functions quantify probabilities for the high range of peak values. However, high river discharges are likely to occur jointly with ‘normal’ sea water level conditions and vice versa, so statistics of ‘daily’ conditions are also relevant. To describe probabilities of the whole range of conditions, histograms were derived from all observed daily discharges in a period of approximately 100 years of measurements. Similarly, histograms of tidal peaks were derived from all observed tidal peaks in a period of approximately 100 years. The histograms are used directly as input for the sampling procedure, so no curve fitting was applied. The probability distribution for the Maeslant barrier is binominal: there is a 1 % probability that the barrier fails to close upon request, and therefore a 99 % probability that the barrier closes upon request. High water events in the Rhine and Meuse rivers often occur simultaneously. This means discharges of these rivers are correlated and this is taken into account in the modeling framework. However, in the current paper this correlation is not relevant as the Rhine is the only river we focus on to determine our optimal importance sampling scheme.

The statistical distribution functions of discharges and sea water levels refer to peak values, while the hydrodynamic simulation model requires time series as input. To describe the temporal evolution of the river discharge, a normalised hydrograph is used, i.e. a dimensionless hydrograph with a peak value equal to 1. For each simulated event, the normalized hydrograph is multiplied by the sampled peak discharge to form a discharge time series, which is used as input of the hydrodynamic simulation model. The normalised hydrograph is based on average durations of threshold exceedances, as observed during high water events on the Rhine and Meuse rivers. The hydrograph of the sea water level is a combination of a standardised surge hydrograph and average tidal conditions. The standardised surge hydrograph is also based on averages of observed high storm surge events. The standardised hydrographs for storm surge and river discharge are applied in each simulated event. The following assumptions are made with regard to “timing”:

  • The peak of the Rhine discharge at Lobith occurs at the same time as the peak of the Meuse discharge at Lith.

  • The peak of the sea water level occurs 2 days after the peak of the river discharge. This means the peaks arrive approximately at the same time in the transitional area, i.e. the area that is influenced by both river discharges and sea water level.

Events with high discharges in the Rhine and Meuse rivers may last several weeks. For long duration events, the probability that the sea water level exceeds a given high threshold at some stage during the event is higher than for short duration events. This is especially relevant for the transitional area, where water levels are influenced by both river discharges and sea water levels. In the probabilistic model for the statutory safety assessment of flood defences, the total duration of a river induced flood event in the Rhine river is assumed to be in the order of 30 days (Geerse 2005). This duration includes the rising and falling limb of the hydrograph, which means high river discharges only occur during a smaller sub-period. In our model, the duration of this sub-period is equal to τ tidal periods and starts at τ/2 tidal periods before the peak discharge and ends at τ/2 tidal periods after the peak discharge. The value of τ is chosen to be 12 tidal periods, i.e. about 6.5 days. The value of τ is applied in the sampling procedure of the (peak) sea water level. The probability distribution function, F M(m), for the peak sea water level is available for the tidal period:

$$ F_{M}^{{}} \left( m \right) = P\left[ {M < m} \right] $$
(8)

This means the function F M(m) describes the probability that the maximum sea water level during a single tidal period is less than or equal to m. In the Monte Carlo procedure, the maximum sea water level of a period of τ tidal periods will be sampled. This value has the following distribution function:

$$ F_{M}^{*} \left( m \right) = P\left[ {M < m} \right]^{\tau } = \left( {F_{M}^{{}} \left( m \right)} \right)^{\tau } $$
(9)

Note that this formula is based on the assumption of independence between subsequent tidal peaks. Equation (9) shows the assumed duration τ influences the distribution function from which the peak sea water level is sampled. An increase in the value of τ increases the probability of higher peak sea water levels being sampled. This is exactly the duration effect that needed to be incorporated in the approach: the longer the duration of a high discharge event, the higher the probability that the sea water level exceeds a given high threshold at some stage during this event.

4.3 Hydrodynamic simulations

The Sobek hydrodynamic model (see e.g. Stelling and Verwey 2005) was used to compute water levels at all potential breach locations of Fig. 1, for the selected combinations of river discharges, sea water levels and barrier states. The formation and consequences of breaches are also simulated in this hydrodynamic model. Breaches occur if the river water level at a location exceeds the maximum water level that a dike section can withstand, as sampled from the derived fragility curves. The process of breaching is not further considered in the remainder of this paper, even though it is highly relevant for the estimated societal flood risk. This is because the focus of the paper is on the development of efficient Monte Carlo importance sampling techniques and it is most practical to test these on the relatively simplified case in which it is assumed no breaches can occur. This will be further explained in Sect. 4.4. For more information on the hydrodynamic modeling of breaches and resulting societal flood risks, the interested reader is referred to De Bruijn et al. 2014.

4.4 Test set for selecting importance sampling strategies

Section 3 describes criteria for the selection of efficient sampling schemes. One of the criteria is the standard deviation of the Monte Carlo estimator. In order to quantify this standard deviation, the Monte Carlo simulation needs to be repeated multiple times with different (random) seeds. In order to prevent having to carry out millions of time-consuming model simulations, the tests for the selection of sampling strategies were only carried out for the hydraulic loads, i.e. not for breaches and flood consequences. To construct the test procedure, hydraulic simulations were carried out for combinations of seven sea water levels, 11 river discharges and 2 barrier situations, so in total 7 × 11 × 2 = 154 simulations. The simulated sea water levels and river discharges cover the complete range of events that are relevant for flood risk assessments. In the simulations, dike breaching was not modelled. For this particular test, the river discharges of the Rhine and Meuse were assumed to be fully correlated, to further simplify the test procedure. The simulated maximum water levels at the 171 potential breach locations, as obtained from the 154 simulations, served as a lookup table for the Monte Carlo test simulations. In this way, water levels at the 171 potential breach locations can be derived for all potential realisations of the random load variables with negligible computation time.

Another advantage of the relatively low number of random variables of the test case is that results of the Monte Carlo simulations can be compared with the “exact” results as computed with numerical integration. The computations with numerical integration were carried out on a very fine grid consisting of 400,000 combinations of river discharges and sea water levels. This grid was applied for both barrier states, i.e. ‘functioning’ and ‘malfunctioning’. T-year water levels were derived for all potential breach locations for a range of values of T. The computed T-year water levels of the numerical integration procedure were compared with analytical results for locations in the non-tidal area, which showed that the error in water levels as estimated with the numerical integration procedure were less than two millimeters. This is considered small enough to serve as the reference for the detection of errors (bias) in the Monte Carlo simulations.

5 Results and analysis

5.1 Sampling strategies for the non-tidal area

In total six different sampling strategies were tested. The strategies are labeled ISS1… ISS6 and the associated distribution functions and parameters are summarized in Table 1. The first tests for importance sampling strategies were only carried out for locations in the non-tidal area. For these locations, the river discharge is the only random variable of interest, i.e. the influence of the sea water level and barrier state is negligible. This means the most efficient sampling strategies for these locations only need to focus on high river discharges. The following two importance sampling strategies were tested:

Table 1 Overview of sampling strategies for the annual maximum discharge of the Rhine river at Lobith (QR_AM), the daily maximum discharge of the Rhine river at Lobith (QR_D), the annual maximum sea water level at Maasmond (SWL_AM), the tidal peak of the sea water level at Maasmond (SWL_T) and the functioning of the barrier at Maasmond (B). Functions f and h1,…,h4 are sampling density functions as defined in the bottom part of the Table, the values between brackets are the corresponding function parameters
Full size table

  • ISS1: Sampling from the highest quantiles of river discharges only, with sampling probability densities proportional to actual probability densities;

  • ISS2: Uniform sampling of river discharges.

In formula, this means the following sampling density functions are applied on the variable discharge:

$$ h_{1} \left( x \right) = \left\{ {\begin{array}{*{20}c} {0\quad \quad \;\quad \quad ;\;x \le x_{T} } \\ {\frac{f\left( x \right)}{{1 - F\left( {x_{T} } \right)}}\quad ;\;x > x_{T} } \\ \end{array} } \right. $$
(10)
$$ h_{2} \left( x \right) = \left\{ {\begin{array}{*{20}c} {0\quad \quad \;\quad ;\;x \notin \left[ {x_{L} ,x_{U} } \right]} \\ {\frac{1}{{x_{U} - x_{L} }}\quad ;\;x \in \left[ {x_{L} ,x_{U} } \right]} \\ \end{array} } \right. $$
(11)

In which x T is the threshold discharge above which discharges are sampled in strategy 1 (ISS1), x L and x U are the lower and upper bounds of the interval from which discharges are sampled in strategy 2 (ISS2) and f(x) is the actual density function of the discharge. The generic variable name ‘x’ is used in the equations above because these sampling functions will be applied on other random variables later on as well. In strategy 1, the sampling density for discharges above threshold x T is proportional to the original density function f(x), whereas in strategy 2 the probability density is uniform for all discharges in the interval [x L , x U ]. Threshold x T was taken equal to the 100-year discharge (≈12.700 m3/s for the Rhine at Lobith), x L and x U are taken equal to 10,000 m3/s and 24,000 m3/s respectively. These bounds were carefully chosen make sure that [a] the interval is not too large and hence the sampling method inefficient and [b] the interval is large enough to have all discharges included that are relevant for flood risk in the non-tidal area.

Monte Carlo simulations were carried out 100 times for both strategies to obtain the standard deviation of computed T-year water levels. Furthermore, the mean value of the T-year water level over the 100 simulations was compared with the “exact” results from numerical integration to quantify the (potential) bias that may be introduced by importance sampling methods. Figure 2 shows the resulting bias and standard deviation of the 100, 1,000 and 10,000-year water level of the following sampling strategies: [a] crude Monte Carlo with 100,000 simulated years, [b] crude Monte Carlo with 1,000 simulated years [c] ISS1 with 1,000 simulated years and [d] ISS2 with 1,000 simulated years. The subplots on the left show the bias and the subplots on the right show the standard deviation for estimated water levels at 7 locations in the non-tidal area with return periods of 100 years (top panel), 1,000 years (centre panel) and 10,000 years (lower panel). These return periods cover the range that is most relevant for flood risk estimates in the area.

Fig. 2
figure 2

Bias (left) and standard deviation (right) for estimated water levels with return periods of 100 years (top panel), 1,000 years (centre panel) and 10,000 years (lower panel); comparison of results of importance sampling strategies 1 and 2 with 1,000 simulated years and crude MC with 1,000 and 100,000 simulated years. All locations are discharge dominated

Full size image

It is no surprise that the crude Monte Carlo results for n = 100,000 are more accurate than the crude Monte Carlo results for n = 1,000. For n = 1,000 the absolute value of the bias is larger and the standard deviation is substantially larger. Furthermore, the 10,000 year water level could not be obtained with n = 1,000 samples, as it requires at least 10,000 samples to quantify this water level without the (undesired) use of extrapolation techniques. The positive value of the bias as observed in the left panel subplots may require some further explanation. Formally, the bias as defined in Sect. 3 is equal to 0 for crude Monte Carlo sampling. In other words: the error in the Monte Carlo estimate reduces to 0 if n goes to infinity. The bias in Fig. 2 for the crude Monte Carlo methods is therefore caused by the fact that a limited set of samples is used. Increasing the number of samples will decrease the bias, which is demonstrated by the fact that the bias for n = 100,000 is much smaller than for n = 1,000.

Since errors of 0.1 m or more in estimated water levels are considered unacceptable for flood risk analysis in this area, n = 1,000 simulated years is not sufficient for crude Monte Carlo simulation, whereas n = 100,000 leads to an acceptable bias and standard deviation. However, it would be unpractical to carry out 100,000 hydraulic model simulations whereas n = 1,000 would be acceptable. This is the reason why importance sampling is required in our probabilistic framework. Figure 2 shows that both importance sampling strategies lead to acceptable results, i.e. errors well below 0.1 m, for n = 1,000 simulated years. Results of strategy 1 are nearly the same as the crude Monte Carlo results with n = 100,000 years. The reason is that for the analysis of events with return periods > = 100 years the two methods are essentially the same, since strategy 1 [a] only samples from discharges with return period > 100 years and [b] was applied with a factor 100 lower number of samples. So with ISS1, similar results can be obtained as crude Monte Carlo with a factor 100 lower computation time. Note that this is only the case for return values of 100 years and higher, for lower return periods this importance sampling strategy will not provide results. This is no problem if only the extreme events are relevant, but this is not always the case as will be demonstrated in the next section.

Figure 2 shows that strategy 2 provides even more accurate results than strategy 1 and the crude Monte Carlo simulations, especially for the 1,000-year and 10,000-year water level. The reason is that in strategy 2 the extremely high discharges up to 24,000 m3/s have a significantly higher probability of being sampled in comparison with strategy 1 and crude Monte Carlo sampling. This gives the method the potential to provide more reliable estimates for particularly the high return periods.

5.2 Sampling strategies for all locations

So far, the analysis has focused on locations for which the river discharge is the only relevant variable. For these locations, sampling strategy 2 turned out to be very efficient. However, this success is partly explained by the fact that this sampling strategy only focuses on river discharges. For sea water dominated locations this strategy is less efficient, as can be seen from Fig. 3 (red open circles). This Figure shows results for all 171 potential breach locations. Locations are ordered based on the longitudinal coordinate, which means sea-dominated locations (tidal area) are on the left and river dominated locations (non-tidal area) are on the right. Clearly, the bias with sampling strategy 2 is unacceptably large for locations in the tidal area.

Fig. 3
figure 3

Bias (left) and standard deviation (right) for estimated water levels with return periods of 100 years (top panel), 1,000 years (centre panel) and 10,000 years (lower panel); comparison of results of importance sampling strategies 2, 3 and 4 with 1,000 simulated years

Full size image

In order to develop a sampling strategy that provides reliable results for all locations, using a limited set of 1,000 simulated years, importance sampling on sea water levels is required as well. Therefore, a uniform sampling strategy (ISS3) is adopted for the sea water level, with bounds 2 m + NAP and 7 m + NAP. This is done for event type (ii), i.e. for events with the annual maximum sea water level. For event type (i) (annual maximum discharge with co-inciding sea water level) the bounds 1.2 m + NAP and 6 m + NAP are adopted (see Table 1 for the details of the sampling strategies). For river discharges, strategy 3 uses the same sampling distributions as strategy 2.

Figure 3 compares the results for strategies 2 and 3. In general, strategy 3 results in a reduction of standard deviations in comparison with strategy 2 for locations in the tidal area (location id’s 1–100), but the bias for these locations is still large. Furthermore, it can be seen that for locations in the non-tidal area (location id’s 100–171) the standard deviation for strategy 3 is higher than for strategy 2, even though the same sampling strategies for river discharges were applied. This is due to the fact that for these locations the lower sea water levels are more relevant than high sea water levels and strategy 3 shifts the sampling density to the higher sea water levels. This demonstrates that a sampling strategy can increase the accuracy for one location and at the same time decrease the accuracy for another location. This is the reason why importance sampling in a delta like the Rhine–Meuse delta is more challenging than for rivers where only discharges are relevant.

Another noteworthy aspect of Fig. 3 is that the bias for locations in the tidal area (id < 100) is large for sampling strategy 3. This is due to the fact that the lower bound of the uniform sampling strategy for the river discharge is relatively high (10,000 m3/s). Such a high value is efficient for river dominated locations because for these locations only high discharges will result in relevant high water levels. However, for locations in the tidal area, low and moderate discharges are relevant as well, because high sea water levels usually coincide with low/moderate river discharges. Ignoring these events in the sampling scheme clearly results in an underestimation of design water levels for these locations. Therefore, in a subsequent sampling strategy 4 (ISS4) the lower bounds of the uniform sampling distributions for river discharges where reduced to 6,000 m3/s for event type (i), i.e. the events with annual maximum river discharges, and to 500 m3/s for event type (ii), i.e. the events with annual maximum sea water levels. Figure 3 demonstrates that this has the desired effect on the bias, which is close to zero for all locations for sampling strategy 4.

With the bias reduced to near zero, the next objective is to adapt the sampling strategy in such a way that the standard deviation is further reduced, without simultaneous increase of the bias. The first point of consideration is the set of river dominated locations (id’s > 100), for which the standard deviation of the 10,000-year water level is close to 0.1 m. Figure 3 shows that these relatively large numbers arose when sampling strategy 3 was introduced, in sampling strategy 2 these numbers were much smaller. In sampling strategy 3, importance sampling for sea water levels was introduced, which resulted in a significant reduction of standard deviations for locations in the tidal area. However, this was at the expense of the standard deviations for discharge dominated locations. For discharge dominated locations, events with high discharges in combination with moderate to low sea water levels are relevant. The introduction of importance sampling for high sea water levels caused a decrease in the number of samples of moderate/low sea water levels, i.e. a decrease in the number of samples that are relevant for discharge dominated locations. This gave rise to the increase in the standard deviation of the Monte Carlo estimate for river dominated locations. In order to decrease the standard deviation of these locations, the obvious way is to increase the probability of sampling lower sea water levels. The problem is that this will be at the expense of the accuracy for sea water level dominated locations, which is the reason why sampling strategy 3 was introduced in the first place.

In order to obtain accurate probability estimates for both discharge dominated and sea water level dominated locations, the sampling strategy for sea water level therefore has to be a compromise between the importance sampling function on one hand and the original density function (i.e. no importance sampling) on the other hand. This compromise is reached by dividing the relevant range of sea water levels into two intervals [x 1, x 2] and [x 2, x 3], with x 1 < x 2 < x 3. The first interval represents the low/moderate sea water levels and the second interval represents the high/extreme sea water levels. Since both intervals are relevant for the flood risk in the area, we decided to give equal probability weights to both. In other words: each individual sea water level sample has a 0.5 probability of being low/moderate (interval 1) and also a 0.5 probability of being high/extreme (interval 2). In the first interval, the sampling density is taken proportional to the original density function, f(x). In the second interval, the sampling density is taken uniform. In formula:

$$ h_{3} \left( x \right) = \left\{ {\begin{array}{*{20}c} {\frac{0.5f(x)}{{F\left( {x_{2} } \right) - F\left( {x_{1} } \right)}}\quad ;\;x \in \left[ {x_{1} ,x_{2} } \right]} \\ \\ {\quad \frac{0.5}{{x_{3} - x_{2} }}\quad \;\quad \quad ;\;x \in \left[ {x_{2} ,x_{3} } \right]} \\ \end{array} } \right. $$
(12)

This sampling strategy for sea water levels is only applied for event type (i), i.e. events that represent annual maximum discharges in combination with a coinciding sea water level. Figure 4 shows the results for sampling strategy 5, which uses function h 3. For river dominated locations (id > 100) the standard deviations are now all below 0.05 m. This is a significant reduction in comparison with sampling strategy 4, while the bias remains in the same order of magnitude.

Fig. 4
figure 4

Bias (left) and standard deviation (right) for estimated water levels with return periods of 100 years (top panel), 1,000 years (centre panel) and 10,000 years (lower panel); comparison of results of importance sampling strategies 5 and 6 with 1,000 simulated years and crude MC with 100,000 simulated years

Full size image

Unfortunately, the new sampling strategy caused an increase in the estimate of the 10,000 year water level for some locations in the tidal area (location id < 100 in the lower right subplot of Fig. 4. The estimated 10,000 year water level with sampling strategy 5 is around 0.1 m for these locations. For these locations, extremely high water levels are caused by a combination of high sea water levels and a malfunctioning barrier. The probability of failure to close upon request for this barrier is 1 in 100, so a malfunctioning barrier only occurs in 1 % of the samples on average. The fact that in the Monte Carlo simulations there are only a few samples of this type of event is the main reason why the standard deviation of the Monte Carlo estimate is relatively high for sea water level dominated locations: one or two samples more (or less) may lead to significant changes in the estimated T-year water levels. The obvious way to reduce this effect is to increase the probability of sampling events in which the barrier fails to close upon request. Since the random variable ‘barrier’ has only two states (functioning or malfunctioning), the importance sampling distribution is binomial:

$$ h_{4} ( x) = \left\{ \begin{array}{ll} p_{1} & ;{\text{malfunctioning\;barrier}} \\ 1 - p_{1} & ;{\text{functioning\;barrier}} \\ \end{array} \right. $$
(13)

In sampling strategy 6 (ISS6), the probability of a malfunctioning barrier, p 1, was chosen to be 10 %, whereas the actual probability is estimated to be 1 %. Of course, this increase with a factor 10 needs to be corrected for in the usual manner in the Monte Carlo estimator. For samples in which the barrier malfunctions, the correction factor is equal to 1/10, because the sampling probability of a malfunctioning barrier was increased with a factor 10. For samples in which the barrier closes upon request, the correction factor is equal to 99/90, because the sampling probability of a functioning barrier was decreased from 99 to 90 %.

Figure 4 compares the results for sampling strategies 5 and 6. The objective of reducing the remaining “high” standard deviations has clearly been successful. With sampling strategy 6, the standard deviations in the estimated 100, 1,000 and 10,000 year water levels are all less than 0.06 m. Further fine-tuning of the sampling strategy did not lead to significant further improvements since an improvement for one location is almost automatically at the expense of the quality of the results for other locations. Sampling strategy 6 is therefore chosen as the preferred option in the framework for societal flood risk analysis. Figure 4 also compares the results of sampling strategy 6 for 1,000 simulated years with the crude Monte Carlo results with 100,000 simulated years. It can be seen that for the 100-year water level the crude Monte Carlo method performs better due to its abundance in the applied number of samples. However, for the 10,000-year water level the importance sampling strategy clearly outperforms the crude Monte Carlo approach, because the bias and standard deviation are lower for all locations. For many locations, the crude Monte Carlo method results in a standard deviation of more than 0.1 m, whereas with importance sampling this standard deviation is less than 0.06 m for all locations and all considered T-year water levels. So in spite of the fact that for the Crude Monte Carlo method 100 times more samples were used, the importance sampling method provides overall more accurate estimates T-year water levels. This clearly shows the added value of importance sampling: with 100 times lower computation time, more accurate results can be obtained.

6 Conclusions

This paper described the benefits of the application of importance sampling in a probabilistic framework for societal flood risk analysis in the Rhine–Meuse delta in the Netherlands. The choice of efficient importance sampling techniques in a delta like the Rhine–Meuse delta is more challenging than for non-tidal rivers where only discharges are relevant, because the relative influence of the forcing factors like river discharge and sea water level differ from location to location. As a consequence, sampling methods that are efficient and accurate for one location may be very inefficient for other locations or, worse, may introduce errors in computed design water levels. Several sampling strategies were tested and results were compared in terms of bias and standard deviation in the probability estimate. The analysis resulted in an efficient sampling strategy which reduces the required model simulation time by a factor 100 compared to crude Monte Carlo simulation, while at the same time the probability estimates of the relevant extreme water levels are more accurate for all locations considered in the area. This is a very valuable result, as it reduces the required computation times of the probabilistic framework to acceptable quantities, while at the same time the output is more accurate.